全文HTML
--> --> -->在过去的二十多年, 纳米光学和等离激元学(plasmonics)的兴起也促进了光学力的研究和光镊等技术的发展. 与细胞、电介质等不同, 金属纳米结构由于具有与光的特殊的相互作用以及突破衍射极限的亚波长操控而引起了广泛兴趣. 之前认为金属结构的表面会反射光, 因而无法像电介质颗粒那样折射光从而产生光学梯度力. 而1994年的一个实验[8]证明了当金属颗粒的尺寸小于波长时, 可被稳定地捕获, 且其捕获力远大于同尺寸的电介质颗粒. 这是因为光与金属纳米颗粒的相互作用主要取决于入射光的电场与金属表面自由电子集体振荡之间的耦合, 也就是局域表面等离激元(localized surface plasmons, LSPs). 当入射光的频率与电子集体振荡的本征频率匹配时, 就产生局域表面等离激元共振(localized surface plasmon resonances, LSPRs). 共振峰的峰位、数量以及电荷位移、阻尼特性等, 均可由金属颗粒的形状、尺寸、排布、材料、周围环境折射率等来调控. 在共振激发的条件下, 等离激元金属纳米结构具有高度局域的近场[9], 可作为纳米天线[10—12], 增强和调控光与物质相互作用(吸收、散射), 因而不仅在增强光谱[13]、超灵敏传感[14], 而且在光学捕获和操纵方面[15—26]具有良好的表现, 尤其是填补了处于亚纳米(原子、分子)和微米(细胞)尺度之间的纳米级光学操纵的空白[27]. 具体而言, 金属纳米颗粒具有较大的波长相关的极化率, 尤其是近场耦合的等离激元金属纳米颗粒, 由于电场主要集中在颗粒表面, 且随间距变大而迅速变小, 所以电场梯度较大, 而梯度力正比于场强梯度, 从而可增强光学力, 甚至改变力的方向, 例如通过调控入射光频率相对于颗粒的偶极子共振峰的红移或蓝移, 梯度力可为吸引或排斥[28]. 相似地, 早期的工作也认为将激光波长调谐到特定的光学跃迁, 可增强光学力, 从而实现对原子和分子的捕获[29].
传导表面等离激元(propagating surface plasmons, PSPs)与LSPs的理论机制和应用不尽相同, 而且其近场增强、电场梯度和光学力增强相对较小, 本综述也主要关注金属纳米颗粒的LSPs对光学力的增强与调控. 此外, 也未涉及超材料(metamaterials)、二维原子晶体材料等其他有可能具有等离激元特性的材料. 本文内容的组织侧重于应用的角度, 首先简要介绍金属纳米颗粒间隙增强光学力的原理和计算, 之后是光镊作用于等离激元金属纳米颗粒的各类实例, 接着介绍作用于其他颗粒的各类“等离激元镊”(plasmonic tweezer), 最后考虑偏振效应、新型光场以及手性纳米结构下的光学力. 在介绍国际研究新进展的同时, 也关注国内****的研究.
麦克斯韦应力张量法是计算光学力的基本方法, 在包裹颗粒的任意闭合面s上对麦克斯韦应力张量T进行积分, 得到光学力
2
2.1.Mie理论与光学力计算
Xu和K?ll[31]较早地利用广义Mie理论和麦克斯韦应力张量法, 计算了在平面波入射下, 银纳米颗粒二聚体在等离激元共振处的光学力和光学势, 增强的光学力产生并作用于颗粒聚集体. 如图1(a)和图1(b)所示, 在mW/μm2级入射光强的共振激发下, 光势阱最大, 紧密靠近的颗粒被光学力拉到一起, 同时单分子可被捕获在颗粒的连接处. 该效应可极大地放大表面增强拉曼散射(SERS)等光谱, 提升单分子探测的敏感性. Brus等[32]计算了在可见光入射下, 半径为30 nm的金或银纳米颗粒间的光学(引)力, 这些力的共振位置与近场电磁强度的共振位置相近. 光学力比范德瓦尔斯力强, 在MW/cm2级强度入射下, 可用于聚集金属颗粒. 同时发现光学力大小与间隙大小或近场增强因子并不呈线性关系, 如图1(c)所示, 这也是因为光学力取决于场的梯度而非绝对强度.
图 1 (a)银纳米颗粒二聚体和三聚体间隙中心点的光学势[31]; (b)纳米间隙附近光学势的空间分布[31]; (c)光学力与电场增强的比较[32]; (d)偏振平行或垂直于大小不对称二聚体轴时的光学力[33]; (e)光学力与范德瓦耳斯力的比较[34]; (f)领结型二聚体的光学力分布[37]Figure1. (a) Simulated optical potential U(λ) at the gap between Ag nanoparticles (d = 1 nm) in a trimer and a dimer system in water with a plane wave polarized parallel to the symmetry axis[31]; (b) spatial variation of optical potential U around a trimer (R = 25 nm, d = 1 nm) gap excited at a surface plasmon resonance (λ = 760 nm)[31]; (c) a comparison of the field enhancement to the optical force at the surface of one nanoparticle in the gap[32]; (d) calculated optical force for Ag and Au nanoparticle heterodimers (R1 = 10 nm, R2 = 10?40 nm, d = 2 nm) in the parallel and perpendicular polarization with different energies[33]; (e) the resonant optical force for Ag dimer (R = 30 nm), compared to the van der Waals attraction (black) with the energy of 3 eV (blue) and 3.3 eV (red)[34]; (f) optical force map of a bowtie antenna shows hot spots near the gap and two sides[37].
K?ll等[33]比较了金或银的同质和异质等离激元二聚体在不同平面波入射下的光学力. 如图1(d)所示, 颗粒间光学力的计算利用了Mie理论结合麦克斯韦张量, 以及其他近似方法. 对于尺寸不同的异质二聚体, 光学力也可能是排斥力而非吸引力. Chu和Mills[34]也计算了银纳米颗粒之间, 以及颗粒与平面间由激光引起的光学力. 如图1(e)所示, 当间隙在0.5—2.0 nm的范围时, 光学力的强共振与等离激元共振激发相联系, 此外, 等离激元共振引起的光学力也随着距离而振荡. 对这些力的测量将为等离激元增强光场的探测提供手段.
Li等[35]利用广义Mie理论(包括高阶多极子、延迟效应), 分析了在会聚的高斯光下银或金纳米颗粒聚集体的光学力. 对于两个相互作用的金属颗粒, 梯度(吸引)力主要由多极子等离激元激发产生, 存在于间隙较小时. 而激发的偶极子场主要产生于间隙与颗粒半径相当或更大时. 长距离时的力可以是吸引或排斥, 这依赖于偶极子的相位, 由激发波长以及偶极子等离激元共振决定. 等离激元共振波长附近的斥力可以很大而超过高斯光束的光学捕获.
2
2.2.数值方法与光学力计算
Quidant等[36]利用格林并矢法(Green dyadic method)和麦克斯韦应力张量法, 计算了LSPRs下金纳米颗粒间的增强的光学(结合)力, 并与介质颗粒、非共振颗粒进行比较. 在适当的入射波长下, 短距离的作用力可使颗粒聚集, 在间隙处产生强的局域“热点”, 同时也证实了金纳米颗粒聚集体的增强拉曼信号实验.Mohseni等[37]给出了Au-SiO2-Au三明治结构的领结型(bowtie)纳米天线“热点”附近的光学力空间分布(波长1550 nm). 如图1(f)所示, 利用了FDTD和麦克斯韦张量法进行模拟, 得到了场强和光学力的精细分布. Gray等[38]利用FDTD分析了双锥体金纳米颗粒二聚体的近场和远场性质, 该二聚体有三种形态: 肩靠肩(side-by-side)、尾靠尾(head-to-tail)、肩靠尾(face-on). 随着间隙的减小, 后两种都表现出共振峰的红移, 而第一种为蓝移. 利用麦克斯韦张量法计算其中一个颗粒对另一个颗粒的光学力, 得到了大的吸引力和弱的排斥力. 尾靠尾(head-to-tail)二聚体之间的光学力可比同样大小的金纳米球二聚体的大10倍.
2
3.1.光镊下的等离激元金属纳米颗粒多聚体
等离激元纳米颗粒在光学操纵中有较好的表现, 尤其是对于颗粒多聚体的操纵. 这是由于表面等离激元及其引起的高度局域的近场, 可由金属纳米颗粒的尺寸和形状来调控, 所以利用吸引或排斥的梯度力可实现颗粒的尺寸相关的捕获和筛选. 利用光镊与暗场光谱相结合, 可实现等离激元纳米颗粒的光学操纵和光谱[39]. 由于其LSPRs, 光学捕获和操纵得到的金属纳米单颗粒或聚集体可作为有效的近场光学探针, 用于表面增强光谱[24]、近场光学显微镜、生化传感等方面. 如图2(a)所示, K?ll等[40]利用光镊来移动单个银纳米颗粒, 使其与另一个固定的颗粒之间形成近场耦合, 也就形成了具有SERS活性的二聚体, 平均的SERS强度增加了20倍. Gucciardi等[41]在有生物分子的溶液中, 利用辐射压力来局域地推动金纳米棒聚集, 实现了中性pH下的非接触的生物分子SERS探测. 金属纳米颗粒成对形成的二聚体也是纳米光学领域的经典体系[13,42]. 二聚体间的作用力还可用比色分析法(colorimetric assay)来测量[43], 这是基于LSPRs强近场耦合的等离激元杂化(plasmon hybridization). Baumberg等[44]利用等离激元引起的金纳米颗粒的激光穿线(laser threading), 产生了(12 ± 2) nm宽的线. 该精度得以实现首先是由于纳米颗粒化学组装成了间隙为0.9 nm的链. 如图2(b)所示, 成线大规模出现在水中, 可通过新的近红外共振的杂化的链/棒型的电荷转移等离激元(charge transfer plasmons)来反映. 线的宽度取决于链的模式共振、纳米颗粒尺寸、链长以及激光峰值功率. 此外, 利用各向异性颗粒的其他等离激元模式, 可增强光学捕获的梯度力, 提高捕获势的强度. Scherer等[45]将捕获激光调谐到纵向等离激元共振的长波侧, 其极化率的实部可导致吸引的梯度力. 并利用另一飞秒激光, 通过激发双光子荧光来探测被捕获的纳米颗粒. Liu等[46]基于两个平行的大小不同(面积相差5倍)的纳米金板形成的等离激元纳米腔, 计算得到了光致负光压(吸引力), 并利用LC谐振模型给出解释.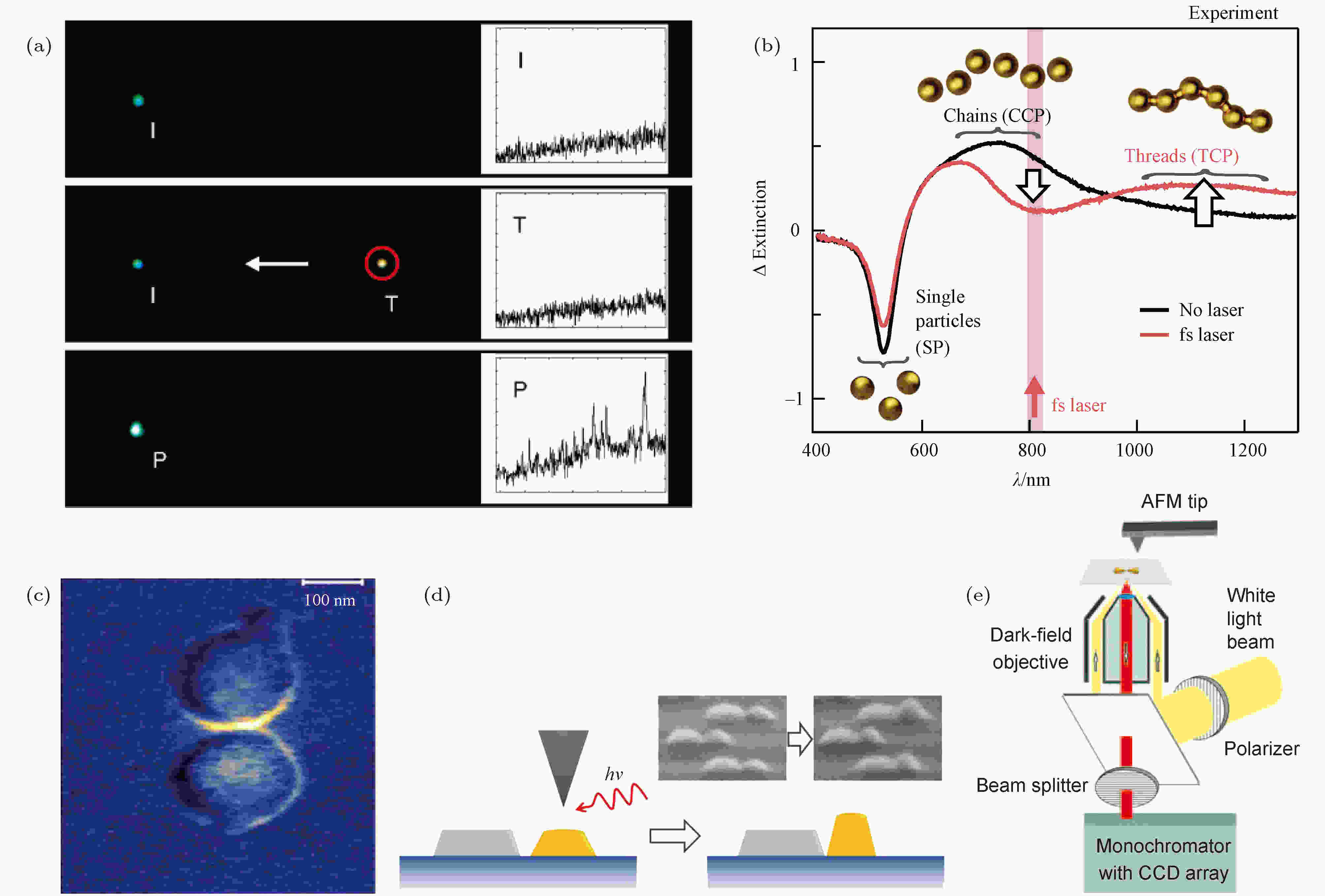
图 2 (a)光学捕获形成颗粒二聚体后的SERS的增强[40]; (b)激光辐射金纳米颗粒成链及其共振峰的变化[44]; (c)二聚体的光学力成像[47]; (d)AFM辅助的Al-Au纳米盘二聚体形变[49]; (e) AFM和暗场散射光谱仪结合实现纳米光学力控制[50]Figure2. (a) Dark-field images of an Ag nano particle and its dimer. The immobilized particle (I) and trapped particle (T) shows no SERS signal. When T being near-field contact with I, the dimer (P) shows an enhanced SERS signal[40]. (b) The threads develop after adding CB molecules and incident fs laser. A dip at the laser wavelength and a peak at the TCPs emerge[44]. (c) Photo-induced force image of an e-beam fabricated gold dimers. The incident polarization is parallel to the dimer axis[47]. (d) Schematic and SEM images of reshaping of Al-Au nanodisk heterodimers before (left) and after (right) illumination[49]. (e) Schematic of the optical manipulation set-up consisting of an AFM and a dark-field scattering spectroscopy system[50].
Nordlander等[47]发展了等离激元纳米结构的光致力显微镜(photoinduced force microscopy), 可测量受光激发下的等离激元纳米结构和扫描探针之间的光学力. 如图2(c)所示, 利用该方法, 基于铝-金纳米圆盘异质二聚体, 实现了波长相关的近场增强和光学力成像[48]. 他们还通过入射在原子力显微镜 (atomic force microscope, AFM)探针和铝-金异质二聚体的间隙处, 实现了金纳米圆盘的方向性光学变形, 减小了两个纳米圆盘的间隙[49]. 金属纳米结构的光学变形一般需要先用强激光实现融化, 之后在表面张力下变为更圆的形态. 如图2(d)所示, 这一过程有三个因素: 一是金晶格的光热软化, 二是铝纳米圆盘作用于金纳米圆盘的光学力, 三是来自附近AFM探针的光学力. 异质二聚体的非对称变形可通过电镜或光谱的变化观测到. 如图2(e)所示, Bratschitsch等[50]通过AFM的针尖来精细操纵领结型金纳米天线的两个三角板的长度和间隙. 光学响应可由暗场散射光谱得到. 当间隙尺寸达到几十纳米时, 等离激元模式分裂为两个偶极子共振.
2
3.2.光镊对等离激元金属纳米颗粒的筛选
光镊除了用于移动金属纳米颗粒的位置, 甚至形成多聚体之外, 还有一类重要应用是对颗粒进行筛选, 这主要是基于光学力对颗粒的几何尺寸或结构的敏感性. Oddershede等[51]利用三维功率谱分析发现, 对于直径小于100 nm的金纳米颗粒, 其光阱刚度(trap stiffness)正比于颗粒的体积; 但对于更大的颗粒, 虽然光阱刚度也随颗粒尺寸增长, 但其斜率更小.Quidant等[52]模拟了介质衬底上的金颗粒在入射光束下受到的光学力. 类似于原子操纵, 根据入射波长是否位于等离激元频带, 而分成两种不同的捕获. 即通过调整入射波长, 衬底界面上的颗粒可被选择性地引导或固定. 光学打印(optical printing)就是一种基于光学筛选的常见应用, 作为利用光学力的全光方法, 可在纳米级精度下将胶体纳米颗粒加到衬底上. Stefani等[53]利用不同功率和波长的激光, 研究金或银纳米颗粒的光学印片的准确性. 当光波长调谐到纳米颗粒的LSPRs时, 随着激光功率的减小, 精度提高. 然而当波长不在LSPRs时, 精度与激光功率无关. Huergo等[54]将Na2S还原金盐得到的金纳米颗粒选择性地打印到衬底上, 入射激光调谐到等离激元共振频率, 金纳米三角表现出近红外的共振. 横向生长引起等离激元共振的红移, 而增厚则引起共振的蓝移. 该纳米三角有极细的线宽, 表现出接近各向同性的散射.
金属纳米颗粒的光学力(尺寸)筛选受制于较宽的偶极子等离激元共振. 而源于窄态和宽态干涉的Fano共振的线宽比一般的偶极子等离激元峰窄, 所以基于Fano共振有可能实现超灵敏的光学力筛选. Li等[55]利用Fano干涉引起的散射(吸引)力, 实现了对等离激元纳米颗粒的尺寸超敏感的捕获和筛选. 理论计算如图3(a)和图3(b)所示, 在高斯光束激发下, 金属纳米颗粒在其Fano共振处的散射在横向上是不对称的, 导致净的Fano干涉引起的横向散射力, 其大小与梯度力是可比拟的. 由于相邻等离激元模式间的干涉的相位敏感性, Fano散射力对于颗粒尺寸和激发光频率是超敏感的, 实现了金或银纳米颗粒的10 nm精度, 或者硅核-金壳纳米颗粒的几个纳米壳厚的尺寸选择. Lin等[56]理论证明了在适当的可见光条件下, Fano共振可引起负的光学散射力, 作用于等离激元金核-银壳纳米颗粒上. 如图3(c)和图3(d)所示, 在零阶贝塞尔光束入射下, 处于Fano共振的等离激元纳米表现出净的纵向的反向光学散射力, 也就是Fano共振引起的负的光学散射力. 由Mie理论得到的消光谱表明, Fano共振是来源于同时激发的多极子的干涉, 其可以是一个宽的电偶极子模式与一窄的电四极子模式, 或者还会伴随宽的一个四极子与一个八极子. 该Fano共振引起的负的光学散射力在核壳结构、均匀结构、空心金属颗粒等也都得到证明. 此外, 通过选择性激发Fano共振附近的等离激元暗模, 还可重构横向光学力[57]. Qiu等[58]利用Ge2Sb2Te5核-Au壳的偶极子与四极子间的Fano共振, 在球表面形成非对称的能流, 使高斯光束产生垂直于光传播方向的横向(lateral)光学力. 当相变材料Ge2Sb2Te5从非晶向结晶相变时, 还可改变横向力的方向. Gao等[59]研究了增益核(染料分子)-金属壳(银)的Fano增强的光学力, 并利用非局域的等效媒质理论发现非局域效应会移动光学力的共振峰, 并增强负的光学力[60]. 此外, 也有介质核-二维材料壳结构的这方面研究[61,62].
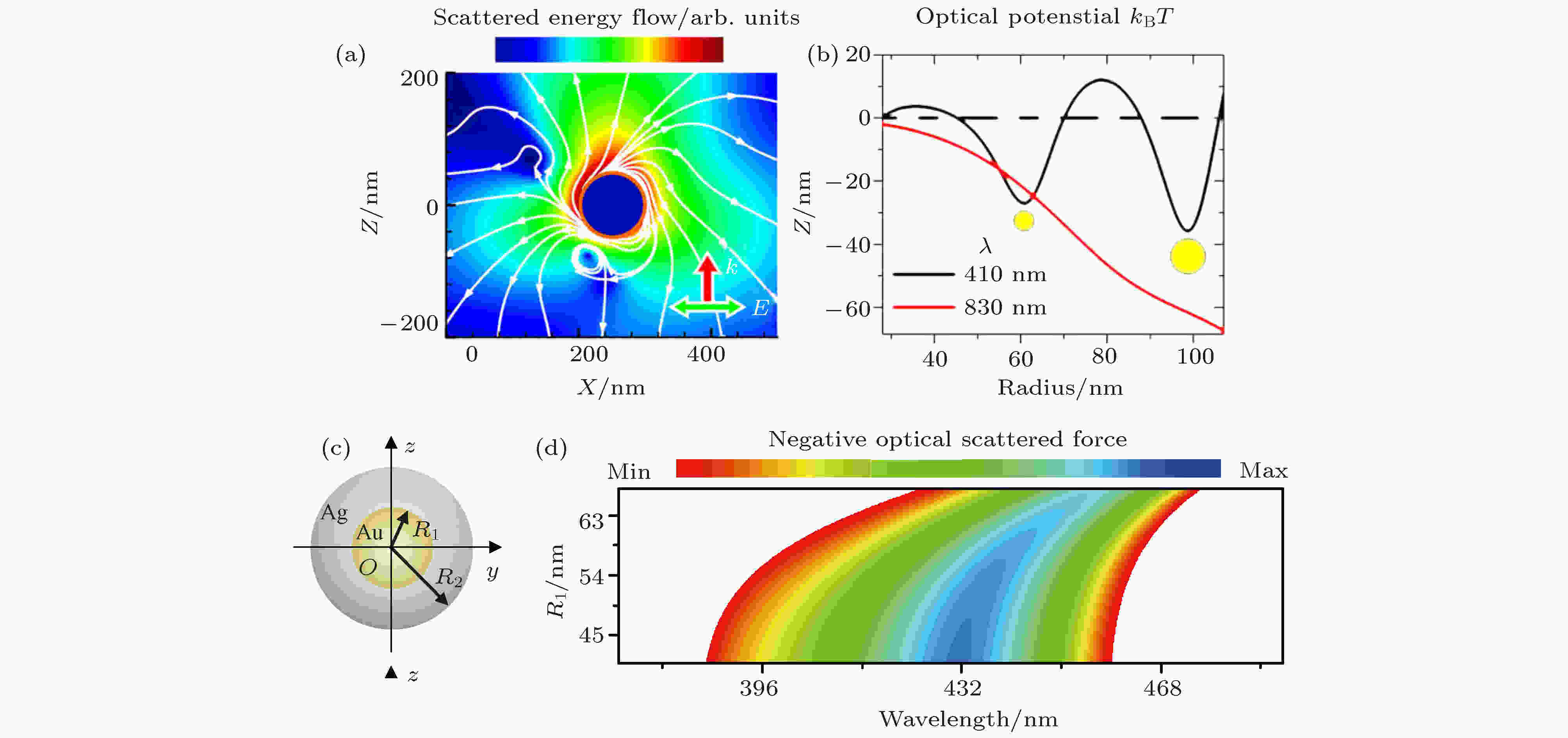图 3 (a)硅核-金壳纳米颗粒能流在高斯激发下的能流[55]; (b)光学势与颗粒半径的关系[55]; (c)金核-银壳纳米颗粒示意图[56]; (d)光学力与波长、核半径的关系[56]Figure3. (a) Energy flow of a Si-Au core-shell sphere under Gaussian beam excitation. The particle is positioned at x = w0/2. The beam waist w0 = 0.5 μm. The white curve and color scale are the direction and logarithmic modulus of the energy flow, respectively[55]. (b) Potential well as a function of the radius under the excitation of λ = 410 nm (black) and 830 nm (red)[55]. (c) Schematic of an Au-Ag core-shell sphere[56]. (d) Phase diagrams of longitudinal optical force Fz acting on the sphere[56].
微流控不仅在增强光谱方面有重要应用[63], 也可将其与光学力结合来筛选颗粒. 传统的离心方法可大量地分离纳米颗粒, 但精度不高. Nan和Yan[64]利用由光的相位梯度产生的动态可调的光学力来全光筛选银或金纳米颗粒. 光的相位梯度导致的尺寸相关的光学力会以不同的速度来驱动溶液中的不同尺寸的颗粒, 导致沿着光线陷阱(optical line traps)的分离. 利用一系列不同的光线来产生不同的捕获势(trapping potentials), 就可实现分辨率为10 nm的70—150 nm直径的金和银纳米颗粒的精细筛选. 此外, 光镊可实现液体环境中稳定的单纳米颗粒精密操纵, 但对于流动体系中的大量纳米颗粒也会有问题, 这是由于较难控制所有的位置随机分散的纳米颗粒. Yang等[65]利用光学力和流体力(hydrodynamic forces)来筛选流体中的金纳米颗粒, 同时达到高精度和相对大的产率. 这是利用了反向撞击流来产生滞止点, 其附近的流速变得非常小. 因而被流体力约束在小区域内的不同尺寸的纳米颗粒, 可被适当功率的激光分离.
2
4.1.“单个颗粒型”等离激元镊
单个金属纳米颗粒的表面等离激元共振激发, 在其周围形成电场增强和梯度, 即可用于捕获其他颗粒. 如图4(a)所示, Quidant等[68]在玻璃衬底上制备了金纳米方片阵列, 形成二维分布的等离激元镊. 与传统的光镊相比, 等离激元镊可使单颗粒介质珠(聚苯乙烯)在较低强度的非会聚光下稳定捕获在金纳米方片的边缘(光势阱最大)的稳定位置, 而且还能从混合物中筛选某种颗粒. 之后, 他们又定量分析了基于金纳米圆片阵列的表面等离激元的光镊[69], 可在低激光强度下捕获微米级胶体, 显示了几十飞牛(fN)力下的稳定捕获. 相对于传统的三维光镊, 等离激元镊对于样品的尺寸更具选择性, 并可通过入射光的参数来调控捕获的性质.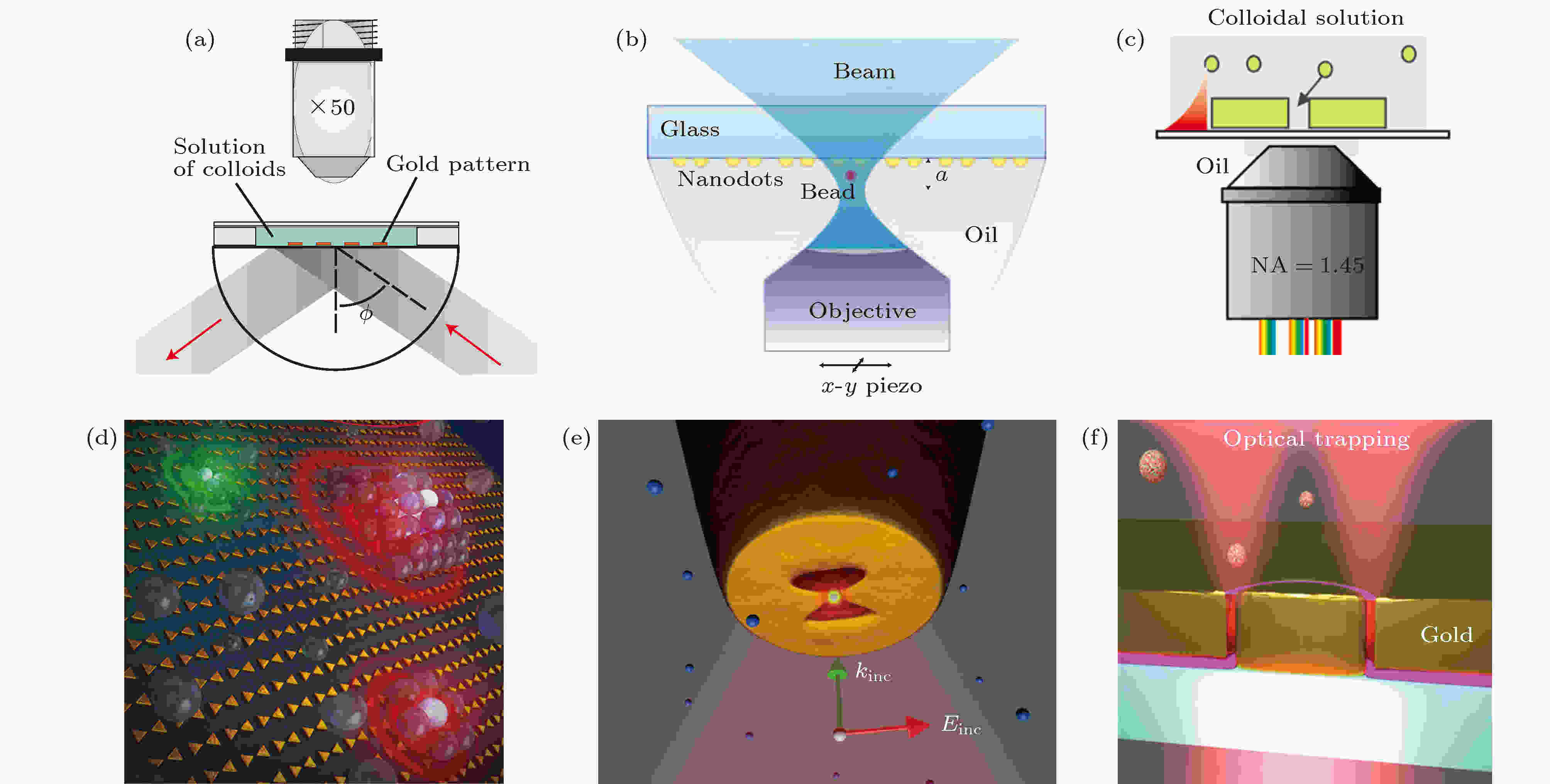
图 4 金属纳米颗粒形成的等离激元镊 (a)单颗粒阵列[68]; (b)纳米颗粒二聚体阵列[79]; (c)纳米棒二聚体[80]; (d)领结型二聚体[82]; (e)领结型纳米孔[84]; (f)同轴纳米孔[85]Figure4. Plasmonic tweezer: (a) Schematic of the gold particle pattern[68]; (b) schematics of a nanodots substrate[79]; (c) schematic of the individual dimer with a 10 nm gap[80]; (d) Au bowtie nano antenna arrays for highly efficient manipulation[82]; (e) SIBA trapping of a holey fiber, the incident polarization is parallel along the gap axis to excite its transverse mode[84]; (f) optical trapping with a gold coaxial nano-aperture (10 nm gap)[85].
Xu等[70]理论研究了在平面波入射下, 杂化二聚体中的低折射率介质颗粒受到的拉力, 其物理机制在于Au颗粒与SiO2介质颗粒间的近场电磁耦合, 因此还可通过几何参数的变化来调控光学力. 此外, 在没有强度梯度的情况下, 也可用一束高斯光来拉动颗粒, 产生没有横向分量的纯的光学拉力. Ng等[71]利用一后向散射力来把颗粒一直拉到光源, 其物理机制是通过辐射多极子的干涉来增大前向散射力. 实现负的光学力(拉力)的必要条件是同时激发颗粒中的多极子, 如果沿着传播方向的所有光子动量的叠加很小, 则光学吸引力是可能的.
等离激元金属纳米线是传导的表面等离激元的载体[72—74]. Xu等[75]利用银纳米线在水溶液中来光学捕获、推动和引导纳米颗粒方向性移动. 激光激发银纳米线的一端, 产生局域的和传导的表面等离激元. 表面等离激元引起的光学力可捕获水溶液中的纳米颗粒, 捕获的纳米颗粒还会沿着或直或弯的银纳米线, 移动到激光的入射点. 对于V形银纳米线, 颗粒的运动方向还可由入射偏振来调控. 除了金属纳米线外, Qiu等[76]实现了在锥形光纤固体环境下微纳物体的光学力操纵. 在超连续光下, 将光学力与基于光热效应的光泳力(photophoretic force)相结合, 驱动微米级的金片在锥形光纤上往复运动. 实现了光学拉力以及金片振荡. Sirbuly等[77]也发展了一种纳米光纤光学力换能器, 利用强的近场等离激元与电介质的相互作用来高灵敏(亚pN)地测量局域光学力.
2
4.2.“间隙型”等离激元镊
等离激元金属纳米颗粒的间隙具有较强的光场局域, 因而与4.1节所述单个颗粒相比, 间隙是一个更有效和稳定的捕获其他颗粒的位置. Quidant等[78] 利用玻璃衬底上的金纳米棒二聚体产生大的光强梯度, 将活的大肠杆菌光学捕获数小时. 一些细菌在被捕获的同时, 其朝向也被二聚体的对称性所固定. 如图4(b)所示, Grigorenko等[79]在传统光镊中利用金颗粒二聚体阵列形成三维亚波长等离激元镊, 可极大地增强捕获效率, 在更小的激光功率下实现纳米级的控制. 将聚苯乙烯球紧紧捕获到衍射极限以下的纳米间隙上, 同时将布朗运动减小了一个数量级. 如图4(c)所示, Martin等[80]利用金纳米棒二聚体, 将10 nm的金纳米颗粒捕获在其间隙中, 形成新的金纳米颗粒与金纳米棒二聚体之间的等离激元近场耦合. 通过探测该耦合导致的共振峰红移, 可实时记录单颗粒的捕获. 因而有望将等离激元捕获与基于LSPRs的传感相结合, 将样品移动到特定的高敏感“热点”区域. Tsuboi等[81]利用三角锥形金纳米颗粒二聚体阵列捕获了量子点, 并通过量子点的荧光观测到捕获现象. 如图4(d)所示, Toussaint等[82]利用领结型金纳米天线阵列实现了颗粒的高效、多功能的捕获、操纵和筛选, 具有低输入功率和低数值孔径. 捕获响应作为入射波长、偏振、颗粒直径以及阵列间隙的函数. Sasaki等[83]利用金纳米方块二聚体的棱边耦合来调控光势阱, 可得到更稳定的捕获.2
4.3.“孔洞型”等离激元镊
与等离激元金属纳米颗粒的间隙相比, 各种形态的纳米孔洞除了具有一定的光场增强外, 有的还可使得被捕获的颗粒通过. Quidant等[86]提出了自诱导反作用(SIBA)捕获, 将光学捕获所需的局域场强减少了一个数量级以上. 被捕获的对象在增强回复力方面有主动性. 利用金膜上纳米孔的强度实时变化的透射共振, 实现了对直径小至50 nm单个聚苯乙烯球的SIBA捕获. 之后又将SIBA与等离激元调控相结合, 实现了矩形纳米孔对22 nm聚苯乙烯单颗粒或二聚体的共振捕获[87], 并提出了品质因子来量化捕获效率. 此外, 还通过等离激元纳米腔中的纳米颗粒捕获, 直接证明了光学势的自重构(self-reconfiguration), 有利于优化基于SIBA捕获的表现[88]. 如图4(e)所示, Quidant等[84]利用基于位于金包锥形光纤尖端的领结型孔等离激元镊, 实现了50 nm单颗粒介质的三维纳米光学捕获和探测. 而且被捕获的样品还能在非常低的捕获强度下, 数分钟移动数十微米.Bawendi等[89]基于领结型纳米孔, 利用相对低的1.56 MW/cm2的1064 nm连续光, 捕获了30 nm的二氧化硅包裹的量子点. 由于纳米孔的强的电场增强, 还实现了量子点的双光子激发. Lee等[90]利用一对移动的点光源, 实现了对小于5 nm颗粒的非荧光捕获和探测. 通过等离激元领结型三维锥形孔洞中的5 nm间隙, 可使共振光子进入5 nm × 5 nm × 7 nm的极小体积, 并在低强度的1560 nm连续光下捕获4 nm的CdSe/ZnS量子点, 此外1560 nm飞秒脉冲的泵浦可在三维锥形尖端产生强无背景的二次谐波点光源.
Oh等[85]利用金膜上原子沉积得到的10 nm间隙的在785 nm共振的同轴纳米孔阵列实现光学捕获. 如图4(f)所示, 这些同轴孔具有尖锐的势阱(potential well), 在激光功率低至4.7 mW时, 仍可捕获30 nm的聚苯乙烯球. 通过简单的透射测量, 就可以得到被捕获物的实时无标记的探测.
Sainidou和García de Abajo[91]以金膜上的圆形纳米孔来捕获金纳米棒. 由于纳米孔表面等离激元引起的光学力会影响纳米棒的位置, 所以通过激发光的变化, 可调整纳米棒在纳米孔中的位置. Deng等[92]实现了金纳米腔与金纳米棒间的光机(optomechanical)相互作用. 金纳米棒的强的LSPR模式杂化, 导致金膜上纳米腔的等离激元共振模式分裂为成键(bonding)模式和反键(antibonding)模式. 当等离激元镊被反键模式激发, 纳米棒会受到光学推力而离开纳米腔. 反之, 当工作在键合模式, 纳米棒受到光学拉力而被捕获在纳米腔里. 由于金纳米棒和金纳米腔之间的强的共振近场相互作用, 金纳米棒受到的光学(拉)力会比同样尺寸的介质纳米棒的高两个数量级. 光学势的形状和位置也可由激光波长来调控, 并用于纳米区域的金纳米棒的操纵.
2
5.1.光学角动量与自旋-轨道耦合
光同时具有线性动量和轨道动量. 线性动量可用于光镊, 激光束作用于颗粒, 可产生将颗粒拉到光束中心的力. 角动量可转移到颗粒上, 使其旋转. 入射偏振变化引起的近场增强和热点分布的变化带来的角动量, 为光学力的操纵带来了更多的自由度, 例如, 可实现纳米颗粒的朝向控制、旋转和纳米马达[93]. 如图5(a)所示, Tong等[94]利用线偏振的近红外激光, 证明了长度为几十纳米到几微米的单颗粒等离激元纳米结构的光学对准(alignment)和旋转. 银纳米棒、金纳米颗粒二聚体与入射偏振的平行(对准), 是由于其偶极子的长轴方向的极化. 而银纳米线会与入射偏振垂直, 并在线的端头链接. 如果入射偏振变化, 线、棒、二聚体将会发生旋转. 旋转的频率约为1 Hz, 这也是由于圆偏光自旋角动量的转化. 如图5(b)和图5(c)所示, K?ll等[93,95,96]基于金纳米球和棒的共振光散射, 利用圆偏光或者改变线偏光的偏振, 使颗粒旋转, 实现了纳米马达. 并通过同时分析等离激元光谱和布朗动力学, 测量了光热效应对光学捕获的影响[97]. Pelton等[98]利用位于纵向等离激元模式附近的激光波长, 证明了单颗粒金纳米棒的三维捕获和朝向. 对共振长波侧的失谐(detuning)可实现几分钟的稳定捕获, 捕获时间与激光功率相关. 而对短波侧的失谐可使得纳米棒从激光焦点处排斥开.
图 5 入射偏振变化引起的金属纳米颗粒转动和纳米马达 (a)银纳米线自转[94]; (b)金纳米颗粒自转[95]; (c)金纳米棒自转[96]; (d)纳米颗粒绕金纳米柱公转[99]; (e)二聚体转向[100]Figure5. Rotation and plasmonic nanomotor. (a) The dark-field images show a silver nanowire is rotated by turning the incident polarization (red arrows)[94]. (b) Schematic of the gold nanoparticle trapped between two glass planes rotates by absorbing spin angular momentum from the circularly polarized beam[95]. (c) Schematic of the gold nanorod rotates in solutions through plasmonic torques of circularly polarized beam[96]. (d) Schematic of trapping and rotation of a nanosphere by the gold nanopillar with linearly polarized light[99]. (e) Schematic of the silver nanoparticle dimer orient along the incident polarization. Two orthogonal polarizations can determine the dimer angle by the difference in the spectral intensity peak[100].
当有其他颗粒存在时, 对于原颗粒的旋转可带来新的影响. 如图5(d)所示, Crozier等[99]利用模板剥离制备的等离激元金纳米柱, 证明了对直径110 nm的聚苯乙烯颗粒的捕获和旋转. 通过改变入射光偏振, 可动态调控金纳米柱边缘的与偏振平行的两个电场最强的“热点”, 从而可稳定地捕获纳米颗粒, 并使其也随着“热点”绕金纳米柱边缘转动. 而当入射偏振不变时, 被捕获的纳米颗粒也基本不运动. 当利用圆偏光时, 产生旋转的能流, 也使颗粒发生旋转. Rohrbach等[100]发现在光镊中形成的80 nm银纳米颗粒二聚体, 朝向沿着激光的电场方向, 可在水平面上稳定地旋转. 因而纳米颗粒的朝向和自组装可由光散射方法来控制. 如图5(e)所示, 通过测量两个正交偏振的光谱强度的最大值的差别, 来确定不同等离激元耦合强度的二聚体的方位角. 精度可达几度, 而不依赖于频率或纳米颗粒的间距. Zheng等[101]引入了一种基于C型刻蚀的等离激元共振结构的4.5 μm长的传送带. 通过旋转入射光的偏振, 可实现长距离地操纵聚苯乙烯纳米球.
自旋-轨道耦合也为表面等离激元光学操纵提供了新的自由度. 光子自旋和轨道之间的耦合一般是较弱的, 但在等离激元金属纳米结构中却较容易探测到增强的自旋-轨道相互作用(spin-orbit interaction, SOI). Xu等[102]利用圆偏光被单颗粒金纳米球散射, 在纳米球附近形成扭曲的手性传播轨迹, 揭示了表面等离激元近场的强的SOI. 类似的由强的SOI引起的自旋相关的轨迹也出现在金纳米线端头, 有望实现等离激元纳米光路中的光子自旋筛选. 光学力依赖于场强梯度来产生局域的作用, 有的是仅可在光传播的方向上推动颗粒. 但Zayats等[103]发现, 自旋-轨道耦合, 也就是入射圆偏光的自旋转化为横向的动量, 可导致横向的光学力, 作用于衬底上的颗粒, 而且伴随着反冲作用力(recoil mechanical force). 这一违反直觉的力的作用方向既非场强梯度也非传播方向, 其可由平面波的偏振来调控, 而且大小也与其他光学力可比拟. Shalin等[104]发现在等离激元界面附近的颗粒可受到光学拉力(optical pulling forces). 对于这种负的反作用力, 有两个主要因素: 一是入射波和反射波之间的干涉引起具有非对称散射模式的旋转偶极子, 二是PSPs的方向性激发可增强散射光的线性动量. PSPs的强的非对称激发是由旋转偶极子与PSPs间的自旋-轨道耦合来决定. 根据动量守恒, 作用于颗粒的力的指向与入射波的传播方向相反. Crozier等[105]利用FDTD模拟也发现, PSPs可增强对金纳米颗粒的推动. 增强的光学力是由于PSPs带来的场增强, 以及金颗粒与金膜之间的近场耦合.
2
5.2.新型光场
虽然标准的高斯光束已是有利的光镊工具, 但改变光场的相位和幅度还可能带来更多不寻常的光束形态, 为颗粒操纵带来新的自由度[106]. 实际上, 新型光场的不寻常的强度、偏振和相位结构, 已经用于光操纵领域[107].利用椭圆光束或螺旋相位结构光束, 通过光与物质间的角动量转移, 可引起颗粒的旋转. 但光热效应以及轴向力将可实现的旋转频率限制在了几赫兹. 这一问题理论上可通过透明颗粒的角动量转移来克服, 如图6(a)所示, Friese等[108]利用光镊, 在双折射方解石微米颗粒上引起光学力矩. 颗粒与入射偏振面平行, 因而可以一定的角度旋转, 或者以一定的旋转频率自旋. 由于这些颗粒是透明的, 因此可在较高功率下三维捕获而不产热, 旋转频率达350 Hz. 光学力对纳米颗粒的作用通常是两部分的叠加: 偶极子的梯度力以及散射的压力. 散射力一般与坡印亭矢量成比例, 反映了动量的方向和大小. 但Sáenz等[109]发现, 对于具有非均匀螺旋度(nonuniform helicity)的光场而言, 还会有额外的非保守力, 与自旋角动量的旋度成比例. 如图6(b)所示, Dholakia等[110]利用环形光场得到螺旋形相前, 将纳米颗粒约束在涡旋中心(暗), 实现了等离激元共振附近的捕获, 以及由轨道角动量转移而产生的颗粒旋转. 如图6(c)所示, Scherer等[111]利用光涡旋(拉盖尔-高斯光束)的光子轨道角动量, 引起介质表面的10 μm长的单个银纳米线的旋转. 旋转由线偏光与银纳米线的等离激元相互作用来控制, 而线偏光产生的力矩可产生角加速度. Huang等[112]利用金膜上刻蚀的单个阿基米德螺旋线的等离激元近场, 来选择性地捕获或旋转光学各向同性的介质微球. 当左旋光入射时, 近场角动量为零, 其等离激元近场形成的会聚点可稳定捕获微球. 当右旋光入射时, 产生等离激元涡旋, 微球发生旋转.
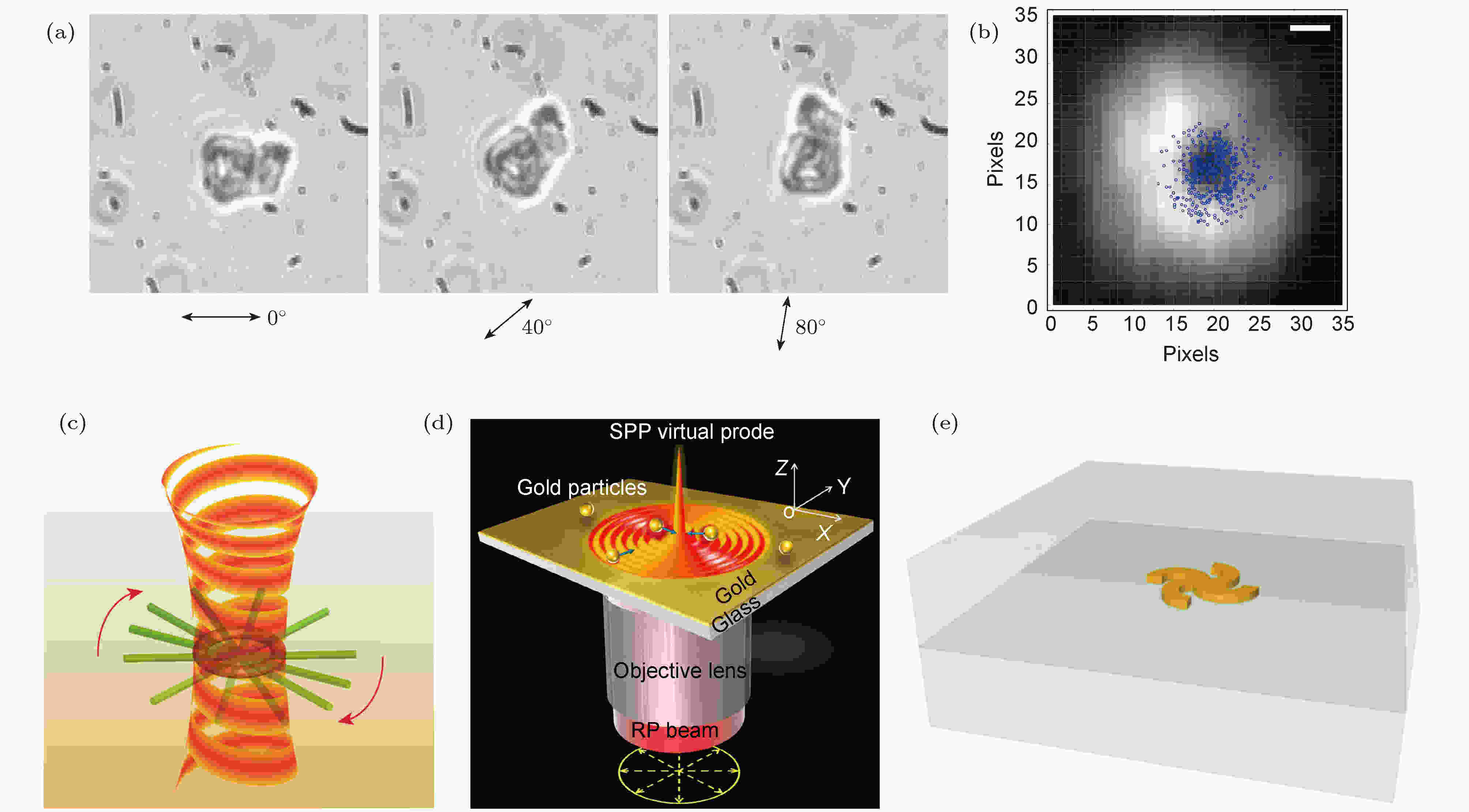图 6 (a)方解石晶体自转[108]; (b)拉盖尔-高斯光入射下的单个金纳米颗粒运动情况的空间分布[110]; (c)光涡旋引起银纳米线自转[111]; (d) PSPs捕获金颗粒[114]; (e)万字形金纳米马达[118]Figure6. (a) A calcite crystal is parallel with the polarization of the laser beam[108]; (b) spatial points of the movement of a gold nanoparticle with Laguerre-Gaussian beam of L = 2 at λ = 488 nm with 120 mW laser power[110]; (c) schematic of the rotation of a Ag nanowire on a glass substrate induced by an optical vortex[111]; (d) schematic of the metal particles trapped by a PSPs virtual probe[114]; (e) schematic of the gold nano-motor, sandwiched between two silica disks (300 nm thick, 2.2 mm × 2.2 mm). The large silica disk reduces the Brownian motion of the nanoparticles[118].
除涡旋光束之外, 另一种常见的矢量光束是高度会聚的径向(radially)偏振光束, 其强的轴向分量提供了大的梯度力. Zhan等[113]利用径向偏振光束实现了金属瑞利颗粒的稳定的三维捕获, 同时, 轴向分量不会产生沿着光轴的坡印亭矢量, 因此不会产生轴向的散射/吸收力. 由于梯度力和散射/吸收力的空间色散, 可实现稳定的三维捕获. 如图6(d)所示, Yuan等[114]利用高数值孔径显微镜和径向偏振光束来激发和聚焦金膜的表面等离激元, 形成等离激元镊. 散射力和梯度力产生的合力可吸引和捕获金纳米颗粒, 这与没有金膜时的光镊产生的排斥力相反. 实际上, 等离激元镊的捕获不仅仅只是一个梯度力与一个相反的散射力之间的平衡, 而是来自于所有梯度力和散射力的叠加. 此外, 通过产生一个坑型(crater-shaped)的势阱, 可得到双等离激元镊[115], 从而可精确地控制纳米间隙的数量和增强. Taylor等[116]发现, 适当结构的入射光场在与散射颗粒作用时, 可实现类似分光膜的作用. Lindquist等[117]利用等离激元全息, 实现了纳米颗粒的捕获和操纵. 计算机控制的空间光调制器产生的全息, 照射在牛眼(bull’s eye)银纳米结构的圆周, 实现等离激元波之间的干涉相长和相消, 得到一个可在表面移动的向中心传播的聚焦“热点”. 改变作为位置的函数的等离激元波的相位就可控制会聚点的位置, 进而使得被捕获在焦点处的200 nm直径纳米颗粒可移动到结构的任何位置上.
2
5.3.手性等离激元金属纳米颗粒
如果金属纳米颗粒为不对称、手性或其他特殊形状, 也可为光学操纵带来奇异的效果. 由于手性等离激元的作用, 利用手性匹配的圆偏甚至线偏的入射光, 就可产生旋转的能流, 使颗粒发生旋转. 由于光可以对任何其遇到的物体施加辐射压力, 通常认为会向前推动颗粒. 实际上任何具有光子动量的入射平面波都会沿着入射方向推动颗粒, 而与颗粒的性质无关. Wang和Chan[119]发现如果一个手性颗粒位于任何一个左右对称的衬底上, 那么在与入射光子动量垂直的方向上可产生一个奇异的横向光学力. 该力是由于颗粒球的结构手性与衬底表面反射光之间的耦合产生, 进而可将具有相反手性的手性颗粒推到相反的方向. 如图6(e)所示, Zhang等[118]证明了当线偏光入射时, 通过改变入射光的波长, 就可激发一个螺旋十字形金纳米结构不同的等离激元模式, 进而可控制一个体积是其4000倍的二氧化硅微米圆盘的旋转方向和速度. 这是由于在两个共振波长处, 分别对应着两个最大的但反向的坡印亭矢量, 进而得到两个最大的但方向相反的旋转速度.对于左手和右手对映异构体, 圆偏光产生的作用力大小不同, 因而可用于化学混合物的手性辨识以及手性纳米结构的可控组装. 然而, 对映选择性(enantioselective)的光学力较难量化, 因为其相对较小(亚pN), 且为亚微米分辨. Dionne等[120]利用手性AFM探针与等离激元镊结合, 增强并可视化了光学力. 在圆偏光激发下, 等离激元镊对于探针的作用力取决于光和探针的手性. 例如对于左手性探针而言, 横向力在左旋光下是吸引的, 而在右旋光下是排斥的. 对于相反手性的两个样品, 力的差别可超过10 pN. 探针的手性光学力成像横向分辨率在2 nm, 对于不同手性的力也会有不同的空间分布. Lin等[121]发现, 当线偏振平面波入射到一对手性相反的纳米颗粒时, 可产生横向光学力, 可侧向移动该手性颗粒二聚体, 移动方向取决于两个颗粒的距离和手性. 横向光学力来自于多重散射所导致的光学势梯度, 更依赖于颗粒的手性, 而非材料的损耗. Capolino等[122]利用光致力显微镜近场表征高度会聚的径向偏振光束, 对于手性样品, 实现了突破衍射极限的纳米级分辨率的近场激发和探测. 其利用了纳米针尖受到的光致梯度力, 机械探测到悬臂的受迫振荡. Phillips等[123]提出了一种变形的颗粒作为被动力的夹钳, 用作表面形貌成像的光捕获探针. 通过光束和颗粒形状的变化, 控制动量由光子向机械体系的转移.
