摘要: 本文对GaN基InGaN/GaN多量子阱结构、蓝紫光发光二极管(light-emitting diode, LED)的电流噪声进行了测试, 电流测试范围为0.1—180 mA. 根据电流噪声的特点, 结合LED中载流子之间的产生-复合机制, 探讨了电流注入下LED中载流子的产生与复合机制和低频噪声产生的机理. 结论表明, 随着电流从0.1 mA逐渐增大到27 mA, LED中的电流噪声具有低频产生-复合(generation-recombination, g-r)噪声的特性; 当电流逐渐增大到50 mA及以上时, 电流噪声的行为接近1/
f 噪声. 采用电子元器件中公认的电流噪声模型, 拟合了低频电流噪声功率谱密度与频率之间的关系, 结合LED中载流子的输运机理和复合机制, 从理论上分析了LED在电流注入时g-r噪声幅值和转折频率的变化规律. 本文的结果提供了一种检测和表征多量子阱结构蓝紫光LED在电流逐渐增大过程中发光机制转变的有效手段, 为提高其发光量子效率提供理论依据.
关键词: 低频噪声 /
发光二极管 /
产生-复合噪声 /
复合机理 English Abstract Low-frequency generation-recombination noise behaviors of blue/violet-light-emitting diode Wang Dang-Hui Xu Tian-Han School of Materials Science and Engineering, Xi’an Shiyou University, Xi’an 710065, China Received Date: 07 February 2019Accepted Date: 08 April 2019Available Online: 06 June 2019Published Online: 20 June 2019Abstract: During the past two decades, GaN-based light-emitting diode has been used as a high-quality light-source. Low-frequency noise as a diagnostic tool for quality control and reliability estimation has been widely accepted and used for semiconductor devices. Understanding the origin of efficiency-droop effect is key to developing the ultimate solid-state light source. Various mechanisms that may cause this effect have been suggested, including carriers’ escape, loses due to dislocations, and the Auger effect. In this study, we investigate the low-frequency noise behaviors of GaN-based blue light-emitting diode with InGaN/GaN multiple quantum wells. The measured currents range from 0.1 mA to 180 mA. According to the characteristics of power spectral density of current noise and the generation-combination mechanism between electrons and holes in the active region of light-emitting diode (LED), we adopt the well-known model of low-frequency noise to fit the relationship between power spectral density of current and frequency, and find that there exists a transition between generation-combination and 1/f noise when the light-emitting diode begins to work. In other words, it can be derived that the low-frequency noise behaviors are dominated by generation-combination noise when the currents are between 0.1 mA and 27 mA; with the current gradually increasing, the origin source of low-frequency noise in blue/violet-light LED will transit to the 1/f noise. Through the analysis of the transport and recombination mechanism of the carriers, and combination with the model of low-frequency noise, we analyze the corner frequency of the generation-recombination noise. The results of this paper provide an effective tool and method to study the conversion of light-emitting diodes.Keywords: low-frequency noise /light-emitting diode /generation-recombination noise /recombination mechanisms 全文HTML --> --> --> 1.引 言 GaN基宽禁带光电子半导体材料具有在0.7—6.2 eV之间的直接、连续可调的带隙特性, 是实现半导体蓝光及紫光/深紫外光发光二极管(light-emitting diode, LED)、激光二极管和GaN基功率器件的关键材料. 目前, GaN基LED多采用多量子阱(multiple quantum well, MQW)结构作为发光活性区. 在施加正向偏置时, 由于外加电压基本都在耗尽层上, 抵消并减弱了内建电场, 降低了势垒高度, 因此多数载流子就容易越过势垒注入对方形成少数载流子. 于是处于高能态的电子和空穴相遇复合, 同时把多余的能量以电磁波的形式释放, 从而实现固态发光. 基于p-n结理论的LED发光原理如图1 所示, 图中箭头所示为电子与空穴辐射复合发射可见光的传播方向. 发光活性区中少数载流子之间的辐射复合是引起LED发光的主要原因.[1 -4 ] . 在电子元器件的工作过程中(尤其是开启过程), 电子与空穴在电场作用下的扩散与漂移、陷阱能级或缺陷能级对载流子的俘获与发射, 以及杂质与晶格的散射作用等物理过程, 均能引起载流子数目的涨落和迁移率的涨落, 这些过程中蕴涵着丰富的噪声信息[5 -8 ] . 我们知道, GaN基LED的实质是InGaN/GaN MQW结构, 其发光区域主要集中在p-GaN的有源区, 载流子的溢出、发光活性区中的位错对载流子的俘获以及Auger效应被认为是引起LED量子效率降低的主要原因. 当电流注入时, MQW结构LED中的载流子复合、非辐射复合以及载流子数目涨落中包含的大量信息往往被许多研究者忽略. LED中的产生-复合 (generation-recombination, g-r)噪声起源于器件中陷阱对少数载流子的随机俘获或者发射, 引起了电流传导过程中载流子数目和迁移率的涨落. 当载流子被俘获时, 会诱发引起迁移率、扩散系数、电场强度、势垒高度以及空间电荷区宽度等方面的涨落[9 -12 ] . 低频噪声作为一种有效的、敏感的无损检测技术, 其中的低频1/f 噪声和g-r噪声中分别包含着半导体器件中载流子的扩散、漂移、涨落等输运信息和发光活性区中载流子的产生、复合以及被杂质缺陷的俘获等信息. 研究g-r噪声的产生机理、噪声幅值和特征频率等参数, 以及这些参数与电子流之间的关系等问题, 对深入了解LED的发光机理、LED在大电流注入下的电流噪声特性, 以及在高电流密度注入下LED的质量与可靠性评估具有重要的研究意义. 本文采用低频噪声对LED高电流密度注入下的载流子输运行为和低频g-r噪声的行为之间的相关性进行了研究.图 1 p-n结型LED发光原理图Figure1. Principle schematic of p-n junction LED.2.实 验 实验所采用的LED均是采用金属有机化学气相沉积(metal-organic chemical vapor deposit, MOCVD)技术, 以异质外延的方式生长在蓝宝石衬底之上. 具体的生长工艺如文献[13 ]所示, 对LED的低频噪声测试是在西安电子科技大学噪声检测与无损诊断实验室完成的. 在LED的低频噪声测试实验中, 测试频率的范围为1—100 kHz, 测试电流的范围为0.1—180 mA. 为了保证电流值的精确性, 对LED串联了一个可变电阻R d , 其阻值范围为10—10000 Ω; 相应的前置偏压的范围为0.1—3.0 V, 通过改变串联电阻的大小实现开启LED并逐渐增大电流的目的. 根据图2 所示的低频噪声测试原理, 电流噪声的功率谱密度SI (power spectral density, PSD)为SI 为测试的电流噪声PSD (单位为A2 /Hz); N V _MEAS${{\rm{V}} / {\sqrt {{\rm{Hz}}} }}$ ). 图2 中CAMP为放大器; R F 为可调节并联电阻器; Digitizer为数字化的数据处理设备. 通过(1 )式和图2 , 可以获得不同电流下LED的噪声PSD.图 2 LED低频噪声测试原理图Figure2. Measurement schematic of low frequency noise for LED.3.实验结果与讨论 23.1.伏安特性 3.1.伏安特性 图3 给出了室温下对LED进行光致发光(photoluminescence, PL)测试的结果. 从图3 可以看出, LED发光的峰值波长为428 nm, 属蓝紫光范畴. 电学性能测试的伏安(V -I )特性曲线如图4 所示. 从图4 可以看出, 当施加约2.52 V的正向偏置时, LED开始发光.图 3 LED室温PL测试Figure3. PL measurement at room temperature.U 下(2 < U < 6), LED的理想因子γ 为[14 ] R p 为并联电阻, R s 为串联电阻, I s 为反向饱和电流, ${k _{\rm{B}}}$ 为玻尔兹曼常数, T 为开氏温度, I 为流经二极管的电流, q 为真空中的单位静电荷. 根据文献[15 ]中的LED模型, 结合图4 的曲线可知, 实验中LED的寄生电阻可忽略不计. 通常情况下, R p 的数量级远大于R s . (2 )式可改写为图 4 LED的V -I 特性测试曲线Figure4. V -I characteristic transfer curve of LED.3 )式对V -I 特性曲线进行拟合, 得到LED的理想因子γ = 5.43, 这表明LED内部存在串联电阻的特性. 众所周知, 当理想因子γ = 1时, LED中扩散电流占主导地位; 当理想因子γ = 2时, LED中复合电流占主导地位. 但是实际上, LED的理想因子γ 通常远大于2. 高的理想因子不能用扩散理论和复合理论进行解释, 而必须采用隧穿理论进行解释, 此时隧穿电流变得更加重要. 在LED施加正向偏置时, 由于一部分电压降在LED的串联电阻R s 上, 使得外加电压引起的势垒降低会小一些, 结区周围的表面非辐射复合引起了一些附加电流[15 ] . 因此, LED正向V -I 特性用一个非理想的二极管方程描述:I nr0 是反向非辐射复合电流; I n , I p , I n0 , I p0 , I nr 分别为电子对电流的贡献、空穴对电流的贡献、反向电子电流、反向空穴电流及非辐射复合电流. 注入到工作区的一些载流子可能会发生非辐射复合而降低内量子效率, Auger复合是一种本征的非辐射复合过程. 在Auger复合中, 电子空穴对释放的能量被多数载流子(即n型材料中的电子和p型材料中的空穴)吸收. 但是在发射可见光的宽禁带半导体中, Auger过程相对较弱, 非辐射复合主要是来源于深杂质能级.3.2.低频噪声特性 -->3.2.低频噪声特性 为了进一步研究电流注入下LED的低频噪声特性, 对LED分别施加了不同大小的电流(0.1, 10, 27, 50, 80和180 mA), 并测量了不同电流注入下LED中的低频电流噪声, 测试结果如图5 所示. 从图5 可以看出, 随着测试电流的逐渐增加, LED的低频电流噪声也逐渐增加. 当电流从0.1 mA逐渐增大到27 mA时, 电流噪声功率谱具有g-r噪声的特征, 而且随着电流的逐渐增大, g-r噪声的特征逐渐消失. 当测试电流增加到50 mA时, 低频噪声的行为接近于标准的闪烁噪声(即1/f 噪声, 此时γ = 1). 文献[16 , 17 ]认为, 当电流越小(小于0.1 mA)时, LED低频电流噪声的行为具有接近产生g-r噪声的趋势, 引起这种噪声变化的原因是由于非辐射复合的隧穿过程, 这种非辐射复合的隧穿过程是由于扩展的缺陷体系延伸到了LED的光学活性区. 在低电流注入下, g-r噪声在低频噪声中是主要的噪声机制, 它起源于p-n结势垒之间复合电流的涨落[18 -21 ] .图 5 InGaN/GaN LED的电流噪声PSD与频率的关系图Figure5. Relationships between current PSD and frequency for InGaN/GaN LED.图5 还可知, 在电流大于27 mA时, InGaN/GaN MQW LED中低频1/f 噪声的成分在逐渐增加; 而在电流为0.1—27 mA时, 低频噪声中的g-r噪声源的成分在逐渐降低. 一般情况下, 电子器件中的低频噪声是由三部分构成[18 -20 ] , 如下式所示:A 为白噪声的幅值; f 为频率; 第二项为闪烁噪声(flicker noise)项, B 为闪烁噪声的幅值, γ 为闪烁噪声的频率指数因子, 当γ = 1时为1/f 噪声, 表明载流子之间的产生与复合达到平衡; 第三项为Lorentzian噪声, C 为Lorentzian噪声的幅值, ${f_0} = {1 / {\left( {2{\text{π}}{\tau _0}} \right)}}$ 为g-r噪声的转折频率, 其中${\tau _0}$ 为Lorentzian噪声的时间常数, α 为Lorentzian噪声的频率指数因子, 当α = 2时为标准的g-r噪声. 采用(5 )式对LED的电流噪声PSD进行频率范围为1—100000 Hz曲线拟合, 拟合曲线如图6 所示, 低频噪声(包括1/f 和g-r)参数的提取结果如表1 所列.图 6 根据(5 )式拟合g-r噪声参数Figure6. Fitting results of g-r noise using Eq. (5 ).低频噪声类型 测试电流/mA 0.1 10 27 50 80 180 白噪声 5.14 × 10–18 1.10 × 10–17 6.12 × 10–17 2.36 × 10–17 9.23 × 10–18 9.23 × 10–18 1/f 噪声 $\displaystyle\frac{{4.61 \times {{10}^{ - 16}}}}{{{f^{0.65}}}}$ $\displaystyle\frac{{1.82 \times {{10}^{ - 15}}}}{{{f^{0.83}}}}$ $\displaystyle\frac{{1.01 \times {{10}^{ - 13}}}}{{{f^{0.90}}}}$ $\displaystyle\frac{{5.29 \times {{10}^{ - 13}}}}{{{f^{0.95}}}}$ $\displaystyle\frac{{{\rm{3}}.{\rm{32}} \times {{10}^{ - 1{\rm{2}}}}}}{{{f^{{\rm{1}}.{\rm{09}}}}}}$ $\displaystyle\frac{{{\rm{5}}.{\rm{04}} \times {{10}^{ - 1{\rm{1}}}}}}{{{f^{{\rm{1}}.{\rm{09}}}}}}$ g-r噪声 $\displaystyle\frac{{{\rm{4}}.{\rm{07}} \times {\rm{1}}{{\rm{0}}^{ - {\rm{19}}}}}}{{{\rm{1}} + (\frac{f}{{14000}}{)^{1.84}}}}$ $\displaystyle\frac{{7.38 \times {\rm{1}}{{\rm{0}}^{ - {\rm{18}}}}}}{{{\rm{1}} + (\frac{f}{{990{\rm{0}}}}{)^{1.96}}}}$ $\displaystyle\frac{{1.32 \times {\rm{1}}{{\rm{0}}^{ - {\rm{17}}}}}}{{{\rm{1}} + (\frac{f}{{1560}}{)^{2.02}}}}$ 低频噪声起源 1/f + g-r噪声 1/f + g-r噪声 1/f + g-r噪声 1/f 噪声 1/f 噪声 1/f 噪声
表1 根据(4 )式提取出的低频噪声参数Table1. Extraction results of low-frequency noise using Eq. (4 ).表1 可以看出, 随着电流的不断增大, 样品中白噪声的幅值($A = 4{K_{\rm{B}}}TR$ )变化很小, 这表明整个测试系统的温度和样品的电阻保持稳定, 背景噪声的影响较小. 而1/f 噪声的幅值A 随着电流的增大而增大; 闪烁噪声的指数因子γ 随测试电流的增大而逐渐从0.65逐渐增大到0.83, 0.90, 0.95和1.09, 说明在大电流注入下, 样品中的低频噪声行为逐渐成为1/f 噪声. 当电流从0.1 mA逐渐增大到27 mA时, 低频Lorentzian噪声的成分逐渐演进为g-r噪声(Lorentzian噪声的频率指数因子从1.84变化到2.02), 且只有一个特征频率, 表明LED中的g-r噪声源自于禁带中的一个缺陷能级. 对于极性MQW结构LED而言, 在外加正向偏置电压时, 能带结构会发生倾斜, 对于费米能级的位置也将发生改变, 从而使杂质能级与费米能级交叉点的位置发生变化. 因此, g-r噪声的特征频率发生了改变, g-r噪声的幅值逐渐从$1.32 \times {\rm{1}}{{\rm{0}}^{ - {\rm{19}}}}$ 增大到${\rm{4}}.{\rm{07}} \times {\rm{1}}{{\rm{0}}^{ - {\rm{17}}}}$ . 从表1 还可以看到, 对g-r噪声而言, 随着注入电流的逐渐增大, 特征频率变得越来越低, 这意味着g-r噪声的时间常数越来越大; 反之, 当杂质能级越靠近能带中间时, 由于杂质能级近似等于E i , 即相当于本征状态n 0 = p 0 = n i , 故f 0 越小[21 -23 ] .表1 的提取结果, 对1/f 噪声和g-r噪声的参数与电流之间的相关性进行分析, 结果如表2 所示.低频噪声类型 测试电流/mA 0.1 10 27 50 80 180 1/f 噪声幅值 $B = {I^{3.834}}$ $B = {I^{7.370}}$ $B = {I^{8.285}}$ $B = {I^{_{^{^{_{9.436}}}}}}$ $B = {I^{_{^{10.4647}}}}$ $B = {I^{13.8273}}$ g-r噪声幅值 $C = {I^{^{_{4.0980}}}}$ $C = {I^{8.5660}}$ $C = I{}^{12.0212}$ g-r噪声时间常数 $\tau = {I^{0.9978}}$ $\tau = {I^{_{2.3969}}}$ $\tau = {I^{3.1520}}$
表2 低频1/f 噪声和g-r噪声参数与电流之间的指数关系Table2. Exponent relationships between parameters of 1/f noise and g-r noise and measured currents.表2 可以看出, 随着电流的逐渐增大, 1/f 噪声和g-r噪声的幅值B 与电流I 之间的相关性越来越大, 这与图5 及文献中的结论是一致的. 图7 对测试LED的电流噪声PSD涨落SI /I 2 与电流I 之间的相关性进行了分析. 从整个测试电流的范围来看, SI /I 2 与电流I 之间呈二次函数的关系, 但是在高电流范围内(电流大于10 mA时), 两者之间具有良好的线性关系, 这与文献[23 , 24 ]中的结论是一致的. 即在低电流阶段, LED中的低频噪声主要来自于g-r噪声, 随着电流的增大, 1/f 噪声逐渐成为低频噪声中的主要起源.图 7 电流噪声PSD涨落SI /I 2 与电流I 之间的关系演变Figure7. Fluctuation evolution relationships of current PSD SI /I 2 and current I .4.结 论 本文对LED的电流噪声进行了测试, 电流范围为0.1—180 mA. 根据电流噪声的特点, 结合LED中载流子的产生-复合机制, 通过对低频电流噪声PSD的拟合, 探讨了高电流注入下LED的载流子产生与复合机制. 结果表明, 随着电流从0.1 mA逐渐增大到27 mA, LED中的电流噪声具有低频g-r噪声的特性; 当电流逐渐增大到50 mA时, 电流噪声的行为开始接近于低频1/f 噪声. 根据载流子的复合机制, 结合LED中低频噪声的结电流模型, 从理论上分析了LED在高电流注入时的转折频率的变化规律. 本文的结果提供了一种表征InGaN/GaN MQW LED发光机制转变的有效手段, 为提高其发光量子效率提供理论依据. 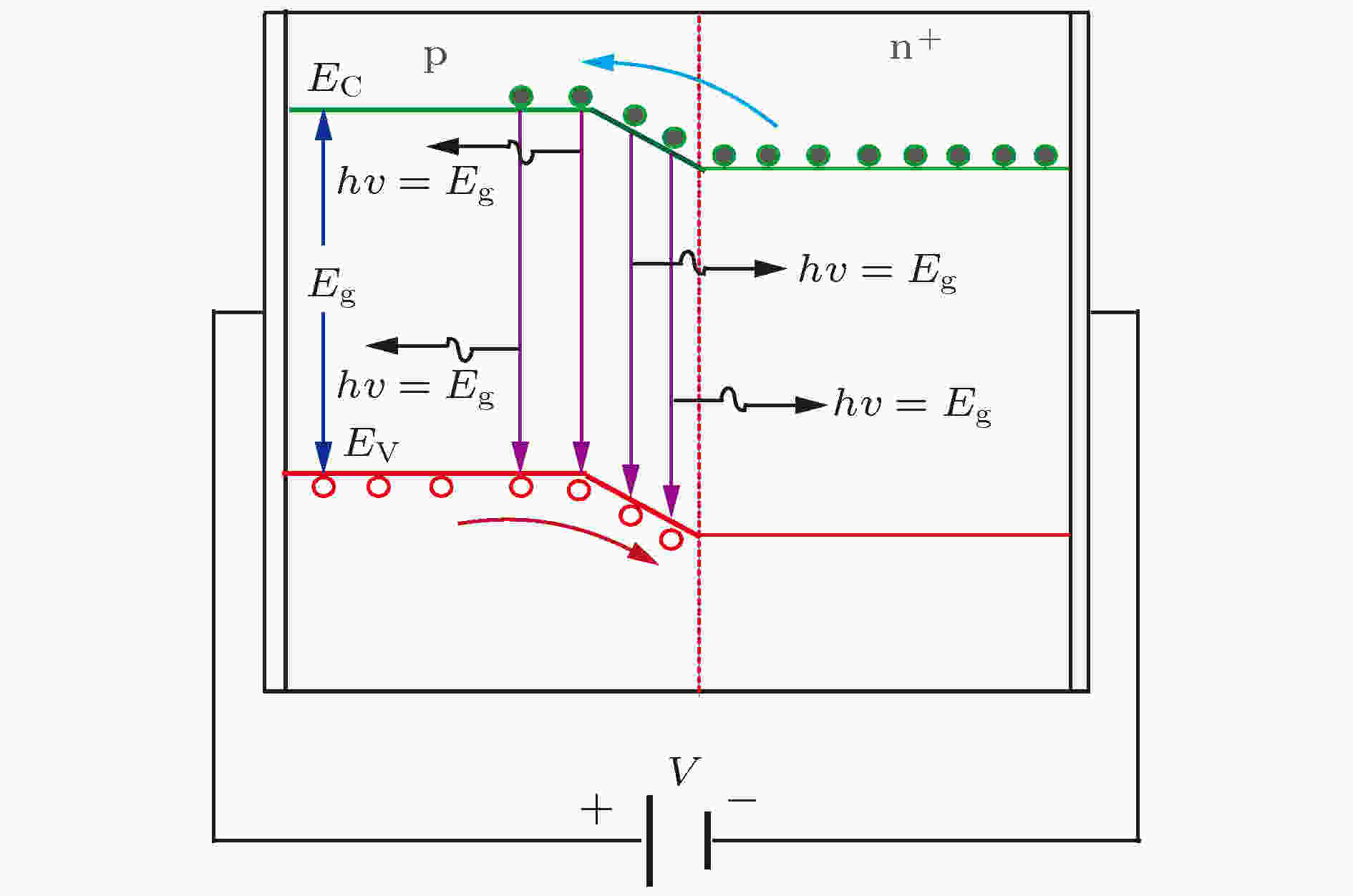 图 1 p-n结型LED发光原理图
图 1 p-n结型LED发光原理图
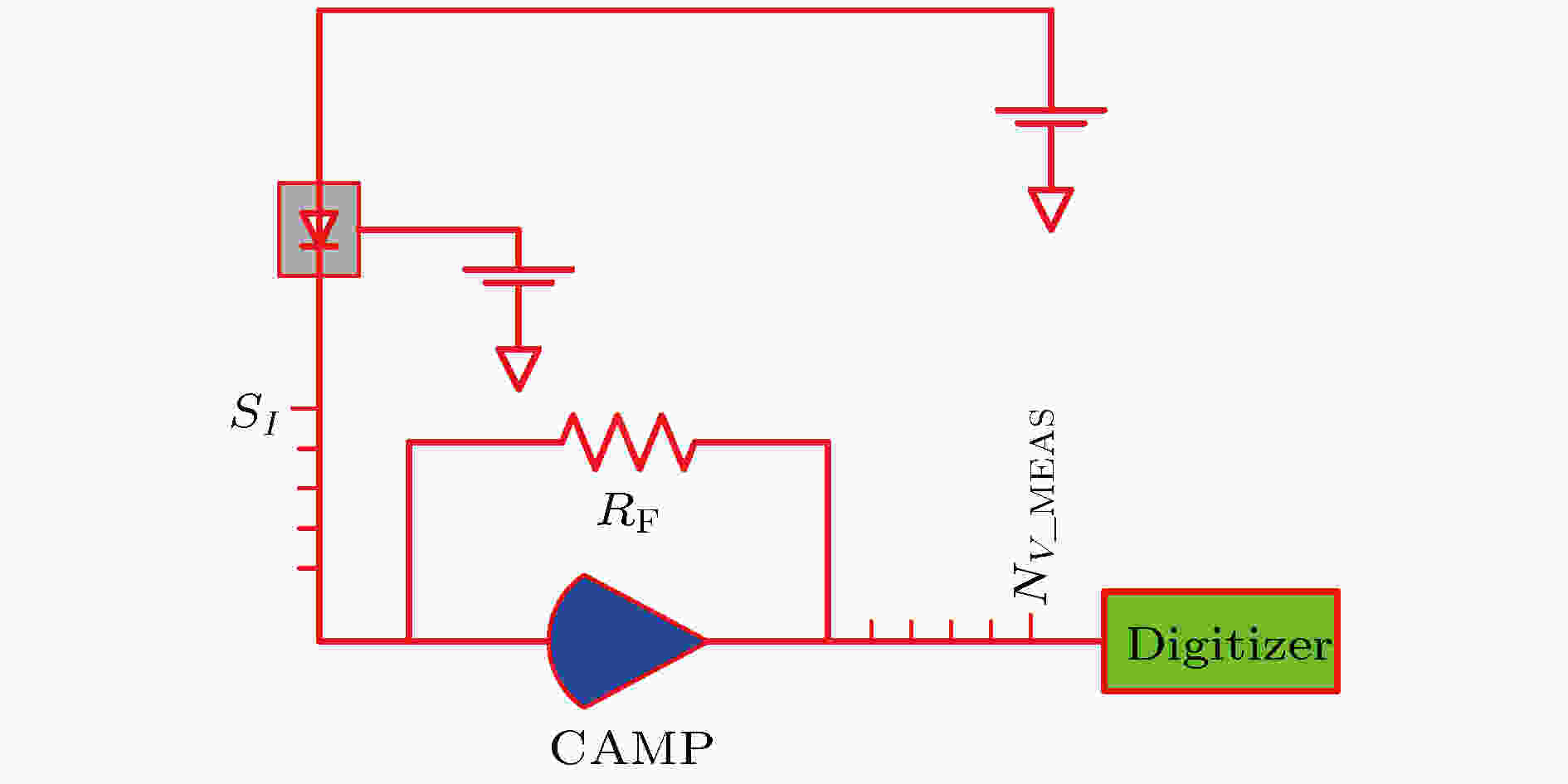 图 2 LED低频噪声测试原理图
图 2 LED低频噪声测试原理图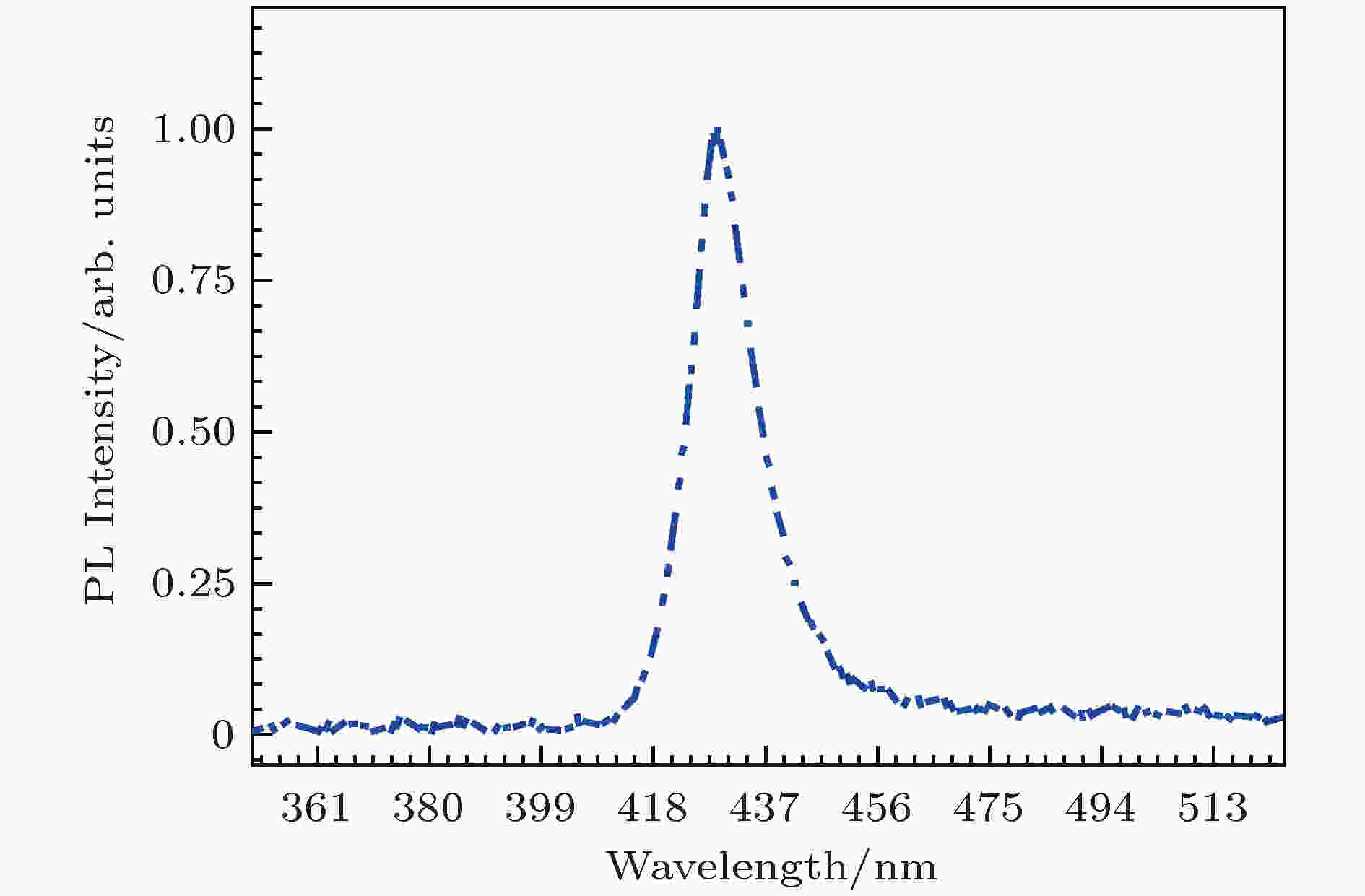 图 3 LED室温PL测试
图 3 LED室温PL测试
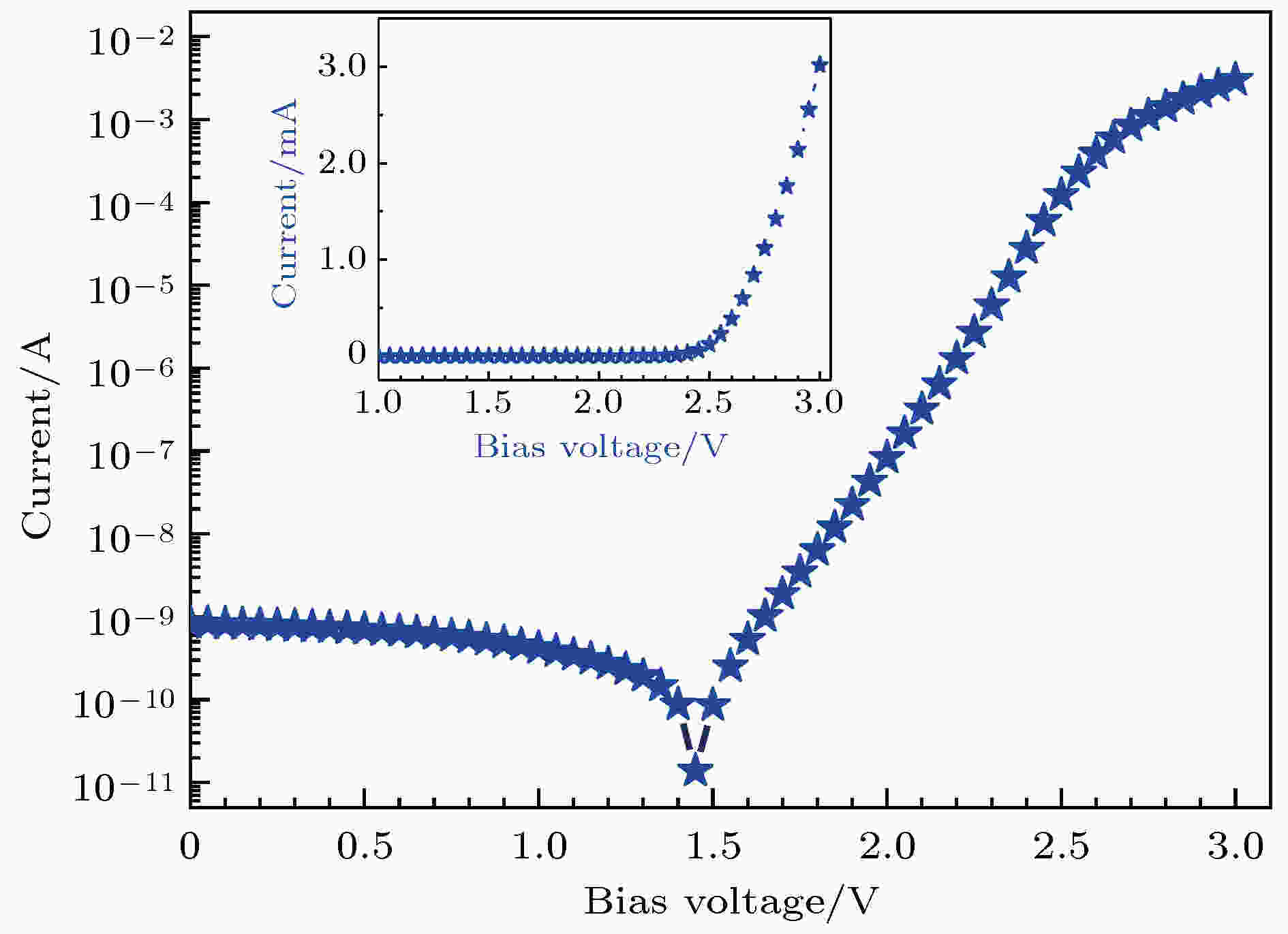 图 4 LED的V-I特性测试曲线
图 4 LED的V-I特性测试曲线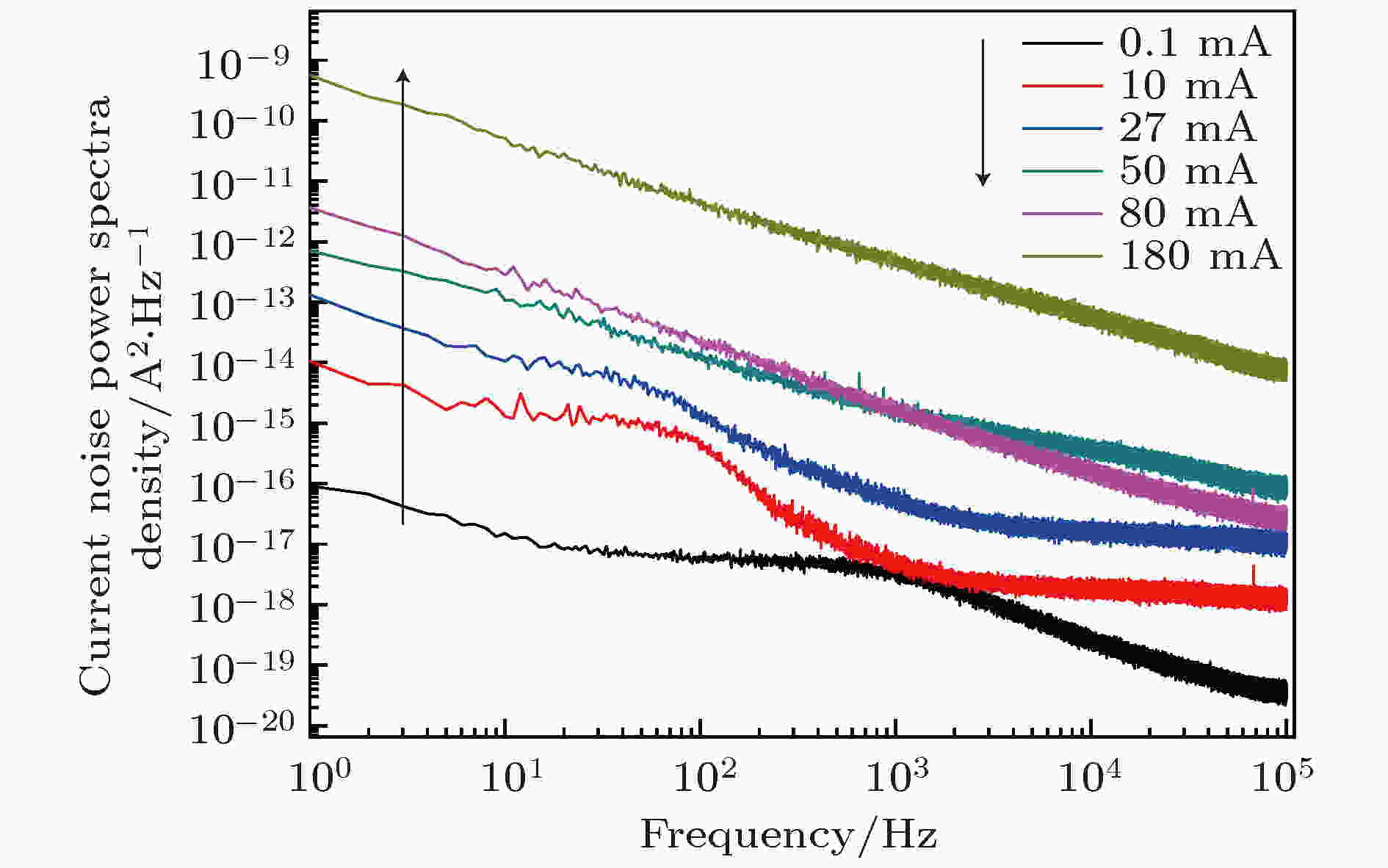 图 5 InGaN/GaN LED的电流噪声PSD与频率的关系图
图 5 InGaN/GaN LED的电流噪声PSD与频率的关系图

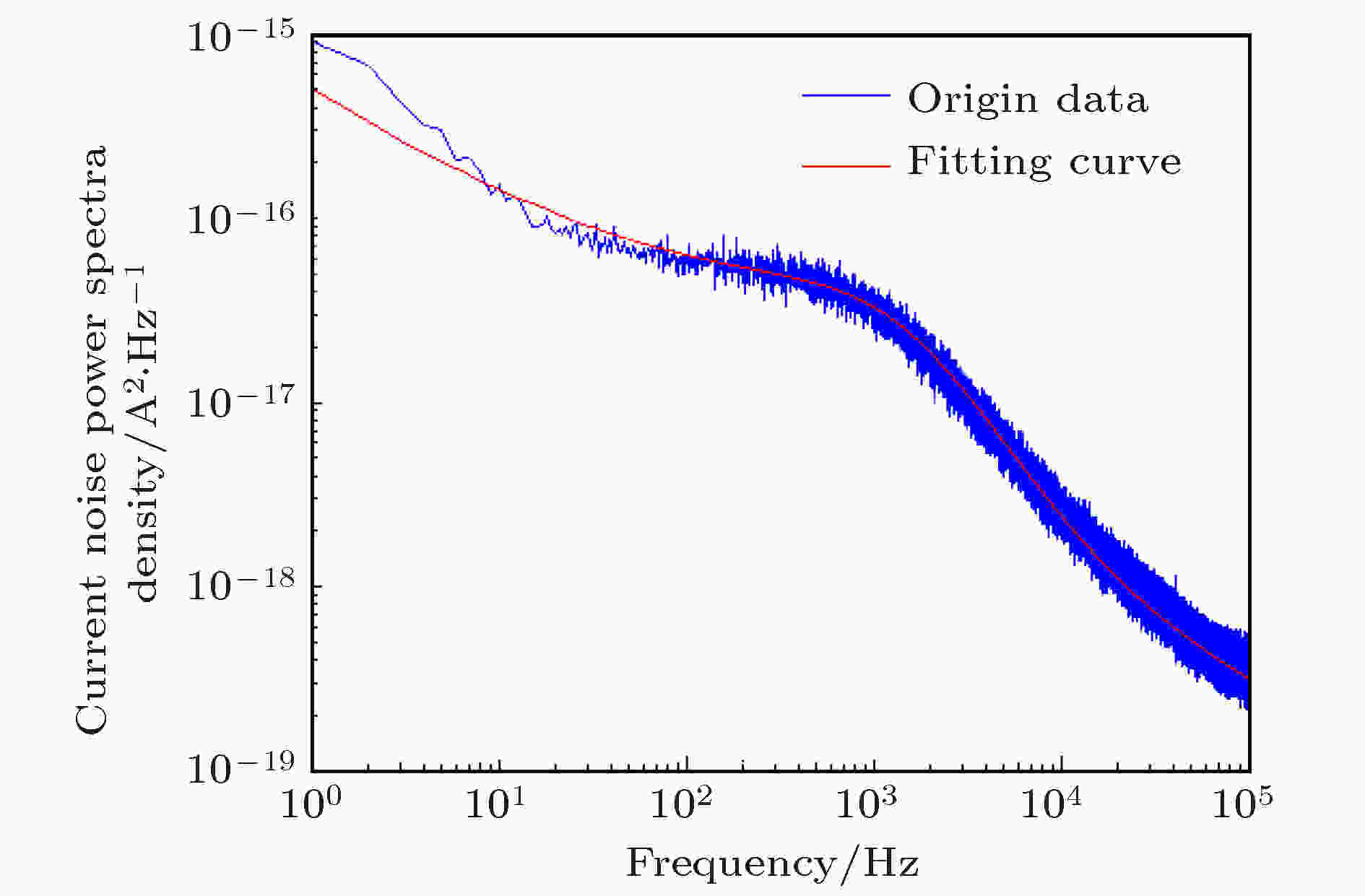 图 6 根据(5)式拟合g-r噪声参数
图 6 根据(5)式拟合g-r噪声参数


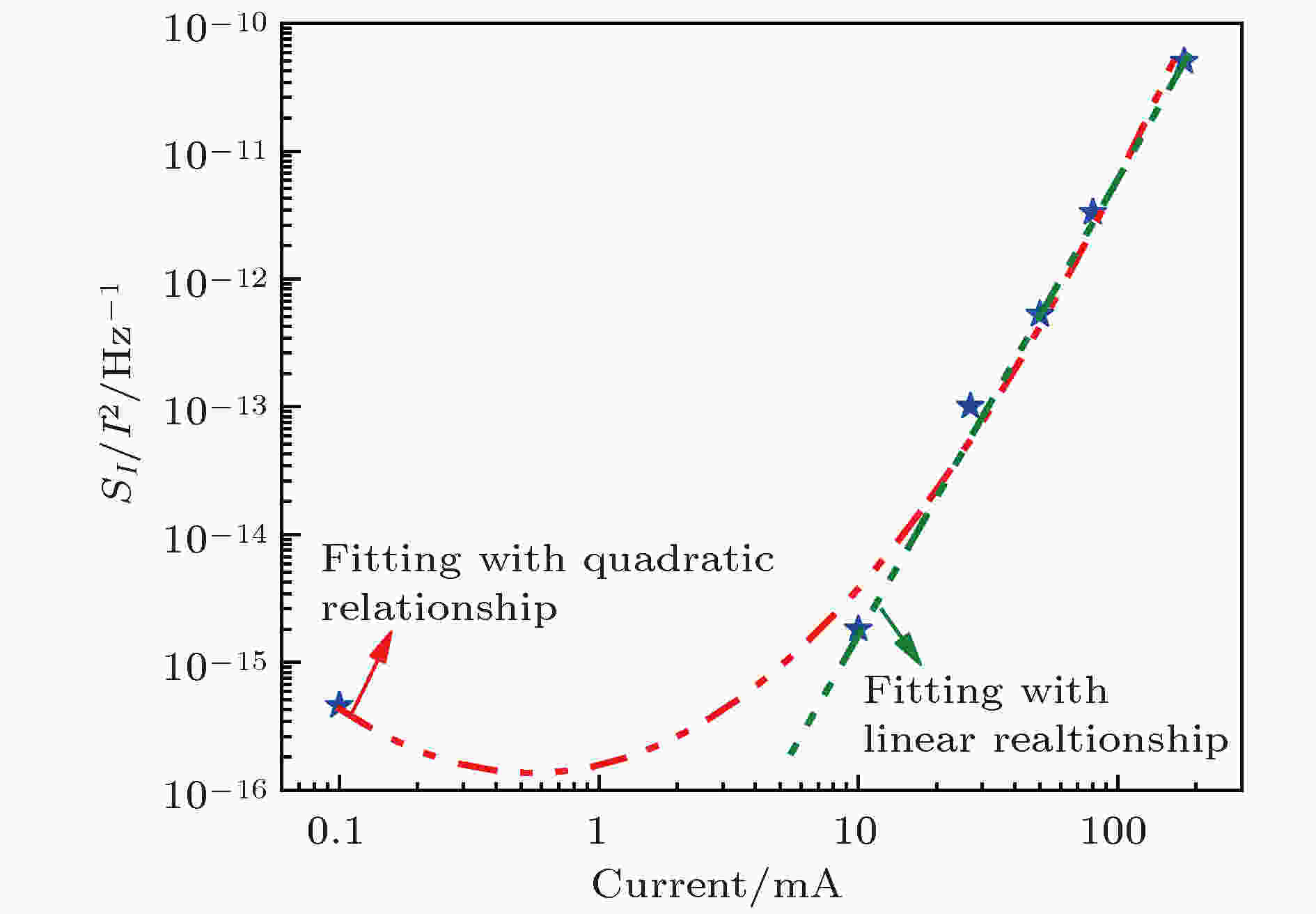 图 7 电流噪声PSD涨落SI/I2与电流I之间的关系演变
图 7 电流噪声PSD涨落SI/I2与电流I之间的关系演变