摘要:采用第一性原理计算方法, 研究了二维单层硒化锗(GeSe)的5种同分异构体结构的稳定性和在应力调控下的电子性质变化规律. 计算结果表明: 5种同分异构体结构都具有热力学稳定性; α-GeSe是直接带隙半导体, β-GeSe, γ-GeSe, δ-GeSe和ε-GeSe都是间接带隙半导体. α-GeSe在应力调控下出现了直接到间接带隙的转变和半导体到金属性质的转变. β-GeSe和γ-GeSe在应力的作用下具有可调节的间接带隙范围. 当沿δ-GeSe双轴方向施加压缩应力为1%和4%时, δ-GeSe的能带从间接带隙转变成直接带隙. 通过沿ε-GeSe的扶手椅形方向施加10%的拉伸应变, 出现了从间接带隙到直接带隙的转变; 继续增加拉伸应变到20%, 能带结构一直保持直接带隙的特征, 其可调范围为1.21—1.44 eV. 沿δ-GeSe双轴方向施加10%拉伸应变时, 也出现了从间接带隙到直接带隙的转变; 该直接带隙在双轴拉伸应变增加到19%前一直保持, 可调范围为0.61—1.19 eV.
关键词: 第一性原理/
单层GeSe/
应变/
电子性质

English Abstract

全文HTML

--> --> -->

单层二维材料由于其独特的电子特性和潜在的光电应用引起了广泛关注^[1-4], 例如石墨烯、二硫化钼(MoS₂)、六方氮化硼(h-BN)以及磷烯等^[1,5-7]. 在这些二维材料中, 由于石墨烯缺乏带隙、h-BN带隙过大等因素, 使它们不能完全满足半导体器件应用^[6-8]. 而MoS₂因为其自身的夹层结构大大降低了电子迁移率^[9-11]. 黑磷作为一种具有直接带隙为1.0 eV的半导体, 其在半导体电子材料领域的应用倍受关注^[12-15], 但是单层黑磷在室温下容易与空气发生反应^[16]. 因此, 寻找具有室温稳定性和良好性能的类石墨烯材料非常重要.
近年来, 已经有大量关于类黑磷翘曲二维化合物的报道, 例如单层二维材料GeX和SnX (X = S, Se, Te). 理论研究表明, IV族单层的卤化物具有优异的压电性能, 在纳米和光电子学方面具有应用前景^[17-20]. 其中, 单层二维材料GeSe与磷烯的几何构型相似, 因具有抗氧化性^[21,22], 因此在空气中比磷烯更稳定, 逐步成为了研究热点^[23-27]. 单层GeSe是单硫族化合物中具有最大直接带隙的半导体^[28]. 硫族化合物在地球上的储量丰富, 且具有环保、低毒等特征. 在探测器、能量转换装置、触摸传感器等方面有许多应用^[29]. 单层二维材料GeSe共有5种同素异形体结构, 包括α-GeSe, β-GeSe, γ-GeSe, δ-GeSe和ε-GeSe^[30]. 当前实验已成功制备出了α-GeSe和γ-GeSe, 它们可作为光学器件的候选材料^[31,32]. 相关理论研究表明, 单层α-GeSe在这5种同素异形体结构中是直接带隙半导体, 其他4种结构是间接带隙半导体材料^[30,33]. 先前的第一性原理计算指出, 双层α-GeSe的带隙可以通过应变来调控^[34]. 有关理论研究也预测了点缺陷工程可以提高有毒气体分子在α-GeSe单层表面的吸附能力^[35]. 对于单层β-GeSe点缺陷的研究表明, 空位和磷原子的取代可以有效地减小其带隙并增加其磁矩^[36]. 已有理论研究发现应变能调节二维单层α-GeSe和γ-GeSe的电子特性^[30,37-40], 证实了应变是调控GeSe二维材料能带结构的直接有效方法. 然而到目前为止仍然没有相关GeSe 5种同素异形体结构在应力调控下的系统研究, 进一步研究应变对GeSe 5种同素异形体光电性质的影响非常必要.
本文系统研究了单层GeSe 5种同分异构体结构的电子性质. 通过施加外部平面应力, 发现单层GeSe在应力的调控下表现出很敏感的电子和光学性质.

为了获得单层GeSe的5种同素异形体的平衡结构、稳定性和应变调控下能带结构的变化, 我们使用VASP(Vienna ab initio simulation package)软件包^[41,42], 采用了基于密度泛函理论(DFT)^[43,44]的第一性原理平面波计算方法. 计算中的交换关联能使用了广义梯度近似(GGA)的Perdew-Wang交换关联泛函(PW91)^[44-46]. 为了克服半局域交换相关函数带隙不足的问题, PW91和HSE06泛函分别被用于研究能带结构^[47]. 在结构弛豫和总能量的计算中, 平面波的截断能量为500 eV. 5种结构的几何优化和自洽计算分别使用9 × 9 × 1和13 × 13 × 1的Monkhorst-Pack^[48]K点网格进行采样. Z轴方向使用20 ? (1 ? = 0.1 nm)的真空层以避免相邻层超胞之间的相互作用. 在结构优化过程中, 所有原子上力的收敛设定不超过0.01 eV/?. 自洽场(SCF)计算中使用的总能量收敛标准为10^–6 eV. 同时计算了吸收系数和振动频率, 振动频率的计算位移设定在正负两个方向上都移动. 结合能的计算公式^[49]定义为

${E_{\rm{b}}} = \left( {{E_{{\rm{GeSe}}}} - n{E_{Ge}} - \left( {N - n} \right){E_{{\rm{Se}}}}} \right)/N,$

其中E_Ge, E_Se和E_GeSe分别是Ge原子、Se原子和GeSe单层的总能量; N是总原子数; n是Ge原子的数量; N–n是Se原子的数量.

单层GeSe 5种同分异构体优化的几何结构如图1所示. 弛豫后得到的晶格常数和结合能的绝对值如表1中所示. 通过对比它们的结合能, 可以得出这5种同分异构体结合能的最大差值不超过0.06 eV/atom. 为了进一步阐明结构热力学的稳定性, 模拟单层GeSe的5种同分异构体结构的振动频率, 获得的振动频率表明, α-GeSe, β-GeSe, γ-GeSe, δ-GeSe和ε-GeSe的虚拟频率占据零点能的比率很小, 分别为0.05%, 0.04%, 0.05%, 0.05%和0.03%, 如表2所示. 这一结果也进一步证明它们的结构具有热力学稳定性. 对于α-GeSe, β-GeSe, γ-GeSe, δ-GeSe和ε-GeSe, 使用PW91函数计算的能隙为1.14, 2.30, 1.77, 1.58 eV和1.78 eV; 使用HSE06杂化泛函方法计算的相应能隙为1.66, 3.04, 2.52, 2.24 eV和2.50 eV; 模拟结果与之前相关文献的报道^[31]非常吻合.

	α-GeSe	β-GeSe	γ-GeSe	δ-GeSe	ε-GeSe
E0	73.88	39.55	77.92	151.22	179.68
Ef/i/meV	0.037	0.016	0.041	0.077	0.664
Ef/i/E0	0.05%	0.04%	0.05%	0.05%	0.03%

表25种GeSe同分异构体结构的振动频率计算结果 (E₀代表零点能, E_f/i代表虚拟频率, E_f/i/E₀为虚拟频率占据零点能的比例)
Table2.Calculated results of vibration frequencies of five isomers of GeSe (E₀ represents zero energy, E_f/i represents virtual frequency, E_f/i/E₀ denotes virtual frequency occupies the proportion of zero energy).

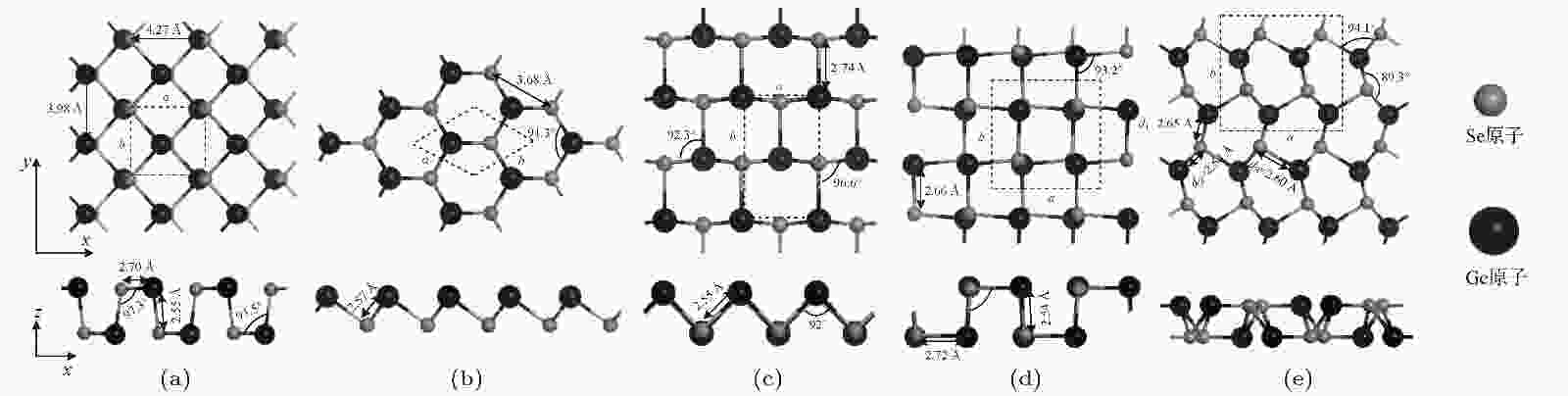图 1 单层GeSe的5种同分异构弛豫后结构的俯视图和侧视图(图中a和b表示晶格常数)　(a) α-GeSe; (b) β-GeSe; (c) γ-GeSe; (d) δ-GeSe; (e) ε-GeSe
Figure1. Top view and side views of relaxed structures of five isomers of GeSe monolayer (in the figures, a and b denote the lattice constants, respectively): (a) α-GeSe; (b) β-GeSe; (c) γ-GeSe; (d) δ-GeSe; (e) ε-GeSe.

	α-GeSe	β-GeSe	γ-GeSe	δ-GeSe	ε-GeSe
a/?	4.27	3.68	3.67	5.80	6.85
b/?	3.98	3.68	5.89	5.84	6.43
h/?	2.52	1.45	1.76	2.52	1.72
|Eb|/eV·atom–1	4.14	4.12	4.11	4.13	4.08
Eg/eV	1.14	2.30	1.77	1.58	1.78

表1弛豫后单层GeSe 5种同分异构体的结构参数 ( a和b分别是晶格常数, h为GeSe的翘曲高度, E_b是相对于单个原子之间的结合能, E_g为基本带隙)
Table1.Relaxed structural parameters of five isomers of GeSe monolayer (a and b are the lattice constants, respectively. h is the buckling height of GeSe; E_b is the bind energy per atom; E_g is the fundamental band gap).

单层GeSe 5种同素异形体结构的吸收系数如图2所示. 可以发现, 这5种同素异形体在不同能量下具有多个吸收峰. 其中, α-GeSe和δ-GeSe在室温下对可见光具有较强的吸收强度, 最高的吸收峰在6 eV附近; 而ε-GeSe的吸收峰最高. α-GeSe和ε-GeSe相比其他3种结构的谱线的峰值比较平滑, 同时谱线较宽, 这也表明两个结构的能级均匀分布. 先前的研究普遍认为α-GeSe是直接带隙半导体, 而其他4种同素异形体是间接带隙半导体^[30]_. 然而, 间接带隙半导体中的电子吸收光子从价带顶跃迁到导带底需要声子参与, 此过程是通过与声子交换动量来实现的, 这将极大地限制跃迁并降低跃迁的转化率^[50]. 为了更好地探究能带调控规律, 我们探索了单层GeSe 5种同素异形体在应力调控下的能带结构变化.
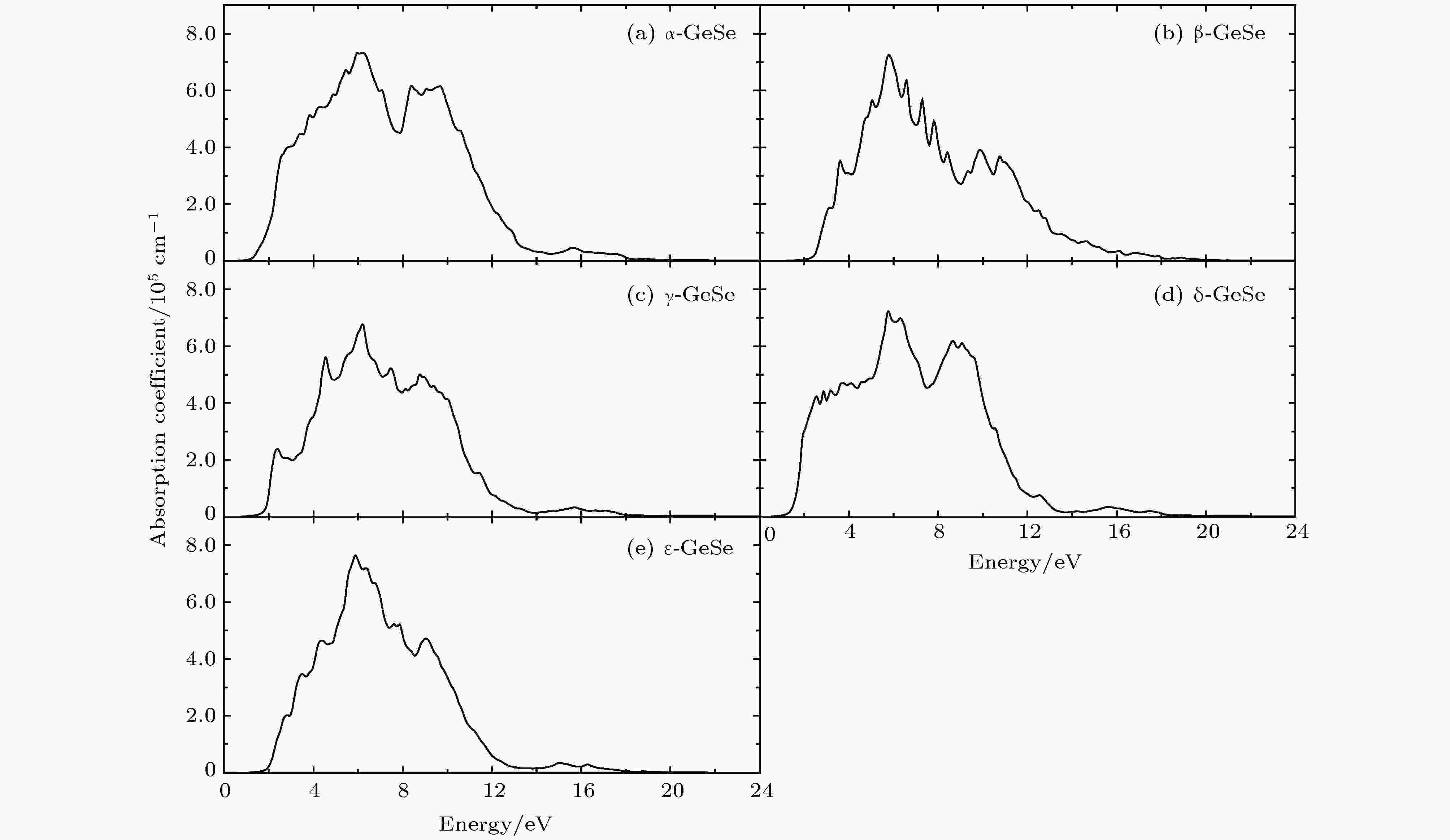图 2 5种GeSe单层同分异构体的吸收系数
Figure2. Absorption coefficients for five isomers in GeSe monolayer.

我们计算了单层GeSe 5种同素异形体结构的能带, 以及在单轴和双轴应变下的能带变化规律. 单轴方向包括扶手椅形和锯齿形两个方向. 基于单轴和双轴方向的应变, 使用拉伸和压缩应变来调节带隙, 以实现优异的电子性质和潜在的光学性质. 单轴应变计算中, 固定一个方向(扶手椅形或者锯齿形方向), 并在另外两个方向上弛豫了结构. 当应用双轴应变时, 固定扶手椅形和锯齿形在真空层的方向上进行驰豫计算. 这5种同素异形体中, 已经有研究报道了α-GeSe和γ-GeSe在应变下的能带结构变化^[37-40]. 为了验证计算的准确性, 通过计算得到了不同应变下这两种结构的能带, 结果表明与报道的文献基本一致^[25]. 图3显示了在单轴和双轴应变下5种同素异形体结构的能带变化. 如图3(a)所示, 对α-GeSe施加–10%到10%的应变时, 带隙出现了从直接到间接、从半导体到金属性的转变, 具体能带结构的变化展示在附录材料图A1中. 从图3(b)可以看出, 当β-GeSe施加0—10%的单轴或双轴拉伸应变时, 带隙减小. 锯齿形方向施加0—1%的压缩应变时, 带隙略微增加; 当应变从1%增加到10%时, 带隙从2.33 eV减小到1.35 eV. 当在扶手椅型和双轴方向上从0增加到施加10%的压缩应变时, 带隙从2.30 eV减小到0.67 eV. 如图3(c)所示, 应变调控下γ-GeSe的带隙变化趋势与β-GeSe相似. γ-GeSe的带隙从1.78 eV变化到0.3 eV, 应变区域内没有出现半导体到金属或间接到直接的带隙转化. δ-GeSe在施加沿扶手椅形和双轴方向应变下带隙变化的趋势几乎相同. 如图3(d)所示, 当施加双轴压缩应变σ_xy = –2%和σ_xy = –4%时转变为直接带隙, 其值分别为1.29 eV和1.17 eV. 图3(e)表示在不同应变下ε-GeSe带隙的变化. 当沿扶手椅形和双轴方向的拉伸应变分别增加到10%时, ε-GeSe出现了直接带隙. 为了考察更大应变下ε-GeSe能带的调节情况, 继续增加拉伸应变来分析ε-GeSe在应力调节下的能带, 详细分析如下.
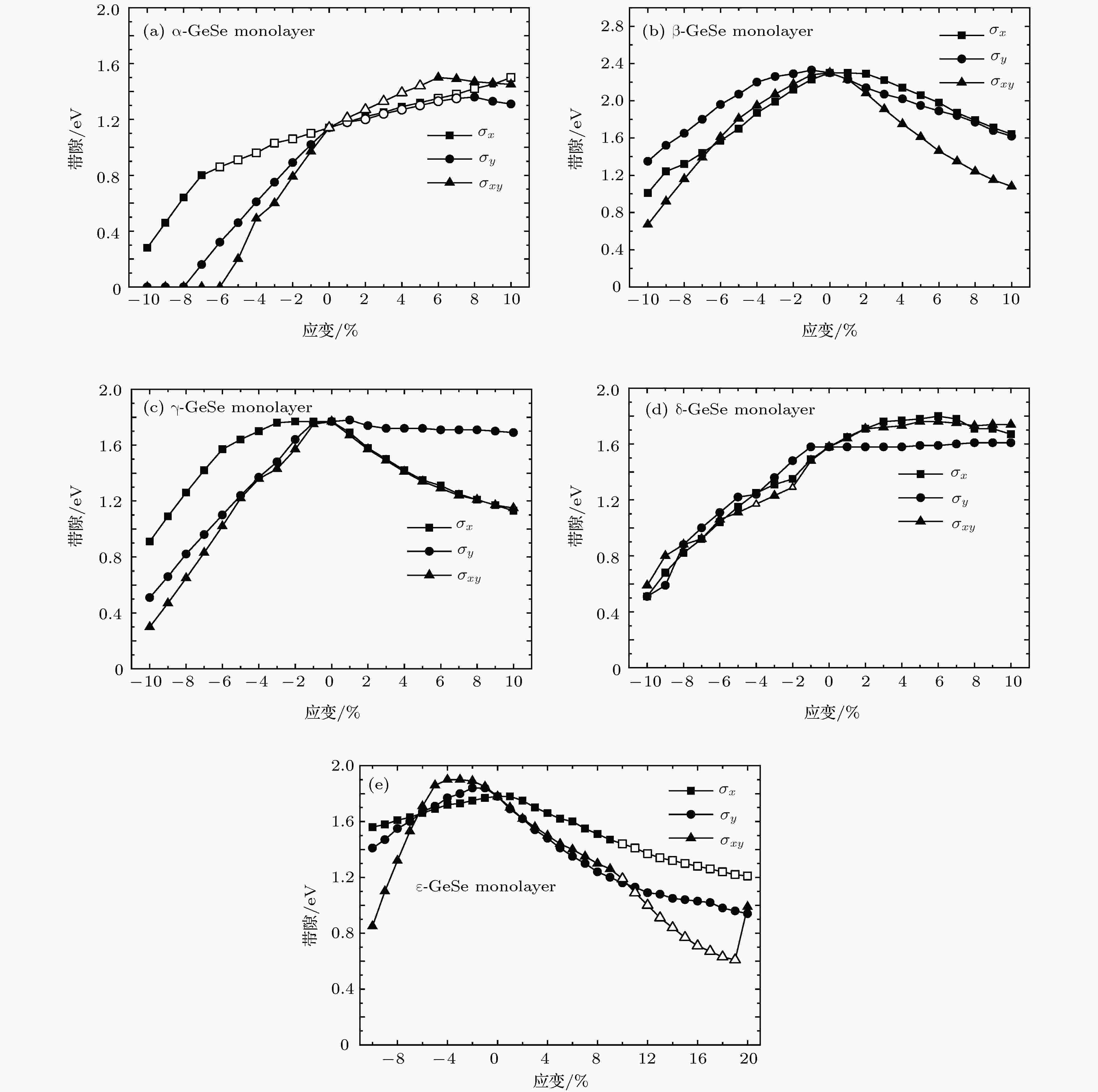图 3 带隙随平面内应变的变化图(方块表示沿扶手椅(σ_x)方向的应变, 圆圈表示沿锯齿形(σ_y)方向的应变, 三角形代表双轴(σ_xy)应变, 实心和空心符号分别表示间接和直接带隙)
Figure3. Variation of band gap along with the applied in-plane strain (The square represents the strain along armchair (σ_x) direction, while the circle represents the strain along zigzag (σ_y) direction, the triangle represents the bi-axial (σ_xy) strain, the solid and hollow symbols denote the indirect and direct band gap, respectively)

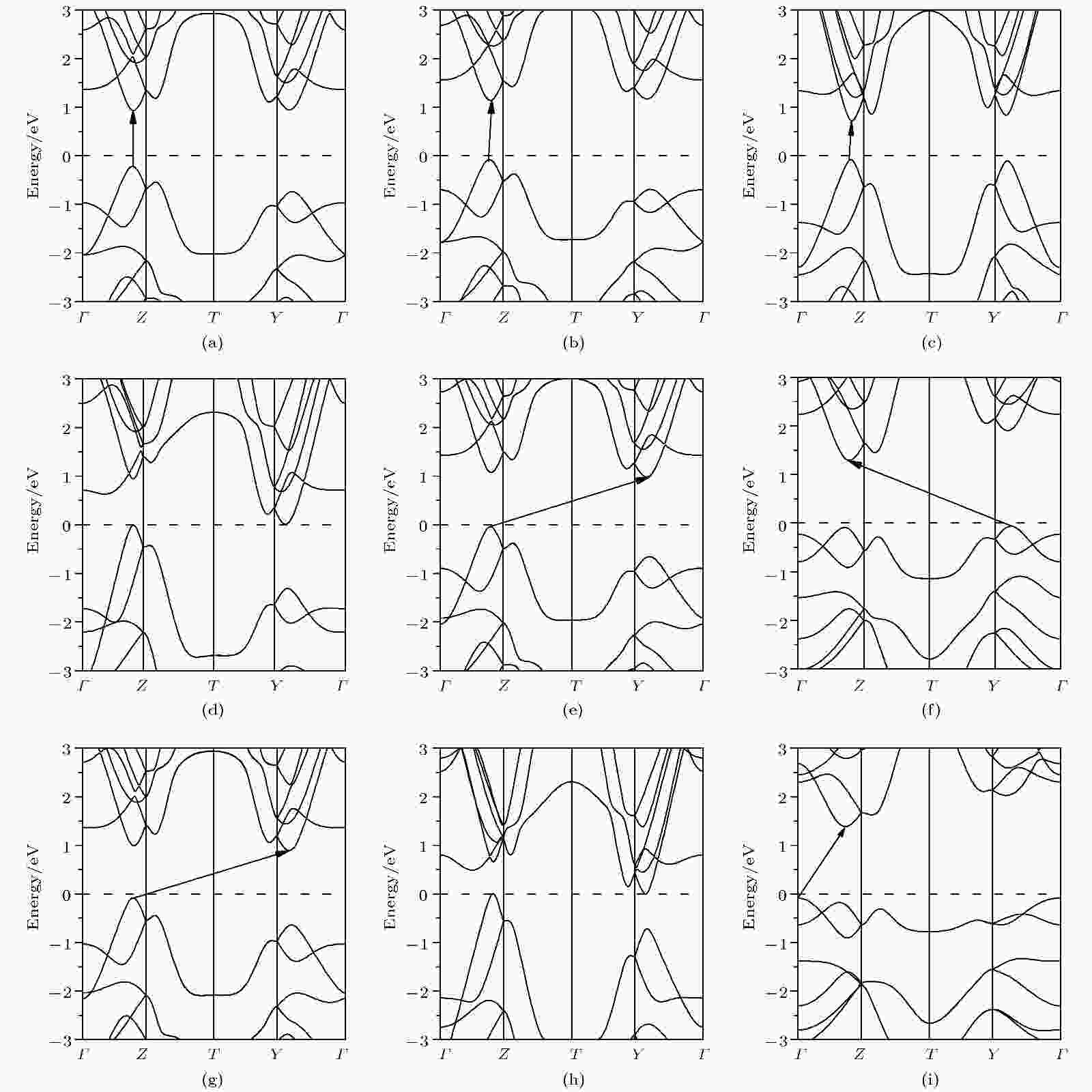图 A1 单层α-GeSe在应变调控下能带结构　(a) σ = 0; (b) σ_x = 2%; (c) σ_x = 7%; (d) σ_y = –8%; (e) σ_y = –1%; (f) σ_y = 8%; (g) σ_xy = –1%; (h) σ_xy = –6%; (i) σ_xy = 8%
FigureA1. Band structures of α-GeSe monolayer under applied strains: (a) σ = 0; (b) σ_x = 2%; (c) σ_x = 7%; (d) σ_y = –8%; (e) σ_y = –1%; (f) σ_y = 8%; (g) σ_xy = –1%; (h) σ_xy = –6%; (i) σ_xy = 8%.

图3(e)中的方块表示单层ε-GeSe沿着扶手椅形方向施加从–10%到20%的应变下带隙的变化. 当施加从0到10%的压缩应变时, 带隙呈现出从1.78 eV到1.56 eV的微小下降. 当施加0—9%的拉伸应变时, 带隙从1.78 eV略微降低至1.47 eV. 随着拉伸应变增加到10%, 带隙出现了从间接到直接的转变; 并且从10%到20%的拉伸应变下单层ε-GeSe保持直接带隙的特征, 直接带隙的范围从1.44 eV减小到1.21 eV. 图4(b)和图4(c)展示了扶手椅形方向上施加应变的部分能带图. 能带分析表明, 在没有应变的情况下, 如图4(a)所示, 导带最小值(CBM)和价带最大值(VBM)的位置分别位于Γ-Z路径上和Γ点. 随着拉伸应变改变了结构参数, CBM的位置在10%应变下从Γ-Z路径变为Γ点, 此时VBM保持在Γ点, 这导致了能带结构从间接到直接半导体的转变. 继续增加从10%到20%的拉伸应变, CBM和VBM的位置保持不变, 直接带隙随应变的增加而减小. 表3列出了ε-GeSe单层在扶手椅形方向上施加拉伸应变后的结构参数, 通过分析可知原子结构的距离d₂的增加和θ (Ge-Se-Ge)的增加可能导致能量的变化, 从而使能带出现从间接到直接半导体的转化, 并且沿扶手椅形方向施加应变带隙的变化都是线性的.
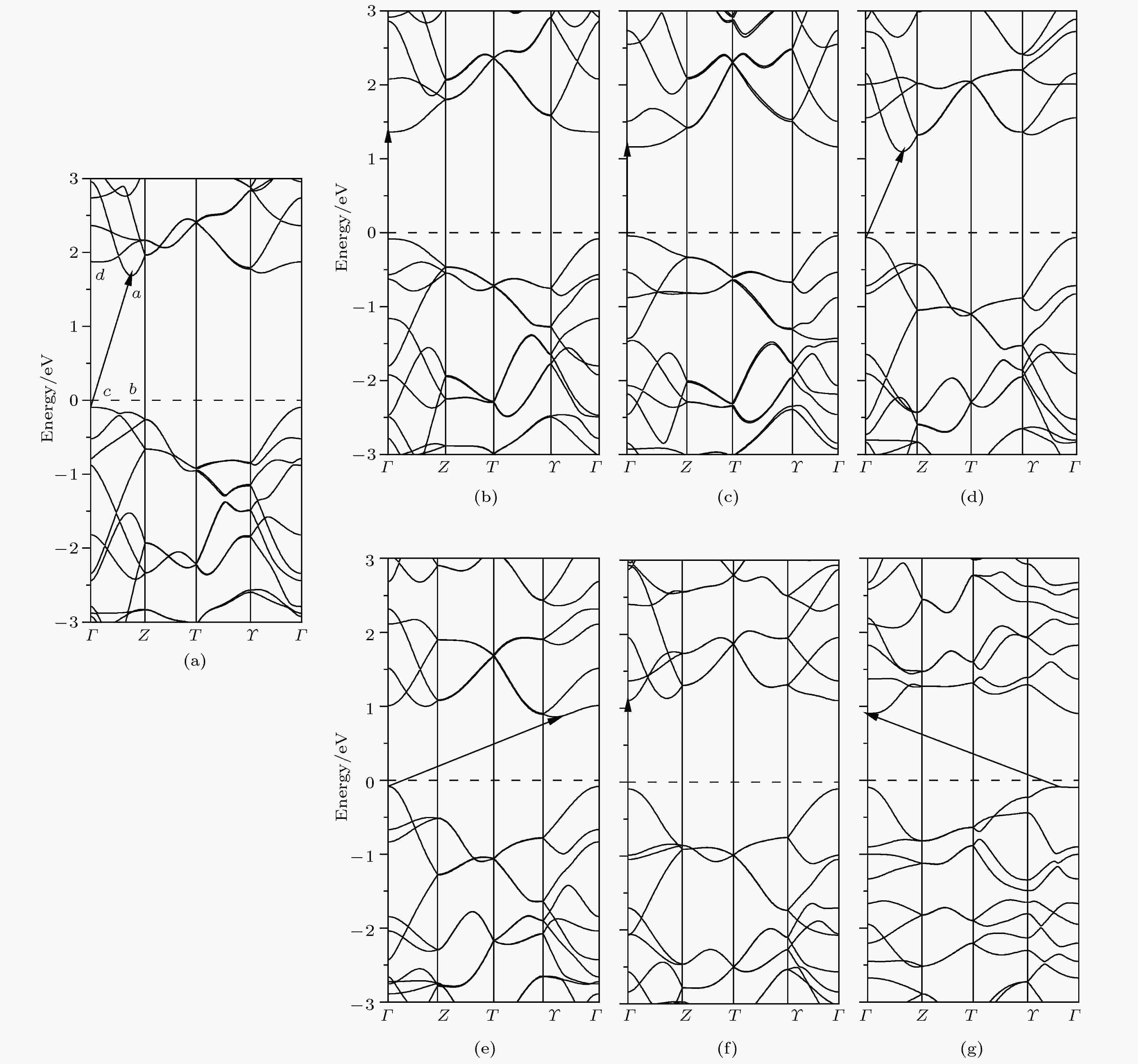图 4 应变调控下ε-GeSe单层的能带结构 (σ_x, σ_y和σ_xy分别表示沿扶手椅形、锯齿形和双轴方向的应变箭头表示导带最小值 (CBM)指向价带最大值 (VBM)的方向)　(a) σ = 0 (图中a表示ε-GeSe的导带最小值, b表示与a相同路径点的价带点, c是ε-GeSe的价带最大值, d是与c的相同路径点的导带点); (b) σ_x = 10%; (c) σ_x = 20%; (d) σ_y = 10%; (e) σ_y = 20%; (f) σ_xy = 10%; (g) σ_xy = 20%
Figure4. Band structures of ε-GeSe monolayer under applied strains (σ_x, σ_y, σ_xy represent the strains along the armchair, zigzag and biaxial directions, respectively. The arrow represents the direction from the conduction band minimum (CBM) to the valence band maximum (VBM)): (a) σ = 0 (in the figure, a represents the conduction band minimum of ε-GeSe, b represents the valence band point corresponding to the same path point of a, c is the valence band maximum of ε-GeSe, d is the conduction band point corresponding to the same path point of c); (b) σ_x = 10%; (c) σ_x = 20%; (d) σ_y = 10%; (e) σ_y = 20%; (f) σ_xy = 10%; (g) σ_xy = 20%.

Strain/%		d1/?	d2/?	d3/?	θ1	θ2	Eg/eV
	σx	2.68	2.51	2.60	85.6	86.7	1.56 (ind.)
–10	σy	2.60	2.58	2.56	98.2	85.1	1.41 (ind.)
	σxy	2.60	2.52	2.52	89.6	77.8	0.85 (ind.)
	σx	2.67	2.51	2.60	87.4	87.2	1.61 (ind.)
–8	σy	2.61	2.57	2.57	97.1	85.8	1.55 (ind.)
	σxy	2.60	2.52	2.54	90.2	80.3	1.32 (ind.)
	σx	2.67	2.52	2.60	89.1	87.8	1.66 (ind.)
–6	σy	2.61	2.56	2.58	96.3	86.6	1.67 (ind.)
	σxy	2.61	2.52	2.56	90.8	82.8	1.71 (ind.)
	σx	2.66	2.52	2.60	90.9	88.3	1.72 (ind.)
–4	σy	2.62	2.55	2.59	95.5	87.5	1.77 (ind.)
	σxy	2.62	2.53	2.57	91.7	85.5	1.90 (ind.)
	σx	2.65	2.53	2.60	92.4	88.8	1.75 (ind.)
–2	σy	2.63	2.55	2.59	94.8	88.4	1.84 (ind.)
	σxy	2.64	2.53	2.59	92.7	87.4	1.89 (ind.)
0		2.65	2.54	2.60	94.1	89.3	1.78 (ind.)
	σx	2.65	2.55	2.60	95.8	89.7	1.75 (ind.)
2	σy	2.67	2.54	2.60	93.3	90.5	1.62 (ind.)
	σxy	2.67	2.55	2.60	95.8	91.3	1.62 (ind.)
	σx	2.64	2.56	2.60	97.2	90.2	1.66 (ind.)
4	σy	2.69	2.54	2.60	93.2	91.6	1.48 (ind.)
	σxy	2.68	2.56	2.60	98.0	92.6	1.50 (ind.)
	σx	2.63	2.57	2.61	99.0	90.2	1.60 (ind.)
6	σy	2.71	2.54	2.60	92.8	92.8	1.35 (ind.)
	σxy	2.70	2.57	2.60	100.2	93.7	1.40 (ind.)
	σx	2.63	2.59	2.61	100.8	90.4	1.51 (ind.)
8	σy	2.74	2.54	2.60	92.8	94.1	1.24 (ind.)
	σxy	2.71	2.59	2.60	102.6	94.9	1.30 (ind.)
	σx	2.62	2.60	2.61	103.5	89.9	1.44 (dir.)
10	σy	2.77	2.54	2.59	93.0	95.5	1.16 (ind.)
	σxy	2.73	2.60	2.60	105.1	96.1	1.19 (dir.)
	σx	2.62	2.61	2.62	105.5	90.0	1.37 (dir.)
12	σy	2.80	2.54	2.59	92.9	96.8	1.09 (ind.)
	σxy	2.75	2.61	2.59	107.7	97.6	1.00 (dir.)
	σx	2.61	2.62	2.62	108.2	89.4	1.32 (dir.)
14	σy	2.84	2.53	2.58	93.2	98.3	1.05 (ind.)
	σxy	2.77	2.62	2.58	110.3	99.4	0.84 (dir.)
	σx	2.60	2.63	2.63	110.8	89.0	1.28 (dir.)
16	σy	2.87	2.53	2.57	93.4	100.0	1.03 (ind.)
	σxy	2.78	2.64	2.57	112.6	101.7	0.67 (dir.)
	σx	2.60	2.63	2.63	113.1	88.8	1.24 (dir.)
18	σy	2.92	2.52	2.56	93.5	102.0	0.98 (ind.)
	σxy	2.79	2.65	2.55	115.2	103.7	0.63 (dir.)
	σx	2.59	2.64	2.64	115.6	88.3	1.21 (dir.)
20	σy	2.96	2.51	2.54	94.1	103.8	0.94 (ind.)
	σxy	2.72	2.70	2.54	123.7	108.1	0.99 (ind.)

表3ε-GeSe沿扶手椅形(σ_x)、锯齿形(σ_y)和双轴(σ_xy)方向平面应变优化后的几何参数及能隙(负应变表示压缩应变, 正应变表示拉伸应变; d₁, d₂和d₃ (如图1(e)所示)分别表示Ge和Se原子之间的距离, θ₁表示θ (Ge-Se-Ge)的键角, θ₂表示θ (Se-Ge-Se)的键角; E_g (eV)表示对应应变下的带隙, (ind.)表示间接带隙，(dir.)表示直接带隙)
Table3.Summary of the optimized geometric structures and energy gaps for ε-GeSe under in-plane strains along the armchair (σ_x), zigzag (σ_y) and biaxial (σ_xy) directions (Negative values of strain denote compress strains, while positive values denote tensile strains. d₁, d₂ and d₃ (as shown in Fig. 1(e)) represent the distance between Ge and Se atoms, respectively. θ₁ represents the θ (Ge-Se-Ge) bond angle. θ₂ represents the θ (Se-Ge-Se) bond angle. E_g (eV) is the band gap under the corresponding strain，（ind.）is the indirect band gap, (dir.) is the direct band gap)

沿锯齿形方向施加应变后的带隙变化如图3(e)中的圆圈所示. 分析可知, 随着拉伸应变从1%增加到20%, 带隙的变化近似于线性. 对ε-GeSe单层施加从1%到3%的压缩应变时, 带隙从1.78 eV略微增加到1.84 eV. 当压缩应变从4%增加到10%, 带隙从1.77 eV减小到1.41 eV. 部分不同应变下能带结构的变化如图4(d)和图4(e)所示. 在锯齿形方向上施加拉伸或者压缩应变没有出现从间接到直接带隙或从半导体到金属的转变.
图3(e)中的三角形表示在双轴应变下单层ε-GeSe的带隙变化趋势. 施加0—5%的压缩应变时, 带隙从1.78 eV增加到1.90 eV. 当施加从6%到10%的压缩应变时, 带隙从1.71 eV减小到0.85 eV. 从表3分析压缩应变从0到10%诱导能带变化的原因是由于原子之间的键长和θ (Ge-Se-Ge)及θ (Se-Ge-Se)的逐渐减小. 当施加1%至9%的拉伸应变时, 原子d₁和d₂之间的距离随着每增加1%应变增加约0.01 ?, 角度θ (Ge-Se-Ge)和θ (Se-Ge-Se)也呈线性增加. 在此阶段单层ε-GeSe能带结构的导带在Γ点处能量快速减小, 并且CBM和VBM的位置保持不变. 将双轴拉伸应变继续增加到10%, 带隙出现了间接到直接的转变. 当拉伸应变从10%连续增加到19%时, 能带结构保持直接带隙特征. 如果拉伸应变增加到20%, 能带结构变为带隙增加的间接半导体. 从表3中分析可知, 当d₁, d₂, θ (Ge-Se-Ge)和θ (Se-Ge-Se)增加到一定程度时开始导致d₃减小, 带隙出现间接到直接的转换, 并且这些参数都呈现线性变化. 当拉伸应变增加到20%时, 带隙呈现增加并变成间接带隙. 部分不同应变条件下的能带结构如图4(f)和图4(g)所示. 结果表明, 在双轴应变条件下, 单层ε-GeSe在应力的调控下出现了从间接到直接带隙的转换, 直接带隙可调范围为0.63—1.19 eV.
为了进一步说明ε-GeSe单层的能带受应力调控的效应, 分别计算了ε-GeSe单层在扶手椅方向、锯齿形方向和双轴方向下施加20%的拉伸应力下结构的振动频率. 结果表明该结构在20%的拉伸应力下结构具有稳定性, 具体的结构图和振动频率计算结果展示在附录材料的图A2和表A1中.
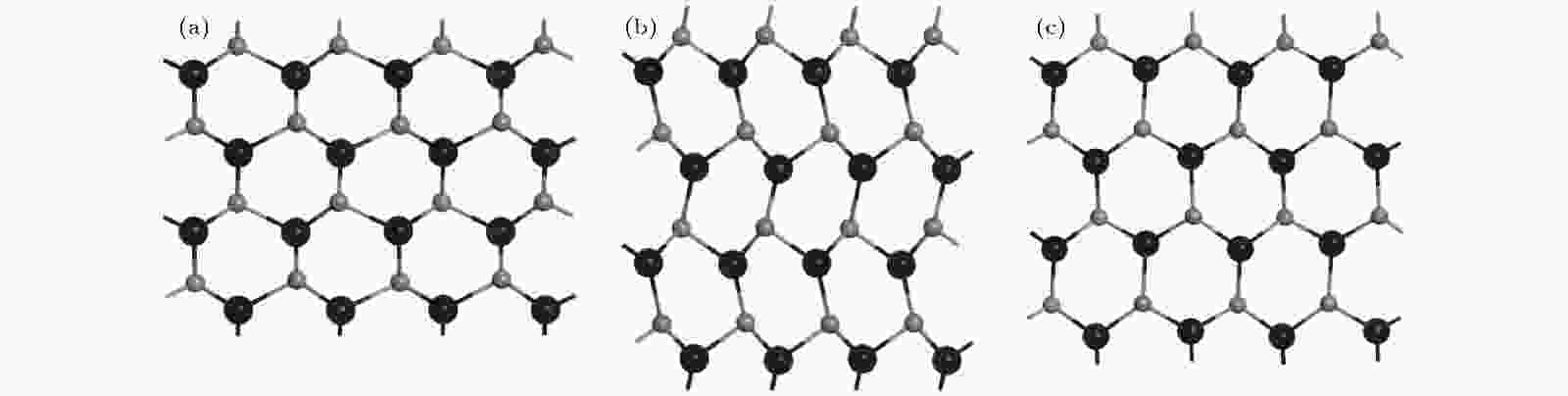图 A2 ε-GeSe单层施加20%拉伸应变下优化后的结构　(a) 扶手椅方向; (b) 锯齿形方向; (c) 双轴方向
FigureA2. Optimized structures of ε-GeSe monolayer under 20% tensile strain, respectively: (a) Armchair direction; (b) zigzag direction; (c) biaxial direction.

	σx = 20%	σy = 20%	σxy = 20%
E0/meV	165.49	156.07	132.56
Ef/i/meV	2.650	0.030	0.005
Ef/i/E0	1.60%	0.02%	0.03%

表A1单层ε-GeSe在施加20%拉伸应变下优化后的结构的振动频率的计算结果
TableA1.Calculated optimized results of vibration frequencies of ε-GeSe monolayer under application of 20% tensile strain.

图5所示为ε-GeSe单层的等值面部分电荷密度图. 其中图5(a)—(d)分别对应于图4(a)的点a, b, c和d处的密度. 图5中4个图对比可以看出, (d)图中该结构的Ge原子周围局域电荷密度较强, 由之前的分析可知, d点随着扶手椅和双轴方向上的拉伸应变的增加能量减小, 使单层ε-GeSe转变为直接带隙, 这也意味着该点在应变的调控下更加敏感的主要原因是Ge原子的贡献. 计算结果表明, 单层GeSe在平面应变调控下表现出较强的敏感性, 特别是应变调谐下的ε-GeSe, 表现出更大范围变化的电子特性.
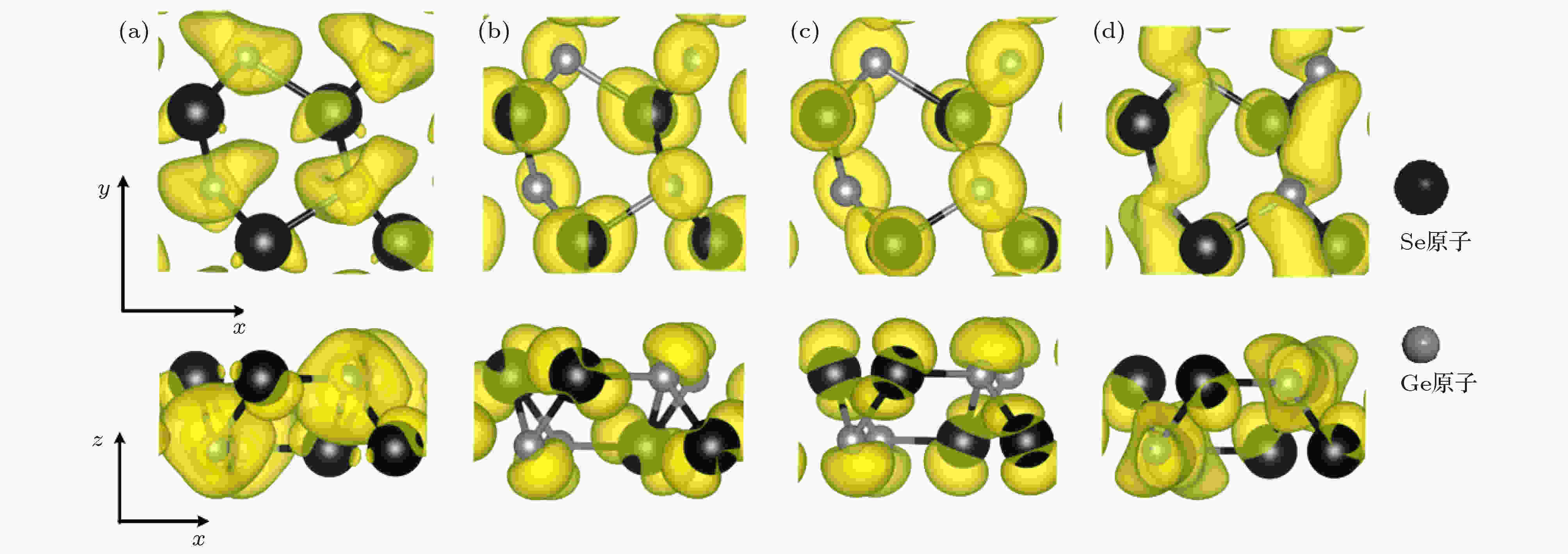图 5 单层ε-GeSe部分电荷密度的等值面 ((a), (b), (c), (d)分别对应于图4(a)中a, b, c和d所标注的点)
Figure5. Isosurfaces of partial charge densities of monolayer ε-GeSe ((a), (b), (c), (d) are corresponding points to a, b, c and d in Fig. 4(a), respectively).

运用第一性原理计算方法, 系统研究了单层GeSe的5种同分异构体结构的稳定性和应变调控下的电子性质变化. 结果表明, 5种同分异构体结构(α-GeSe, β-GeSe, γ-G0eSe, δ-GeSe, ε-GeSe)是热力学稳定的, α-GeSe是直接带隙半导体, 而其他4种同分异构体是间接带隙半导体. α-GeSe的能带在应变下具有从间接到直接带隙的变化. β-GeSe和γ-GeSe在施加应变下具有可调节的间接带隙范围. 当施加双轴压缩应变时, δ-GeSe在σ_xy = –2%且σ_xy = –4%变为直接带隙. 通过沿ε-GeSe的扶手椅形方向施加10%的拉伸应变, 出现了从间接带隙到直接带隙的转变. 继续增加拉伸应变到20%, 能带结构一直保持直接带隙的特征. 沿双轴方向施加10%拉伸应变时, 也出现了从间接带隙到直接带隙的转变. 能带结构在双轴拉伸应变增加到19%时一直保持直接带隙的特征. 总体来看, ε-GeSe单层在应变的调控下直接带隙可在0.61 —1.44 eV之间调节. 相比而言, ε-GeSe在应变的调控下可调的直接带隙范围比α-GeSe更大.

图A1为单层α-GeSe在部分应力调控下的能带结构图. 图A1(a)为单层α-GeSe不加应力下的能带图. 可以看出该结构是具有直接带隙的二维材料. 从图A1(b)和(c)中可以看出当施加沿扶手椅方向的拉伸或者压缩应力时都存在直接带隙到间接带隙的转变. 图A1(d), (e)和(f)分别为在锯齿形方向上施加应力后的部分能带图. 当在锯齿形方向上施加8%的压缩应力时带隙减小为零, 结构呈现金属性; 当施加1%的压缩应力和8%的拉伸应力时, 能带出现了直接带隙到间接带隙的转变. 图A1(g), (h)和(i)分别为在双轴方向施加应力后的部分能带图. 当双轴方向上施加6%的压缩应变时带隙减小为0, 出现了半导体到金属性的转变; 当施加1%的压缩应力和8%的拉伸应力时, 能带出现了直接到间接的转变.
图A2为单层ε-GeSe在不同方向施加20%的拉伸应力下优化后的结构图. 表A1为单层ε-GeSe在不同方向施加20%的拉伸应力下的振动频率计算结果. 可以看出扶手椅、锯齿形和双轴方向施加20%的拉伸应力下结构的虚频占据零点能的比例分别为0.16%, 0.02%和0.03%. 这一结果说明该结构在20%的拉伸应力下仍然具有热力学稳定性.