摘要:社会舆论的形成是个体行为及其关联与社会环境影响共同作用的结果. 在受到环境因素影响的同时, 个体行为也反过来影响社会环境, 从而呈现出耦合演化的特点. 本文在Ising模型的基础上, 建立了一个包含社会张力累积和消解过程的舆论形成模型, 研究了个体行为和社会环境的耦合演化行为. 利用朗道的平均场理论, 重点分析了在不同舆论疏解系数下系统演化的定态解及其稳定性, 以及系统定态解随参数变化的分支行为. 同时使用计算机模拟方法对平均场理论的结果进行了印证. 研究结果表明, 将系统与环境的耦合演化机制加入Ising模型后, 系统会展现出一定的自组织特性. 当疏解系数较小时, 系统会出现不同程度上的整体一致舆论, 产生宏观有序状态; 当疏解系数较大时, 系统则稳定在无序状态. 同时, 存在一个临界参数, 使系统从任何初始状态出发均自发演化到临界的分支点状态.
关键词: 舆论形成/
Ising模型/
耦合演化/
自组织临界

English Abstract

全文HTML

--> --> -->

进入21世纪以来, 信息网络技术的飞速发展, 深刻地改变着社会经济形态, 使得我们的社会成为一个强关联的复杂系统. 社会舆论形成也因此与网络上的信息传播紧密地联系在了一起, 网络社会所特有的实时互动和虚拟性等特点, 使得社会舆论的形成和发展具有了新的特性, 迫切需要我们利用复杂性研究的视角和方法, 认识和理解其中的核心科学问题.
实际上, 对社会舆论形成机制和演化规律的研究早已成为科学探索的一个重要议题. ****们从不同的角度提出了多种舆论动力学模型^[1]. 其中, 统计物理中的Ising模型, 由于其中自旋粒子向上或向下的两种状态, 可以自然地刻画人们观点的左右区分、或支持与反对的态度, 因而被广泛应用到舆论形成的研究中^[2]. 在这一类模型中, 研究者将个体抽象为系统中的粒子, 粒子的状态表示个体持有的观点, 定义粒子间的微观交互规则及粒子状态转变规则, 在给定的初始状态分布下, 个体按模型规则进行交互, 推动着宏观舆论的演化, 最终可能演化到所有个体的观点出现统一、极化和分裂现象. 类比于Ising模型对铁磁物质相变的理解, 舆论形成也被描述为通过相变产生有序现象的过程. 在Ising模型的基础上, 研究者们又提出了一系列经典的舆论动力学模型, 例如: 投票者模型^[3]、多数决定模型^[4]、Sznajd模型^[5]、Deffuant模型^[6]以及Krause-Hegselmann模型^[7]等. 随着复杂网络研究的兴起, 社会个体之间相互作用的网络结构对舆论形成的影响也成为广受关注的一个重要主题. 人们发现在复杂网络的框架下, 能够更好地理解舆论形成现象^[8-12], 而网络结构和舆论行为的共同演化模型^[13]、羊群现象与种族分割等的讨论^[14,15], 则更全面地描述了结构和行为的相互关系. 我国许多研究团队也在这一方向上开展了卓有成效的工作. 程洁和狄增如^[8]研究了舆论形成和网络结构的耦合演化, 并利用社会层次熵描述了最终舆论分布的结果; 罗植等^[16]研究了网络空间结构对舆论形成的影响; 李振鹏和唐锡晋^[17-20]则利用多主体模型以及数学分析, 深入研究了平衡结构等微观结构性质对舆论形成的影响.
考查已有基于Ising模型的舆论形成模型, 可以发现大部分工作对主体行为的适应性以及系统与环境的相互作用关系刻画不够. 相关研究关注的是系统在一定外界环境下(相当于热力学系统的温度)演化的平衡态, 虽然随后发展的Majority Vote Game等模型已拓展到非平衡系统的定态^[21-25], 但这些模型没有考虑系统状态对环境的反馈影响, 也没有强调个体的适应性行为. 因此, 我们需要改进模型以刻画系统个体行为与环境之间的耦合演化行为, 更好地揭示社会系统舆论形成的机制和演化规律. 实际上, 随着多层耦合网络研究的深入和发展, 通过网络耦合讨论系统协同演化的研究已经越来越受到科研工作者的关注^[26-29].
以经典Ising模型为代表的热力学系统, 热浴所给定的环境温度并不受系统与环境交互的影响. 但社会系统有所不同, 系统中个体的行为不仅受社会环境或氛围的影响, 反过来还会作用于社会, 导致社会整体环境的变化. 具体到舆论形成过程, 个体所组成的社会系统所处的政治、经济、文化等各种环境因素可以用一个社会张力指数来刻画, 它对应于Ising模型中的逆温度参数$ \beta \left( {\beta = \displaystyle\frac{1}{{kT}}} \right)$, 社会张力指数越大, 人群的非理性和从众行为的倾向越显著, 从而越容易发生舆论的极化行为(类似于Ising的有序相变), 产生舆论的一致性. 同时, 个体的行为, 特别是与舆论相关的现实世界和网络虚拟世界中的集群行为, 会在很大程度上反馈于社会, 影响和改变社会张力指数.
本文建立了一个包含社会张力累积和消解过程的舆论形成模型, 研究个体行为和社会环境的耦合演化行为. 类比于具有自组织临界行为的沙堆模型, 我们将引入社会张力的缓慢增加以及通过舆论集群行为的形成而产生的消解过程, 探讨系统与环境的相互作用关系所导致的系统演化以及有序结构的涌现行为. 在第2节中, 我们将首先介绍模型建立的基本思路, 然后在Ising模型平均场理论的基础上, 通过非线性动力学方程来刻画系统演化的自组织行为, 对系统与环境的耦合机制进行模拟分析.
在动力学模型中, 系统仍将依据朗道平均场理论给定的自由能函数, 具有演化到势函数最小的性质, 同时, 我们引入环境逆温度的自积累机制, 以及集群行为对社会张力的疏解机制, 探究不同参数条件下系统演化的稳定状态, 得到系统定态随参数变化的分支图. 我们发现, 当社会疏解等效系数等于1时, 系统从任意给定的初始状态出发, 都会自发演化到临界的分支点状态, 产生类似于沙堆模型的自组织临界演化性质. 在第3节中, 我们使用Monte Carlo方法得到了上述机制的数值模拟结果, 与平均场中的分析结果进行互相验证, 并探察系统存在随机性时的演化特征. 第4节对研究结果进行了总结和讨论.

以沙堆模型为代表的自组织临界性理论为理解现实世界中普遍存在的临界现象提供了新的角度^[30,31], 被广泛应用于自然、社会和工程等领域. Brunk认为, 其基本思想同样适用于理解社会. 他基于自组织临界性概念, 提出了社会崩溃理论^[32,33]: 能量缓慢积累; 局部失去稳定性, 累积和雪崩所造成的耗散过程, 共同驱动着系统达到自组织临界态. 显然, 这一过程对于我们正确认识和理解社会舆论的形成机制和演化规律富有指导意义. 在我们的耦合演化模型中, 个体的舆论取向以及个体之间的相互作用仍由Ising模型描述, 模型中节点的自旋方向代表节点的不同态度, 逆温度$ \beta \left( {\beta = \displaystyle\frac{1}{{kT}}} \right)$就对应于环境的社会张力指数. 但与Ising模型给定β不同, 我们类比于沙堆模型引入社会张力的累积效应和释放过程. 首先, 类似于沙粒的不断增加, 引入一个社会张力指数的累积过程(对应于温度的逐步降低), 同时, 假定系统由于自发涨落或外界刺激而产生一个或几个舆论集团时, 就会释放情绪并通过社会治理导致社会张力指数的疏解(对应于温度的升高). 显然, 在已有的Ising模型的基础上, 社会张力累积和疏解过程之间的竞争将大大丰富模型所能展示的系统演化行为. 下面首先构建基于平均场理论的系统演化动力学模型.
2

-->

2.1.耦合演化的舆论生成模型

在模型建立和讨论部分, 为了方便起见, 仍然选取温度T作为模型参数和变量. 由朗道1937年提出的平均场理论, Ising模型在不同温度下的热力学势如图1所示.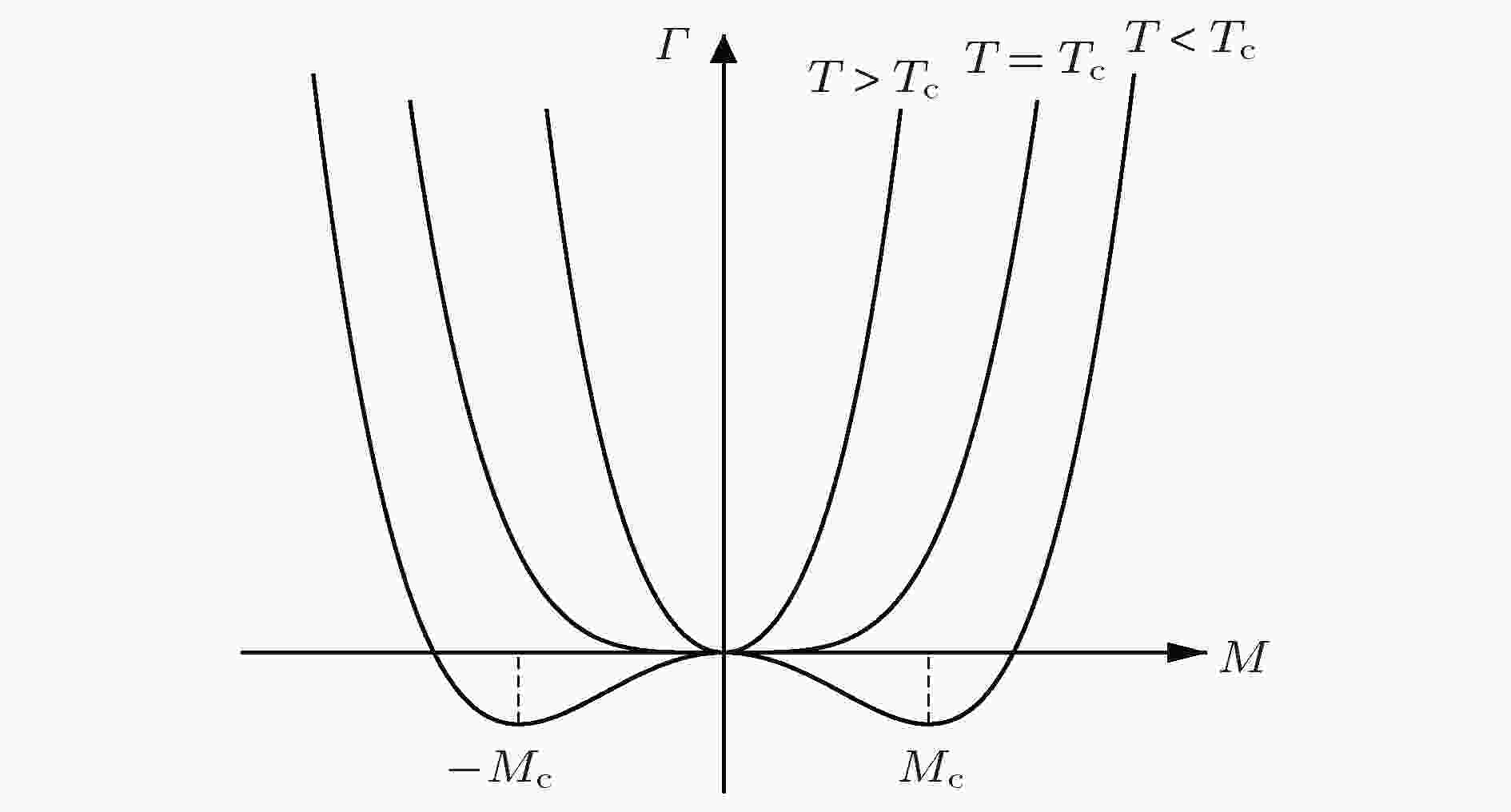
图 1 不同温度下的热力学势
Figure1. The Landau potential under different temperatures.

从图1中可以看到, 当T > T_c时, M₀ = 0是稳定的解, 在T = T_c时成为临界点, T < T_c时, M₀ = 0解失稳, 出现 ± M_c两个新的非0的稳定解.
考虑一个单轴各向异性的铁磁体系统. 系统的初始温度为T(0), 初始平均磁矩为M(0). 由于势函数Γ的存在, 磁矩随时间的变化可由以下梯度系统描述:

$\frac{{{\rm{d}}M}}{{{\rm{d}}t}} = - \nabla \varGamma = - \frac{{\partial \varGamma }}{{\partial M}}.$

由Ising模型势函数$\varGamma \left( M \right) = {T_0}\left( T \right) +\displaystyle\frac{1}{2}{a_2}\left( {T - {T_{\rm{c}}}} \right)$$ \times {M^2} + \displaystyle\frac{1}{4}{a_4}{M^4}$, 可得一般情况下平均场理论下平均磁矩的动力学方程:

$\frac{{{\rm{d}}M}}{{{\rm{d}}t}} = - {a_2}\left( {T - {T_{\rm{c}}}} \right)M - {a_4}{M^3}.$

耦合演化模型的核心是建立系统状态对环境温度的反馈作用, 即系统对于温度产生的影响.首先给出相关的动力学方程如下:

$\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = - \alpha + \beta \left( {{\rm{tanh}}{S_\infty } + \left| M \right|} \right),$

其中α, β均为实数, M为平均磁矩, S_∞表示Ising模型相同取向的自旋所形成的最大联通集团. 在已有的研究中, 我们知道在临界点附近, Ising集团具有分形结构, 分形维数为$ D = \displaystyle\frac{{187}}{{96}} \approx 1.95$^[25], 利用关联长度$ \xi \propto {\left| {T - {T_{\rm{c}}}} \right|^{ - \nu }}$作为最大联通集团的线度指标, 可知$ {S_\infty } \propto {\xi ^D} \propto {\left| {T - {T_{\rm{c}}}} \right|^{ - \nu D}}$, 对于二维晶格有ν = 1. 为方便理论分析并不失一般性, 设

${S_\infty } = \begin{cases} b{{\left( {T - {T_{\rm{c}}}} \right)}^{ - 2}}, & T > {T_{\rm{c}}}, \\ \infty , & T \leqslant {T_{\rm{c}}},\end{cases}$

而tanh函数是一个归一化函数, 将最大联通集团的影响转换到[0, 1]区间.
这一动力学方程所描述的社会张力的变化来源于两部分. 一个是系统社会张力的累积过程, 用Ising系统的自主降温描述; 另一个是社会张力的内部消解, 与最大联通集团的形成相关, 表示舆情积累到一定程度后所出现的群体一致行为会疏解社会张力, 使Ising系统温度升高. 在这里我们定义了一个等效疏解系数$ c = {\beta }/{\alpha }$, 表示社会系统中张力积累和疏解之间的竞争关系.
这样得到了系统与环境的耦合演化的舆论生成模型, 由M与T随时间变化组成的动力学方程组构成,

$\quad \left\{ {\begin{aligned}&{\frac{{{\rm{d}}M}}{{{\rm{d}}t}} = - {a_2}\left( {T - {T_{\rm{c}}}} \right)M - {a_4}{M^3},\qquad \qquad \quad \left( {\rm 5a} \right)}\\&{\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = - \alpha + c\alpha \left( {{\rm{tanh}}{S_\infty } + \left| M \right|} \right).\qquad \qquad \quad \left( {\rm 5b} \right)}\end{aligned}} \right.$

2 -->

2.2.动力学方程的定态解与分支行为

在动力学演化中, 我们关心的是系统演化的极限行为, 系统的定态解及其稳定性起着重要作用.
进一步, 我们希望了解系统极限行为与疏解系数c之间的关系, 即系统的定态解随参数c的分支行为, 所以首先通过$ \displaystyle\frac{{{\rm{d}}M}}{{{\rm{d}}t}} = 0,{\rm{}}\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = 0$, 求出系统的定态解, 然后通过线性稳定性分析获得其稳定性随参数的变化.
由方程(5a)可求得定态解M和T的函数关系, M = 0即或$ M = \pm k\sqrt {{T_{\rm{c}}} - T} $, 其中$ k = {{{a_2}}}/{{{a_4}}}$, 这是由Ising模型的性质所决定的, 给定一个外界温度T, 最终系统将会演化到一个稳定的值, 并由朗道势函数的形式可知, 当T ≥ T_c时, M = 0稳定; T < T_c时, M = 0失稳, $ M = \pm k\sqrt {{T_{\rm{c}}} - T} $稳定.
对于方程(5b), 当给定参数c > 1时, 方程右函数若有定态解, 则要求$ \tanh {S_\infty }$ + M < 1, 如果T ≤ T_c, 由(4)式可知, $ \tanh {S_\infty }=1$, 由上述讨论M ≠ 0, 故$ \tanh {S_\infty }$ + |M| > 1; 而当T > T_c时, 有$ \tanh {S_\infty }$ ≤ 1且M = 0, 可以满足方程解的条件$ \tanh {S_\infty }$ + |M| < 1, 所以得到, 当参数c > 1时, 系统最终应演化到T > T_c的定态. 同理, 也可以分析出, 当给定参数c < 1时, 系统将演化到T ≤ T_c的定态. 注意到, 参数c = 1是系统以上两种定态的分支点.
由上述分析就可以得到定态解, c和M, T之间的对应关系.
1)当c < 1时T ≤ T_c, 得到动力学方程为

$\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = - \alpha + c\alpha \left( {1 + \left| M \right|} \right),\tag{6a}$

通过右函数为0, 可以得到M的定态解, $ M = {1}/{c} - 1.0$.
进一步代入$M = \pm k\sqrt {{T_{\rm{c}}} - T} $, 可求出T的定态解,

$T = {T_{\rm{c}}} - \frac{1}{{{k^2}}}{\left( {\frac{1}{c} - 1.0} \right)^2}.$

2)当c ≥ 1时, T > T_c, 得到动力学方程为

$\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = - \alpha + c\alpha \left[ {{\rm{tanh}}\left( {b{{\left( {T - {T_{\rm{c}}}} \right)}^{ - 2}}} \right) + \left| M \right|} \right],\tag{6b}$

代入M =0, 解得定态解

$T = \sqrt {\frac{b}{{{\rm{artanh}}\left( {{1}/{c}} \right)}}} + {T_{\rm{c}}}.$

通过线性稳定性分析, 可以进一步确定定态解的稳定性, 并得到系统定态解随参数c的分支行为, 如图2和图3所示.
图 2 M-c 定态解分支图
Figure2. The bifurcation solutions of M-c function.

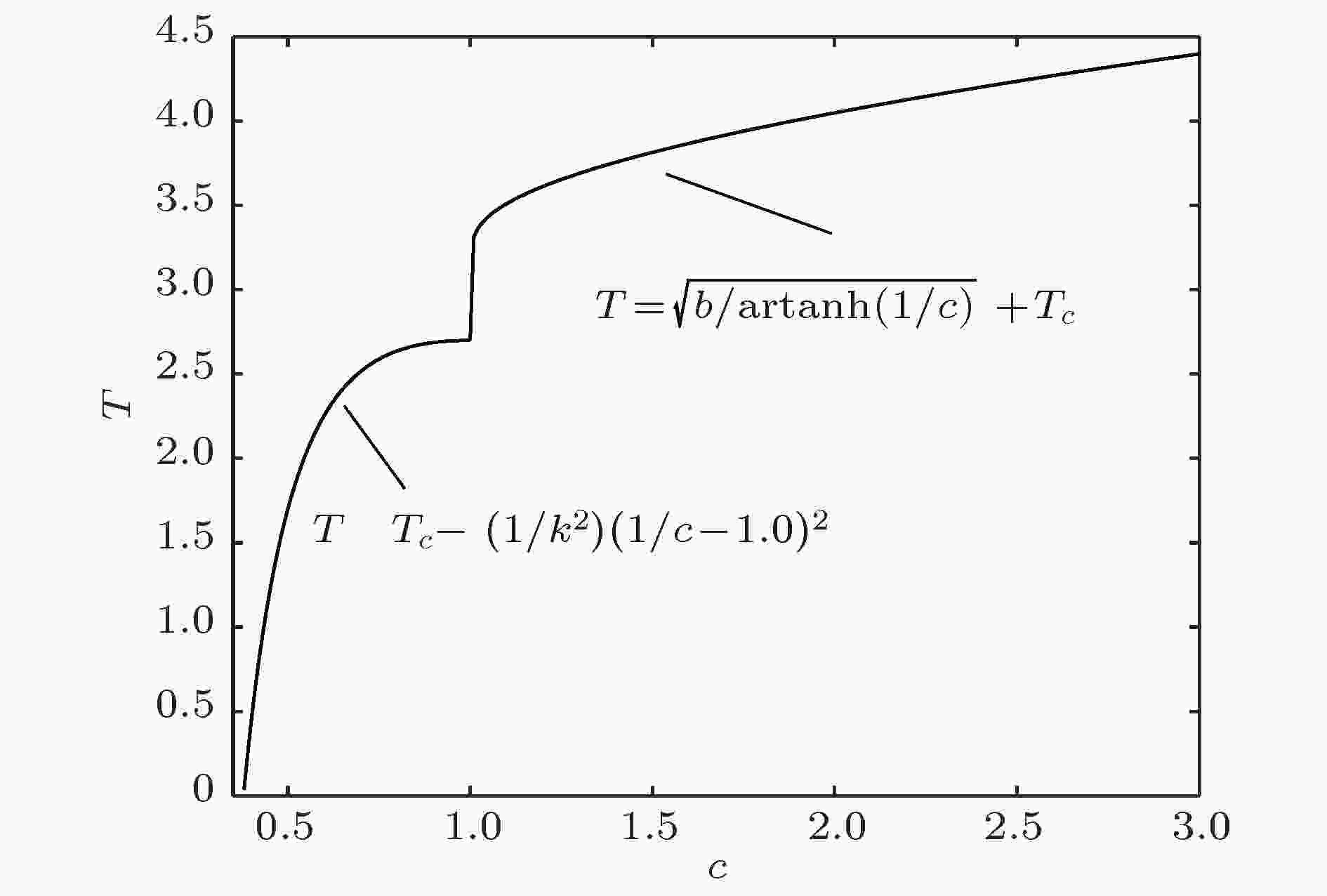图 3 T-c 定态解函数图像
Figure3. The function of stationary solutions.

从图中可以看到, 当疏解系数c ≥ 1的时, 社会系统中小集团形成后产生的疏解强度较大, 系统的磁矩将稳定为0, 社会不会产生舆论极化行为, 温度保持在临界温度上方. c = 1是一个特殊的临界点, 当c = 1时, 由线性稳定性分析可知, (M = 0, T = T_c)是一个高阶稳定不动点, 从任何初始条件出发, 系统都会自发演化到临界分支点, 形成类似于沙堆模型的向自组织临界态的演化行为.
以上系统与环境耦合的演化机制模型, 加入了系统对环境温度的影响, 使系统主体行为不再单纯地只受环境影响, 而展现出自组织的演化特性. 模型定义了疏解系数c, 反映了社会系统中社会张力的积累和疏解过程, 得出了在不同系数下的系统演化结果, 使得我们对该舆论动力学演化过程认识更加深入. 第3节将通过计算机数值模拟, 对以上结论进行印证, 并考虑在随机性存在的情况下, 系统随时间演化的不同状态及最终的稳态分布.

2

-->

3.1.模拟方法

考虑二维正方形晶格的Ising系统, 取边长L = 50, 并采用循环边界条件. 此时, 平均每个自旋可翻转一次所需的仿真周期数量为一个Metropolis步, 即2500个仿真周期算作一个Metropolis步. 对于每一个仿真周期都需要按

$E = - \sum\nolimits_{\left\langle {i,j} \right\rangle } {{s_i}{s_j}} $

计算出系统的总能量, 并在每一个仿真周期中依据总能量变化, 以一定概率来接受或拒绝每自旋的翻转,

${s_i}\left( {t + 1} \right) = \left\{ {\begin{aligned}&{{s_i'},}\quad {{\text{以概率}}\mu ,}\\&{{s_i}\left( t \right),}\quad {{\text{以概率}}1 - \mu .}\end{aligned}} \right.\tag{8a}$

概率μ为

$\mu = {\rm{min}}\left\{ {\exp \left( {\frac{{E\left( {{s_i}\left( t \right)} \right) - E\left( {{s_i'}} \right)}}{{kT}}} \right),1} \right\},\tag{8b}$

其中k为玻尔兹曼常数, 取为1; 开始时, 给定系统的初始温度T, 取5000个Metropolis步, 使系统首先演化到当前温度的平衡态.
之后引入温度调节机制, 每500个Metropolis步进行一次温度调节. 我们计算系统最后10个Metropolis步中全部仿真周期中磁矩的绝对值和最大联通集团面积的平均值, 通过如下方式对温度T进行调整:

$\Delta {T_t} = - \alpha + c\alpha \left( {\frac{{{S_L}}}{{{L^D}}} + M} \right),\tag{9a}$

${{T}_{t+1}}={{T}_{t}}+ {\Delta {T}_{t}},\tag{9b}$

与平均场理论中的参数设置相似, α, c为常数; M为平均绝对磁矩; S_L表示在L × L格子系统中相同自旋形成的最大联通集团中自旋的个数, 即最大联通集团的面积. 在模拟中L^D为理论上L × L格子系统中在临界点时最大联通集团面积, 其中D表示该结构的分形维数, 依据已有研究结果^[25], 在模拟中我们取D = 1.95.
对于给定的参数c, 多次重复以上过程, 并记录系统在当前参数下达到稳态后的磁矩状态, 进行系综平均, 进而给出系统磁矩的概率分布. 具体的算法过程如下.
Step 1　确定初始稳态分布. 给定初始温度T₀, 生成L × L的初始数组, 数组中元素分别在 ± 1中等概率取值, 按照Metropolis算法进行5000个Metropolis步, 实现初始平衡分布.
Step 2　温度调节. 以系统状态演化最后10个Metropolis步系统状态的平均值为基础, 按(9a)和(9b) 式调节温度.
Step 3　系统状态演化. 按照Metropolis算法, 改变系统自旋状态, 演化500个Metropolis步.
Step 4　判断系统演化是否达到稳态. 若否, 返回Step 2, 继续系统演化; 若是, 绘制出系统平均磁矩绝对值、温度值和最终稳态分布.
在本文中, 我们使系统分别在社会疏解系数c取2.5, 1.3, 0.8时进行演化, 以模拟系统最终演化至无序态、临界态、有序态三种情况.
2 -->

3.2.模拟结果

1) c = 2.5
如图4所示, 系统温度随时间演化不断上升, 最终达到定态; 系统绝对平均磁矩逐渐减小到0, 并一直保持在0附近.
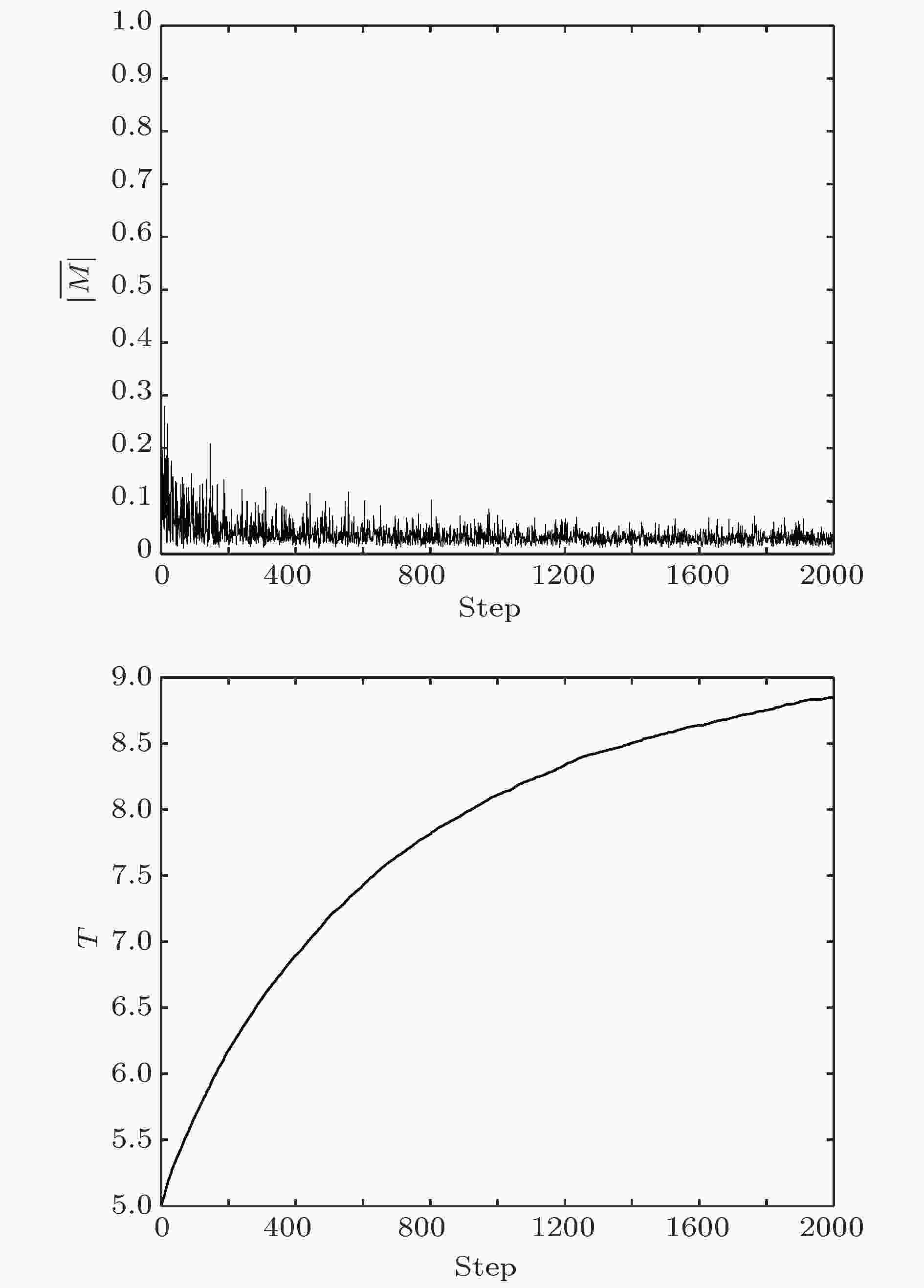图 4 c = 2.5时系统状态演化行为
Figure4. Evolution of the system state given c = 2.5.

取系统演化到定态时最后500个Metropolis步的平均磁矩, 并在不同初始条件下系统演化重复6次, 得到3000个平均磁矩值进行系综平均, 得到的统计分布如图5.
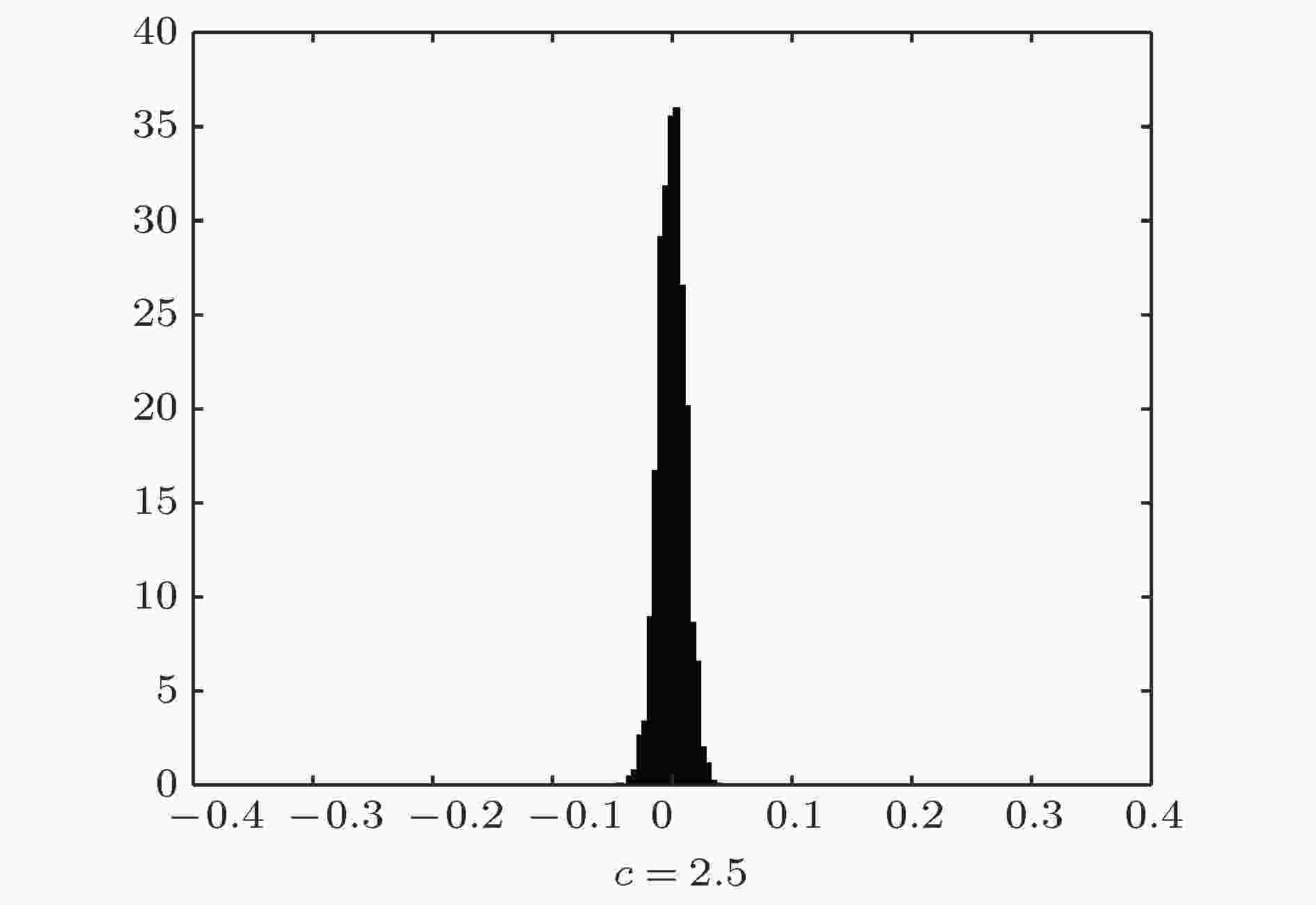图 5 c = 2.5时系统定态时磁矩M的统计分布
Figure5. Distribution of the magnetic moments (M) after system evolved to the stationary state, given c = 2.5.

由图5看出, 系统磁矩分布于区间(–0.04, 0.04), 经计算, 该分布的峰态系数K ≈ 3, 偏态系数S ≈ 0, 故该分布接近均值为0的正态分布, 说明此时系统演化至了无序态, 与平均场理论中的结果一致.
2) c = 1.3
如图6所示, 系统温度和绝对平均磁矩随着时间演化都始终在一定区间内波动.
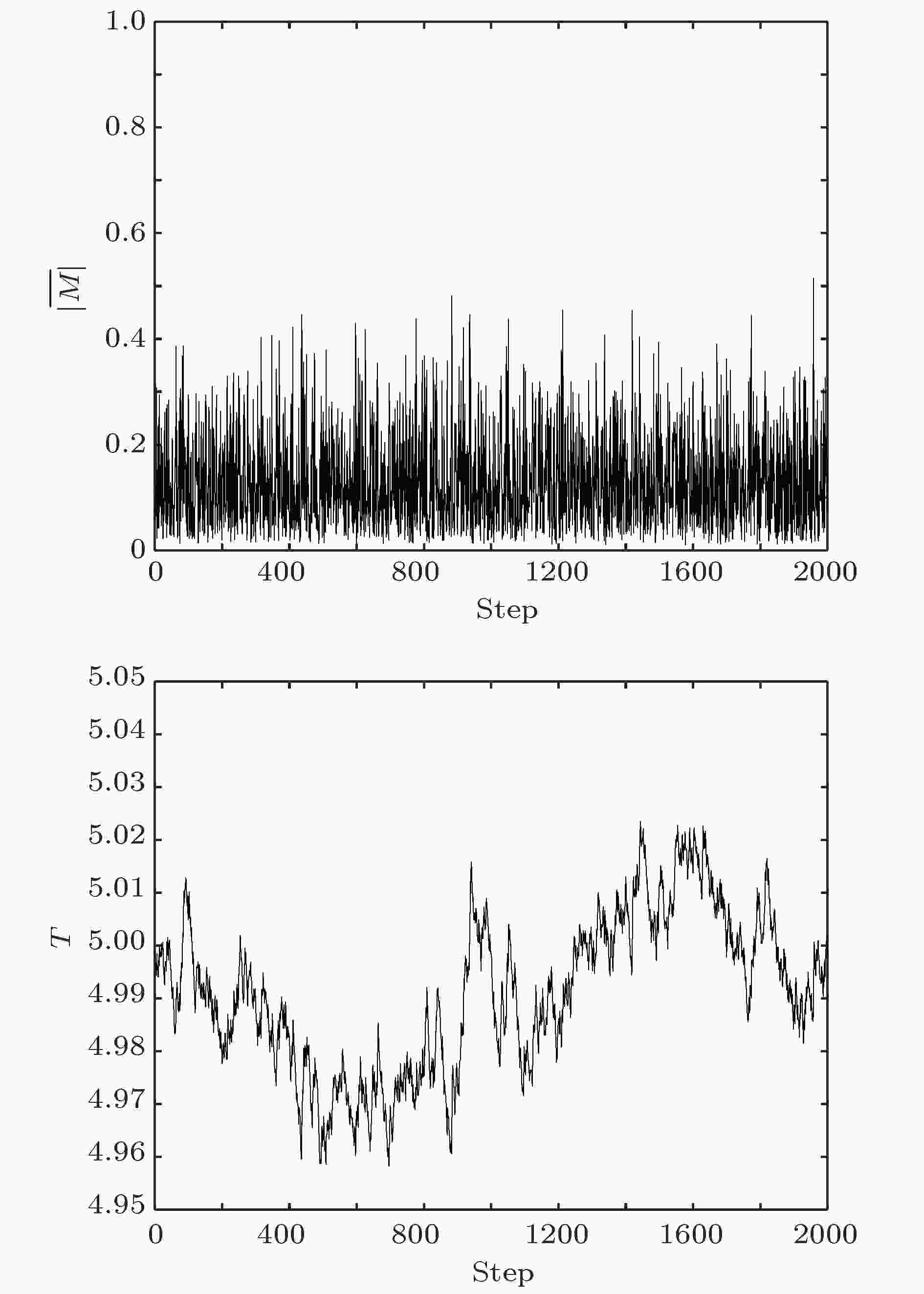图 6 c = 1.3时系统状态演化行为
Figure6. The evolution of system state given c = 1.3.

同样地, 取系统演化到定态时最后500个Metropolis步的平均磁矩, 并使系统在定态条件下重复演化16次, 得到8000个平均磁矩值进行系综平均, 得到统计分布如图7所示.
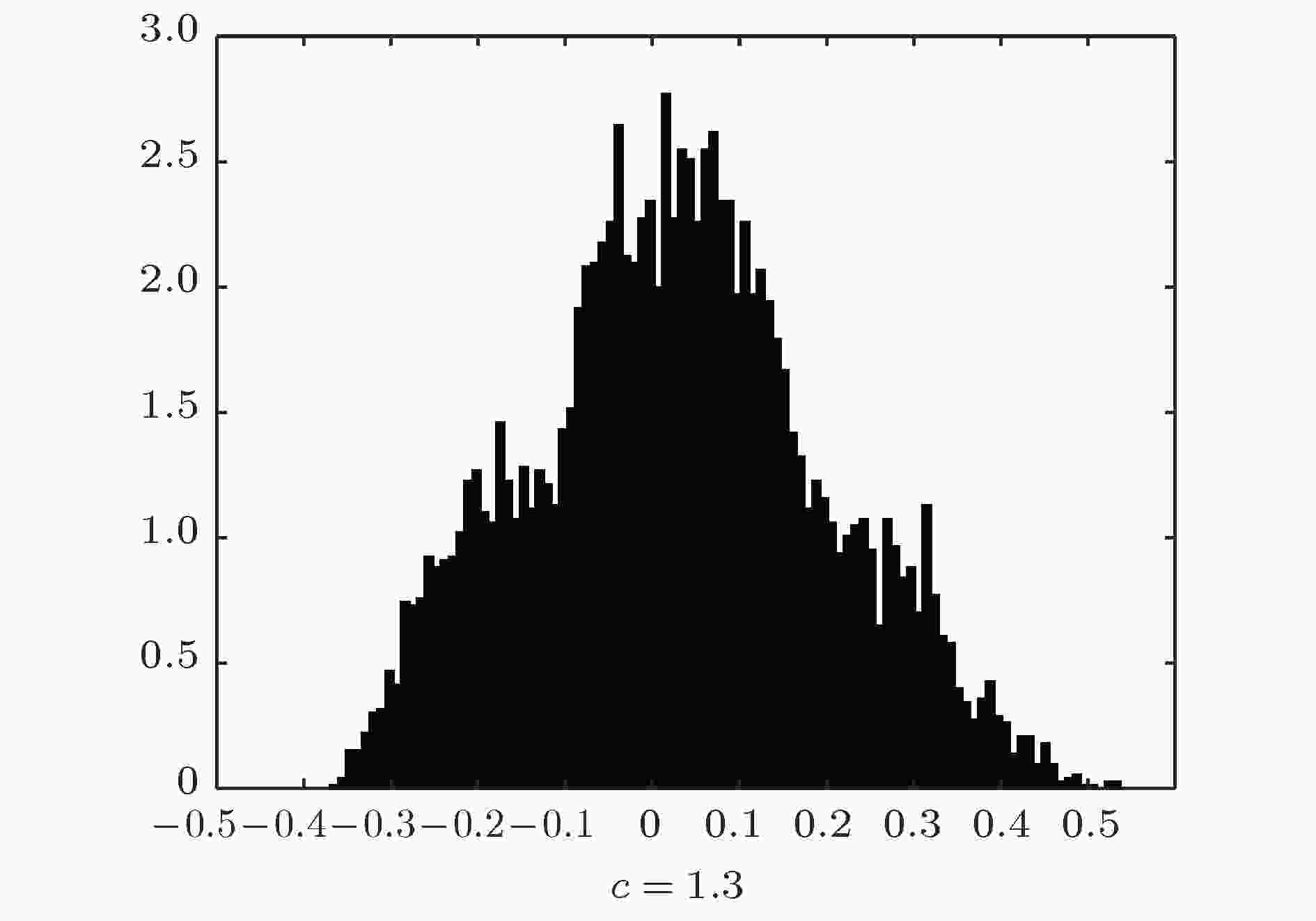图 7 c = 1.3时系统定态时磁矩M的统计分布
Figure7. Distribution of the magnetic moments (M) after system evolved to the stationary state, given c = 1.3.

此时, 系统的平均磁矩在(–0.4, 0.6)的区间内, 分布范围远远超过c = 2.5时的情形, 且峰态系数K ≈ 2.5, 小于正态分布的情形, 表明系统在均值0附近有较大的涨落.
由于随机性的存在, 仅仅通过对给定参数下系统演化及稳态分布的观察, 很难准确找到平均场理论中得到的临界点参数. 在后续的研究中, 我们将利用有限尺度标度理论及统计方法, 确定耦合演化系统的临界有效疏解系数c, 并定性地确定系统是否具有临界性质, 进而定量刻画系统的临界行为, 包括标度律和临界指数.
3) c = 0.8
如图8所示, 温度随时间演化不断降低, 最终达到定态; 系统平均磁矩从0上升, 表现出一定程度的极化行为.
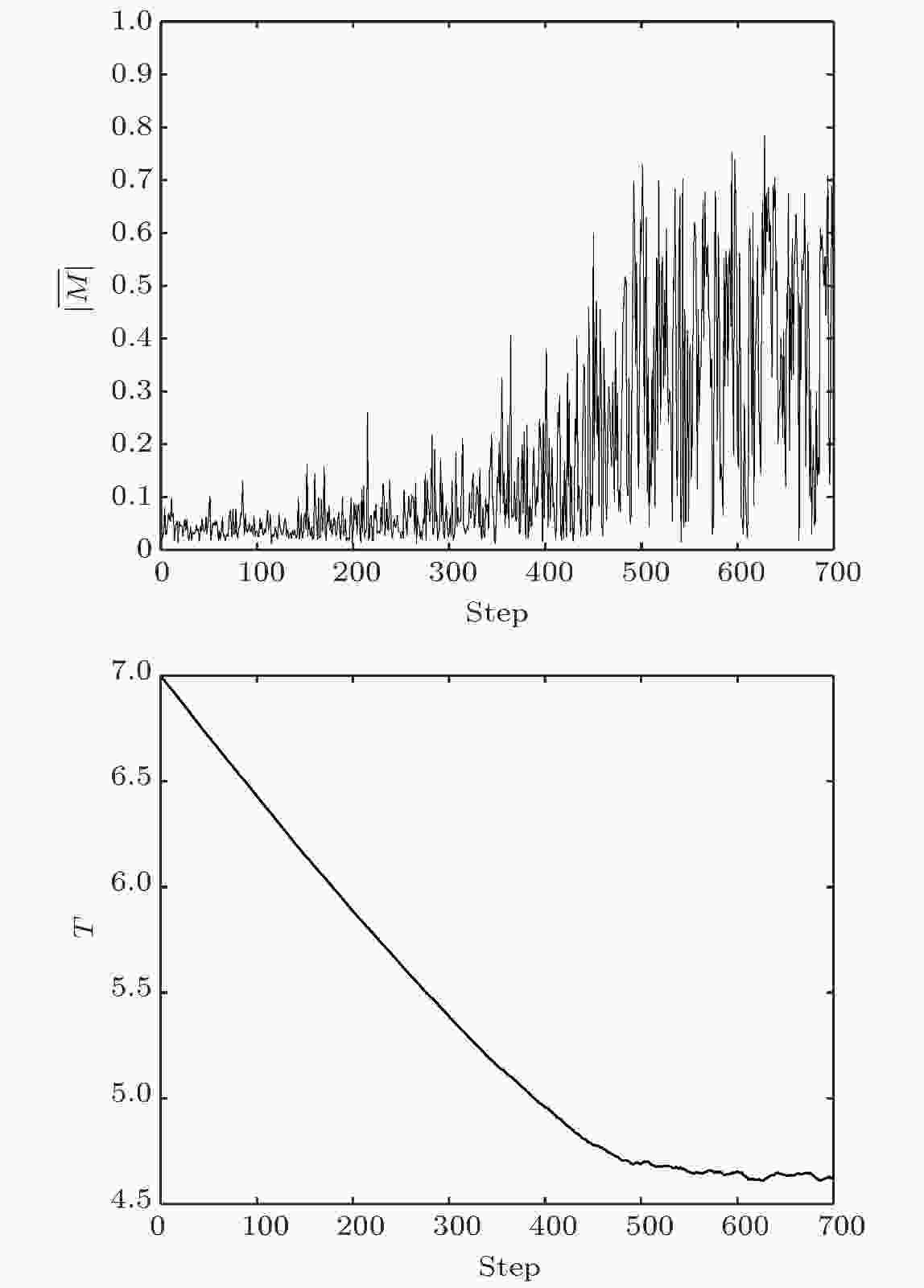图 8 c = 0.8时系统状态演化行为
Figure8. The evolution of system state given c = 0.8.

为验证系统降温过程中出现的与前文所述两种情形所对应的暂态, 我们观察了系统磁矩分布随时间的变化. 我们使系统重复演化9次, 在每一次演化中记录每一次变温演化时500个Metropolis步的平均磁矩, 每一个时间步得到4500个平均磁矩进行系综平均, 绘制出系统的平均磁矩分布随时间的演化图像, 如图9所示.
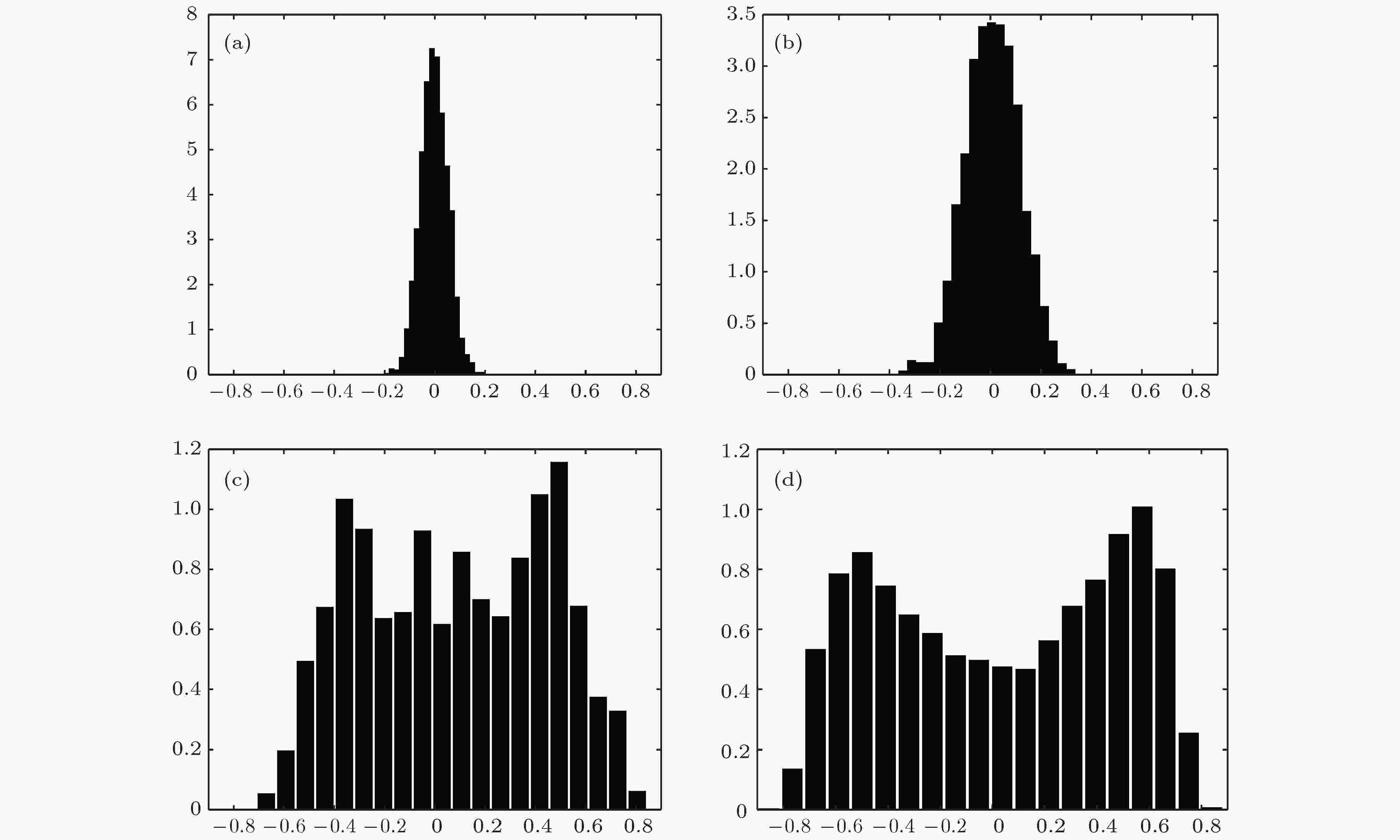图 9 c = 0.8时系统磁矩M的统计分布随时间的变化　(a) t = 100; (b) t = 300; (c) t = 500; (d) t = 600—700
Figure9. Distribution of the magnetic moments (M) when the system is evolving to the stationary state, given c = 0.8: (a) t = 100; (b) t = 300; (c) t = 500; (d) t = 600?700.

从图9的时间演化过程中可以看出, 系统磁矩分布经历了从单峰分布的暂态逐渐向均匀分布的暂态过渡, 最终达到的稳态分布为双峰分布, 并表现出一定程度的极化行为. 可以说明系统经历了从完全无序演化到有序极化的稳态的过程.
需要说明的是, 之所以可以对最后100步取平均, 是因为系统在最后100步时已经达到了稳态, 统计性质在每一个时间步是相同的.

在Ising模型的基础上, 考虑系统主体行为对环境的反馈作用, 构造出了具有自组织特性的舆论形成耦合演化模型, 更深入地探讨了社会系统舆论形成和传播的自组织行为. 在平均场理论下, 建立了Ising模型状态的演化特性与系统外界温度调解之间的关系, 通过舆论疏解系数的构建, 明确了在不同参数条件下系统最终达到的稳定状态, 进一步研究了系统在耦合机制下的自组织行为特性, 并应用Monte Carlo模拟对平均场结果进行了验证.
研究发现, 耦合演化模型会显示出一定的自组织演化特性, 自发向新的稳定状态演化, 显示出更加丰富的演化规律. 系统最终到达的稳定状态与我们定义的舆论等效疏解系数有关: 当c > 1时, 系统不会出现一致性的社会舆论, 平均磁矩为0, 系统会稳定在无序状态; 当c < 1时, 系统的舆论疏解能力较差, 最终会显示出不同程度上的整体一致舆论, 产生宏观有序状态; 而c = 1, 是动力系统演化的一个分支点. Monte Carlo模拟的结果也证明存在这样一个参数临界值, 使得社会整体舆论显示出上述特点.
本研究提出的具有自组织特性的舆论形成模型为今后的研究奠定了一定的理论基础, 后续的研究一方面可以进一步深入研究耦合演化系统的临界性质, 如利用有限尺度标度理论确定系统是否进入了临界态, 计算系统的临界指数, 并进而确定系统临界行为的普适类等; 另一方面可以在舆论形成机制认识的基础上, 进一步发展评估、预警指标以及干预、治理措施, 为现代社会治理提供新思路与新方法.