摘要:超表面是由亚波长单元组成控制电磁波的人工结构, 研究发现通过对其进行编码排列可实现对电磁波能量的任意控制. 本文利用四种形状相同、尺寸不同的人字形结构单元, 结合其不同相位响应和不同的相位灵敏度设计了太赫兹频率编码器, 通过进行特定编码, 在频率改变的情况下, 实现了对电磁波能量辐射调控. 分别设计了1-bit, 2-bit周期和非周期太赫兹频率编码器, 通过数值计算和仿真模拟验证了上述特性, 而且该结构对太赫兹波辐射主瓣能量有很好的分散作用, 可以有效减少雷达散射截面, 雷达散射截面缩减在θ = 0, φ = 0方向上最大可达29 dB, 在太赫兹波隐身中具有巨大应用价值.
关键词: 编码超表面/
太赫兹调控/
相位灵敏度

English Abstract

全文HTML

--> --> -->

不同于传统材料, 超表面是由周期或非周期亚波长单元组成的人工结构, 由于其不寻常的电磁响应^[1,2], 对电磁波的相位和振幅具有很强的控制作用. 超表面作为二维超材料具有厚度薄、带宽、损耗小等优点, 近年来引起了广泛关注^[3-8], 已经在隐身^[9]、天线^[10,11]、微波器件^[12]、光学器件^[13]方面展示出巨大的应用前景. 与传统的通过调节电子场和磁界面的极化率来控制电磁波的方法相比, 编码超材料的主要思想是通过设计编码单元的各种编码序列来有效地控制电磁波^[14-17] . 文献[16]提出了一种具有缺口的轮式结构作为基本编码粒子单元, 分别设计了1-bit, 2-bit和3-bit编码超表面, 在空间编码模式下, 实现了对太赫兹波能量的控制. 最近有关编码超材料结构已有一些报道^[18-20]. 然而, 上述数字编码仅仅是在空域编码进行, 并未利用频域特性进行编码处理.
本文设计的频率编码器采用了空域-频域结合的方式, 利用了单元频率不同的相位响应灵敏度, 通过低和高相位灵敏度对数字“0”和“1”的单元进行编码设计. 编码在不改变空间编码模式的情况下, 可实现对电磁波能量辐射的各种灵活控制, 而且对电磁波能量辐射具有很好的分散作用, 能有效减少雷达散射截面, 雷达散射截面缩减值在θ = 0, φ = 0方向上最大可达到29 dB, 在太赫兹波隐身中具有巨大应用价值.

在频率编码器中, 不同基本单元需要具有相同的初始相位响应和相位对频率的敏感性, 随着工作频率的增加, 不同单元反射相位值将不同. 单元结构在频率上的相位响应可利用泰勒级数表示为

$\begin{split}\varphi (f) =\, &{\alpha _0} + {\alpha _1}(f - {f_0}) + {\alpha _2}{(f - {f_0})^2} +\cdots \\ &+ {\alpha _n}{(f - {f_0})^n} + {\alpha _{n + 1}}{(f')^{n + 1}},\end{split}$

其中, ${f_0} \leqslant f' \leqslant f$, f₀是初始频率, α₀是初始频率处相位响应, α₁是工作频率上的相位灵敏度, α_n是相位响应的第n阶.
在忽略表达式的高阶时, 工作频带内基本单元间的相位差是恒定的, 代表所设计编码器基本单元的相位信息. 此时 (1) 式可简化为

$\varphi (f) \approx {\alpha _0} + {\alpha _1}(f - {f_0}).$

(2) 式表明, 单元的相位响应随频率的变化而变化. 每个单元相位响应与初始频率点相位值和相位灵敏度有关, 这也意味着相邻单元间的相位差不仅与初始相位响应α₀有关, 还与相位灵敏度α₁有关. 在这种情况下, 利用初始频率和截止频率上的相位响应来近似确定单元的线性相位灵敏度, 参数α₁表示为

${\alpha _1} = \left[ {\varphi \left( {{f_1}} \right) - \varphi \left( {{f_0}} \right)} \right]/\left( {{f_1} - {f_0}} \right).$

本文的单元结构如图1(a)和图1(b)所示. 人字形单元结构位于介质层聚酰亚胺膜(h = 20 μm, 介电常数为3.0, 损耗角正切值为0.03)上, 底层是金属铜片(0.2 μm). 人字形结构是由同一个厚0.2 μm的矩形按顺时针以120°依次旋转两次得到, 具体参数为: P = 100 μm, W = 40 μm, 初始值L = 20 μm. 利用CST软件对单元结构进行反复优化仿真, 改变人字形金属结构长度L, 得到了在初始频率具有相等相位值, 且在工作频率范围内具有不同相位灵敏度的四个基本单元结构分别为A单元(图2(a))、B单元(图2(b))、C单元(图2(c))和D单元(图2(d)). 它们对应的长度L分别为48, 40, 34和20 μm. 图2(e)和图2(f)为A, B, C和D四个基本单元结构在0.4—1.0 THz之间的太赫兹波反射率和反射相位曲线. 从图中可以看出, 在频率范围内四个基本单元的太赫兹波反射率都位于0.8以上, 接近于全反射, 且它们在初始频率f₀ = 0.4 THz处具有相同的初始相位响应$\alpha _{\rm{0}}^{\rm{A}} = \alpha _{\rm{0}}^{\rm{B}} = \alpha _{\rm{0}}^{\rm{C}} = \alpha _{\rm{0}}^{\rm{D}} \approx 8{\text{π}}/9$. 为了验证太赫兹频率编码器远场能量模式随频率的增加而变化, 本文分别设计了1-bit, 2-bit太赫兹频率编码器, 如图3所示. 图3(a)为以“0-0, 0-1, 0-0, 0-1”序列沿x方向排列1-bit周期太赫兹频率编码器; 图3(b)为以 “0-0, 0-1, 0-0, 0-1/0-1, 0-0, 0-1, 0-0” 序列棋盘式排列1-bit周期太赫兹频率编码器; 图3(c)为以“00-00, 00-01, 00-10, 00-11”序列沿x方向排列2-bit周期太赫兹频率编码器; 图3(d)为2-bit随机太赫兹频率编码器; 图3(e)为2-bit非周期太赫兹频率编码器.
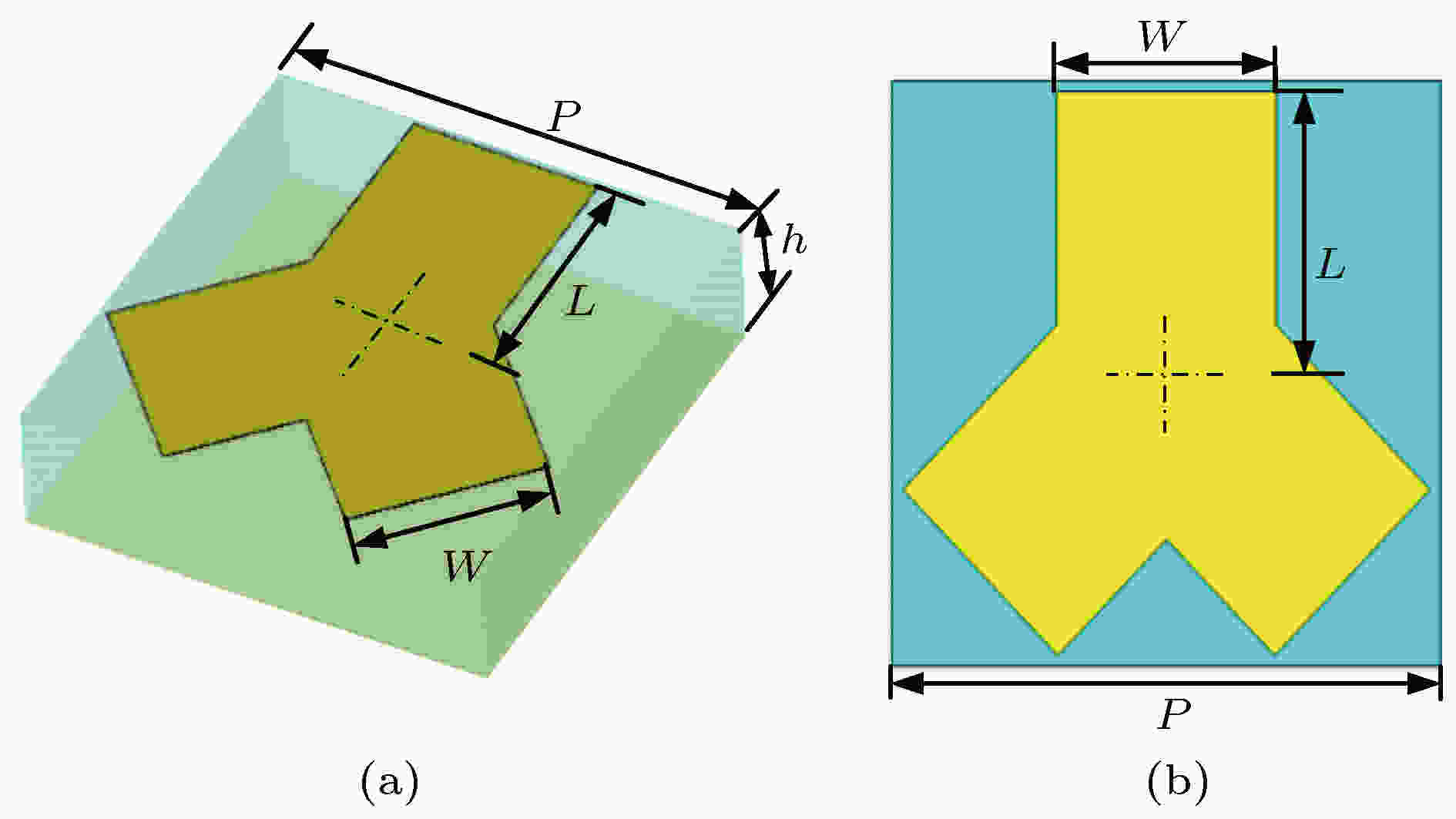图 1 人字形超表面单元结构　(a)单元结构三维立体图; (b)单元结构二维平面图
Figure1. Herringbone metasurfaceunit structure: (a) Three-dimensional of unit structure; (b) two-simensional of unit structure.

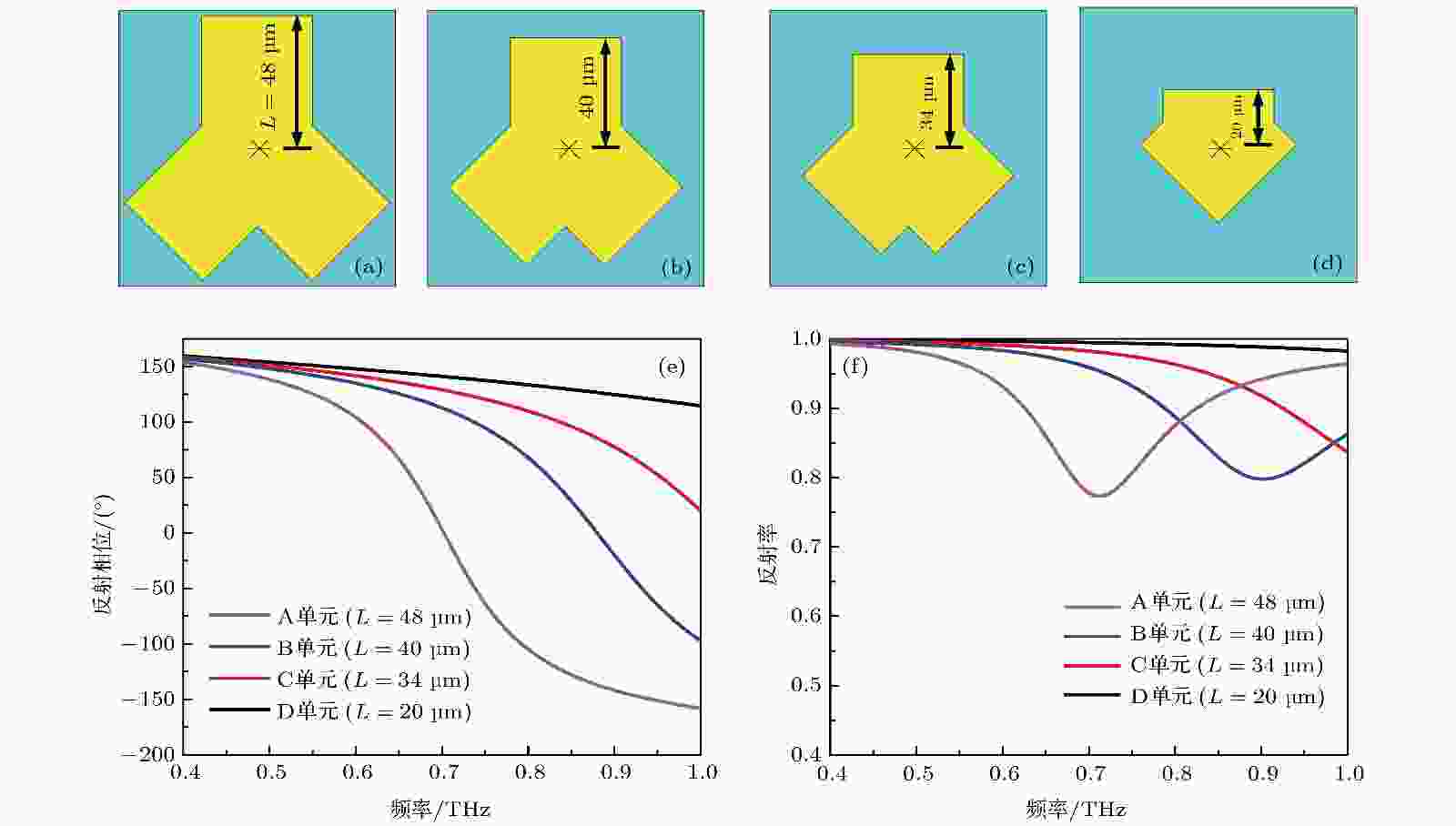图 2 4种人字形超表面基本单元结构及其特性曲线　(a) A单元(L = 48 μm); (b) B单元(L = 40 μm); (c) C单元(L = 34 μm); (d) D单元(L = 20 μm); (e) 4种单元在0.4 THz到1.0 THz下的反射率; (f) 4种单元在0.4 THz到1.0 THz下的反射相位
Figure2. The basic unit structure and characteristic curves of four kinds of herringbone metasurface: (a) Unit A (L = 48 μm); (b) unit B (L = 40 μm); (c) unit C (L = 34 μm); (d) unit D (L = 20 μm); (e) reflectivity of four unitsfrom 0.4 THz to 1.0 THz; (f) reflection phase of four units from 0.4 THz to 1.0 THz.

图 3 太赫兹频率编码器　(a)以“0-0, 0-1, 0-0, 0-1”序列沿x方向排列1-bit周期太赫兹频率编码器; (b)棋盘式1-bit周期太赫兹频率编码器; (c)以“00-00, 00-01, 00-10, 00-11”序列沿x方向排列2-bit周期太赫兹频率编码器; (d) 2-bit随机太赫兹频率编码器; (e) 2-bit非周期太赫兹频率编码器
Figure3. The terahertz frequency coding metasurface: (a) 1-bit periodic terahertz frequency coding metasurface arranged along x direction with “0-0, 0-1, 0-0, 0-1” sequence; (b) chessboard 1-bit periodic terahertz frequency coding metasurface; (c) 2-bit periodic terahertz frequency coding metasurface arranged along x direction with “00-00, 00-01, 00-10, 00-11” sequence; (d) 2-bit random terahertz frequency coding metasurface; (e) 2-bit non-periodic terahertz frequency coding metasurface.

只需要A和C两种单元结构设计1-bit太赫兹频率编码器. 结合图2(f)得到表1两个单元的相位响应特性. 在初始频率f₀ = 0.4 THz时, $ \alpha _{\rm{0}}^{\rm{A}} = $$\alpha _{\rm{0}}^{\rm{C}} \approx 8{\text{π}}/9$, 两个单元的空间域参数是相同的. 两个单元在工作频带上有着不同程度的相位灵敏度.

单元结构	α0/(°)	1-bit相位响应
		近似α0/(°)	空域码	α1/(°)·THz–1	近似α1/(°)·THz–1	频域码	编码状态
	154	160	“0”	–312/0.6	0/0.6	“0”	“0–0”
	158	160	“0”	–138/0.6	180/0.6	“1”	“0–1”

表11-bit频率编码器单元
Table1.1-bit frequency terahertz coding metasurface unit.

由 (3) 式可得两个单元相位灵敏度分别为

$\left\{ {\begin{aligned}& {\alpha _1^{\rm A} = [{\varphi ^{\rm{A}}}({f_1}) - {\varphi ^{\rm{A}}}({f_0})]/({f_1} - {f_0}) = ( - 158^\circ - 154^\circ )/(1.0 - 0.4) \approx 0/{\rm{0}}{\rm{.6(rad/THz)}}} \\ & {\alpha _1^{\rm D} = [{\varphi ^{\rm{D}}}({f_1}) - {\varphi ^{\rm{D}}}({f_0})]/({f_1} - {f_0}) = (114^\circ - 160^\circ )/(1.0 - 0.4) \approx {\text{π}}/{\rm{0}}{\rm{.6}}({\rm{rad/THz}})} \end{aligned}} \right..$

因此, 将$\alpha _{\rm{1}}^{\rm{A}}$编码为“0”, 将$\alpha _{\rm{1}}^{\rm{B}}$编码为“1”, 用来表征A, C两个单元的频率特性, 得到A, C两个单元的最终编码状态分别为“0-0”和“0-1”. 为了进一步分析1-bit太赫兹频率编码器的工作性能, 分别设计了以序列“0-0, 0-1, 0-0, 0-1” 沿x方向进行编码(见图3(a))和以数字序列“0-0, 0-1, 0-0, 0-1/0-1, 0-0, 0-1, 0-0”棋盘式进行编码(见图3(b))的太赫兹频率编码器. 为了减小耦合效应, 每个编码粒子采用3×3个相同单元组成的超级单元进行编码排布.
利用CST软件对两种1-bit太赫兹频率编码器进行建模计算, 结果如图4—图7所示. 图4和图6为1-bit太赫兹频率编码器三维远场散射图, 图5和图7为1-bit太赫兹频率编码器二维电场图. 由图4(a)可以看出, 在用数字序列“0-0, 0-1, 0-0, 0-1”沿x方向进行编码的1-bit太赫兹频率编码器, 当初始频率f₀ = 0.4 THz, 垂直入射的太赫兹波被垂直反射. 产生这种现象是由于A和C两个单元在初始频率f₀ = 0.4 THz处具有一样的相位响应, 相邻单元相位差为0°, 等同于一块完美导体, 所以垂直入射的太赫兹波被原路垂直反射回去. 随着工作频率逐渐增加, 反射波束由原来一束指向z轴的主能量转换为两束对称光束(见图4(b)和图4(c)). 当频率增加到f₁ = 1.0 THz时, 因A和C两个单元之间相位差变为180°, 原主瓣几乎消失, 在θ₁ = 30°处产生两束z轴对称的光束, 如图4(d)所示. 此时, 俯仰角为θ₁ = sin^–1(λ/Γ₁)=30°, 其中Γ₁ = 2×3×100 μm = 600 μm为编码序列一个周期的物理长度, λ为自由空间波长. 图5(a)—(d)分别为对应图4(a)—(d)的二维电场图, 从图5中的光斑点位置也很好地验证了计算结果.
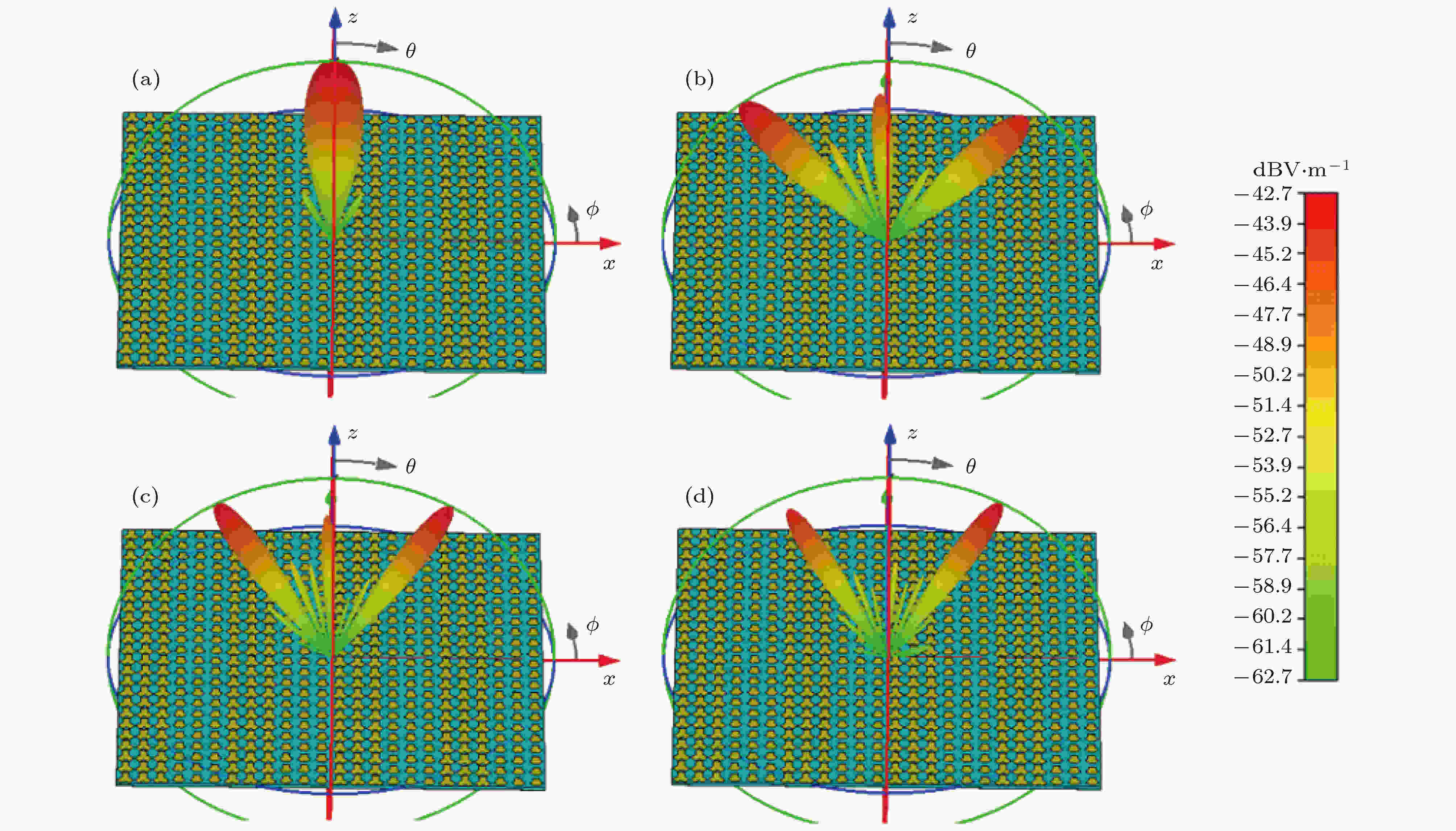图 4 序列“0-0, 0-1, 0-0, 0-1”沿x方向上周期排布的1-bit太赫兹频率编码器　(a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Figure4. 1-bit terahertz frequency coding metasurface arranged periodically along x direction with sequence “0-0,0-1, 0-0, 0-1”: Three-dimensional far-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

图 5 序列“0-0, 0-1, 0-0, 0-1”沿x方向上周期排布的1-bit太赫兹频率编码器　(a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的二维电场图
Figure5. 1-bit terahertz frequency coding metasurface arranged periodically along x direction with sequence“0-0, 0-1, 0-0, 0-1”: Two-dimensional electric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

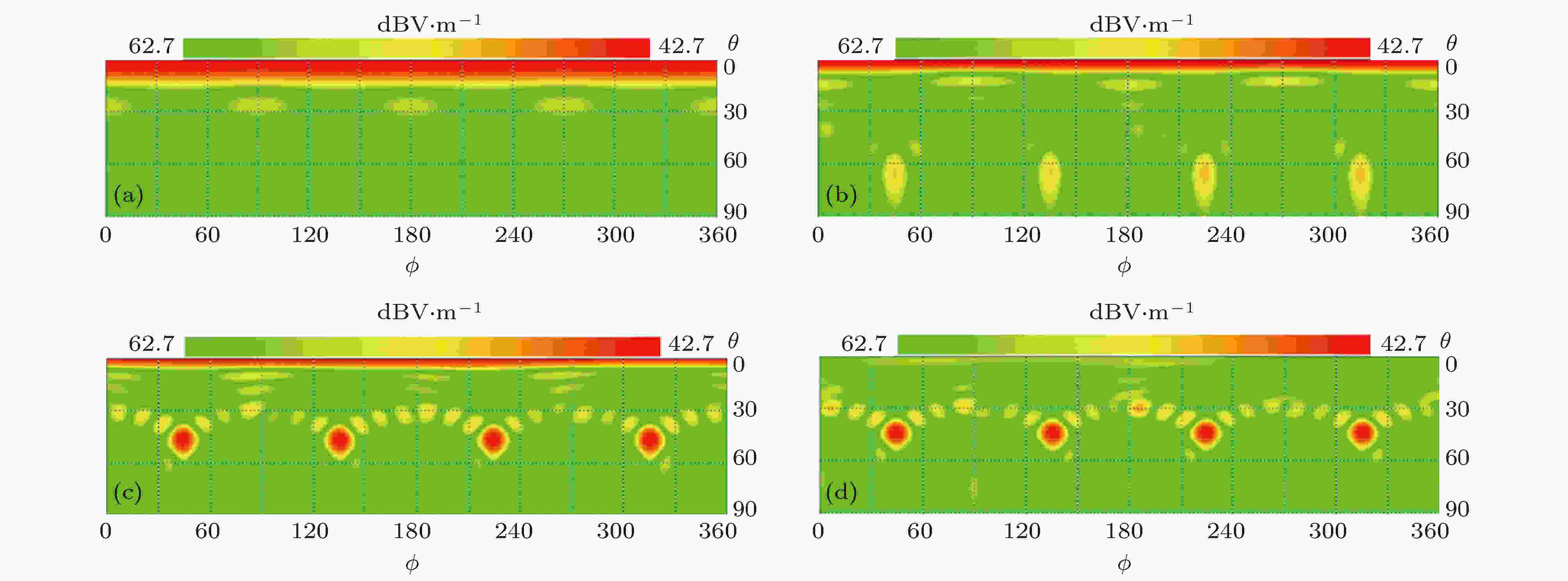图 7 棋盘式1-bit太赫兹频率编码器　(a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的二维电场图
Figure7. Chessboard 1-bit terahertz frequency coding metasurface: Two-dimensional electric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

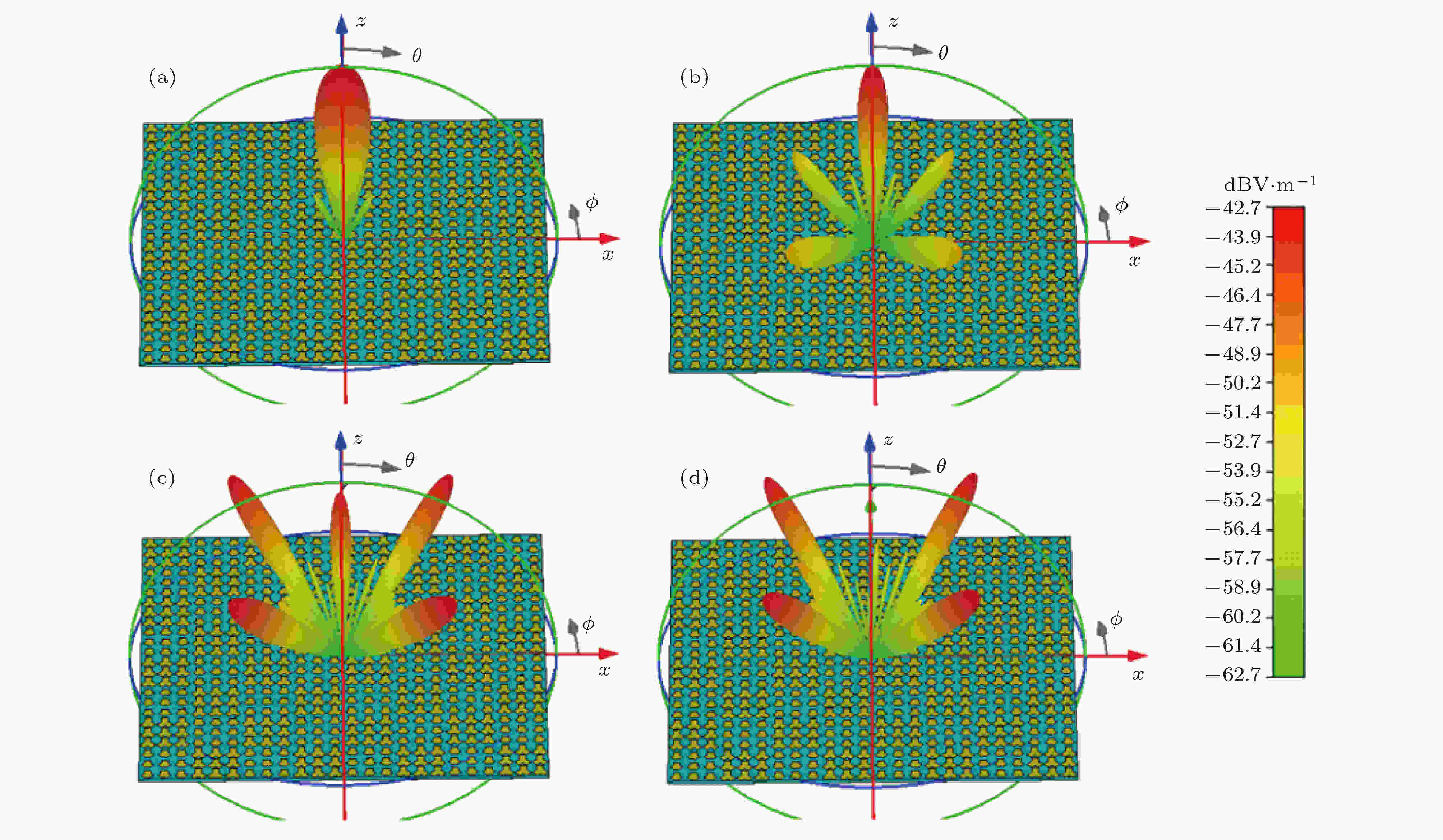图 6 棋盘式1-bit太赫兹频率编码器　(a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Figure6. Chessboard 1-bit terahertz frequency coding metasurface: Three-dimensional far-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

图6(a)—(d)给出了棋盘式分布的1-bit太赫兹频率编码器远场散射能量随频率变化而变化的过程.随着频率的增加, 在初始频率f₀ = 0.4 THz处产生的反射太赫兹波光束沿着z轴主瓣逐渐变化为四束对称光束, 主瓣能量变得越来越弱, 四束对称光束能量越来越强. 当频率f₁ = 1.0 THz时, 在俯仰角θ₂ = 45°处产生四束对称光束, 此时θ₂ = sin^–1(λ/Γ₂) = 45°(Γ₂ = $\sqrt {\rm{2}} $×3×100 μm ≈ 424 μm), 结果如图6(d)所示. 图7(a)—(d)分别为对应图6(a)—(d)的二维电场图, 从图7中的光斑点位置也很好地验证了计算结果.

为进一步验证太赫兹频率编码器远场能量模式随频率的变化关系, 本文设计了2-bit太赫兹频率编码器. 2-bit太赫兹频率编码器粒子采用A, B, C和D四个单元, 图2(e)和图2(f)分别显示了四个单元频率上的反射率和相应的相位曲线. 从图2中可以清楚地看出, 四个单元在初始频率f₀ = 0.4 THz处具有几乎相同的初始相位响应α₀ ≈ $8{\text{π}} /9 $, 由 (3) 式计算得到A, B, C和D四个基本单元的相位灵敏度为

$\left\{ {\begin{aligned}& {\alpha _1^{\rm A} = [{\varphi ^{\rm{A}}}({f_1}) - {\varphi ^{\rm{A}}}({f_0})]/({f_1} - {f_0}) = ( - 158^\circ - 154^\circ )/(1.0 - 0.4) \approx 0/{\rm{1}}{\rm{.2(rad/THz)}}} \\ & {\alpha _1^{\rm B} = [{\varphi ^{\rm{B}}}({f_1}) - {\varphi ^{\rm{B}}}({f_0})]/({f_1} - {f_0}) = ( - 97^\circ - 157^\circ )/(1.0 - 0.4) \approx {\text{π}}/{\rm{1}}{\rm{.2}}({\rm{rad/THz}})} \\ & {\alpha _1^{\rm C} = [{\varphi ^{\rm{C}}}({f_1}) - {\varphi ^{\rm{C}}}({f_0})]/({f_1} - {f_0}) = (20^\circ - 158^\circ )/(1.0 - 0.4) \approx 2{\text{π}}/{\rm{1}}{\rm{.2}}({\rm{rad/THz}})} \\ & {\alpha _1^{\rm D} = [{\varphi ^{\rm{D}}}({f_1}) - {\varphi ^{\rm{D}}}({f_0})]/({f_1} - {f_0}) = (114^\circ - 160^\circ )/(1.0 - 0.4) \approx 3{\text{π}}/{\rm{1}}{\rm{.2}}({\rm{rad/THz}})} \end{aligned}} \right..$

上述计算可得到A, B, C和D四个单元在初始频率处具有相同的相位响应, 但在频率范围内相位灵敏度却不一样. 当太赫兹波垂直入射到太赫兹频率编码器时, 由太赫兹编码器产生的远场能量与${\left| {1 + {{\rm{e}}^{{\rm{j}}\varphi }}} \right|^2}$成正比, 其中φ是基本单元间的相位差, 只需用同一个太赫兹频率编码器改变不同的工作频率点就可以实现对太赫兹波反射能量的不同控制.
为了观察其产生的现象, 利用CST对图3(c)和图3(d)两种设计方案进行了仿真, 结果如图8—图11所示. 图8和图10分别是以序列“00-00, 00-01, 00-10, 00-11”沿x方向排列的2-bit周期太赫兹频率编码器的三维远场散射以及二维电场图. 图9和图11分别是2-bit随机太赫兹频率编码器的三维远场散射以及二维电场图. 图8(a)和图9(a)是在初始频率f₀ = 0.4 THz时, 太赫兹波垂直照射到2-bit周期太赫兹频率编码器所产生的结果. 由于四个基本单元在f₀ = 0.4 THz处相位差为
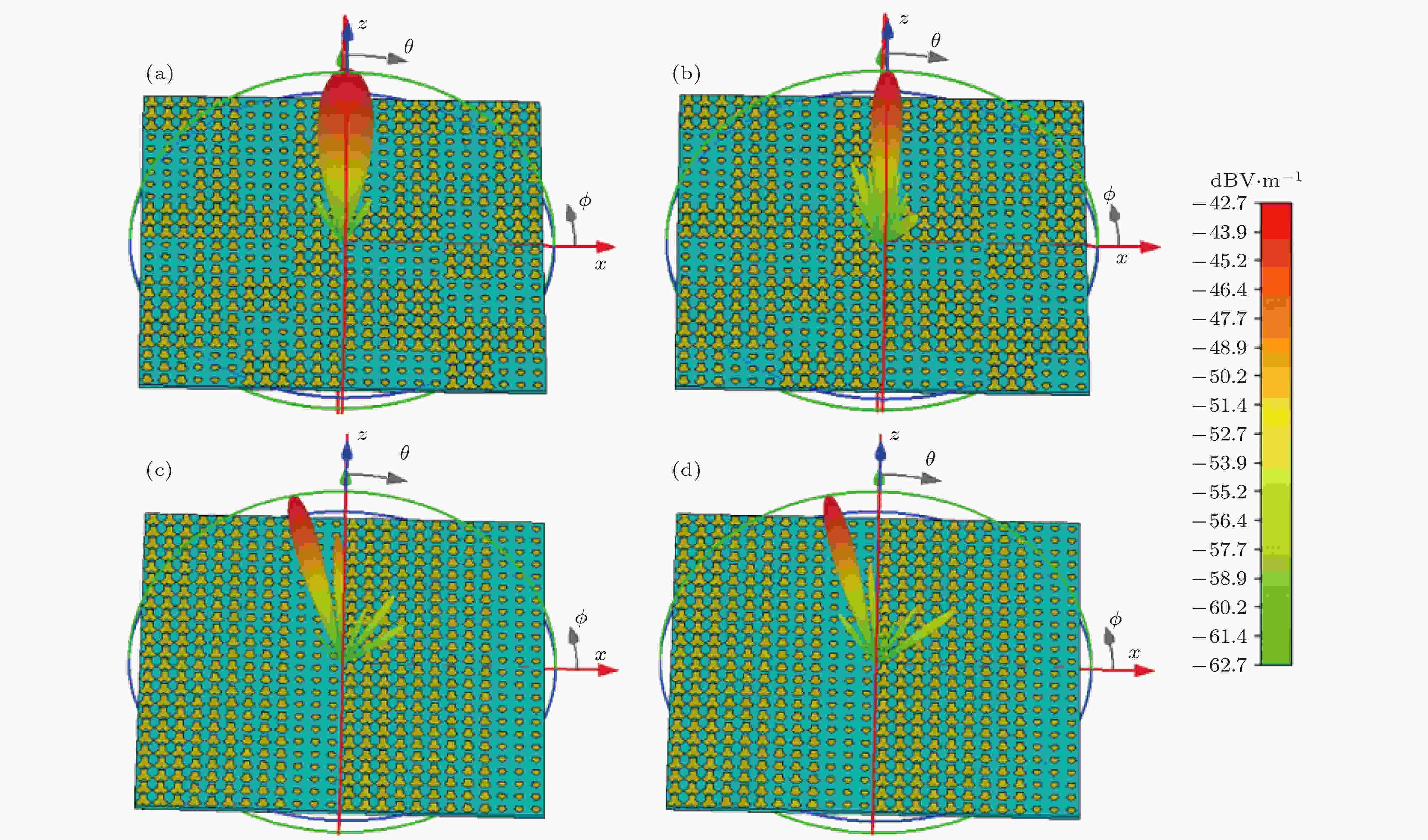图 8 “00-00, 00-01, 00-10, 00-11”周期排布的2-bit太赫兹频率编码器　(a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Figure8. 2-bit periodic terahertz frequency coding metasurfacearranged along x direction with “00-00, 00-01, 00-10, 00-11” sequence: Three-dimensionalfar-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

图 11 2-bit太赫兹随机频率编码器　(a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时二维电场图
Figure11. 2-bit random terahertz frequency coding metasurface:two-dimensional electric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

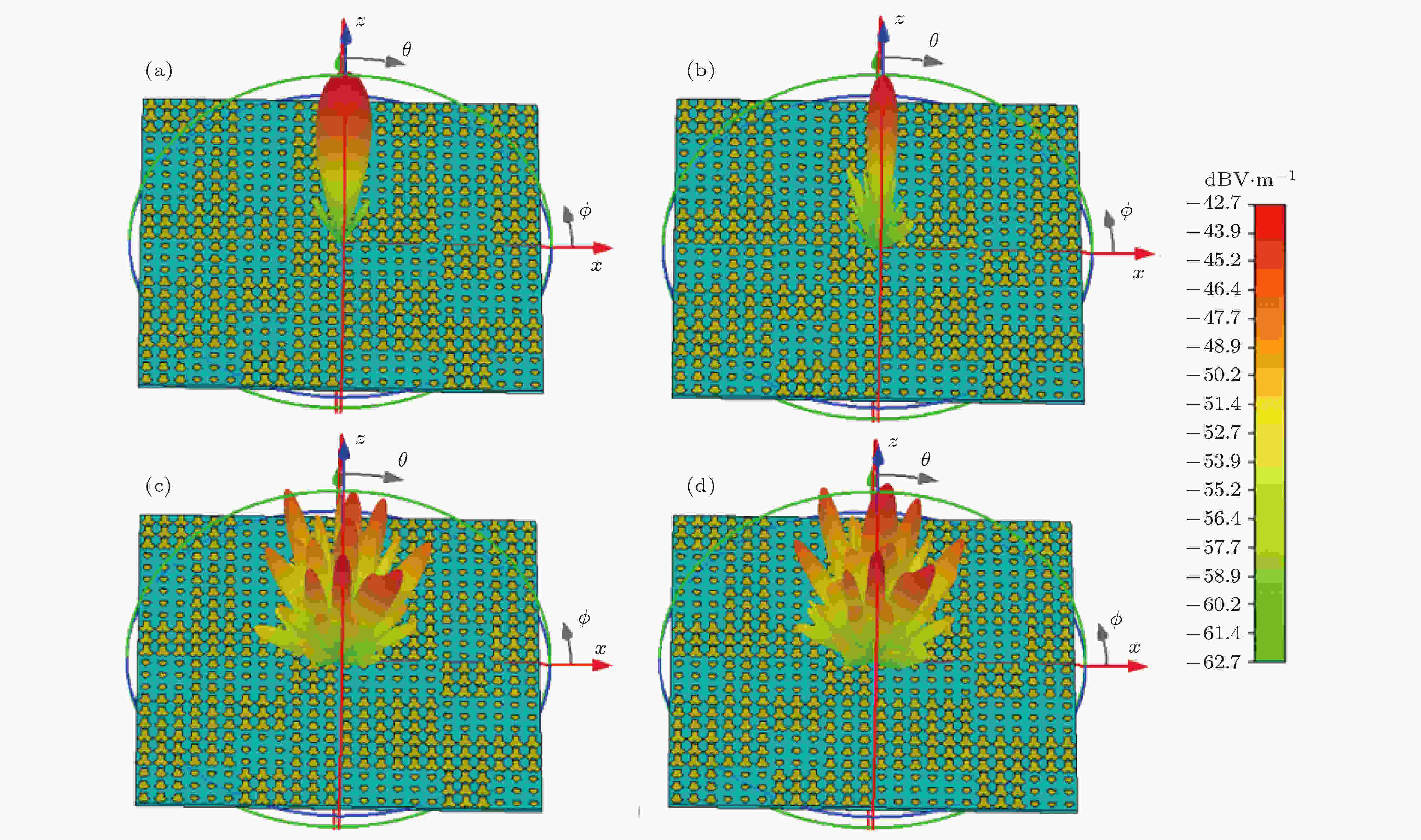图 10 2-bit太赫兹随机频率编码器　(a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Figure10. 2-bit random terahertz frequency coding metasurface: Three-dimensional far-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

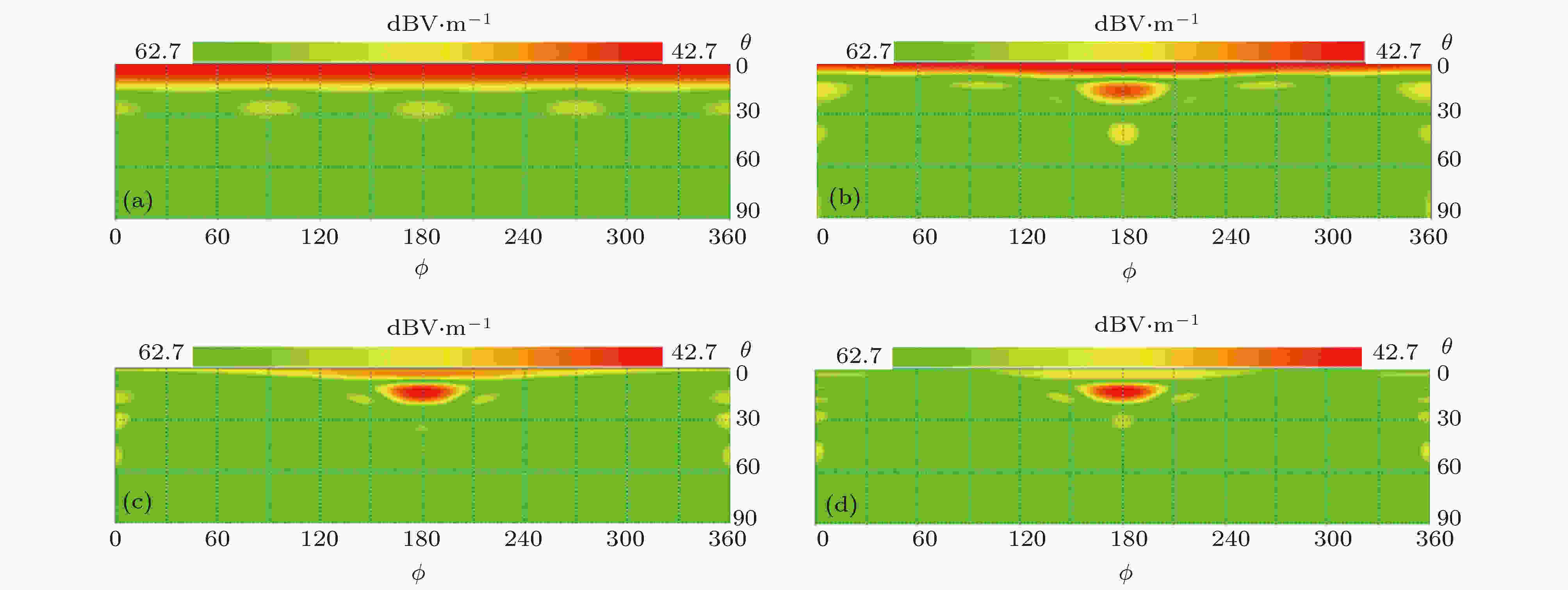图 9 “00-00, 00-01, 00-10, 00-11”周期排布的2-bit太赫兹频率编码器　(a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的二维电场图
Figure9. 2-bit periodic terahertz frequency coding metasurface arranged along x direction with “00-00, 00-01, 00-10, 00-11” sequence: Two-dimensionalelectric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

$\begin{split}&{\varphi ^{\rm{B}}}\left( {{f_0}} \right) - {\varphi ^{\rm{A}}}\left( {{f_0}} \right) \approx {\varphi ^{\rm{C}}}\left( {{f_0}} \right) - {\varphi ^{\rm{B}}}\left( {{f_0}} \right) \\ \approx & \; {\varphi ^{\rm{D}}}\left( {{f_0}} \right) \quad - {\varphi ^{\rm{C}}}\left( {{f_0}} \right) \approx {\varphi ^{\rm{A}}}\left( {{f_0}} \right) - {\varphi ^{\rm{C}}}\left( {{f_0}} \right) \approx 0.\end{split}$

当太赫兹波垂直照射到2-bit周期太赫兹频率编码器, 太赫兹波将沿着θ = 0o原路反射回去. 随着频率增加到f₁ = 1.0 THz时, 相邻单元间的相位差变为

$\begin{split} &{\varphi ^{\rm{B}}}\left( {{f_1}} \right) - {\varphi ^{\rm{A}}}\left( {{f_1}} \right) \approx {\varphi ^{\rm{C}}}\left( {{f_1}} \right) - {\varphi ^{\rm{B}}}\left( {{f_1}} \right) \\ \approx &\; {\varphi ^{\rm{D}}}\left( {{f_1}} \right) - {\varphi ^{\rm{C}}}\left( {{f_1}} \right) \approx {\varphi ^{\rm{A}}}\left( {{f_1}} \right) - {\varphi ^{\rm{C}}}\left( {{f_1}} \right)\\ \approx &\; {\text{π}}/2,\end{split}$

此时, 2-bit周期太赫兹频率编码器产生的结果如图8(d)和图9(d)所示. 从图8(d)可以看出, 以序列“00-00, 00-01, 00-10, 00-11”沿着x方向排列的2-bit周期太赫兹频率编码器, 垂直入射的太赫兹波由原本沿着θ = 0°原路反射, 并随着频率增加, 反射波束由原来一束指向z轴正方向的主能量转换为一束逐渐偏离z轴正方向光束(见图8(b)—(d)). 最终在f₁ = 1.0 THz处与z轴成θ₃ = 14.5°反射太赫兹波, 其中θ₃ = sin^–1(λ/Γ₃) = 14.5°(Γ₃ = 4×3×100 μm = 1200 μm), 其相对应的二维电场如图9(d)所示.
对于2-bit随机太赫兹频率编码器所得到的结果如图10(d)所示. 太赫兹波垂直入射后, 由原始一束主瓣变为逐渐被散射到多个方向, 形成了无数的太赫兹波光束, 其对应的二维电场如图11(d)所示. 根据能量守恒定律, 将极大地缩减每个光束的能量, 可以很好地缩减雷达散射截面. 在频率为1.0 THz下雷达散射截面缩减在θ = 0, φ = 0方向上最大可达29 dB, 如图12所示. 当垂直入射的太赫兹波频率介于f₀与f₁(从0.4 THz到1.0 THz)之间时, 2-bit随机太赫兹频率编码器将发生轻度漫反射现象, 形成越来越多的散射波, 使原本集中的太赫兹波能量分散到多个方向, 结果如图10(b)和图10(c)所示, 对应的二维电场如图11(b)和图11(c)所示.
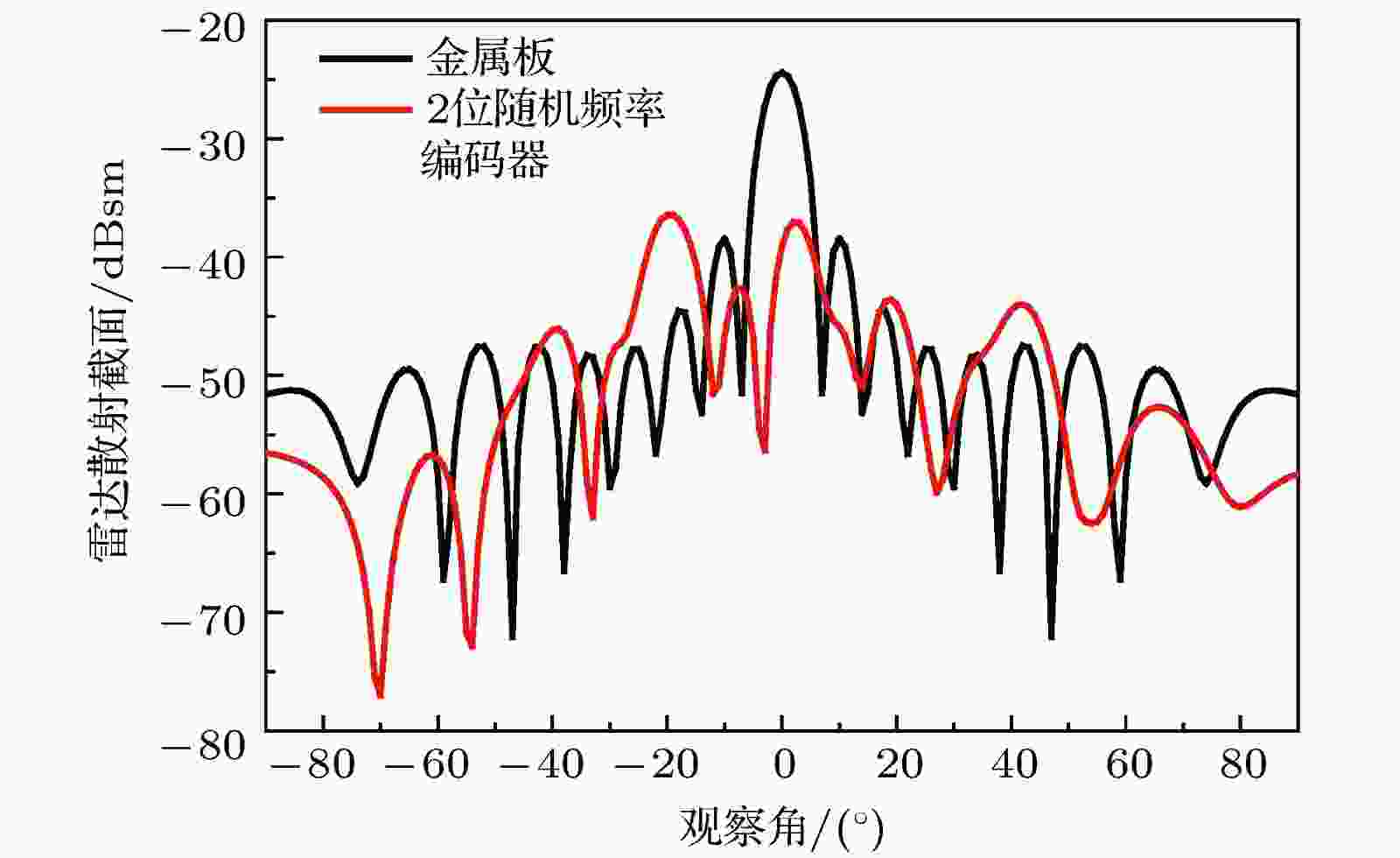图 12 2-bit太赫兹随机频率编码器和金属板在1.0 THz处的雷达散射截面分布
Figure12. Radar cross section distribution of 2-bit terahertz random frequency coding metasurface and metal plate at 1.0 THz.

根据广义斯涅耳定律, 当太赫兹波垂直照射到超表面时, 其反射角可表示为

$\theta = \sin {}^{ - 1}\left(\frac{{{\lambda _0}}}{{2{\text{π}}}}\frac{{{\rm{d}}\varphi }}{{{\rm{d}}x}}\right),$

式中, λ₀为对应频率f的波长, dφ/dx是分界面上沿x方向的相位梯度. 由于非周期性太赫兹频率编码器在工作频率上具有均匀分布的相位响应, 因此可以利用广义斯涅耳定律, 只需改变工作频率可以使主波束的方向发生变化, 即主瓣方向随频率的变化而变化. 采取3×3超级单元形式以A, B, C, D四个基本单元依次沿x方向排列组成非周期太赫兹频率编码器, 四个基本单元在整个工作频率范围内的相位响应为:

$\left\{ {\begin{aligned}& {{\varphi ^{\rm{A}}}(f) \approx \alpha _{\rm{0}}^{\rm{A}}+\alpha _{\rm{1}}^{\rm{A}}(f - {f_0}) = 8{\text{π}}/9} \\ & {{\varphi ^{\rm{B}}}(f) \approx \alpha _{\rm{0}}^{\rm{B}}+\alpha _{\rm{1}}^{\rm{B}}(f - {f_0}) = 8{\text{π}}/9 + {\text{π}}/0.6(f - {f_0})} \\ & {{\varphi ^{\rm{C}}}(f) \approx \alpha _{\rm{0}}^{\rm{C}}+\alpha _{\rm{1}}^{\rm{C}}(f - {f_0}) = 8{\text{π}}/9 + 2{\text{π}}/0.6(f - {f_0})} \\ & {{\varphi ^{\rm{D}}}(f) \approx \alpha _{\rm{0}}^{\rm{D}}+\alpha _{\rm{1}}^{\rm{D}}(f - {f_0}) = 8{\text{π}}/9 \!+\! 3{\text{π}}/0.6(f \!-\! {f_0})}.\end{aligned}} \right.$

联合上述方程可以得到奇异偏转角公式如下:

$\theta = {\sin ^{ - 1}}[0.{\rm{4}}2 \times (1 - {f_0}/f)],$

上式表明非周期性太赫兹编码器在整个工作频率中的调控性能, 即反射太赫兹波主瓣方向只与工作频率大小有关. 当频率f从初始频率f₀ = 0.4 THz增加到f₁ = 1.0 THz时, $0.{\rm{4}}2 \times (1 - {f_0}/f)$相应的从0增加到0.25, 此时垂直入射的太赫兹波的反射光束相应地从0°转移到14.5°, 反射太赫兹波三维远场如图13所示, 相应的二维电场如图14所示.
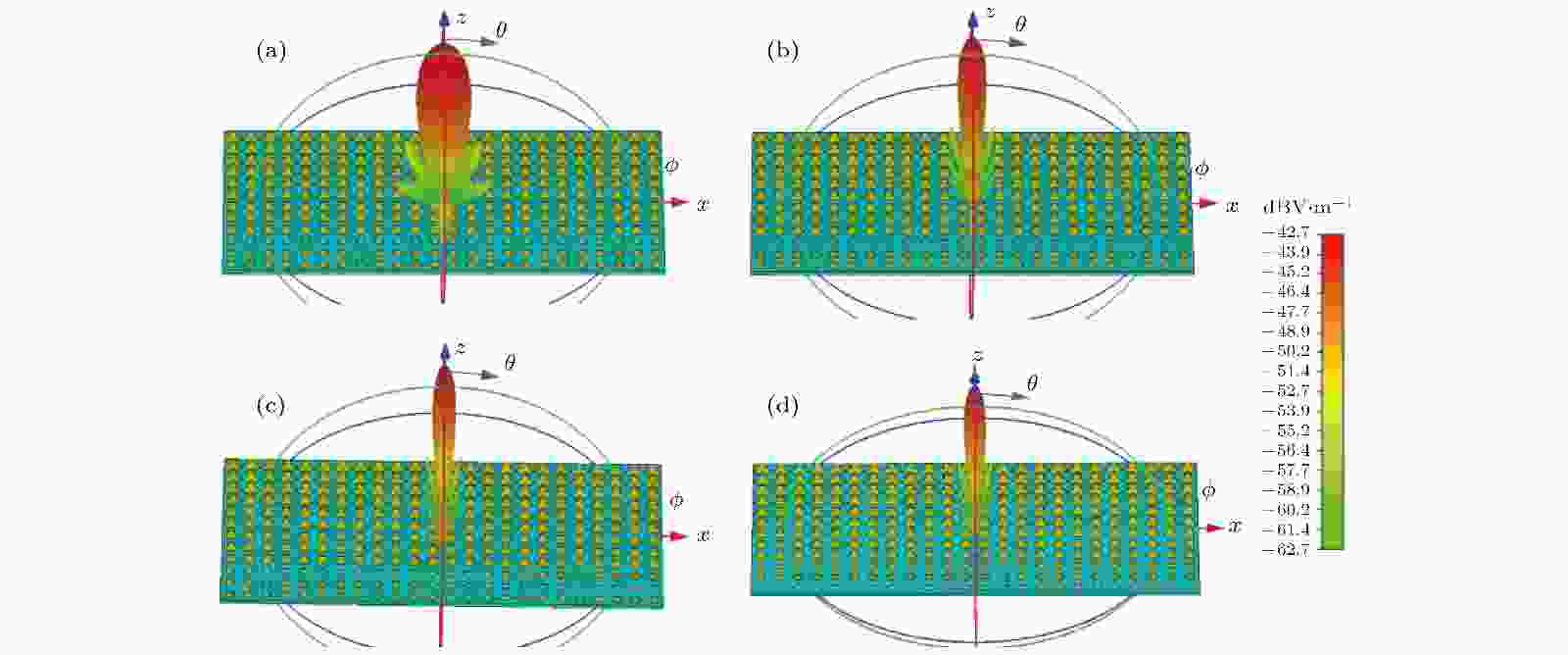图 13 2-bit非周期排布太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Figure13. Fig. 10. 2-bit non-periodic terahertz frequency coding metasurface: Three-dimensional far-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

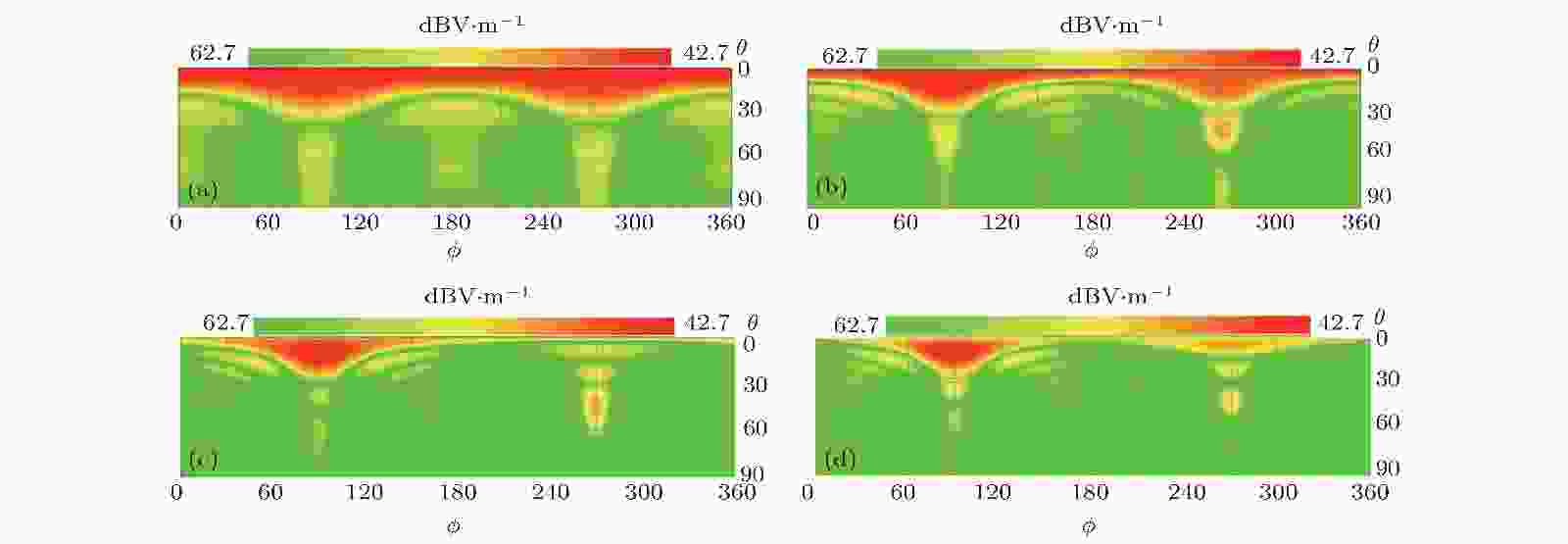图 14 2-bit非周期排布太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的二维电场图
Figure14. Fig. 10. 2-bit non-periodic terahertz frequency coding metasurface: Two-dimensional electric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.

利用了四个相同形状、不同尺寸的单元相位灵敏度不同的特性, 设计了一种人字形结构太赫兹频率编码器, 实现了从0.4—1.0 THz太赫兹波编码调控. 通过预设1-bit, 2-bit和非周期太赫兹编码, 实现了对太赫兹波能量反射波束任意角度的调控. 同样地, 在不重新设计结构的情况下, 随着工作频率的改变, 该器件也可以实现对太赫兹波能量反射角任意的调控. 而且还有效地减少了雷达散射截面, 在θ = 0, φ = 0方向上最大缩减值可达到29 dB. 数值计算和仿真模拟验证了这一特性, 在太赫兹波隐身中具有巨大应用价值.