摘要:纳米流动系统具有高效、经济等优势, 在众多领域具有广泛的应用前景. 因该类系统具有极高的表面积体积比, 致使界面滑移效应对流动具有显著影响. 本文采用分子动力学方法以两无限大平行非对称壁面组成的Poiseuille流动为对象, 分析了壁面粗糙度与润湿性变化对通道内流体流动的影响. 对于不同结构类型的壁面, 需要通过水动力位置来确定固液界面位置, 准确计算固液界面位置有助于更好地分析界面滑移效应. 研究结果表明, 上下壁面不对称会引起通道内流场参数分布的不对称, 壁面粗糙度及润湿性的变化会影响近壁面附近流体原子的流动特性, 由于壁面凹槽的存在, 粗糙壁面附近的数密度分布低于光滑壁面一侧. 壁面粗糙度及润湿性的变化会影响固液界面位置, 肋高变化及壁面润湿性对通道中速度分布影响较大, 界面滑移速度及滑移长度随肋高和润湿性的增大而减小; 肋间距变化对通道内流体流动影响较小, 界面滑移速度和滑移长度基本保持恒定.
关键词: 粗糙度/
润湿性/
界面滑移/
分子动力学

English Abstract

全文HTML

--> --> -->

对纳米流体的深入研究是科技微型化导致的必然趋势, 纳米流体具有优于常规介质的特性, 包括运输、传热、吸附等性能, 对纳米流体的深入研究将更有利于科技微型化的发展. 纳米量级流体在流动时存在许多微尺度效应, 包括分子力效应、低雷诺数效应以及表面张力效应等. 相比于宏观尺度, 微尺度条件下对流体流动规律的研究受实验条件和测量精度的限制, 使得数值模拟成为了微尺度流动的主要研究方法. 而以微观原子之间的作用模型为基础的分子动力学, 因不引入常规假设, 能以原子级精度描述流体在近邻壁面处的流动特性, 是目前研究微尺度流动问题的主要数值模拟方法.
通常宏观尺度下流体在通道内的流动特性都是基于无滑移边界条件进行研究, 因为壁面产生的表面效应对近壁处流体流动特性影响较小. 然而, 随着流动通道尺寸的减小, 比表面积急剧增加, 微尺度下固体壁面对近壁处流体的影响直接关系到通道内整体的流动特性分布^[1-3]. Sun和Ebner^[4]研究了固液界面间作用强度大小对流体流动特性的影响, 发现当固液原子间作用力较强时, 流体在壁面处几乎无滑移, 而当作用力较弱时, 流体在壁面处会产生较大的边界滑移. Voronov等^[5]利用分子动力学对Couette流动进行模拟, 结果显示滑移长度与接触角相关, 对于疏水性表面, 接触角会增大, 滑移长度也会随之增大, 但也会出现随着接触角增大滑移长度减小的情况. 胡海豹等^[6]利用分子动力学对超疏水纳米通道内流体流动特性进行研究, 结果表明当接触角大于150°时, 滑移速度和滑移长度出现随接触角增大而减小的反常现象, 并进一步证明了改变固液原子间的势能参数表征的润湿性不能用来准确表示超疏水壁面对流体的影响. Nagayama和Cheng^[7]对纳米通道内的Poiseuille流动进行分析, 发现改变壁面与流体间的势能参数以及添加在流体部分的驱动力均会影响固液界面间流体原子的运动特性, 固液间相互作用越强, 边界滑移速度越小, 而添加的驱动力越大, 滑移速度也越大. Barisik和Beskok^[8]以及Shi等^[9]利用智能壁分子动力学方法模拟研究了纳米通道内气体原子的流动特性, 结果表明近壁区域内气体的速度、密度和压力的变化趋势仅由壁面力场决定, 不受通道高度以及密度的影响. 张冉等^[10]利用分子动力学分析了纳米通道内近壁区域流体的流动特性, 同样发现近壁区域的气体流动特性仅由壁面力场决定, 壁面对气体原子的势能作用越强, 气体在近壁区域的密度越大, 直至形成吸附层. Voronov等^[5]利用分子动力学方法对Couette流动中流体的滑移现象进行了研究, 发现固液间势能强度以及平衡距离的减小均倾向于增大接触角, 而减小势能强度会增加滑移长度, 减小平衡距离会减少滑移长度, 说明接触角与滑移长度间的关系并不唯一. Cieplak^[11]同样利用分子动力学方法对Couette流动进行研究, 主要探究了固液间的作用强度以及不同流体介质对流体滑移的影响, 结果表明, 滑移长度与固液间的作用有直接关系, 而与流体介质无关.
可见, 目前科研工作者大多集中于进行固液间相互作用等因素对通道内流体流动影响规律的研究, 且固体表面多是光滑壁面. 实际上, 任何固体表面都不可能是绝对光滑的, 当宏观尺度转为纳微尺度, 流动通道尺度急剧减少, 比表面积也随之急剧增加, 固体表面的粗糙程度对流体流动的作用也相应凸显. 因此, 粗糙壁面对流动的影响机理研究已逐渐成为当前纳微尺度传热传质研究中的重点^[12]. 张程宾等^[13]利用分子动力学方法对含粗糙壁面纳米通道内的流体流动进行了研究, 发现粗糙壁面会限制近壁区流体原子的运动, 导致流体流动速度及滑移速度降低. Rahmatipour等^[14]利用分子动力学对含粗糙壁面的纳米通道内的肋高变化进行了研究, 结果显示, 相比于光滑壁面, 随着肋高的增大, 壁面附近流体的密度波动范围逐渐增大, 但波动的峰值均低于光滑壁面. Toghraie等^[15]对含纳米颗粒的粗糙通道内的流体流动特性进行了研究, 通过设定肋高与肋间距的比值来获取不同壁面粗糙度, 结果表明通道内流体的温度及速度分布并不随着粗糙度的增大而增大, 而是由凹槽内限制的流体原子数量决定, 限制的流体原子数量数量越多, 流体流动速度越小, 反之流动速度越大. 但由该文献的物理模型可知, 在研究粗糙度变化时, 粗糙壁面上肋的尺寸及数量也发生了变化, 故不能很好地诠释壁面肋间距及肋高变化对近壁区流体的影响.
综上所述, 目前研究壁面的粗糙度变化对流动的影响还不够详细, 而针对粗糙壁面润湿性变化的研究更是较少. 为深入揭示纳微尺度下粗糙壁面对流体流动的影响机理, 本文拟构建含粗糙壁面的纳米通道内流体流动的分子动力学模型, 并与光滑壁面进行对比, 分析粗糙壁面肋高及肋间距对流体流动特性的影响. 在此基础上, 讨论壁面润湿性对壁面附近流体原子的影响, 并揭示粗糙壁面与光滑壁面润湿性变化的异同.

纳米通道流体流动的分子动力学模型如图1(a)所示. 模拟通道尺寸为L_x × L_y × L_z = 18.20σ × 19.68σ × 7.87σ, 纳米通道上壁为光滑壁面, 下壁为粗糙壁面, 壁面由铜原子构成, 流体单原子氩均匀分布于上下壁面之间, 且均按照面心立方结构进行排列. 图1(b)为纳米结构示意图, 壁面长度为L_x = 18.20σ, 壁面厚度D = 2.95σ, 粗糙壁面肋间距为a, 肋高为h, 肋长度为b, 通道整体高度为H, 光滑壁面与切面间为平直流道, 高度为H'. 计算统计时, 对通道高度H进行分层, 其中统计流场中数密度分布时分为70层, 对速度分布进行统计时分为44层. 整个模拟系统在x, z方向上设置周期性边界条件, 在y方向上设置固定边界条件.
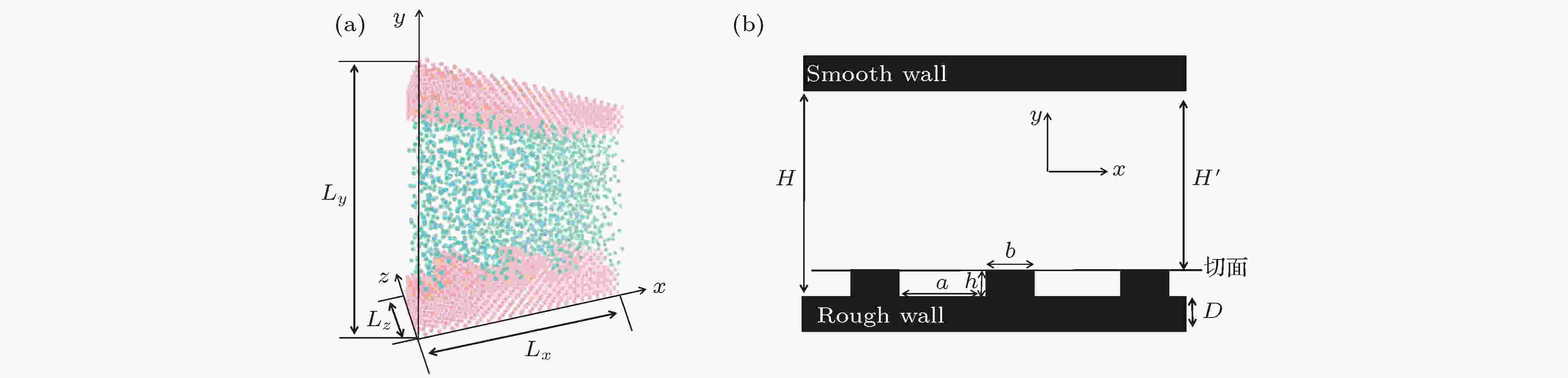图 1 (a) 模拟系统图; (b) 纳米结构示意图
Figure1. (a) Simulation system; (b) schematic of nanostructure.

流体原子间以及固液原子间的势能作用均采用Lennard-Jones (12-6)势能模型, 其表达式为

$U({r_{ij}}) = \left\{ \begin{aligned}& 4\varepsilon \left[ {{{\left(\frac{\sigma }{{{r_{ij}}}}\right)}^{12}} - {{\left( {\frac{\sigma }{{{r_{ij}}}}} \right)}^6}} \right], \quad r < {r_{\rm{c}}}, \\ & 0, \quad\quad\quad\quad \quad \quad \quad \quad \quad \quad \quad\; r \geqslant {r_{\rm{c}}},\end{aligned} \right. $

式中${r_{ij}}$为原子间的距离, $\varepsilon $为能量参数, $\sigma $为尺寸参数, ${r_{\rm{c}}}$为截断半径. 流体氩原子间的能量参数$\varepsilon = 1.67 \times {10^{ - 21}}$ J, 尺寸参数$\sigma = 0.3405$ nm. 壁面固体原子势能参数${\varepsilon _{\rm{s}}} = 40\varepsilon $, 尺寸参数${\sigma _{\rm{s}}} = 0.69\sigma $, 截断半径取${r_{\rm{c}}} = 2.5\sigma $.
固液原子间的作用力大小决定了壁面润湿性, 流体在壁面铺展得越充分, 固液界面间的接触角越小, 可认为润湿性越好. 而对于光滑壁面而言, 接触角的理论公式为

$\cos \theta = 2\frac{{{\varepsilon _{{\rm{sl}}}}}}{\varepsilon } - 1, $

式中$\theta $为光滑壁面接触角, ${\varepsilon _{{\rm{sl}}}}$为固液原子间的能量参数. 而对于粗糙壁面, (2)式将不再适用, 针对本文所研究的物理模型, 粗糙壁面润湿性可表示为

$\cos {\theta _r} = r\cos \theta, $

$r = \frac{{b + a + 2h}}{{b + a}}, $

式中$r$表示粗糙壁面的粗糙程度; $a$, $b$及$h$为图1(b)中所示参数. 令$\dfrac{{{\varepsilon _{{\rm{sl}}}}}}{\varepsilon } = c$, $c$为固液原子间的势能系数. 本文模拟工况与对应粗糙度下的接触角如表1所列.

模拟工况	r	θ/(°) (c = 1.0)	θ/(°) (c = 0.75)	θ/(°) (c = 0.5)	θ/(°) (c = 0.25)
h = 0	0	0	60	90	120
h = 0.45σ, a = 3.6σ	1.143	0	55.21	90	124.79
h = 0.9σ, a = 3.6σ	1.286	0	50	90	130
h = 1.35σ, a = 3.6σ	1.429	0	44.44	90	135.56
h = 1.8σ, a = 3.6σ	1.571	0	38.22	90	141.78
h = 1.8σ, a = 2.7σ	1.667	0	33.64	90	146.36
h = 1.8σ, a = 4.5σ	1.500	0	41.38	90	138.62
h = 1.8σ, a = 5.4σ	1.444	0	43.80	90	136.20

表1不同模拟工况下对应的粗糙度与接触角
Table1.Corresponding roughness and contact angle under different simulation conditions.

对于壁面原子与流体原子间的尺寸参数σ_sl, 由Lorentz-Berthelot混合法进行计算:

${\sigma _{{\rm{sl}}}} = \frac{{(\sigma + {\sigma _{\rm{s}}})}}{2}.$

平板间的Poiseuille流动是通过在x方向上施加外部驱动力来驱动流体流动的, 并利用抛物线求解Navier-Stokes方程. Poiseuille流动被定义为在通道高度H (y方向上由0到H)内的流动, Navier-Stokes方程可简化为^[16]

$\frac{{{\partial ^2}{u_x}}}{{\partial {y^2}}} = - \frac{{\rho {g_x}}}{{\mu} }, $

式中${\mu} $为剪切黏度, ${u_x}$为x方向上的流动速度, $\rho $为流体密度. 对(6)式连续进行两次积分, 将中心对称条件$\dfrac{{\partial {u_x}}}{{\partial y}}\left| {_{y = \frac{H}{2}}} \right. = 0$和边界滑移条件${u_x}\left| {_{y = 0}} \right. = $${u_{\rm{s}}}$或${u_x}\left| {_{y = H}} \right. = {u_{\rm{s}}}$依次代入, 其中${u_{\rm{s}}}$为边界滑移速度, Poiseuille流动的速度场可表示为

${u_x} = \frac{{\rho {g_x}}}{{2{\mu} }}y(H - y) + {u_{\rm{s}}}.$

固液界面间的滑移规律可以由滑移长度${l_{\rm{s}}}$表示, 表达式为^[17-20]

${l_{\rm{s}}} = \frac{{{u_{\rm{s}}}}}{{{{(\partial {u_x}/\partial y)}_{\left| y \right| = H}}}}, $

式中${(\partial {u_x}/\partial y)_{\left| y \right| = H}}$为固液界面处流体的速度梯度. 对于粗糙壁面滑移长度的确定, 需要根据水动力位置来研究^[21]. 图2(a)和图2(b)所示分别为Couette流动和Poiseuille流动示意图, 图2(a)中${y_{\rm{C}}}$为外推线性的速度直线达到壁面速度时对应的位置, 图2(b)中${y_{\rm{P}}}$为外推抛物线的速度曲线达到壁面速度的对应位置. 通过文献[21]可知, 粗糙壁面滑移长度可表示为${l_{\rm{s}}} = \sqrt {(y_{\rm{C}}^2 - y_{\rm{P}}^{{2}})} $, 而水动力位置可表示为${y_{\rm H}} = {y_{\rm{C}}} + {l_{\rm{s}}}$.
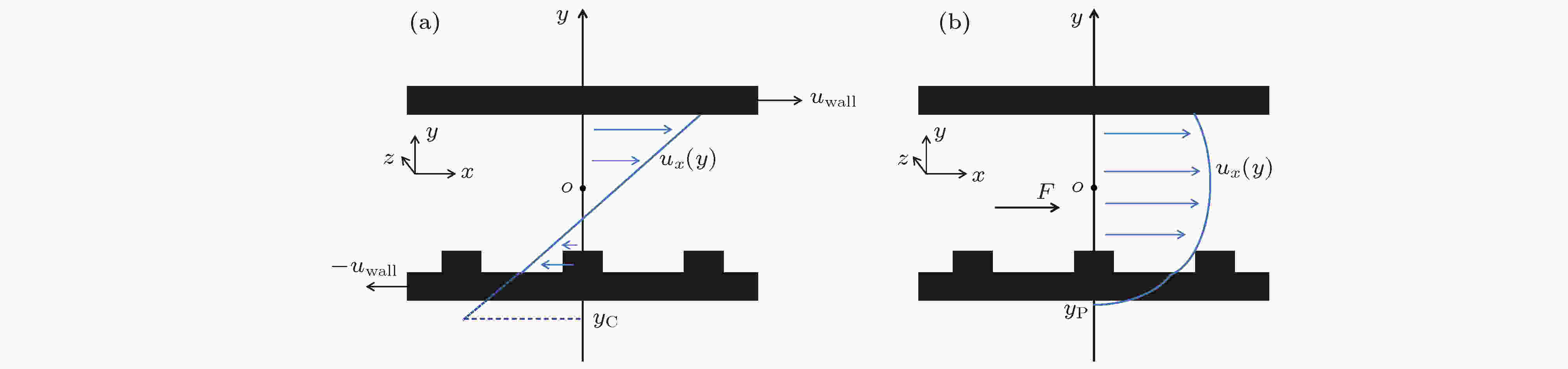图 2 模型结构示意图　(a) Couette流动; (b) Poiseuille流动
Figure2. Schematic of nanostructure: (a) Couette flow; (b) Poiseuille flow.

本文模拟过程中, 改变壁面粗糙度会影响通道内流体密度与压力的变化, 但变化幅度较小, 通道中流体原子的密度基本保持在(1.23 ± 0.01) g/cm³范围内, 造成的计算误差可以忽略. 粗糙壁面肋的长度b = 2.7σ, 肋的数量为3. 采用Velocity-Verlet算法对流体原子运动方程进行求解, 时间步长为1 fs. 首先利用正则系综对初始模型进行弛豫, 利用Nose-Hoover恒温算法将系统温度恒定在$T = 0.827\varepsilon /{k_{\rm{B}}}$, 流体原子的速度遵循高斯分布, 进行50万步使系统达到稳定. 弛豫后对模型入口处厚度为2.0σ的流体区域施加沿x正方向的水平驱动力F = 0.05ε/σ, 采用正则系综对系统进行温度控制, 共运行400万步, 前200万步使系统达到稳定, 后200万步对流场中所需参数进行计算统计. 分析模型水动力位置时需要计算Couette流动的速度场分布, 设置上下壁面在水平位置上以相同的速度反向运动, 速度大小为$v = 0.15\sqrt {\varepsilon /m} $. 模拟采用LAMMPS程序编写^[22].

为了验证模型及参数设置的正确性, 本文基于两平行光滑平板间的Poiseuille流动, 对不同壁面润湿性下流体在通道内的密度分布进行验证. 具体参数设置如下: 流体采用单原子氩, 其中$\varepsilon = 1.67 \;\times$$ {10^{ - 21}}$ J, $\sigma = 0.3405$ nm; 固液原子间的距离参数${\sigma _{{\rm{sl}}}}=0.2872$ nm, 无量纲化后, 取固液原子间的势能系数c = 2.0, 1.0, 0.6, 0.2; 上下壁面设置为固体刚性壁面, 截断半径r_c = 2.5σ.
图3所示为不同固液原子间势能系数c对应的微通道内流体的无量纲密度分布. 由图3可知, 模拟数据与文献[23]所给数据基本相符, 在近壁面区域内, 由于表面效应的存在使得流体密度分布均出现了有序振荡现象, 流体密度不均匀; 而在通道中心的主流区, 流体受壁面的影响较小而趋近于平缓. 因此, 可认为本文建立理论模型、选用算法及编写的程序准确可靠.
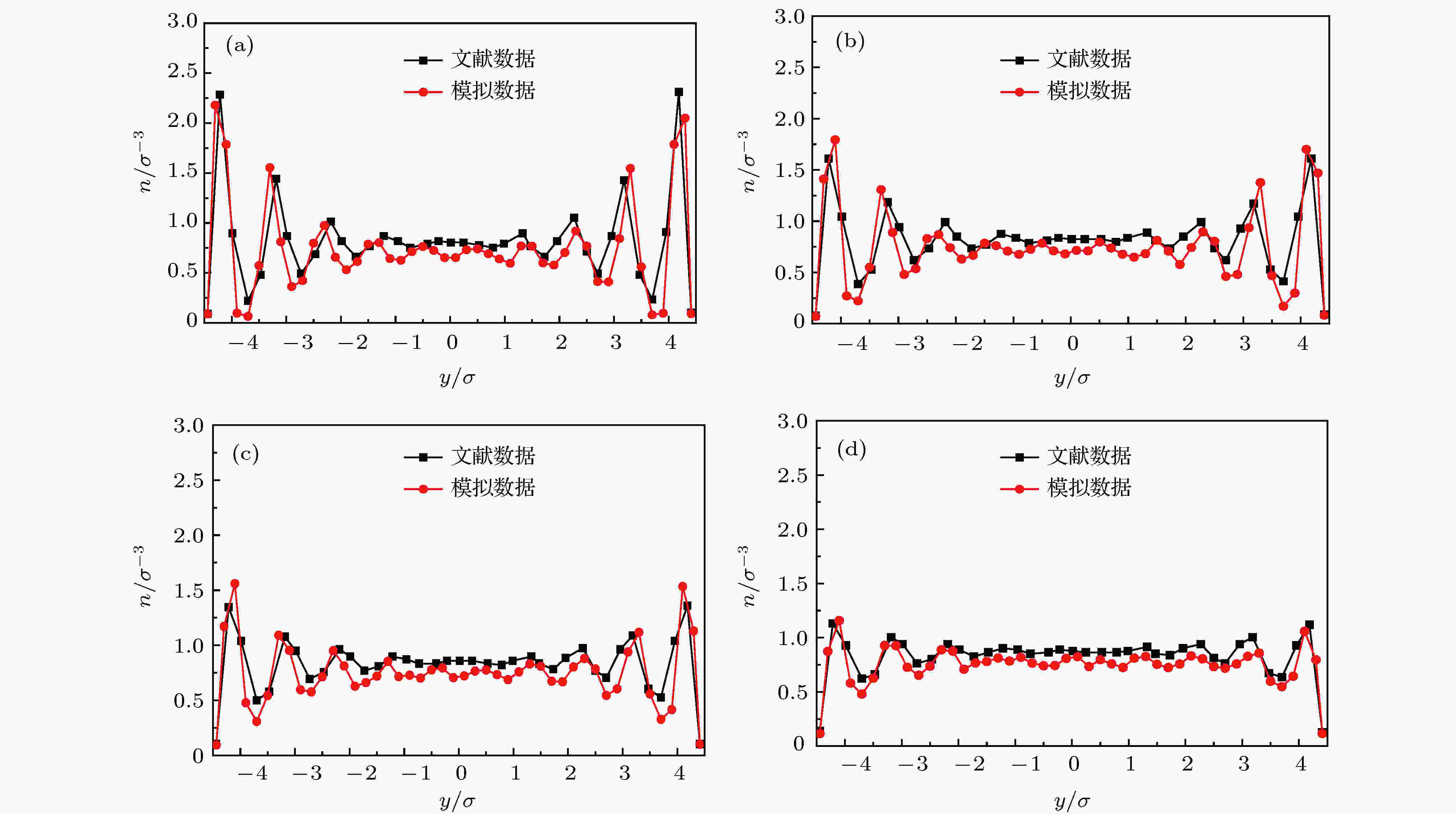图 3 不同势能系数c下流体沿z方向的密度分布　(a) c = 2.0; (b) c = 1.0; (c) c = 0.6; (d) c = 0.2
Figure3. Density profiles in the z-direction with different energy coefficient c: (a) c = 2.0; (b) c = 1.0; (c) c = 0.6; (d) c = 0.2.

2

-->

4.1.壁面粗糙度变化对流动特性的影响

本节以固液原子间势能系数c = 0.75, 对应的光滑接触角θ = 60°时的工况为例. 通过改变粗糙壁面上肋高及肋间距研究壁面粗糙度对通道内流体数密度及速度分布的影响.
3 -->

4.1.1.数密度分布

为研究肋高变化对近壁区流体数密度的影响, 固定肋间距$a = 3.6\sigma $不变, 分别取肋高$h = 0.5\sigma ,$$1.0\sigma ,1.5\sigma ,2.0\sigma $, 研究微通道内流体流动数密度分布曲线规律. 如图4所示, 横坐标为沿y方向的高度, 纵坐标为无量纲数密度$\rho * = \rho {\sigma ^3}$. 由图4可知, 由于壁面效应使得近壁区流体原子分布不均匀, 近壁区域流体数密度分布出现明显的振荡现象, 而通道主流区域流体受壁面影响较小, 数密度分布基本保持恒定. 由于通道壁面形状的不对称, 导致流场中数密度分布的不对称, 由图4(a)和图4(b)所示, 光滑壁面附近流体的数密度波动幅度要大于粗糙壁面, 且呈现逐渐衰减趋势. 通过改变肋高h来改变壁面粗糙度, 实现不同粗糙表面构造. 图4(a)结果显示, 当h较小时, 近壁区流体数密度波动呈现逐渐衰减趋势, 但随着肋高的增大, 近壁区流体数密度分布出现一次回升现象, 这是由于凹槽内的壁面与切面处的壁面对流体均有影响, 导致数密度分布呈现衰弱、增强、再衰弱的趋势. 为研究肋间距a变化对通道内流体数密度分布的影响, 固定肋高$h = 2.0\sigma $不变, 分别取长度$a = 2.7\sigma ,\;3.6\sigma ,\;4.5\sigma ,$$5.4\sigma $, 结果如图5所示. 由图5(a)和图5(b)可知, 纳米通道内流体在不同肋间距下数密度的振荡周期一致, 肋间距a变化对近壁区数密度影响较小. 因此, 可认为肋间距a的变化基本不影响壁面粗糙度对流体数密度分布.
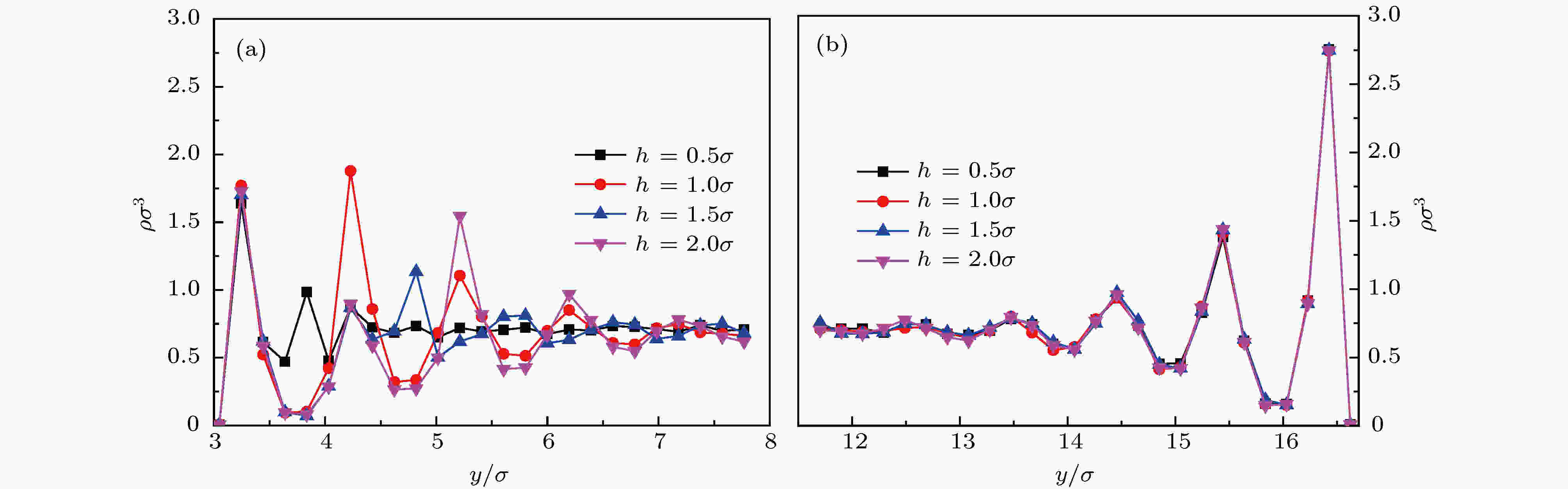图 4 肋高h对壁面附近流体数密度分布的影响　(a)粗糙壁面; (b)光滑壁面
Figure4. Effect of rib height h on the distribution of fluid number density near wall surface: (a) Rough wall surface; (b) smooth wall surface.

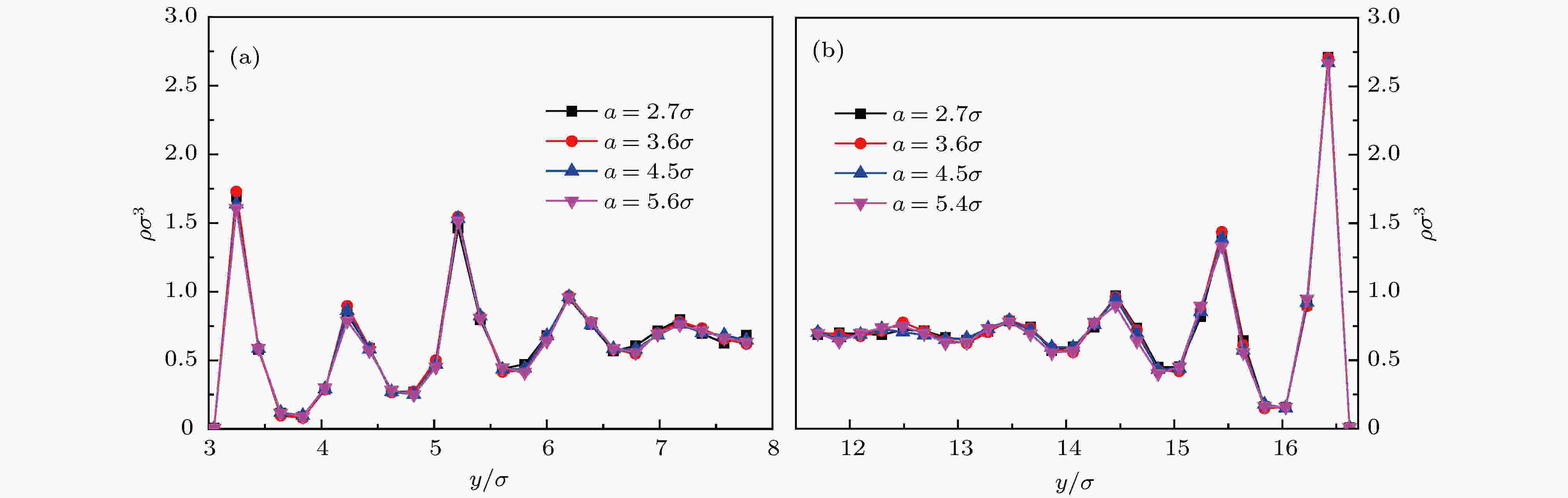图 5 肋间距a对壁面附近流体数密度分布的影响　(a)粗糙壁面; (b)光滑壁面
Figure5. Effect of rib spacing a on the distribution of fluid number density near wall surface: (a) Rough wall surface; (b) smooth wall surface.

3 -->

4.1.2.速度分布

壁面粗糙度变化引起的通道内流体数密度的变化, 也会导致通道内流体流速分布的变化. 为确定模型水动力位置, 分别计算Couette流动及Poiseuille流动时通道内的速度分布, 更深一步地分析边界滑移机理. 图6(a)和图6(b)为不同肋高对两种流动状态下速度分布的影响, 横坐标为沿y方向上的通道高度分布, 纵坐标为无量纲速度$u * = u/{(\varepsilon /m)^{1/2}}$. 图6结果显示, 微通道内流体速度分布呈现不对称性, 壁面粗糙度的存在使近壁区流体剪切产生了额外黏性耗散, 其次粗糙壁面凹槽内流体原子的运动受到限制, 难以从凹槽内逃脱进入主流区域, 导致Couette流动中壁面更容易带动流体运动, 速度大小分布高于光滑壁面一侧, 而在Poiseuille流动中则刚好相反, 流体的运动受到壁面的阻碍, 速度大小分布低于光滑壁面一侧. 随着肋高h的增大, 凹槽内限制的流体原子数量增多, 产生的黏性耗散越大, 不同结构壁面附近的速度分布差异越明显. 通过两种流动状态下的速度分布可推算出固液边界位置及滑移长度, 本文主要分析Poiseuille流动时的滑移机理, 通过施加不同外部驱动力F = 0.03ε/σ, F = 0.05ε/σ, F = 0.07ε/σ来获取滑移长度计算的标准差η, 并取不同驱动力下滑移长度的平均值作为分析结果. 图7所示为不同肋高h下滑移长度标准差分布. 图8所示为不同肋高h对Poiseuille流动中通道内滑移速度及滑移长度的影响. 分析结果显示, 光滑壁面一侧的滑移速度及滑移长度要高于粗糙壁面一侧, 随着肋高h的增大, 粗糙壁面一侧滑移速度及滑移长度逐渐减小, 与Schmatko等^[24]研究粗糙高度对界面处滑移速度的影响结论一致. 图9为肋间距a变化对两种流动状态下速度分布的影响. 由图9可知, 两种流动状态下肋间距a的变化对流场中速度分布影响较小, 这是由于肋间距a变化不会产生额外的黏性耗散, 且凹槽限制流体原子的数量不会产生太大差异. 图10为不同肋间距a下滑移长度标准差分布. 图11(a)和图11(b)为肋间距a变化对Poiseuille流动时通道内滑移效应的影响, 可以看出肋间距a变化对滑移速度及滑移长度的影响较小. 通过分析壁面粗糙度对速度分布的影响, 发现肋高h的变化会影响水动力位置的变化, 对边界滑移影响较大; 而肋间距a变化对通道内速度分布影响较小, 水动力位置变化不大, 故对边界滑移影响较小.
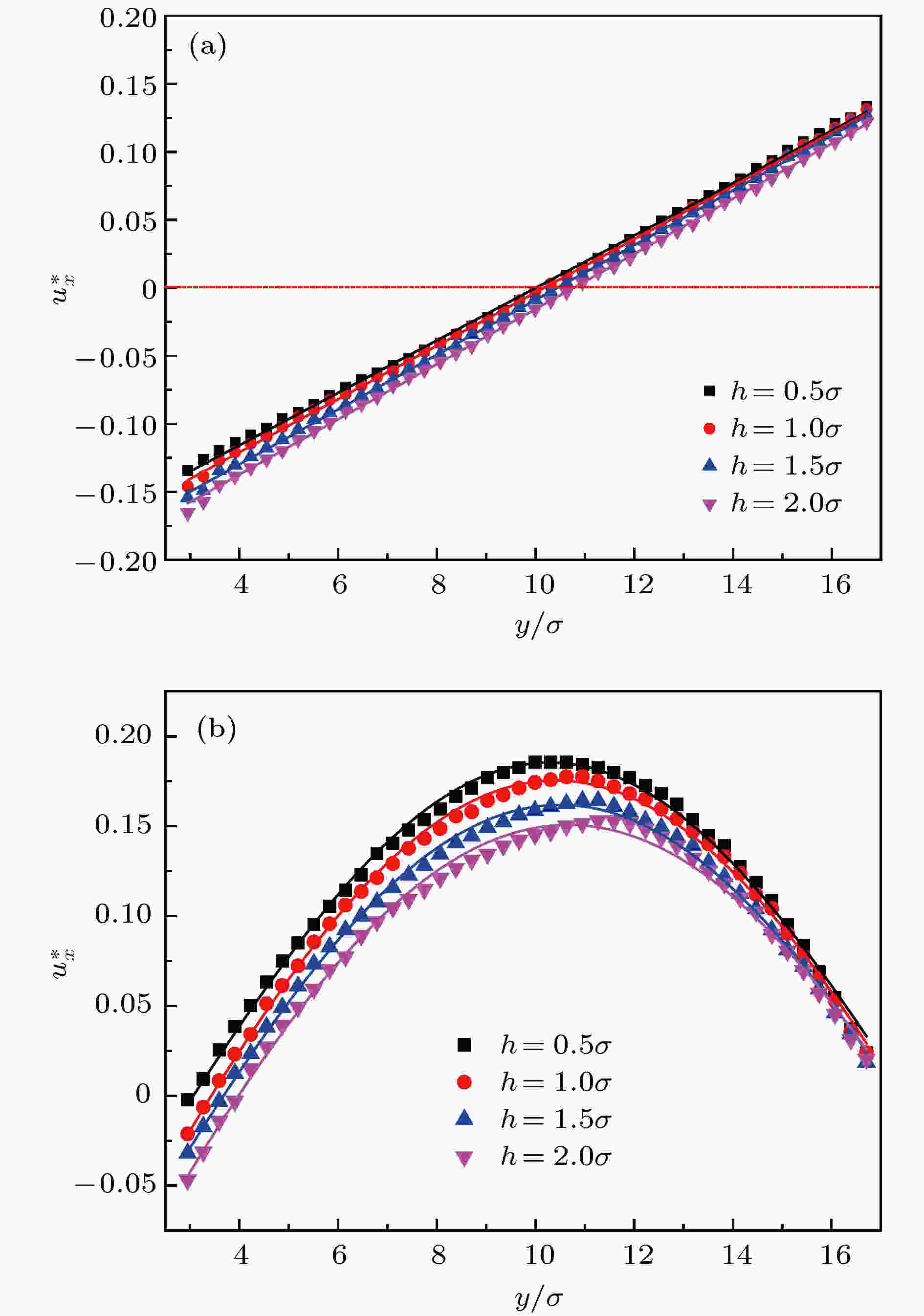图 6 不同肋高h下流体沿y方向的速度分布　(a) Couette流动; (b) Poiseuille流动
Figure6. Velocity profiles in the y-direction with different rib height h: (a) Couette flow; (b) Poiseuille flow.

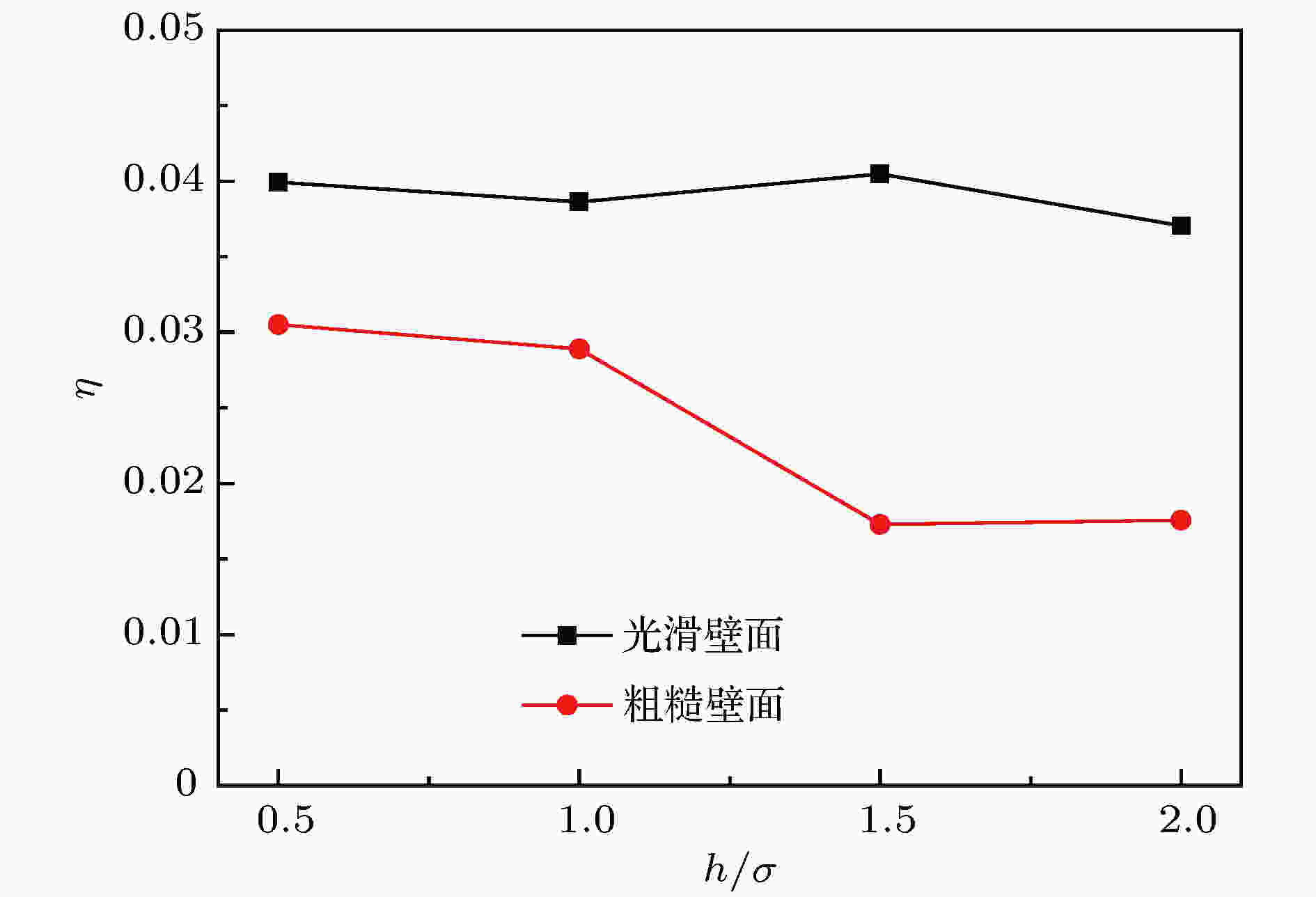图 7 不同肋高h下滑移长度标准差分布
Figure7. Standard deviation distribution of slip length with different rib height h.

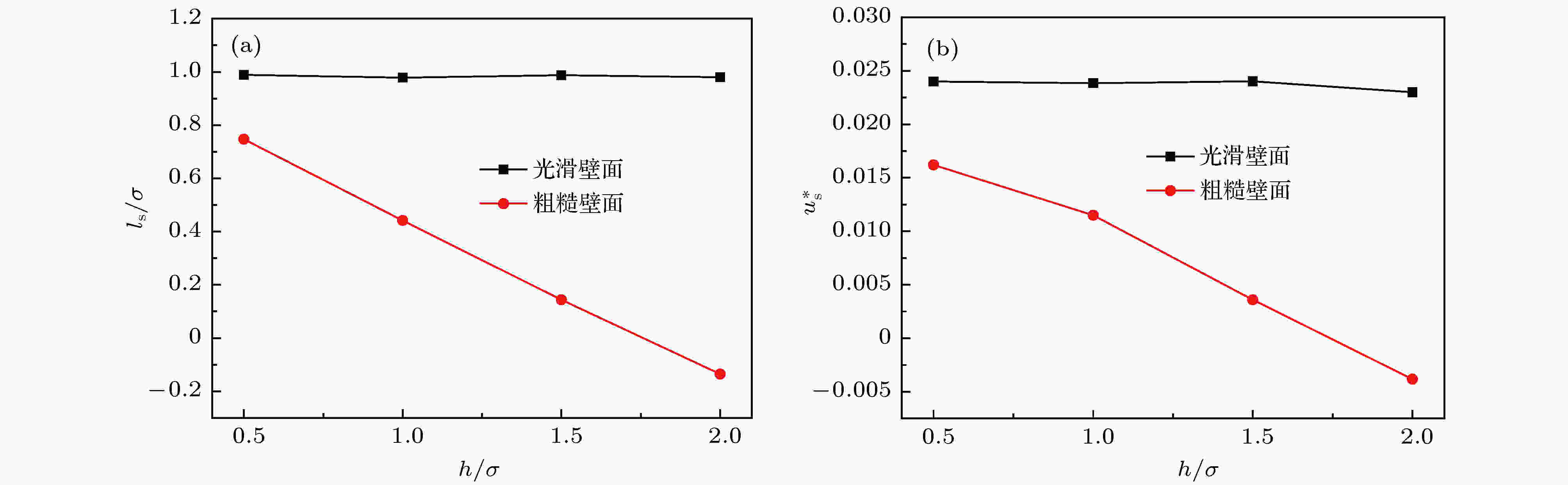图 8 (a) 肋高h对滑移长度的影响; (b) 肋高h对滑移速度的影响
Figure8. (a) Effect of rib height h on the slip length; (b) effect of rib height h on the slip velocity.

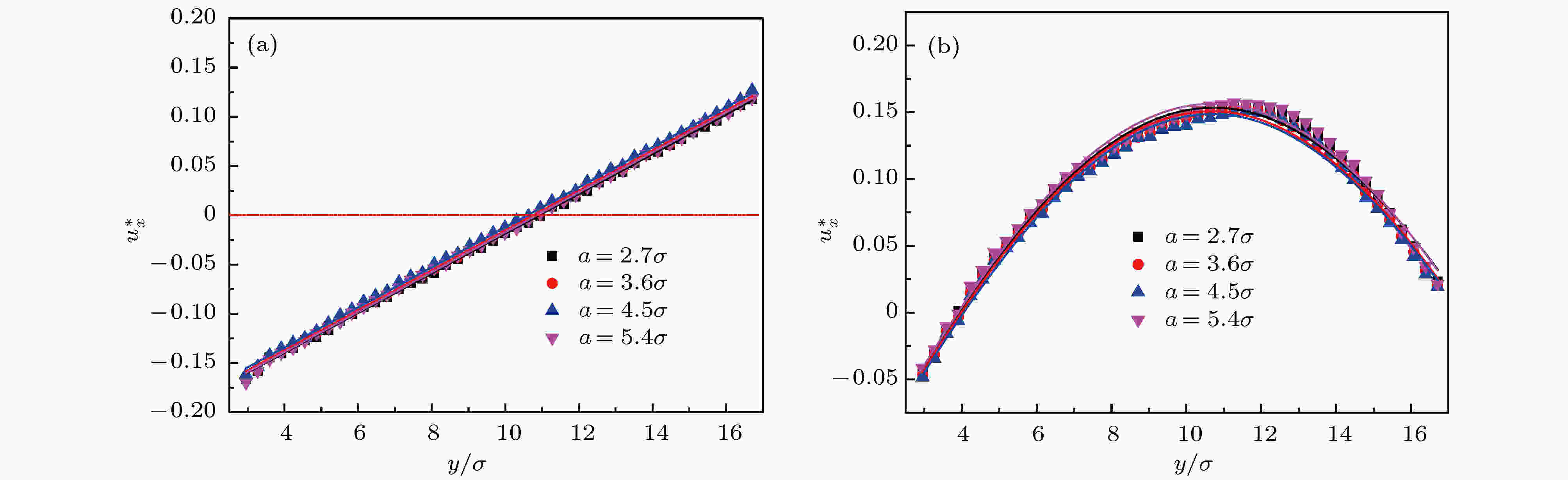图 9 不同肋间距a下流体沿y方向的速度分布　(a) Couette流动; (b) Poiseuille流动
Figure9. Velocity profiles in the y-direction with different rib spacing a: (a) Couette flow; (b) Poiseuille flow.

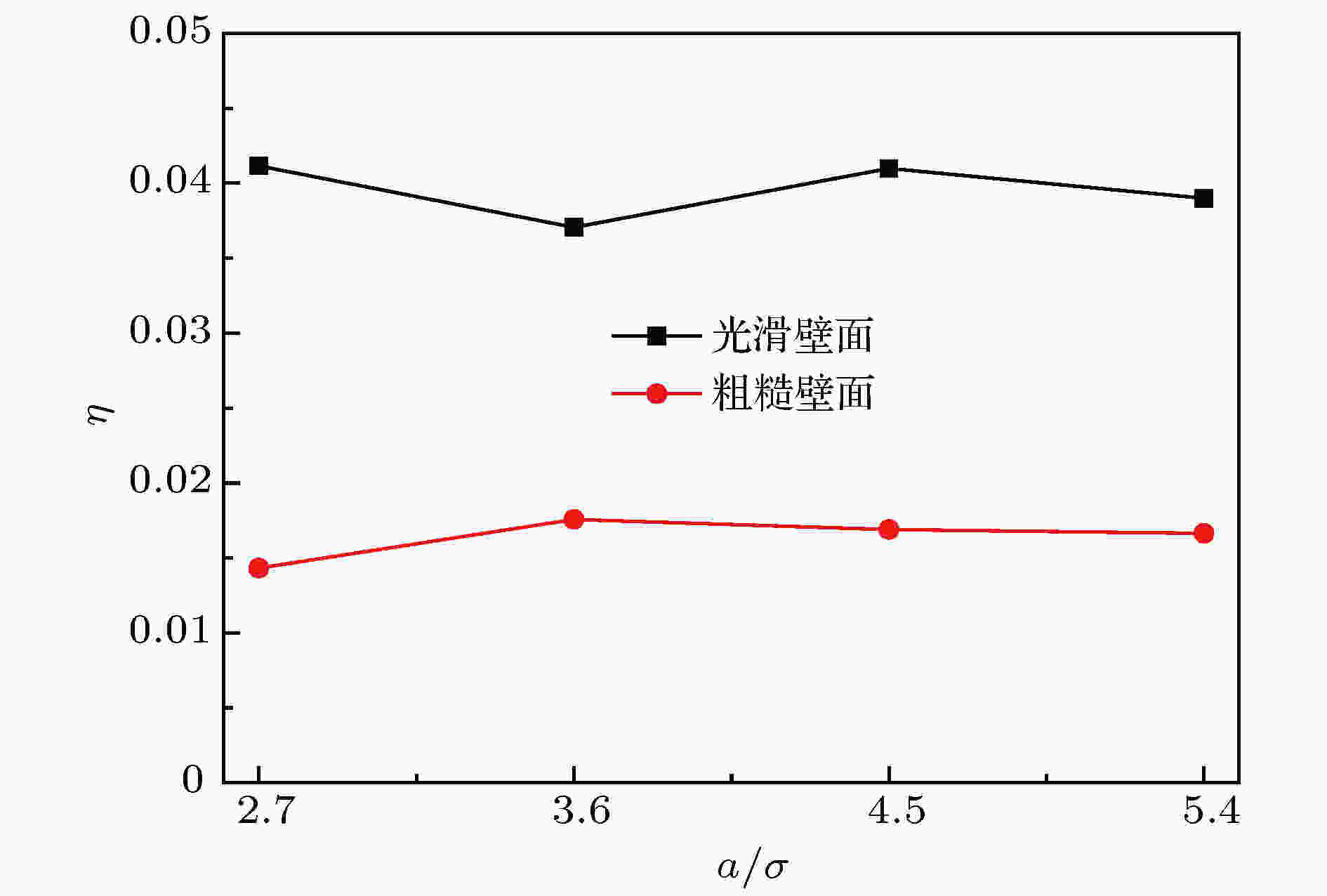图 10 不同肋间距a下滑移长度标准差分布
Figure10. Standard deviation distribution of slip length with different rib spacing a.

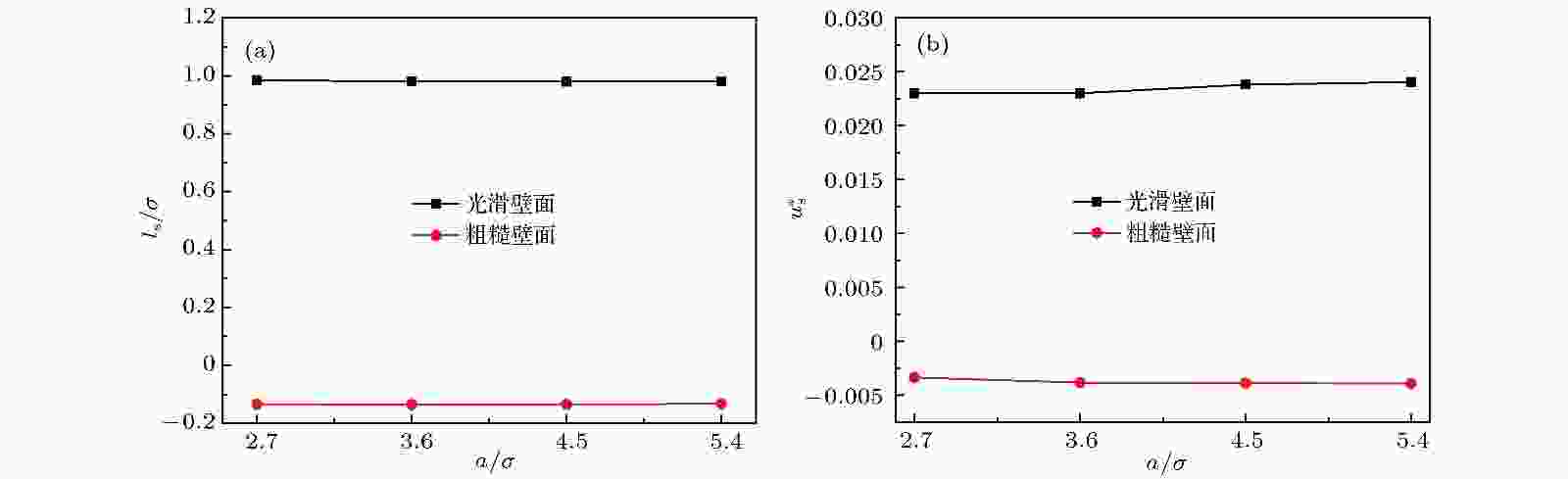图 11 (a) 肋间距a对滑移长度的影响; (b) 肋间距a对滑移速度的影响
Figure11. (a) Effect of rib spacing a on the slip length; (b) effect of rib spacing a on the slip velocity.

2 -->

4.2.壁面润湿性变化对流动特性的影响

3 -->

4.2.1.壁面润湿性变化对数密度的影响

壁面润湿性决定了固体壁面与流体间的相互作用, 不仅会影响固液界面处动量的传递, 也会改变近壁区流体原子的分布状态^[25]. 为研究壁面润湿性对微通道内流动的影响, 固定凹槽高度$h = 2.0\sigma $, 长度$a = 3.6\sigma $, 对势能系数c = 1.0, 0.75, 0.5, 0.25下流体在通道内的流动特性分别进行研究. 图12为不同润湿性下对应的通道内流体数密度分布, 由图12可知, 无论是粗糙壁面还是光滑壁面, 壁面与流体间的作用力越强, 壁面润湿性越好, 壁面附近吸附的流体原子数量越多, 近壁区流体的数密度均随着势能系数的增大而增大. 对于粗糙壁面, 当固液界面间的势能系数c ≤ 0.5时, 随着固液间势能系数c的减小, 凹槽内流体原子的数密度有所下降, 但下降幅度小于光滑壁面, 且凹槽内流体数密度要大于切面附近. 而当固液间的势能系数c = 0.25时, 对应的接触角最大, 凹槽内流体原子的数密度明显减少, 如图12(a)所示, 凹槽内的数密度波动峰值要低于切面附近, 说明此时凹槽对流体原子几乎处于排斥状态.
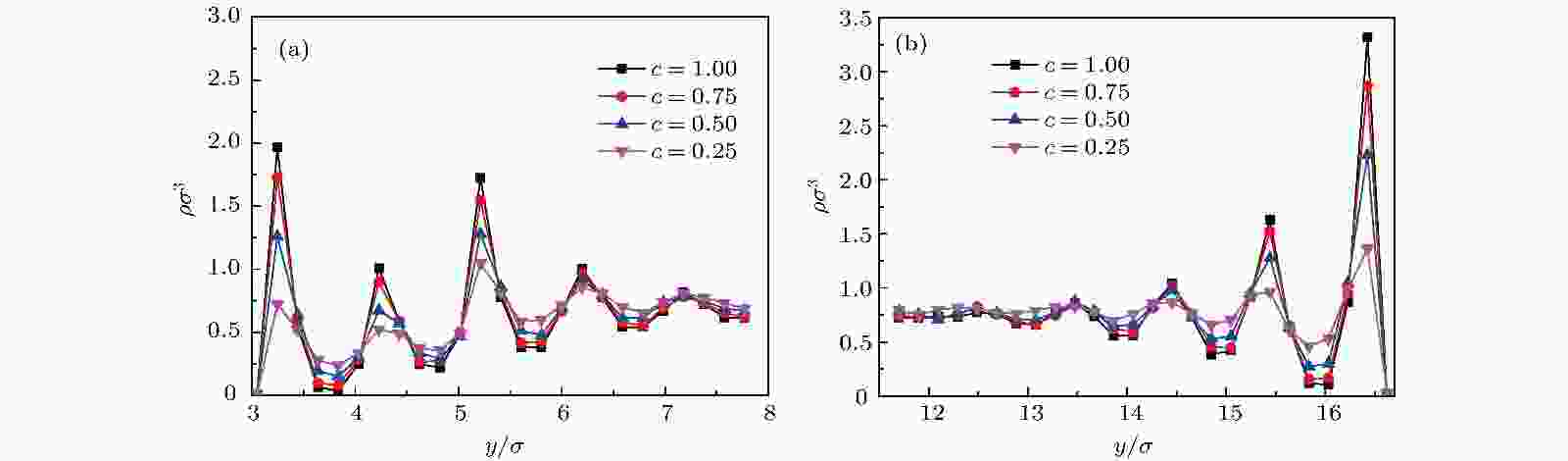图 12 势能系数c对壁面附近流体数密度分布的影响　(a)粗糙壁面; (b)光滑壁面
Figure12. Effect of energy coefficient c on the distribution of fluid number density near wall surface: (a) Rough wall surface; (b) smooth wall surface.

3 -->

4.2.2.壁面润湿性变化对速度分布的影响

图13为势能系数c变化对两种流动状态下通道内速度分布的影响. 结果显示, 随着势能系数c的增大, 固液原子间的作用力逐渐增强, 两种流动状态下速度分布呈现相反的变化趋势. 如图13(a)所示, Couette流动中通道内的速度分布随着势能系数c的增大而增大, 而图13(b)显示Poiseuille流动中通道内的速度分布随势能系数c的增大而减小. 另外值得一提的是, 对于Couette流动来说, 粗糙壁面附近流体速度变化幅度要大于光滑壁面一侧, 而Poiseuille流动则刚好相反. 图14为不同势能系数c下滑移长度标准差分布. 图15(a)和图15(b)分别为Poiseuille流动中通道内的滑移速度及滑移长度分布, 可以发现, 随着势能系数c的增大, 无论是光滑壁面还是粗糙壁面, 滑移速度和滑移长度分布均逐渐降低. 通过分析可知, 改变势能系数c会影响通道内的速度分布, 使水动力位置发生变化, 并对边界滑移影响较大.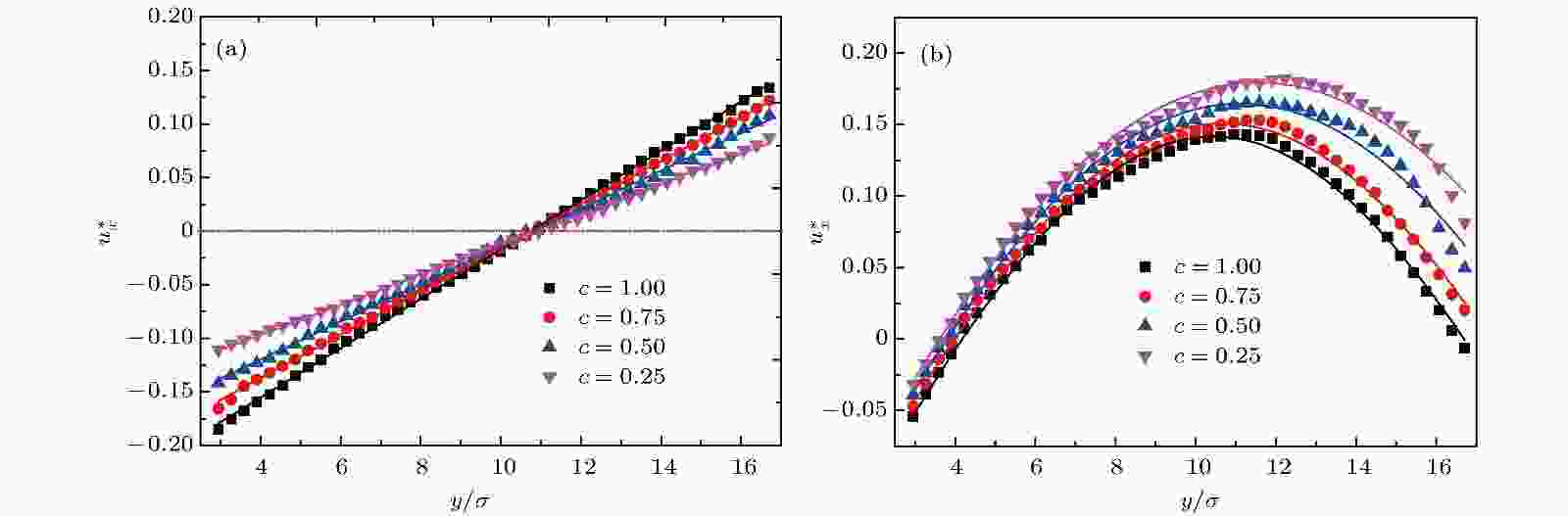
图 13 不同势能系数c下流体沿y方向的速度分布　(a) Couette流动; (b) Poiseuille流动
Figure13. Velocity profiles in the y-direction with different energy coefficient c: (a) Couette flow; (b) Poiseuille flow.

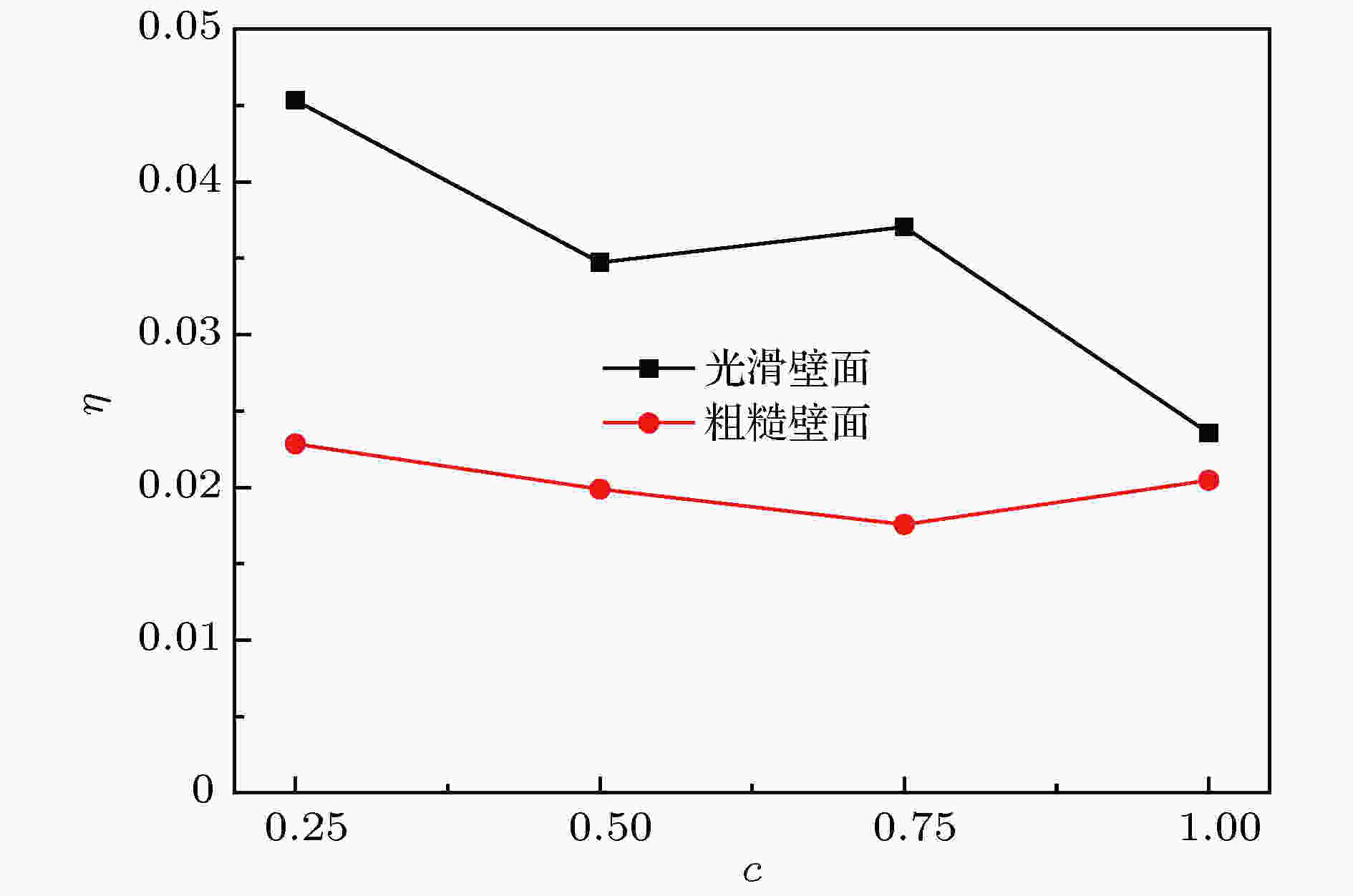图 14 不同势能系数c下滑移长度标准差分布
Figure14. Standard deviation distribution of slip length with different energy coefficient c.

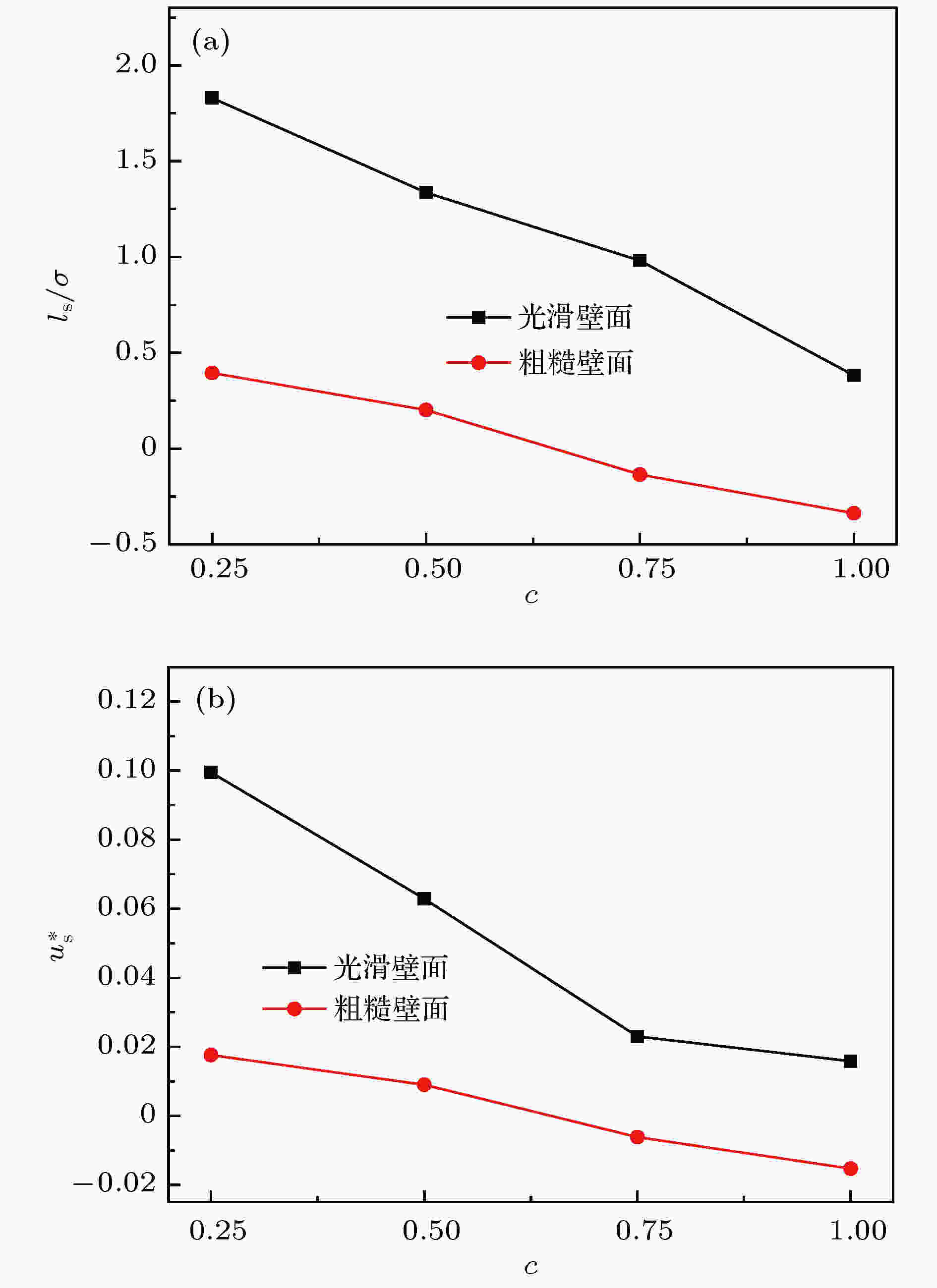图 15 (a) 势能系数c对滑移长度的影响; (b) 势能系数c对滑移速度的影响
Figure15. (a) Effect of energy coefficient c on the slip length; (b) effect of energy coefficient c on the slip velocity.

本文采用分子动力学方法研究了含粗糙壁面纳米通道内流体的流动特性, 探讨了不同壁面粗糙度以及壁面润湿性对通道内流体的数密度和速度场分布的影响, 所得结论如下.
1)相比于光滑壁面, 粗糙壁面附近流体的数密度分布较低, 随着肋高的增大, 密度波动呈现一次回升现象; 改变肋间距对近壁区流体影响较小, 数密度波动趋势基本一致; 无论是光滑壁面还是粗糙壁面, 增大壁面润湿性均会使近壁区数密度波动增大.
2)通过分析Couette流动和Poiseuille流动时通道内的速度场分布确定模型的固液边界位置. 分析结果表示, 改变肋高及壁面润湿性会明显影响通道内的速度分布, 使固液边界位置发生偏离, 而肋间距变化对固液边界位置影响较小.
3)以Poiseuille流动为主, 分析了壁面粗糙度及润湿性对界面滑移的影响. 结果表明, 粗糙壁面一侧滑移速度及滑移长度均小于光滑壁面一侧, 且随着肋高及壁面润湿性的增大, 滑移速度和滑移长度逐渐减小; 肋间距变化对界面滑移影响较小, 滑移速度及滑移长度分布基本恒定.