删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

O<sup>+</sup>+H<sub>2</sub> → OH<sup>+</sup>+H反应的动力学研究

本站小编 Free考研考试/2021-12-29
摘要:采用含时量子波包方法结合二阶分裂算符传播子对初始态为(v = 0, j = 0)的O+ + H2 → OH+ + H反应体系在0.01—1.00 eV的碰撞能范围内进行了态分辨理论水平上的动力学计算. 对反应概率、积分截面、微分截面以及固定初始态的热速率常数等动力学信息进行了计算并与文献报道的实验和理论结果进行了比较. 结果表明本文的理论结果与实验结果十分符合. 从微分截面的散射信息可知, 在低碰撞能范围内, 插入反应机制在反应中占据主导地位. 随着碰撞能的增加, 反应机制逐渐由插入机制变为抽取反应机制.
关键词: OH2+体系/
反应概率/
积分截面/
微分截面

English Abstract


全文HTML

--> --> -->
1.引　言
离子与分子类型反应的研究在星际化学、电荷转移、燃烧化学以及化学键的弱相互作用等领域都有着重要的意义[1-3]. 此外, 包含离子的碰撞反应也是解释反应过程中多通道竞争现象的重要反应类型[4]. 由于电子在不同电子态之间的跃迁导致多数的离子与分子类型反应存在透热效应, 因此无论是非绝热势能面的构建还是非绝热动力学的计算都充满了挑战. 而O+ + H2反应是一个比较特殊的离子与分子反应, 在中低碰撞能下, 该反应是在绝热势能面上进行的. 这样的特性使得O+ + H2反应体系无论是在实验上[5-15]还是在理论上[16-24]都受到了广泛的关注.
实验上, 1987年Burley等[9]采用导向离子束质谱测量了基态氧离子与H2分子及其同位素反应的速率常数、分子比以及积分截面等动力学信息. 采用电荷转移探测方法、八极离子囚禁技术和2—4倍的八极装置, Li等[12]在0.02—12.0 eV的碰撞能范围内测量了O+(4S, 2D, 2P)+ H2(D2)反应的积分截面.
理论上, 2004年Martínez等[16]采用599个从头算能量点构建了OH2+体系的解析势能面. Martínez等[16-19]基于该势能面进行了一系列的动力学研究. 2005年, 采用准经典轨线方法(QCT), Martínez等[17]计算了O+与H2分子及其D2, HD同位素的反应. 紧接着采用非含时的量子机制的紧密耦合方法结合超球坐标, Martínez等[18]在0.04—1.24 eV的碰撞能范围内进一步研究了O+ + H2反应. 2006年, 采用含时量子机制的实波包方法, Martínez等[19]重新计算了O+离子与H2分子及其同位素的反应. 文中把反应概率和积分截面与之前应用非含时量子方法计算的结果进行了比较, 以此来检测科里奥利耦合效应在反应过程中的作用. 之后基于Martínez等[16]的势能面, Xu等[21], Gómez-Carrasco等[22], Bulut等[23]使用含时量子波包方法(TDWP)进行了O+ + H2反应体系的动力学计算, 报道了该反应的反应概率、积分截面和速率常数等动力学性质. 由于Martínez等[16]的势能面仅包含599个从头算能量点, 不足以精确描述具有两个势阱一个势垒的复杂反应体系, 2018年, Li等[24]采用置换不变多项式神经网络方法对63000个从头算能量点进行了拟合, 构建了新的势能面. 并采用TDWP方法在新的势能面基础上进行了动力学计算. 文中对反应概率、积分截面和微分截面等动力学信息进行了报道, 并与之前的实验与理论结果进行了比较.
之前的研究主要集中于介绍势能面的性质, 并且对于长程相互作用势的描述还不充分. 本文对该体系在核间距较远的地方增加了一些从头算点并重新拟合构建了新势能面. 图1给出了当氢分子固定在平衡位置, O+离子线性接近氢分子的图像. 由图1不难看出, 新势能面在长程相互作用势上对于老势能面有了很大的改善. 在新的势能面的基础上, 进行了O+ + H2反应的动力学计算. 本文的结构如下: 第2小节简略介绍TDWP方法; 第3小节对动力学结果进行详细的分析和讨论; 第4小节给出结论.
图 1 新旧两个势能面的长程相互作用势比较
Figure1. Comparison of the long range interaction potential for the old and new potential energy surfaces

2.动力学计算方法
作为一个强有力的计算工具, TDWP方法广泛应用于原子与双原子散射反应[25-27]以及包含多原子的反应[28, 29]中. 关于TDWP方法的详细信息可以参考文献[30], 本文仅简单介绍TDWP方法. 对于一个给定的总角动量J, O+ + H2体系的哈密顿量可以写为
$\hat H = - \frac{{{\hbar ^2}}}{{2{{\mu} _R}}}\frac{{{\partial ^2}}}{{\partial {R^2}}} - \frac{{{\hbar ^2}}}{{2{{\mu} _r}}}\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{{{{(\hat J - \hat j)}^2}}}{{2{{\mu} _R}{R^2}}} + \frac{{{{\hat j}^2}}}{{2{{\mu} _r}{r^2}}} + V,$
其中${{\mu} _R}$和${{\mu} _r}$分别为R和r方向的约化质量, J是总角动量, j是H2分子的转动角动量. 含时波函数是由体坐标下的平动、振动和转动基矢构成$\left\{ {u_n^v(R){\varphi _v}(r)y_{jK}^{JMp}(\hat R,\hat r)} \right\}$,
$\begin{split}&\psi _{{v_0}{j_0}{K_0}}^{JMp}(R,r,t) \\[5pt ]= \;& \sum\limits_{n,v,j,K} {F_{nvjK,{v_0}{j_0}{K_0}}^{JMp}} (t)u_n^v(R){\varphi _v}(r) \\ & \times y_{jK}^{JMp}(\hat R,\hat r),\end{split}$
其中下标n为平动基, p为体系的宇称, (v0, j0, K0)是体系的初始振-转态, M是总角动量J在空间坐标系下z轴的投影.
在采用TDWP方法计算过程中, 二阶分裂算符[31]用来传播初始波包. 如果$\psi \left( {R,r,t} \right)$是t时刻的波包, 那么经过一个时间步, 波包可以写为
$\begin{split} &\psi (R,r,t) \\ =\; &{{\rm{e}}^{ - {\rm{i}}V{\varDelta _t}/(2\hbar) }}{{\rm{e}}^{ - {\rm{i}}{T_j}{\varDelta _t}/(2\hbar) }}{{\rm{e}}^{ - {\rm{i}}({T_r} + {T_R}){\varDelta _t}/\hbar }} \\ &\times {{\rm{e}}^{ - {\rm{i}}{T_j}{\varDelta _t}/(2\hbar) }}{{\rm{e}}^{ - {\rm{i}}V{\varDelta _t}/(2\hbar) }} \times \psi (R,r,t + {\varDelta _t}),\end{split}$
其中V是体系的势能, ${T_j} = [{(J - j)^2}/(2{{\mu} _R}{R^2})] + $${j^2}/(2{{\mu} _r}{r^2})$是角动量算符, ${T_r} = - \left[ {{\hbar ^2}/(2{{\mu} _r})} \right]\left( {{\partial ^2}/{\partial ^2}r} \right)$和${T_R} = - \left[ {{\hbar ^2}/(2{{\mu} _R)}} \right]\left( {{\partial ^2}/{\partial ^2}R} \right)$分别为r和R方向的径向动能算符.
最终, 通过传播初始波包和抽取态-态散射矩阵, 可以得到体系的反应概率、积分截面、微分截面和速率常数:
$P_{{v_0}{j_0}{k_0}}^J(E) = \frac{\hbar }{{{{\mu} _R}}}{\mathop{\rm Im}\nolimits} \left[ {\left\langle {\psi (E)\left| {\delta (r - {r_0})\frac{\partial }{{\partial r}}} \right|\psi (E)} \right\rangle } \right]\!,$
$\begin{split}{\sigma _{{\upsilon _v}{j_v} \leftarrow {\upsilon _0}{j_0}}} =\; & \frac{{\text{π}}}{{(2{j_0} \!+\! 1)k_{{\upsilon _0}{j_0}}^2}}\!\sum\limits_{{K_v}} {\sum\limits_{{K_0}} {\sum\limits_J {(2J \!+\! 1)} } }\\ & \times|S_{{\upsilon _v}{j_v}{K_v} \leftarrow {\upsilon _0}{j_0}{K_0}}^J{|^2},\end{split}$
$\begin{split}&\frac{{{\rm{d}}{\sigma _{{\upsilon _v}{j_v} \leftarrow {\upsilon _0}{j_0}}}(\vartheta ,E)}}{{{\rm{d}}\varOmega }} \\=\; & \frac{1}{{2{j_0} + 1}}\sum\limits_{{K_v}} {\sum\limits_{{K_0}} {|\frac{1}{{2{\rm{i}}k_{{\upsilon _0}{j_0}}^2}}} }\\ &\times\sum\limits_J {(2J + 1)d_{{K_v}{K_0}}^J} (\vartheta )S_{{\upsilon _v}{j_v}{K_v} \leftarrow {\upsilon _0}{j_0}{K_0}}^J{|^2},\end{split}$
$\begin{split}{k_{{v_0}{j_0}}}(T) = & {\left( {\frac{{8kT}}{{{\text{π}}{\mu} }}} \right)^{1/2}}{\left( {{k_{\rm{B}}}T} \right)^{ - 2}} \\ & \times \int_0^\infty {E{{\rm{e}}^{ - E/{(k_{\rm{B}}}T)}}} {\sigma _{{v_0}{j_0}}}(E){\rm{d}}E,\end{split}$
其中ψ(E)可以通过对含时波函ψ(t)进行快速傅里叶变换得到, ${{S}}_{{\upsilon _v}{j_v}{K_v} \leftarrow {\upsilon _0}{j_0}{K_0}}^J$是散射矩阵, $\vartheta $为散射角, kB为玻尔兹曼常数.
3.结果与讨论
图2给出了O+ + H2反应势能面在90°, 120°, 150°和180°时的最小能量路径, 其中180°对应线性的O+-H-H结构也是体系的最小能量反应路径. 由图2可知, O+ + H2反应是一个放热反应, 其放热能约为0.54 eV(考虑了零点能). 随着碰撞能的增加, O+ + H2反应可以在偏离最小反应路径的位置进行, 在反应路径上多出一个势垒和一个势阱, 并且随着角度的减少, 势垒高度不断增加. 进一步了解势能面的特性, 读者可以参考文献[24].
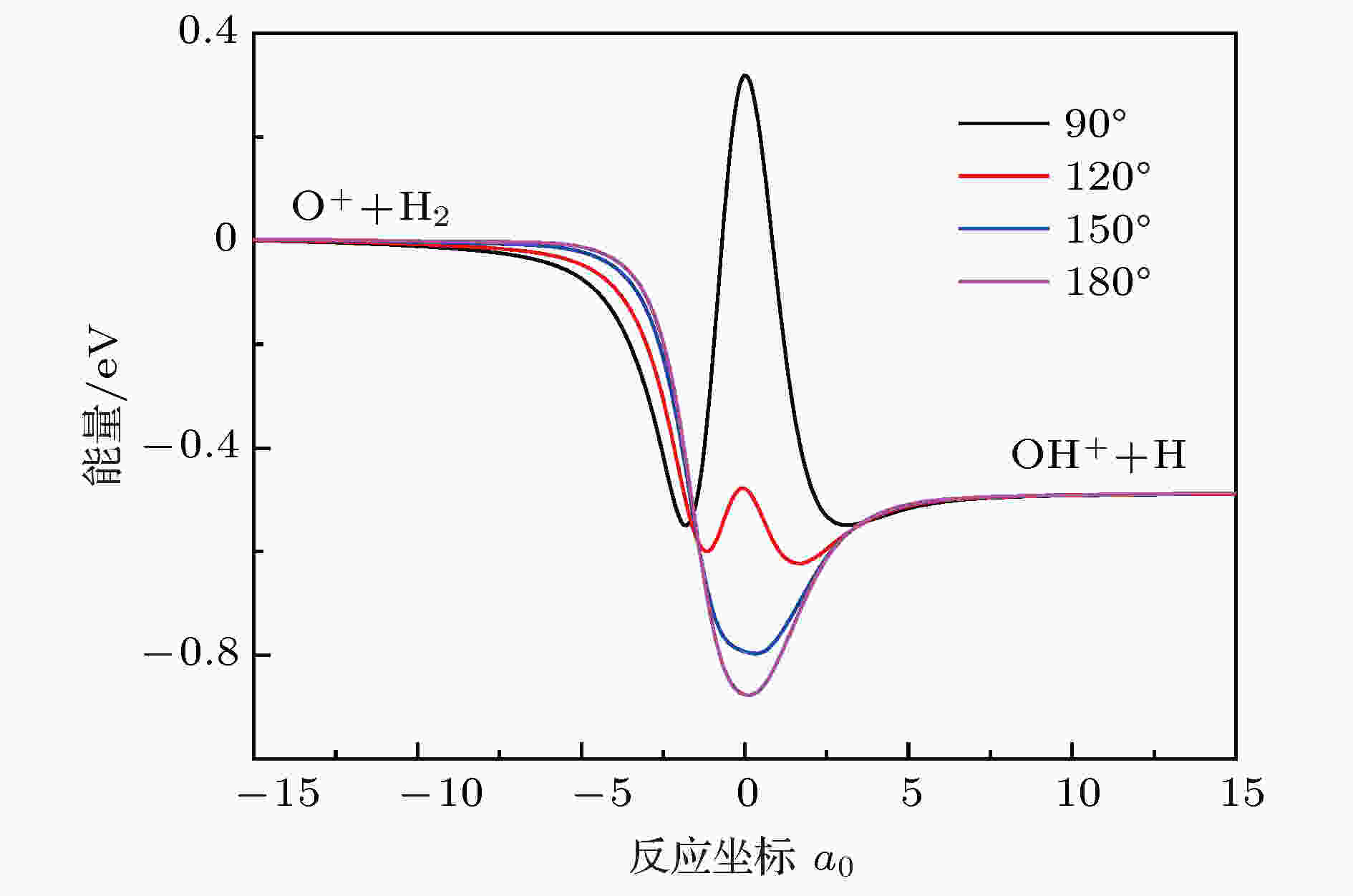图 2 90°, 120°, 150°和180°的最小能量路径
Figure2. The minimum energy paths at 90°, 120°, 150°, and 180° angles

为了获得收敛的动力学结果, 在进行动力学计算之前需要对诸多动力学参数进行调试. 本文计算了总角动量J = 0的反应概率, 得到了最优的动力学参数, 并将这些参数用于J大于0的计算中. 具体的参数见表1
格点范围和大小$R \in \left[ {0.1,16} \right],{N_R} = 279,N_R^{{\rm{int}}} = 159$
$r \in \left[ {0.1,15} \right],{N_r} = 279,N_r^{{\rm{asy}}} = 159$
初始波包Rc = 11.0, ${k_0} = \sqrt {2{E_0}{\mu_R}} $
${\varDelta _R} = 0.2 {\rm{exp}}\left[ { - \dfrac{{{{\left( {R - {R_{\rm{c}}}} \right)}^2}}}{{2\varDelta _R^2}}} \right]{\rm{cos}}\left( {{k_0}R} \right)$;

其中E0 = 0.5 eV
总传播时间 30000
最大总角
动量J 		70


表1计算中使用的参数(除了特殊声明, 均采用原子单位a.u.)
Table1.Parameters used in the calculation (The atomic unit is used in the calculation unless otherwise stated)

2
3.1.反应概率
-->

3.1.反应概率

图3给出了若干总角动量J的反应概率. 由图可知, 在反应概率上有很多共振峰, 并且这些共振峰随着能量和总角动量J的增加而变宽, 振幅变小. 这是由于在最小能量路径上有一个支持很多束缚态和准束缚态的深势阱. 随着碰撞能和J的增加, 中间络合物O+-H-H的寿命变短, 因此反应概率上的共振峰变得不那么明显了. 此外, 还可以发现, 对于J < 40, 随着碰撞能的增加其反应概率逐渐降低. 这是一个典型的放热反应特征, 这是因为随着碰撞能以及离心势的增加O+离子的速率越来越快, H2分子来不及与O+离子形成OH键, O+离子就跑开了, 因此反应概率会越来越低. 而对于J > 60, 其反应概率随着碰撞能的增加逐渐升高. 结合图1, 本文认为这是因为随着碰撞能和离心势的增加, O+ + H2反应已经不局限在最小反应路径上, 反应可以在其他角度的能量路径上进行, 在反应路径上将会有势垒的存在, 这导致反应概率随着碰撞能的增加而增加.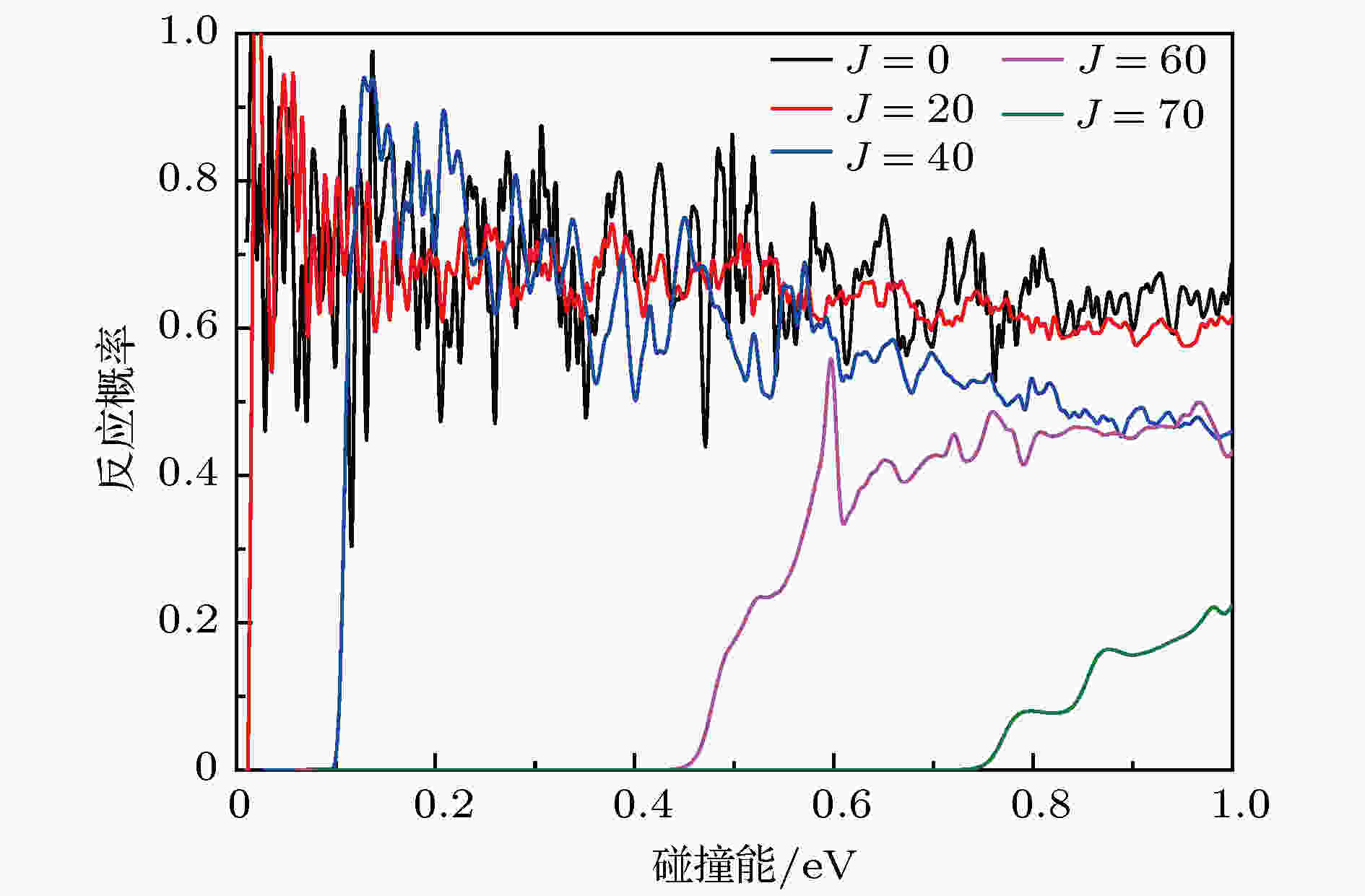
图 3 对于几个选定的总角动量J在能量范围0—1.0 eV的反应概率
Figure3. The total reaction probabilities for several selected total angular momentum J in the collision energy from 0 to 1.0 eV

图4给出了J = 0反应概率的振动分辨. 由图可知, 产物OH+ (v′ = 0, 1)的振动态在低能时就是打开的, 随着碰撞能的增加, 其他振动激发态陆续打开, 这表明随着碰撞能的增加有更多的能量转化为体系的内能. 从图4中不难看出, v′ = 0和v′ = 1所占据的反应概率的比重一直是最高的. 随着产物振动态的增加, 其所占的比例越低. 这表明在O+ + H2→ OH+ + H反应过程中振动激发的效率不高, 这可能是因为OH+产物振动态之间的能隙间隔过宽所致.
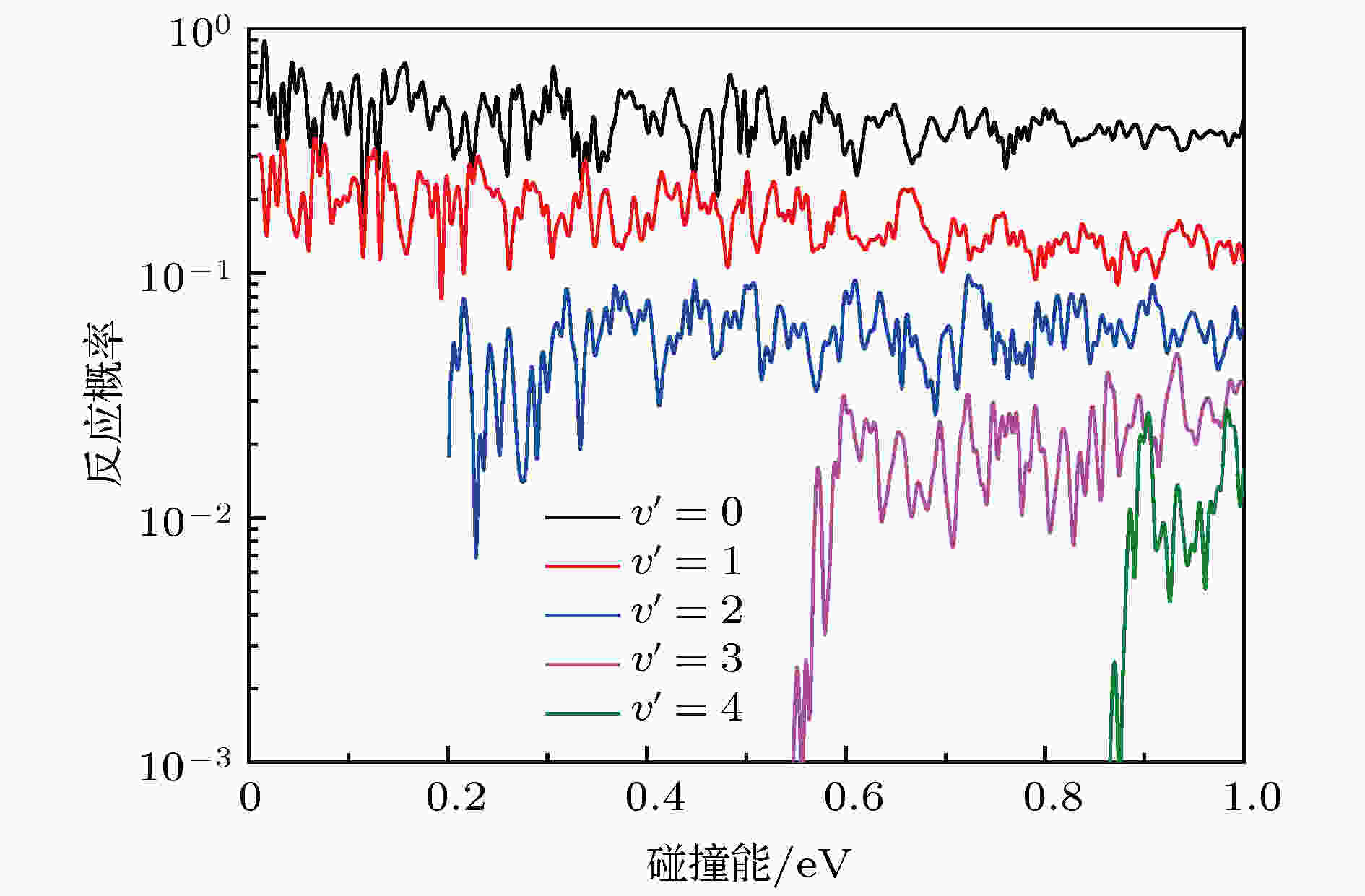图 4 总角动量J = 0反应概率的振动分辨
Figure4. The vibrational resolved reaction probabilities of the total angular momentum J = 0

图5给出了J = 0反应概率的转动分辨. 图5展示了所有共振结构的特征, 如上所述, 这是由反应路径上的深势阱所致. 产物OH+ (v′= 0)的转动通道在j′= 11之前都是打开的. 在图5中仅列出j′从0到5的反应概率. 对比J = 0反应概率的振动分辨, 发现OH+的转动激发更容易实现. 图5有一个奇怪的现象, 产物OH+(v′= 0, j′ = 1)的激发效率远低于其他转动态. 这可能是过渡态产物的特性导致的.
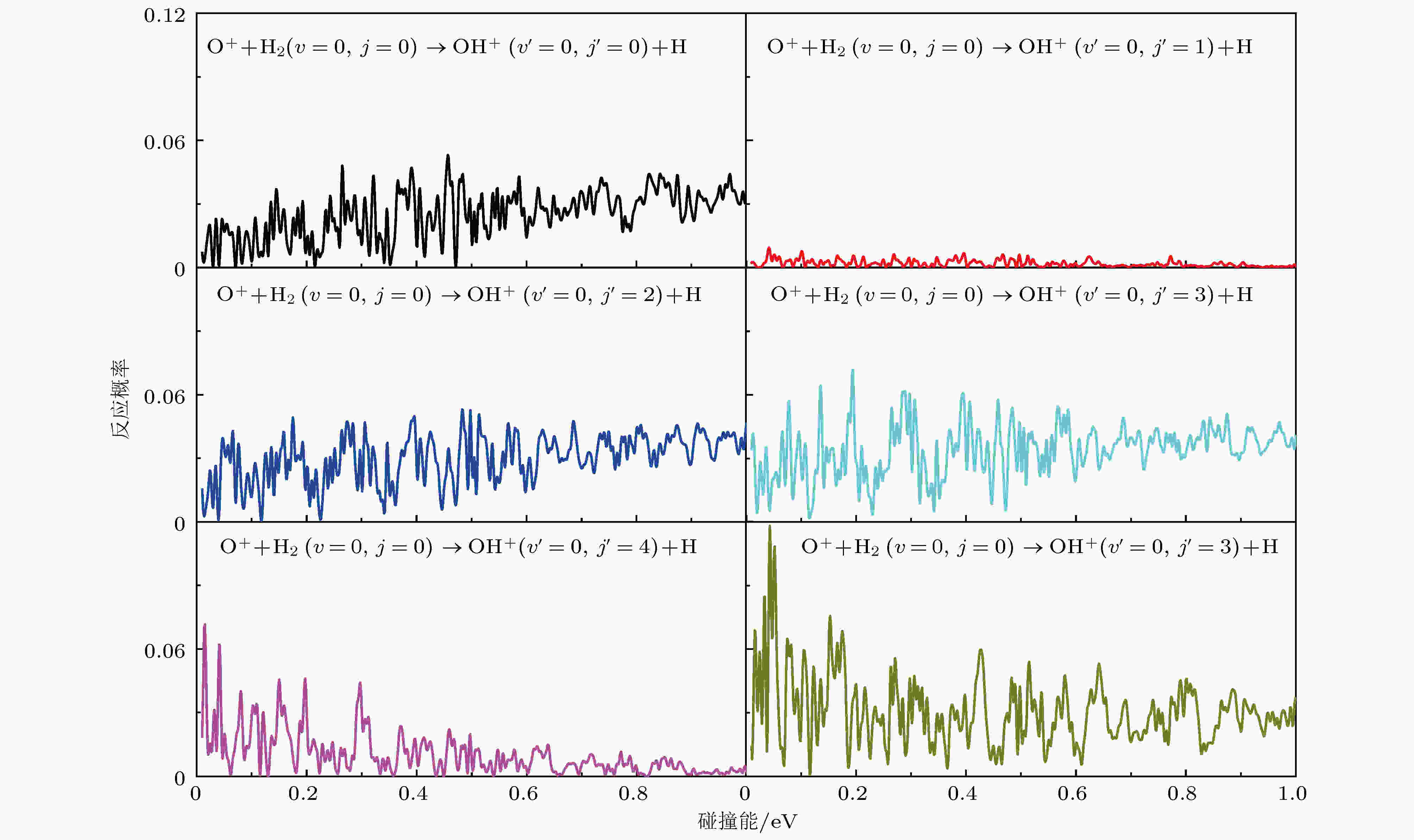图 5 O+ + H2(v = 0, j = 0) → OH+ (v' = 0, j' ) + H反应在总角动量J = 0时转动分辨的反应概率
Figure5. Rotationally resolved reaction probabilities for the O+ + H2 (v = 0, j = 0) → OH+(v' = 0, j' ) + H reaction at total angular momentum J = 0

2
3.2.积分截面
-->

3.2.积分截面

图6给出了O+ + H2反应体系在0.01—1.0 eV能量范围内的总积分截面. 为了与理论和实验文件进行比较, 由文献[22]获得理论结果和文献[8]得到的实验结果也在图6中给出. 由图6可知, 总积分截面随着碰撞能的增加而降低. 比较文献[22]的理论结果与本文的结果, 当碰撞能小于0.1 eV时, 文献[22]的结果高于本文结果, 当碰撞能大于0.4 eV时, 本文的结果略高于文献[22]的结果. 通过与实验结果的比较可知, 本文结果与实验结果符合得更好, 而文献[22]的结果在低碰撞能范围内略高于实验结果.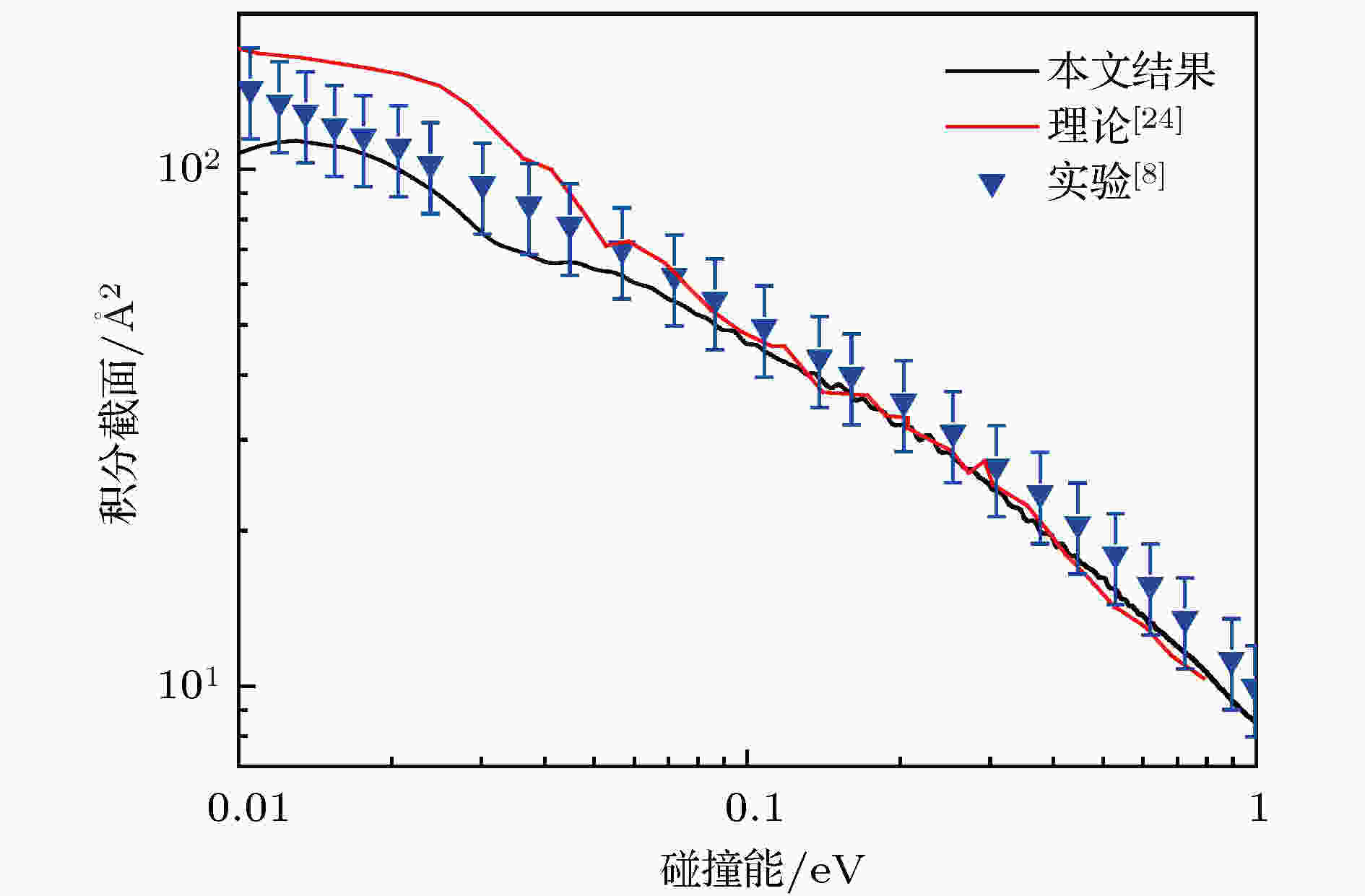
图 6 O+ + H2反应的积分截面以及文献[22]的理论结果和文献[8]的实验结果
Figure6. The integral cross section of the O+ + H2 reaction as well as the theoretical and experimental results obtained from Ref. [22] and Ref. [8], respectively

2
3.3.微分截面
-->

3.3.微分截面

图7给出了O+ + H2反应若干能量点的微分截面. 由图7可知, 微分散射的信号主要集中在前向(0°)和后向(180°)的方向上. 边缘散射的信号分布很少, 并且随着碰撞能的升高逐渐降低. 从图7左图相应的低能部分可以看出, 前向散射的信号和后向散射的信号都非常明显, 但是偏向于前向散射. 在低碰撞能时, 反应主要是在最低能量路径上进行, 反应路径上的深势阱所产生的中间络合物具有很长的寿命. 因此, 产物既可以向前又可以向后散射, complex-forming反应机制占据主导地位. 从图7右图可以看出, 随着碰撞能的增加, 反应已经不局限于最小能量路径上, 反应路径上出现了一个势垒两个势阱, 前向散射明显高于后向散射. 这说明O+离子碰撞H2分子直接形成OH键并带走一个H原子, 没有经过过多的振荡, 表明反应机制逐渐由间接的插入机制转变为直接的抽取机制.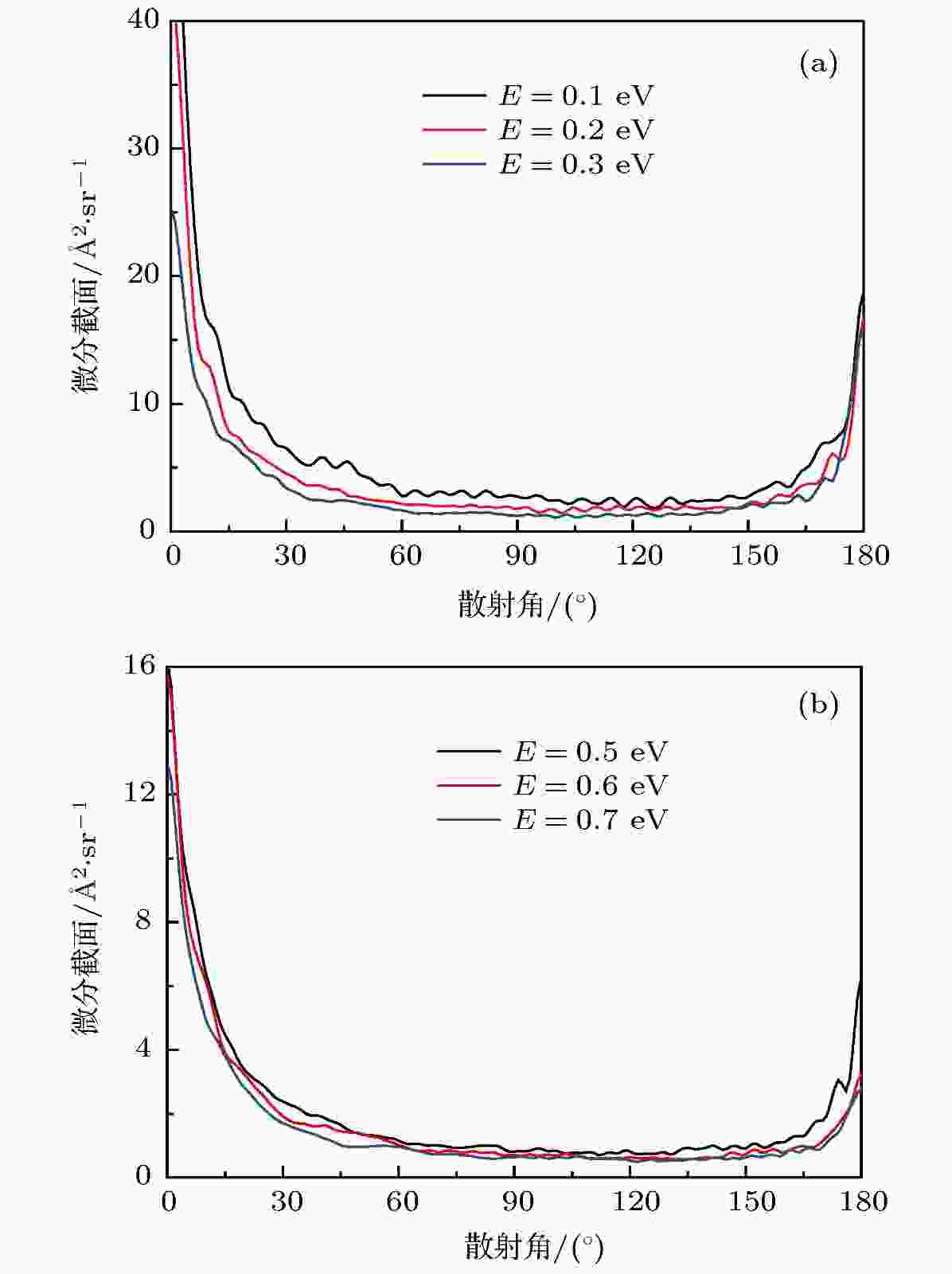
图 7 O+ + H2反应若干能量点的微分截面　(a)低能部分; (b) 高能部分
Figure7. The differential cross sections of O+ + H2 reaction for several collision energies: (a) The low energy; (b) the high energy part

2
3.4.速率常数
-->

3.4.速率常数

图8给出了O+ + H2反应在200—1000 K温度范围内的速率常数. 从图8可以看出, 随着温度的增加, 速率常数以约1.25的因子增加. 通过与实验比较发现, 本文的理论结果明显偏低. 速率常数可以通过积分截面获得, 由图6可以看出本文的积分截面与实验结果十分吻合, 所以预期本文的速率常数结果将会与实验结果有比较好的符合. 然而通过图8可以看出, 两者有较大的差别. 本文认为导致这个差距的原因主要源于和实验数据进行对比需要包含反应物H2分子的转动激发态的影响, 而本文的计算为初始态为(v = 0, j = 0)的动力学计算, 没有包含转动激发的影响.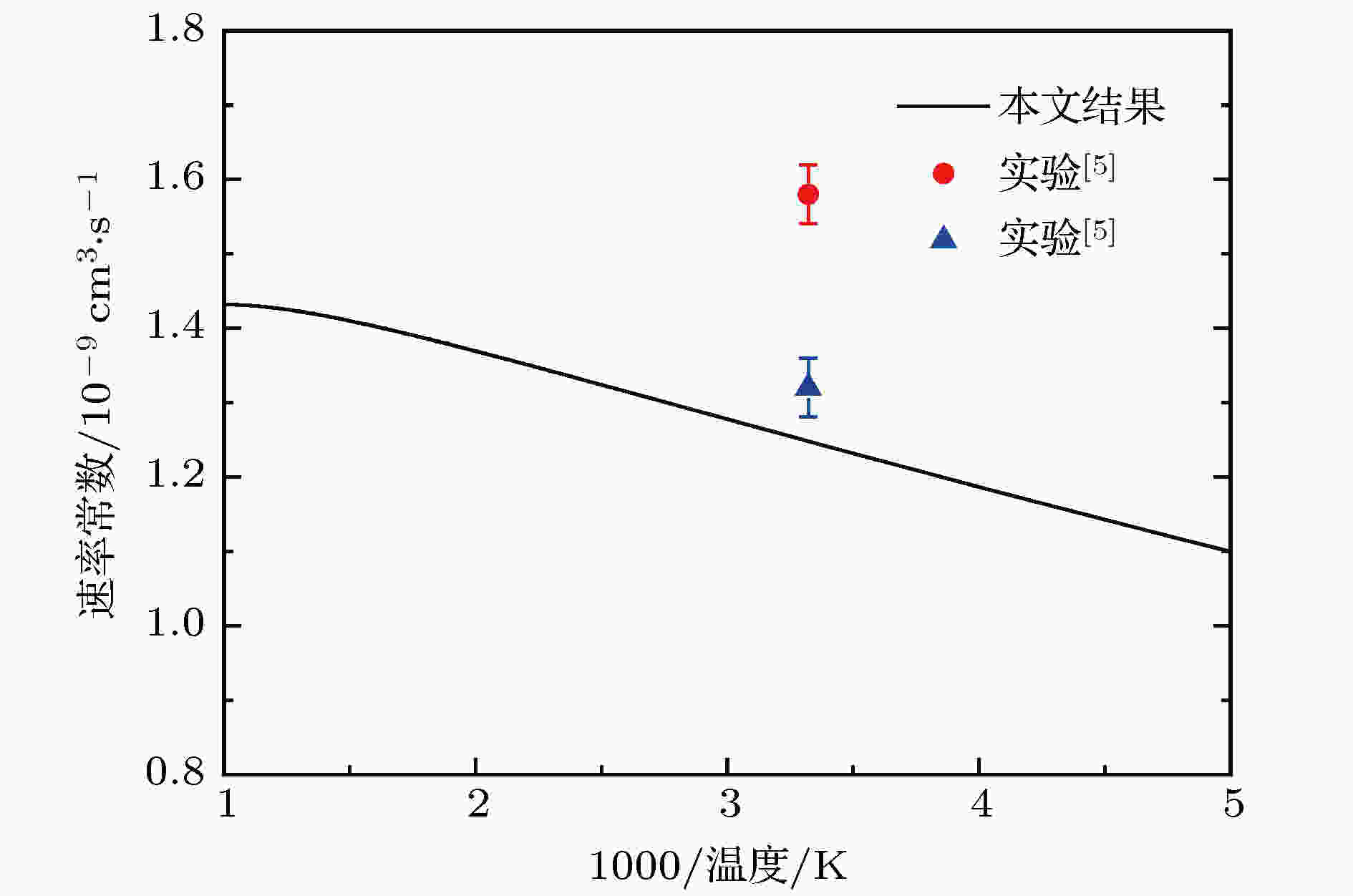
图 8 O+ + H2反应的速率常数和文献[5]的实验结果
Figure8. The rate constant of the O+ + H2 reaction and the experimental values obtained from Ref. [5] in the temperature range of 200 to 1000 K

4.结　论
本文采用含时量子波包方法和二阶分裂算符传播子, 并基于新势能面进行O+ + H2 → OH+ + H反应的态-态动力学计算. 对反应概率、积分截面、微分截面和速率常数等动力学信息进行了计算, 并与之前的理论和实验结果进行了比较. 结果表明本文得到的积分截面与实验符合得很好, 而本文的速率常数值低于实验值. 从微分截面得到的信息可知, 在反应过程中的低能部分complex-forming反应机制占据主导地位. 随着碰撞能的升高, 反应机制由间接变为直接, 在高能部分抽取反应机制占据主导地位.
相关话题/概率 实验 计算 文献 信息
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于共心球透镜的多尺度广域高分辨率计算成像系统设计
    摘要:针对实时广域高分辨率成像需求,充分利用具有对称结构的多层共心球透镜视场大且各轴外视场成像效果一致性好的特点,设计基于共心球透镜的多尺度广域高分辨率计算成像系统.该系统基于计算成像原理,通过构建像差优化函数获得光学系统设计参数,结合球形分布的次级相机阵列进行全局性优化,提高系统性能的同时有效简化 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • W波段分布作用速调管的设计和实验研究
    摘要:基于运动学理论、感应电流定理和电荷守恒定律,分析了分布作用谐振腔的渡越时间效应,推导了各个谐振腔工作于${\text{π}}$模的电子注与微波之间的能量转换系数、电子负载电导和电子负载电纳,计算结果显示采用分布作用谐振腔有利于提高速调管的工作效率.利用三维电磁仿真软件,设计了一款工作于W波段的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Ce-La-Th合金高压相变的第一性原理计算
    摘要:采用第一性原理计算对Ce0.8La0.1Th0.1在高压下fcc-bct的结构相变、弹性性质及热力学性质进行了研究讨论.通过对计算结果的分析,发现了合金在压力下的相变规律,压强升高到31.6GPa附近时fcc相开始向bct相转变,到34.9GPa时bct相趋于稳定.对弹性模量的计算结果从另一角 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 螺旋锥束计算机断层成像倾斜扇束反投影滤波局部重建算法
    摘要:螺旋锥束计算机断层成像(CT)作为常用的临床诊断工具,如何尽可能地减少其辐射剂量是热点研究领域之一.局部成像利用准直器减小射线直照区域,能够有效降低CT辐射剂量.然而,局部成像会造成投影数据横向截断,产生局部重建问题.现有螺旋反投影滤波(BPF)算法只能实现局部曲面重建,难以实现局部体区域重建 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 量子微波制备方法与实验研究进展
    摘要:量子微波信号既保留了经典微波信号的空间远距离传播能力,又具有非经典的量子特性,为微波频段量子通信、量子导航及量子雷达等基于大尺度动态空间环境无线传输的量子信息技术提供了可资利用的重要信号源.按照腔量子电动力学系统、超导电路量子电动力学系统和腔–光(电)–力学系统三大类型实验平台,归纳、分析了微 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光声光谱检测装置中光声池的数值计算及优化
    摘要:利用光声光谱技术进行痕量气体的检测具有独特的优势,光声池是系统装置中最为重要的核心部件,它决定着整机性能的优劣.以一圆柱形共振型光声池为研究对象,基于声学与吸收光谱学的基本理论,建立了光声池声场激发的数学模型;利用数值模拟方法对光声池空腔结构进行了声学模态仿真,获得了前8阶声学模态值以及声压可 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 正弦波沟槽对湍流边界层相干结构影响的TR-PIV实验研究
    摘要:利用高时间分辨率粒子图像测速(time-resolvedparticleimagevelocimetry,TR-PIV)技术,在不同雷诺数下对光滑壁面和二维顺流向、三维正弦波(two/threedimensional,2D/3D)沟槽壁面湍流边界层流场进行了实验测量,从不同沟槽对湍流边界层相干 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 激光加载下金属锡材料微喷颗粒与低密度泡沫混合实验研究
    摘要:金属材料的微喷是冲击加载下金属表面发生的一种动态破碎现象,微喷研究在很多领域都具有重要意义,包括惯性约束聚变(ICF)和烟火制造等.由于激光实验特有的优势,近几年国内外开展了很多利用强激光驱动冲击加载研究材料微喷过程的实验.利用泡沫材料对微喷颗粒进行静态软回收虽然可以获得颗粒的形态分布、颗粒尺 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • W-In体系溶质晶界偏聚行为的第一性原理计算
    摘要:基于第一性原理构建了钨基合金体系的溶质偏聚模型,以W-In体系为例研究了不同浓度下溶质的晶界偏聚行为和成键特征,从电子结构层面揭示了W-In体系的键合作用,预测了W-In体系界面稳定性随溶质浓度的变化规律.结合键布居、电荷密度、差分电荷密度和态密度等电子结构分析,发现了W-In体系中溶质原子在 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种基于分支过程的信息流行度动力学模型
    摘要:Web2.0时代,建模和预测在线信息流行度是信息传播中的重要问题.本文基于社交网络系统信息传播的机制,通过假设和简化,提出了分支过程的概率模型,来描述在线社交网络信息的流行度动力学过程.对典型在线社交网络系统的信息流行度数据和网络结构数据进行了分析,统计结果表明信息流行度衰减遵循幂律分布(幂指 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.