摘要: 采用双层线性耦合Lengyel-Epstein模型, 在二维空间对简单正四边和超点阵四边形进行了数值分析. 结果表明: 当两子系统波数比
N >1时, 随耦合强度的增大, 基模的波矢空间共振形式发生改变, 系统由简单六边形自发演化为结构复杂的新型斑图, 除已报道的超六边形外, 还获得了简单正四边和多种超点阵四边形, 包括大小点、点线、白眼和环状超四边等斑图. 当耦合系数
$\alpha $ 和
$\beta $ 在一定范围内同步增大时, 两子系统形成相同波长的I型简单正四边; 当
$\alpha $ 和
$\beta $ 不同步增大时, 由于两图灵模在短波子系统形成共振, 系统斑图经相变发生I型正四边→II型正四边→超点阵四边形的转变; 当系统失去耦合作用时, 短波子系统波长为
$\lambda $ 的I型正四边斑图迅速失稳并形成波长为
$\lambda $ /
N 的I型正四边, 随模拟时间的延长, 两子系统中不同波长的正四边均会经相变发生I型正四边→II型正四边→六边形的转变.
关键词: Lengyel-Epstein模型 /
超点阵四边形 /
图灵失稳 English Abstract Numerical investigation on square Turing patterns in medium with two coupled layers Li Xin-Zheng Bai Zhan-Guo Li Yan School of Sciences, Hebei University of Science and Technology, Shijiazhuang 050018, China Fund Project: Project supported by the Natural Science Foundation of Hebei Province, China (Grant No. A2017208081) and the Educational Commission of Hebei Province, China (Grant No. ZD2016025).Received Date: 10 December 2018Accepted Date: 05 January 2019Available Online: 01 March 2019Published Online: 20 March 2019Abstract: In this paper, the simple and superlattice square patterns in two-dimensional space are investigated numerically by the two-layer coupled Lengyel-Epstein model. When the wave number ratio of Turing modes is greater than one, our results show that the spatial resonance form of the fundamental mode is changed with the increase of coupling strength, and simple hexagon pattern evolves spontaneously into a new pattern with a complicated structure. In addition to the reported superlattice hexagonal pattern, simple square pattern and superlattice square pattern are obtained, such as the complicated big-small spot, spot-line, ring and white-eye square pattern. The characteristics of simple and complicated superlattice square pattern are investigated by the intermediate process of evolution. When the coupling parameters $\alpha $ and $\beta $ increase synchronously within a certain range, the type I square patterns of the same wavelength are obtained in the two subsystems. When the coupling parameters $\alpha $ and $\beta $ increase asynchronously, the type I square pattern can evolve into the type II square pattern on the same spatial scale through phase transition. Then, the new subharmonic modes are generated, and the complicated superlattice square patterns are obtained due to the resonance between the two Turing modes in a short wavelength mode subsystem. The influence of coupling between two subsystems on the square pattern is investigated. When the type I square pattern of wavelength $\lambda $ emerges, the square pattern will quickly lose its stability in the short wavelength mode subsystem, since the coupling coefficient is equal to zero. Finally a new square pattern of wavelength $\lambda $ /N is formed. The type I square patterns of two subsystems successively evolve into the type II square patterns through the phase transition. The spots move relatively with the extension of simulation time, and a new mode is generated and forms three-wave resonance in two subsystems, and then the hexagonal pattern dominates the system. Our results also show that the type II square pattern spontaneously transforms into a hexagonal pattern.Keywords: Lengyel-Epstein model /superlattice square pattern /Turing instability 全文HTML --> --> --> 1.引 言 丰富多样的斑图广泛存在于自然界和多个实验系统中, 如太空中的螺旋状星系、云朵的条状排列、心肌组织的螺旋波电信号、反应扩散系统和非线性光学系统中的超点阵斑图等[1 -5 ] . 它是系统发生动力学分岔和某种时空对称性破缺的结果, 一般在时间上静止、空间上呈周期分布的静态斑图由图灵失稳引起, 而随时间呈周期变化的动态斑图则由霍普夫失稳或波失稳引起. 图灵斑图主要有六边形、四边形和条纹等, 在反应扩散系统中, 因为振幅方程在临界点附近不存在$ A \to -A$ 反向对称, 方程的二阶项不为零, 所以四边形斑图相对不稳定较难获得, 成为研究的难点. 目前, 研究人员已在不同实验系统中获得了正方形和多种超四边斑图. Gal等[6 ] 在Rayleigh-Bénard对流系统中利用导热系数较差的玻璃作为边界获得了稳定的正方形斑图; Wagner等[7 ] 利用外加驱动频率在法拉第实验中获得了正四边斑图, 并观察到四边形到六边形的转变; Yang等[8 ] 利用方形图案观察到周期性光驱动下CDMA (chlorine dioxide-iodine-malonic-acid)系统中的超四边图形; Dong等[9 ,10 ] 利用介质阻挡放电装置获得了多种类型的超四边形斑图, 并分析了图形随驱动电压的变化. 除实验研究外, 人们在理论上也对四边形斑图做了大量研究工作. Page等[11 ] 利用Gierer-Meinhardt方程加四边形挡板获得了大小点超四边斑图; Yang等[12 ] 利用Brusselator模型外加周期性驱动获得了振荡正四边形; Li等[13 ] 利用双层耦合Lengyel-Epstein模型获得了图灵失稳下自发形成的一种稳定正方形斑图; Judd和Silber[14 ] 预言了格子态超四边的存在, 但未能利用理论模型获得其斑图. 可见利用反应扩散理论模型对自发形成的超四边斑图研究结果相对较少, 有待进一步深入研究.2.理论模型 自从图灵[15 ] 利用包含反应和扩散项的数学模型成功解释某些图纹的产生机理后, 多个理论模型被提出并用于研究不同系统中的斑图动力学行为[16 -20 ] , 如Brusselator模型、Schnackenberg模型、复Ginzburg-Landau理论方程、FitzHugh-Nagumo模型和Lengyel-Epstein模型等, 其中, Lengyel-Epstein 模型在研究反应扩散系统的图灵斑图中应用最广. 文中采用双层线性耦合的Lengyel-Epstein反应扩散方程, 在无量纲的情况下, 该模型的数学表达式为$u$ 和$v$ 分别为活化子和阻塞子的浓度; ${D_u}$ 和${D_v}$ 分别为变量$u$ 和$v$ 的扩散系数; $\alpha $ 和$\beta $ 为两子系统的活化子和阻塞子之间的线性耦合强度; a 和b 为动力学控制参数, 文中固定${a_1} = {a_2} = 15$ 和${b_1} = {b_2} = 9$ . 系统的均匀定态解: $({u_{10}},{v_{10}},{u_{20}},{v_{20}}) =$ $ \left( {\displaystyle\frac{{{a_1}}}{5},1 + \displaystyle\frac{{{a_1}^2}}{{25}},\frac{{{a_2}}}{5},1 + \displaystyle\frac{{{a_2}^2}}{{25}}} \right)$ , 利用微扰对定态解做线性稳定性分析得到本征值方程:${A} = \left( {\begin{array}{*{20}{c}}{ - 1 + 4\left( {\displaystyle\frac{{a_1^2 - 25}}{{a_1^2 + 25}}} \right) - \alpha }&{ - 20\displaystyle\frac{{a_1^{}}}{{a_1^2 + 25}}}&\alpha &0\\{{b_1}\left( {\displaystyle\frac{{a_1^2 - 25}}{{a_1^2 + 25}}} \right)}&{ - 5b_1^{}\displaystyle\frac{{a_1^{}}}{{a_1^2 + 25}} - \beta }&0&\beta \\\alpha &0&{ - 1 + 4\left( {\displaystyle\frac{{a_2^2 - 25}}{{a_2^2 + 25}}} \right) - \alpha }&{ - 20\displaystyle\frac{{a_2^{}}}{{a_2^2 + 25}}}\\0&\beta &{{b_2}\left( {\displaystyle\frac{{a_2^2 - 25}}{{a_2^2 + 25}}} \right)}&{ - 5b_2^{}\displaystyle\frac{{a_2^{}}}{{a_2^2 + 25}} - \beta }\end{array}} \right)$ , ${D} = \left( {\begin{array}{*{20}{c}}{{D_u}_1}&0&0&0\\0&{{D_v}_1}&0&0\\0&0&{{D_u}_2}&0\\0&0&0&{{D_v}_2}\end{array}} \right)$ , $\lambda$ 为波长的特征值, I 图1 所示). 因控制参数[21 ] $b = 9 > {b_{\rm{H}}} = \displaystyle\frac{{3{a^2} - 125}}{{5a}} = $ 7.3, 所以系统为局域渐近稳定, 通过调节扩散系数${D_u}$ 和${D_v}$ 的比值, 使b 满足图 1 两子系统图灵模型的色散曲线Figure1. Dispersion curves of Turing mode in two subsystems.$b < {b_{\rm{T}}} = \displaystyle\frac{{3{a^2} + 125 - 4a\sqrt {10({a^2} + 25)} }}{{5a{D_u}}}{D_v}$ ,${b_{\rm{H}}} < {b_{\rm{T}}}$ ($b_{\rm{H}}$ 是系统发生霍普夫失稳的临界值, $b_{\rm T}$ 是系统发生图灵失稳的临界值), 所以图灵失稳先于霍普夫失稳发生, 系统会形成空间呈周期性分布的静态图灵斑图.N × N (128 × 128)个格子的二维平面上进行, 时间积分步长$\Delta t = 0.02$ 个时间单位, 空间积分步长为$\Delta x = \Delta y = 1.0$ , 边界条件选用周期性边界条件.3.数值模拟结果与分析 23.1.简单正四边的数值分析 3.1.简单正四边的数值分析 因复杂斑图均是由简单斑图相互作用构成, 所以研究简单正四边对于超四边斑图的了解非常重要, 但反应扩散系统的振幅方程中二阶项不为零, 所以系统一般不会选择正方形斑图, 而是六边形或条纹斑图. 文中利用两个不同波长的模通过线性耦合使系统出现稳定的简单正四边斑图, 两子系统的扩散参数: (${D_{{u_1}}}$ , ${D_v}_{_1}$ , ${D_{{u_2}}}$ , ${D_v}_{_2}$ ) = (23.75, 326.85, 46.30, 671.25). 图2(a) 和图2(b) 分别为无耦合$\alpha = \beta = 0$ 时两子系统生成的小点和大点简单六边形, 空间尺度的波长比为$1:\sqrt 2 $ , 从空间傅里叶频谱显示两子系统基模的三个波矢均满足空间共振形式: ${{{k}}_3} = - {{{k}}_1} - {{{k}}_2}$ ; 当同步增大耦合强度时, 系统逐渐形成简单正四边斑图, 图2(c) 给出当层层耦合强度$\alpha = \beta = 0.10$ 时, 两子系统生成相同空间尺度波长为$\lambda $ 的I型简单正四边斑图, 空间傅里叶频谱显示基模的两个波矢: ${{{k}}_1} \bot {{{k}}_2}$ ($\left| {{{{k}}_1}} \right| = \left| {{{{k}}_2}} \right|$ ), 两波矢虽不能满足空间共振形式, 但系统斑图可稳定存在, Dong等[22 ] 利用介质阻挡放电实验装置在一定的实验条件下观察到随驱动电压的升高放电丝斑图经历六边形→正四边形的相变现象.图 2 无耦合时两子系统生成的六边形(a), (b)及耦合时生成的正四边形(c)Figure2. Hexagonal patterns (a), (b) without coupling and square pattern (c) with coupling in the two subsystems.图3(a1) 和图3(b1) ), 令$\alpha = \beta = 0$ , 去掉耦合作用, 发现短波子系统中的正四边迅速失稳并演化为波长为$\lambda /\sqrt 2 $ 的I型简单正四边斑图, 长波子系统斑图空间尺度不变(图3(a2) 和图3(b2) ), 随模拟时间延长两子系统中的I型简单正四边先后经相变演化为II型简单正四边斑图, 但空间尺度不变(图3(a3) 和图3(b3) ), 生成的II型简单正四边不能长时间稳定存在, 斑点位置随模拟时间逐渐发生变化, 并最终演化为六边形(图3(a4) 和图3(b4) ). 从稳定正四边到六边形的演化过程来看: 耦合项的存在会消除振幅方程中二阶项的影响, 从而改变原波矢的空间共振形式, 使两系统形成简单正四边斑图, 因为长波模的失稳强度大于短波模(如图1 所示), 所以长波模为主动模, 短波模为从动模, 两子系统形成空间尺度相同的四边形; 当去掉耦合作用后, 短波模由从动模变为主动模, 且两模在各自系统中的波矢大小和方向不会瞬间改变, 因此短波模会形成新的I型正四边, 且与原图形的空间尺度比为$1:\sqrt 2 $ , 而长波子系统斑图的空间尺度保持不变; 耦合作用消失后, 由于两子系统振幅方程中的二阶项的影响, 系统会重新选择稳定模式, 因此I型正四边发生失稳, 并经过相变演化为II型正四边, 随II型正四边斑点位置的移动, 两波矢不再相互垂直, 同时系统会产生一个新的模, 逐渐满足三波共振形式, 系统最终形成稳定的六边形斑图, 并且发现长波子系统斑图的失稳时间早于短波子系统, 可见II型正四边是I型正四边由稳定到不稳定的一个过渡态. 若短波子系统出现空间尺度为$\lambda /\sqrt 2 $ 的I型正四边后, 令$\alpha = \beta = 0.10$ , 让两子系统恢复耦合, 长波模会再次起主导作用, 短波子系统会重新形成波长为$\lambda $ 的稳定I型简单正四边. 在其他整数倍波数比时也有相同的模拟结果.图 3 失去耦合后两子系统中正四边斑图的自发演化Figure3. Spontaneous evolution of square patterns in two subsystems after loss of coupling.3.2.超点阵四边形的数值分析 -->3.2.超点阵四边形的数值分析 两个不同波长的模相互作用时可形成新的空间共振关系, 从而系统出现包含多个空间尺度模的复杂超点阵斑图[23 ] , 本文利用两个不同尺度的模经线性耦合后, 获得了大小点、白眼和点线等复杂超四边, 其中大小点和白眼超四边已在介质阻挡放电实验中观察到[9 -10 ,24 ] .图4 给出两子系统波数比$\sqrt 2 :1$ 时, 大小点超四边斑图的形成过程. 不难发现系统首先形成由长波模构成的I型简单正四边, 随时间延长短波子系统的正四边发生相变形成II型正四边, 长波子系统的斑图不变, 稳定一段时间后短波子系统的II型正四边会进一步演化, 每一个斑点周围形成一个晕圈, 与此同时长波子系统的I型正四边不再稳定, 发生相变演化为II型正四边, 随模拟时间延长短波子系统每四个斑点的中心位置出现新的小斑点, 系统逐渐形成大小点嵌套的复杂四边形, 空间傅里叶频谱显示有两套不同的矢量结构: ${{{q}}_1} \bot {{{q}}_2}$ , ${{{k}}_1} \bot {{{k}}_2}$ ($\left| {{q}} \right| = \sqrt 2 \left| {{k}} \right|$ ), 且两套波矢满足: ${{{k}}_1} \!+\! {{{k}}_2} = {{{q}}_1}$ , $ - {{{k}}_1} + {{{k}}_2} = {{{q}}_2}$ , 沿对角线方向的波形空间分布也可看出系统具有两种不同强度的波形. 分析其原因是短波模与长波模的竞争引起I型正四边的失稳, 当生成II型正四边时短波模与长波模逐渐由竞争关系形成空间共振, 从而系统产生大小点超四边斑图. 当系统形成超四边后, 令$\alpha = \beta = 0$ , 去掉耦合作用, 短波子系统中的大点迅速被小点所取代, 形成II型简单正四边(如图3(a3) 所示), 且两子系统正四边的空间尺度比为$1:\sqrt 2 $ , 从而说明超四边是由不同尺度的模相互作用形成.图 4 (a)—(f)大小点超四边的形成过程, 模拟时间顺序为463.8, 827.9, 893.2, 927.8, 957.4, 975.0; (g) 空间傅里叶频谱; (h) 波形空间分布($\alpha = 0.085$ , $\beta = 0.11$ , 其余参数见图2 )Figure4. (a)?(f) Formation process of big-small spot square pattern, and the simulation time sequence is as follows: 463.8, 827.9, 893.2, 927.8, 957.4, and 975.0; (g) Fourier spectrum; (h) waveform diagram ($\alpha = 0.085$ , $\beta = 0.11$ , the other parameters is the same value of Fig. 2 ).图5 所示. 当波数比为2 : 1时, 系统形成类似于大小点的复杂超四边, 也是由大小点嵌套形成, 不同的是每一个小点的边缘有一圈暗环, 属于复杂斑点; 当波数比为3 : 1时, 系统形成点线超四边, 大点成正四边排列, 大点的中心为亮点、外面是一暗环, 每一个大点由8个小斑点围绕, 并平均地分布在四边, 同侧的小斑点呈直线排列; 当波数比为4 : 1时, 系统生成环状超四边, 单元点呈正四边排列, 每一个单元点分成三层, 其中心为一亮点, 中间是一暗环, 最外面是一个大的亮环; 当波数比为5 : 1时, 系统生成白眼超四边, 每一单元的中心为白色斑点, 外面则是一暗环. 从二维傅里叶频谱可以看到: 波数比为整数时超四边的两基模波矢相互平行(${{{q}}_i}//{{{k}}_i}$ ), 在两套基矢$ { q}_i $ 和${ k}_i $ 间有新的次谐振波矢出现, 这是由于基模间相互作用可产生新的次谐振模, 次谐振模与基模间满足三波共振关系. 波数比2 : 1时最为简单, 只显示一个大小为$\sqrt 2 \left| { k}_i \right|$ 的次谐振模(见图5(a2) ), 这是因${ q}_i $ 与$ - { k}_i $ 相互作用时会产生新的次谐振波矢${ k}^{\prime}_i $ (${ q}_i - { k}_i = { k}^{\prime}_i $ ), 又因$\left| { q}_i \right| = 2\left| { k}_i \right|$ , 所以$\left| { k}^{\prime}_i\right| = \left| { k}_i \right|$ , ${ k}^{\prime}_i $ 与${ k}_i $ 重合, 因此${ k}^{\prime}_i $ 未显示, 基模${ k}_i $ 与垂直方向上的次谐振模${ k}^{\prime}_j $ ($i \ne j$ )相互作用会产生新的次谐振模, 如${ k}_1 + { k}^{\prime}_2 = { k}^{\prime\prime}_1 $ ($\left| { k}^{\prime\prime}_1 \right| = \sqrt 2 \left| { k}_i \right|$ ); 当波数比N 大于2时, 两基模${ q}_i $ 和$ -{ k}_i $ 相互作用生成大小为$(N - 1)\left| { k}_i \right|$ 的次谐振模, 次谐振模与基模$ - { k}_i$ 相互作用又会产生尺度为$(N - 2)\left| { k}_i \right|$ 的模, 直至一倍新生模为止, 两垂直方向的模相互作用, 又会产生非整数次谐振模, 因此傅里叶频谱图显示除整数倍模外, 还有多个非整数倍尺度模产生, 并且随波数比的增大新生次谐振模的数量增加明显.图 5 不同波数比时系统形成的超四边形 (a)复杂大小点四边, Du 1 = 11.885, Dv 1 = 163.425, Du 2 = 46.30, Dv 2 = 671.25, $\alpha = 0.075$ , $\beta = 0.11$ ; (b) 点线四边, Du 1 = 2.95, Dv 1 = 41.15, Du 2 = 25.75, Dv 2 = 382.05, $\alpha = 0.085$ , $\beta = 0.11$ ; (c)环状四边, Du 1 = 2.95, Dv 1 = 41.15, Du 2 = 45.90, Dv 2 = 677.05, $\alpha = 0.085$ , $\beta = 0.11$ ; (d)白眼四边, Du 1 = 2.95, Dv 1 = 41.15, Du 2 = 71.0, Dv 2 = 1065.25, $\alpha = 0.075$ , $\beta = 0.11$ Figure5. Square superlattice pattern at different wavenumber ratios: (a) Complex big-small spot square pattern, Du 1 = 11.885, Dv 1 = 163.425, Du 2 = 46.30, Dv 2 = 671.25, $\alpha = 0.075$ , $\beta = 0.11$ ; (b) spot-line square pattern, Du 1 = 2.95, Dv 1 = 41.15, Du 2 = 25.75, Dv 2 = 382.05, $\alpha = 0.085$ , $\beta = 0.11$ ; (c) ring square pattern, Du 1 = 2.95, Dv 1 = 41.15, Du 2 = 45.90, Dv 2 = 677.05, $\alpha = 0.085$ , $\beta = 0.11$ ; (d) white-eye square pattern, Du 1 = 2.95, Dv 1 = 41.15, Du 2 = 71.0, Dv 2 = 1065.25, $\alpha = 0.075$ , $\beta = 0.11$ .4.结 论 本文利用双层线性耦合Lengyel-Epstein模型, 通过分析斑图的演化过程, 研究了简单正四边和超点阵四边形斑图的形成机制. 发现在控制参数a 和b 确定时, 两子系统的耦合强度和波数比在四边形斑图的形成过程中发挥了重要作用. 随耦合系数的增加, 系统可实现简单六边形到简单正四边形的相变, 耦合项的存在会消除振幅方程中二次项的影响, 研究表明生成的I型正四边经相变转化为相同空间尺度的II型正四边, 当两基模在短波子系统发生共振时, 其系统会形成包含多个尺度模的超点阵正四边, 通过调节两图灵模的波数比获得了多种超四边, 包括大小点、点线、环状和白眼等超四边; 在失去耦合作用时, 因为四边形的波矢不满足空间共振形式, 所以系统会重新选择斑图的稳定存在形式, 随模拟时间延长两子系统中II型正四边的单元点空间位置逐渐发生改变, 将会出现一个新的模, 使系统的模满足三波共振形式. 本文的研究结果对于非线性系统超点阵斑图的深入研究具有重要的借鉴作用. 






















 图 1 两子系统图灵模型的色散曲线
图 1 两子系统图灵模型的色散曲线
















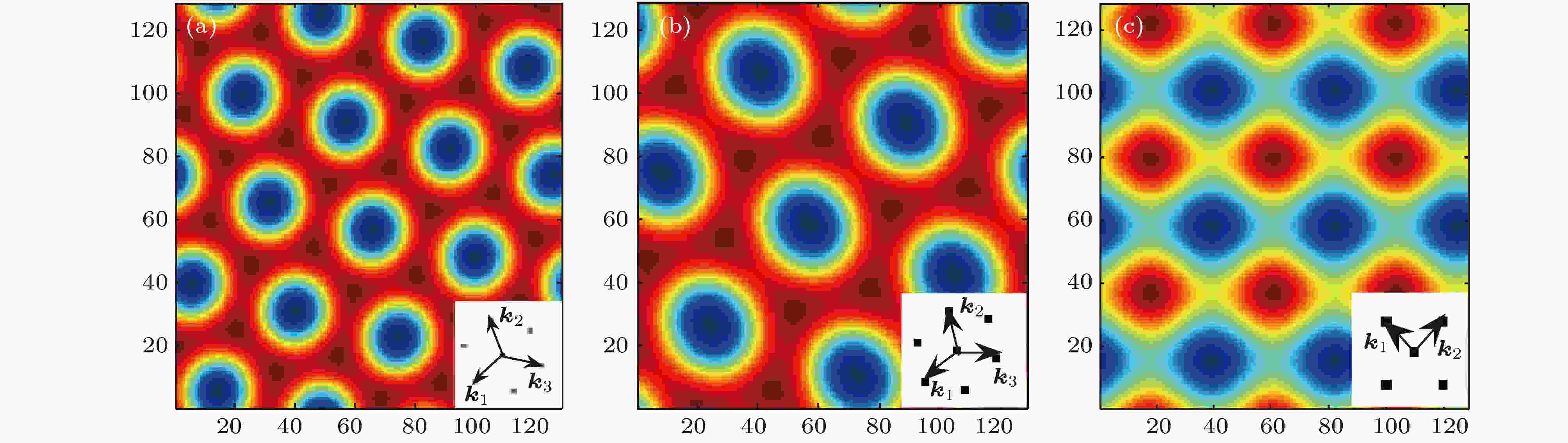 图 2 无耦合时两子系统生成的六边形(a), (b)及耦合时生成的正四边形(c)
图 2 无耦合时两子系统生成的六边形(a), (b)及耦合时生成的正四边形(c)







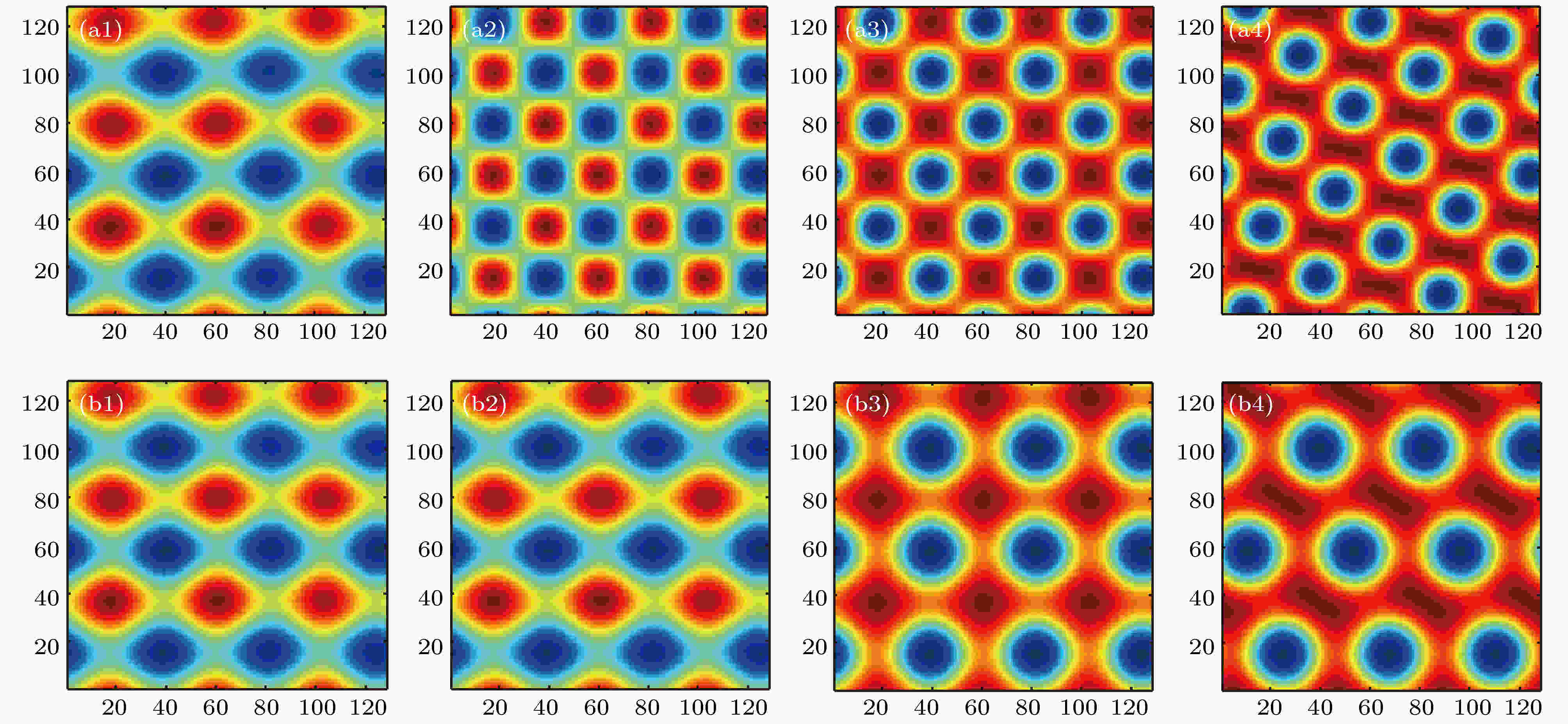 图 3 失去耦合后两子系统中正四边斑图的自发演化
图 3 失去耦合后两子系统中正四边斑图的自发演化







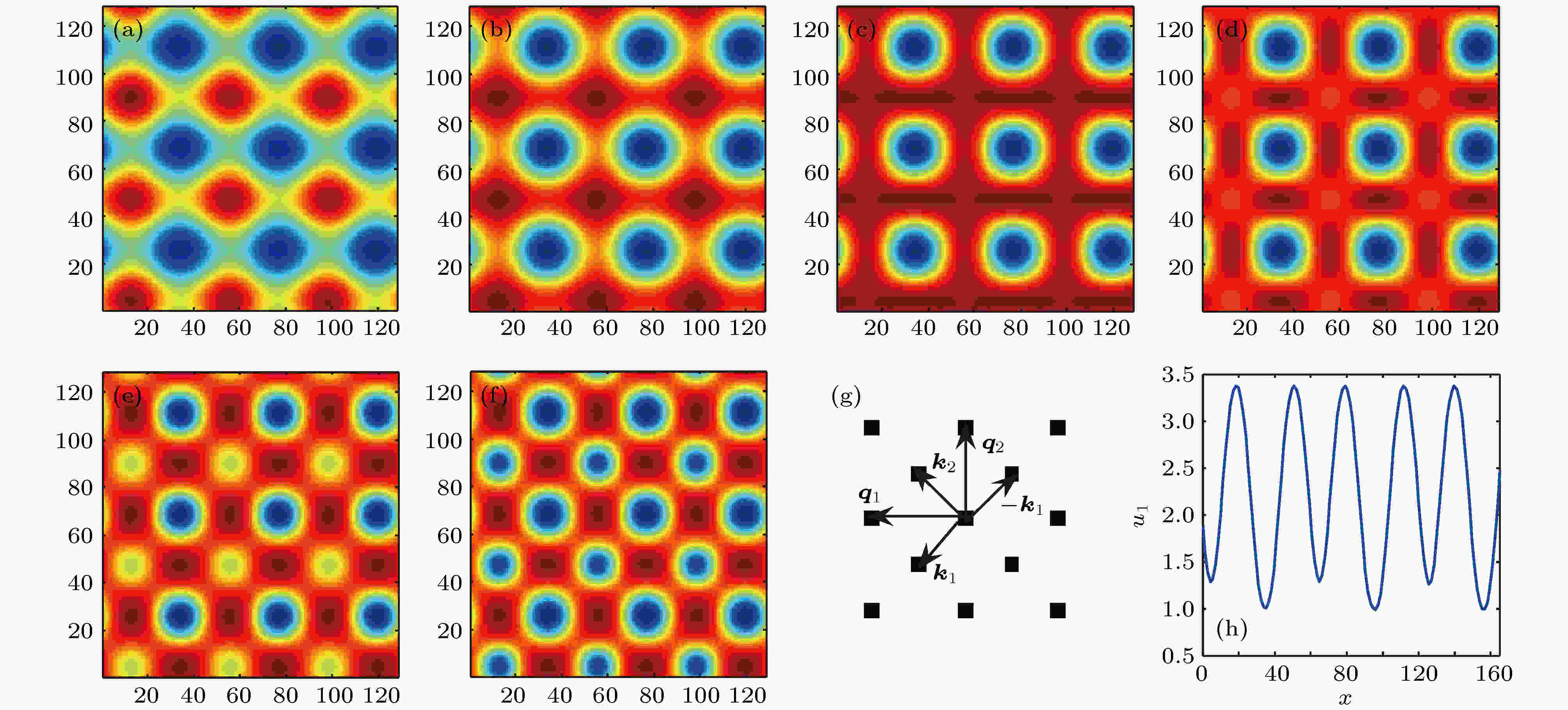 图 4 (a)—(f)大小点超四边的形成过程, 模拟时间顺序为463.8, 827.9, 893.2, 927.8, 957.4, 975.0; (g) 空间傅里叶频谱; (h) 波形空间分布(
图 4 (a)—(f)大小点超四边的形成过程, 模拟时间顺序为463.8, 827.9, 893.2, 927.8, 957.4, 975.0; (g) 空间傅里叶频谱; (h) 波形空间分布(








































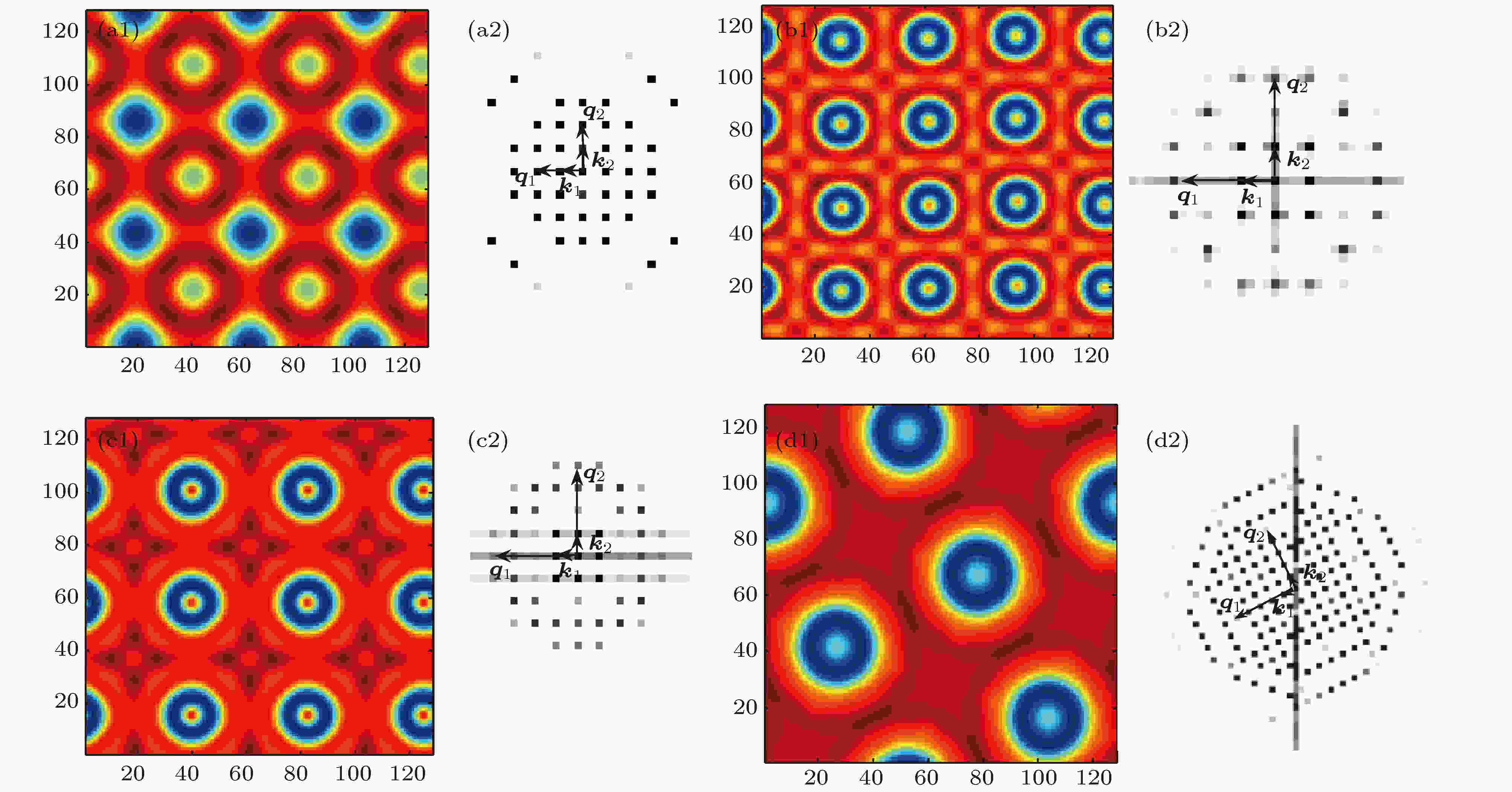 图 5 不同波数比时系统形成的超四边形 (a)复杂大小点四边, Du1 = 11.885, Dv1 = 163.425, Du2 = 46.30, Dv2 = 671.25,
图 5 不同波数比时系统形成的超四边形 (a)复杂大小点四边, Du1 = 11.885, Dv1 = 163.425, Du2 = 46.30, Dv2 = 671.25, 





















































