摘要:复杂声学环境中人耳附近空间降噪是有源噪声控制研究的重要课题, 目前采用的主要方法为有源降噪头靠(AHR)和虚拟声屏障(VSB). 本文简述AHR与VSB的发展历史和研究现状, 介绍其物理原理和设计方法, 评述其在实际应用中的优缺点, 讨论了目前存在的问题与未来相关的研究方向. 已有理论、数值仿真和实验研究验证了相关技术在人耳附近空间产生静区的可行性. AHR系统需要较少控制源, 系统相对简单易实现, 但静区范围较小, 结合虚拟传声器技术和人头跟踪技术后可实现随人头移动的静区, 降噪频率可达中高频; VSB产生的静区范围较大, 但控制源个数较多, 系统复杂和成本高, 可通过代价函数和控制源优化, 以及主被动混合控制技术来提高有效降噪频率范围和减少控制源个数.
关键词: 有源噪声控制/
有源降噪头靠/
虚拟声屏障/
静区

English Abstract

全文HTML

--> --> -->

传统降噪方法采用材料和结构进行隔声、吸声和消声, 在中高频可有效降噪, 但因应用场合对材料和结构的体积和重量限制, 在低频时性能下降^[1]. 有源噪声控制技术通过引入控制声源影响初级噪声源的辐射和传输来实现降噪, 具有体积小、重量轻和低频降噪性能好的特点^[2]. 有源降噪技术可针对噪声源进行控制以降低声源的总辐射功率^[3,4]. 有源降噪技术也可用于传播路径的控制, 如与传统声屏障结合的有源声屏障通过在屏障顶部放置控制声源减少入射波的衍射, 从而增大声屏障的插入损失^[5-8].
对于保护接收者, 有源降噪耳机通过电路提升耳机低频降噪性能, 获得较好的宽带降噪效果^[9,10], 但耳机佩戴有时给人耳带来不适或压迫感. 因此有必要探讨在人耳附近空间产生静区的技术^[11-23], 该技术有广阔的应用场景, 尤其在噪声级高、噪声源众多且难以定位的复杂噪声环境. 如在舰船舱室、飞机机舱和列车车厢中降低操作人员和乘客附近的噪声, 在生产车间降低操作人员附近的噪声, 甚至可在卧室人耳附近降低传来的鼾声^[24].
目前在人耳附近空间产生静区的方法主要有两类: 一是有源降噪头靠(active HeadRest, AHR), 一般由2个控制声源、2个误差传声器和有源控制 器组成, 通过降低误差传声器处噪声在人耳附近形成静区^[11-13]; 二是虚拟声屏障(virtual sound barrier, VSB), 使用控制声源阵列与传声器阵列围成封闭几何形状包围目标区域, 阻挡来自各个方向的噪声, 在目标区域内形成静区, 因其不影响空气和光线的传播, 像一个无形的屏障对噪声起作用, 故称为VSB ^[20,21].
本文针对复杂声学环境中人耳附近空间降噪问题, 分别介绍AHR系统和VSB系统的发展历史与现状、原理、设计方法和应用, 并讨论目前存在的问题和未来的研究方向.

2

-->

2.1.发展历史和现状

AHR系统如图1所示, 扬声器作为控制声源, 通过控制器调节扬声器输出在人耳旁的误差传声器附近产生静区. AHR的概念最早可追溯至Olson和May^[25]于1953年提出的“电子吸声器”, 他们使用模拟电路调节扬声器的输出以抵消传声器处的噪声, 在传声器附近产生静区, 并展望了在汽车和工厂的应用前景. 由于当时电子技术水平限制, 相关系统难以应用于实际, 其研究也陷入沉寂. 随电子技术水平的进步, 直到20世纪80年代, 有源噪声控制的研究才渐渐复苏并最终蓬勃发展, 人耳附近空间降噪也重新受到关注.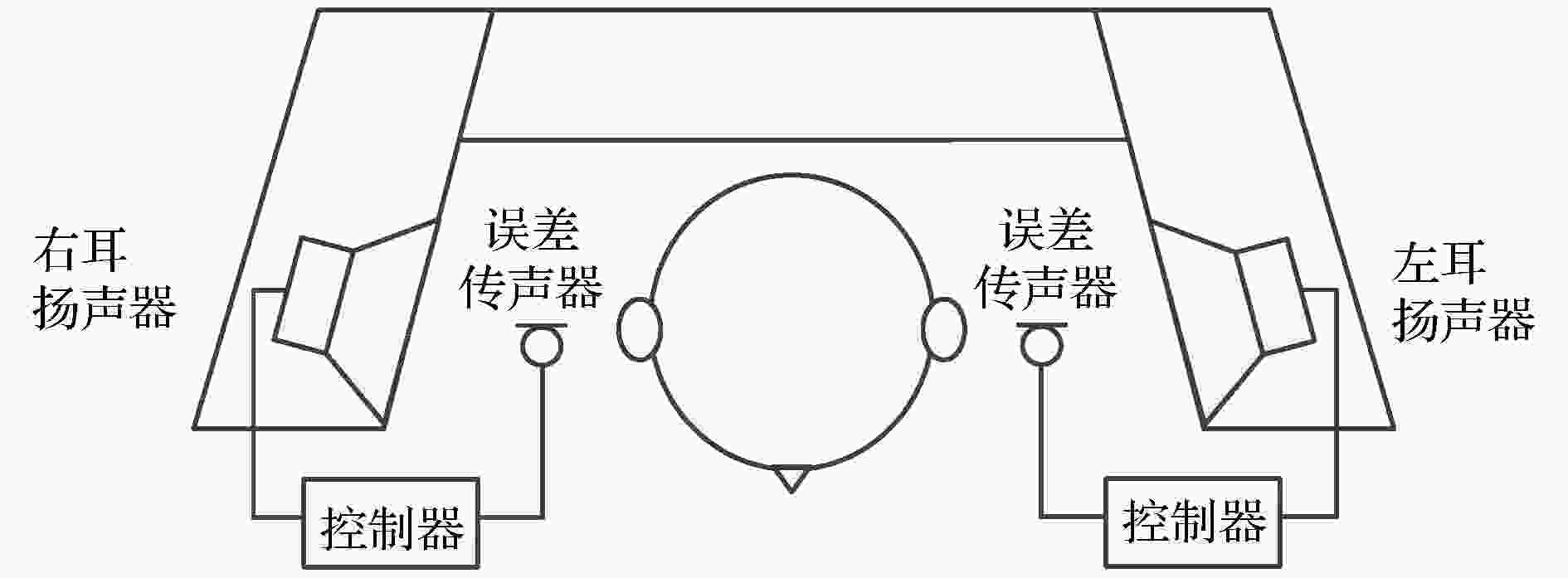
图 1 AHR示意图
Figure1. Schematic drawing of AHR.

降噪量超过10 dB的静区大小是评价AHR性能的重要参数. 英国南安普顿大学声与振动研究所(ISVR)在该领域有一系列重要研究. Elliott等^[11]应用空间相关函数理论分析扩散场中一个控制源在远场产生的静区, 发现其形状是直径小于1/10声波波长的球. 而在控制源近场, 用无限大障板上的活塞作为控制声源, 其近场某点的静区形状在低频是厚度不超过1/10声波波长的球壳, 在高频则是直径小于1/10声波波长的球^[26,27]. 无论是在控制源远场还是近场, 若同时控制某点的声压和质点速度, 都能获得更大静区^[28,29].
实际应用中, AHR周围可能存在反射体和反射面, Garcia-Bonito和Elliott^[12]将控制声源建模为表面有振动速度分布的球体, 同时考虑人头衍射的影响, 研究此时的静区分布, 发现人头衍射对控制有好处. Garcia-Bonito等^[30]进一步研究在扩散场中4种反射表面对静区大小的影响, 结果表明反射表面增大了静区. Rafaely^[31-32]提出了空间时间相关函数, 并用于研究控制声源在宽频混响声场中产生的静区, 指出静区大小与频率等于频带中心频率的单频情况相若.
由前述可知, AHR系统静区直径不超过1/10声波波长, 因此误差传声器必须靠近人耳, 有时不方便. 可在头靠系统中引入虚拟传声器布放技术(virtual microphone arrangement), 将误差传声器(此时称物理传声器)移至离人头较远的位置, 在人耳处假设虚拟传声器, 使用物理传声器预测虚拟传声器处的噪声, 从而使控制声源在虚拟传声器处产生静区^[13,14,33]. 早期研究假设物理传声器与虚拟传声器的初级声场相等, 故系统性能依赖于两者的匹配程度, 在500 Hz以下低频段降噪效果较好, 但在500 Hz以上频段性能下降, 甚至导致噪声增大^[14].
为解决这一问题, Roure和Albarrazin^[34]提出了远程传声器技术(remote microphone technique), 事先测量物理传声器(称为远程传声器)与虚拟传声器(称为近端传声器)的初级声场间的传递函数, 系统运行时可更准确地以远程传声器处的声场信号来估计虚拟传声器处的声场. 为进一步降低估计误差, 可使用多个远程传声器估计近端传声器处的声场. 研究表明, 在扩散声场以及远程传声器指向近端传声器方向的定向声场中, 使用4个远程传声器可显著提高性能^[35].
虚拟传声器技术与远程传声器技术均需在使用前测量控制源到物理传声器和虚拟传声器间声场传递函数, Kestell^[36,37]提出使用多个物理传声器的信号通过插值来外推预测虚拟传声器的声压, 该方法无需预先测量与虚拟传声器相关的声场传递函数, 系统对声场传递函数的变化具有较好的鲁棒性, 然而预测精度仅在物理传声器和虚拟传声器的间距远小于波长时才较高. 有源噪声控制中的虚拟传感问题本质上为预测问题, Petersen等^[38]提出使用卡尔曼滤波进行预测, 通过预先计算的参数对物理传声器处的信号进行处理估计近端传声器的信号, 滤波算法中已包含了测量误差的影响, 但该方法适用于相对低阶的系统.
人头移动引起的声场变化会降低虚拟误差信号与近端误差信号的估计精度, 进而影响降噪效果和系统的稳定性^[16]. 针对该问题, Petersen等^[39]提出移动虚拟传感技术, 在一维管道的实验结果表明, 对于窄带噪声有效地产生了能跟随指定目标的静区. 对于三维声场中的AHR, 移动虚拟传声器技术需要知道目标区域即人头的位置信息^[40], 可通过三维头部跟踪系统实现^[16,17,41]. 预先测量并存储不同人头位置对应的声场传递函数, 使用摄像系统实时跟踪人头移动位置, 调用对应的传递函数进行计算并控制噪声, Elliott等^[17]对1000 Hz以下宽带噪声取得近20 dB的降噪量. 为避免使用复杂的头部跟踪系统, Lei等^[42]通过改进次级路径模型, 使之在人头活动范围内与真实次级路径保持较高匹配度, 提高了人耳位置处降噪量, 扩大了人头允许移动范围.
2 -->

2.2.原理、设计方法

室内扩散声场是一种复杂的噪声环境, 可用于分析AHR的性能. 设初级声场为扩散声场, 当控制源远离误差点时, 次级声场也为扩散声场, 围绕误差点的静区大小依赖于扩散声场的统计特性. 初级声场中声压的空间分布可视为一个高斯随机过程, 空间相关函数反映空间中任意两点间的声压相关性^[11]. 纯音扩散声场中声压的归一化空间相关函数为^[43]

$\rho (\Delta x) = \sin (k\Delta x),$

式中$\Delta x$为空间两点的距离; k为声波的波矢. 在稳态扩散声场中, 用远场控制声源使误差点x₀处的声压降为零, 此时误差点x₀附近任一点${{ x}_0} + \Delta { x}$的声压空间均方值由整个空间声场的声压空间均方值与声场空间相关函数决定, 即

$ \left\langle {|p({{ x}_0} + \Delta { x}){|^2} } \right\rangle = \left\langle {|p({ x}){|^2} } \right\rangle [1 - {\rho ^2}(\Delta x)],$

式中“$ \left\langle { } \right\rangle$”表示空间平均; $\Delta x$为该点与误差点间的距离; $ \left\langle {|p({ x}){|^2} } \right\rangle $为整个空间所有点的平均值^[11], 该式得到了仿真与实验的验证^[11,44]. 实验表明控制后的室内整体均方声压大幅提升, 是控制前的3.8倍, 代入(2)式可得

$\frac{{\left\langle {|p({{ x}_0} + \Delta { x}){|^2} } \right\rangle }}{{ \left\langle {|{p_{\rm{p}}}({ x}){|^2}} \right\rangle }} = 3.8[1 - {\rho ^2}(\Delta x)],$

式中p_p(x)为初级场的声压. (3)式显示控制后空间某点的降噪量仅和该点与误差点的空间相关函数有关. 据此可算出10 dB静区为一球形, 直径约为1/10声波波长.
当误差点位于控制源近场时, 在该点附近的次级声场中以直达声为主, 经室内壁面反射造成的混响声可忽略, 则近场的次级声场声压分布仅与控制源辐射阻抗有关. 使用位于y_s的控制声源控制位于x₀的近场误差点声压为零, 对于误差点附近任一点${{ x}_0} + \Delta { x}$(满足$\left| {k\Delta { x}} \right| < 1$), 有

$\frac{{ \left\langle {|p({{ x}_0} + \Delta { x}){|^2}} \right\rangle}}{{\left\langle {|{p_{\rm{p}}}({{ x}_0}){|^2} } \right\rangle}} \approx {\left| {\frac{{\nabla {Z_{\rm{d}}}({{ x}_0}|{{ y}_{\rm{s}}}) \cdot \Delta { x}}}{{{Z_{\rm{d}}}({{ x}_0}|{{ y}_{\rm{s}}})}}} \right|^2},$

式中p_p(x₀)为初级场误差点的声压; Z_d(x₀|y_s)为控制源和误差点间的直达声阻抗传递函数^[27].可见控制后误差点附近场点的降噪量仅和控制源辐射特性及误差点和场点距离有关.
使用点源控制源与活塞控制源进行分析, 将其声阻抗传递函数代入(4)式, 结果表明误差点距离控制源很近时10 dB静区范围很小, 直径不及1/10声波波长, 当误差点渐远, 10 dB静区范围逐渐扩大, 其直径上限为1/10声波波长^[26,27]. 在中高频静区形状与控制源辐射特性相关, 而在低频静区形状为环绕控制源的球壳.
不论是在控制源远场还是近场, 误差点位于刚性反射表面或其附近时, 静区大小均有不同程度的增加^[12,30]. 对于控制源远场, 由于反射面的影响, 空间相关函数值增大, 静区大小在反射面法向上增大, 误差点越靠近反射面效果越明显. 其物理解释为此时反射体表面声压梯度为0, 等效于控制系统同时控制了误差点处的声压和误差点附近的声压梯度, 因此静区得以增大^[30]. 对于控制源近场, 将人头建模为一刚性球, 研究表明有人头存在时, 静区“趋向”人头, 使静区大小有微小的增大, 人头对次级声场的散射是主要原因, 而初级声场的散射作用可忽略不计^[12].
AHR的静区直径较小, 故误差传声器必须靠近人耳. 虚拟传声器技术以原误差传声器位置为虚拟传声器位置, 物理传声器移至离人头较远的位置. 图2为单通道虚拟传声器的示意图, 物理传声器处的声压和虚拟传声器处的声压分别为^[14]
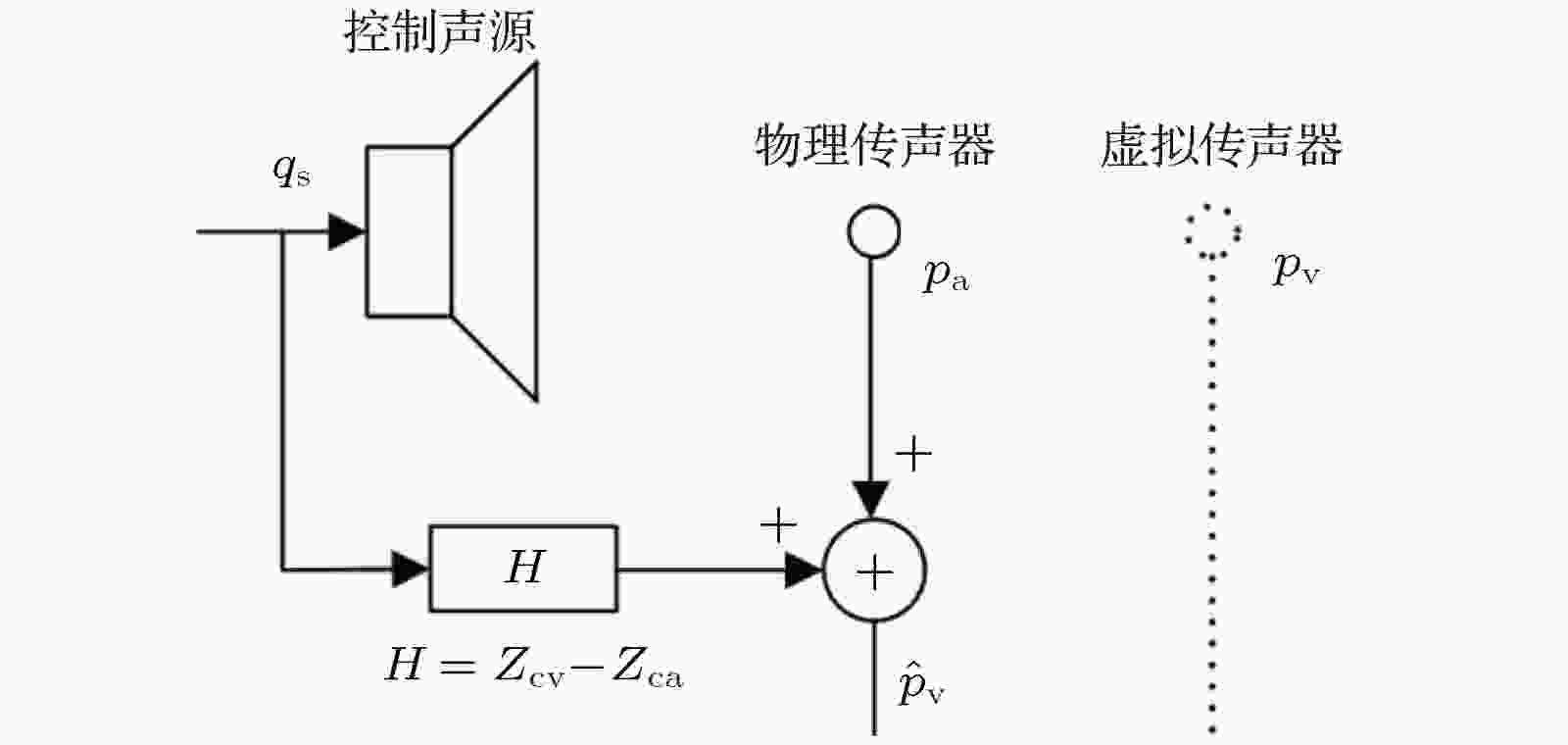图 2 单通道虚拟传声器示意图^[14]
Figure2. Schematic drawing of single-channel virtual microphone arrangement^[14].

$\left\{ \begin{aligned}&{p_{\rm{a}}} = {p_{{\rm{pa}}}} + {Z_{{\rm{ca}}}}{q_{\rm{s}}},\\&{p_{\rm{v}}} = {p_{{\rm{pv}}}} + {Z_{{\rm{cv}}}}{q_{\rm{s}}},\end{aligned} \right.$

式中p_pa和p_pv分别为物理传声器和虚拟传声器处的初级声压; Z_ca和Z_cv分别为控制声源到物理传声器和虚拟传声器处的传递函数; q_s为控制声源源强. 假设初级声场在低频随空间位置变化较小, 在物理传声器与虚拟传声器较近条件下, 可假设p_pa ≈ p_pv, 则虚拟传声器处的声压可估计为^[14]

${\hat p_{\rm{v}}} \approx {p_{{\rm{pa}}}} + {Z_{{\rm{cv}}}}{q_{\rm{s}}} = {p_{\rm{a}}} + ({Z_{{\rm{cv}}}} - {Z_{{\rm{ca}}}}){q_{\rm{s}}}.$

已知Z_ca, Z_cv和q_s, 测得物理传声器的声压p_a, 便可估计出虚拟传声器处的声压${\hat p_{\rm{v}}}$并使用控制声源进行控制.
物理传声器与虚拟传声器的初级声压差别随着频率增大而增加, 故相关系统在低频段降噪效果较好, 但在500 Hz以上频段性能下降, 甚至导致噪声增大^[14]. 远程传声器技术事先测量远程物理传声器与近端虚拟传声器的初级声场间的传递函数(称为观测滤波器), 较准确地估计近端传声器处的声场^[34]. 设p_pv = Gp_pa, G为观测滤波器, 则近端传声器处的声压可估计为

${\hat p_{\rm{v}}} = G{p_{{\rm{pa}}}} + {Z_{{\rm{cv}}}}{q_{\rm{s}}} = G({p_{\rm{a}}} - {Z_{{\rm{ca}}}}{q_{\rm{s}}}) + {Z_{{\rm{cv}}}}{q_{\rm{s}}},$

已知G, Z_ca, Z_cv和q_s, 可通过p_a估计出近端传声器处的声压${\hat p_{\rm{v}}}$. 可见(6)式是(7)式中G = 1的特例.
近端传声器声压的估计误差是影响控制系统性能的重要因素, 其误差来源包括远程传声器个数和位置以及初级声场特性^[35]. 以估计误差的均方值为代价函数, 可求出观测滤波器的最优解^[45], 对于远程传声器多于近端传声器的超定条件, 需选择合适的正则参数以在系统估算误差和鲁棒性之间取得较好的平衡^[35]. 使用4个远程传声器对1个近端传声器进行估计, 相对于1个远程传声器而言, 在扩散声场以及初级源位于远程传声器后面(近端传声器为前面)的自由场中, 估计误差小于10 dB和20 dB的近端传声器可选区域明显扩大. 若在初级源位于远程传声器侧面的自由场中, 则可选区域变化较小. 远程传声器数量不变, 优化其位置分布需同时考虑阵列几何结构与初级声场的空间匹配度与观测滤波器中可逆矩阵的条件数, 空间匹配度高与较低的条件数可获得较准确的预测精度^[35].
2 -->

2.3.应　用

有源降噪技术在汽车领域有部分应用研究, 其中汽车发动机低频降噪是小空间的全局控制问题, 已在多款车型中商用. 与此不同, 轮胎/道路噪声包含较高频率分量, 属于局域空间降噪问题. 目前大部分相关研究是在人耳附近布放误差传声器, 使用车门扬声器进行控制, 虽属人头附近局域降噪, 但不完全属于AHR^[46]. AHR使用安装于座椅两侧的扬声器作为控制声源, 通过反馈、前馈以及前反馈混合控制算法在人耳处降噪, 降噪效果约3—4 dBA^[47].
AHR系统应用研究中的一个重要问题是人头移动导致降噪性能将下降. 移动虚拟传声器技术可让静区随头部移动, 但该技术需要知道目标区域即人头的位置信息. 最近的研究表明, 通过三维头部跟踪系统实现人头位置跟踪^[16-17,41], 调用预先测量并存储的与人头位置对应的声场传递函数, 可准确估计虚拟传声器位置处的声压并控制. 该AHR系统如图3所示, 包含2个控制源, 4个远程传声器和1套人头跟踪系统, 人耳处为近端传声器位置. 人头活动区域可划分为20个位置(图中网格点), 事先测量人头在不同位置时的声场传递函数并储存, 人头移动时, 跟踪系统判断其所在位置, 调用相应的传递函数计算虚拟传声器位置处的声压并驱动控制源降噪. 在噪声环境中, 测量该系统有源降噪和人头跟踪过程中人耳处的实时噪声信号, 结果表明, 当人头保持不动并开启有源降噪系统情况下, 双耳获得有效降噪; 人头移动到不同位置, 有源降噪系统保持工作但人头跟踪系统关闭时, 降噪效果显著下降; 有源降噪系统与人头跟踪系统同时开启, 尽管人头仍在移动, 降噪效果将获得较大改善^[16].
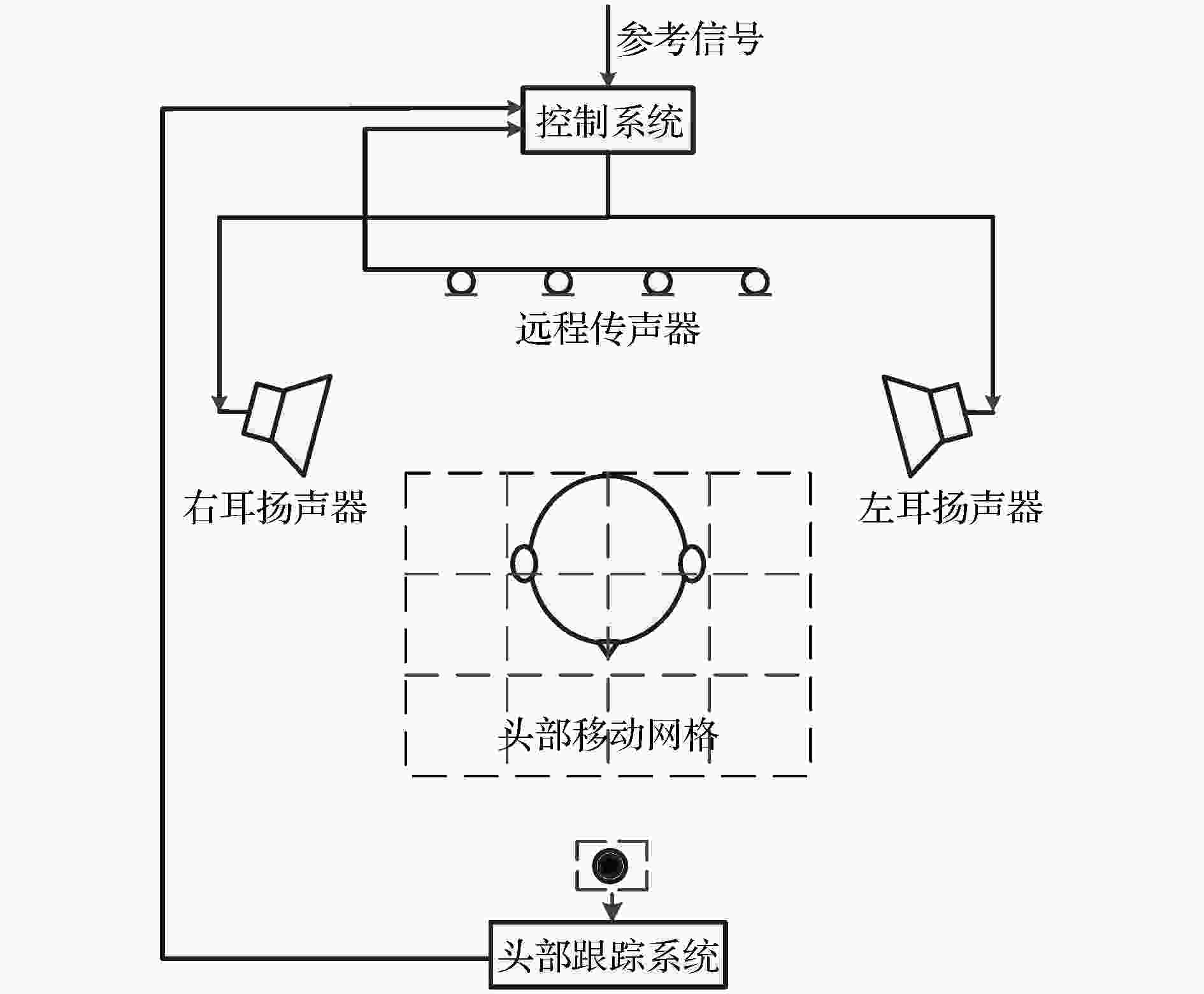图 3 使用远程传声器技术和人头跟踪系统的AHR系统^[16]
Figure3. AHR system integrated with remote microphone technique and head tracker system^[16].

2

-->

3.1.发展历史和现状

在人耳附近空间产生静区的另一类方法为VSB, 类似的研究包括边界声压控制(boundary pressure control)^[23]. VSB一般离声源较远, 属于声场控制, 其主要机理是通过控制声源吸收或反射初级噪声. VSB系统的理论基础是Huygens原理和K-H( Kirchhoff-Helmholtz)积分方程, 即若某一空间内部没有声源, 则该空间内的声场完全由该空间边界上的声压及其梯度决定. 因此, 若在该区域外部或者边界上放置控制声源, 通过控制声源产生的声场调整上述边界的声压及其梯度, 使其减小或者为零, 则可整体降低边界包围区域的声压^[48].
利用Huygens原理来实现有源声控制的思想在20世纪70年代前后出现, Jessel, Malyuzhinets和Canevet提出了JMC理论, 指出在封闭曲面使用连续分布的单极子源和偶极子源的组合可实现对入射声波的完美吸收^[49-52]. Mangiante^[53]在三维空间应用扬声器近距离包围初级噪声源实现低频噪声辐射控制, 但该实验的控制原理是降低初级噪声源的声辐射功率, 而不全是基于Huygens原理的声场控制. Ise^[19]应用K-H方程进行“边界控制”研究, 在二维平面上布置一圈误差传声器, 通过控制外圈控制声源阵列的输出, 使误差传声器处的声压和质点速度为0, 达到控制误差传声器圈内的声场的目的, 然而研究只限于二维上的理论分析和数值仿真.
Qiu等^[20]提出的VSB系统将K-H方程的研究扩展到三维空间, 使用圆柱状结构的控制声源阵列和误差传声器阵列, 通过控制误差传声器处的声压, 在传声器阵列包围的空间内部产生静区, 仿真结果验证了VSB系统降噪的可行性, 然而缺乏实验验证且静区范围仅与人头大小相若, 人头不便活动. Zou等^[21]完成了16通道圆柱状VSB系统的理论和实验研究, 在半径为0.2 m, 高为0.2 m的柱状区域, 对550 Hz以下的噪声, 获得10 dB以上的全空间降噪, 与此同时, 系统对周围声场的影响有限. 研究还表明系统性能与控制源和传感器的位置和数量有关, 降噪量随着频率升高而近似线性降低.
Zou和Qiu^[22]进一步研究了引入人头后, 人头散射对VSB系统性能的影响, 发现此时VSB系统性能随着物理配置的变化趋势与未引入人头时是一致的, 但人头散射使系统性能略有提高, 实验结果还表明, 系统对人头移动有较好的鲁棒性. Epain和Friot^[23]使用边界声压控制方法控制球形体积内的声压, 原理与VSB系统相同, 30个误差传声器分布于半径为0.3 m的球壳上, 30个控制声源分布于半径为0.6 m的球壳, 在整个球形区间内均获得有效降噪, 其中区间内的2个典型测点在100—500 Hz的宽带噪声的降噪量约20 dB.
VSB系统控制不同的物理量会有不同的控制效果. 以误差传感器的声势能密度和为代价函数, 在低频可取得较好的降噪效果, 但声压降低量不很均匀, 且由于内部空间特征值问题, 降低了有效降噪的上限频率; 以声动能密度和为代价函数, 声压降低量最为均匀, 但低频的降噪效果不好; 以声能量密度和为代价函数, 降噪效果最好且具有较均匀的声压降低量分布^[54]. VSB系统中也可使用虚拟传感器技术, 将物理传感器布放于目标区域边界, 虚拟传感器布放于目标区域中的优化位置可提升降噪效果, 且避免传感器在目标区域中与人头形成冲突, 系统的性能和控制声源与物理传感器的距离有关, 也和初级声场的复杂程度及虚拟传感器位置声场预测方法有关^[55].
Rao^[56]研究控制源的指向性对VSB系统性能的影响, 指出对于最小均方优化法的VSB系统, 指向性控制源相比单极子声源可获得更大的降噪量, 此外, 指向性控制源可降低VSB系统对外部声场的影响. 实际应用中, VSB系统周围可能存在反射面. 初步研究表明, 墙面附近的VSB降噪性能随频率变化的曲线在自由场环境的降噪曲线上下波动, 降噪量随反射面的距离呈周期性变化. 此外, 墙面反射导致VSB系统的性能对初级声场的入射角度变得敏感^[56,57].
2 -->

3.2.原理和设计方法

VSB的理论依据是形如式(8)的K-H积分方程:

$p({{r}}) = \int_S {[{\rm{G}}({{r}}|{{s}})\nabla p({{s}}) - p({{s}})\nabla {\rm G}({{r}}|{{s}})]} \cdot {{n}}{\rm{ d}}S,$

式中边界S包围体积V; p(s)为边界S上点s处的声压; p(r)为体积V内点r处的声压; n为边界S的外法向单位矢量; G(r|s)为自由空间的格林函数^[48], 表达式为

${\rm{G}}({{r}}|{{s}}) = \frac{1}{{4{\text{π}}|{{r}} - {{s}}|}}{{\rm{e}}^{ - {\rm{j}}k|{{r}} - {{s}}|}}.$

(8)式给出了某一内部没有声源的空间, 其内部声压和边界上声压及其梯度的关系^[48] , 描述了声场的内在性质, 是Huygens原理的一种数学表达, 即某一空间内的声场完全可用其边界上的声压及其梯度决定. 因此, 可通过控制空间外部或者边界上的控制声源调节该声场边界上的声压及其梯度控制该空间内声场, 这是VSB系统的基本原理.
图4是VSB系统的示意图, 由立体结构的扬声器阵列和传声器阵列构成, 在传声器阵列围成的封闭空间内部产生静区. 对于初级噪声源位置和辐射声场随时间变化的场合, VSB系统通过误差传声器和自适应系统动态调整控制扬声器的输出来控制噪声. 对于稳定的初级噪声场, 可以省去监测用的误差传声器, 控制扬声器的输出可根据初级声场的分布和静区的位置事先设计.
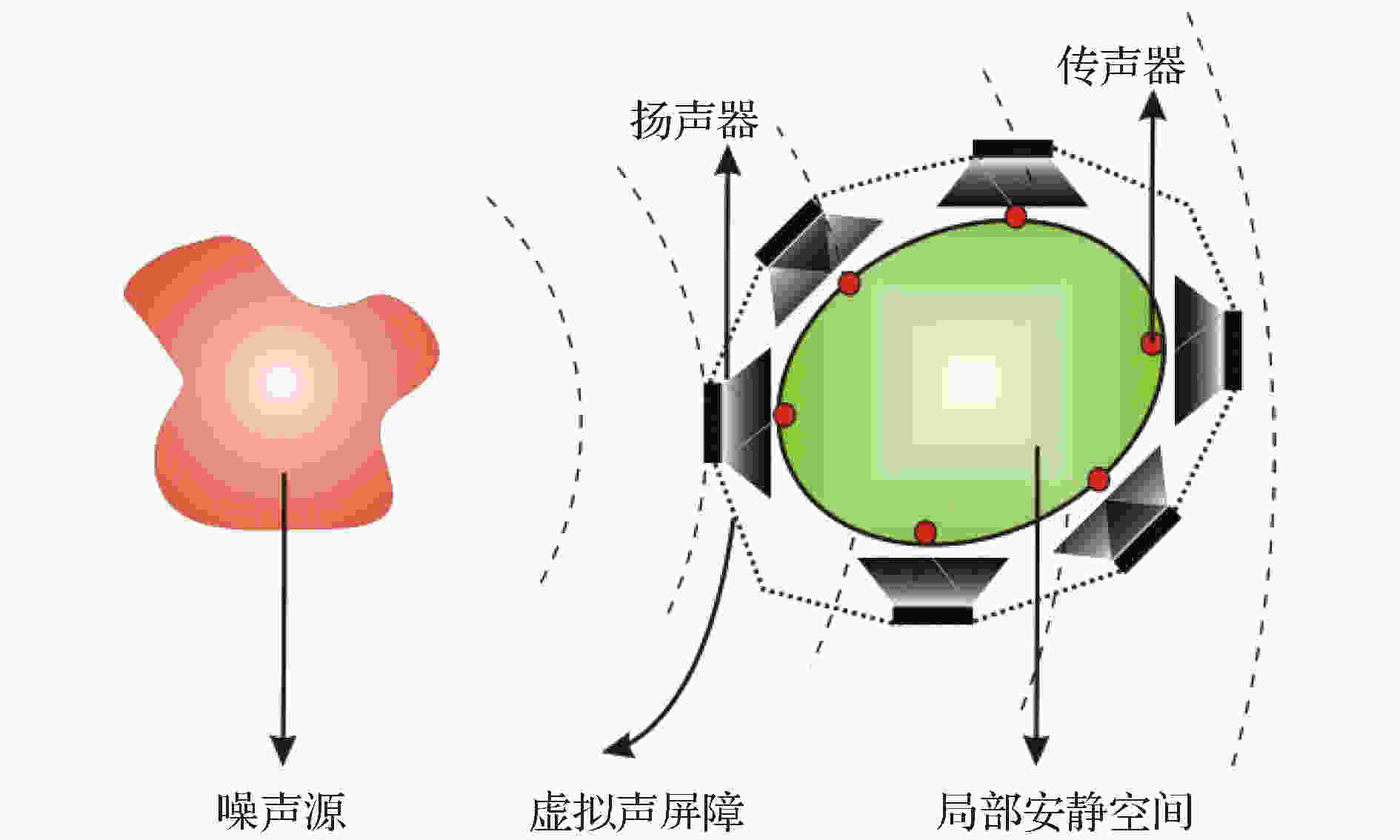图 4 VSB系统示意图
Figure4. Schematic drawing of a VSB system.

VSB系统的降噪机理可能有多种. 若VSB系统距离初级声源很近, 导致控制声源与初级声源相互作用降低噪声, 其机理为降低噪声源的辐射阻抗; 若VSB系统在低模态的封闭空间中, 可通过控制源产生的模态耦合初级声源产生的模态来降噪, 其机理是控制源降低了初级声源的负载. 以上两种属于自由场的全局控制与封闭空间的全局控制范畴^[58], 并非一般意义的VSB系统. 用于局部区域控制的VSB系统一般远离初级噪声源, 其降噪机理为对初级声场的声能量进行吸收或反射. 在边界上使用连续分布的单极子源和偶极子源的组合可实现对入射声波的完美吸收, 若单独使用单极子源或偶极子源, 其机理为对入射声波的反射^[48] . 例如使用单极子源控制位于区域边界的传声器处的声压为零形成声学软边界, 将入射到静区的初级声反射回去, 其机理为声反射, 会导致控制后总声场的能量增大.
VSB系统主要有2种设计方法: 针对稳定初级声场的展开法, 适合时变初级声场和自适应系统的最小均方优化法. 下面以在某一噪声场中产生半径为r_v的球形VSB静区为例进行说明. 设系统的坐标原点定在球形静区的中心, 控制源布放在球面上, 静区内没有任何声源和散射体.
1) 初级声场展开法
波数为k的初级噪声场中任意一点$ {{r}} =(r,\theta ,$$ \phi )$处的声压可表示为^[59]

${p_{\rm{p}}}({{r}}) = \left\{ \begin{aligned}&\sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {A_n^m(k){{\rm{j}}_n}(kr){\rm{Y}}_n^m(\theta ,\phi )} } {\rm{, }}\quad r < {r_{\rm{v}}},\\&\sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {C_n^m(k){{\rm{h}}_n}(kr){\rm{Y}}_n^m(\theta ,\phi )} } {\rm{, }}\quad r > {r_{\rm{v}}},\end{aligned} \right.$

式中$A_n^m(k)$和$C_n^m(k)$为球谐函数${\rm{Y}}_n^m(\theta ,\phi )$的系数; j_n(kr) 为第一类n阶球Bessel函数; h_n(kr) 为第一类n阶球Hankel函数; ${\rm{Y}}_n^m(\theta ,\phi )$的表达式为^[59]

${\rm{Y}}_n^m(\theta ,\phi ) = \sqrt {\frac{{(2n + 1)}}{{4{\text{π}}}}\frac{{(n - \left| m \right|)!}}{{(n + \left| m \right|)!}}} {\rm{P}}_n^{\left| m \right|}(\cos \theta ){{\rm{e}}^{ - {\rm{j}}m\phi }},$

式中${\rm{P}}_n^{\left| m \right|}( \cdot )$是连带Legendre函数.
在球形区域边界布放连续控制声源构建VSB系统产生次级声场, 根据(8)式的K-H方程, 空间内声压由边界上声压及其梯度决定, 即

$\!\!\begin{split}{p_{\rm{s}}}({{r}}) =& \int_0^{2{\text{π}}} {\int_0^{\text{π}} {\left[ {\frac{{\partial {p_{\rm{s}}}({{{r}}_{\rm{v}}})}}{{\partial {{n}}({{{r}}_{\rm{v}}})}}{\rm G}({{r}}|{{{r}}_{\rm{v}}})} \right.} } \\&-\left. { {\rm{j}}k{p_{\rm{s}}}({{{r}}_{\rm{v}}})\frac{1}{{{\rm{j}}k}}\frac{{\partial {\rm G}({{r}}|{{{r}}_{\rm{v}}})}}{{\partial {{n}}({{{r}}_{\rm{v}}})}}} \right]r_{\rm{v}}^2\sin {\theta _{\rm{v}}}{\rm{d}}{\theta _{\rm{v}}}{\rm{d}}{\phi _{\rm{v}}},\end{split}\!\!\!$

式中${{{r}}_{\rm{v}}} = ({r_{\rm{v}}},{\theta _{\rm{v}}},{\phi _{\rm{v}}})$为球面上的一点. 可见边界上的声压及声压梯度分别决定了控制源的偶极子源强D(r_v)和单极子源强S(r_v), 即

$\begin{split}& S({{{r}}_{\rm{v}}}) = \frac{{\partial {p_{\rm{s}}}({{{r}}_{\rm{v}}})}}{{\partial {{n}}({{{r}}_{\rm{v}}})}}, \\& D({{{r}}_{\rm{v}}}) = {\rm{j}}k{p_{\rm{s}}}({{{r}}_{\rm{v}}}) \end{split}, $

其中对偶极子源引入频率归一化系数jk可使偶极子源的指向性与频率无关. VSB系统控制目标是使空间内总声场为零, 即

${p_{\rm{t}}}({{r}}) = {p_{\rm{p}}}({{r}}) + {p_{\rm{s}}}({{r}}) = 0, \;\; \left| {{r}} \right| \leqslant {r_{\rm{v}}}.$

将(10)式与(14)式代入(13)式可得

$S({{{r}}_{\rm{v}}}) = - k\sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {A_n^m(k){{{\rm{j'}}}_n}(k{r_{\rm{v}}}){\rm{Y}}_n^m({\theta _{\rm{v}}},{\phi _{\rm{v}}})} } ,$

$D({{{r}}_{\rm{v}}}) = - {\rm{j}}k\sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {A_n^m(k){{\rm{j}}_n}(k{r_{\rm{v}}}){\rm{Y}}_n^m({\theta _{\rm{v}}},{\phi _{\rm{v}}})} } .$

实际应用中, 需要将球面上的连续声源离散化. 若采用N_c个位于${{{r}}_l} = ({r_{\rm{v}} },{\theta _l},{\phi _l})$的控制源, 则控制声源产生的声场为^[56]

${p_{\rm{s}}}({{r}}) = \sum\limits_{l = 1}^{{N_{\rm{c}}}} {r_{\rm{v}}^2{\beta _l}\bigg[ {S{\rm{(}}{{{r}}_l}{\rm{)G}}({{r}}|{{{r}}_l})} \bigg.} \left. { - D{\rm{(}}{{{r}}_l}{\rm{)}}\frac{1}{{{\rm{j}}k}}\frac{{\partial {\rm{G}}({{r}}|{{{r}}_l})}}{{\partial {{n}}({{{r}}_l})}}} \right],$

式中${\beta _l}$为球谐函数的权重系数. 若源强中的球谐函数展开到N阶, 则利用初级声场展开法得到的VSB系统的连续控制声源的源强为

$S({{{r}}_l}) = - k\sum\limits_{n = 0}^N {\sum\limits_{m = - n}^n {A_n^m(k){{{\rm{j'}}}_n}(k{r_{\rm{v}}}){\rm{Y}}_n^m({\theta _l},{\phi _l})} } ,$

$D({{{r}}_l}) = - {\rm{j}}k\sum\limits_{n = 0}^N {\sum\limits_{m = - n}^n {A_n^m(k){{\rm{j}}_n}(k{r_{\rm{v}}}){\rm{Y}}_n^m({\theta _l},{\phi _l})} } .$

2) 最小均方优化法
N_c个一阶控制声源均匀分布在半径为r_v的球形VSB 的球面上, 其坐标为${{ r}_l} = ({r_{\rm{v}} },{\theta _l},{\phi _l})$, 产生的次级声场表示为^[56]

$\!\!\!\!\begin{split}{p_{\rm s}}({{r}}) = &\sum\limits_{l = 1}^{N_{\rm c}} \frac{{q_l}{\rm{e}}^{ - {\rm j}k\left| {{r} - {{r}}_l} \right|}}{4{\text{π}}\left| {{{r}} - {{{r}}_l}} \right|}\\&\times \left[ \alpha \!-\! \left( {1 \!-\! \alpha } \right)\left( 1 \!-\! \frac{\rm j}{k\left| {{r}} - {{r}}_l \right|} \right)\cos \gamma \right] , \!\!\!\!\!\!\end{split}$

式中q_l为第l个控制声源的源强, $ l=1, 2, \cdots, N_{\rm c}$; 等式右边q_l[·]为理想一阶声源的一般表达式^[56]; 指向性权重$\alpha $取值在0和1之间, $\alpha $ = 1声源为单极子, $\alpha $ = 0为偶极子, $\alpha $ = 0.5为三极子, 即心形单指向性声源; $\gamma $为矢量r – r_l与声源轴的夹角.
控制后的总声场为

${p_{\rm{t}}}({{r}}) = {p_{\rm{p}}}({{r}}) + {p_{\rm{s}}}({{r}}).$

拟优化的代价函数可为与误差点的声势能密度和、声动能密度和、总声能量密度和相关的量^[58], 三者可分别表示为

${J_{\rm{p}}} = \sum\limits_{n = 1}^{{N_{\rm{e}}}} {|{p_{\rm{t}}}({{r}}_n^{\rm{e}}){|^2} + \beta {{q}}_{\rm{s}}^{\rm{H}}{{{q}}_{\rm{s}}}} ,$

${J_{\rm{k}}} = \sum\limits_{n = 1}^{{N_{\rm{e}}}} {|{v_{\rm{t}}}({{r}}_n^{\rm{e}}){|^2} + \beta {{q}}_{\rm{s}}^{\rm{H}}{{{q}}_{\rm{s}}}}, $

${J_{\rm{e}}} = \sum\limits_{n = 1}^{{N_{\rm{e}}}} {\left[\frac{1}{{2{\rho _0}c_0^2}}|{p_{\rm{t}}}\left({{r}}_n^{\rm{e}}\right){|^2} + \frac{{{\rho _0}}}{2}|{v_{\rm{t}}}({{r}}_n^{\rm{e}}){|^2}\right] + \beta {{q}}_{\rm{s}}^{\rm{H}}{{{q}}_{\rm{s}}}} ,$

式中${\rho _0}$和c₀分别为空气密度和声速; $ {{{q}}_s} =[{q_1},$$ {q_2}, \ldots ,{q_{Nc}}]^{\rm{T}}$为控制源强的矢量; N_e为拟优化误差点的个数; ${{r}}_n^{\rm{e}}$为第n个误差点位置(图4中的传声器); v_t(r)为声场在误差点的法向质点速度, 参数$\beta $对控制源强的大小进行约束, 能改善仿真结果的可靠性.
将(20)式和(21)式代入(22)—(24)式之一, 代价函数可写成矩阵二次型的形式^[58], 即

$J = {{q}}_{\rm{s}}^{\rm{H}}({{A}} + \beta {{I}}){{{q}}_{\rm{s}}} + {{q}}_{\rm{s}}^{\rm{H}}{{b}} + {{{b}}^{\rm{H}}}{{{q}}_{\rm{s}}} + c,$

式中矩阵A与控制声源到场点的声阻抗传递函数有关; 矩阵b与控制声源到场点的声阻抗传递函数和初级声场有关; 常数c仅和初级声场有关, I为单位矩阵. 以声势能代价函数为例, 表达式分别为^[56,58]:

${{A}} = {{Z}}_{{\rm{ce}}}^{\rm{H}}{{{Z}}_{{\rm{ce}}}}, \;\; {{b}} = {{Z}}_{{\rm{ce}}}^{\rm{H}}{{{P}}_{{\rm{pe}}}}, \;\; c = {{P}}_{{\rm{pe}}}^{\rm{H}}{{{P}}_{{\rm{pe}}}},$

${{{P}}_{{\rm{pe}}}} = {[{p_{\rm{p}}}({{r}}_{\rm{1}}^{\rm{e}}),{p_{\rm{p}}}({{r}}_{\rm{2}}^{\rm{e}}) \cdots {p_{\rm{p}}}({{r}}_{N{\rm{e}}}^{\rm{e}})]^{\rm{T}}}, $

${{{Z}}_{{\rm{ce}}}} \!=\! \left[ \!\!\!\!{\begin{array}{*{20}{c}} {{Z_{\rm{c}}}(\left. {{{r}}_{\rm{1}}^{\rm{e}}} \right|{{r}}_{\rm{1}}^{\rm{c}})}&{{Z_{\rm{c}}}(\left. {{{r}}_{\rm{1}}^{\rm{e}}} \right|{{r}}_{\rm{2}}^{\rm{c}})}&{...}&{{Z_{\rm{c}}}(\left. {{{r}}_{\rm{1}}^{\rm{e}}} \right|{{r}}_{{N_{\rm{c}}}}^{\rm{c}})} \\ {{Z_{\rm{c}}}(\left. {{{r}}_{\rm{2}}^{\rm{e}}} \right|{{r}}_{\rm{1}}^{\rm{c}})}&{{Z_{\rm{c}}}(\left. {{{r}}_{\rm{2}}^{\rm{e}}} \right|{{r}}_{\rm{2}}^{\rm{c}})}&{...}&{{Z_{\rm{c}}}(\left. {{{r}}_{\rm{2}}^{\rm{e}}} \right|{{r}}_{{N_{\rm{c}}}}^{\rm{c}})} \\ \vdots & \vdots &{}& \vdots \\ {{Z_{\rm{c}}}(\left. {{{r}}_{{N_{\rm{e}}}}^{\rm{e}}} \right|{{r}}_{\rm{1}}^{\rm{c}})}&{{Z_{\rm{c}}}(\left. {{{r}}_{{N_{\rm{e}}}}^{\rm{e}}} \right|{{r}}_{\rm{2}}^{\rm{c}})}&{...}&{{Z_{\rm{c}}}(\left. {{{r}}_{{N_{\rm{e}}}}^{\rm{e}}} \right|{{r}}_{{N_{\rm{c}}}}^{\rm{c}})} \end{array}} \!\!\!\! \right], $

$\begin{split} &{Z_{\rm{c}}}(\left. {{{r}}_n^{\rm{e}}} \right|{{r}}_m^{\rm{c}}) \\=& \frac{{{{\rm e}^{ - {\rm{j}}k\left| {{{r}}_n^{\rm{e}} - {{r}}_m^{\rm{c}}} \right|}}}}{{4{\text{π}}\left| {{{r}}_n^{\rm{e}} - {{r}}_m^{\rm{c}}} \right|}} \\ & \times \left[ {\alpha - \left( {1 - \alpha } \right)\left( {1 - \frac{{\rm{j}}}{{k\left| {{{r}}_n^{\rm{e}} - {{r}}_m^{\rm{c}}} \right|}}} \right)\cos {\gamma _{n,m}}} \right], \end{split}$

$\cos {\gamma _{n,m}} = \frac{{({{r}}_n^{\rm{e}} - {{r}}_m^{\rm{c}}) \cdot {{r}}_m^{\rm{c}}}}{{\left| {{{r}}_n^{\rm{e}} - {{r}}_m^{\rm{c}}} \right|\left| {{{r}}_m^{\rm{c}}} \right|}},$

其中(27)式为误差点处的初级声场向量, (28)式为控制源到误差点处的传递函数矩阵, (29)式为位于点${{r}}_m^{\rm{c}}$的控制源到位于点${{r}}_n^{\rm{e}}$的误差点的传递函数.
令代价函数最小化, 可求得VSB系统的控制源的源强^[58], 即

${{{q}}_{\rm{s}}} = - {({{A}} + \beta {{I}})^{ - 1}}{{b}}.$

两种方法得到控制源最优源强后, 可代入(21)式中得到控制后的总声场. VSB系统的性能定义为VSB内部区域降噪前后的声势能差, 即

${\rm{NR}} = 10\lg 10\left(\sum\limits_{i = 1}^{{N_{\rm{v}}}} {{{\left| {{p_{\rm{p}}}({{{r}}_i})} \right|}^2}} /\sum\limits_{i = 1}^{{N_{\rm{v}}}} {{{\left| {{p_{\rm{t}}}({{{r}}_i})} \right|}^2}} \right),$

式中N_v为评价点的个数, 取值与噪声频率有关, 通常每波长至少取6个评价点. VSB系统性能和所优化的代价函数有关, 可采用上述步骤研究不同代价函数, 不同物理系统配置的VSB系统的性能.
2 -->

3.3.应　用

VSB系统在大型电力变压器的低频噪声控制的有相对成熟的应用. 在室内变压器的大门或窗户开口布放平面型的VSB系统, 可阻挡噪声而不影响通风散热. Xue等^[60]在某110 kV室内变压器的现场进行了实验, 在约23.2 m的开口上布放44通道的VSB系统控制变压器通过开口向外辐射的噪声, 在开口外8.3 m × 5 m宽的区域内, 绝大部分区域均得到有效降噪, 100 Hz最大降噪量达23.8 dB, 200 Hz最大降噪量达18.8 dB. 该应用体现了复杂噪声环境中VSB系统产生静区的有效性.
相比AHR系统, 用于人耳附近空间局部降噪的VSB系统可在一个较大区间内形成静区, 但所需控制源个数多, 系统复杂, 目前尚处于实验室样机阶段. 一个圆柱状分布的16通道的VSB系统如图5所示, 16个误差传感器分为两层, 每层各为圆内接正八边形, 两层的距离h_e等于圆半径r_e, 为0.2 m. 16个控制源采用同样的结构, 层间距h_c等于圆半径r_c, 为1.22 m. 半径为a的刚性圆球模拟人头在误差传感器包围的空间内, 球心与VSB系统的中心重合, a = 0.09 m^[58], 使用最小均方优化算法设计自适应的VSB系统.
实验在普通不规则房间进行, 使用3个位于不同方向的扬声器产生初级声场, VSB系统所在空间声场较为均匀, 近似扩散. 由16个驻极体传声器和16个普通音箱构成图5形式的VSB系统放置在房间中间, 采用16通道FxLMS算法的自适应控制器. 初级源距离VSB系统中心约4 m, 与控制源距离始终保持大于0.5波长, 以保证实验所得控制效果不是通过降低初级源的辐射阻抗得到的. 图6为实验环境照片.
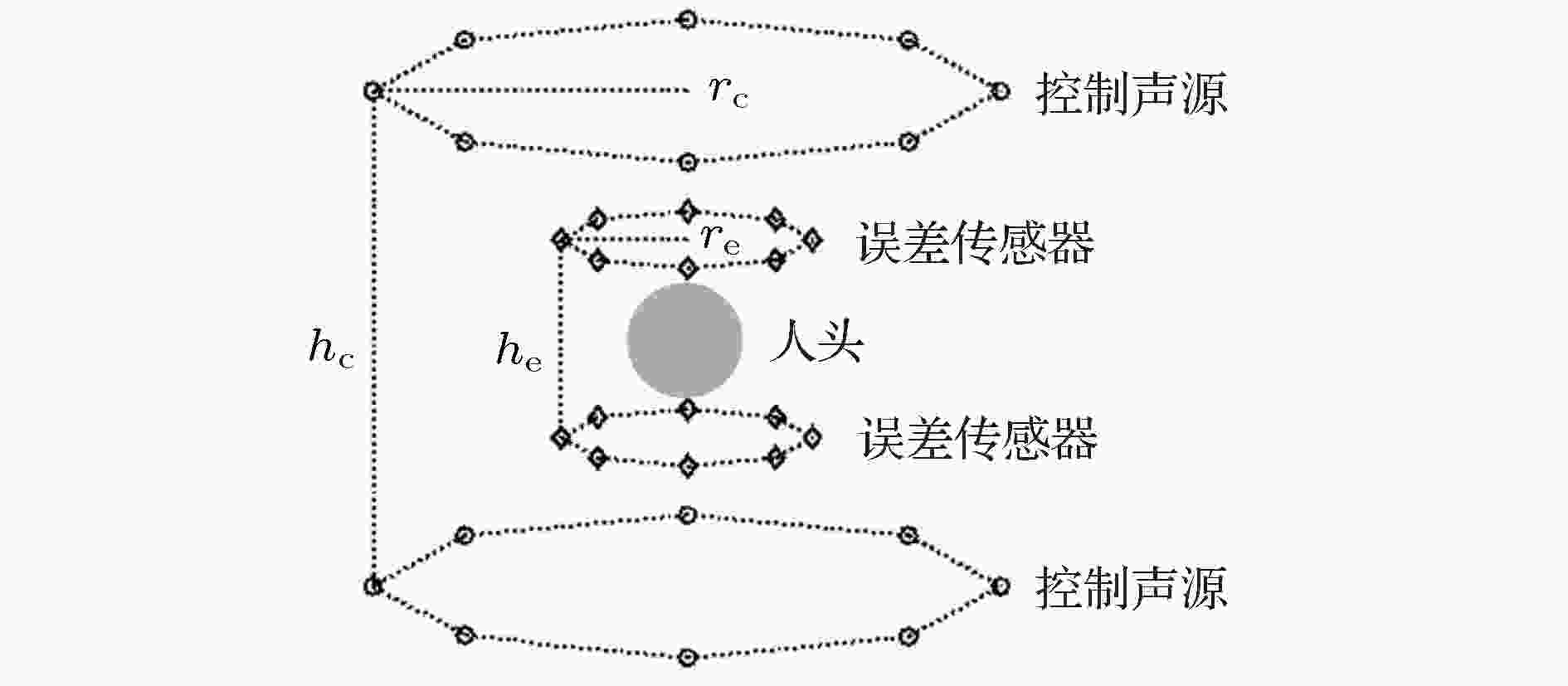图 5 圆柱状分布内含人头的16通道VSB系统^[58]
Figure5. Setup of the 16-channel cylindrical VSB system with a rigid sphere^[58].

图 6 实验环境照片^[58]
Figure6. Photo of experimental setup^[58].

为考察人耳移动的影响, 选择在人头表面绕两耳的水平圆周上的所有点的平均声压降噪量NR来评价系统性能. 图7为NR随频率变化的曲线, 信号频率取值为200—600 Hz, 间距50 Hz. 可见在有无人头情况下, 该VSB系统在所研究的频段都能得到10 dB以上的降噪效果, 但两者略有不同, NR的差值$\Delta {\rm{NR}}$在–0.8—2.6 dB之间, 随频率升高有微小的增加. 在图7曲线前段, 频率小于300 Hz时, 由于实验系统和实验环境限制, 无法测得更大的降噪值, 都在31 dB左右. 图8为频率为500 Hz时, NR随人头移动的曲线, 其中xy平面为水平面, z轴为垂直于水平面方向. 控制器为自适应的, 跟踪时间在秒量级, 实验数据是在系统跟踪收敛后测得的. 人头偏离中心的距离取值为0—0.1 m, 间距0.02 m, 偏离0.1 m时, 人头已接近误差传感器包围区间的边缘. 图8显示当频率为500 Hz, 随着人头偏离系统中心, 降噪效果下降, 最大值为6.2 dB, 但最差的降噪效果仍超过13.3 dB^[58].
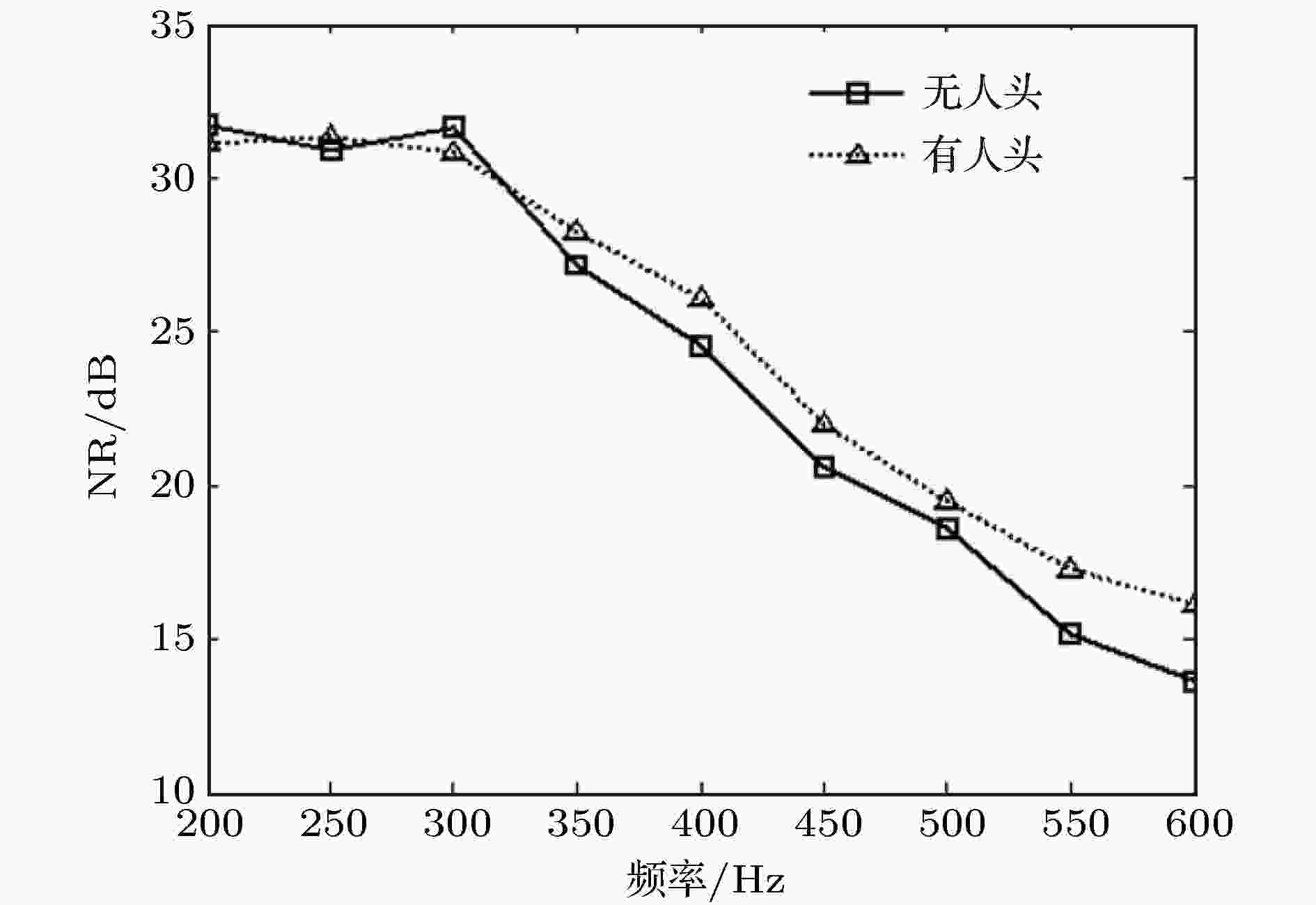图 7 实测VSB系统平均降噪量NR随频率变化的曲线^[58]
Figure7. Experimental results of control performance with respect to the frequency of noise signal^[58].

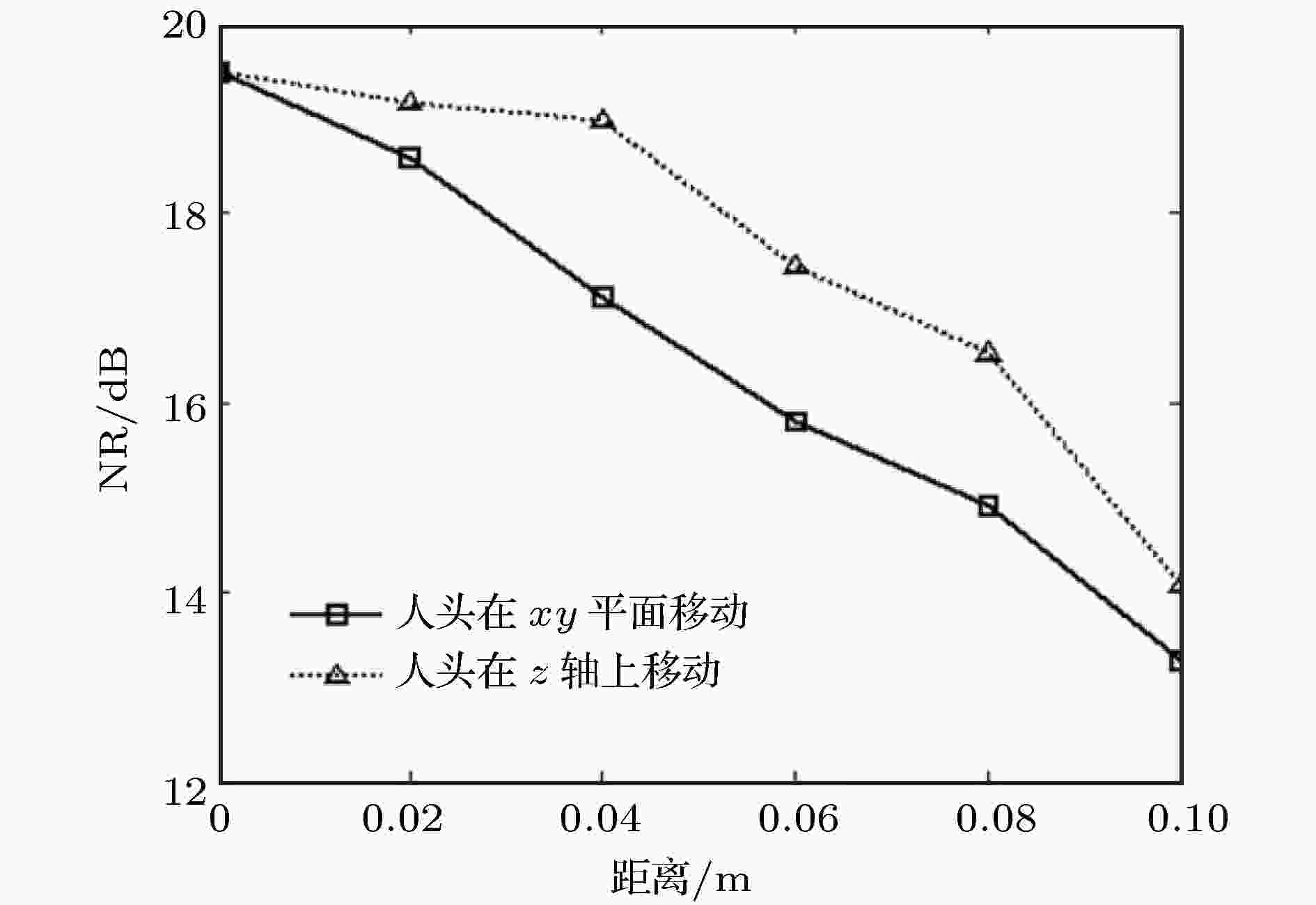图 8 实测人头移动对降噪效果的影响^[58]
Figure8. Experimental results of control performance with respect to the movements of rigid sphere^[58].

综上所述, 复杂声学环境中人耳附近空间降噪的国内外相关研究目前已取得一定进展, 无论是AHR还是VSB方法, 理论、数值仿真和实验均已验证了其可行性, 即在噪声来自于多个方向的复杂噪声场中, 在低频段产生一定大小的静区是可行的. 这两种方法各有优缺点, 目前距实际应用均存在一定距离.
AHR系统所需控制源数少, 物理系统简单, 但其静区范围较小, 误差传声器需靠近人耳才有较好的降噪效果. 虚拟传声器与远程传声器技术可解决误差传声器与人头冲突的问题, 但并没有解决静区范围小的问题. 此外, 人头移动还引起声场传递函数变化, 虚拟传声器或近端传声器的估计误差增大也导致性能下降. 使用头部定位系统跟踪人头移动位置, 降低估计误差可提升效果, 但需要存储传递函数数据, 且使系统变得复杂和昂贵.
VSB系统静区范围较大, 局限性在于降噪有效频率不够高, 所需控制源个数多, 系统复杂度和成本较高. 以文献[21]所述16通道VSB系统为例, 在半径0.2 m高为0.2 m的圆柱形区间获得10 dB降噪的有效频率上限大约为550 Hz, 若尺寸不变, 拟将有效频率提高一倍, 则控制通道数需要增加到64个, 较难实际应用.
静区大小与控制源个数是一对矛盾. 为增大有AHR的静区, 可尝试的方法包括: 同时控制误差点的声压与质点速度^[29]; 增加控制声源使用同一输出形成优化的指向性^[28], 以及增加控制源个数^[61]. 对于远程传声器技术, 可研究在复杂声场中如何提高预测精度, 例如尝试使用圆环状的远程传声器分布; 还可研究高性价比的人头位置跟踪技术. 对于VSB系统而言, 需要考虑如何增加系统的有效频率和作用空间, 或在同样降噪效果情况下减少通道数, 可尝试的研究方向包括:
1) 采用声能量密度作为代价函数, 通过同时获得声场某点的声压和三个正交方向的质点速度来获得声能量密度^[54].
2) 对VSB系统声源的指向性特性进行优化, 或采用双层声源阵列和双层传声器阵列设计VSB系统^[62,63].
3) 采用主被动混合控制的VSB系统, 例如通过将有源噪声控制系统的控制声源和若干无源声学隔板间隔布放, 或者将控制声源放置在类似墙角的专门设计的声学结构中, 通过主被动结合来达到减少控制通道的目的^[64]. VSB系统完全采用扬声器阵列和信号处理的方法来进行声场控制, 而主被动混合VSB系统则通过在声学边界上引入具有不同阻抗的被动声学隔板和能自适应调整的主动声源共同作用, 达到声场控制的目的.
早期有源声屏障研究的应用场景通常为户外噪声环境, 静区范围很大^[5-8]. 近年来针对开放式办公空间的隔断也展开了研究, 静区为人耳附近空间^[65,66]. 噪声源位于隔断一侧, 将控制源布放于隔断顶部形成有源声屏障, 以降低隔断另一侧的座椅顶部40 cm边长区域的噪声, Huang等^[65]的研究表明可在500 Hz以下频段可获得10 dB降噪, 相比于侧墙, 房顶的反射对降噪效果的负面影响更大. Wang等^[66]在隔断上应用前反馈结合的有源降噪系统, 相比仅使用反馈或前馈系统性能更优, 仿真结果表明对于60 cm边长的平面测量区域, 在250 Hz和500 Hz的倍频程分别获得5 dB与3 dB左右的降噪量. 这表明噪声来自某一特定方向特定场合, 利用有源声屏障在人耳附近产生静区是可行的, 目前研究仅限于仿真, 且误差传感器布放于远场, 可进一步结合远程传声器技术并展开实验研究.
以上分析与讨论针对的是相关物理系统, 而具体降噪系统的实现还涉及到系统和算法的研究. 如讨论适用于复杂环境的具强鲁棒性的非自适应算法^[67], 在自适应算法上, 除常规地针对算法的收敛速度、稳定性、降噪效果、计算效率等因素进行分析外, 还可研究算法对非理想抵消路径模型的鲁棒性和稳定性条件以及滤波器阶数不足对算法性能的影响, 研究无次级通道建模的自适应算法. 另外针对VSB系统的高复杂度和高成本, 还可从前馈、反馈、前反馈混合控制结构以及集中和非集中控制策略等方面进行探索.

针对复杂声学环境中人耳附近空间降噪问题, 介绍了AHR和VSB技术的发展历史、原理、设计方法和应用. AHR系统需要较少控制源, 系统相对简单易实现, 但静区范围较小, 结合虚拟传声器技术和人头跟踪技术后可实现随人头移动的静区, 降噪频率可达中高频; VSB产生的静区范围较大, 但控制源个数较多, 系统复杂和成本高, 可通过代价函数和控制源优化, 以及主被动混合控制技术来提高有效频率范围和减少控制源个数. 无论是AHR还是VSB方法, 理论、数值仿真和实验均已验证了其可行性, 即在噪声来自于多个方向的复杂噪声场中, 在低频段产生一定大小的静区是可行的. 这两种方法各有优缺点, 目前距实际应用均有一定距离. 未来最有可能实用的方法是针对具体应用场景, 将这两种方法综合应用, 结合虚拟传声器和声场预测技术, 采用主被动混合结构实现复杂声学环境中人耳附近空间的有效降噪.