摘要: 本文提出了一个基于超绝热捷径技术快速制备超导三量子比特Greenberger-Horne-Zeilinger态的理论方案. 该方案首先在量子Zeno动力学的帮助下得到系统的有效哈密顿量, 之后通过引入与有效哈密顿量具有相同形式的反向导热哈密顿量来构建绝热捷径, 加速了整个系统的演化过程. 该方案不需要初态和目标态之间的直接耦合, 在实验上也更容易实现. 数值模拟结果表明该方案对超导量子比特的自发辐射、波导谐振腔的泄漏以及超导量子比特的退相位是鲁棒的.
关键词: 超绝热捷径 /
超导量子比特 /
Greenberger-Horne-Zeilinger态 English Abstract Superadiabatic scheme for fast generating Greenberger-Horne-Zeilinger state of three superconducting qubits Yu Wan-Rang Ji Xin Department of Physics, College of Science, Yanbian University, Yanji 133002, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11464046).Received Date: 29 October 2018Accepted Date: 03 December 2018Available Online: 01 February 2019Published Online: 05 February 2019Abstract: With the development of quantum information processing (QIP), entangled states have been used in many important fields. One of the well-known entangled states is Greenberger-Horne-Zeilinger (GHZ) state, which provides a possibility for testing quantum mechanics against local hidden theory without using Bell’s inequality. Many schemes of generating the GHZ state have been put forward in various physical systems over the past ten years. Among these physical systems, the superconducting qubits (SQs) have the potential suitability for the integrated devices in QIP and can be controlled easily through modulating electromagnetic signals and designing level configurations. On the other hand, adiabatic passage is a typical method which is used widely to generate entanglements. However, adiabatic passage needs long evolution time to satisfy the adiabatic condition. Therefore, to speed up a slow quantum adiabatic process, a new kind of technique called " shortcuts to adiabatic passage (STAP)” has attracted much attention. The Lewis-Riesenfeld invariants and transitionless quantum driving are famous methods of STAP. But they are difficult to use in the experiment. For the Lewis-Riesenfeld invariants, the driving pulses are not smoothly turned on or off and thus lead to severe impediments in experiment. For transitionless quantum driving, a direct coupling between the initial state and the target state is needed, but is too hard to obtain experimentally. In this paper, we propose a theoretical scheme for fast generating GHZ state of three superconducting qubits via superadiabatic-based shortcuts. Firstly, with the help of quantum Zeno dynamics, we obtain the effective Hamiltonian of the system, then we choose a suitable counterdiabatic Hamiltonian in the same form as the effective Hamiltonian and add it to the effective Hamiltonian in order to construct shortcuts to adiabatic passage, which can make the system evolve along one of the superadiabatic states and thus accelerate the evolution process of the system. More importantly, the superadiabatic scheme does not need an additional coupling between the initial and finial state, which ensures its high experimental feasibility. In addition, numerical simulation results show that the proposed scheme is robust against spontaneous emission, the cavity photon leakage and the dephasing of SQs.Keywords: superadiabatic-based shortcuts /superconducting qubit /Greenberger-Horne-Zeilinger state 全文HTML --> --> --> 1.引 言 随着量子信息学的发展, 纠缠态已经应用在许多前沿领域, 如量子隐形传送、量子密钥分配、量子安全直接通信等[1 -3 ] . 其中一种著名的纠缠态就是Greenberger-Horne-Zeilinger (GHZ)态, 它提供了一种不使用贝尔不等式就可以验证量子力学违背局域隐变量理论的可能性[4 ,5 ] . 迄今为止, 人们在不同的系统中制备了GHZ态, 这些系统包括离子系统[6 ] 、光子系统[7 ] 、原子系统[8 ] 、超导系统[9 ] 等. 相比较而言, 超导系统的优势在于它的可操控性, 即通过调节电磁信号以及能级结构可以让超导量子比特之间的耦合强度达到理想数值[10 -12 ] .[13 ] 利用受激拉曼绝热过程的方法制备了n 量子比特GHZ态, 但是, 受激拉曼绝热过程的方法需要较长的演化时间来抑制非绝热过程, 而长的演化时间势必会对整个系统的消相干造成较大的影响. 为了解决绝热过程演化缓慢的问题, 2017年Zhang等和Wu等分别用无跃迁量子驱动的方法[14 ] 以及Lewis-Riesenfeld不变量的方法[15 ] 在超导系统中制备了GHZ态. 然而, 这两种方法在实验上实现起来分别遇到了不同的挑战. 无跃迁量子驱动的方法需要初态和目标态之间的直接耦合, 这在实际操作中是很难实现的; 在Lewis-Riesenfeld不变量的方法中需要使用短时间截取的两个简谐脉冲, 在现有的实验技术条件下是很难获得这样的脉冲的. 为了克服上述两种方案中的不足之处, 本文提出基于超绝热迭代相互作用的方法来制备GHZ态. 超绝热迭代相互作用作为传统绝热近似的延伸第一次由Berry[16 ] 介绍, 这里通过两次迭代相互作用获得超绝热态作为演化路径, 构建的反向导热哈密顿量与利用量子Zeno动力学化简后的哈密顿量具有相同的形式. 与之前的两种方案相比, 该方案的优点在于不需要初态和目标态之间的直接耦合, 并且该方案中所使用的驱动脉冲可以在曲线拟合的帮助下用两个高斯型脉冲所替代, 这两个优点极大地增加了该方案在实验上实施的可行性. 数值模拟结果显示制备的纠缠态保真度较高, 并且对于波导谐振腔的耗散、超导量子比特的自发辐射以及超导量子比特的退相位是鲁棒的.2.物理模型和有效动力学 如图1 所示, 三个超导量子比特与两个共面的波导谐振腔(CPWRs)通过电容器相互耦合, 三个超导量子比特具有相同的能级结构, 都具有一个激发态${\left| e \right\rangle _j}$ , 两个基态${\left| L \right\rangle _j}$ 和${\left| R \right\rangle _j}$ ($j = 1,2,3$ ). 对于超导量子比特SQ1和超导量子比特SQ3, ${\left| e \right\rangle _1} \leftrightarrow {\left| R \right\rangle _1}$ 和${\left| e \right\rangle _3} \leftrightarrow {\left| L \right\rangle _3}$ 的跃迁分别由拉比频率为${\varOmega _1}(t)$ 和${\varOmega _3}(t)$ 的经典激光驱动. ${\left| e \right\rangle _{1(2)}} \leftrightarrow {\left| L \right\rangle _{1(2)}}$ 的跃迁与CPWR1共振耦合, 耦合强度为${\lambda _{\rm{L}}}$ , ${\left| e \right\rangle _{2(3)}} \leftrightarrow {\left| R \right\rangle _{2(3)}}$ 的跃迁与CPWR2共振耦合, 耦合强度为${\lambda _{\rm{R}}}$ . 在相互作用绘景下, 系统的总哈密顿量为($\hbar = 1$ )图 1 制备超导三量子比特GHZ态的装置图Figure1. Setup for generating GHZ state of three superconducting qubits.${H_{{\rm{total}}}}$ 是系统的总哈密顿量; ${H_{\rm{C}}}$ 是超导量子比特与共面波导谐振腔之间的相互作用哈密顿量; ${H_{\rm{L}}}$ 是超导量子比特与经典激光之间的相互作用哈密顿量; ${a_{\rm{L}}}$ , ${a_{\rm{R}}}$ 分别是CPWR1和CPWR2的湮灭算符. 为了简便, 令${\lambda _{\rm{L}}} = {\lambda _{\rm{R}}} = \lambda $ . 假定系统的初态为$\left| {{\phi _1}} \right\rangle = {\left| R \right\rangle _1}{\left| L \right\rangle _2}{\left| R \right\rangle _3}{\left| 0 \right\rangle _{\rm{L}}}{\left| 0 \right\rangle _{\rm{R}}}$ , 它表明三个超导量子比特分别处于状态${\left| R \right\rangle _1}$ , ${\left| L \right\rangle _2}$ , ${\left| R \right\rangle _3}$ , 两个共面波导谐振腔处于真空态. 在系统总哈密顿量的作用下, 整个系统的演化会在如下子空间进行:${\varOmega _1}(t),{\varOmega _3}(t) \ll \lambda $ , 整个系统会近似地在${H_{\rm{C}}}$ 的本征值为0的如下不变Zeno子空间Z中进行演化[17 -19 ] :$\left| \varphi \right\rangle = (\left| {{\phi _2}} \right\rangle - \left| {{\phi _4}} \right\rangle + \left| {{\phi _6}} \right\rangle )/\sqrt 3 $ , 相应的投影算符为${\varOmega _{\rm{P}}}(t) = {\varOmega _1}(t)/\sqrt 3 $ , ${\varOmega _{\rm{S}}}(t) = {\varOmega _3}(t)/\sqrt 3 $ . 此时系统可看作是一个有一个激发态$\left| \varphi \right\rangle $ , 两个基态$\left| {{\phi _1}} \right\rangle $ 和$\left| {{\phi _7}} \right\rangle $ 的简单三能级系统. 接下来介绍基于超绝捷径的方法制备超导三量子比特GHZ态$\left| {{\psi _{_{{\rm{GHZ}}}}}} \right\rangle =$ $ ({\left| R \right\rangle _1}{\left| L \right\rangle _2}{\left| R \right\rangle _3} - {\left| L \right\rangle _1}{\left| R \right\rangle _2}{\left| L \right\rangle _3})/\sqrt 2 $ .3.基于超绝热捷径方法快速制备超导三量子比特GHZ态 ${H_{{\rm{eff}}}}(t)$ 的瞬时本征态也称作绝热本征态, 其形式如下:${\eta _0} = 0$ , ${\eta _ \pm } = \pm \varOmega (t)$ , 这里, $\varOmega (t) = \sqrt {{\varOmega _{\rm{P}}}{{(t)}^2} + {\varOmega _{\rm{S}}}{{(t)}^2}} $ , $\tan {\theta _0}(t) = {\varOmega _{\rm{P}}}(t)/$ $ {\varOmega _{\rm S}}(t)$ . 通过幺正操作${U_0}(t) = \sum\limits_{k = 0, \pm } {\left| {{\eta _k}} \right\rangle \left\langle {{\eta _k}(t)} \right|} $ , 将${H_{{\rm{eff}}}}(t)$ 变换到以绝热本征态作为基矢的绝热框架下, 得到新的哈密顿量:$\left| {{{\dot \theta }_0}(t)} \right| \ll \sqrt 2 \varOmega (t)$ , 系统会沿着其中一个绝热本征态进行演化, 但这需要非常长的演化时间. 为了缩短演化时间, 文献[20 , 21 ]提出在${H_{{\rm{eff}}}}(t)$ 中加入一个合适的反向导热哈密顿量, 目的是抑制${H_{{\rm{eff}}}}(t)$ 中不同本征态之间的跃迁. 选取绝热框架下的反向导热哈密顿量$ - {\rm{i}}{\dot U_0}(t){U_0}^\dagger (t)$ , 以$\left\{ {\left| {{\phi _1}} \right\rangle ,\left| {{\phi _7}} \right\rangle ,\left| \varphi \right\rangle } \right\}$ 为基矢, 其可以写为$H_{{\rm{CD}}}^{\rm{1}}(t)$ 需要$\left| {{\phi _1}} \right\rangle $ 和$\left| {{\phi _7}} \right\rangle $ 的直接耦合, 这在实际操作中是很难实现的. 所以, 下面进行二次变换以便找到一个实验可行的反向导热哈密顿量.${H_1}(t)$ 的瞬时本征态也叫超绝热态, 它们的形式如下:${\eta _0}^\prime = 0$ , ${\eta _ \pm }^\prime = \pm \varOmega '(t)$ . 其中, $\varOmega '(t) = \sqrt {{{\dot \theta }_0}{{(t)}^2} + {\varOmega ^2}(t)} $ , $\tan {\theta _1}(t) = {\dot \theta _0}(t)/$ $\varOmega (t)$ . 可以发现, 如果满足边界条件${\theta _1}(0) = 0$ , ${\theta _1}({t_{\rm{f}}}) = 0$ (${t_{\rm{f}}}$ 是演化的最终时刻), 则$\left| {{{\eta '}_0}(0)} \right\rangle = $ $\left| {{{\eta '}_0}({t_{\rm{f}}})} \right\rangle = \left| {{\eta _0}} \right\rangle $ , 即最初、最终时刻超绝热态和绝热态是重合的, 所以找到一个哈密顿量使得超绝热态$\left| {{{\eta '}_0}(t)} \right\rangle $ 与$\left| {{{\eta '}_ \pm }(t)} \right\rangle $ 之间没有相互作用即可.${U_1}(t) = \sum\limits_{k = 0, \pm } {\left| {{{\eta '}_k}} \right\rangle } \left\langle {{{\eta '}_k}(t)} \right|$ 将${H_1}(t)$ 变换到以超绝热本征态作为基矢的框架下, 得到新的哈密顿量:$ - {\rm{i}}{\dot U_1}(t){U_1}^\dagger (t)$ , 以$\left\{ {\left| {{\phi _1}} \right\rangle ,\left| {{\phi _7}} \right\rangle ,\left| \varphi \right\rangle } \right\}$ 为基矢, 其可以写为$H_{{\rm{CD}}}^2(t)$ 与${H_{{\rm{eff}}}}(t)$ 具有相同的形式, 所以选取$H_{{\rm{CD}}}^2(t)$ 作为反向导热哈密顿量是可行的. 这样修正后的系统总哈密顿量为$\varOmega _{\rm{P}}^{\rm{A}}(t) = {\varOmega _{\rm{P}}}(t) + {\varOmega '_1}(t)$ , $\varOmega _{\rm{S}}^{\rm{A}}(t) = {\varOmega _{\rm{S}}}(t) + $ ${\varOmega '_2}(t)$ , ${\varOmega '_1}(t) \!=\! - {\dot \theta _1}(t)\cos {\theta _0}(t)$ , ${\varOmega '_2}(t) \!=\! {\dot \theta _1}(t)\sin {\theta _0}(t)$ . 激光脉冲$\varOmega _{\rm{P}}^{\rm{A}}(t)$ 和$\varOmega _{\rm{S}}^{\rm{A}}(t)$ 可以看作是在激光脉冲${\varOmega _{\rm{P}}}(t)$ , ${\varOmega _{\rm{S}}}(t)$ 上分别增加两个辅助脉冲${\varOmega '_1}(t)$ 和${\varOmega '_2}(t)$ , 并且在曲线拟合的帮助下, 实验上可以使用两个高斯型脉冲代替它们. 如果满足边界条件${\theta _0}(0) = 0$ , ${\theta _0}({t_{\rm{f}}}) = {\text{π}}/4$ , ${\theta _1}(0) = 0$ , ${\theta _1}({t_{\rm{f}}}) = 0$ , 脉冲$\varOmega _{\rm{P}}^{\rm{A}}(t)$ 和$\varOmega _{\rm{S}}^{\rm{A}}(t)$ 就可以驱动整个系统沿着超绝热态$\left| {{{\eta '}_0}(t)} \right\rangle $ 进行演化, 实现GHZ态的制备.4.数值模拟 为了满足边界条件, 选择脉冲${\varOmega _{\rm{P}}}(t)$ 和${\varOmega _{\rm{S}}}(t)$ 的形式如下:${\varOmega _0}$ 是高斯脉冲的振幅, ${t_{\rm{f}}}$ 是操作时间, 选定参数$\tau = 0.15{t_{\rm{f}}}$ , $T = 0.23{t_{\rm{f}}}$ . 通过这两个脉冲, 可以确定${\theta _0}(t)$ 和${\theta _1}(t)$ . 图2 给出了${\theta _0}(t)$ 和${\theta _1}(t)$ 随时间变化的图像, 可以看出对于任意的${\varOmega _0}$ , 均满足边界条件${\theta _0}(0) = 0$ , ${\theta _0}({t_{\rm{f}}}) = {\text{π}}/4$ , 但是${\varOmega _0}$ 数值的大小对边界条件${\theta _1}(0) = 0$ , ${\theta _1}({t_{\rm{f}}}) = 0$ 的影响很大. 为了找到合适大小的${\varOmega _0}$ , 图3 绘制了保真度随${\varOmega _0}$ 变化的图像, 可以看到当${\varOmega _0}$ 的取值在10—50之内时, 均可获得相对较高的目标态保真度, 但是考虑到量子Zeno条件${\varOmega _{1(3)}} \ll \lambda $ , ${\varOmega _0}$ 又不能过大, 因为一旦不满足量子Zeno条件, 系统在演化的过程中会经历更多的耗散. 因此, 为了保证该方案的鲁棒性, 在接下来的讨论中取${\varOmega _0} = 32.6{t_{\rm{f}}}^{ - 1}$ (${\varOmega _0}/\lambda \approx 0.3$ ). 为了进一步说明该方案的可行性, 在图4 中根据脉冲$\varOmega _{\rm{P}}^{\rm{A}}(t)$ 和$\varOmega _{\rm{S}}^{\rm{A}}(t)$ 绘制出$\left| {{\phi _1}} \right\rangle - \left| {{\phi _7}} \right\rangle $ 七个状态的布居转移, 可以看出在$t = {t_{\rm{f}}}$ 时可以近乎完美地获得GHZ态, 并且不包含在GHZ态中的其他状态在整个演化过程中布居占有数很小. 因此, 本文提出的方案是有效的.图 2 ${\theta _0}(t)$ 和${\theta _1}(t)$ 随时间的变化情况Figure2. Dependence on $t$ of ${\theta _0}(t)$ and ${\theta _1}(t)$ .图 3 保真度随${\varOmega _0}$ 的变化情况Figure3. Dependence on ${\varOmega _0}$ of fidelity ( $\lambda = 100{t_{\rm f}}^{ - 1}$ ).图 4 量子态布局随时间的变化Figure4. Population ${P_m}$ of $\left| {{\phi _m}} \right\rangle $ ($m = 1,2,$ 3, ···, 7) versus $t$ (${\varOmega _0} = 32.6{t_{\rm{f}}}^{ - 1},$ $\lambda = 100{t_{\rm{f}}}^{ - 1}$ ).${b_k}(k = 1,2,3, \cdots ,14)$ 是Lindblad算符, 这里共有14个Lindblad算符, 分别对应14个耗散项, 它们是${\gamma _n}(n = 1,2, \cdots, 6)$ 是超导量子比特自发辐射率; ${\kappa _{\rm{l}}}$ 和${\kappa _{\rm{r}}}$ 是波导谐振腔的泄漏率; ${\gamma _{{\phi _{{\rm{L}}j}}}}$ 和${\gamma _{{\phi _{{\rm{R}}j}}}}$ $(j = 1,2,3)$ 是超导量子比特的退相位率. 为了简便, 令${\kappa _{\rm{l}}} = {\kappa _r} = \kappa $ , ${\gamma _{{\phi _{{\rm{L}}j}}}} = {\gamma _{{\phi _{{\rm{R}}j}}}} = {\gamma _\phi }$ .图5(a) —(c) 分别给出了保真度随$\gamma $ 和$\kappa $ 的变化情况, 保真度随$\gamma $ 和${\gamma _\phi }$ 的变化情况, 以及保真度随$\kappa $ 和${\gamma _\phi }$ 的变化情况. 从图5 可以看出, 超导量子比特的自发辐射对系统的保真度几乎没有影响, 这主要是因为如图4 所展现的, 在该方案中, 激发态$\left| {{\phi _2}} \right\rangle $ , $\left| {{\phi _4}} \right\rangle $ 和$\left| {{\phi _6}} \right\rangle $ 在整个演化过程中的布居数几乎为0; 与自发辐射相比, 波导谐振腔的泄漏对系统保真度的影响稍大, 但从图5(a) 和图5(c) 可以看出, 当$\kappa $ 从0变化到$0.01/{t_{\rm{f}}}^{ - 1}$ 时, 系统的保真度变化很小, 所以该方案对波导谐振腔的泄漏也是鲁棒的; 对比图5(a) 、图5(b) 、图5(c) 三个图可以看出, 超导量子比特的退相位对系统的保真度影响最大, 但即使当波导谐振腔的泄漏率$\kappa = 0.01/{t_{\rm{f}}}^{ - 1}$ 且超导量子比特的退相位率${\gamma _\phi } = 0.001/{t_{\rm{f}}}^{ - 1}$ 时, 目标态保真度仍高达99.76%, 而在前面提到的通过无跃迁量子驱动的方法[14 ] 和通过Lewis-Riesenfeld不变量的方法[15 ] 制备GHZ态中, 当$\kappa = 0.01/{t_{\rm{f}}}^{ - 1}$ , ${\gamma _\phi } = 0.001/{t_{\rm{f}}}^{ - 1}$ 时, 保真度分别为0.922和0.87, 所以可以看出本文方案与之前的方案相比对于超导量子比特的退相位是更加鲁棒的.图 5 (a) $\gamma $ 和$\kappa $ 对目标态保真度的影响; (b) ${\gamma _\phi }$ 和$\gamma $ 对目标态保真度的影响; (c) $\kappa $ 和${\gamma _\phi }$ 对目标态保真度的影响Figure5. (a) Denpendence on $\gamma $ and $\kappa $ of fidelity; (b) denpendence on $\gamma $ and ${\gamma _\phi }$ of fidelity; (c) dependence on $\kappa $ and ${\gamma _\phi }$ of fidelity.5.结 论 在量子Zeno动力学的帮助下, 提出了一个实验上可行的理论方案, 通过超绝热捷径技术快速制备超导三量子比特GHZ态. 与无跃迁量子驱动的方法和Lewis-Riesenfeld不变量的方法相比, 该方案的优点在于以超绝热态作为演化路径, 构建的反向导热哈密顿量与利用量子Zeno动力学化简后的哈密顿量具有相同的形式, 不需要初态与目标态之间的直接耦合, 并且所使用的驱动脉冲在曲线拟合的帮助下在实验上可以用两个高斯型脉冲所替代, 这些优点极大地保证了该方案在实验上实施的可行性. 数值模拟结果表明该方案对于超导量子比特的能量弛豫、波导谐振腔的泄漏以及超导量子比特的退相位是鲁棒的. 












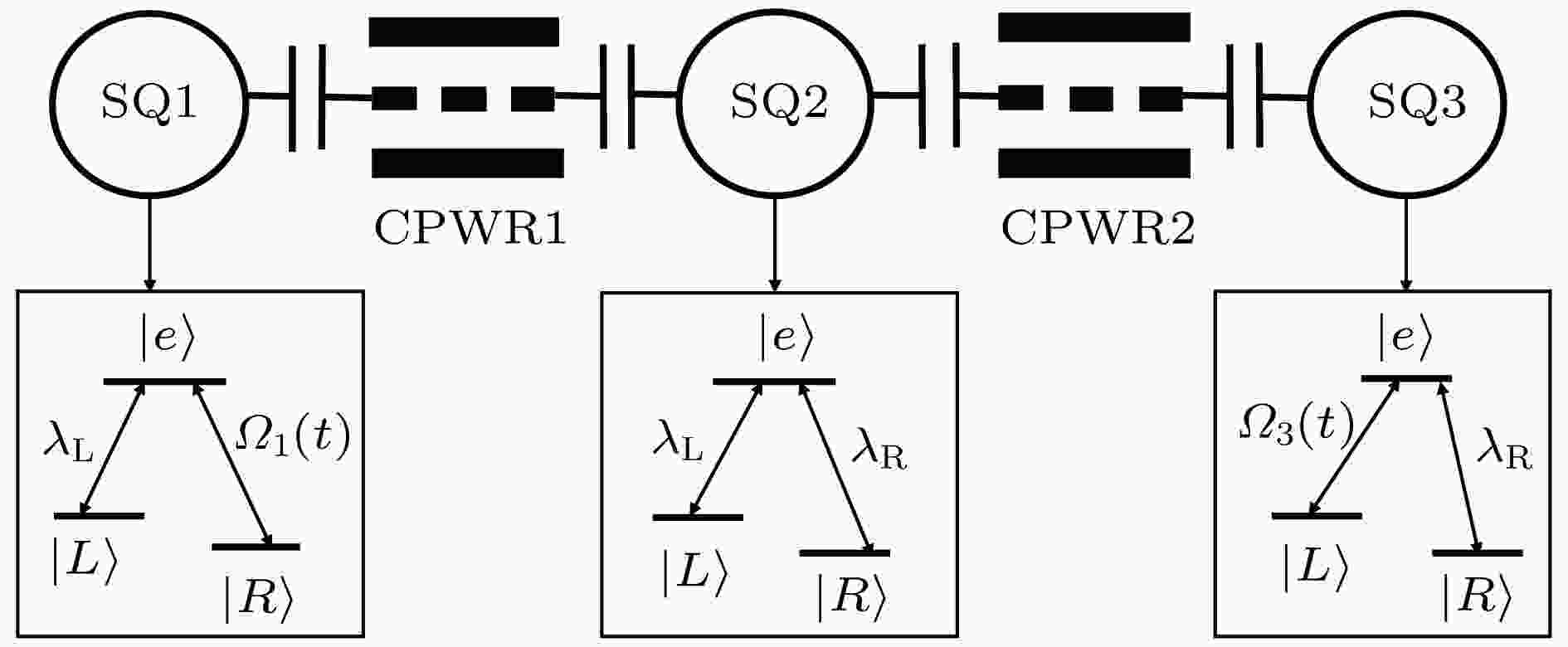 图 1 制备超导三量子比特GHZ态的装置图
图 1 制备超导三量子比特GHZ态的装置图




























































































































































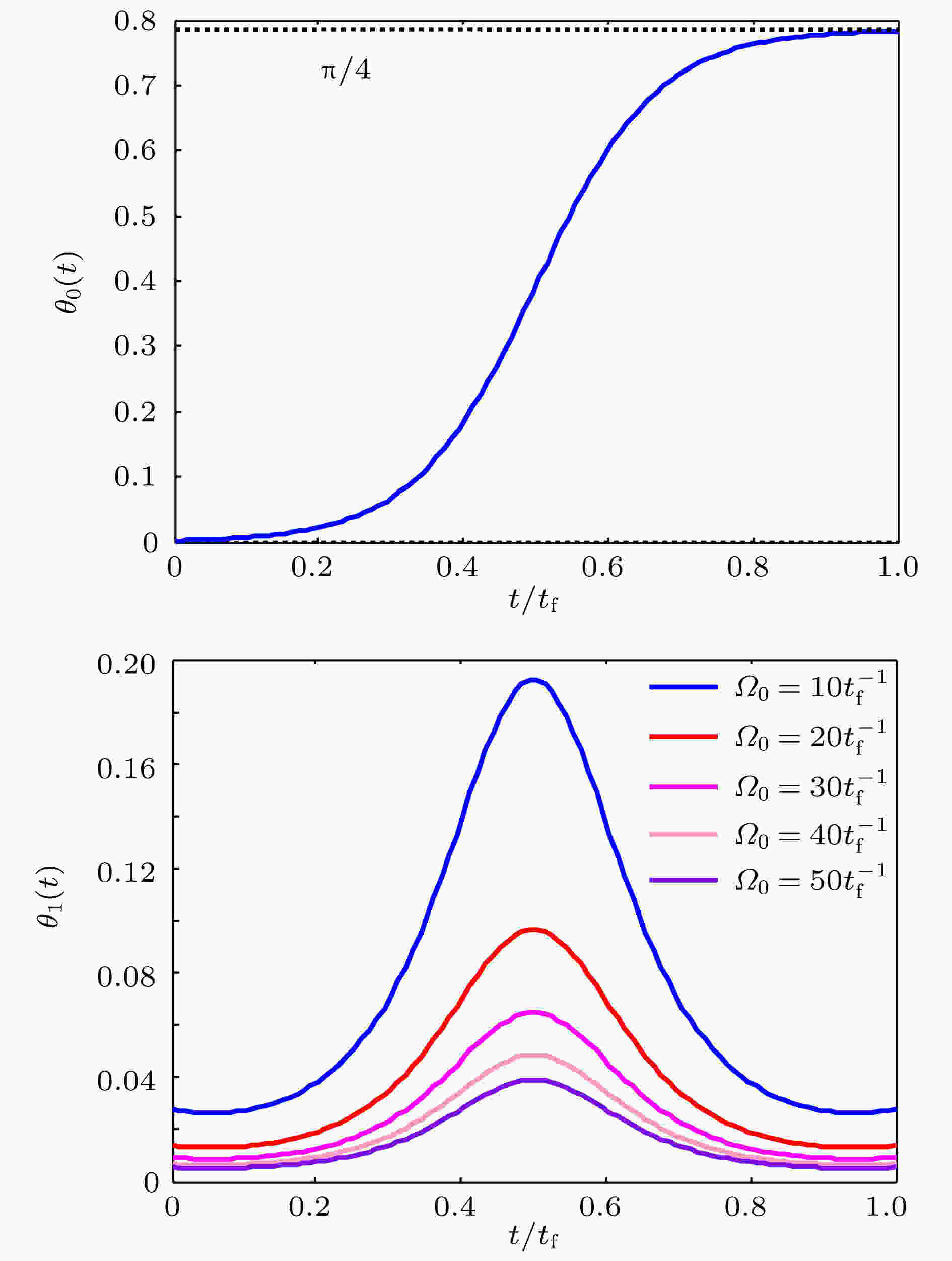 图 2
图 2 




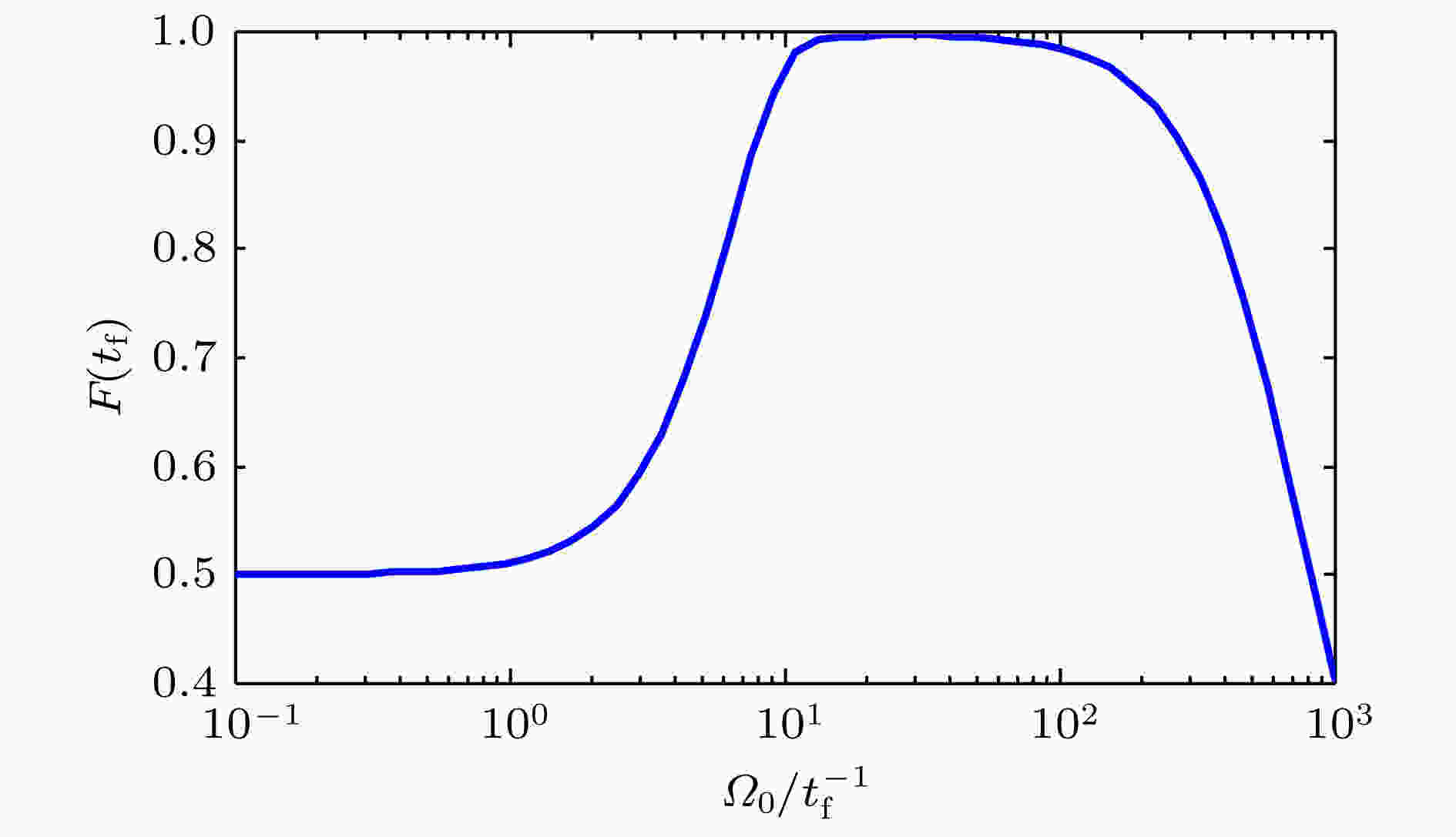 图 3 保真度随
图 3 保真度随


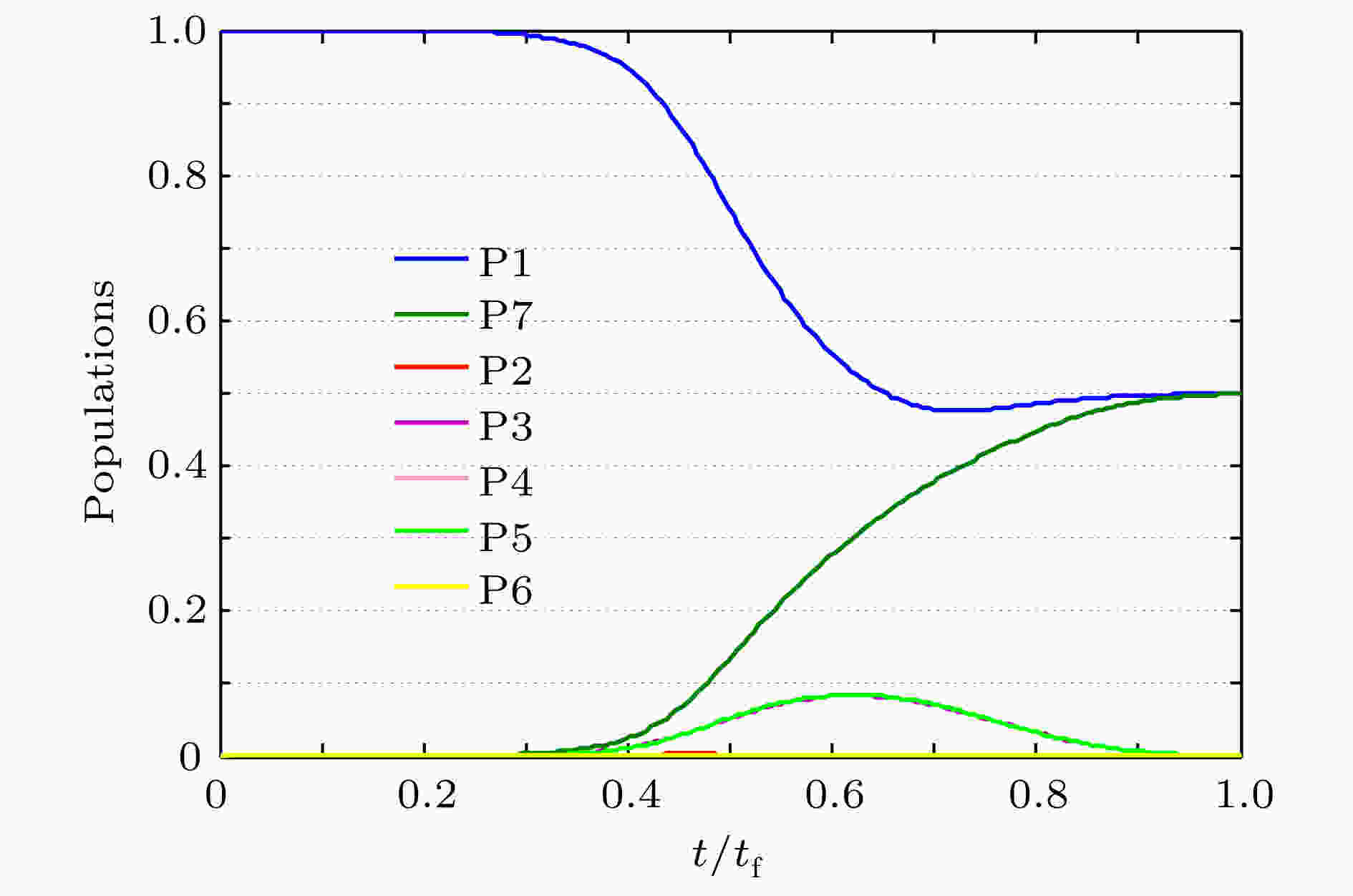 图 4 量子态布局随时间的变化
图 4 量子态布局随时间的变化











































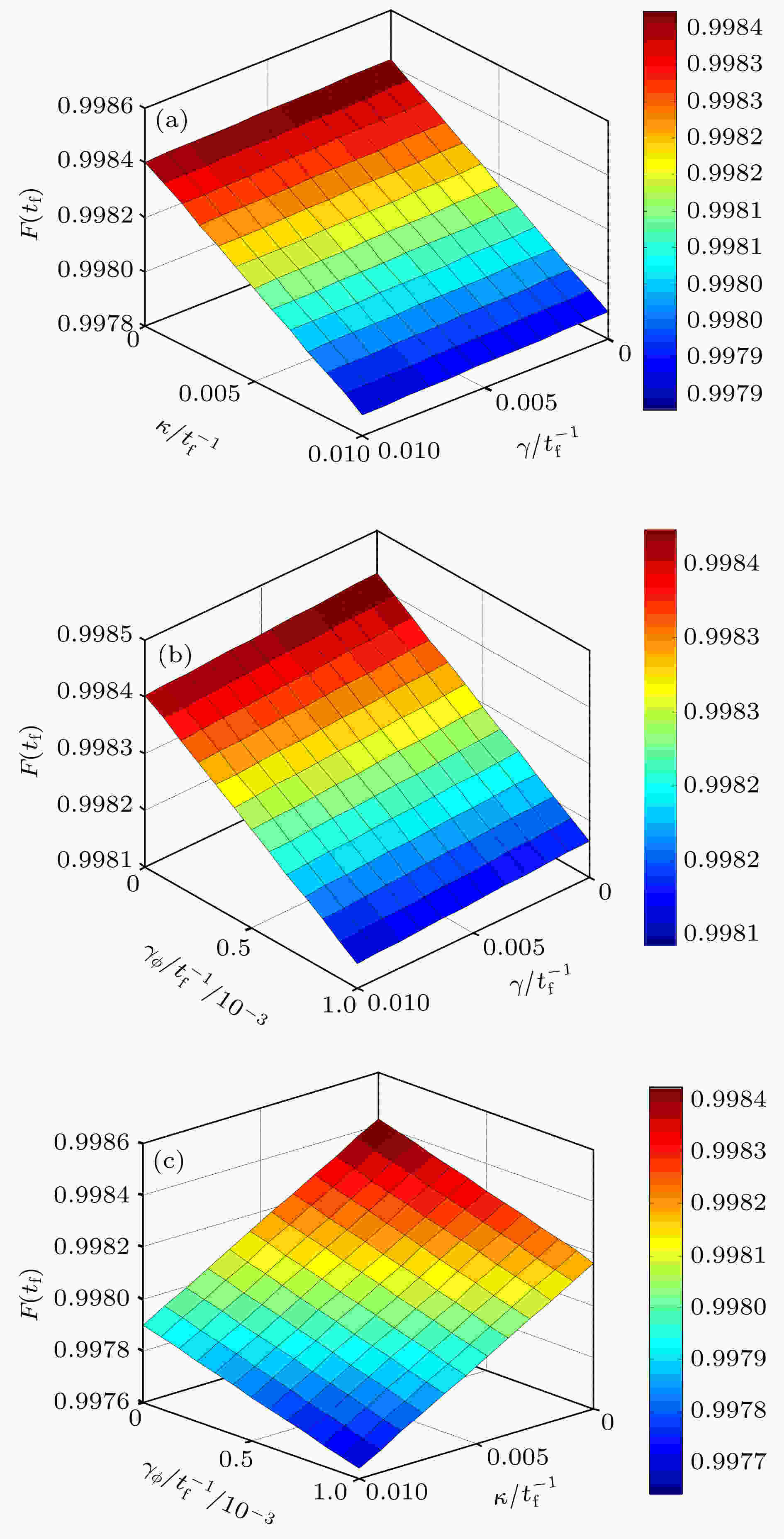 图 5 (a)
图 5 (a) 























