摘要:为了分析飞秒激光烧蚀过程, 在双相延迟模型的基础上建立了双曲型热传导模型. 模型中考虑了靶材的加热、蒸发和相爆炸, 还考虑了等离子体羽流的形成和膨胀及其与入射激光的相互作用, 以及光学和热物性参数随温度的变化. 研究结果表明: 等离子体屏蔽对飞秒激光烧蚀过程有重要的影响, 特别是在激光能量密度较高时; 两个延迟时间的比值对飞秒激光烧蚀过程中靶材的温度特性和烧蚀深度有较大的影响; 飞秒激光烧蚀机制主要以相爆炸为主. 飞秒激光烧蚀的热影响区域较小, 而且热影响区域的大小受激光能量密度的影响较小. 计算结果与文献中实验结果的对比表明基于双相延迟模型的飞秒激光烧蚀模型能有效对飞秒激光烧蚀过程进行模拟.
关键词: 飞秒激光烧蚀/
双相延迟模型/
双曲型热传导方程/
等离子体屏蔽

English Abstract

全文HTML

--> --> -->

飞秒激光烧蚀具有效率高、功率密度高、材料损伤范围小、低烧蚀阈值、加工精度高、加热时间和位置可控性好等优点^[1,2], 因此广泛应用于纳米粒子加工^[3,4]、微机械^[5-7]、表面改性^[8]、激光烧蚀推进^[9]、激光打孔^[10]、激光焊接^[11]等领域.
飞秒激光与材料相互作用的时间较短, 且其热影响范围较小^[12], 通过实验来研究飞秒激光烧蚀的相关物理机制存在较大的困难. 因此, 数学模型在飞秒激光烧蚀研究过程中起到了至关重要的作用^[12]. 目前, 用于飞秒激光烧蚀的模型主要有流体动力学模型^[13-15]、分子动力学模型^[16-18]和双温模型^[19-21](two-temperature model, TTM). 流体动力学模型和分子动力学模型存在建模困难和计算耗时长的问题^[22,23], 因此较为常用的是TTM, 对于TTM的详细描述请见文献[12, 24-26]. 尽管TTM和TTM的改进模型^[27-34]以及TTM与其他方法耦合建立的模型^[35-39]在飞秒激光烧蚀中得到了成功的应用, 但是TTM的有限性验证问题依然存在^[40-43], 其中之一就是在较高激光能量密度下的有限性验证^[43]. 此外, 大部分双温模型中都没有考虑等离子体屏蔽的影响, 这会导致在激光能量密度较高时高估烧蚀深度^[44,45].
尽管基于傅里叶定律的热传导模型在处理大多数工程应用问题时获得了较大的成功^[46], 但是它却无法准确预测一些特殊情况下的温度分布, 比如瞬态、低温和微尺度的温度分布^[47]. 为了克服傅里叶定律的限制, Cattaneo^[48]和Vernotte^[49]通过将双曲型热传导方程与局部热平衡耦合, 首次提出了非傅里叶热传导模型, 该模型被称为Cattaneo-Vernotte (CV)模型. 尽管很多实验证明CV模型的预测结果比基于傅里叶定律的热传导模型的预测结果更准确^[50-53], 但是CV模型仍然存在一些不足^[54,55], 比如该模型假设温度梯度和能量传输同时发生, 从而导致该模型无法描述传热过程中的微结构效应^[55]. 为了考虑传热过程中的微结构效应, Tzou^[56]将微结构效应用宏观方程中的温度梯度延迟时间来描述, 从而提出了双相延迟(dual-phase-lag, DPL)模型. 该模型覆盖了从微观到宏观的物理响应^[57], 可以通过改变延迟时间的取值来转变成傅里叶热传导模型和CV模型, 而且该模型满足热力学第二定律^[58]和玻尔兹曼传输方程^[59]. 目前, DPL模型的有效性已经在很多特殊热传导问题上得到了验证, 比如微纳尺度^[60,61]、生物组织^[62-64]、多孔材料^[65,66]、超流体液氦^[58]和超短脉冲激光加热^[2,58,67-70]中的热传导. 此外, DPL模型有向分数阶DPL模型^[71,72]和其他应用领域^[66]发展的趋势, 但是目前还没有关于DPL模型应用于高能飞秒激光烧蚀的报道.
本文针对飞秒激光烧蚀不同阶段的物理过程, 将DPL模型分别与不同阶段的能量守恒方程相结合建立相应的双曲型热传导方程, 然后在双曲型热传导方程中耦合等离子体膨胀和屏蔽模型, 由此建立了一种飞秒激光烧蚀金属模型. 此外, 该模型中考虑蒸发和相爆炸两种烧蚀机制, 同时还在室温到接近临界温度(${T_{\rm {cr}}}$)范围内考虑靶材的光学和热物性参数随温度的变化. 该模型的建立不仅扩展了DPL模型的应用范围, 而且为飞秒激光烧蚀的数值模拟研究提供了一种易于实施的新方法. 本文以金属铜(Cu)为例, 利用所建立的模型分析等离子体屏蔽、延迟时间的比值和激光能量密度对飞秒激光烧蚀的影响, 通过与文献中实验结果的对比验证模型的有效性.

2

-->

2.1.两个不同阶段的热传导方程

当飞秒激光辐照金属靶材时, 部分激光被反射, 剩余的激光被靶材吸收; 靶材吸收激光能量后被加热, 从而导致靶材的蒸发、相爆炸, 该过程被称为飞秒激光烧蚀. 飞秒激光烧蚀过程可分为两个阶段: 在第一个阶段, 靶材被激光加热并且其表面温度低于沸点, 此时不用考虑靶材蒸发和等离子体屏蔽的影响, 其示意图见图1; 在第二个阶段, 靶材表面被激光加热至高于沸点, 靶材开始被烧蚀并且在靶材表面形成等离子体羽流, 然后等离子体羽流会膨胀并吸收部分激光能量, 其示意图见图2. 本文针对以上两个阶段不同的物理过程, 将DPL模型分别与不同阶段的能量守恒方程相结合建立相应的双曲型热传导方程, 然后在双曲型热传导方程中耦合等离子体膨胀和屏蔽模型, 由此建立了一种飞秒激光烧蚀金属模型. 此外, 由于飞秒激光烧蚀金属靶材时, 靶材的吸收深度远远小于激光束的直径, 因此三维热传导问题可以简化为激光辐照方向的一维热传导问题.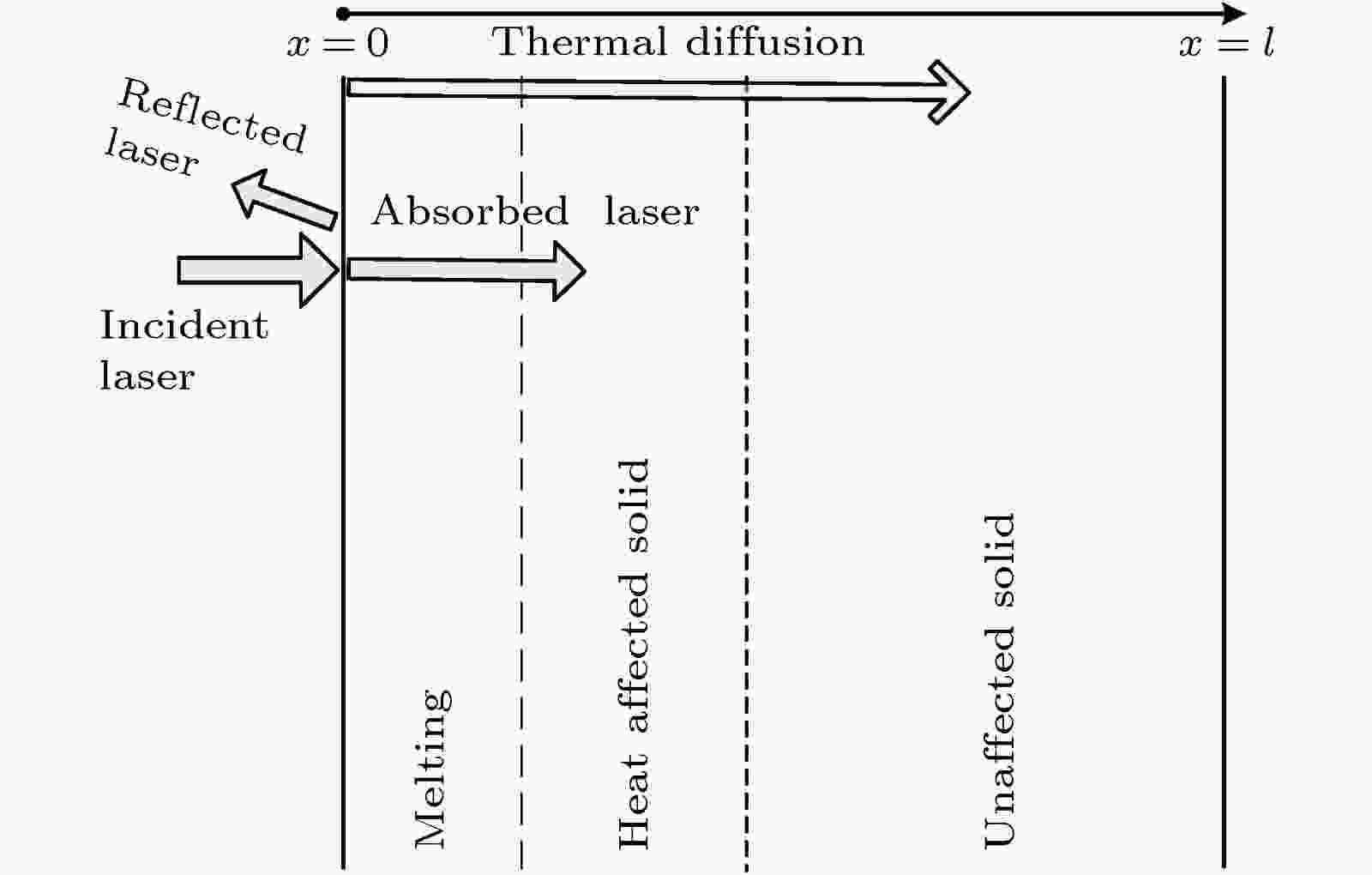
图 1 蒸发开始前激光与靶材相互作用示意图
Figure1. Schematic of laser interaction with target before the initiation of the evaporation.

图 2 蒸发开始后激光与靶材相互作用示意图
Figure2. Schematic of laser interaction with target after the initiation of the evaporation.

3 -->

2.1.1.靶材蒸发前的热传导方程

当靶材的表面温度低于靶材的沸点时, 此时不用考虑靶材蒸发带走的热量和等离子体屏蔽, 因此能量守恒定律^[73]可表示为

$\rho (T){C_p}(T)\frac{{\partial T}}{{\partial t}} = - \frac{{\partial {{q}}}}{{\partial x}} + \dot S, $

其中$\rho (T)$和${C_p}(T)$分别表示随时间变化的密度和比热容, ${{q}}$表示热流密度矢量, $\dot S$是热源项:

$\dot S = \alpha (T)\beta (T){I_{\rm{L}}}(t)\exp \left[ { - \alpha (T)x} \right], $

其中$\alpha (T)$和$\beta (T)$分别表示随温度变化的吸收系数和吸收率, ${I_{\rm{L}}}(t)$表示入射激光到达靶材表面的激光强度.
将方程(1)与DPL模型^[12]相结合:

${{q}} + {\tau _q}\frac{{\partial {{q}}}}{{\partial t}} = - k(T)\frac{{\partial T}}{{\partial x}} - k(T){\tau _{\rm{T}}}\frac{\partial }{{\partial t}}\left(\frac{{\partial T}}{{\partial x}}\right), $

由此可获得双曲型热传导方程

$\begin{split} & \rho (T){C_p}(T)\frac{{\partial T}}{{\partial t}} + {\tau _q}\rho (T){C_p}(T)\frac{{{\partial ^2}T}}{{\partial {t^2}}} = \frac{\partial }{{\partial x}}\left(k(T)\frac{{\partial T}}{{\partial x}}\right) \\ & + {\tau _T}\frac{\partial }{{\partial x}}\left[ {k(T)\frac{\partial }{{\partial t}}(\frac{{\partial T}}{{\partial x}})} \right] + \dot S + {\tau _q}\frac{{\partial \dot S}}{{\partial t}}, \quad\quad\quad\quad\quad (4)\!\end{split}$

其中$k(T)$表示随温度变化的热导率, ${\tau _q}$表示热流矢量延迟时间, ${\tau _T}$表示温度梯度延迟时间. 本文定义${\tau _T}$与${\tau _q}$的比值为B.
热传导方程还包含一个初始条件和两个边界条件:

$\left\{ \begin{aligned} & T(x, t)\left| {_{t = 0}} \right. = {T_0}, \\& k(T)\frac{{\partial T(x, t)}}{{\partial x}}\left| {_{x = l}} \right. = 0, \\ & - k(T)\frac{{\partial T(x, t)}}{{\partial x}}\left| {_{x = 0}} \right. = - \beta (T){I_{\rm{L}}}(t) + \varepsilon \sigma ({T^4} - T_0^4),\end{aligned} \right.$

其中${T_0}$表示室温并假设为300 K, $\sigma $表示斯特藩-玻尔兹曼常数, $\varepsilon $表示靶材的表面发射率.
3 -->

2.1.2.靶材蒸发后的热传导方程

当靶材温度高于靶材的沸点时, 靶材的蒸发效应变得很明显^[74], 蒸发和等离子体屏蔽的影响会变得很重要, 此时能量守恒定律^[73]表示为

$\rho (T){C_p}(T)\frac{{\partial T}}{{\partial t}} = - \frac{{\partial {{q}}}}{{\partial x}} + \dot S + \rho (T){C_p}(T)u(T)\frac{{\partial T}}{{\partial x}}.$

方程(6)与方程(3)结合, 可获得双曲型热传导方程:

$\begin{split}& \rho (T){C_p}(T)\frac{{\partial T}}{{\partial t}} + {\tau _q}\rho (T){C_p}(T)\frac{{{\partial ^2}T}}{{\partial {t^2}}} \\=\, &\frac{\partial }{{\partial x}}\left(k(T)\frac{{\partial T}}{{\partial x}}\right) + {\tau _T}\frac{\partial }{{\partial x}}\left[ {k(T)\frac{\partial }{{\partial t}}\left(\frac{{\partial T}}{{\partial x}}\right)} \right] \\ +\, & \dot S + {\tau _q}\frac{{\partial \dot S}}{{\partial t}} + \rho (T){C_p}(T)u(T)\frac{{\partial T}}{{\partial x}} \\ + \,& {\tau _q}\frac{\partial }{{\partial t}}\left(\rho (T){C_p}(T)u(T)\frac{{\partial T}}{{\partial x}}\right), \end{split} $

其中蒸发速度$u(T)$^[75,76]可表示为

$\begin{split}u(T) = \, & {C_{\rm{s}}}{P_{\rm{b}}}{(2{\rm{π}}{m_{\rm{a}}}{k_{\rm{B}}}{T_{\rm{s}}})^{ - 1/2}}\frac{{{m_{\rm{a}}}}}{{\rho ({T_{\rm{s}}})}} \\ & \times \exp \left[ {\frac{{{L_{{\rm{hv}}}}{m_{\rm{a}}}}}{{{k_{\rm{B}}}}}\left(\frac{1}{{{T_{\rm{b}}}}} - \frac{1}{{{T_{\rm{s}}}}}\right)} \right],\end{split}$

其中${C_{\rm{s}}}$表示蒸发系数, ${P_{\rm{b}}}$表示沸腾压力(一般取值0.1 MPa), ${k_{\rm{B}}}$表示玻尔兹曼常数, ${m_{\rm{a}}}$表示靶材的原子质量, ${T_{\rm{s}}}$和${T_{\rm{b}}}$分别表示表面温度和沸点, $\rho ({T_{\rm{s}}})$表示在温度为表面温度时的密度, ${L_{{\rm{hv}}}}$表示蒸发时的气化潜热.
基于连续温度条件, 此时的初始条件可表示为

$\left\{ \begin{aligned} & T(0 \leqslant x \leqslant l, t = t_{\rm{b}}^{\rm{ + }}) = T(0 \leqslant x \leqslant l, t = t_{\rm{b}}^{\rm{ - }}), \\& \frac{{\partial T}}{{\partial t}}\left| {_{t = t_{\rm{b}}^ + }} \right. = \frac{{\partial T}}{{\partial t}}\left| {_{t = t_{\rm{b}}^ - }, } \right.\end{aligned} \right.$

其中${t_{\rm{b}}}$表示靶材表面温度达到沸点的时间.
基于能量守恒定律, 边界条件可表示为

$\left\{ \begin{split} & k(T)\frac{{\partial T(x, t)}}{{\partial x}}\Big| {_{x = l}} = 0, \\& -k(T)\frac{{\partial T(x, t)}}{{\partial x}}\Big| {_{x = 0}} \\=& - \beta (T){I_{\rm{L}}}(t) + {L_{{\rm{hv}}}}\rho (T)u(T) + \varepsilon \sigma ({T^4} - T_0^4).\end{split} \right.$

2 -->

2.2.等离子体膨胀和屏蔽

蒸发和相爆炸会在靶材表面形成等离子体羽流, 然后等离子体会膨胀并吸收部分激光能量, 因此靶材表面温度达到沸点后应开始考虑等离子体屏蔽的影响. 在等离子体屏蔽模型中, 假设等离子体对激光能量的吸收只考虑逆韧致吸收机制(inverse bremsstrahlung, IB), 因为在激光波长较长时, 其他吸收机制的影响较小^[77]. IB的等离子体吸收系数${\alpha _{{\rm{IB}}}}$^[78]由下式给出:

${\alpha _{{\rm{IB}}}} = \frac{{3.69 \times {{10}^8}{Z^3}n_{\rm{i}}^{\rm{2}}}}{{T_{\rm{p}}^{0.5}{\omega ^3}}}\left[ {1 - \exp \left( - \frac{{h\omega }}{{{k_{\rm{B}}}{T_{\rm{p}}}}}\right)} \right], $

其中$Z$表示平均电荷, ${n_{\rm{i}}}$表示等离子体中的离子密度, ${T_{\rm{p}}}$表示等离子体温度, $\omega $表示激光频率, $h$表示普朗克常数.
等离子体中的离子密度随着温度的变化关系用Saha方程^[79]得到:

$\frac{{n_{\rm{i}}^{\rm{2}}}}{{{n_0}}} \approx 2.4 \times {10^{21}}T_{\rm{p}}^{1.5}\exp \left( - \frac{{I{P_1}}}{{{k_{\rm{B}}}{T_{\rm{p}}}}}\right), $

其中$I{P_1}$表示第一离子能, ${n_0}$表示中性粒子数密度.
假设中性粒子数密度在等离子体屏蔽长度内均匀分布, 则它可表示为

${n_0} = \frac{\rho }{{{m_{\rm{a}}}}}\frac{{{S_{{\rm{ab}}}}}}{{{H_{\rm{p}}}}}, $

其中${S_{{\rm{ab}}}}$表示烧蚀深度, ${H_{\rm{p}}}$表示等离子体屏蔽长度, 它可以表示为

${H_{\rm{p}}} = {S_{{\rm{ab}}}} + \int\nolimits_{{t_{\rm{b}}}}^t {{v_{\rm{p}}}{\rm{d}}t} , $

其中${v_{\rm{p}}}$表示等离子体膨胀速度.
等离子体屏蔽长度随着等离子体向外膨胀而改变, 等离子体的膨胀动力学方程^[78]可表示为

${x_{\rm{p}}}(t)\left( {\frac{1}{t}\frac{{{\rm{d}}{x_{\rm{p}}}(t)}}{{{\rm{d}}t}} + \frac{{{{\rm{d}}^2}{x_{\rm{p}}}(t)}}{{{\rm{d}}{t^2}}}} \right) = \frac{{{k_{\rm{B}}}{T_{\rm{p}}}}}{{{m_{\rm{a}}}}}, $

其中${x_{\rm{p}}}(t)$表示等离子体膨胀距离.
等离子体的膨胀速度可表示为

${v_{\rm{p}}} = \frac{{{\rm{d}}{x_{\rm{p}}}(t)}}{{{\rm{d}}t}}.$

在计算中, 等离子体的初始速度^[80]定义为

${v_0} = \sqrt {8{k_{\rm{B}}}{T_{\rm{b}}}/({\rm{π}}{m_{\rm{a}}})} .$

因此, 激光在穿过等离子体羽流后达到靶材表面的激光强度可表示为

${I_{\rm{L}}}(t) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{I_0}(t), }&{} \end{array}{\rm{ }}t < {t_{\rm{b}}}, } \\[3mm] {{I_0}(t)\exp \left( { - \displaystyle\int_0^{{H_{\rm{p}}}} {{\alpha _{{\rm{IB}}}}{\rm{d}}x} } \right){\rm{, }}\quad t \geqslant {t_{\rm{b}}}, } \end{array}} \right.$

其中${I_0}(t)$表示入射激光强度, 假设其表示为^[76]

${I_0}(t) = {I_{\max }}{\left(\frac{t}{{{t_{\max }}}}\right)^7}\exp \left[ {7\left(1 - \frac{t}{{{t_{\max }}}}\right)} \right], $

其中${I_{\max }}$是峰值激光强度, ${t_{\max }}$表示激光强度达到峰值的时间.
由方程(19)和激光强度与激光能量密度${F_{{\rm{fluence}}}}$的关系可得到峰值激光强度的表达式:

${I_{\max }} = {F_{{\rm{fluence}}}}/\int\nolimits_0^\infty {{{\left( {\frac{t}{{{t_{\max }}}}}\right)}^7}\exp \left[ {7\left( {1 - \frac{t}{{{t_{\max }}}}} \right)} \right]{\rm{d}}t}. $

由方程(19)可得到激光强度与最大激光强度的比值随时间的变化, 如图3所示, 设置为半峰值脉宽(full width at half maximum, FWHM)的激光脉宽也示于图3. 本文中除了3.5节的模型验证, 其他部分的计算结果所用激光脉宽都为170 fs.
图 3 激光强度与最大激光强度的比值随时间的变化(t_p = 170 fs (FWHM))
Figure3. The variation of the ratio of laser intensity to maximum laser intensity with time (t_p = 170 fs (FWHM)).

2 -->

2.3.Cu的材料特性

以上建立的模型中有5个参数(分别是导热系数、密度、比热容、吸收系数和吸收率)会随着温度的变化而变化, 并会影响热传导过程. 通过分阶段拟合文献[81]中的数据, 得到Cu随温度变化的导热系数的表达式为

$k(T) = \left\{ \begin{aligned}& {420.457 - 0.0681T,} \quad{\rm{300\; K < }}T < {T_{\rm m}}, \\ & 111.996 + 0.06152T - 1.5255 \times {{10}^{ - 5}}{T^2} \\ & + 7.69366\times 1{0^{- 10}}{T^3},\quad{T_{\rm m}} \leqslant T \leqslant 0.9{T_{{\rm cr}}}, \end{aligned}\right.$

其中${T_{\rm{m}}}$表示熔点.
对于纯金属而言, 电导率和导热系数在高低温条件下均满足Wiedemann-Lorenz定律^[82], 因此电导率的表达式可表示为

$\sigma (T) = \frac{{k(T)}}{T}\frac{1}{{2.44 \times {{10}^{ - 8}}}}.$

密度可从文献[83]中得到

$\rho (T) = \left\{ {\begin{aligned}& {9224.492 - 0.88711T, \quad {\rm{ 300\;K}} \leqslant T < {T_{\rm{m}}}, } \\ & {8846.882 - 0.609T, \quad \quad {T_{\rm{m}}} \leqslant T \leqslant 0.9{T_{{\rm{cr}}}}. } \end{aligned}} \right.$

比热容^[83,84]可用下式计算:

${C_p}(T) = \left\{ {\begin{aligned}& {356.176 + 0.10228T, \quad {\rm{ 300 K < }}T < {T_{\rm{m}}}, } \\ & \quad \quad \quad {{\rm{ 494, }}\quad\quad\quad\quad \quad {T_{\rm{m}}} \leqslant T \leqslant 0.9{T_{{\rm{cr}}}}.} \end{aligned}} \right.$

吸收系数$\alpha (T)$和吸收率$\beta (T)$的关系式^[76]可表示为:

$\alpha (T) = \frac{{4{\rm{π}}{n_{\rm{I}}}(T)}}{\lambda }, $

$\beta (T) = \frac{{4{n_{\rm{R}}}(T)}}{{{{({n_{\rm{R}}}(T) + 1)}^2} + {n_{\rm{I}}}^2(T)}}, $

其中${n_{\rm{I}}}(T)$和${n_{\rm{R}}}(T)$分别表示消光系数和折射率, 它们的计算方程见文献[76].
模型中用到Cu的其他参数汇总于表1.

参数	符号	取值	文献
熔点/K	${T_{\rm{m}}}$	1357.77	[83]
沸点/K	${T_{\rm{b}}}$	2835.15	[83]
蒸发潜热/J·kg–1	${L_{{\rm{hv}}}}$	4.79937 × 106	[83]
第一电离能/eV	$I{P_1}$	7.72638	[83]
临界温度/K	${T_{{\rm{cr}}}}$	8500.00	[81]
蒸发系数	${C_{\rm{s}}}$	0.82	[85]
热流矢量延迟时间/ps	${\tau _q}$	0.56—5.4	[66]
温度梯度延迟时间/ps	${\tau _{\rm{T}}}$	6.0—63.0	[66]

表1模型中用到的Cu的参数
Table1.Parameters of Cu used in the model.

2 -->

2.4.数值方法

采用有限体积法对导热方程和边界条件进行离散化(计算网格示意图如图4所示), 采用全隐式格式, 则方程(4)和方程(7)对应的离散方程可表示为以下形式: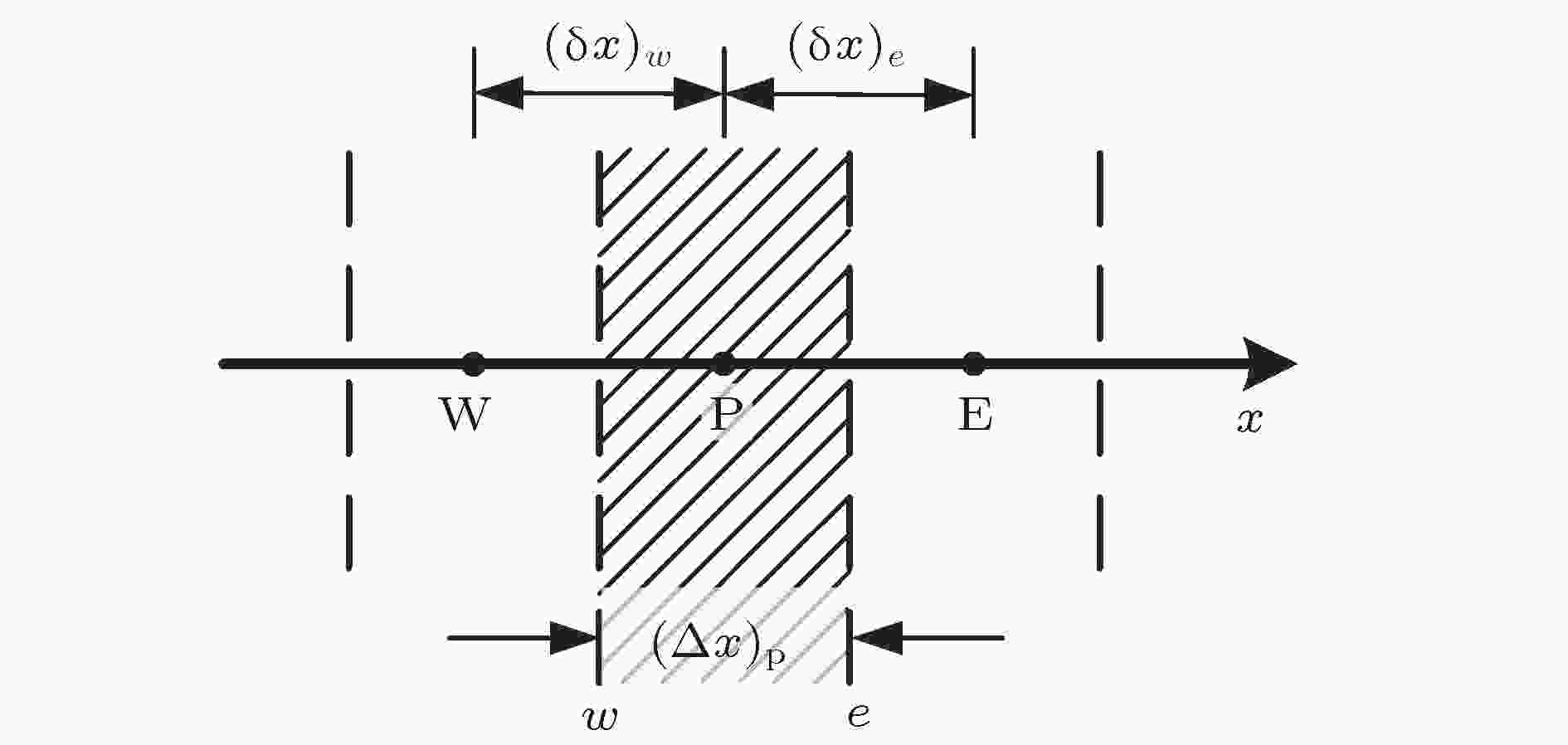
图 4 计算网格示意图
Figure4. Schematic of computational grids.

${a_{\rm{P}}}T_{\rm{P}}^{n + 1} = {a_{\rm{E}}}T_{\rm{E}}^{n + 1} + {a_{\rm{W}}}T_{\rm{W}}^{n + 1} + b.$

以方程(7)为例, 对应的离散方程中的各个系数分别为:

$\left\{ \begin{aligned}& {a_{\rm{E}}} = \frac{{{k_e}}}{{{{(\delta x)}_e}}}\left(1 + \frac{{{\tau _{\rm{T}}}}}{{\Delta t}}\right) + (1 - \omega ){C_p}\rho u\left( {1 + \frac{{{\tau _q}}}{{\Delta t}}} \right), \\& {a_{\rm{W}}} = \frac{{{k_w}}}{{{{(\delta x)}_w}}}\left(1 + \frac{{{\tau _{\rm{T}}}}}{{\Delta t}}\right) - \omega {C_p}\rho u\left( {1 + \frac{{{\tau _q}}}{{\Delta t}}} \right), \\& a_{\rm{P}}^0 = \frac{{\rho {C_p}{{(\Delta x)}_p}}}{{\Delta t}}\left( {1 + \frac{{{\tau _q}}}{{\Delta t}}} \right), \\& {a_{\rm{P}}} = {a_{\rm{E}}} + {a_{\rm{W}}} + a_{\rm{P}}^{\rm{0}}, \\& b = \dot S_{\rm{P}}^{n + 1}{(\Delta x)_p}\left(1 + \frac{{{\tau _q}}}{{\Delta t}}\right) - \dot S_{\rm{P}}^n{(\Delta x)_p}\frac{{{\tau _q}}}{{\Delta t}} \\& + \rho {C_p}u\frac{{{\tau _q}}}{{\Delta t}}\left[ {(1 - 2\omega )T_{\rm{P}}^n + (\omega - 1)T_{\rm{E}}^n + \omega T_{\rm{W}}^n} \right] \\& + \frac{{{\tau _{\rm{T}}}}}{{\Delta t}}\left[ \left(\frac{{{k_e}}}{{{{(\delta x)}_e}}} + \frac{{{k_w}}}{{{{(\delta x)}_w}}}\right)T_{\rm{P}}^n - \frac{{{k_e}}}{{{{(\delta x)}_e}}}T_{\rm{E}}^n \right.\\& \left. - \frac{{{k_w}}}{{{{(\delta x)}_w}}}T_{\rm{W}}^n \right] + \rho {C_p}{(\Delta x)_p}\frac{{{\tau _q}}}{{\Delta t}}{\left(\frac{{\partial T}}{{\partial t}}\right)^n} + a_{\rm{P}}^0T_{\rm{P}}^n,\end{aligned} \right.$

其中$\Delta t$表示时间步长(激光脉宽为170 fs和70 fs时分别设置为0.0005 fs和0.00015 fs); ${k_e}$, ${k_w}$分别表示边界e, w上的导热系数; $\omega = 1/(1 + {(\delta x)_w}/$${(\delta x)_e})$表示几何参数.
方程(4)的全隐式离散方程为无条件稳定, 而为了保证方程(7)的全隐式离散方程的稳定性, 应当满足的条件^[86,87]为

${a_{\rm{E}}} > 0, \quad{\rm{ }}{a_{\rm{W}}} > 0.$

由此推导出应该满足的条件为

$\frac{{{k_w}}}{{{{(\delta x)}_w}}}\left(1 + \frac{{{\tau _{\rm{T}}}}}{{\Delta t}}\right) > {C_p}\rho u\omega \left(1 + \frac{{{\tau _q}}}{{\Delta t}}\right).$

结合两个阶段的初始条件和边界条件, 用三对角追赶法(tridiagonal matrix method, TDMA)求解离散方程(27). 在计算中, 每一靶材层的五个参数在每一步计算中都进行更新. 在第二个阶段的计算中, 需要同时计算等离子体羽流的膨胀和穿过等离子体后的激光强度, 并在每一时间步中进行耦合计算.
靶材蒸发所导致的烧蚀深度利用每一时间步长的蒸发速度进行计算. 在本文的计算中, 相爆炸所导致的烧蚀深度假设只要温度高于0.9${T_{{\rm{cr}}}}$^[76,77]就立刻发生. 由于相爆炸是一个体积移除过程, 因此相爆炸所导致的深度通过移除温度高于0.9${T_{{\rm{cr}}}}$的靶材层来计算得到, 而这些层将在后续的计算中被忽略. 靶材的烧蚀深度是蒸发深度和相爆炸深度之和.

2

-->

3.1.等离子体屏蔽的影响

激光能量密度为20.0 J/cm²时, 有无等离子体屏蔽的激光强度和烧蚀深度随时间的变化如图5所示. 有无等离子体屏蔽时, 激光强度和烧蚀深度曲线有较大的不同. 两条烧蚀深度曲线的分离时间与两条激光强度曲线相同. 这是因为当烧蚀深度达到一定程度时, 在靶材的表面会形成致密的等离子体, 它会吸收部分激光强度, 因此会使得到达靶材表面的激光强度降低. 这反过来又会影响对靶材的烧蚀过程并减缓烧蚀深度的增加.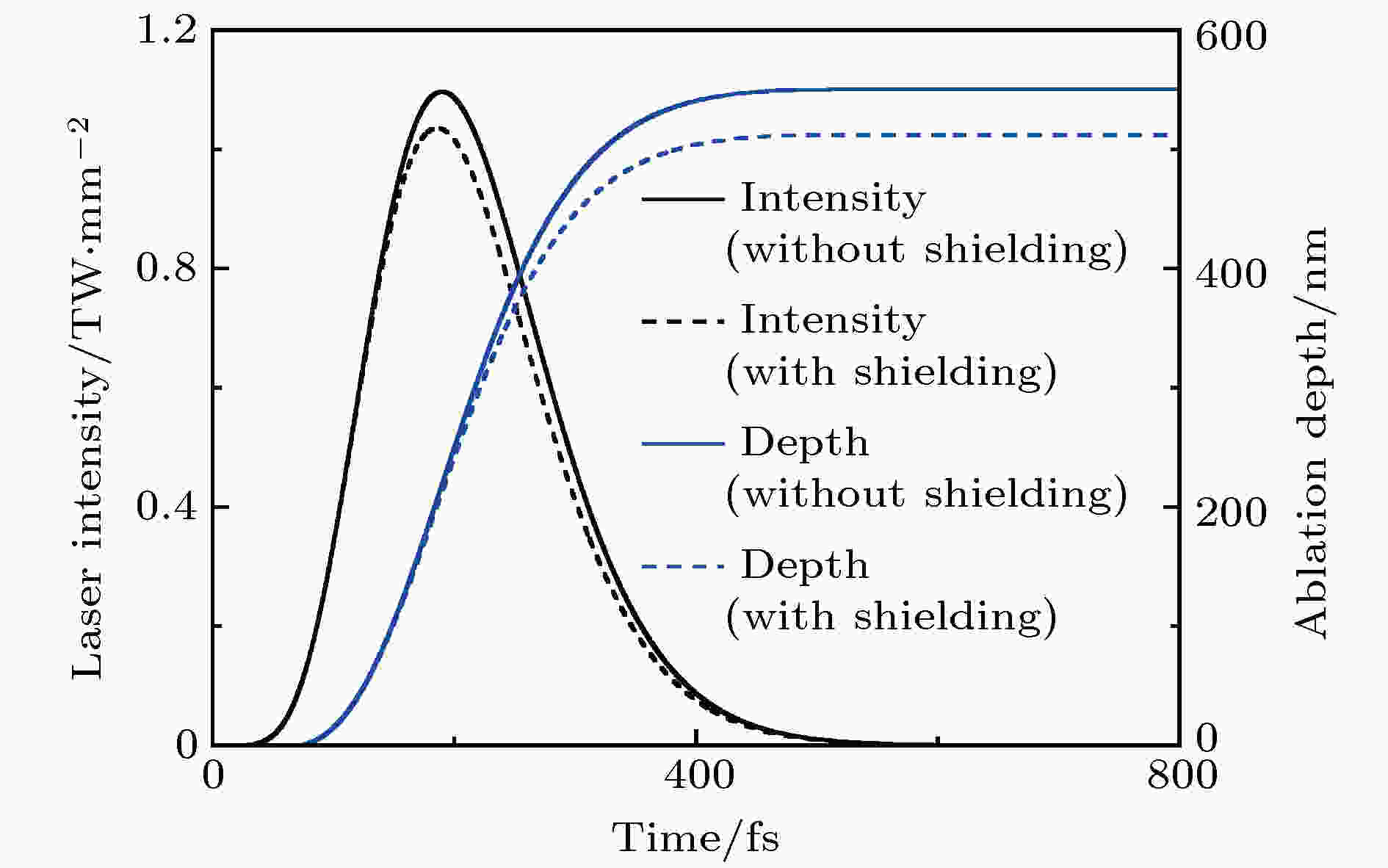
图 5 激光强度和烧蚀深度的对比(F_fluence = 20.0 J/cm²)
Figure5. Comparison of laser intensity and ablation depth (F_fluence = 20.0 J/cm²).

本文将等离子体屏蔽比例定义为等离子体羽流吸收的激光能量密度与入射激光能量密度的比值, 假设有、无等离子体屏蔽时的激光强度曲线(分别对应图5中的黑色虚线和黑色实线)与x轴围成的面积分别为A_w和A_wo, 则等离子体屏蔽比例的计算公式为(1–A_w/A_wo). 图6显示了等离子体屏蔽比例随激光能量密度的变化. 在激光能量密度为35.0 J/cm²以下时, 等离子体屏蔽的比例随着激光能量密度的增加而增加, 这表明等离子体羽流的不透明程度随着激光能量密度的增加而增加. 这意味着等离子体屏蔽对飞秒激光烧蚀过程有较大的影响, 特别是在较高的激光能量密度下. 在本文随后呈现的结果中都考虑了等离子体屏蔽的影响.
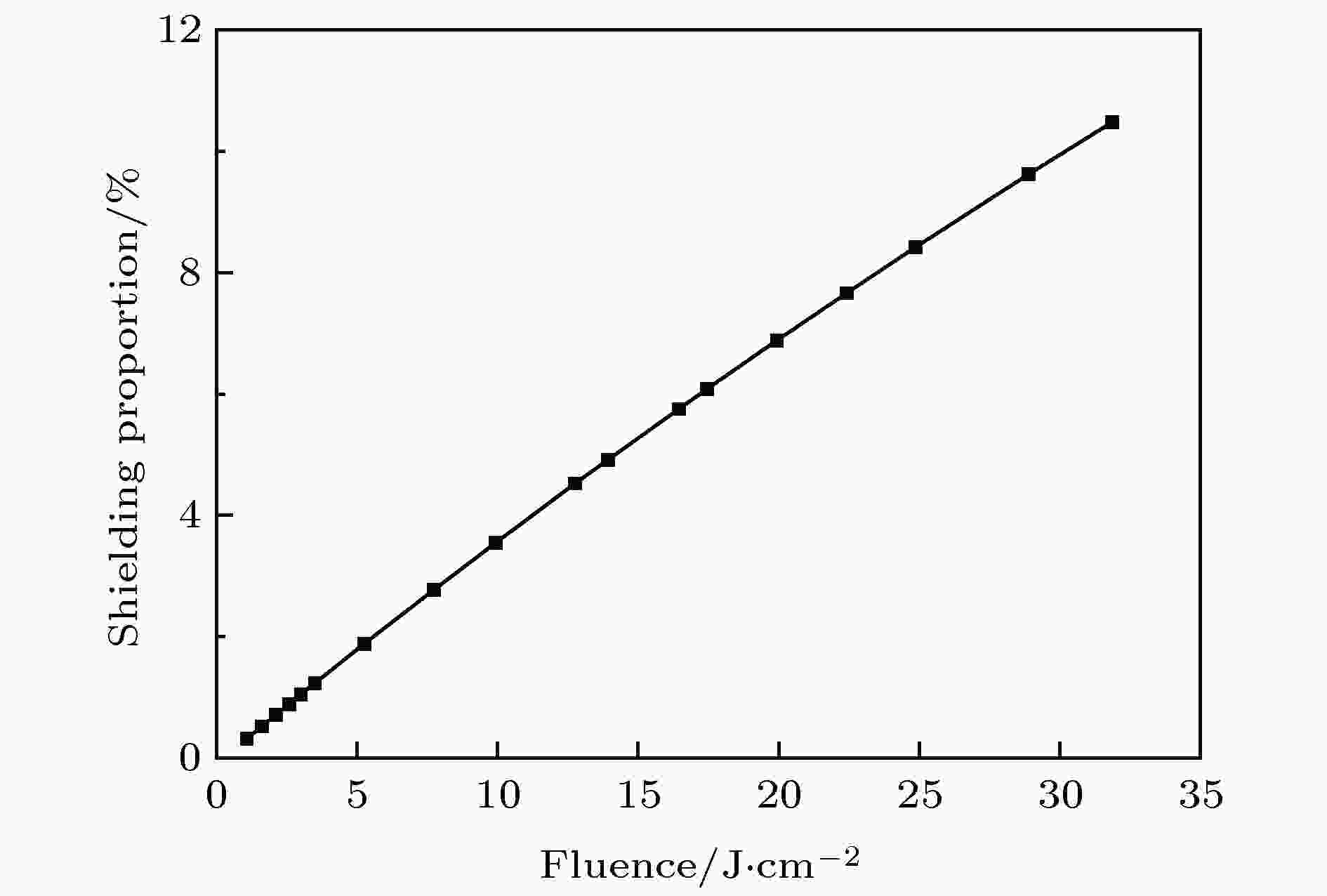图 6 等离子体屏蔽比例随着激光能量密度的变化
Figure6. Variation of plasma shielding proportions with laser fluence.

2 -->

3.2.${{\tau}_{ q}}$不变时, 比值B的影响

不同比值B时, 激光能量密度为0.2 J/cm²、时间为400 fs时的温度沿靶材深度分布情况如图7所示. 靶材表面温度随着比值B的增大而减小, 而热传导的深度随着比值B的增加而增加. 这是因为, 比值B的增加会加快热扩散的程度, 使热量更快地向靶材内部传导, 从而导致在相同的激光能量密度下比值B较高时的表面温度低于比值B较低时的表面温度, 而相应的热传导深度加深^[2].
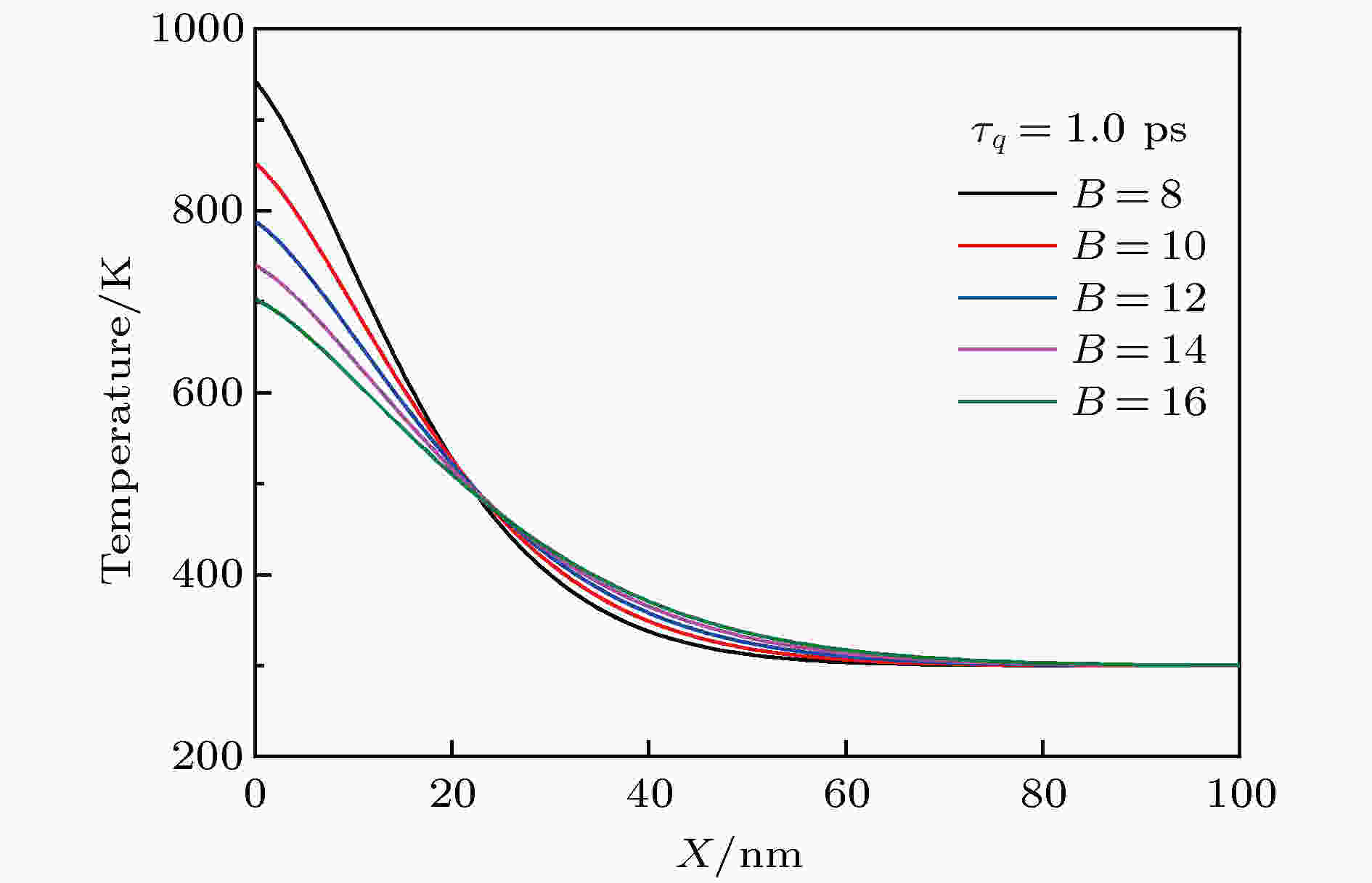图 7 不同比值B (${\tau _q}$不变)时, 温度沿靶材深度的分布(F_fluence = 0.2 J/cm²)
Figure7. Distribution of temperature along the target depth at different ratios B (${\tau _q}$ is constant) (F_fluence = 0.2 J/cm²).

不同比值B情况下, 激光能量密度为10.0 J/cm²时靶材表层的温度变化如图8所示. 不同比值B情况下, 靶材表层温度先缓慢上升, 当温度超过熔点后, 靶材表层温度上升的速度大大加快, 这是因为超过熔点后, 靶材的吸收率提高, 而导热系数降低. 同时可以发现, 比值B越大, 靶材表面温度开始上升的时间越晚, 且上升速度越缓慢. 当靶材表层温度达到0.9T_cr时, 该层靶材由于发生相爆炸而被烧蚀掉.
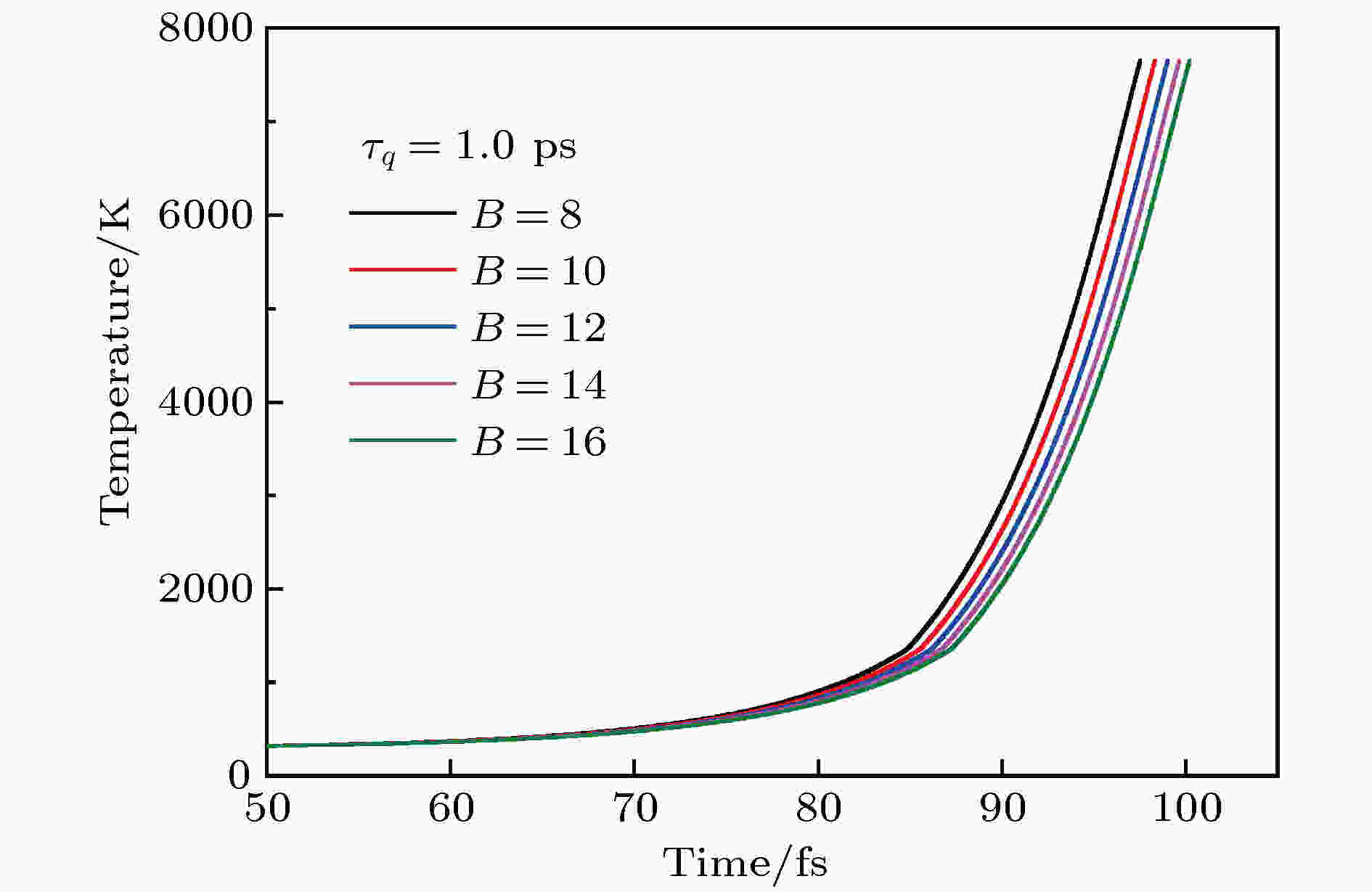图 8 比值B (${\tau _q}$不变)对表层温度的影响(F_fluence = 10.0 J/cm²)
Figure8. The effect of ratios B (${\tau _q}$ is constant) on temperature of surface layer (F_fluence = 10.0 J/cm²).

不同比值B情况下, 激光能量密度为10.0 J/cm²时靶材表面温度变化如图9所示. 需要说明的是, 此时的靶材表面是指烧蚀后的实时表面位置, 它会随着烧蚀深度的变化而变化. 不同比值B情况下, 靶材表面温度都快速上升到0.9T_cr并诱导相爆炸, 由于激光能量的持续注入, 相爆炸会持续发生, 因此温度会维持在0.9T_cr的位置. 当激光能量减小到一定值时, 表面温度不能维持在0.9T_cr, 这意味着相爆炸结束, 靶材表面温度开始下降. 由于模型中使用的激光脉宽为FWHM (如图3所示), 因此在FWHM之外的部分时间内仍然有较强的激光强度, 由此导致了图9中的相爆炸维持时间超过了170 fs.
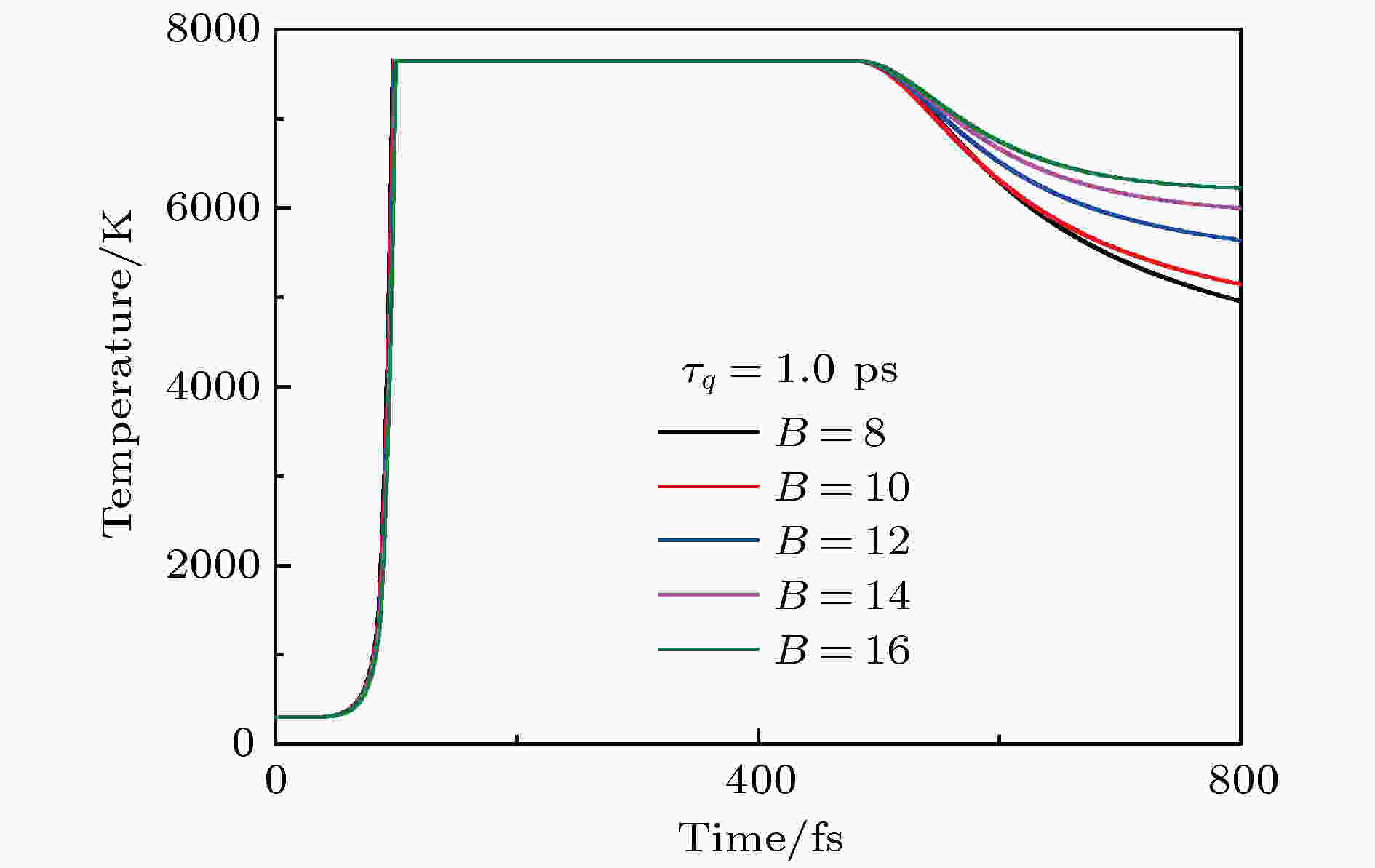图 9 比值B (${\tau _q}$不变)对表面温度的影响(F_fluence = 10.0 J/cm²)
Figure9. The effect of ratios B (${\tau _q}$ is constant) on surface temperature (F_fluence = 10.0 J/cm²).

对比不同比值B条件下的表面温度变化可知, 比值B的改变对靶材温度上升阶段和下降阶段的影响较大, 但是对相爆炸维持时间的影响不大. 在温度下降阶段, 由于B较大时, 热量向内部传导的较多, 内部与表面之间的温度梯度较低, 因此温度下降速度较慢.
不同比值B条件下, 激光能量密度为10.0 J/cm²时烧蚀深度随时间的变化如图10所示. 随着比值B的增加, 烧蚀深度增加. 这是因为在相爆炸开始后, 表面温度会维持在相同的温度下(0.9T_cr), 而比值B增大时, 热量向内部传递的速度加快, 这会使内部温度升高越多, 从而加快烧蚀速度.
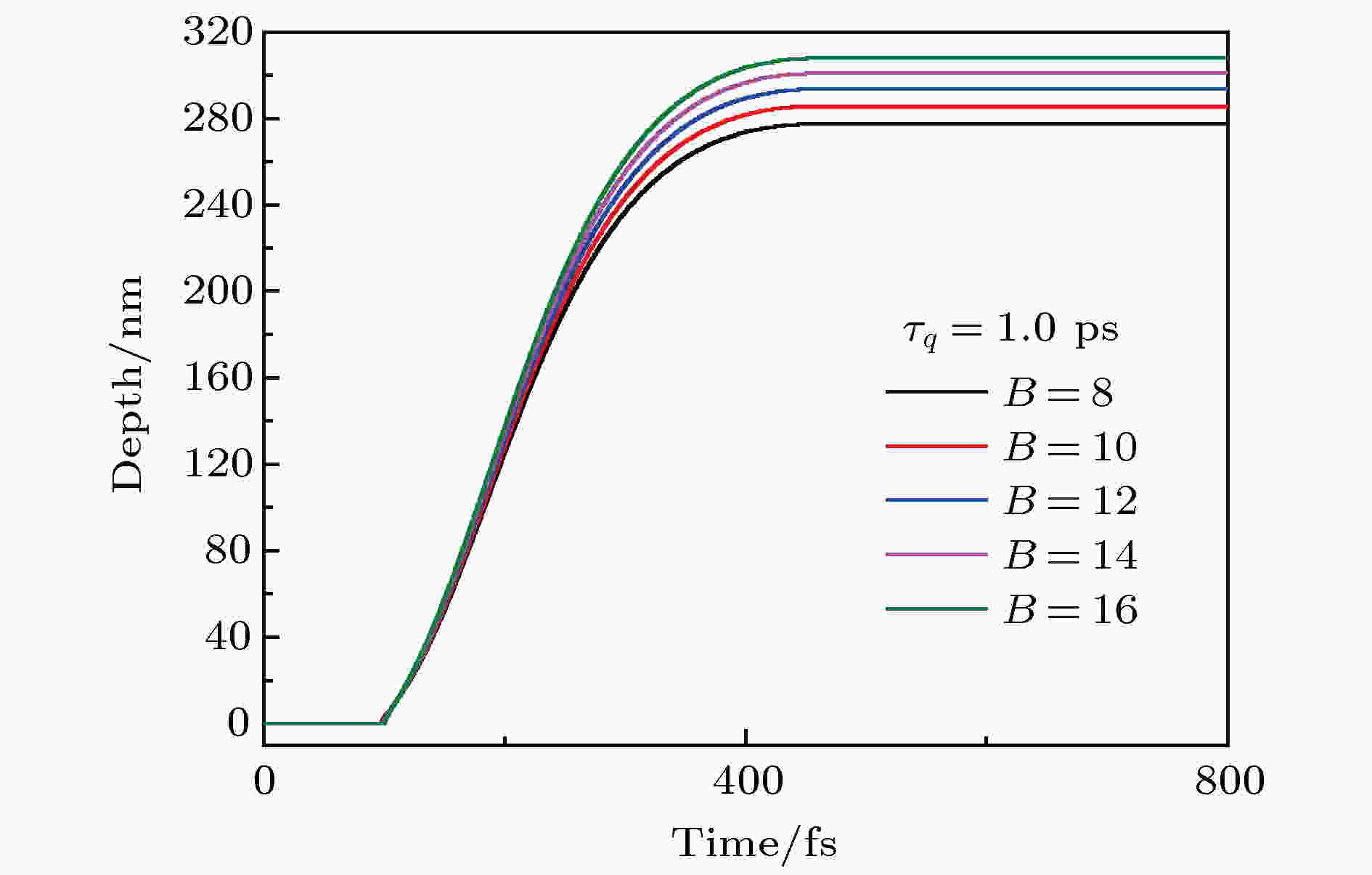图 10 比值B (${\tau _q}$不变)对烧蚀深度的影响(F_fluence = 10.0 J/cm²)
Figure10. The effect of ratios B (${\tau _q}$ is constant) on ablation depth (F_fluence = 10.0 J/cm²).

2 -->

3.3.${{\tau}_{\bf T}}$不变时, 比值B的影响

由于${\tau _q}$和${\tau _{\rm{T}}}$分别代表热传导过程中类波行为和类扩散行为的强度, 当比值B大于1时, 类波行为的强度会衰减, 类扩散行为的强度会增强, 从而使得热传导以超扩散的方式传播^[88], 因此通过改变${\tau _q}$的大小来改变比值B的大小对烧蚀过程的影响与3.2节大体相同. 图11和图12分别为比值B对表面温度和烧蚀深度的影响. 由图11可知, 随着比值B的增加, 温度达到相爆炸温度的时间越晚, 相爆炸结束后温度下降得越缓慢. 由图12可知, 随着比值B的增加, 烧蚀深度增加.
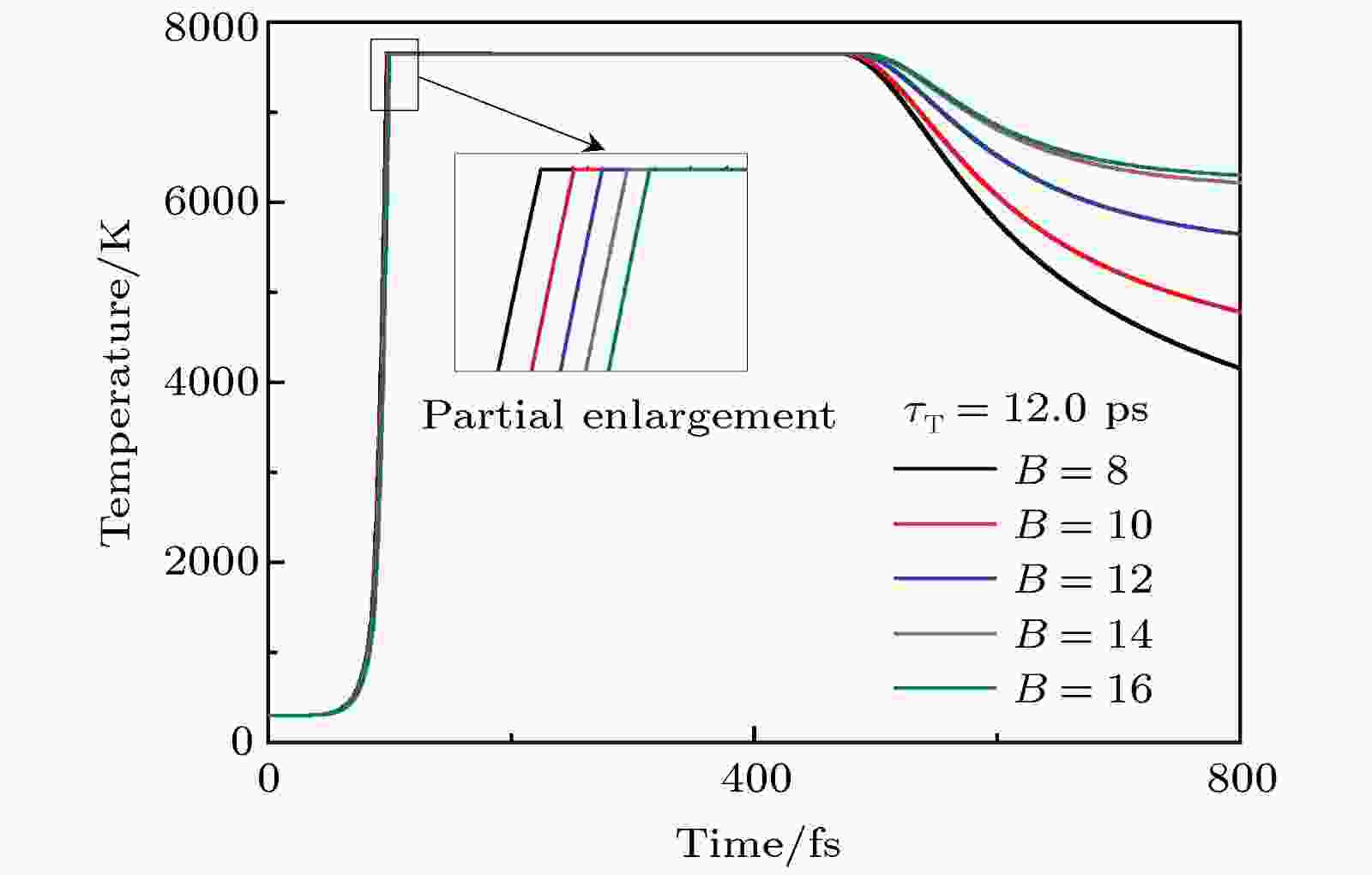图 11 比值B ($\tau _{\rm{T}}$不变)对表面温度的影响(F_fluence = 10.0 J/cm²)
Figure11. The effect of ratios B ($\tau _{\rm{T}}$ is constant) on surface temperature (F_fluence = 10.0 J/cm²).

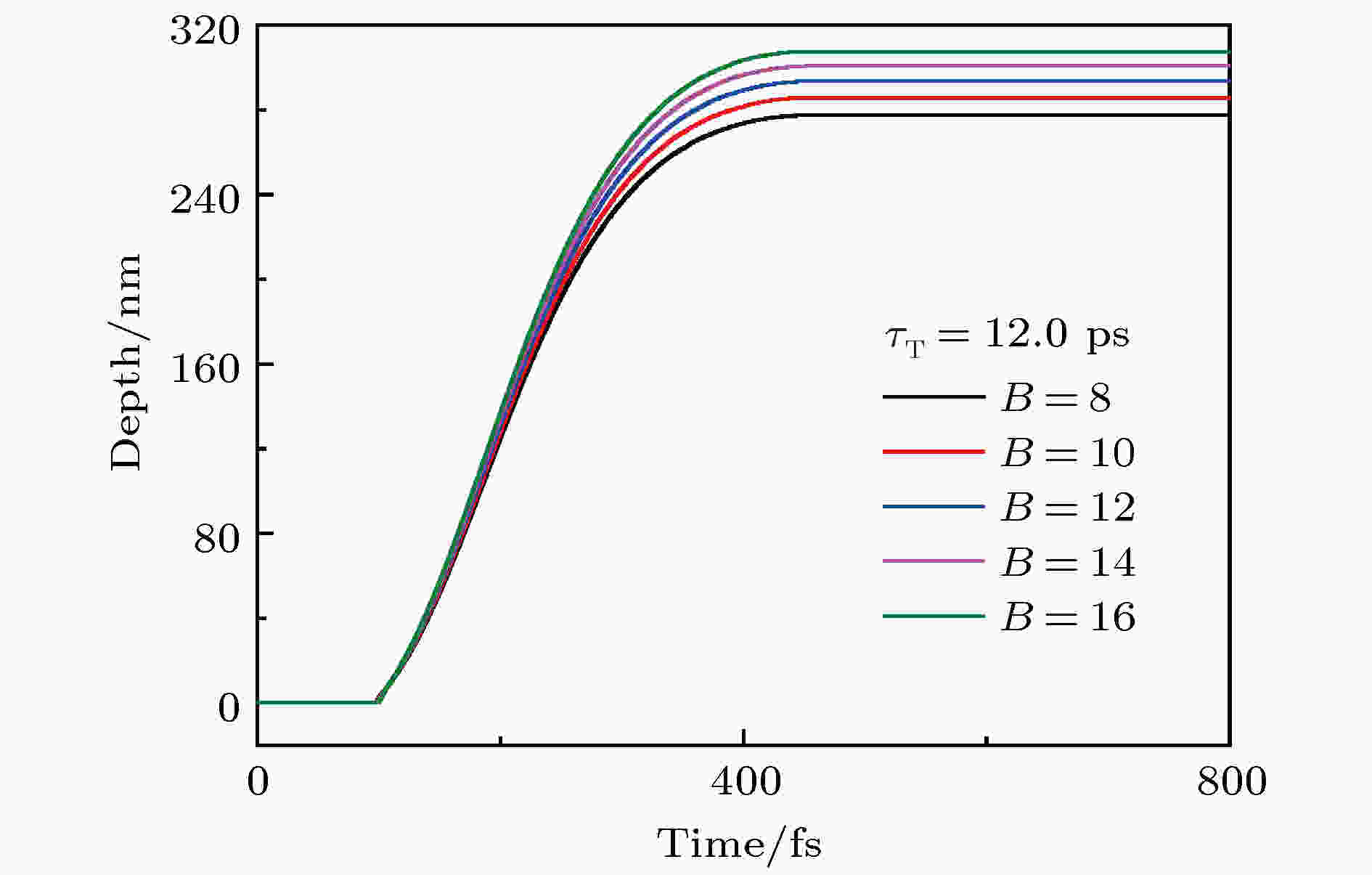图 12 比值B($\tau _{\rm{T}}$不变)对烧蚀特性的影响(F_fluence = 10.0 J/cm²)
Figure12. The effect of ratios B ($\tau _{\rm{T}}$ is constant) on ablation depth (F_fluence = 10.0 J/cm²).

2 -->

3.4.激光能量密度的影响

5种不同激光能量密度下, $\tau _T=$12.0 ps, ${\tau _q}=$1.0 ps时的表面温度对比图如图13所示. 随着激光能量密度的增大, 靶材表面相爆炸开始的时间提前, 且相爆炸结束的时间也会相应延后, 从而使得相爆炸维持的时间增长. 图14给出了5种不同激光能量密度下, $\tau _T=$12.0 ps, ${\tau _q}=$1.0 ps时烧蚀深度随时间的变化趋势. 在烧蚀深度增加的阶段, 激光能量密度越大时烧蚀深度曲线斜率越大, 这表明烧蚀速率越快. 因此, 激光能量密度越大, 烧蚀深度越深. 同时, 不同激光能量密度下, 烧蚀深度差异最大时主要集中在激光的FWHM内, 其他时间内所引起的烧蚀深度差异较小. 此外, 尽管相爆炸温度下蒸发烧蚀速率较快(约为25.0 m/s), 但是由于持续时间较短, 所以导致蒸发深度较小. 即使在激光能量密度为20.0 J/cm²时的蒸发深度仅有0.02 nm, 这表明飞秒激光烧蚀的机制以相爆炸为主. 在纳秒激光烧蚀中, 存在一个由以蒸发烧蚀为主向相爆炸烧蚀为主转变的阈值激光能量密度^[76].
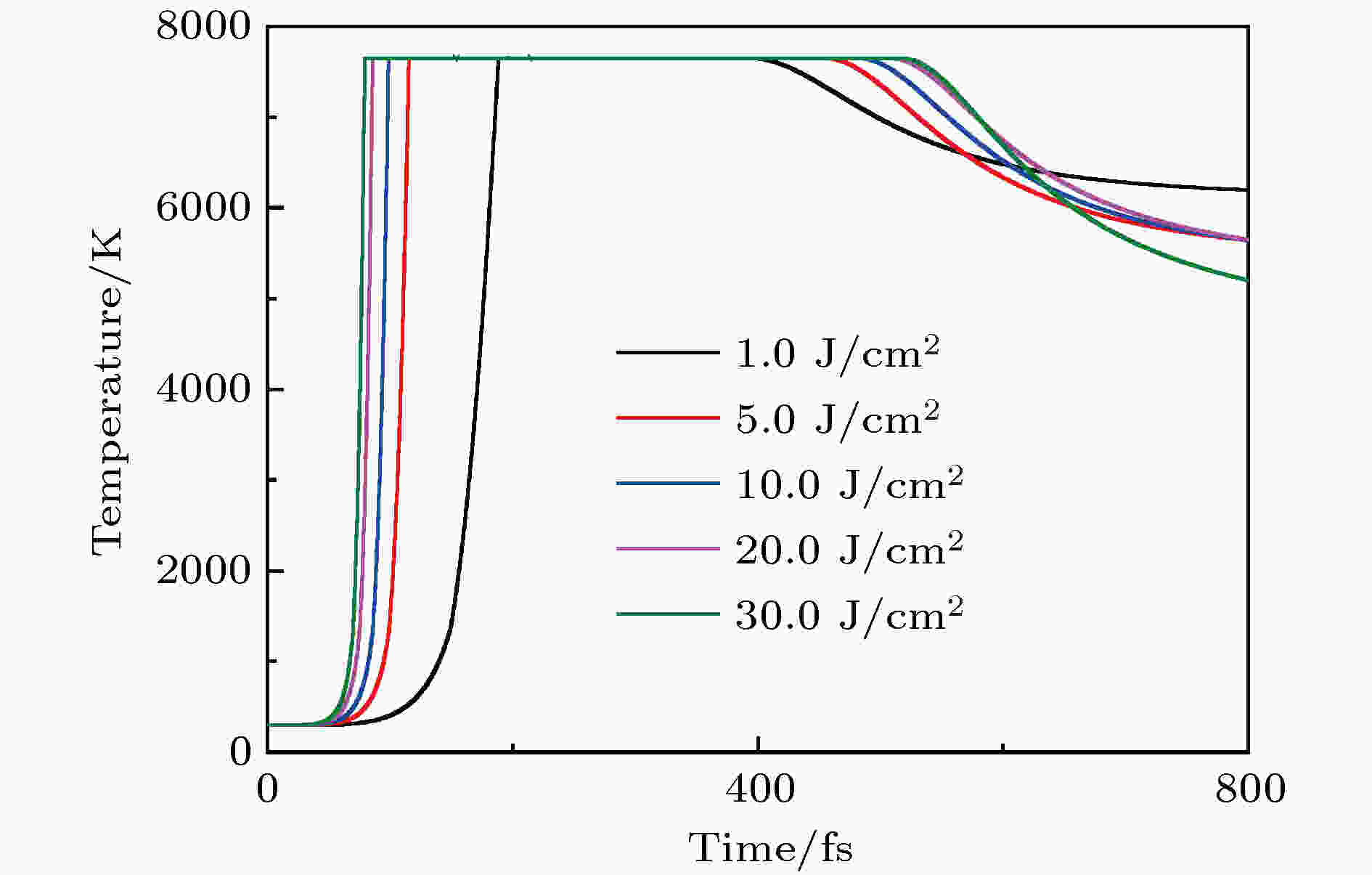图 13 不同激光能量密度下, 表面温度随时间的变化($\tau _{\rm{T}}$ = 12.0 ps, ${\tau _q}$ = 1.0 ps)
Figure13. Surface temperature changes with time at different laser fluence ($\tau _{\rm{T}}$ = 12.0 ps, ${\tau _q}$ = 1.0 ps).

图 14 不同激光能量密度下, 烧蚀深度随时间的变化($\tau _{\rm{T}}$ = 12.0 ps, ${\tau _q}$ = 1.0 ps)
Figure14. Ablation depth changes with time at different laser fluence ($\tau _{\rm{T}}$ = 12.0 ps, ${\tau _q}$ = 1.0 ps).

不同激光能量密度下, 烧蚀深度、超热液体层(温度高于沸点, 低于0.9T_cr)、融化层(温度高于熔点, 低于沸点)和热影响的固体层(温度高于0.4倍的熔点^[89], 低于熔点)随时间的变化如图15所示. 在激光能量密度为1.0 J/cm²时, 由于加热速度较慢, 在开始烧蚀前和烧蚀过程中靶材内部形成了较为明显的热影响的固体层、融化层和超热液体层, 如图15(a)所示. 随着激光能量密度的增加, 对靶材的加热速度和烧蚀速度加快, 从而导致在开始烧蚀前和烧蚀过程中靶材内部没有形成较为明显的热影响的固体层、融化层和超热液体层, 如图15(b)—(d)所示. 同时, 对比图15中各图可以发现, 不同激光能量密度下, 靶材烧蚀结束后的热影响区域的大小(温度高于0.4倍熔点, 低于0.9T_cr)相差不大, 且都不大于100 nm, 这既表明飞秒激光烧蚀的热影响区域较小, 又说明此时的热影响区域的大小受激光能量密度的影响不大.
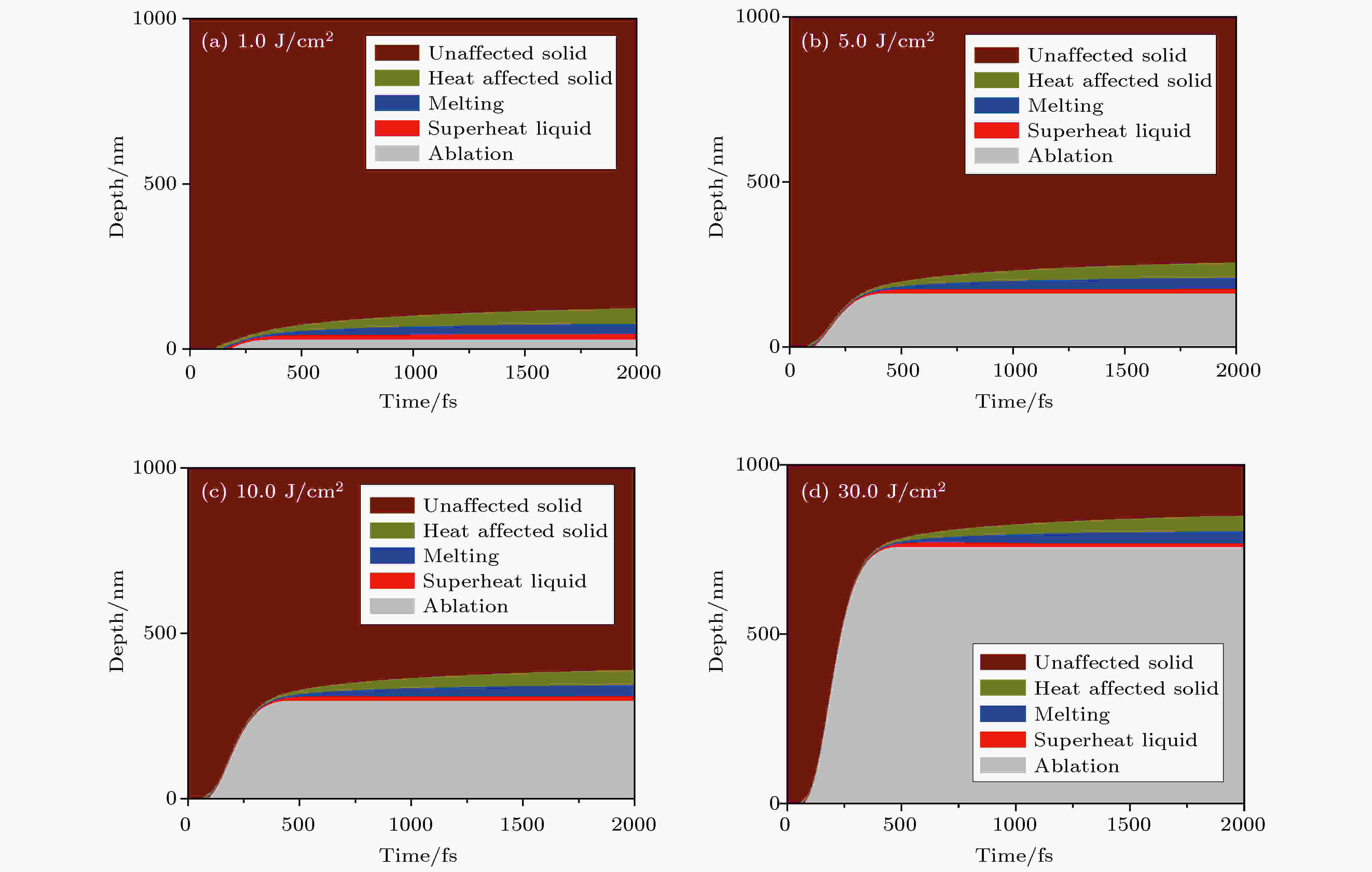图 15 不同能量密度下, 烧蚀深度、超热液体层、融化层和热影响的固体层随时间的变化($\tau _{\rm{T}}$ = 12.0 ps, ${\tau _q}$ = 1.0 ps)
Figure15. The ablation depth, the superheated liquid layer, melting layer and heat affected solid layer as a function of time at different laser fluence ($\tau _{\rm{T}}$ = 12.0 ps, ${\tau _q}$ = 1.0 ps).

2 -->

3.5.模型验证

为了验证模型的有效性, 将烧蚀深度的计算结果与Davydov和Antonov^[90]以及Hashida等^[91]通过实验测得的飞秒激光烧蚀Cu的结果进行对比, 其中Davydov等的实验条件为激光脉宽为170 fs, 激光波长为800 nm, 聚焦点直径约为16.0 ${\rm{μ}m}$; Hashida等的实验条件为激光脉宽为70 fs, 激光波长为800 nm, 聚焦点直径约为41.5 ${\rm{μ}}{\rm m}$. 由这两个实验的聚焦点直径和相应的烧蚀深度可知, 其聚焦点直径远远大于烧蚀深度, 因此可以用一维模型来对其进行模拟. 同时, 计算中分别采用与这两个实验相同的激光参数.
图16和图17分别呈现了文献[90,91]的实验结果与两个理论模型的计算结果的对比, 其中两个理论模型分别为基于DPL模型的热传导模型和傅里叶热传导模型(即把基于DPL模型的热传导模型中的两个延迟时间都设置为0 ps). 由图16和图17可知, 与傅里叶热传导模型相比, 基于DPL模型的热传导模型的计算结果与实验结果吻合得更好, 这表明非傅里叶效应在飞秒激光烧蚀过程中起到了至关重要的作用, 同时也表明基于双相延迟模型的飞秒激光烧蚀模型能有效对飞秒激光烧蚀过程进行模拟.
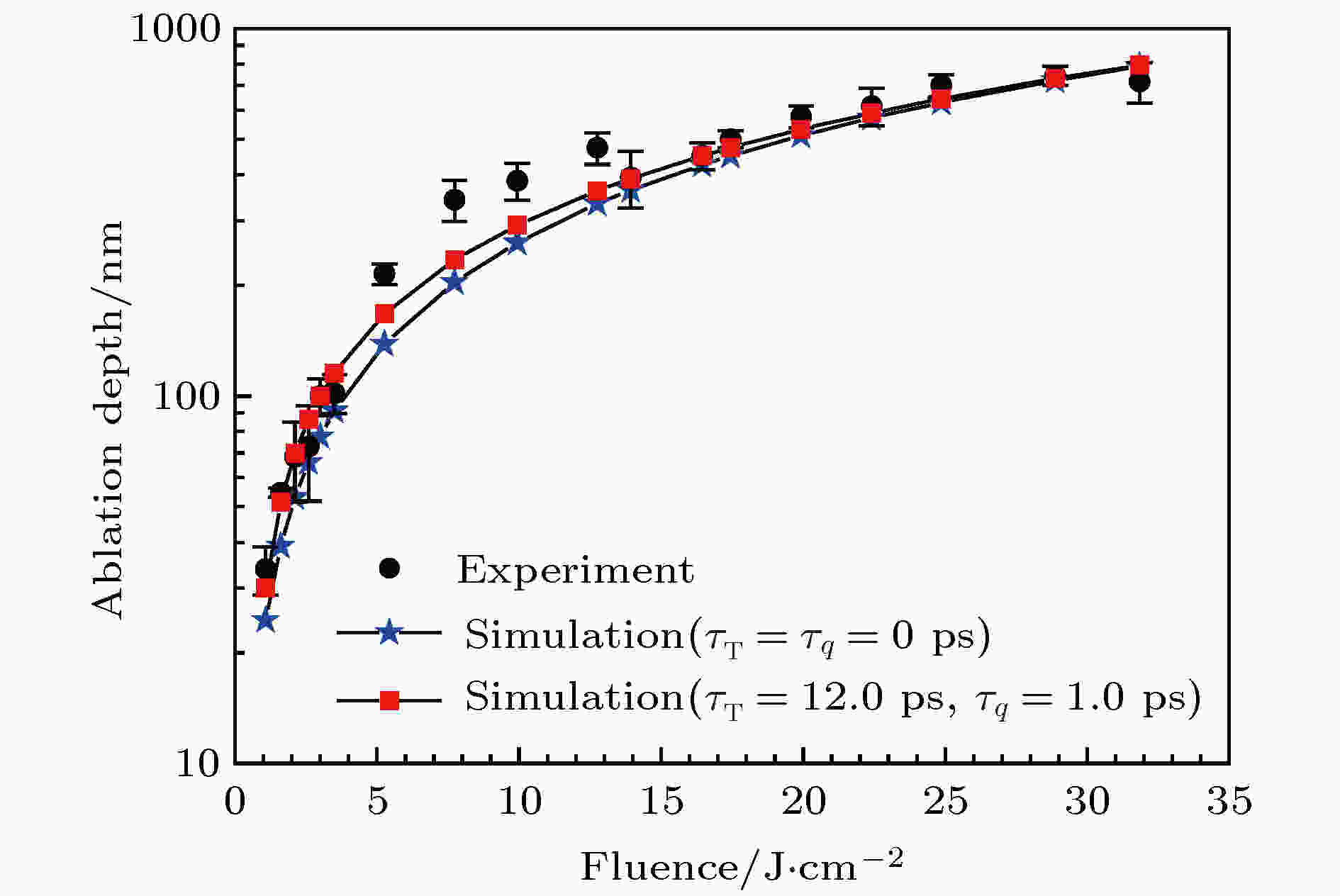图 16 烧蚀深度的计算结果与文献[90]的实验结果对比(t_p = 170 fs (FWHM))
Figure16. Comparison of simulation results of ablation depth with the experimental results from Ref. [90] (t_p = 170 fs (FWHM)).

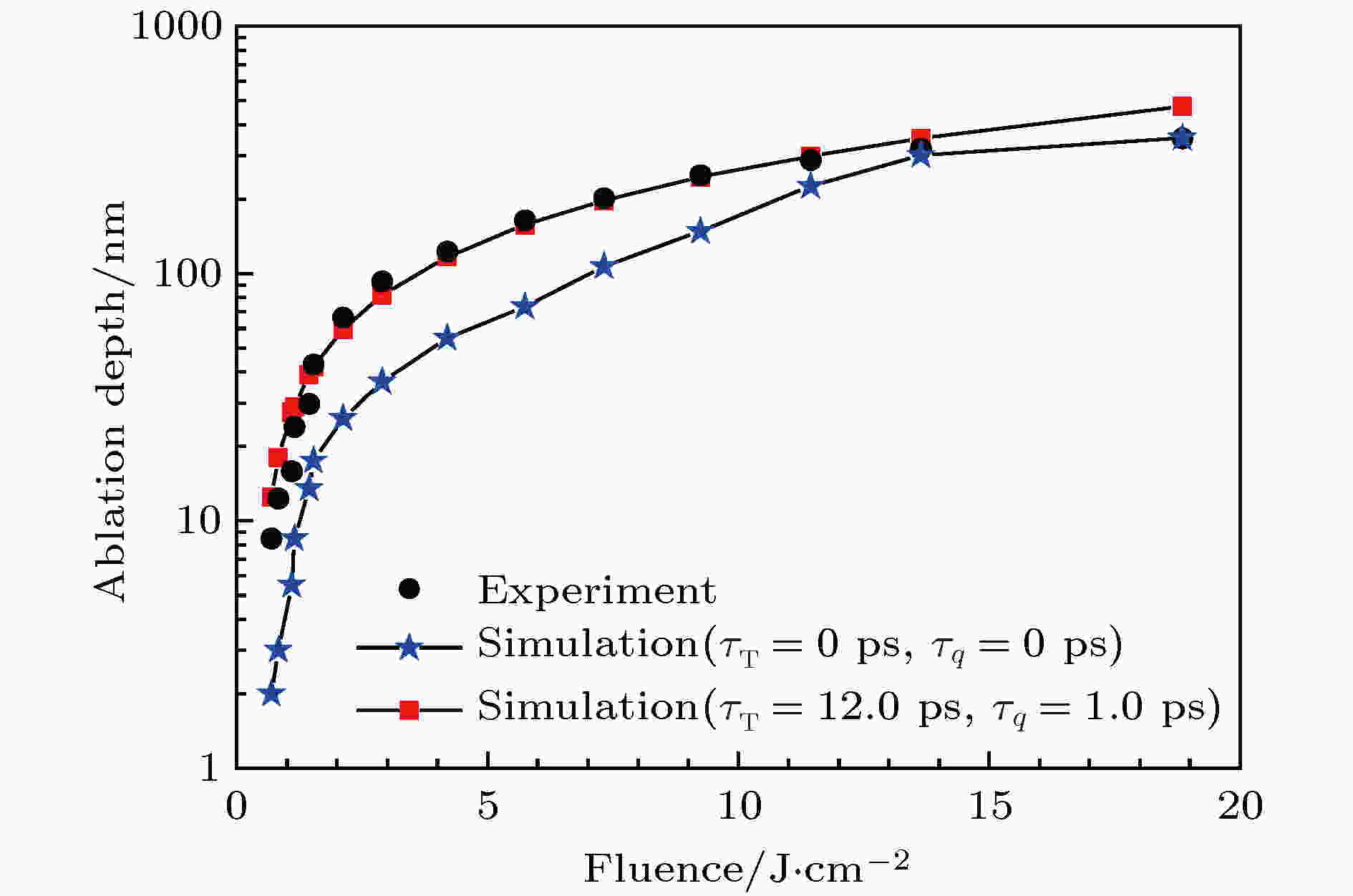图 17 烧蚀深度的计算结果与文献[91]的实验结果对比(t_p = 70 fs (FWHM))
Figure17. Comparison of simulation results of ablation depth with the experimental results from Ref. [91] (t_p = 70 fs (FWHM)).

本文建立了考虑靶材的加热、蒸发和相爆炸, 等离子体羽流的形成和膨胀、等离子体羽流与入射激光相互作用的飞秒激光烧蚀金属模型. 此外, 模型中还考虑了光学和热物性参数随温度的变化. 主要得到以下结论:
1) 等离子体屏蔽在飞秒激光烧蚀过程中起到了至关重要的作用, 特别是在激光能量密度较高时;
2) 延迟时间比值B对靶材表面的温度特性和烧蚀深度特性有较大的影响, 比值B的增加会加快热扩散的程度, 从而使表面温度上升减缓, 但是在烧蚀开始后会加快烧蚀的速度;
3) 烧蚀深度随着激光能量密度的增加而增加, 烧蚀深度产生差异最大的时候主要集中在激光的FWHM内, 飞秒激光烧蚀的热影响区域较小, 且热影响区域的大小受激光能量密度的影响较小;
4) 通过计算结果与实验结果的对比可知, 基于双相延迟模型的飞秒激光烧蚀模型能有效地对飞秒激光烧蚀过程进行模拟.