摘要:为了探索Al_xCrFeNiTi系高熵合金组成成分和弹性性质的关系, 结合固溶体特征参数和第一性原理计算, 研究Al元素含量对Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)合金结构和弹性性质的影响, 并分析合金固溶体特征参数与弹性性质之间的关系. 结果表明: Al_xCrFeNiTi系合金的价电子浓度随着Al含量的增加逐渐减小, 合金在体心立方结构下的形成焓均低于面心立方结构, 说明研究的Al_xCrFeNiTi系合金会形成单一的体心立方结构固溶体; 合金的晶格常数和形成能力强弱随着Al含量的增加而增大, 但合金的结构稳定性略有下降; 当合金元素按照等原子比进行成分配比时, 合金的原子尺寸差异最大; Al_xCrFeNiTi系合金中不同原子之间除了金属键结合外, 还表现出一定的共价和离子键结合特征; 对于Al_xCrFeNiTi系合金而言, 随着热力学熵焓比的增大, 合金体弹模量和韧性随之增大; 随着合金混合焓的增加, 合金在压缩方向的各向异性程度明显降低. 热力学熵焓比和混合焓可作为Al_xCrFeNiTi系高熵合金成分设计的重要参数.
关键词: Al_xCrFeNiTi系高熵合金/
第一性原理计算/
固溶体特征参数/
弹性性质

English Abstract

全文HTML

--> --> -->

一般地, 将五种及五种以上金属元素以等摩尔比或近摩尔比混合得到的合金称为高熵合金^[1-3]. 高熵合金通常为体心立方(body centered cubic, BCC)或面心立方(face centered cubic, FCC)结构的固溶体, 一般认为高熵效应是形成这种独特固溶体结构的主要原因^[2]. 基于这样的固溶体结构, 高熵合金具有传统合金不能比拟的高硬度、高强度、耐腐蚀性、耐磨性和电磁性等综合性质^[4,5]. 目前对于高熵合金的研究多数集中在含AlCrFeNi元素的体系, 并通过添加不同的合金元素对合金的性能进行调控, 以获得具有不同特性的高熵合金体系, 如高耐磨的AlCo_1.5CrFeNi_1.5Ti合金^[6]、高强的AlCoCrFeNiV合金^[7]以及抗高温氧化的AlCrFeMn_0.5NiTi合金^[8]体系等. 研究表明, 高熵合金的结构和性能与合金成分有着密切的联系. 刘瑞文^[9]研究了Al元素对Al_xCoCrFeNiTi_0.5高熵合金结构和性能的影响, 发现随着Al元素的增加, 合金的相结构由FCC固溶体逐渐向BCC固溶体转变, 并且合金的硬度逐渐增加.
对高熵合金成分的表征一般通过合金的固溶体特征参数进行描述, 并结合统计方法进行结构预测. 原子尺寸差$\delta $和热力学熵焓比$\varOmega$通常被用于预测多组元合金分别形成无序固溶体、有序固溶体、金属间化合物和块状非晶时所处的参数区域^[10]. 研究发现当合金的固溶体特征参数在$\delta $ ≤ 6.6%和$\varOmega $ ≥ 1.1时最易形成稳定的固溶体. 同时, 多主元合金的价电子浓度(valance electron concentration, VEC)在预测高熵合金形成单一BCC、单一FCC或BCC+FCC的混合结构上起到很好的效果. 高熵合金的结构稳定性和弹性性质通常采用基于密度泛函理论(density functional theory, DFT)的第一性原理计算进行研究. 对单相TiZrNbMoV_x (x = 0—1.5)高熵合金的弹性性质的第一性原理计算表明^[11], 当合金的VEC在4.72左右时, 该合金具有最优弹性各向异性性质. 尽管在理论上已经有这些对高熵合金结构和弹性性质的研究, 但成分和性能之间的直接关系对于高熵合金体系设计而言仍是需关注的重点.
为了探索高熵合金的组成成分和弹性性质之间的关系, 本文选择Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)系列单相的合金体系进行研究. 该新型无Co的合金体系既包含了高熵合金最常采用的合金元素, 又满足了降低高熵合金成本的设计原则. 合金的组成成分采用固溶体特征参数进行表征, 理论的弹性性质通过第一性原理计算获得. 本文首先研究Al含量变化对合金结构和弹性性质的影响, 最后深入探讨固溶体特征参数与弹性性质之间的关系, 为更好地进行高熵合金体系设计提供理论参考.

2

-->

2.1.固溶体特征参数计算

为了表征不同Al元素含量下Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)合金的组成成分, 引入原子尺寸差异$\delta $、混合焓$ \Delta H_{\rm mix}$、VEC和热力学熵焓比$\varOmega $ 这四个固溶体特征参数. 其中, 原子尺寸差异$\delta $与置换固溶体的形成有关, 计算式为^[12]

$\delta = 100\sqrt {\sum\limits_{i = 1}^n {c_i}{{{(1 - {r_i}/\bar r)}^2}} } , \;\; \bar r = \sum\limits_{i = 1}^n {{c_i}{r_i}} , $

式中, c_i是第i个元素的原子百分比, r_i是该原子的半径. 通常来说, 稳定的置换固溶体的原子尺寸差异$\delta $在1—6之间. 混合焓$ \Delta H_{\rm mix}$是另一个影响固溶体形成的重要参数, 当混合焓的值在$ -0.17$ ≤ $\Delta H_{\rm mix}$ ≤ 0.1 eV区间时^[10], 高熵合金将形成稳定的固溶体结构. 混合焓的计算式为^[13]

$\Delta {H_{{\rm{mix}}}} = \sum\limits_{i = 1,i \ne j}^n {4\varDelta _{{\rm{mix}}}^{AB}{c_i}{c_j}} ,$

其中$\varDelta _{{\rm{mix}}}^{AB}$表示二元合金AB的混合焓, 通过第一性原理计算得出. VEC理论适用于大多数高熵合金, 主要原理是通过描述原子的堆叠特征来判断高熵合金形成的结构, 其计算公式为^[14]

$VEC = \sum\limits_{i = 1}^n {{c_i}{{(VEC)}_i}} , $

其中( VEC )_i表示第i个元素的VEC. 热力学熵焓比$\varOmega $是一个结合热力学熵和焓的复合固溶体特征参数, 其表达式为^[10]

$\begin{split} & \Delta {S_{{\rm{conf}}}} = {k_{\rm{B}}}\ln \omega = - R\sum\limits_{i = 1}^n {({c_i}\ln {c_i})} , \\ & {T_{\rm{m}}} = \sum\limits_{i = 1}^n {{c_i}{{({T_{\rm{m}}})}_i}} , \; \varOmega = \frac{{{T_{\rm{m}}}\Delta {S_{{\rm{conf}}}}}}{{\left| {\Delta {H_{{\rm{mix}}}}} \right|}} , \end{split}$

式中, $\Delta S_{\rm conf}$为固溶体形成时的混合熵, T_m为合金的熔点, $\Delta H_{\rm mix} $是由(2)式所计算的合金的混合焓. 本文对Al_xCrFeNiTi系合金固溶体参数的计算所用到的相关元素的物理参数如表1所列.

元素	原子半径/?	VEC	熔点Tm/℃
Al	1.432	3	660.2
Cr	1.249	6	1857
Fe	1.241	8	1535
Ni	1.246	10	1453
Ti	1.462	4	1660

表1Al_xCrFeNiTi系合金中元素的物理参数^[15]
Table1.Physical parameters of alloying elements in Al_xCrFeNiTi alloys^[15].

2 -->

2.2.第一性原理计算

为了研究Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)高熵合金的结构稳定性和弹性性质, 本文采用基于DFT的第一性原理对Al_xCrFeNiTi系高熵合金进行研究. Al_xCrFeNiTi系合金的晶体结构在基于BCC和FCC结构的超晶胞上建立, 其中所有原子进行随机占位, 并且满足最邻近原子不能为同类型原子的原则^[8]. 合金元素的电子和离子之间的相互作用采用超软贋势进行描述, 电子交换关联函数采用广义梯度近似中的Perdew-Burke-Ernzerhof形式^[16]. 对建立的BCC结构的Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)合金, DFT计算中所使用的k点分别设置为9 × 9 × 4, 8 × 8 × 1, 9 × 9 × 2, 9 × 9 × 3, 9 × 9 × 1和8 × 8 × 2; 对建立的FCC结构的Al_xCrFeNiTi合金, k点分别设置为7 × 6 × 7, 6 × 8 × 1, 7 × 7 × 1, 6 × 6 × 3, 7 × 6 × 1和6 × 8 × 3. 为了兼顾精度和计算速度, 将平面波截断能设置为400 eV. 第一性原理自洽计算的收敛条件为: 每个原子上的力低于0.01 eV/?, 公差偏移小于5.0 × 10^?4 ?, 最大压力小于0.02 GPa和总能量小于5.0 × 10^?6 eV/atom.
材料的多晶体弹性性质, 包括体弹模量B、剪切模量G、杨氏模量E和泊松比$\nu $, 可以根据Voigt-Reuss-Hill (V-R-H)近似结合第一性原理计算获得的弹性常数进行预测, 计算公式分别为^[17]

$\begin{split}& B = \frac{{B_{\rm{V}} + {B_{\rm{R}}}}}{2} , \; G = \frac{{{G_{\rm{V}}} + {G_{\rm{R}}}}}{2}, \\ & E = \frac{{9BG}}{{3B + G}}, \; \nu = \frac{{3B - E}}{{6B}} ,\end{split}$

其中多晶体体弹模量B和剪切模量G分别是根据Voigt和Reuss模型获得的模量的算数平均值. 体弹模量B和剪切模量G的计算公式分别为^[17]

$\begin{split}& B_{\rm{V}}^{} = \frac{1}{9}({C_{11}} + {C_{22}} + {C_{33}}) + \frac{2}{9}({C_{12}} + {C_{13}} + {C_{23}}),\\& {B_{\rm{R}}} = \frac{1}{{({S_{11}} + {S_{22}} + {S_{33}}) + 2({S_{12}} + {S_{13}} + {S_{23}})}},\\& {G_{\rm{V}}} = \frac{1}{{15}}({C_{11}} + {C_{22}} + {C_{33}} - {C_{12}} - {C_{13}} - {C_{23}}) + \frac{1}{5}({C_{44}} + {C_{55}} + {C_{66}}),\\& {G_{\rm{R}}} = \frac{{15}}{{4({S_{11}} + {S_{22}} + {S_{33}}) - 4({S_{12}} + {S_{13}} + {S_{23}}) + 3({S_{44}} + {S_{55}} + {S_{66}})}},\end{split}$

其中C_ij代表材料的单晶弹性常数; S_ij为弹性柔度, 是弹性矩阵C_ij的逆矩阵.
材料的弹性各向异性是一个重要的弹性性质. 基于Voigt和Reuss模型获得的弹性模量, 在压缩方向上的各向异性A_B和剪切方向上各向异性的A_G通常被应用于研究材料的弹性各向异性, 计算式分别为^[18]

${A_B} = \frac{{{B_{\rm{V}}} - {B_{\rm{R}}}}}{{{B_{\rm{V}}} + {B_{\rm{R}}}}}, \; {A_G} = \frac{{{G_{\rm{V}}} - {G_{\rm{R}}}}}{{{G_{\rm{V}}} + {G_{\rm{R}}}}}.$

A_B和A_G的值能够描述合金的弹性各向异性性质, 值越大表明合金在该方向上的各向异性程度越大. 当A_B和A_G的值为0%时, 结构表现为各向同性特征; 而当A_B和A_G的值达到100%时就意味着合金的各向异性特征最大.

2

-->

3.1.Al含量对Al_xCrFeNiTi合金结构的影响

根据经典的多组元合金的VEC理论^[15], 不同的晶体结构有不同的VEC特征, 当VEC < 6.87时形成单一的BCC结构固溶体; 当VEC ≥ 8.00时形成单一的FCC结构固溶体; 在6.87 ≤ VEC < 8.00时形成BCC和FCC结构的混合固溶体. 不同Al元素含量下Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)高熵合金的VEC如图1所示. 除了x = 0时的CrFeNiTi四元合金的VEC略高于6.78外, 其余Al_xCrFeNiTi (x = 0.5, 1, 2, 3, 4)五种合金的VEC均小于6.87, 说明当Al含量的原子百分比为11.11 at.%, 20 at.%, 33.33 at.%, 42.86 at.%和50 at.%时, Al_xCrFeNiTi系合金有可能形成单一BCC结构的固溶体. 此外, 从能量角度描述合金形成不同结构的能力强弱可以通过形成焓H_f进行表征, A_nB_m合金形成焓的计算式为^[19]
图 1 Al含量对Al_xCrFeNiTi系合金的VEC、形成焓和结构的影响, 其中当x = 0, 0.5, 1, 2, 3, 4时, 分别对应Al含量的原子百分比为0, 11.11 at.%, 20 at.%, 33.33 at.%, 42.86 at.%, 50 at.%
Figure1. Effect of Al contents on valence electron concentration, formation enthalpy and structure of Al_xCrFeNiTi alloys. When x = 0, 0.5, 1, 2, 3, 4, the atomic percentages corresponding to Al content are 0, 11.11 at.%, 20 at.%, 33.33 at.%, 42.86 at.%, 50 at.% respectively.

${H_{\rm{f}}} = \frac{{{E_{{\rm{tot}}}} - nE_{{\rm{solid}}}^A - mE_{{\rm{solid}}}^B}}{{n + m}}, $

式中E_tot是单相Al_xCrFeNiTi系合金经晶格优化后得到的平衡结构的总能量, n和m分别是不同合金元素在结构中对应的原子数目, $E_{{\rm{solid}}}^X$是X元素在其初始平衡结构下的能量.
形成焓的数值代表化合物形成前后的能量差异, 拥有更低负值的形成焓的合金晶体结构更容易形成. 采用Broyden-Fletcher-Goldfarb-Shanno方法^[20]对建立的BCC和FCC结构的Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)合金进行晶格结构优化, 获得BCC和FCC结构下Al_xCrFeNiTi系合金的平衡结构, 并根据(8)式计算得到不同Al含量下Al_xCrFeNiTi系合金形成不同结构的形成焓, 结果如图1所示. 可以看出, 在相同的Al含量下, BCC结构Al_xCrFeNiTi合金的形成焓均低于FCC结构下的合金, 这说明从能量角度上分析, 相对于FCC结构, 合金形成BCC结构固溶体所需能量更少, 由此可以推断, BCC结构为Al_xCrFeNiTi系合金优先形成的结构. 另外, 随着Al含量的增加, Al_xCrFeNiTi系合金的形成焓明显下降, 说明合金的形成能力随着Al含量的增加而增强. 与此同时, 由图1可以发现, Al_xCrFeNiTi系合金的VEC随着Al含量的增大也逐渐下降. 固溶体的VEC值越低, 说明合金越易于形成低原子堆垛特征的结构, 即BCC结构, 这是因为这种原子堆垛方式的能量更稳定^[14]. 这与形成焓的计算结果相符合.
VEC理论和形成焓计算结果对Al_xCrFeNiTi (x = 0.5, 1, 2, 3, 4)这五种合金形成结构倾向性的结论完全符合, 但对于四元CrFeNiTi合金, 由于其区别于传统意义上的五元及以上的高熵合金, 虽然其VEC略高于判据中的6.87, 但根据有关四元等摩尔比合金的文献报道^[21]以及形成焓计算可知, 四元CrFeNiTi合金同样形成单一的BCC结构固溶体. 因此, 结合VEC理论和形成焓计算结果, 可以预测Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)合金的晶体结构均为单相的BCC结构. 本文其余有关第一性原理的计算, 包括晶格常数、电子结构和弹性性质等, 对Al_xCrFeNiTi系合金的研究均基于BCC结构.
图2为Al含量对Al_xCrFeNiTi系合金平衡结构下晶格常数和原子尺寸差异的影响. 由于所研究的Al_xCrFeNiTi系合金的晶体结构是基于BCC结构上建立的超晶胞, 在计算充分弛豫后, 组成超晶胞的各个独立的单胞具有相似的晶格常数a, b和c. 为了便于与实验数据进行对比, 采用晶格常数的算术平均数a_avg对Al_xCrFeNiTi系合金的晶格参数进行描述, 计算公式为^[8]
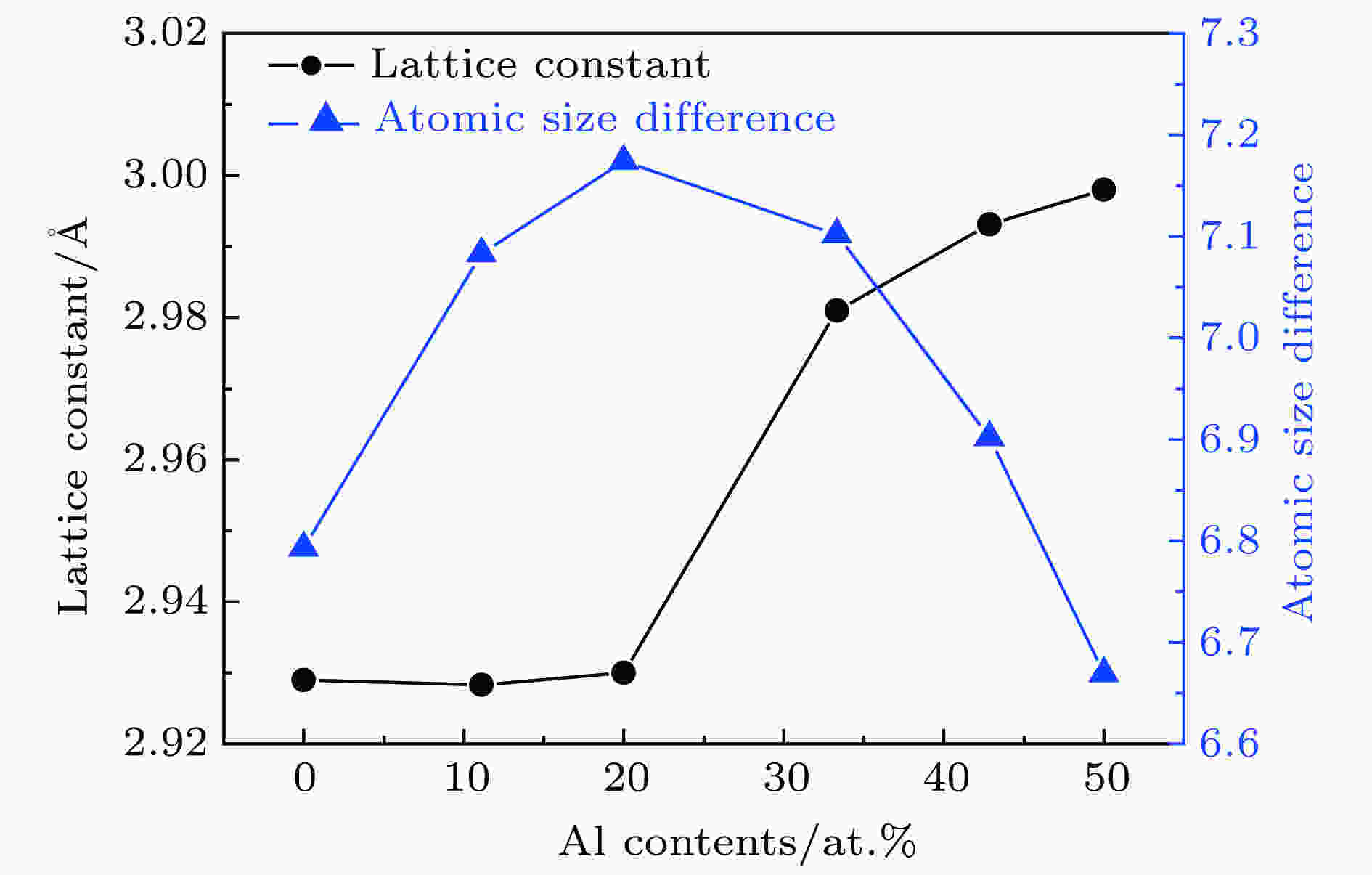图 2 Al含量对Al_xCrFeNiTi系合金的晶格常数和原子尺寸差异的影响
Figure2. Effect of Al contents on lattice constant and atomic size difference of Al_xCrFeNiTi alloys.

${a_{{\rm{avg}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{1}{3}({a_i} + {b_i} + {c_i})} , $

式中a_i, b_i, c_i, 分别表示结构优化后超晶胞中第i个单胞的晶格常数; n是超晶胞中单胞的数目. 根据含AlCrFeNi元素高熵合金的相关文献^[1-5], 形成稳定BCC结构时合金的晶格常数约为2.92 ?. 由图2的晶格常数曲线可知, 当Al元素的原子百分比为0, 11.11%和20%时, Al_xCrFeNiTi (x = 0, 0.5, 1)合金的晶格常数在2.92 ?附近, 形成的BCC结构固溶体更为稳定; 当Al元素的原子百分比为33.33%, 42.86%和50%时, Al_xCrFeNiTi (x = 2, 3, 4)合金的晶格常数在2.98—3.00 ?之间. 这是由于Al元素的原子半径较大, Al元素在合金体系中的比重增大使得Al_xCrFeNiTi系合金的晶格参数明显增大.
从图2中原子尺寸差异$\delta $的曲线可以看出, 虽然合金的晶格常数随着Al含量增大逐渐增加, 但表征晶格畸变程度的原子尺寸差异并非持续增大. 当Al元素原子百分比含量低于20 at.%时, 随着大原子半径的Al元素的增加, 合金的原子尺寸差异逐渐增大; 当Al元素的含量超过20 at.%时, 此时随着Al含量的增加, 合金的原子尺寸差异却逐渐减小; 当Al_xCrFeNiTi系合金中各元素的配比为等摩尔比时, 即合金为AlCrFeNiTi时, 合金的原子尺寸差异到达最大. 这是由于初始较大原子半径的Al原子的加入提高了CrFeNiTi四元合金的晶格畸变程度, 但随着Al元素含量在合金中的比重增加, 使得合金趋向于形成以Al为基体的固溶体, 因此转而使合金的原子尺寸差异即晶格畸变降低.
为了研究Al_xCrFeNiTi系合金的结构稳定性来源, 计算了CrFeNiTi合金、Al₂CrFeNiTi合金和Al₄CrFeNiTi合金在平衡结构下的总态密度, 结果如图3所示. 费米能级处(0 eV)较高的态密度值说明了这三种合金均表现出明显的金属特征. 随着合金体系中Al元素含量的不断增加, 合金的总态密度在低能级处的峰位(?72, ?57, ?44和?24 eV附近)向高能级方向移动, 同时, 总态密度在高能级处(费米能级附近)呈现同样的规律, 说明随着Al含量增加, Al_xCrFeNiTi系合金晶体结构的稳定性有所下降.
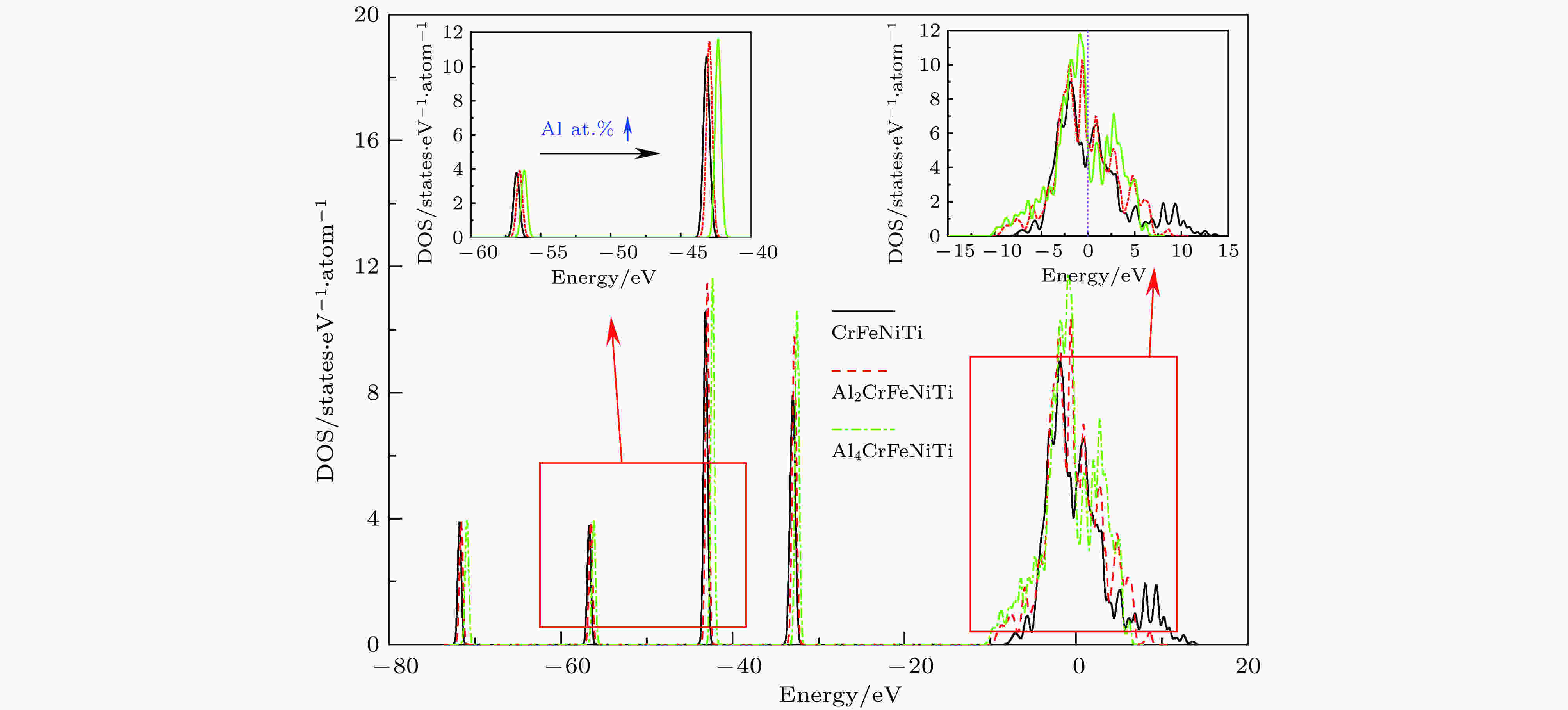图 3 CrFeNiTi, Al₂CrFeNiTi和Al₄CrFeNiTi合金的总态密度
Figure3. Density of states (DOS) of CrFeNiTi, Al₂CrFeNiTi and Al₄CrFeNiTi alloys.

除了分析总态密度的变化趋势之外, 合金的结构稳定性还可以通过计算合金在平衡结构下的结合能E_c进行定性描述. 结合能E_c反映了晶体被分解为单个原子所需要的能量, A_nB_m合金结合能的计算公式为^[19]

${E_{\rm{c}}} = \frac{{{E_{{\rm{tot}}}} - nE_{{\rm{atom}}}^A - mE_{{\rm{atom}}}^B}}{{n + m}}, $

其中E_tot是合金在平衡结构下的总能量, n和m分别是不同合金元素在结构中对应的原子数目, $E_{{\rm{atom}}}^X$是孤立X原子的能量. 更低的结合能E_c说明分解该晶体结构需要更大的能量, 此时该晶体结构的稳定性更高. 计算获得的Al_xCrFeNiTi (x = 0, 0.5, 1, 2, 3, 4)合金在平衡结构下E_c分别为?5.64, ?5.48, ?5.31, ?5.18, ?5.04和?4.96 eV/atom, 说明随着Al含量增加, Al_xCrFeNiTi合金的结合能不断升高, 分解合金结构所需能量减小, 合金的结构稳定性逐渐下降. 这与态密度的分析结果完全一致.
差分电荷密度和原子布居数能够描述合金键合之后原子电荷分布的变化情况, 可以用来研究不同元素对合金中成键的贡献. 以Al₂CrFeNiTi合金作为例子, 图4(a)为选取的包含所有组成原子的部分(110)截面上的差分电荷密度分布图. 原子之间电荷密度的明显增加说明成键后合金内形成离域的价电子云, 这是原子间形成金属键结合的显著特点. 此外, Fe和Ni原子在得电子区域以及Al和Ti原子在失电子区域均表现出一定的方向性, 说明这些原子的键合可能具有离子结合的特征; 而Cr-Cr原子之间存在一定共价键特征的差分电荷密度分布. 图4(b)为BCC结构的Al_xCrFeNiTi系合金在平衡结构下不同元素的原子布居数分析结果. 由于在计算过程中同种元素的每一个原子都具有极其相似的得失电子的能力, 因此在图4(b)中不同元素的原子布居数是该种元素所有原子的原子布居数的平均值. 当原子布居数的平均值为正时, 意味着该元素在键合之后失去电子, 而布居数为负值则意味着得到电子; 更小的负值(或更大的正值)说明该元素具有更强的得(失)电子的能力^[22]. 由图4(b)可知, Al原子和Ti原子在成键后均是失去电子, 而Ni原子和Fe原子均得到电子. Cr原子除了在四元CrFeNiTi合金时失去电子, 在其余Al_xCrFeNiTi (x = 0.5, 1, 2, 3, 4)合金中均得到电子. 价电子主要从Al原子和Ti原子的s轨道上转移到了Cr原子、Ni原子和Fe原子上, 并且Ti原子展现出比Al原子更强的失电子的能力. 随Al元素含量的增加, Cr和Ni原子得电子能力呈现出增强的趋势, 而Fe原子基本保持不变. 另外, 除四元CrFeNiTi合金以外, 其余合金中Fe元素与Ti元素的布居数随Al元素含量变化的曲线上呈一定的对称分布特征, 可以推测Ti原子失去的电子有可能主要迁移到Fe原子上. 在合金中存在元素电荷迁移现象意味着有不同元素原子之间存在一定的离子键作用力, 这有利于合金形成稳定的结构. 结合差分电荷密度和原子布居数分析, 在Al_xCrFeNiTi系合金中原子之间的键和作用既有金属键结合作用又存在一定的共价和离子键结合作用, 这样的多种键合相互作用, 使得合金具有较好的结构稳定性.
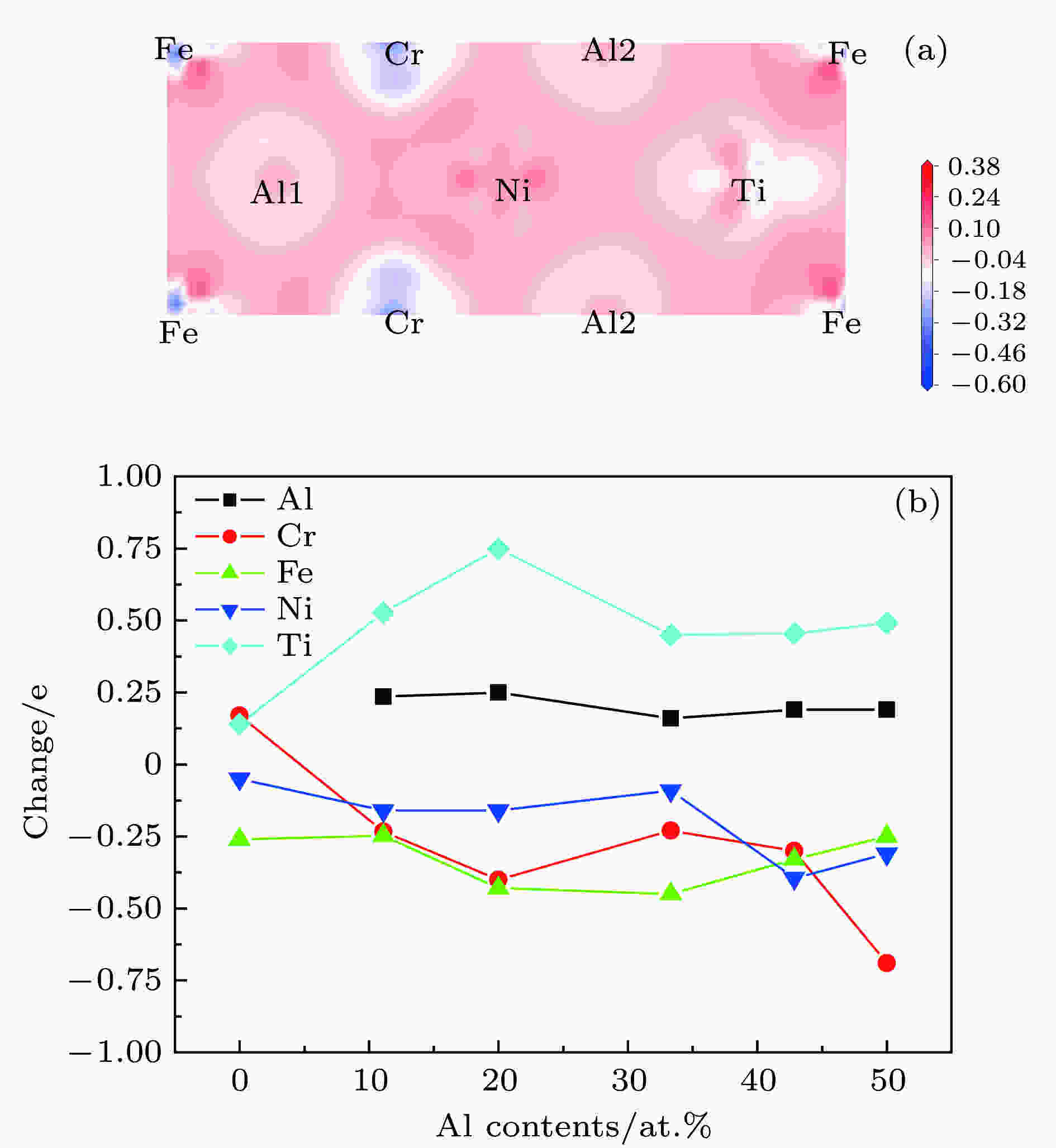图 4 Al_xCrFeNiTi系合金的电荷分布　(a) Al₂CrFeNiTi在(110)面的差分电荷密度; (b) Al_xCrFeNiTi系合金的原子布居数
Figure4. Charge distribution of Al_xCrFeNiTi alloys: (a) Electron density difference map on (110) plane for Al₂CrFeNiTi; (b) the atomic Mulliken population of Al_xCrFeNiTi alloys.

2 -->

3.2.Al含量对Al_xCrFeNiTi合金弹性性质的影响

材料的弹性常数是直观表述材料弹性性质的重要参数, 反映了晶体结构的力学稳定性, 对研究合金的弹性性质如弹性模量和弹性各向异性等具有重要意义. 表2为通过第一性原理计算获得的不同Al含量下Al_xCrFeNiTi系合金的弹性常数C_ij.

合金	弹性常数Cij/GPa
	C11	C12	C13	C22	C23	C33	C44	C55	C66
CrFeNiTi	276.1	158.8	158.8	276.1	158.8	274.4	46.1	46.1	95.0
Al0.5CrFeNiTi	233.3	173.6	136.1	233.3	136.1	246.5	87.1	87.1	102.9
AlCrFeNiTi	198.1	139.3	139.3	198.1	139.3	218.1	90.3	90.3	91.5
Al2CrFeNiTi	158.3	118.4	118.4	158.3	118.4	245.8	75.7	75.7	80.7
Al3CrFeNiTi	191.6	124.9	130.4	191.6	130.4	148.2	104.6	104.6	77.3
Al4CrFeNiTi	213.4	91.6	91.6	213.4	91.6	207.1	99.8	99.8	106.9

表2不同Al含量下Al_xCrFeNiTi系合金的弹性常数C_ij
Table2.Elastic constant C_ij (in GPa) of Al_xCrFeNiTi alloys with different Al contents.

合金的机械稳定性可通过弹性常数进行判断. 对于本文研究的基于BCC结构下的Al_xCrFeNiTi系合金, 基态下(0 K, 0 GPa)机械稳定性判据为^[23]

$\begin{split}& {C_{ij}} > 0;\;{C_{11}}{\rm{ + }}{C_{22}} > 2{C_{12}};\;{C_{11}}{\rm{ + }}{C_{33}} > 2{C_{13}}; \\ & {C_{22}}+{C_{33}} > 2{C_{23}};\\& {C_{11}}+{C_{22}} + {C_{33}} + 2{C_{12}} + 2{C_{13}} + 2{C_{23}} > 0.\end{split}$

结合表2中获得的Al_xCrFeNiTi系合金的弹性常数, 可知所有数据均满足弹性稳定性判据, 说明Al_xCrFeNiTi系合金在基态下均具有良好的机械稳定性, 同样说明了Al_xCrFeNiTi系合金具有稳定的晶体结构.
为了预测Al_xCrFeNiTi系合金的弹性性质, 采用(5)和(6)式中的 V-R-H近似方法, 计算得到了多晶体Al_xCrFeNiTi系合金的弹性常数, 结果如图5所示. 体弹模量B反映晶体在外部压力下抵抗体积变形的能力, 剪切模量G是晶体在剪切应力下抵抗可逆变形的度量, 杨氏模量E是表征晶体在弹性极限内抗压或抗拉的物理量^[23]. 从图5可以看出, 合金的体弹模量B分布在130—200 GPa之间, 剪切模量G大小从50到80 GPa, 杨氏模量E在130—240 GPa之间. 随着Al_xCrFeNiTi系合金中Al含量的增多, 合金的体弹模量B整体呈下降趋势, CrFeNiTi的体弹模量B最大; 剪切模量G整体变化不大, Al₄CrFeNiTi的剪切模量G最大; 杨氏模量E呈先升高后下降最后上升的趋势, Al₄CrFeNiTi的杨氏模量E最大. 因此, Al含量的增加使得Al_xCrFeNiTi合金抵抗体积变形的能力逐渐减弱, 而抵抗可逆变形以及在弹性范围内抗压的能力有所提高.
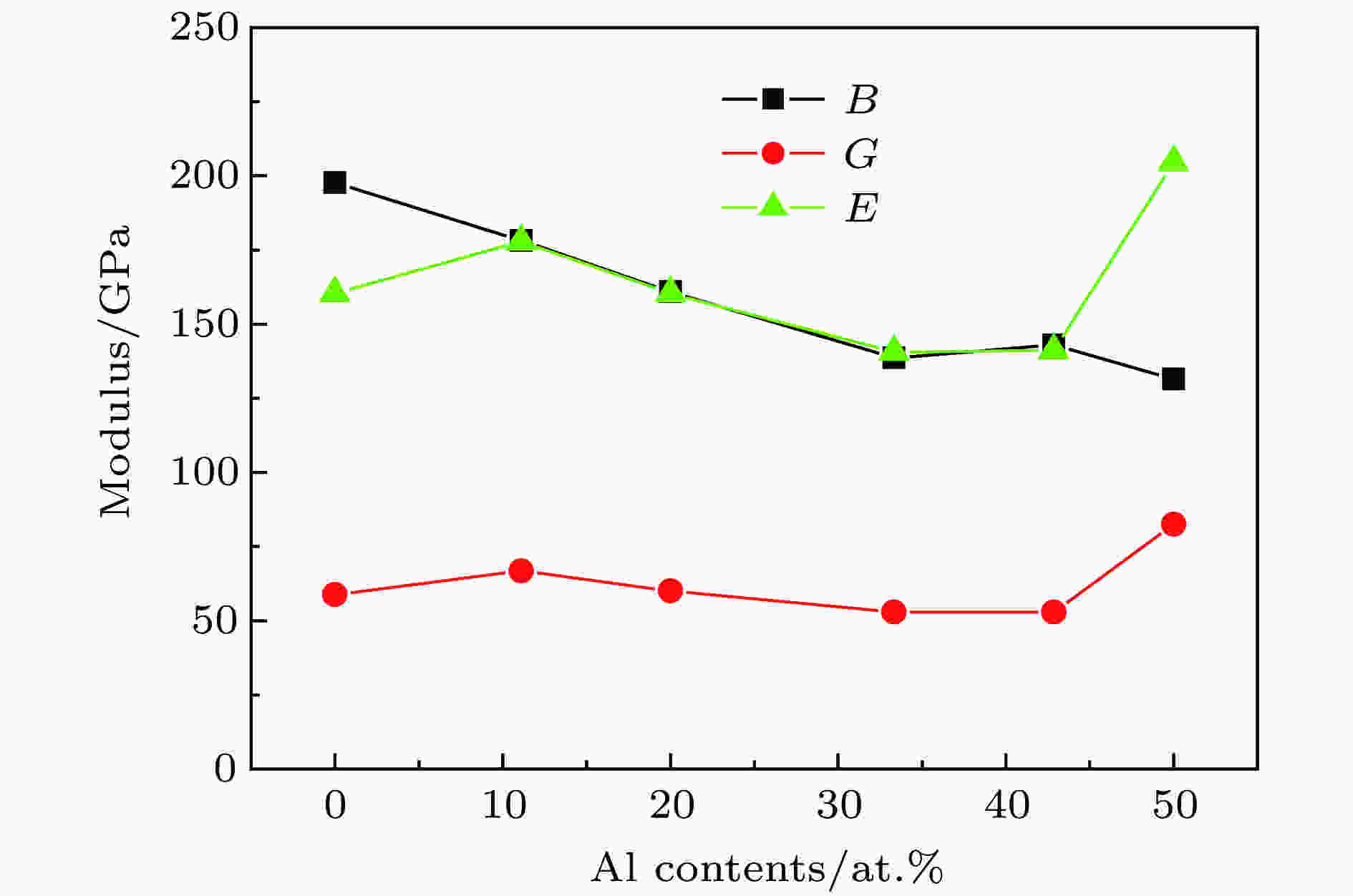图 5 Al含量对Al_xCrFeNiTi系合金弹性模量的影响
Figure5. The effect of Al contents on elastic constants Al_xCrFeNiTi alloys.

脆韧性是材料一个非常重要的性质, 用来描述材料在断裂前吸收能量和进行塑性变形的能力, 通常综合使用体弹模量和剪切模量的比值B/G、泊松比$\nu $和(${C_{12}}-{C_{44}} $)这三个参数对合金的脆韧性进行预测. 当合金同时满足B/G > 1.75, $\nu $ > 0.26和(${C_{12}}-{C_{44}}$) > 0时, 合金表现出韧性特征, 否则呈脆性^[24]. 图6为Al含量对Al_xCrFeNiTi系合金的B/G、泊松比$\nu $和($ {C_{12}}-{C_{44}}$)的影响. 除了Al₄CrFeNiTi呈现脆性(其中, B/G大约为1.5, 泊松比$\nu $约为2.3, (${C_{12}}-{C_{44}}$)为?18 GPa)外, 其余的CrFeNiTi, Al_0.5CrFeNiTi, Al₁CrFeNiTi, Al₂CrFeNiTi和Al₃CrFeNiTi合金均表现明显的韧性特征. 并且随着Al含量的增加, 这三个参数均呈缓慢下降趋势, 其中B/G曲线和泊松比$\nu $曲线变化一致. 在Al_xCrFeNiTi系合金中CrFeNiTi合金的B/G、泊松比$\nu $和($ {C_{12}}-{C_{44}}$)均为最大, 说明CrFeNiTi合金的韧性最好, Al_xCrFeNiTi系合金的韧性随着Al含量的增加而降低, 而当Al的原子百分比含量增大至50%时, 合金由韧性转变为脆性.
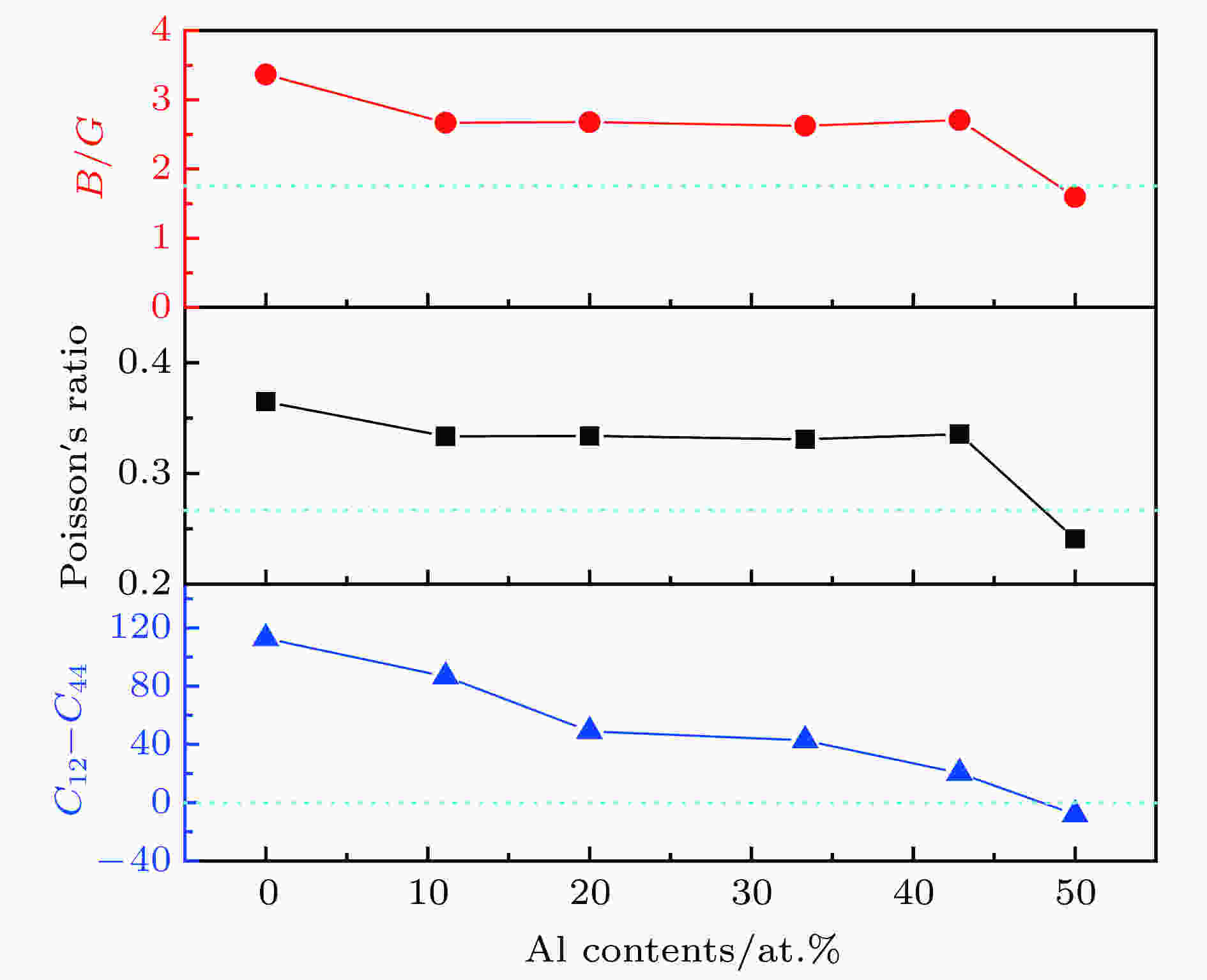图 6 Al含量对Al_xCrFeNiTi系合金的B/G、泊松比$\nu $和(C₁₂?C₄₄)的影响
Figure6. Effect of Al contents on B/G, Poisson’s ratio $\nu $ and (C₁₂?C₄₄ ) of Al_xCrFeNiTi alloys.

2 -->

3.3.Al_xCrFeNiTi系合金固溶体特征参数与弹性性质的关系

高熵合金组成成分和弹性性质之间的关系是高熵合金体系成分设计所关注的重点, 结合研究获得的Al含量对Al_xCrFeNiTi系合金弹性性质的影响, 通过固溶体特征参数对合金的组成成分进行表征, 并作为横坐标, 以计算获得的合金弹性性质作为纵坐标, 探索Al_xCrFeNiTi系合金成分和弹性性质的关系. 图7为Al_xCrFeNiTi系合金固溶体特征参数和弹性性质之间的关系. 从图7(a)可以看出, 剪切模量G、杨氏模量E与热力学熵焓比$\varOmega $ 虽然没有明显的关系, 但体弹模量B和B/G都随着热力学熵焓比$\varOmega $的升高呈上升趋势. 这说明通过调整元素成分改变Al_xCrFeNiTi系合金的热力学熵焓比$\varOmega $, 可以控制合金抵抗压缩时体积变形和韧脆性的能力. 当提高合金的热力学熵焓比$\varOmega $时, 合金将获得更好的抵抗压缩时体积变形和韧性的能力. 对于合金的弹性各向异性而言, 仅存在与混合焓$\Delta H_{\rm mix}$有明显的关系, 如图7(b)所示. 在压缩方向上的各向异性程度A_B随着混合焓$\Delta H_{\rm mix}$的增加而下降, 这说明若想在压缩方向上获得各向同性特性较好的Al_xCrFeNiTi系合金, 可以通过改变成分提高合金的混合焓$\Delta H_{\rm mix}$来实现.
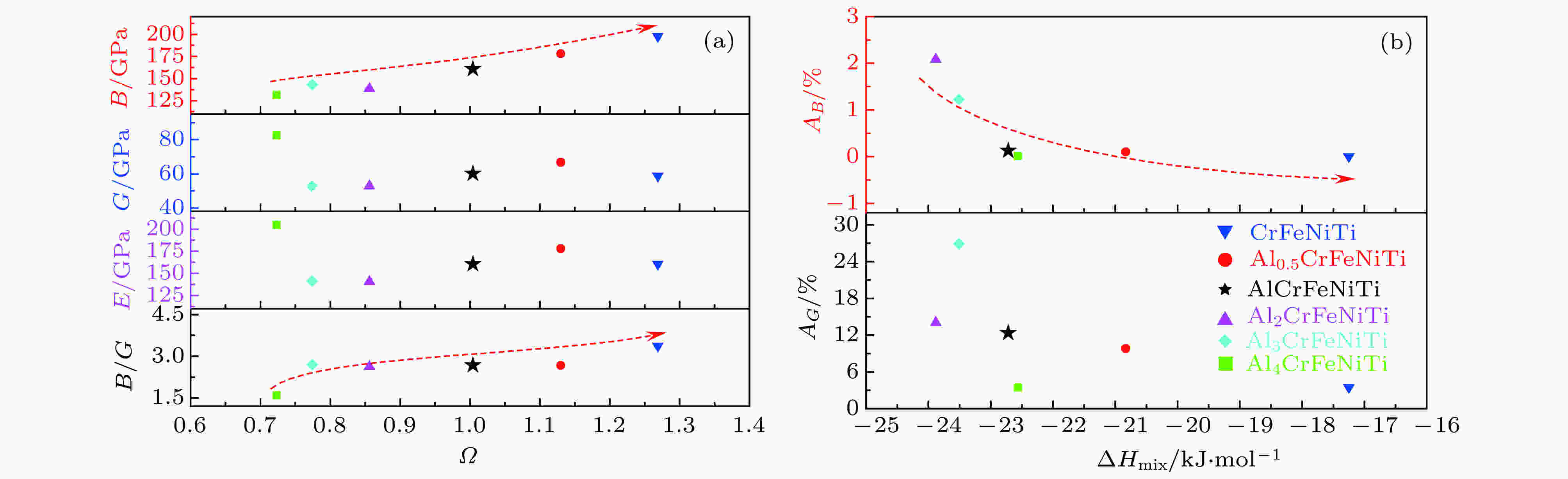图 7 Al_xCrFeNiTi系合金固溶体特征参数和弹性性质之间的关系　(a) 热力学熵焓比$\varOmega $与B, G, E, B/G的关系; (b) 混合焓$ \Delta H_{\rm mix}$与A_G, A_B的关系
Figure7. Correlativity between solid solution characteristics and elastic properties of Al_xCrFeNiTi alloys: (a) Ratio of thermodynamic entropy to enthalpy and B, G, E, B/G; (b) formation entahlpy $ \Delta H_{\rm mix}$ and A_G, A_B.

为了进一步验证Al_xCrFeNiTi系合金弹性各向异性的性质, 根据图7(b)选取了弹性各向异性较小的CrFeNiTi和各向异性较大的Al₂CrFeNiTi的两个合金, 对其杨氏模量E在三维空间里各向异性的曲面表示进行研究, 结果如图8所示. 由于建立的Al_xCrFeNiTi系合金的晶体结构属于四方晶系晶体结构, 相应的杨氏模量E在三维空间里各向异性的曲面可以根据(12)式进行计算^[25]:
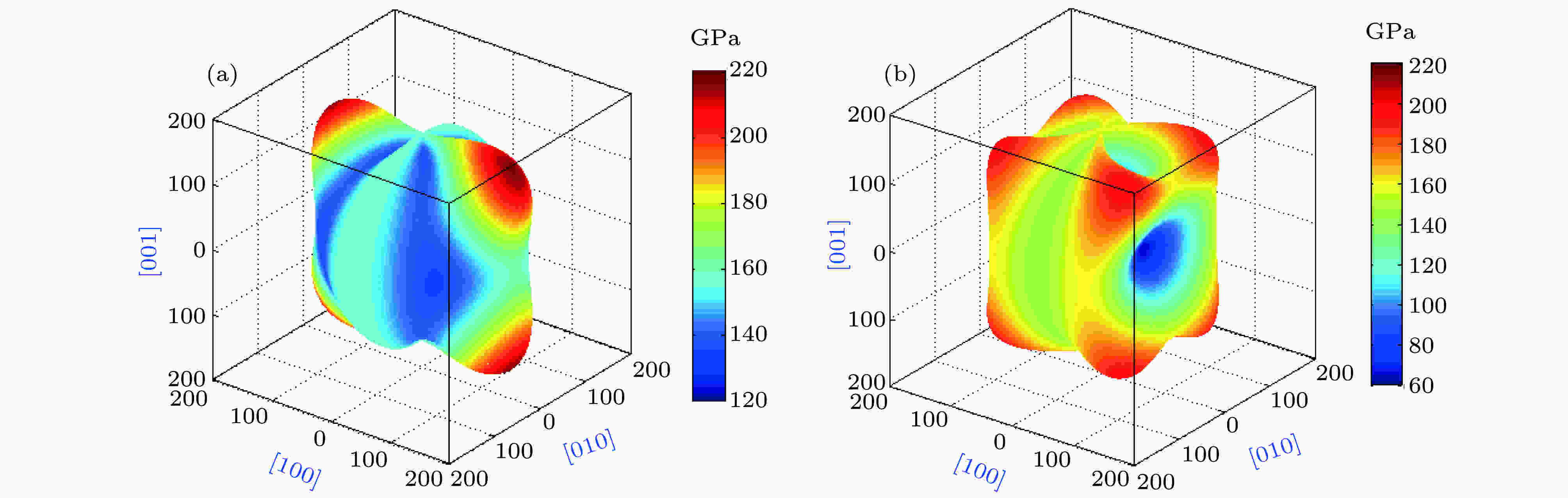图 8 合金杨氏模量E的各向异性　(a) CrFeNiTi; (b) Al₂CrFeNiTi
Figure8. Anisotropy of Young modulus E of CrFeNiTi, Al₂CrFeNiTi alloys: (a) CrFeNiTi; (b) Al₂CrFeNiTi.

$\begin{split}\frac{1}{E} = & \left[ {\left( {l_1^4 + l_2^4} \right){s_{11}} + l_3^4{s_{33}} + l_1^2l_2^2\left( {2{s_{12}} + {s_{66}}} \right)} \right.\\& \left. { + l_3^2\left( {1 - l_3^2} \right)\left( {2{s_{13}} + {s_{44}}} \right)} \right],\end{split}$

其中l₁, l₂和l₃分别是X, Y和Z轴方向上的余弦; S_ij是弹性柔度. 在三维空间上的图形越接近球形说明所研究的结构越趋近于各向同性特征, 反之表现为各向异性特征. 从图8可以看出, CrFeNiTi, Al₂CrFeNiTi合金的弹性模量三维曲面图均不是球形, 说明这两个合金都表现出一定的各向异性特征, 但CrFeNiTi合金的三维曲面图相对于Al₂CrFeNiTi合金的三维曲面图更接近球形特征, 表明Al₂CrFeNiTi合金显示了更为明显的弹性各向异性特征. 该结论与图7(b)中合金的弹性各向异性大小结论相符合. 尽管可以通过热力学熵焓比$\varOmega $和混合焓$\Delta H_{\rm mix} $对Al_xCrFeNiTi系合金的弹性性质进行设计, 但仍需要在理论和实验方面进行进一步的探索, 为高熵合金的成分设计提供参考.

1) 研究的Al_xCrFeNiTi (x = 0.5, 1, 2, 3, 4)系合金的VEC均低于6.87, 且BCC结构下的形成焓均要低于FCC结构下的形成焓, 合金将形成单一的BCC结构固溶体. 随着Al元素含量的增加, Al_xCrFeNiTi系合金的VEC逐渐降低, 但合金的形成能力不断增强; 晶格参数随着Al含量增加不断上升, 合金的原子尺寸差异(反映合金晶格畸变的程度)先上升后下降.
2) Al_xCrFeNiTi系合金的总态密度随着Al含量的增加往高能级方向移动, Al和Ti在成键后均是失去电子, 而Ni和Fe均得到电子. Al_xCrFeNiTi系合金的原子之间形成复合的键和作用.
3) 随着Al含量的增加, Al_xCrFeNiTi系合金的体弹模量B呈下降趋势而剪切模量G整体变化不大, 韧性则逐渐降低. 其中Al₄CrFeNiTi合金呈明显的脆性特征.
4) 热力学熵焓比$\varOmega $和混合焓$\Delta H_{\rm mix} $可作为Al_xCrFeNiTi系合金弹性性质预测的参数. 随着热力学熵焓比$\varOmega $的升高, 合金的体弹模量B和B/G明显升高; 随着混合焓$\Delta H_{\rm mix} $的增加, 合金在压缩方向的各向异性程度A_B逐渐下降.