删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

增材制造316钢高周疲劳性能的微观力学研究

本站小编 Free考研考试/2022-01-01


引 言


近年来, 增材制造作为一项新兴的技术已经广泛应用于功能性部件的快速成形当中. 增材制造技术相对于传统的减材制造具有“自下而上”逐层累积的特点, 是一种从无到有的制造方式. 这为过去受到传统制造方式约束而难以成形的复杂结构件的制造提供了便利, 使其在航空航天工业、能源工业以及核工业得到了广泛应用. 由于增材制造工艺过程中存在复杂的热力学过程, 这导致增材制造成形件的力学性能尤其是疲劳性能与传统制造工艺成形件存在较大的区别. 更重要的是, 增材制造工艺成形过程中的局部热历史可以直接控制, 进而可以通过控制增材制造成形件的微观结构来获得特定的宏观力学性能. 这一特点大大刺激了关于成形工艺对增材制造成形件的疲劳性能影响的研究需求[1-3]. 为此, 大量****对这一问题进行了研究. Yadollahi等[4]研究了打印方向与热处理工艺对选择性激光熔化成形不锈钢疲劳行为的影响, 他们发现制造过程中形成的缺陷以及打印方向对疲劳行为有显著的影响. Greitemeier等[5]研究了表面粗糙度对直接金属激光烧结和电子束熔化Ti-6Al-4V疲劳寿命的影响, 他们发现材料的疲劳寿命随着表面粗糙度的增加而下降. Riemer等[6]研究了选择性激光熔化成形316L不锈钢的疲劳性能, 他们分析了选择性激光熔化成形316L不锈钢的微观结构并考虑了工艺参数?微观结构?疲劳性能之间的关系. Cao等[7]对比了选择性激光熔化成形316钢和轧制316钢的疲劳性能, 发现选择性激光熔化成形316钢相较于轧制316钢具有更高的疲劳极限.

在上述工作中, 大部分****对增材制造成形件疲劳性能的研究主要考虑以下3个方面: 缺陷、微观结构和表面粗糙度. 然而对于本文研究的奥氏体316不锈钢, 相比于缺陷, 材料疲劳裂纹萌生对微观结构更加敏感[8]. Pegues等[8]发现尽管大多数增材制造成形材料在循环载荷下的失效主要是由于工艺过程中引入的缺陷造成, 然而对于激光束粉床熔化奥氏体不锈钢, 大多数导致材料失效的疲劳微裂纹周围并未出现材料缺陷. 因此他们得出激光束粉床熔化奥氏体不锈钢的疲劳裂纹萌生相较于缺陷与材料微观结构特征更相关. Gordon等[9]研究发现直接能量沉积304L不锈钢工艺过程中引入的缺陷对总体疲劳性能的影响可以忽略. 基于上述对增材制造奥氏体不锈钢疲劳裂纹萌生机理的研究, 本文将材料微观结构作为主要影响高周疲劳性能的因素而忽略缺陷对疲劳性能的影响. 另外, 由于疲劳实验件会进行表面抛光处理, 本文忽略了表面粗糙度带来的影响.

除了上述关于增材制造成形件疲劳性能的实验研究之外, 一些****提出了增材制造材料疲劳性能的预测模型. Romano等[10]使用基于缺陷的模型预测了增材制造AlSi10Mg的疲劳极限, 他们对材料的初始缺陷尺寸进行建模并通过基于断裂力学的裂纹扩展模型预测了增材制造AlSi10Mg的S-N曲线. Ebrahimi和Mohammadi[11]根据所提出的有限元模型对直接金属激光烧结Hybrid钢的疲劳寿命进行了预测, 通过使用von-Mises屈服准则、雨流法和Miner理论计算了直接金属激光烧结Hybrid钢的循环寿命. Vayssette等[12]根据轮廓测定法和断层摄影技术获得的表面扫描图像建立了有限元模型, 通过使用非局部基于Crossland准则的疲劳指数预测了选择性激光熔化Ti-6Al-4V的高周疲劳性能. 在上述工作中, 提出的疲劳模型都是基于宏观物理量建立的, 其局限性在于不能有效考虑材料微观结构对疲劳性能的影响. Przybyla和McDowell[13-14]提出了一种考虑材料微观结构的统计学有限元模型来量化微观结构对疲劳寿命的影响, 他们使用晶体塑性理论研究代表体单元的局部力学响应. Robert等[15]基于多晶有限元模型研究了几何缺陷对纯铜高周疲劳性能的影响, 发现将晶体塑性理论和介观高周疲劳准则结合可以很好地预测缺陷尺寸对疲劳性能的影响. 尽管上述工作考虑了晶粒内部位错滑移对疲劳性能的影响, 然而晶界对疲劳性能的影响这一关键因素在这些模型中仍未能得到体现. 为此, 本文使用弹塑性内聚力模型以及晶界介观高周疲劳准则考虑晶界对疲劳性能的影响. 同时, 使用晶体塑性理论和Papadopoulos疲劳准则来研究晶粒内部位错滑移对疲劳性能的影响. 因此, 本文得以将中位错滑移与晶界对疲劳性能的影响同时考虑.


1.
计算模型



1.1
晶体塑性模型


本文使用基于Huang[16]的工作, 使用唯象学晶体塑性材料用户子程序来模拟晶粒内部的力学行为. 这里采用$(alpha )$表示一个滑移系, 它对应着一个滑移面和一个滑移方向, 其中滑移面的法向量为$ {boldsymbol{l}}^{(a)} $, 滑移方向向量为$ {{boldsymbol{s}}^{(alpha )}} $. 滑移应变率$ {dot gamma ^{(alpha )}} $仅取决于分解切应力$ {tau ^{(alpha )}} $[17]







$$ {dot gamma ^{(alpha )}} = {dot a^{(alpha )}} {frac{{{tau ^{(alpha )}}}}{{{g^{(alpha )}}}}} {left| {frac{{{tau ^{(alpha )}}}}{{{g^{(alpha )}}}}}
ight|^{n - 1}} $$
(1)

其中$ {dot a^{(alpha )}} $代表参考应变率, $ {g^{(alpha )}} $代表当前滑移系的强度, n代表应变率敏感因子. 作用于滑移系$alpha $上的分解切应力$ {tau ^{(alpha )}} $可以通过应力张量${boldsymbol{sigma }}$与方向张量$ {{boldsymbol{m}}^{(alpha )}} $的乘积进行计算, 即







$$ {tau ^{(alpha )}} = {{boldsymbol{m}}^{(alpha )}}:{boldsymbol{sigma }} $$
(2)







$$ {{boldsymbol{m}}^{(alpha )}} = frac{1}{2}left( {{{boldsymbol{l}}^{(alpha )}} otimes {{boldsymbol{s}}^{(alpha )}} + {{boldsymbol{s}}^{(alpha )}} otimes {{boldsymbol{l}}^{(alpha )}}}
ight) $$
(3)

当前强度$ {g^{(alpha )}} $的演化可以通过滑移硬化模量$ {h_{alpha beta }} $进行计算. 这里分别是自硬化模量和潜硬化模量. 根据Peirce等[18]提出的硬化准则, 自硬化模量和潜硬化模量可以通过所有滑移系上的Taylor累积切应变$ gamma $进行计算, 即







$$ {dot g^{(alpha )}} = sumlimits_beta {{h_{alpha beta }}} {dot gamma ^{(beta )}} $$
(4)







$$ {h_{alpha alpha }} = {h_0}{{{
m{sech}}} ^2}left( {frac{{{h_0}gamma }}{{{tau _s} - {tau _0}}}}
ight) $$
(5)







$$ {h_{alpha beta }} = q{h_{alpha alpha }}{text{ }},; {alpha ne beta } $$
(6)







$$ gamma = sumlimits_alpha {int_0^t {left| {{{dot gamma }^{(alpha )}}}
ight|} } {text{d}}t $$
(7)

其中$ {h_0} $和$ {tau _0} $分别是初始硬化模量和初始屈服应力, 初始屈服应力$ {tau _0} $等于当前强度的初始值${g^{(alpha )}}(0)$. $ {tau _s} $是塑性流动初始时的参考应力, q是硬化因子.


1.2
弹塑性内聚力模型


本模型同时考虑了线弹性、塑性流动、线性硬化和损伤演化. 首先, 弹塑性分离位移可以分解为以下两部分







$$ {boldsymbol{delta }} = {{boldsymbol{delta }}^e} + {{boldsymbol{delta }}^p} $$
(8)

其中$ {{boldsymbol{delta }}^e} $和$ {{boldsymbol{delta }}^p} $分别是$ {boldsymbol{delta }} $的弹性部分和塑性部分. 为了建立一致性内聚力模型, 自由能密度函数定义为







$$ begin{gathered} psi = psi left( {{{boldsymbol{delta }}^e},d,{{bar delta }^p}}
ight) = frac{1}{2}left[ {(1 - d)({boldsymbol{delta }} - {{boldsymbol{delta }}^p}) cdot {{boldsymbol{D}}^e} cdot ({boldsymbol{delta }} - {{boldsymbol{delta }}^p}) + H{{bar delta }^{{p^2}}}}
ight] end{gathered} $$
(9)

其中d和H分别是损伤因子和线性硬化模量. $ {bar delta ^p} $是有效塑性应变. $ {{boldsymbol{D}}^e} $是界面初始弹性张量, 其可以表示为







$$ {{boldsymbol{D}}^e} = {K_n}{boldsymbol{n}} otimes {boldsymbol{n}} + {K_t}({boldsymbol{I}} - {boldsymbol{n}} otimes {boldsymbol{n}}) $$
(10)

其中$ {K_n} $和$ {K_t} $分别是法向和切向的刚度, n是界面的单位法向量, I是二阶单位张量. 损伤因子可以表示为







$$ d = left{ begin{array}{l}dfrac{{{delta ^f}left( {left| {bf{delta }}
ight| - {delta ^d}}
ight)}}{{left| {bf{delta }}
ight|left( {{delta ^f} - {delta ^d}}
ight)}},;{delta ^d} < left| {bf{delta }}
ight| < {delta ^f}1,;;;left| {bf{delta }}
ight| geqslant {delta ^f}0,;;;left| {bf{delta }}
ight| leqslant {delta ^d}end{array}
ight. $$
(11)

其中$ {delta ^d} $和$ {delta ^f} $是材料参数, $ left| cdot
ight| $代表欧几里得范数.

结合式(9), 牵引应力$ {boldsymbol{sigma }} $可以表示为







$$ {boldsymbol{sigma }} = frac{{partial psi }}{{partial {{boldsymbol{delta }}^e}}} = (1 - d){{boldsymbol{D}}^{text{e}}} cdot ({boldsymbol{delta }} - {{boldsymbol{delta }}^p}) $$
(12)

此处牵引应力$ {boldsymbol{sigma }} $可以进一步分解为







$$ {boldsymbol{sigma }} = {}^n{boldsymbol{sigma }} + {}^t{boldsymbol{sigma }} = ({boldsymbol{n}} otimes {boldsymbol{n}}) cdot {boldsymbol{sigma }} + ({boldsymbol{I}} - {boldsymbol{n}} otimes {boldsymbol{n}}) cdot {boldsymbol{sigma }} $$
(13)

其中法向牵引应力可以进一步表示为







$$ {}^n{boldsymbol{sigma }} = {}^nsigma {boldsymbol{n}} $$
(14)

采用以下形式的屈服函数来避免两个相邻表面的界面穿透[19]







$$ varPhi = left| {{}^t{boldsymbol{sigma }}}
ight| + leftlangle {{}^nsigma }
ight
angle - (sigma _y^0 + H{bar delta ^p}) $$
(15)

其中$ leftlangle cdot
ight
angle $表示McCauley括号, $ sigma _y^0 $代表初始屈服应力. 根据式(15), 关联流动向量N可以表示为







$$ {boldsymbol{N}} = frac{{partial varPhi }}{{partial {boldsymbol{sigma }}}} = {}^n{boldsymbol{N}} + {}^t{boldsymbol{N}} = frac{{leftlangle {{}^nsigma }
ight
angle }}{{{}^nsigma }}{boldsymbol{n}} + frac{{{}^t{boldsymbol{sigma }}}}{{left| {{}^t{boldsymbol{sigma }}}
ight|}} $$
(16)

其中$ {}^n{boldsymbol{N}} $和$ {}^t{boldsymbol{N}} $分别是N的法向部分和切向部分. 关联流动法则可以表示为







$$ {{boldsymbol{dot delta }}^p} = dot{epsilon} {boldsymbol{N}} = dot{epsilon} left( {frac{{leftlangle {{}^nsigma }
ight
angle }}{{{}^nsigma }}{boldsymbol{n}} + frac{{{}^t{boldsymbol{sigma }}}}{{left| {{}^t{boldsymbol{sigma }}}
ight|}}}
ight) $$
(17)

其中$ dot{epsilon} $是塑性乘子, $ dot{epsilon} $等于等效塑性应变率.


1.3
高周疲劳准则


为了研究选择性激光熔化成形316钢和冷轧成形316钢的高周疲劳行为, 本文分别对晶粒内部和晶界使用不同的高周疲劳准则.

针对晶粒部分, 本文采用由Papadopoulos[20]提出的介观疲劳准则. 该准则假设如果给定滑移系的累积塑性滑移不超过临界值, 则晶粒内部将不会有疲劳裂纹萌生. 为此, 通过介观物理量表示的Papadopoulos疲劳准则可以写为







$$ begin{split} & {f^{{text{grain}}}} = frac{1}{b}sqrt {leftlangle {tau _{s,a}^2}
ight
angle } + frac{a}{b}mathop {max }limits_t left[ {leftlangle {{sigma _n}(t)}
ight
angle }
ight] leqslant 1 hfill & sqrt {leftlangle {tau _{s,a}^2}
ight
angle } = sqrt 5 sqrt {frac{1}{{{N_s}}}sumlimits_{g = 1}^{{N_g}} {left[ {frac{1}{{{N_g}}}sumlimits_{s = 1}^{{N_s}} {tau _{s,a}^2(g,s)} }
ight]} } hfill & leftlangle {{sigma _n}(t)}
ight
angle = frac{1}{{{N_p}}}sumlimits_{g = 1}^{{N_g}} {left[ {frac{1}{{{N_g}}}sumlimits_{s = 1}^{{N_p}} {{sigma _n}(g,p,t)} }
ight]} hfill end{split} $$
(18)

其中$ {tau _{s,a}} $为每一个滑移系中的分解切应力幅值, $ {sigma _n} $为每一个滑移面的正应力, $ {N_s} $和$ {N_p} $为单个晶粒中滑移系和滑移面的个数, $ {N_g} $为多晶集中晶粒的个数, $ {f^{{text{grain}}}} $为晶粒的疲劳因子, a和b是材料参数, 他们可以根据完全反向弯曲疲劳极限f?1和完全反向扭转疲劳极限t?1进行计算, 本文取f?1为97.0 MPa和t?1为168.0 MPa[21]. $ sqrt {leftlangle {tau _{s,a}^2}
ight
angle } $是多晶集中所有滑移系中分解切应力的平均值, $ leftlangle {{sigma _n}(t)}
ight
angle $是多晶集中所有滑移面上正应力的平均值.

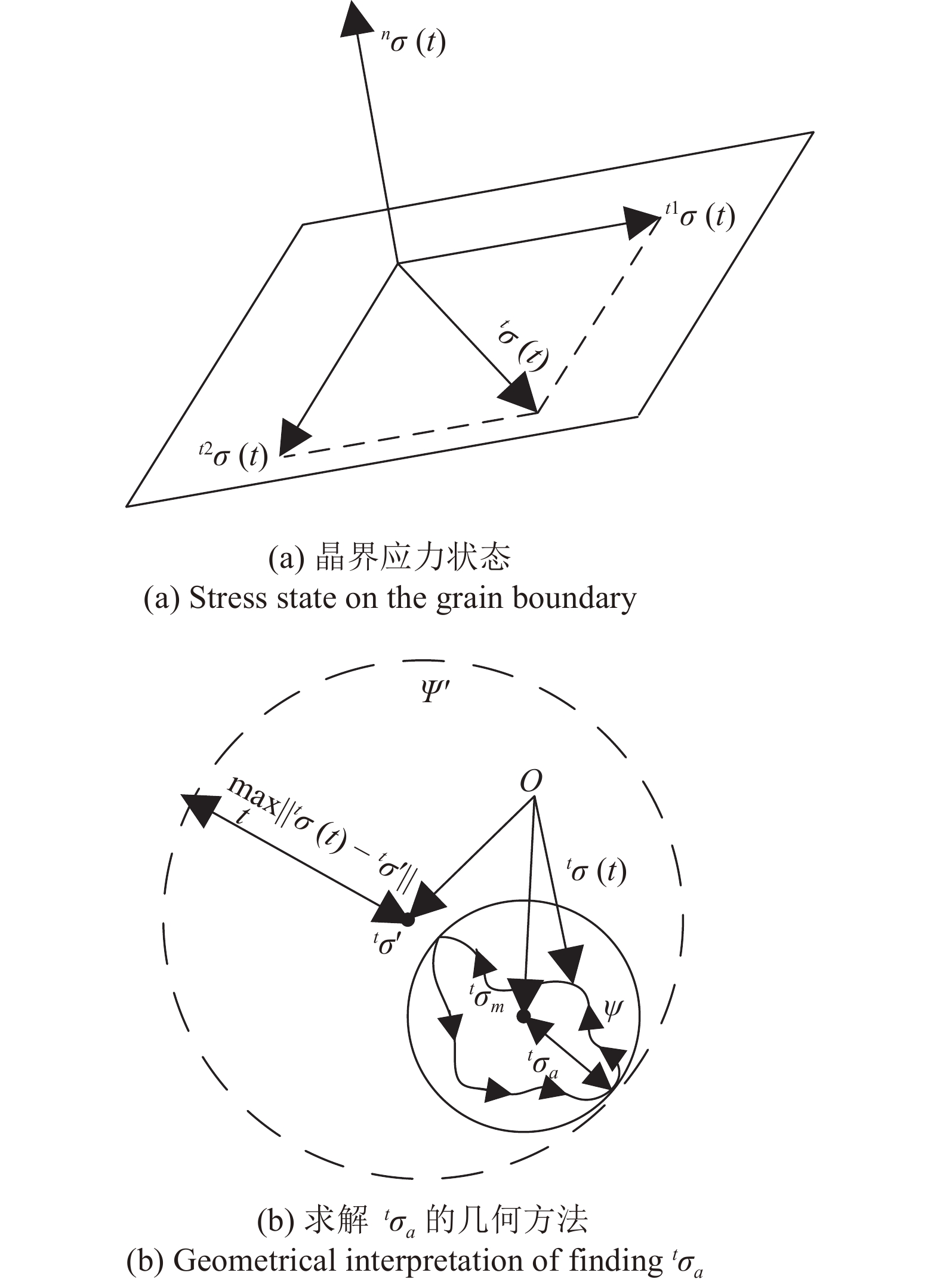
为了研究晶界处的高周疲劳行为, 本文使用了一种新的安定性理论的介观疲劳准则. 该准则假定如果晶界处的应力在介观上处于弹性安定状态, 则晶界上将不会发生疲劳裂纹萌生. 该准则与Dang-Van疲劳准则[22]类似, 区别在于该准则不需要像Dang-Van疲劳准则一样需要宏观介观应力的相互准换, 因为该准则可以直接使用内聚力模型计算出的介观物理量. 该准则为







$$ left. begin{array}{l} {f^{{text{gb}}}} = dfrac{1}{b}leftlangle {{}^t{sigma _a}}
ight
angle + dfrac{a}{b}mathop {max }limits_t left[ {leftlangle {{}^nsigma (t)}
ight
angle }
ight] leqslant 1 hfill leftlangle {{}^t{sigma _a}}
ight
angle = dfrac{1}{{{N_b}}}displaystylesumlimits_{s = 1}^{{N_b}} {{}^t{sigma _a}(b)} hfill leftlangle {{}^nsigma (t)}
ight
angle = dfrac{1}{{{N_b}}}displaystylesumlimits_{b = 1}^{{N_b}} {{}^nsigma (b,t)} hfill end{array}
ight} $$
(19)

其中$ {}^t{sigma _a} $为晶界介观切应力幅值, $ {}^nsigma $为晶界介观正应力, $ {N_b} $为多晶集中晶界的数量, $ {f^{{text{gb}}}} $为晶界的疲劳因子, a和b是与Papadopoulos准则中一样的材料参数. 计算$ {}^t{sigma _a} $之前, 需要了解晶界处的应力状态. 如图1所示, 晶界上的应力可以分为正应力和切应力, 其中切应力又可以在平面内分解为两部分. $ {}^n{boldsymbol{sigma }} $的方向总是垂直于晶界, 但是$ {}^t{boldsymbol{sigma }} $的方向会随时间发生变化. 切应力的加载路径如图1所示, $ {}^t{sigma _a} $即加载路径的最小包络圆的半径, 具体算法可以参照文献[23].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-396-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
求解$ {}^t{sigma _a} $示意图



Figure
1.
Illustration of finding$ {}^t{sigma _a} $



下载:
全尺寸图片
幻灯片



2.
多晶模型建立与材料参数确定



2.1
多晶模型建立


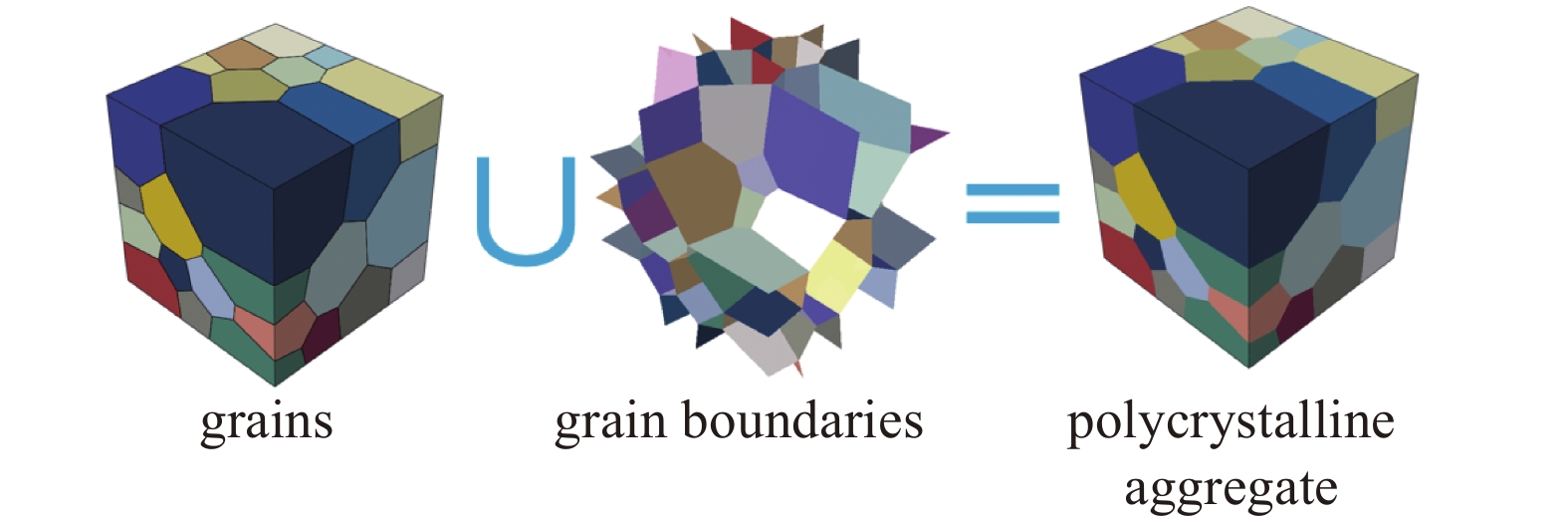
本文研究的选择性激光熔化成形316钢和轧制316钢的晶粒尺寸分别为10.01 μm和4.55 μm[7]. 由于本文采用内聚力模型来模拟晶界处的力学行为, 如果考虑实际的晶粒形貌将会给内聚力单元的建立带来困难. 为了方便起见, 本工作忽略了晶粒形貌的影响, 在晶体塑性仿真中统一将晶粒形貌简化为等轴晶. 本文采用开源软件Neper[24]来生成如图2所示由等轴晶粒组成的代表体单元, 其中Voronoi多面体代表等轴晶粒, 零厚度界面代表晶界. 本文使用四面体单元(C3D4)和三维零厚度内聚力单元(COH3D6)分别划分晶粒网格和晶界网格.


2.2
材料参数优化流程


本文通过拉伸实验的应力应变曲线、微观力学模型计算结果以及反问题优化方法相结合来确定材料本构参数. 本文使用信赖域反射算法[25]来寻找材料参数使得实验获得应力应变曲线与仿真获得应力应变曲线最大程度契合. 定义$ {sigma _i} $和$ {varepsilon _i} $为实验获得的应力应变曲线中的点集, $ {boldsymbol{sigma }} = fleft( {{boldsymbol{varepsilon }},{boldsymbol{p}}}
ight) $为仿真获得的应力预测, p为5个材料参数, 优化问题的数学模型可以表达为







$$ left. begin{array}{l} {text{find}}:{boldsymbol{p}} = ({h_0},{tau _s},{tau _0},n,q) hfill {text{min}}:Oleft( {boldsymbol{p}}
ight) = sumlimits_{i = 1}^n {left| {{sigma _i} - fleft( {{varepsilon _i};{boldsymbol{p}}}
ight)}
ight|} = left| {{boldsymbol{sigma }} - fleft( {{boldsymbol{varepsilon }},{boldsymbol{p}}}
ight)}
ight| hfill {text{s}}{text{.t}}{text{.}}:{l_b} leqslant {p_j} leqslant {u_b},;j = 1,2,...,5 hfill end{array}
ight} $$
(20)

其中ub和lb为模型参数的上界和下界.


2.3
晶粒材料参数


晶粒材料参数由弹性常数和晶体塑性本构参数共同组成. 本节使用代表体单元来模拟拉伸实验曲线从而标定材料参数.

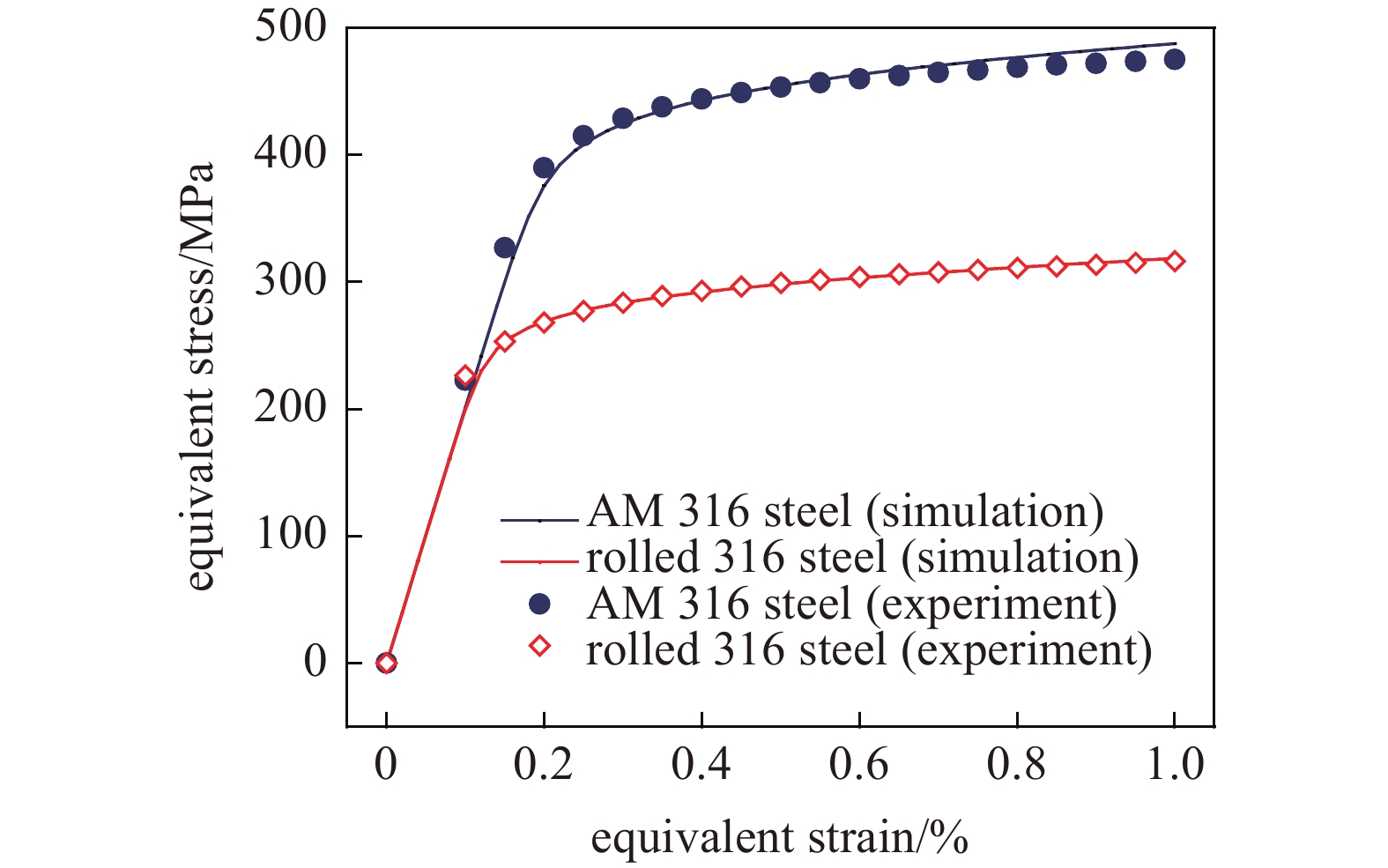
本节计算均采用如图3所示由50个随机取向晶粒组成的代表体单元. 为了避免过刚性响应, 本文在每个晶粒中至少划分20个网格[26]. 为了考虑晶粒尺寸的区别, 本文根据文献[7]中的实验结果分别选取增材制造316钢代表体单元边长和轧制316钢代表体单元边长为37 μm和17 μm. 增材制造316钢和轧制316钢的弹性常数统一选取为Ciiii=206 GPa, Ciijj=206 GPa, Cijij=206 GPa[27]. 对于面心立方金属, 拉伸实验已经足够用来获得晶体塑性本构参数, 在当前参数鉴定流程下不再需要其他实验[28]. 通过周期性边界条件对代表体单元施加宏观应变, 可以很容易计算出代表体单元的平均应力, 结合式(21), 可以得到增材制造316钢和轧制316钢晶体塑性本构参数如表1所示. 如图4所示, 根据优化所得本构参数进行仿真获得的应力应变曲线与实验曲线契合度很高.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-396-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
代表体单元



Figure
3.
Representative volume element (RVE)



下载:
全尺寸图片
幻灯片





表
1
通过拉伸实验确定的晶粒材料参数



Table
1.
Material parameters of the grains obtained by the uniaxial tensile experiments



table_type1 ">
Materialh0/MPaτs/MPaτ0/MPanq${dot a^{(alpha )}}$
AM 316 steel 171 214 156 59 1.11 0.001
rolled 316 steel 107 213 99 77 1.17 0.001





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-396-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
单轴拉伸实验曲线仿真预测



Figure
4.
Prediction of the uniaxial tensile experiments



下载:
全尺寸图片
幻灯片



2.4
晶界材料参数


本文针对于晶界共有7个材料参数(Kn, Kt, σy0, H, t, δd和δf)需要测定. 晶界的刚度可以定义为







$$ left. {begin{array}{*{20}{l}} {{K_n} = dfrac{{{C_{iiii}}}}{t}} {{K_t} = dfrac{{{K_n}}}{{2(1 + mu )}}} end{array}}
ight} $$
(21)

其中泊松比μ取为0.3. 在本文采用的基于牵引应力-分离位移描述的内聚力模型中, 晶界本构厚度t对牵引应力和分离应变之间的关系没有影响. 另外由于内聚力单元的刚度很弱, 晶界厚度对多晶体有限元计算结果的影响也很弱. 如果选取一个很小的晶界厚度, 不但计算结果几乎不受影响, 还会大大减少计算效率. 因此本文选取1 μm作为晶界的厚度. 为了方便起见, 本文选取拉伸应力应变曲线残余应变为0.2%, 对应的应力为初始屈服应力σy0. 线性硬化模量H通过应变强化阶段的斜率来确定. 由于本文仅考虑裂纹初始前的状态, 因此δd和δf控制的损伤演化阶段对结算结果没有影响. 综上所述, 弹塑性内聚力模型的材料参数如表2所示.




表
2
晶界材料参数



Table
2.
Material parameters of the grain boundaries



table_type2 ">
MaterialKn/(GPa·μm?1)Kt/(GPa·μm?1)σy0/MPaH/(MPa·μm?1)δd/μmδf/μmt/μm
AM 316 steel20679.2344510740.050.11
rolled 316 steel20679.232859450.050.11





下载:
导出CSV
|显示表格



3.
仿真结果与讨论


本节将晶体塑性理论、弹塑性内聚力模型以及分别针对于晶粒和晶界的介观疲劳准则相结合以研究增材制造316钢和轧制316钢的高周疲劳性能.

本节采用表1和表2中的材料参数进行数值仿真. 如图2所示, 代表体单元由50个晶粒和218个晶界组成. 与前文相同, 增材制造316钢和轧制316钢的代表体单元边长分别取37 μm和17 μm. 通过一般性周期性边界条件[29]对代表体单元施加幅值为250 MPa、应力比为0的循环应力载荷. 为了节约计算时间, 本节模拟10个循环周期以使代表体单元在介观下达到弹性安定状态. 结合文中所述两种介观疲劳准则即可解分别求得晶粒和晶界的疲劳因子. 对于增材制造316钢, 晶粒和晶界疲劳因子fgrain和fgb分别为0.617和0.306. 对于轧制316钢, 晶粒和晶界疲劳因子fgrain和fgb分别为0.659和0.340. 显然, 无论是晶粒疲劳因子和晶界疲劳因子, 轧制316钢的计算结果皆大于增材制造316钢. 这说明增材制造316钢相较于轧制316钢具有更好的高周疲劳性能, 这与文献[7]中的实验结果相符.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-396-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
多晶集的微观结构



Figure
2.
Microstructure of the polycrystalline aggregate



下载:
全尺寸图片
幻灯片


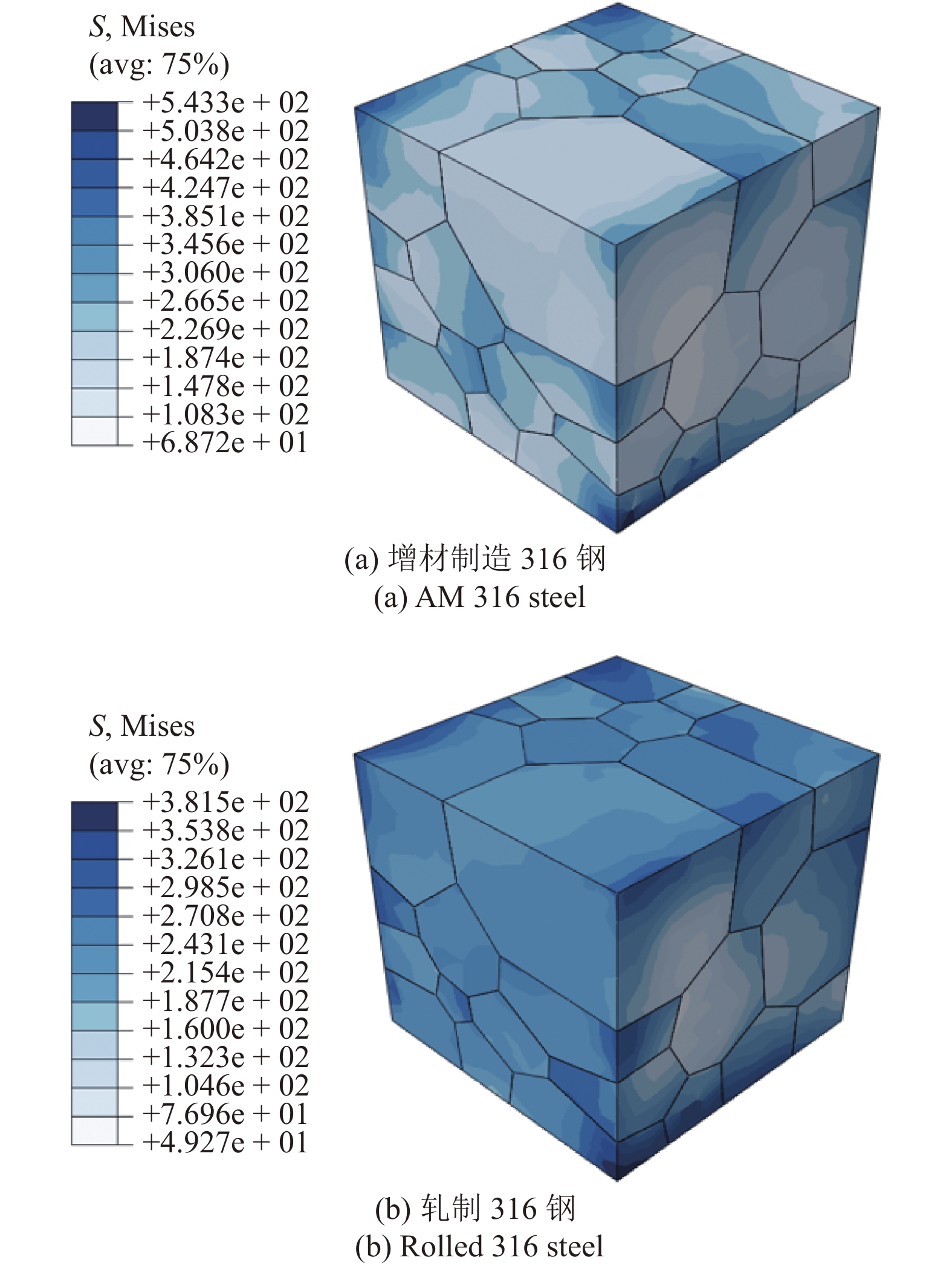
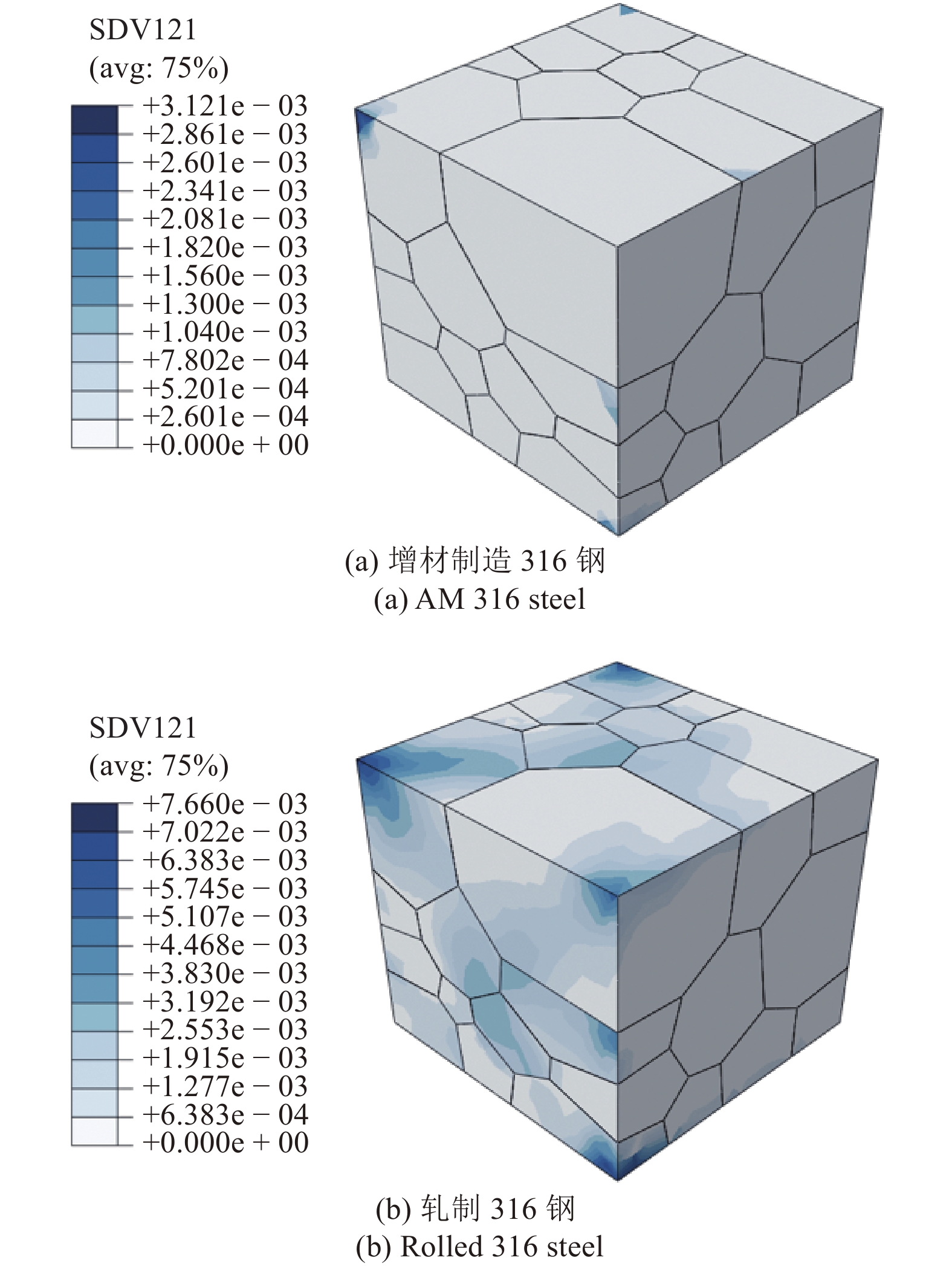
接下来本文将根据图5所示增材制造316钢和轧制316钢晶粒内部的Mises等效应力、图6所示增材制造316钢和轧制316钢晶粒内部的累积剪切应变、图7所示的增材制造316钢晶界处的等效应力和等效塑性应变以及图8所示的轧制316钢晶界处的等效应力和等效塑性应变来解释上述仿真结果. 首先对于晶粒部分, 增材制造316钢晶粒中的最大正应力以及切应力幅值的均值为95.88 MPa和59.87 MPa, 相较于轧制316钢对应值98.96 MPa和63.96 MPa更小. 结合式(18), 显然增材制造316钢的晶粒疲劳因子会小于轧制316钢的晶粒疲劳因子. 值得一提的是, 尽管增材制造316钢的最大Mises等效应力543.3 MPa大于轧制316钢的最大Mises等效应力381.5 MPa(图5所示), 增材制造316钢中Papadopoulos疲劳准则涉及的介观最大正应力和切应力幅值却小于轧制316钢所对应的值. 另外, 增材制造316钢中累积剪切应变的最大值3.121 × 10?3也小于轧制316钢中累积剪切应变的最大值7.660 × 10?3. 一般来说, 大的应力更容易产生位错[30]. 而位于驻留滑移带和基底界面处的位错是疲劳裂纹萌生的主要成因[7]. 因此材料中一般应力越小疲劳性能越好. 然而, 尽管Papadopoulos疲劳准则中所涉及的物理量是与应力相关的, 具有更大Mises等效应力的增材制造316钢与轧制316钢相比却拥有更小的晶粒疲劳因子. 这是由于基于弹性安定理论的Papadopoulos疲劳准则可以有效考虑晶粒内部的局部塑性滑移.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-396-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
晶粒内部的Mises等效应力



Figure
5.
von Mises equivalent stress in the grains



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-396-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
晶粒内部的累积剪切应变



Figure
6.
Total cumulative shear strain in the grains



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-396-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



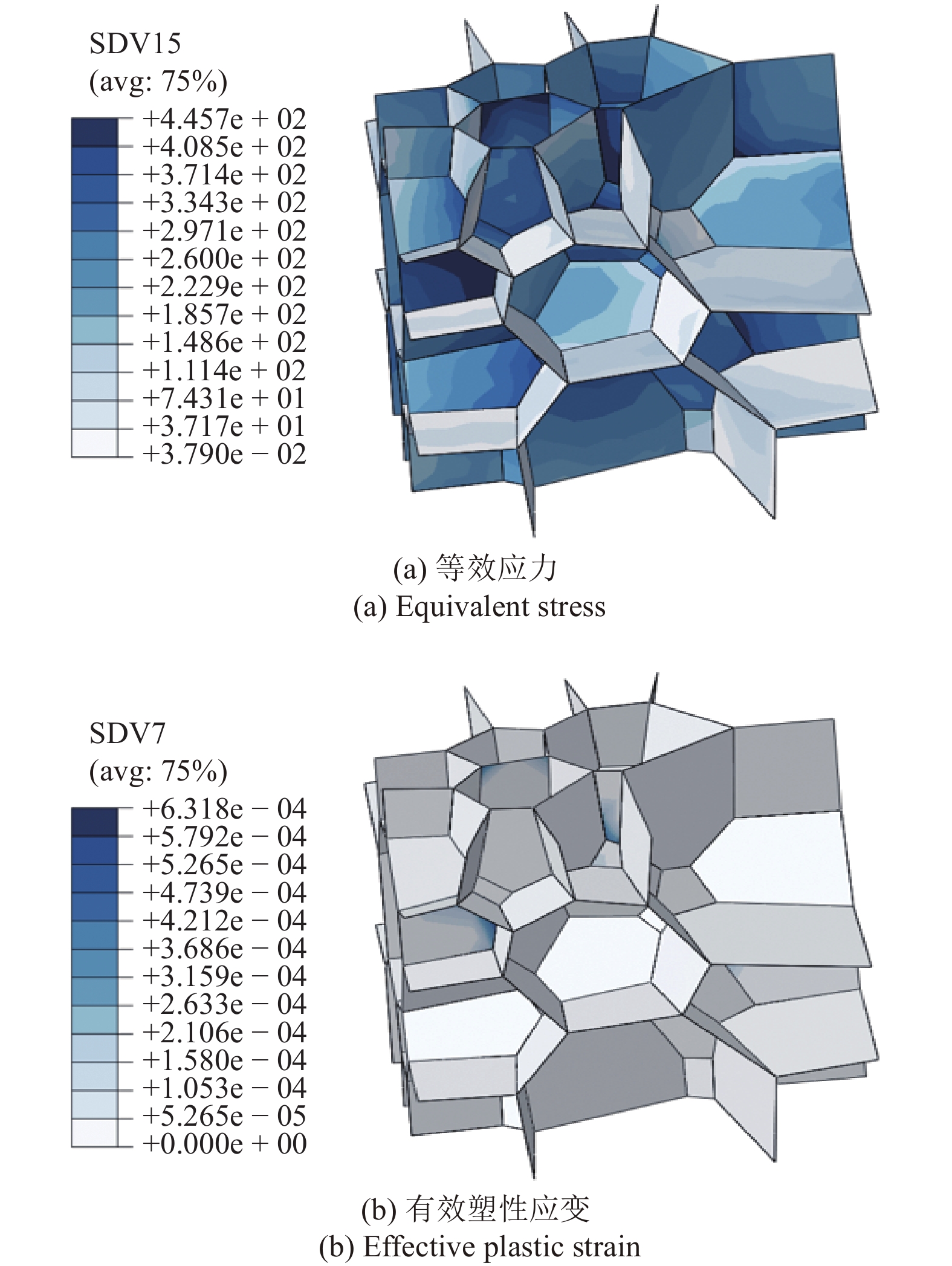
图
7
增材制造316钢晶界



Figure
7.
Grain boundary of AM 316 steel



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-396-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



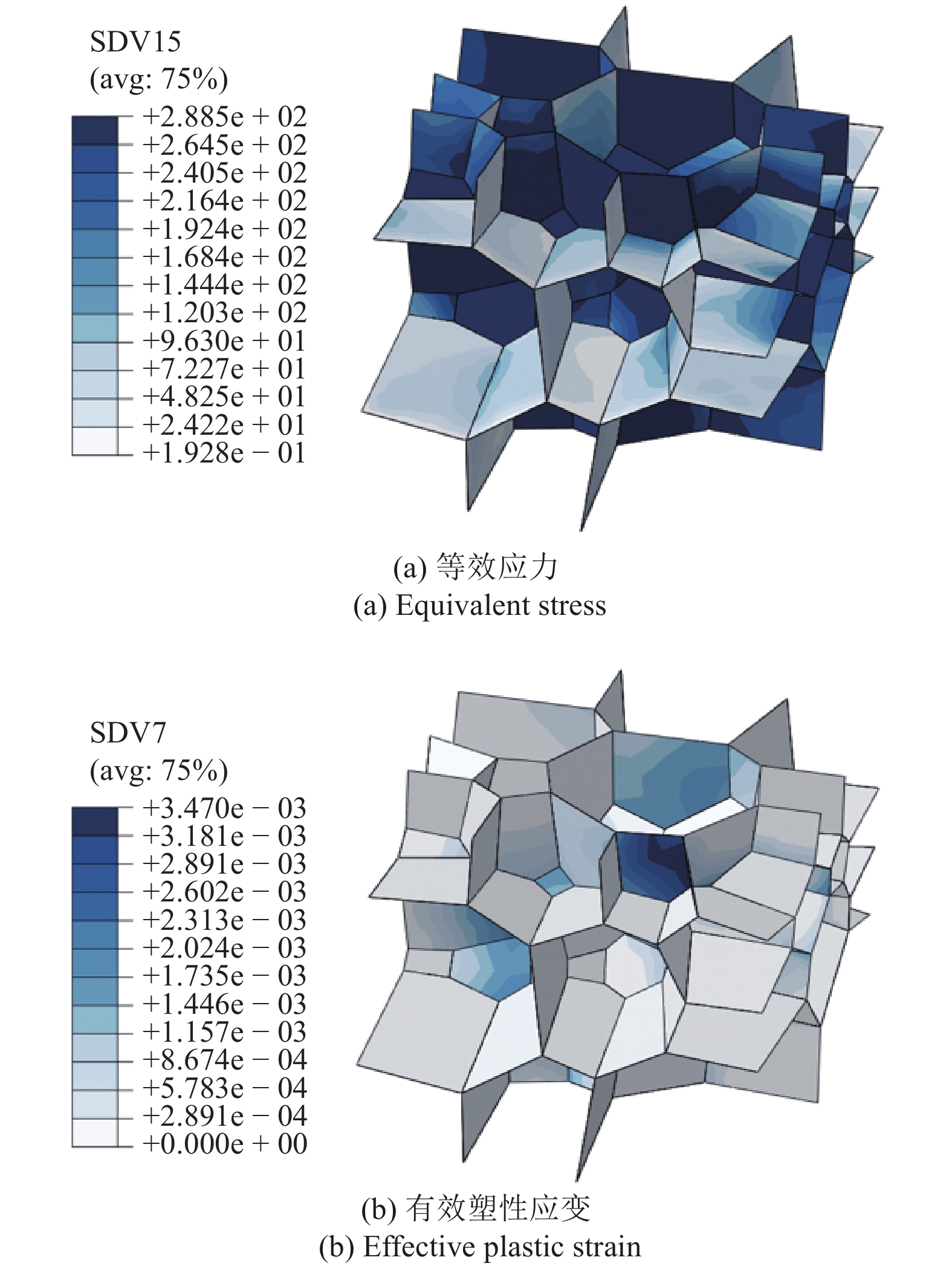
图
8
轧制316钢晶界



Figure
8.
Grain boundary of rolled 316 steel



下载:
全尺寸图片
幻灯片


接下来针对于晶界部分, 尽管增材制造316钢晶界处的最大等效应力值445.7MPa大于轧制316钢晶界中对应值288.5 MPa, 增材制造316钢晶界处的有效塑性应变$ {bar delta ^p} $的最大值6.318 × 10?4却小于轧制316钢晶界中对应值3.470 × 10?3. 事实上, 这是由于增材制造316钢晶界的屈服应力445 MPa大于轧制316钢晶界的屈服应力285 MPa造成的. 因为介观尺度上的局部塑性会造成疲劳裂纹初始, 所以晶界处具有较小等效塑性应变的增材制造316钢有更好的高周疲劳性能. 同样地, 增材制造316钢晶界处的介观切应力幅值和最大正应力的均值为29.65 MPa和99.94 MPa, 相较于轧制316钢对应值32.94 MPa和100.75 MPa更小, 这也证明了本文针对于晶界所使用的基于弹性安定理论的介观疲劳准则可以有效地考虑晶界处局部塑性的影响.

根据本文提出的微观力学模型得到的仿真结果与文献[7]中的实验结果相符. 针对于晶界的介观疲劳准则可以有效地反映出局部塑性对高周疲劳性能的影响. 结合晶体塑性理论和Papadopoulos疲劳准则可以考虑位错滑移对晶粒高周疲劳性能的影响. 本文建立的微观结构-疲劳性能之间关系可以日后应用于增材制造316钢的疲劳性能优化.


4.
结论


本文通过微观力学方法研究了增材制造316钢和轧制316钢的高周疲劳性能. 为了考虑发生于晶粒与晶界中局部塑性的影响, 分别使用晶体塑性理论与弹塑性内聚力模型来模拟晶粒和晶界的力学行为. 为了同时研究滑移带和晶界对疲劳裂纹初始的影响, 分别使用了Papadopoulos疲劳准则和一种基于安定性理论的介观高周疲劳准则.

仿真结果显示选择性激光熔化316钢相较于轧制316钢具有更好的高周疲劳性能, 这与文献中的疲劳实验数据相吻合. 同时仿真结果也证明了所使用的晶界高周疲劳准则可以有效反映局部塑性对高周疲劳性能的影响. 本文建立的微观结构?疲劳性能之间关系可以日后应用于选择性激光熔化316钢的疲劳性能优化.

相关话题/制造 塑性 材料 成形 实验
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 金属增材制造中的缺陷、组织形貌和成形材料力学性能
    引言自青铜器时代以来,金属材料在人类文明发展进程中起到了至关重要的作用.随着社会的不断发展和科技的不断进步,对材料的综合性能提出了更高的要求,所设计的材料结构也逐渐朝轻量化、复杂化和低能耗方向发展.然而,在制备如超材料[1-2]等轻质结构时,传统金属制造技术往往需要经过繁琐且复杂的加工步骤,且相关的 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 选区激光熔化成形区粗糙表面对铺粉质量的影响:离散元模拟
    引言选择性激光熔化(SLM)通过逐层铺粉和选择性熔化粉末来打印三维零件[1].增材制造零件的质量受许多参数影响,例如激光功率[2]、扫描速度[3]、扫描策略等[4].打印零件之前的一个关键程序是在建筑平台上铺粉.在铺粉过程中,粉末的状态会影响铺粉过程,因为粉末在基板上的流动能力决定着每一层粉末的连续 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 激光选区熔化增材制造中的粉体热动力学行为
    引言激光选区熔化(SLM)采用高能束激光熔化细微金属粉末,通过逐道、逐层熔融堆积的方式成形三维零件.SLM可以成形近全致密、性能接近锻件且具有精细复杂结构的金属零件,是增材制造(3D打印)领域的前沿与热点技术[1-2].近年来,SLM技术开始在航空航天、国防科技、定制化生物医疗等领域关键结构部件的制 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 增材制造微结构演化及疲劳分散性计算
    引言增材制造通过不断添加材料来完成零件的加工成型,满足了工业对零件形状、功能、材料的更高要求,成为当前材料加工技术发展的前沿方向.与传统制造工艺相比,增材制造在成形原理、材料形态、制件性能上发生了根本改变,具有材料浪费少、加工工序少、加工周期短、零件结构设计自由、易于实现形状复杂零部件快速成型等优点 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 面向增材制造的熔池凝固组织演变的相场研究
    引言激光增材制造技术因制造柔性高、周期短、材料局限小等优点,极适合复杂整体构件的制造与高附值零件的快速修复,在航空航天、能源动力等领域具有广阔的应用前景[1-3].然而,金属粉末在高能激光束的辐照下快速熔化与冷却.熔池内部涉及许多瞬态及冶金过程,特别是糊状区的非平衡快速凝固过程对枝晶组织生长和晶粒演 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 微磁检测应力和塑性区的磁弹塑耦合理论
    引言钢铁材料因其具有良好的力学以及机械性能,被广泛应用于重大机械、土木交通工程、管道输运等领域.长期服役中钢铁类构件或结构的突发破坏导致恶性工程事故频发,探索针对钢铁材料应力状态和塑性变形的无损检测方法,有望通过结构局部危险点的及时发现来有效预防结构整体垮塌事故,具有重大的研究价值和现实意义.常规无 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 激光冲击下CoCrFeMnNi高熵合金微观塑性变形的分子动力学模拟
    引言激光冲击强化技术利用激光穿过约束层,作用于烧蚀层产生大量等离子体,等离子体继续吸收激光能量发生爆炸从而产生冲击波作用于金属表面.当冲击波峰值压力大于材料的屈服强度时,激光冲击使材料发生超高应变率(>106s?1)的塑性变形,造成材料表面出现残余压应力分布并且发生表面晶粒细化[1-3].与传统的机 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 低频振动隔离和能量采集双功能超材料
    引言超材料是一种具有人工周期性设计的复合材料,它具有天然材料所不具备超常物理特性[1-4].例如,由亚波长结构组成的声学超材料具有可以抑制声波或弹性波传播的带隙[5].超材料的应用主要包括机械波衰减[6-8]、低频隔振[9-11]和能量采集[12-13]等.实际的工程中,如一些特殊工况下(飞行器帆板 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度强化学习算法的颗粒材料应力?应变关系数据驱动模拟研究
    引言在研究泥沙、岩土、粉体等颗粒材料宏观力学行为时,通常在连续介质力学框架下建立其唯象本构模型,通过引入内变量来描述颗粒材料的路径相关、历史相关等特性[1-5].虽然基于连续假设的唯象本构模型在描述颗粒材料宏观力学特性时具备很好的工程适用能力,但是颗粒材料由于其自身的离散特性,具有摩擦性,剪胀性,压 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 均匀电场中气泡上升特性的实验研究
    引言强化传热技术在能源动力、石油工程、航空航天、化工等领域具有广泛的应用前景,而利用电场进行强化换热,能够有效减小换热器的体积和重量,提高能源利用效率[1-2].电场强化沸腾换热技术通过电场力控制气泡的生成、脱离、变形与运动[3-5],降低气泡脱离尺寸[6-7],加速气泡脱离频率[8],从而实现换热 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.