删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

激光选区熔化增材制造中的粉体热动力学行为

本站小编 Free考研考试/2022-01-01


引 言


激光选区熔化(SLM)采用高能束激光熔化细微金属粉末, 通过逐道、逐层熔融堆积的方式成形三维零件. SLM可以成形近全致密、性能接近锻件且具有精细复杂结构的金属零件, 是增材制造(3D打印)领域的前沿与热点技术[1-2]. 近年来, SLM技术开始在航空航天、国防科技、定制化生物医疗等领域关键结构部件的制造方面获得应用, 成为极具发展潜力和研究价值的增材制造技术[3].

自然界的物质按照其存在形态可以分为3类: 流体、固体和颗粒[4-5]. 其中, 颗粒物质是指由大量粉末颗粒集群而形成的物质体系. 由于体系内粉末颗粒的离散性和结构各项异性, 颗粒物质的力学行为无法用流体力学等经典连续介质理论进行描述, 成为21世纪的百个自然科学难题之一[6]. SLM制造工艺采用的金属粉末是典型的颗粒物质. 成形过程中, 铺粉器首先将微米级散状粉末铺设成薄层粉末床, 然后激光热源对粉末床进行扫描与熔融. 粉末在铺设与熔融两个工艺过程中, 可呈现出分层、团聚、挤压、飞溅和剥蚀等典型的颗粒物质复杂热/动力学行为[7], 与零件的孔隙、球化、裂纹等成形缺陷及最终力学性能紧密相关[8]. 因此, 深入研究SLM成形过程中的粉体热/动力学行为, 对SLM零件成形性能的提升和颗粒物质力学理论的探索均具有重要工程及科学意义[9].

目前, 关于SLM粉体热/动力学行为的实验研究方法主要有高倍高速光学成像[10]、纹影成像[11]和X射线同步辐射成像[12]等在线监测手段, 而理论研究方法比较主流的分别是离散单元法(DEM)[13]和计算流体力学(CFD)[14]建模仿真计算.

针对SLM的粉末铺设工艺环节, Parteli和 Poschel[15]提出了DEM软球计算模型, 考虑粉末的弹塑性接触力和范德华黏结力, 对非球形粉末的辊筒式铺设过程进行了计算模拟. Chen等[13]通过DEM建模仿真, 从颗粒尺度较系统地分析了316L粉末在刮板式铺设过程中的速度场、压力场和质量场等动力学信息演变规律. 随后, ****们基于DEM数值模拟, 分别研究了粉末形貌尺寸和粒度分布[16]、铺设机构几何形状[17]、铺设层厚[18]、铺设速度[19]等工艺参数对粉末床致密度、粗糙度、均匀度等铺设质量的影响规律. 通常认为[13,20-21]: 辊筒式粉末铺设对粉末具有挤压效应, 比刮板式更容易获得致密的粉末床; 铺粉速度的提升和层厚的减少不利于粉末流动的均匀性和连续性, 将降低粉末床铺设致密度; 由于范德华力导致的团聚效应, 超细粉末容易引起堵塞现象, 也不利于粉末的铺设. 粉末铺设的颗粒尺度实验研究相对较少. Chen等[13]基于光学成像对金属粉末铺设过程中的宏观动态形态进行了标定与测试, 另外, 还采用激光轮廓仪测试了粉末床的表面形貌质量[21]. 美国阿贡实验室[22]通过高能X射线同步辐射仪观测了微米粉末颗粒在铺设过程中的运动轨迹. 这些实验研究, 对基于DEM数值模拟研究的验证具有积极意义.

SLM粉末床熔融过程中, 粉末床的剥蚀[10]与飞溅[23]是两个重要且复杂的热/动力学行为. 基于高倍高速光学摄像在线监测, Matthews等[10]研究了SLM粉末床的熔化损耗情况, 发现激光扫描过程中, 熔池热影响区域外围的粉末颗粒会被吸入熔池, 从而沿着熔化道在粉末床上形成剥蚀区域. 剥蚀会在熔化道中引起更多的气孔, 并影响粉末熔融的连续性和稳定性. Bidare等[11]采用纹影成像法观测了SLM粉末床熔融过程, 发现了熔池中喷射出来的高速金属蒸汽羽流, 并分析了不同激光参数作用下粉末床整体的剥蚀与飞溅运动. Cunningham等[24]采用X射线同步辐射成像法观测了熔池深孔、蒸汽喷射及粉末运动状态, 分析了粉末运动与熔池热动力学行为直接的关系. 基于上述实验观测, 通常推测: 高能束激光作用下, 熔池内部喷发的高速蒸汽羽流带动环境保护气体形成内旋涡流, 涡流驱动散体粉末从而形成剥蚀和飞溅现象[10]; 粉末剥蚀与飞溅随着环境压力的降低而加剧[25]; 羽流喷射方向对激光扫描速度的增加最为敏感, 依次出现前喷、垂直和后喷3种典型状态[11]. 现有的SLM粉末床熔融模型主要能模拟熔池熔融的固?液态转变过程[8,26–30], 计算过程中将散体粉末床视作连续的块体介质, 因此无法针对粉末床剥蚀与飞溅的热/动力学行为进行仿真模拟. 虽然Bidare等[11]基于有限元理论实现了熔池金属羽流与环境气体流场的计算, 但散体粉末颗粒仍未被包含在模型中. 近期, Chen和Yan[31]针对SLM粉末床的热力运动, 提出了基于DEM和FVM耦合理论的多相流仿真模型, 为SLM剥蚀与飞溅的理论计算预测提供了新的思路. 另外, 关于如何消除SLM剥蚀与飞溅运动对成形过程的负面影响, 目前主要采用添加侧向风进行粉末清除[23,32-33]的被动方法. 如何从源头控制粉末床的热/力运动, 进而控制和消除SLM剥蚀与飞溅现象, 有待进一步研究.

本文介绍了DEM与CFD联合建模仿真在SLM粉体热/动力学行为研究中的应用. 结合光学监测等实验手段, 对SLM粉末铺设工艺环节的粉体动力学及粉末床熔融的粉体热/动力学行为规律进行了探讨. 研究对加深理解SLM工艺中散体粉末介质热/动力学行为机制及改善SLM成形工艺具有重要科学及工程意义.


1.
研究方法



1.1
DEM/CFD联合建模



1.1.1
粉末铺设模型

粉末铺设工艺过程采用软球DEM理论[34]构建. 考虑粉末铺设过程中单个粉末颗粒的平动、转动和温度变化, 根据牛顿运动定律与傅里叶传热定律建立粉末颗粒的状态方程



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure1" />



图
1
SLM粉体热/动力学模型



Figure
1.
Thermal dynamic model of SLM



下载:
全尺寸图片
幻灯片








$$ {m}_{text{P}text{, }text{1}}frac{text{d}{{boldsymbol{u}}}_{text{P,1}}}{text{d}t}={{boldsymbol{F}}}_{text{P-E}} + {{boldsymbol{F}}}_{text{g,1}} + {displaystyle sum ({{boldsymbol{F}}}_{text{n}text{, }text{12}} + {{boldsymbol{F}}}_{{
m{t}}text{, }12} + {{boldsymbol{F}}}_{text{c}text{, }text{12}})} $$
(1)







$$ {I}_{text{P}text{, }text{1}}frac{text{d}{{boldsymbol{omega}} }_{text{P}text{, }text{1}}}{text{d}t}={displaystyle sum {{boldsymbol{R}}}_{text{P},1}times {{boldsymbol{F}}}_{text{t,12}}} $$
(2)







$$ {m_{{text{P,1}}}}{c_{{text{P,1}}}}frac{{{text{d}}{T_{{text{P,1}}}}}}{{{text{d}}t}} = {Q_{{
m{P }}- {
m{E}}}} + sum {{Q_{{text{P,12}}}}} $$
(3)

式中, mP,1, IP,1, TP,1, RP,1和cP,1分别为粉末颗粒的质量、转动惯量、温度、半径和比热容; uP,1和ωP,1分别为粉末颗粒自身的速度和角速度; Fg,1为粉末自身重力; Fn,12和Ft,12为粉末颗粒之间的法向和切向弹塑性接触力, 采用标准的Hertz-Mindlin接触方程[13]计算; Fc,12为粉末颗粒之间范德华黏结力, 采用JKR经验公式[35]计算; QP,12为粉末颗粒之间的热流量, 遵循傅里叶接触传热定律; FP-E和QP-E分别为外界环境对粉末颗粒的作用力和热量传输. 如图1(a)所示, 分别建立了刮板式和滚筒式两种典型的SLM粉末铺设模型. 其中w为滚筒转速; V和H分别为粉末铺设速度与层厚.


1.1.2
粉末熔融模型

粉末铺设计算完成后, 将DEM模型中粉末床的颗粒位置与几何信息导入至CFD模型, 进行SLM粉末床熔融的计算. 熔体的质量、动量、能量守恒N-S方程







$$ nabla cdot ({
ho _{text{M}}}{{boldsymbol{u}}_{text{M}}}) = 0 $$
(4)







$$ begin{split} &frac{partial }{{partial t}}({
ho _{text{M}}}{{boldsymbol{u}}_{text{M}}}) + nabla cdot ({
ho _{text{M}}}{{boldsymbol{u}}_{text{M}}}{{boldsymbol{u}}_{text{M}}}) = &quad- nabla P + {
ho _{text{M}}}{boldsymbol{g}} + nabla cdot (mu nabla {{boldsymbol{u}}_{text{M}}}) + {S_{text{m}}} end{split}$$
(5)







$$ frac{partial }{{partial t}}({
ho _{text{M}}}h) + nabla cdot ({
ho _{text{M}}}{{boldsymbol{u}}_{text{M}}}h) = nabla cdot left( {knabla {T_{text{M}}}}
ight) + {S_{text{h}}} $$
(6)

式中ρM, uM, P和TM分别为熔体的密度、速度、压强和温度状态变量; μ和k分别为熔体黏度和导热系数; Sm为动量源项; Sh为热源项. 其中, 熔体界面采用VOF界面追踪法描述[14]. Sh中的高斯激光热源以面热源的形式加载[36].


1.1.3
粉末?气体的流?固驱动建模

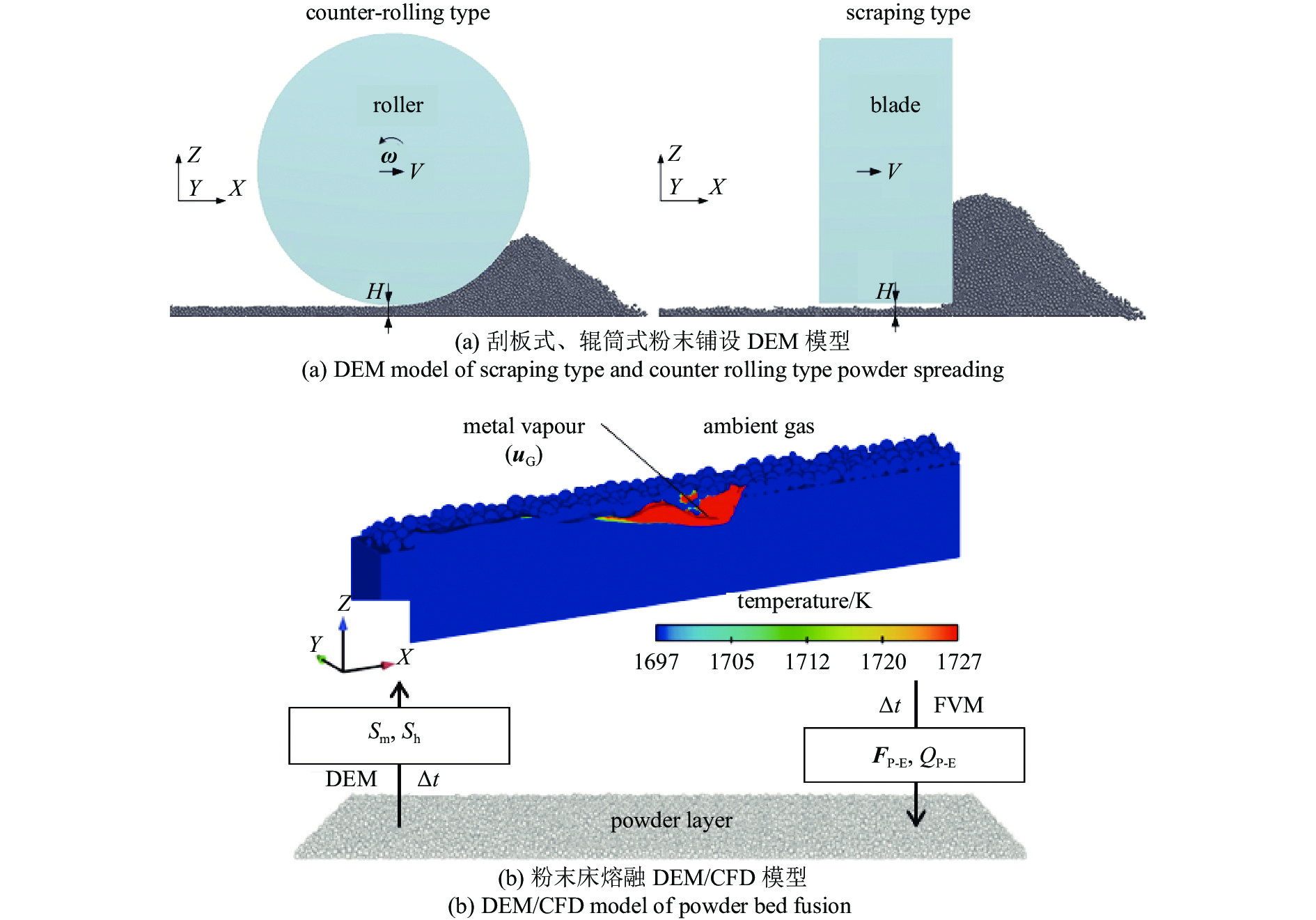
如图1(b)所示, 为模拟气相(熔池蒸汽和环境气体)热力驱动作用下粉末的动力学行为, 首先, 根据Knudsen-layer法则[37]计算熔池界面的羽流气体速度uG







$$ {{boldsymbol{u}}_{text{G}}} = {{{M}}_{text{n}}}left(frac{{gamma {B_{text{o}}}{T_{{text{sur}}}}}}{{{phi _1}{m_1} + {phi _2}{m_2}}}
ight)^{frac{1}{2}} $$
(7)

式中, Mn为马赫数; γ为单原子气体热容比; B0为波尔兹莫常数; Tsur为熔池界面的温度; m1和m2分别熔池蒸汽和环境气体的摩尔质量; φ1和φ2 分别为气体体积分数.

然后, 基于Euler-Lagrange耦合原理[31], 计算式(1) ~ 式(3)中气相对粉末颗粒的热力驱动作用力







$$ left. begin{array}{l} R{e_{text{P}}} = dfrac{{2Rleft| {{{boldsymbol{u}}_{text{G}}} - {{boldsymbol{u}}_{text{P}}}}
ight|{
ho _{text{G}}}}}{{{mu _{text{G}}}}} hfill {{boldsymbol{F}}_{{
m{P }}- {
m{E}}}} = dfrac{{12{text{π}} {R^2}}}{{R{e_{text{P}}}}}{
ho _{text{G}}}({{boldsymbol{u}}_{text{G}}} - {{boldsymbol{u}}_{text{P}}})left| {{{boldsymbol{u}}_{text{G}}} - {{boldsymbol{u}}_{text{P}}}}
ight| = qquadquad 6{text{π}} R({{boldsymbol{u}}_{text{G}}} - {{boldsymbol{u}}_{text{P}}}){mu _{text{G}}} hfill end{array}
ight} $$
(8)







$$ {Q_{{
m{P }}- {
m{E}}}} = {h_{{
m{P }}- {
m{E}}}}{A_{text{P}}}({T_{text{G}}} - {T_{text{P}}}) $$
(9)

式中, ReP为球形粉末颗粒的雷诺数; uG, ρG和μG分别为气相速度、密度和动黏度; AP为球形颗粒表面积; hP?E为粉末与气相之间的对流传热系数, 由Gunn’s法则[38]确定.

依据动量守恒、能量守恒原理, 粉末颗粒对气相的热力反作用为







$$ {S_{text{m}}} = frac{{ - displaystylesumnolimits_j {{{boldsymbol{F}}_{{
m{P }}- {
m{E}}}}} }}{{{V_{{text{mesh}}}}}} $$
(10)







$$ {S_{text{h}}} = frac{{ -displaystyle sumnolimits_j {{Q_{{
m{P }}- {
m{E}}}}} }}{{{V_{{text{mesh}}}}}} $$
(11)

其中, Vmesh为计算域中有限单元的的体积.

以SLM工艺中常用的316L不锈钢粉末为对象, 分别对SLM粉末铺设及粉末床熔融过程进行计算模拟. DEM模型中, 粉末颗粒密度、摩擦系数、恢复系数、导热系数等物性参数的设置详细见文献[13, 31], 其中: 粉末的摩擦系数通过“安息角标定法”校准; 恢复系数通过“自由落体回弹法”校准; 粉末的杨氏模量通常采用真实值的10% ~ 20%, 用以增加迭代时间步长而降低模型计算量. 熔池模型中, 熔池金属蒸汽(Fe)和环境气体(Ar)热物性参数主要参考于焊接熔池的蒸汽与保护气体物理参数, 详细见文献[39]. 为降低计算量: 粉末铺设模型中, 铺粉器方向(Y方向)采用2 mm的循环边界计算域; 粉末床熔融模型中, 采用2 mm × 3 mm × 4 mm计算域. 在计算粉末与气相耦合运动中: 仅考虑“粉末熔融模型”中熔池羽流(金属蒸汽与环境气体)与散体粉末颗粒之间热物性参数的动态耦合, 以获得粉末床的热/动力学演变规律[31]; 熔体的液?固相变过程不包含与耦合模块之中. 目前, 用于粉末运动建模的DEM软件平台有LIGGGTS, PFC, ROCKY-DEM等; 用于熔池建模的CFD软件平台主要有OPENFORM, FLOW-3D和FLUENT等; 基于上述耦合原理搭建数据交互模块, 可以实现SLM粉体热/动力学行为计算预测.


1.2
SLM成形过程监测


粉末铺设及熔融实验分别在课题组自行开发的SLM增材制造装备(YLR-200-SM-AC: 光纤激光器波长、功率和光斑直径分别为1070 nm和200 W和100 μm)上开展, 如图2所示. 粉末材料为粒径0 ~ 100 μm的SLM专用316L不锈钢粉末, 且粉末粒径可根据需求进行筛分配置.

如图2(a)所示, 粉末铺设实验在装备的铺粉机构上进行. 铺粉机构分别配置直角刮板式和辊筒式两种典型的铺粉模块. 辊筒直径及转动速度分为10 mm和2π rad/s. 当粉末颗粒被铺设在基板上之后, 采用0.1 mg精密天平(mettler-toledo ME104)测量基板上的粉末质量mT, 然后可计算粉末床的相对致密度







$$ {
ho _{text{R}}} = frac{{{m_{text{T}}}}}{{{
ho _{text{P}}}{{S}}H}} times 100% $$
(12)

其中, S和ρP分别基板表面积和粉末颗粒的材料密度.

图2(b)所示为SLM成形过程原位监测实验. 如图所示, 在成形腔体外安装一台高速光学相机(photron fastcam mini AX200, 最大采样率为每秒5000 帧). 在相机镜头前配置一个截止波长为250 ~ 800 nm的滤光片, 以降低羽流亮度, 增强图像对比度. 相机与建筑基底距离约400 mm, 视场12 mm × 5 mm, 采集图像1024 × 428像素. 通过我们改进的图像处理方法(支持向量机(SVM)和卷积神经网络(CNN)[40]), 提取并量化激光扫描过程中粉末层的特征. 激光扫描后的粉末床形貌可通过SEM成像法观测.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-2.jpg'"
class="figure_img
figure_type2 ccc " id="Figure2" />



图
2
SLM监测实验



Figure
2.
Experimental monitor on SLM



下载:
全尺寸图片
幻灯片



2.
结果与讨论



2.1
粉末铺设动力学行为



2.1.1
粉末流动物理机制

SLM粉末铺设过程中存在3种基本的流动物理机制: 粉末黏结、壁面边界和粉末渗流效应. 以刮板式粉末铺设为例, 图3(a)所示为粉末黏结机制, 其中, 粉末为不同尺寸的单一粒径. 分子范德华力引起的黏结力是散体粉末颗粒间存在的固有作用力, 其在球形粉末间的作用大小可用黏结系数B表示, 定义为范德华力与重力的比值



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
SLM粉末铺设的粉末流动数值模拟



Figure
3.
Simulated powder flowing in powder spreading process of SLM



下载:
全尺寸图片
幻灯片








$$ B = frac{{{F_{{text{c,12}}}}}}{{{m_{text{P}}}g}} propto frac{psi }{{{
ho _{text{P}}}R_{text{P}}^2}} $$
(13)

式中, ψ为粉末颗粒的表面能. 由式(14)可知, 对于给定粉末材料, 粉末粒径越小, 黏结效应越大. 如图3(a)所示, 随着粉末粒径从60 μm至10 μm变小, 由范德华力引起的黏结作用变强, 因而粉末在铺设过程中的团聚现象越严重, 越不利于形成致密均匀的粉末床.

图3(b)为壁面边界机制. 在漏斗送料、谷仓送料、渠道送料等流道颗粒流情况中[41], 由于流道特征尺寸与粉末颗粒尺寸接近同一量级, 流道壁面与颗粒之间容易形成瞬态“力链拱桥”[42], 降低粉末流动连续性. SLM粉末铺设过程中, 如图所示, 由于刮板与基板之间的间隙通道接近粉末尺寸, 这种壁面效应同样存在, 会降低粉末流动的连续性与稳定性, 导致粉末床致密性和均匀性下降. 并且, 层厚越小(通道越小)、粉末粒径越大, 则这种壁面阻隔作用越明显.

图3(c)为渗流机制. 渗流是颗粒物质在流动过程中的另一固有现象[43]: 流动过程中, 由于粉末颗粒之间存在尺寸和密度等物性差异, 密度大的颗粒和尺寸小的颗粒会逐渐下层, 出现颗粒分流. 图3(c)中, 粗粉末(50 ~ 80 μm)与细粉末(0 ~ 20 μm)按1:3质量比均匀混合. 如图所示, 在粉末铺设过程中, 由于渗流作用, 初始均匀混合的粉末出现分流/分离. 细粉末在流动中更倾向于下沉, 导致粉末床出现了一定的分层现象, 从而降低其均匀性. 并且, 粗粉末之间的空隙也导致粉床的致密性下降.

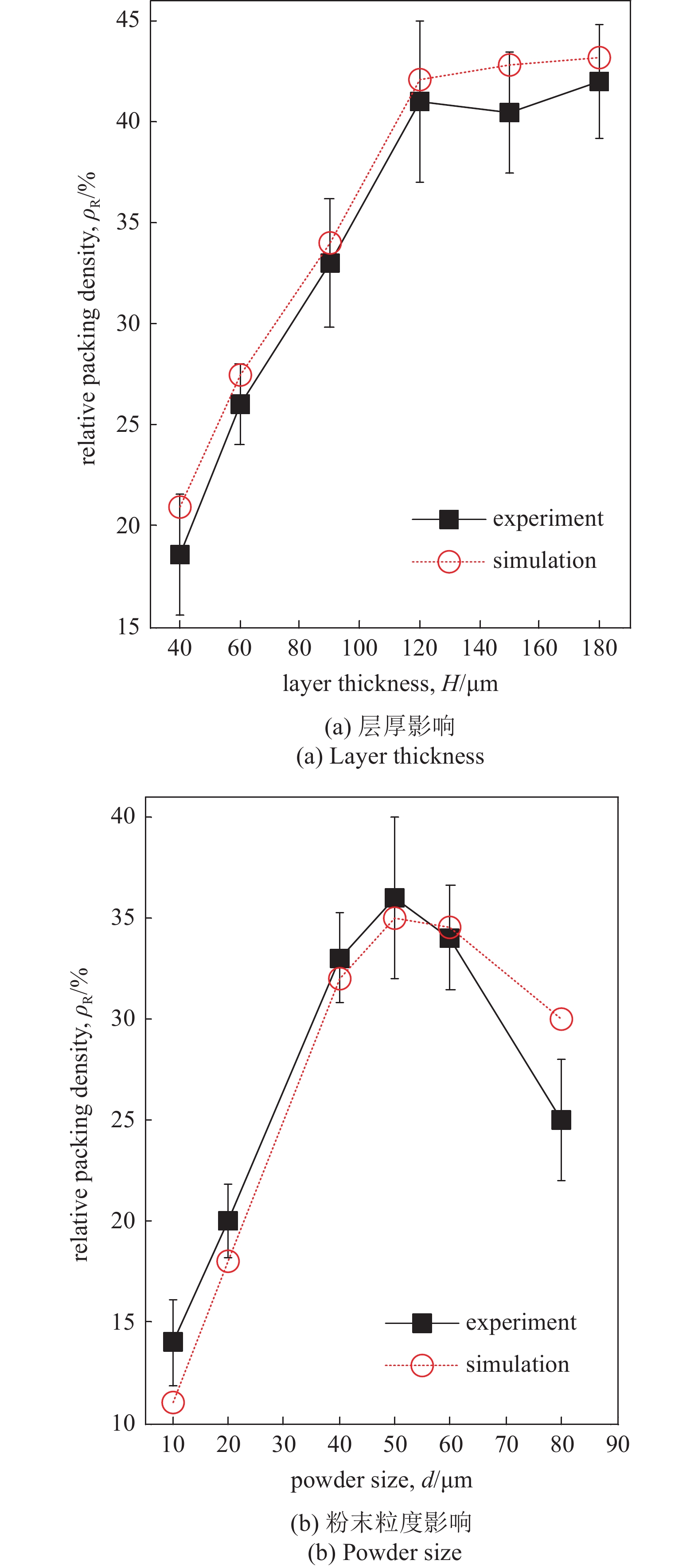
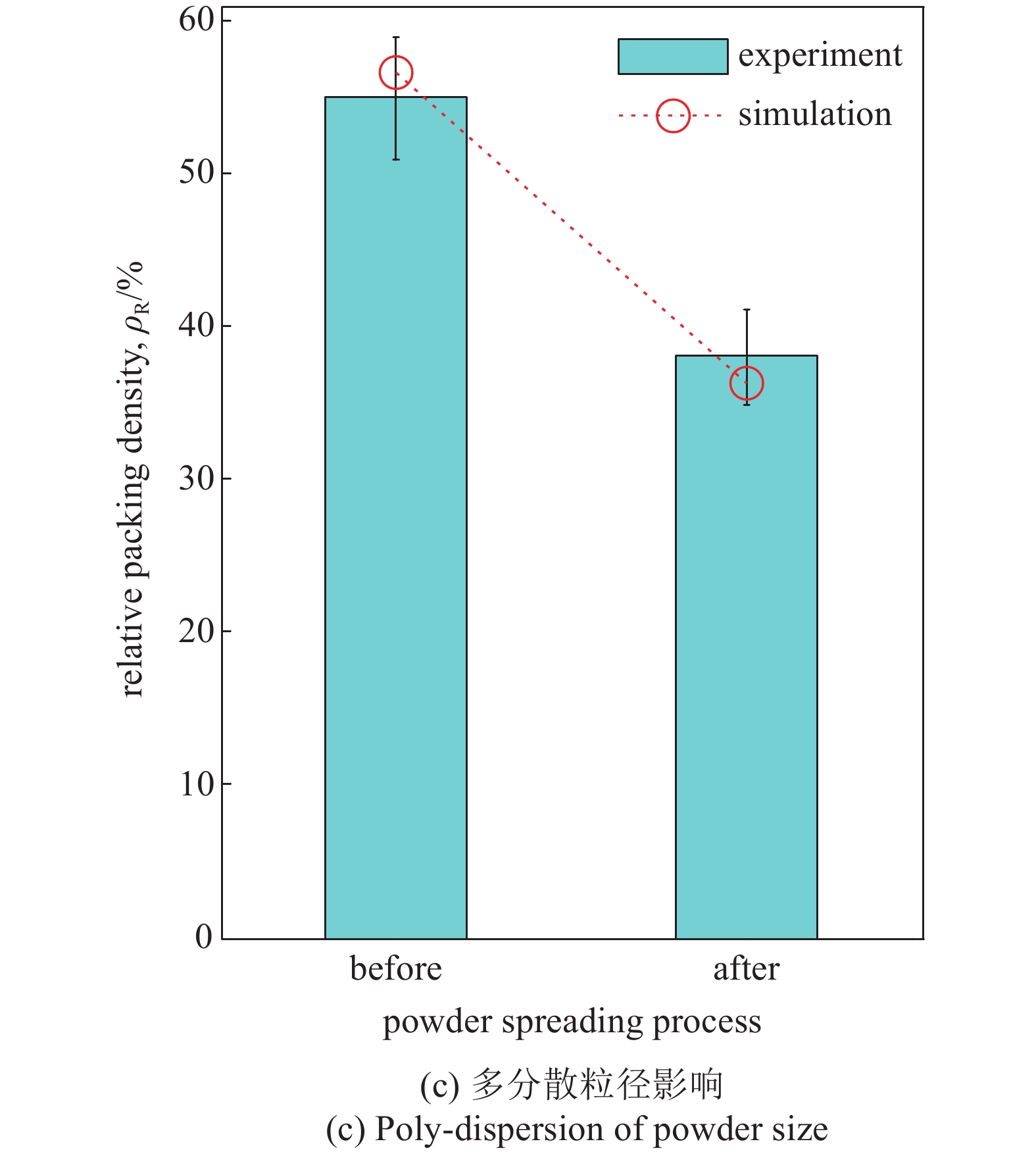
如上所述, 这3种主要物理机制均与粉末粒径等工艺参数紧密相关, 因此, 3种物理机制同时支配SLM的粉末铺设过程, 并决定粉末床最终的致密度等铺设质量. 以刮板式粉末铺设为例, 图4为实验和数值模拟中粉末床致密度随工艺参数的变化规律. 对于给定工况, 如图4(a)所示, 随着粉末床铺设层厚的增加, 壁面边界效应导致的粉末堵塞效果变弱, 粉末铺设过程中流动更顺畅, 因而粉末床的致密度逐渐增大. 如图4(b)所示, 随着粉末粒径逐渐变小, 壁面边界效应的削弱有利于粉末床致密度的提升, 然而, 黏结效应同时也增强且不利于粉末床致密度提升. 在大于约50 μm范围内, 壁面边界机制占主导, 因此致密度随粉末粒径减少而增大. 在小于50 μm范围内, 粉末黏结机制逐渐占主导作用, 因此致密度随粉末粒径减少而减小. 图4(c)为双峰粒径混合粉末的铺设致密度, 其中, 粗粉末与细粉末按1:3质量比均匀混合. 如图, 由于铺设过程的渗流分层, 铺设后的致密度远小于其初始致密度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-4-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4-1" />



4
粉末床致密度测试与模拟结果



4.
Experiment and simulation results showing the evolutions of packing density of powder layer with



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
粉末床致密度测试与模拟结果 (续)



Figure
4.
Experiment and simulation results showing the evolutions of packing density of powder layer with (continued)



下载:
全尺寸图片
幻灯片



2.1.2
粉末床挤压效应

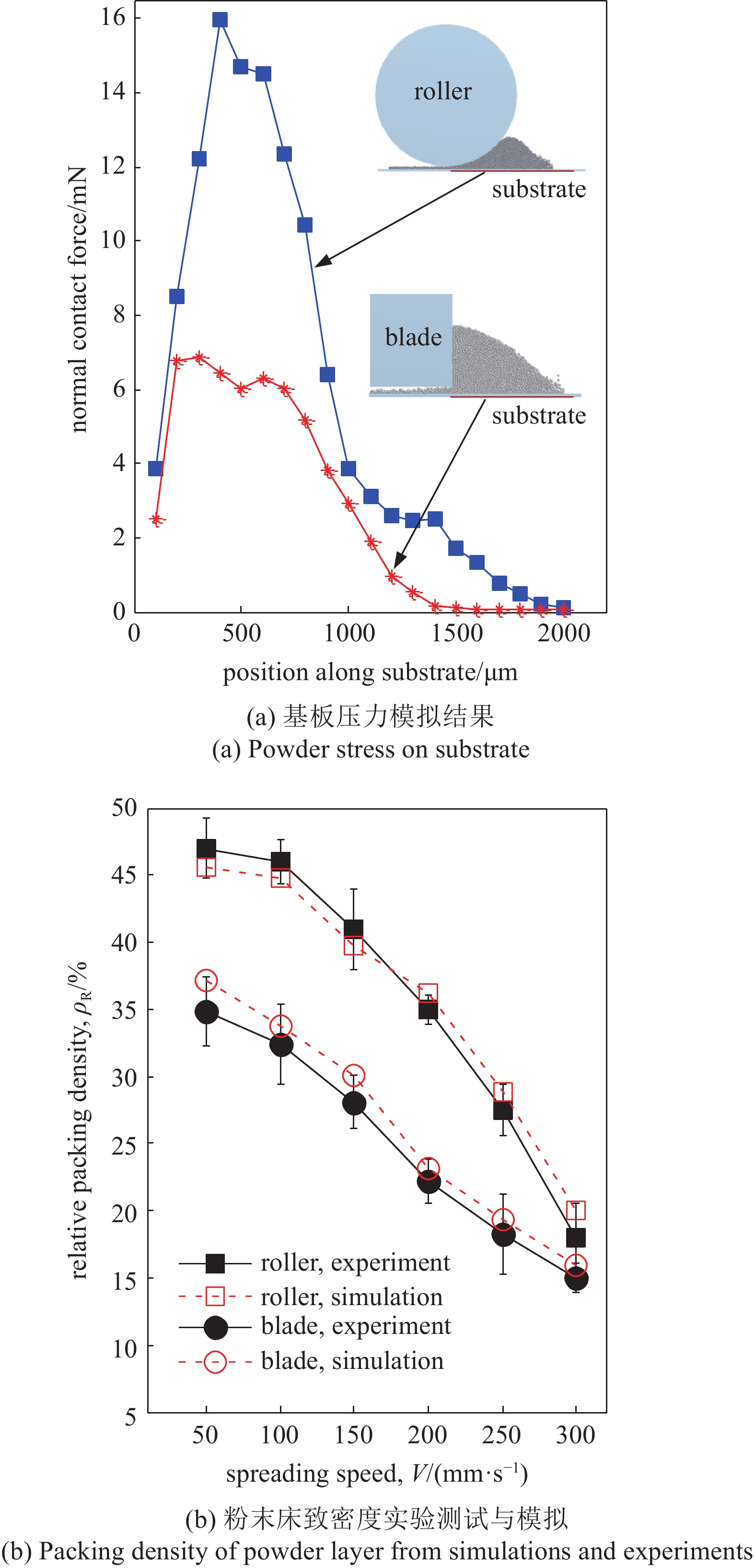
目前, 刮板式和辊筒式是两种典型的SLM粉末铺设方案. 通常直观地认为, 辊筒在铺设过程中对散体粉末具有挤压和紧实作用, 因此所获得的粉末床比刮板式更加致密. 图5为两种粉末铺设模式的对比. 如图所示, 在粉末粒径、铺粉速度、层厚等参数一致的情况下, 辊筒式的基板压力远大于刮板式(图5(a)), 其通过底部的粉末质量流也更高. 如图5(b)所示, 随着铺粉速度的增加, 两种模式的粉末床致密度均降低, 但是由于辊筒式的粉末压实效应, 其粉末床致密度均大于同等工艺参数条件下的刮板式铺粉. 值得注意的是, 虽然辊筒式可以获得更致密的粉末床, 但粉末对基板(或前一层熔融粉床)的压力更大, 由此导致的刮擦和碰撞也可能更严重. 在某些粉末床增材制造工艺中, 如文献[44], 辊筒严重的挤压和刮擦有可能中断或直接破坏整个零件的制造.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
刮板式与辊筒式粉末铺设对比



Figure
5.
Comparison between scraping type and counter-rolling type powder spreading



下载:
全尺寸图片
幻灯片



2.2
粉末床熔融热/动力学行为



2.2.1
飞溅与剥蚀运动

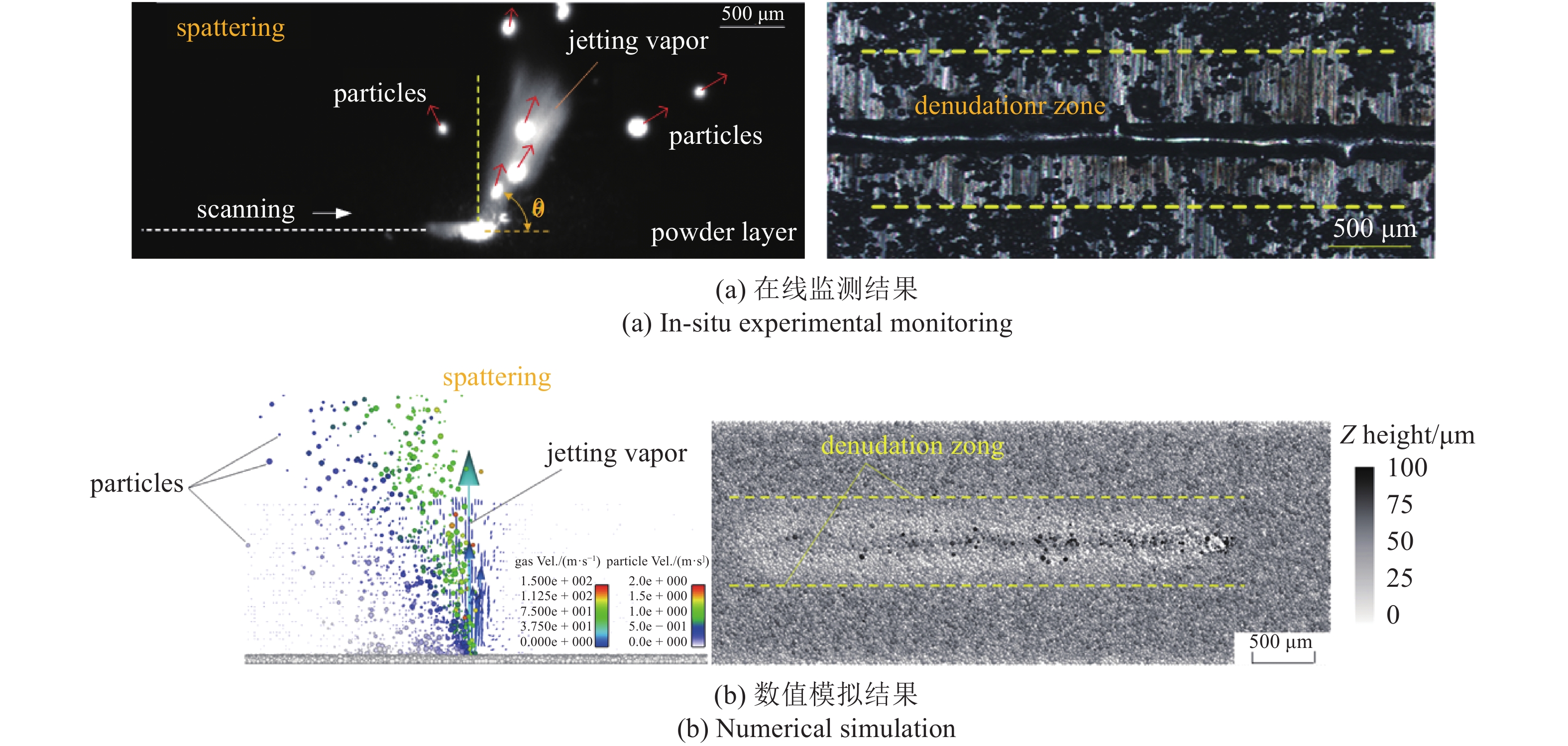
SLM激光对粉末床熔融过程中, 粉末床的飞溅与剥蚀是两个紧密相关的热/动力学现象. 如图6(a)所示, 高能束激光作用在粉末床并高速移动. 在激光作用范围内, 粉末颗粒在激光热作用下发生熔化与凝固. 但是, 激光作用范围之外, 即靠近熔池外围区域的粉末颗粒并非静止, 而是不停地向熔池区域移动. 最终, 沿着熔化道周围的粉末床形成了剥蚀[10]现象. 剥蚀区域的粉末颗粒变得更少, 因而不利于下一道激光熔融. 另外, 粉末颗粒在进入熔池的同时, 随着熔池蒸汽一起喷发, 形成飞溅[23]现象. 飞溅的粉末在重力下回落, 可能对粉末床造成撞击破坏, 也可能对冲击和破坏熔融的粉末床区域. 图6(b)的数值模拟较好地复现了粉末床飞溅和剥蚀运动的在线监测结果, 表明DEM/CFD联合建模仿真是计算和预测SLM粉末床热/动力学行为的有效手段.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-6.jpg'"
class="figure_img
figure_type2 ccc " id="Figure6" />



图
6
粉末床熔融过程中的飞溅与剥蚀运动



Figure
6.
Spattering and denudation in powder bed fusion process



下载:
全尺寸图片
幻灯片



2.2.2
多相耦合驱动机制

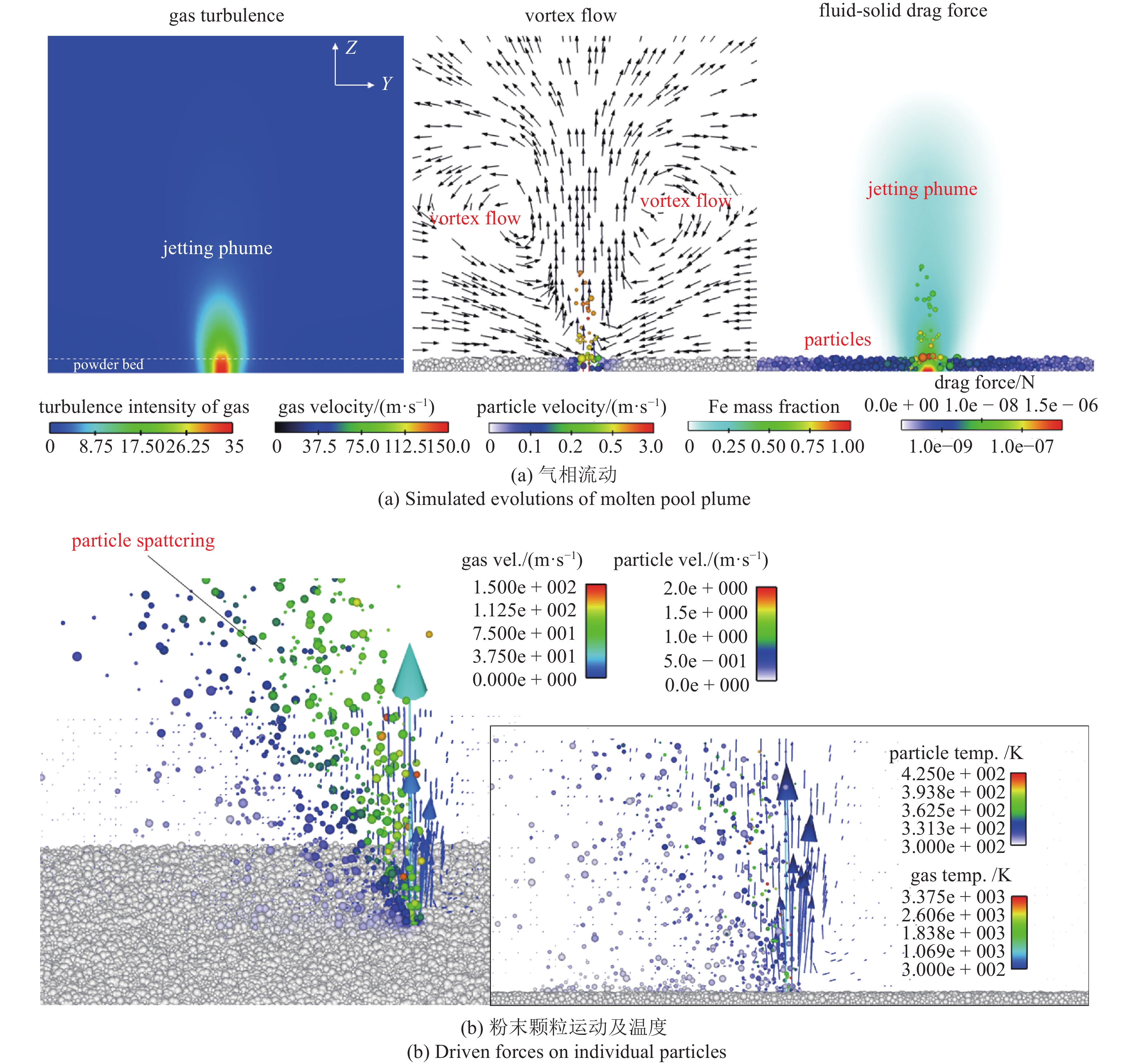
SLM粉末床的剥蚀和飞溅现象本质上是一个流?固热力耦合驱动的物理过程. 如图7(a)计算结果显示: 激光对粉末床熔融过程中, 金属蒸汽(Fe)从熔池中高速喷发, 并且由于能量的湍流耗损和扩散, 形成辐射状的羽流; 喷发的金属蒸汽带动周围的环境保护气体(Ar), 从而在熔池周围形成了内旋的涡流; 内旋的涡流在粉末颗粒上产生流?固驱动力. 如图7(b)所示, 当涡流对粉末的在流?固拖拽力超过粉末之间的摩擦阻力情况下, 内旋的环境气体涡流驱动熔池周围的粉末颗粒向熔池内运动, 形成剥蚀现象. 另外, 粉末颗粒被吸卷进入熔池之后, 一部分颗粒又被高速喷发的金属蒸汽驱动, 顺着羽流向外喷射而形成飞溅现象. 由于高速金属蒸汽的驱动力远大于粉末本身重力, 粉末的飞溅速度往往可以达到数米每秒.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
粉末颗粒?气相耦合流动



Figure
7.
Gas-solid coupled driving force on powder particles



下载:
全尺寸图片
幻灯片


根据上述分析, 通过以下几种方法可削弱或消除粉末剥蚀和飞溅对SLM成形的负面影响. 首先, 可以在成形腔体内安装内循环的侧向风, 将飞溅粉末颗粒吹除清理, 以达削弱飞溅负面影响的效果. 这种方法目前在SLM成形装备普遍使用[33]. 另外, 还可以从源头上消除粉末剥蚀和飞溅运动. 比如, 可以通过预烧结将准备熔融区域的粉末固定, 用以抵抗内旋涡流和羽流的驱动力, 进而消除剥蚀和飞溅运动. 或者, 可以通过调节激光能量的分布状态, 使熔池温度保持在沸点以下, 从源头上消除羽流和环境气体流动, 进而达到消除粉末剥蚀与飞溅运动. 以上方法值得进一步探索和研究.


2.2.3
热浮力驱动机制

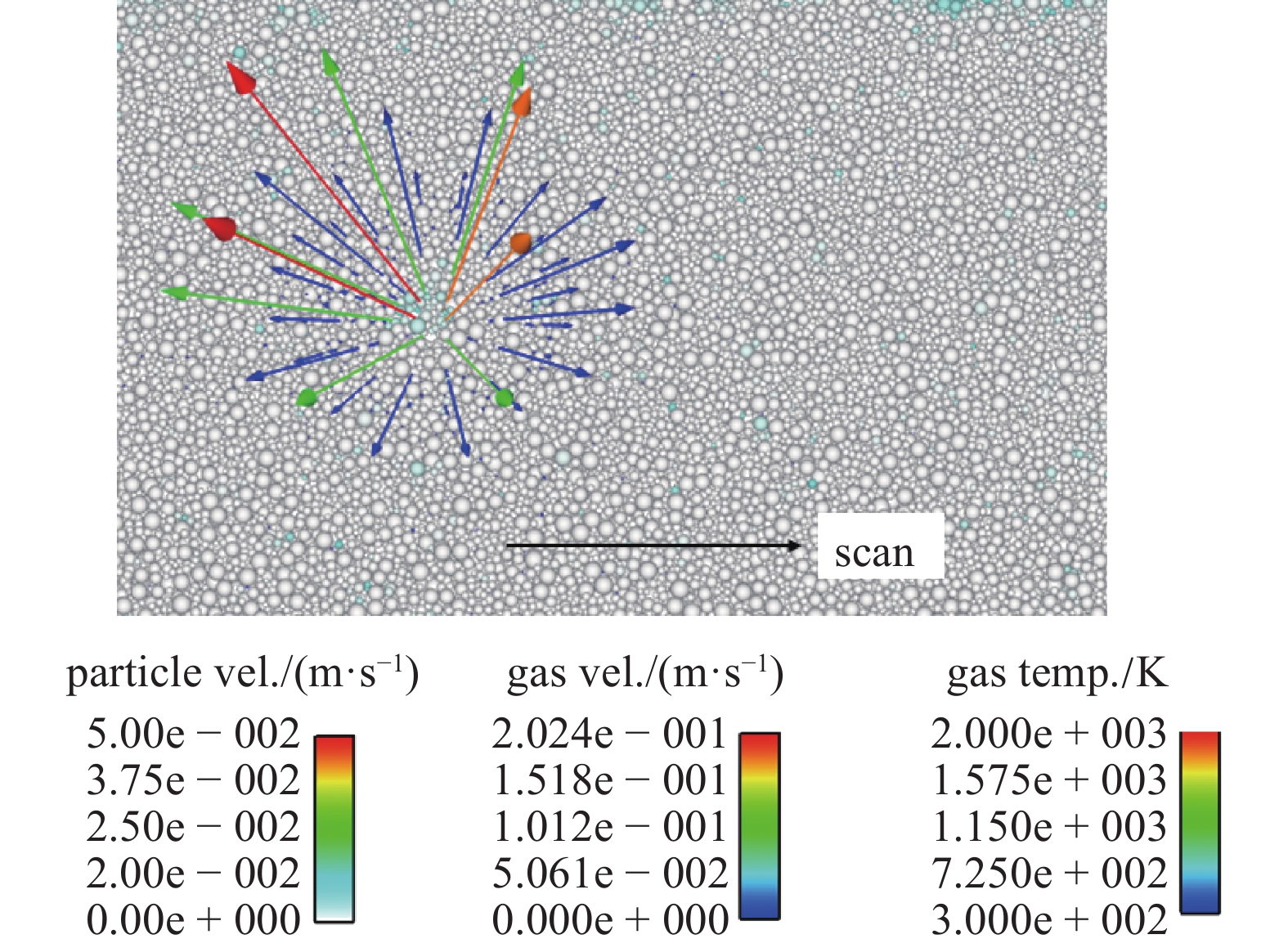
除了羽流引起的驱动力, 部分****认为环境气体受热膨胀的热浮力(thermal buoyancy force[11])也是引发粉末床颗粒运动的因素. 为验证此推测, 将DEM/CFD模型中的金属蒸汽模块去除后重新计算了SLM粉末床的扫描过程. 正常情况下, 金属蒸汽从熔池喷发, 引起环境气体内旋涡流, 并由此带动粉末颗粒运动而形成剥蚀和飞溅现象. 当金属蒸汽从模型中去除之后, 如图8所示, 环境气体(Ar)在激光热量作用下发生膨胀并形成热浮力流动. 但是, 与羽流引起的内旋涡流不同, 热浮力流动是以激光光斑为中心, 形成由内向外的辐射式流动. 另外, 如图所示, 热浮力引发的气体流动速度约为2 m/s, 远小于羽流的喷射速度(约150 m/s, 如图7). 因此, 虽然热浮力流动对粉末有一定加热和拖拽作用, 但流动强度不足以驱动粉末颗粒运动. 如图8所示, 颗粒在粉末床中的运动速度及形态变化可忽略不计. 由此可见, 环境气体的热浮力不是粉末床剥蚀和飞溅运动的主要引发因素.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-403-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
环境气体热浮力作用下的颗粒行为演变计算. 其中, 金属蒸汽羽流被去除



Figure
8.
Evolutions of trajectory and temperature of powder particles under the thermal buoyancy effects without the metal vapor



下载:
全尺寸图片
幻灯片



3.
结 论


针对金属粉末介质在SLM成形过程中的热/动力学行为, 介绍了DEM与CFD联合建模仿真在SLM建模仿真方面的应用. 结合光学监测等实验手段, 从颗粒尺度探讨了SLM的粉末铺设和粉末熔融过程的物理行为机制, 主要结论如下.

(1) SLM粉末铺设存在3种物理机制: 粉末黏结、壁面边界和粉末渗流. 其中, 粉末黏结效应由粉末颗粒间的范德华黏结力导致, 在铺粉过程中容易引起粉末颗粒的团聚, 不利于形成致密的粉末床. 壁面边界效应由颗粒介质的力链结构特征导致, 在铺粉过程中可引起粉末堵塞. 粉末渗流主要由粉末颗粒间的尺寸/密度差异导致, 容易引发颗粒流分离和分层, 不利于形成均匀的粉末床. 3种机制相互竞争, 共同决定粉末床的致密度等铺设质量.

(2)辊筒式铺粉由于对粉末的挤压作用, 其粉末流量更大、所得粉末床也比刮板式更致密. 但是, 辊筒式铺粉的基板/熔融层所受压力也更强, 更容易对已成形层面造成挤压或者刮擦损伤.

(3)激光对粉末床熔融过程中, 金属蒸汽从沸腾的熔池中高速喷射而出, 形成辐射状羽流. 羽流带动环境保护气体流动, 在熔池周围形成内旋的涡流. 在流?固热力耦合作用力下, 内旋的涡流驱动熔池周围的粉末颗粒运动, 形成剥蚀现象. 同时, 吸卷进入熔池的部分粉末颗粒又被高速喷射的羽流驱动, 形成粉末飞溅现象. 因此, SLM粉末床的剥蚀和飞溅本质上是流?固热力耦合的多相流行为.

(4)由于热浮力效应, 环境保护气体受热后膨胀、并在熔池周围形成向外辐射的流场. 但是, 热浮力引起的环境气体流动没有内旋的涡流, 并且, 其流动速度远小于熔池羽流引发的流动速度. 因此, 热浮力引起的环境气体流动不足以驱动粉末床颗粒, 在剥蚀和飞溅行为中不起主导作用.

基于DEM与CFD耦合建模, 可以计算和预测SLM中粉末颗粒的温度和运动状态. 结合光学在线监测等实验方法, 可以对SLM成形过程中粉末颗粒物质的热/动力学行为进行有效探索.

相关话题/计算 运动 激光 成形 环境
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 选区激光熔化成形区粗糙表面对铺粉质量的影响:离散元模拟
    引言选择性激光熔化(SLM)通过逐层铺粉和选择性熔化粉末来打印三维零件[1].增材制造零件的质量受许多参数影响,例如激光功率[2]、扫描速度[3]、扫描策略等[4].打印零件之前的一个关键程序是在建筑平台上铺粉.在铺粉过程中,粉末的状态会影响铺粉过程,因为粉末在基板上的流动能力决定着每一层粉末的连续 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 激光定向能量沉积的粉末尺度多物理场数值模拟
    引言金属增材制造技术作为一种具有变革性的先进数字化制造技术,在航空、航天、交通等领域中具有广泛的应用前景[1-2],得到了国内外****和工业界的广泛关注和高度重视.同轴送粉激光定向能量沉积(laserdirectedenergydeposition,L-DED)技术则是其中的一种代表性技术,具有成 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于半解析VOF-DEM的激光直接沉积多尺度过程模拟
    引言与传统的铸造等减材制造技术相比,增材制造技术有着设计灵活、制造周期短、制造复杂几何构型能力强等不可替代的优越性,因此逐渐被广泛运用到航空航天精密器件、生物组织或义肢、梯度功能材料[1]、印刷电子[2],甚至土木工程领域的大型构件的制造中,且被认为是“第三次工业革命”的标志[3].其中,基于金属粉 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 增材制造微结构演化及疲劳分散性计算
    引言增材制造通过不断添加材料来完成零件的加工成型,满足了工业对零件形状、功能、材料的更高要求,成为当前材料加工技术发展的前沿方向.与传统制造工艺相比,增材制造在成形原理、材料形态、制件性能上发生了根本改变,具有材料浪费少、加工工序少、加工周期短、零件结构设计自由、易于实现形状复杂零部件快速成型等优点 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 激光冲击下CoCrFeMnNi高熵合金微观塑性变形的分子动力学模拟
    引言激光冲击强化技术利用激光穿过约束层,作用于烧蚀层产生大量等离子体,等离子体继续吸收激光能量发生爆炸从而产生冲击波作用于金属表面.当冲击波峰值压力大于材料的屈服强度时,激光冲击使材料发生超高应变率(>106s?1)的塑性变形,造成材料表面出现残余压应力分布并且发生表面晶粒细化[1-3].与传统的机 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一种新的玻尔兹曼方程可计算模型构造与分析
    引言近年来,随着对临近空间战略意义认识的加深,各航空航天大国发展了众多临近空间飞行器.为满足长航时、大载荷、高超声速巡航等需求,这类临近空间飞行器通常整体尺寸较大,各部件间差异显著,飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象,传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 页岩凝析气藏相平衡的快速准确计算方法
    引言随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注,天然气作为一种相对较为清洁的能源得到了广泛的重视[1].近年来在非常规油气藏勘探和开发技术上的迅猛发展,使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2].中国 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.