删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

激光定向能量沉积的粉末尺度多物理场数值模拟

本站小编 Free考研考试/2022-01-01


引言


金属增材制造技术作为一种具有变革性的先进数字化制造技术, 在航空、航天、交通等领域中具有广泛的应用前景[1-2], 得到了国内外****和工业界的广泛关注和高度重视. 同轴送粉激光定向能量沉积(laser directed energy deposition, L-DED)技术则是其中的一种代表性技术, 具有成形精度高、速度快且加工尺寸限制小的优点. 该技术主要通过输送气流裹挟金属粉末进入高功率激光热源作用区域, 使材料熔化沉积在基体表面凝固后形成熔覆层, 通过逐道扫描逐层搭接实现构件的制备. 现阶段, 在实际加工过程中, L-DED成形件受制于表面质量差、尺寸偏差大等形貌缺陷[3-4], 以及微裂纹、孔洞等冶金缺陷[5-6]. 这些缺陷制约了该技术的进一步发展和广泛应用. 因此探究不同工艺参数下的熔覆层成形机理, 对实现增材制造控形控性以及提高成形效率具有重要意义. 然而, L-DED制造过程是一个十分复杂的多尺度、多物理场耦合问题, 包括高度动态且随机性强的粉末传输[7-8]、高热源能量密度下的激热激冷和金属熔池的动态凝固, 并且涉及工艺参数量巨大[9-10], 单纯通过实验手段进行熔覆层成形机理研究十分困难且具有效率低、周期长、代价高昂等缺点[11]. 因此, 采用数值模拟方法研究该问题是一项重要且高效的手段.

目前, 国内外****针对L-DED的熔覆层成形机理已开展了相关研究工作. 依据所建立的分析模型不同, 已有L-DED数值模拟工作可大致分为两类. 第一类为基于连续体假设的热流耦合模拟[12-13], 将落入熔池的粉末等效成为连续体, 不显式考虑粉末的输送过程, 侧重于高效求解熔覆层形貌与温度场. 为简化计算, Knapp等[14]依据实验结果将落入熔池的粉末所形成的熔覆层假设为半椭球形状并结合生死单元技术, 建立了L-DED的热流耦合模型, 研究了考虑Marangoni效应的熔池内流动和传热过程. Lian等[15]则将粉末所形成的熔覆层假设为立方体, 建立了更加高效的L-DED热流耦合模型, 分析了IN718合金单道多层中各层熔池的尺寸和温度场演化过程. 为获得更为准确的熔覆层演化形貌. Zhao等[16]则通过水平集函数法进行熔池自由表面追踪, 避免了对熔覆层形貌的假设, 研究了L-DED成形316L不锈钢材料, 所预测的熔池尺寸与实验结果吻合良好. 虽然可高效求解熔池的尺寸与温度场, 该类模型由于未显式考虑粉末输送过程及其对熔池的影响, 并暗含进入熔池的粉末材料温度为同一均值的假设, 则无法用于研究与粉末颗粒相关的熔覆层成形机理.

第二类L-DED数值模拟工作则为显式考虑粉末的热流耦合模型, 简称为粉末尺度热流耦合模型. 在该类模型中, 粉末处理方式依据求解精度不同可分为3种. 第1种是将粉末在控制方程中以源项的形式予以考虑[17-18], 即在熔池上表面施加相应携带温度、速度信息的质量源. 基于该种方式, Sun等[19]模拟了L-DED成形316L不锈钢合金材料单道熔覆层形貌, 结果表明粉末对于其在熔池落点的流场和温度场有显著的影响, 即导致落点处熔池温度降低并且流场方向发生改变. 第2种方式是采用拉格朗日质点法模拟粉末的输运过程, 其中将粉末等效为一个包含材料信息(质量、速度、温度)的质点[20-21]. 基于该种方式, Wang等[22]建立了L-DED全过程的粉末尺度热流耦合模型, 分析了激光焦平面和加工平面相对位置与单道多层的表面不平整缺陷的内在关联, 结果表明多层打印中正离焦状态是造成上表面粗糙的关键因素. 第3种方式则是对粉末颗粒采用离散元[23-24]或者无网格法[25]进行精确离散求解, 对粉末输送、落入熔池过程进行统一建模求解. 针对该类高精度粉末尺度模型, Dao和Lou[26]采用光滑粒子流体动力学无网格法进行求解, 初步模拟了处于半熔或未熔状态的粉末落入熔池的全过程, 但限于计算规模小而没有将数值模拟结果与实验结果进行对比. 对比3种方法可知, 计算规模和精度依次提高, 但计算效率和求解问题的规模依次降低. 同时, 相比于第3种方法, 前两种方法均将进入熔池粉末的温度设为同一温度值, 如液相线温度, 并没有准确考虑粉末依赖于飞行路径的加热过程以及相应的粉末基板能量分配比例. 然而, Tan等[27]开展的不同粉末速度下L-DED单层单道实验结果表明, 粉末落入熔池前的温度分布和粉末基板能量分配比例对实际熔覆层形貌具有显著的影响. 因此, 亟需发展一种即考虑依赖于飞行路径的粉末温度分布以及相应的粉末基板能量分配比例, 又具有高效计算效率的L-DED粉末尺度多物理场模型.

本文在第2种粉末尺度的热流耦合模型基础上, 发展了激光-粉末交互拉格朗日质点模型, 并结合熔池的热流耦合模型, 建立了考虑激光-粉末-熔池交互过程的粉末尺度多物理场模型. 基于该模型, 本文预测了不同工艺参数、送粉模式下TC17合金材料单道熔覆层尺寸与形貌和相应的粉末温度分布和粉末基材能量吸收比, 揭示了L-DED技术单道熔覆层成形机理并深入讨论了粉末温度对熔覆层形貌的影响机理.


1.
多物理场模型及其实现


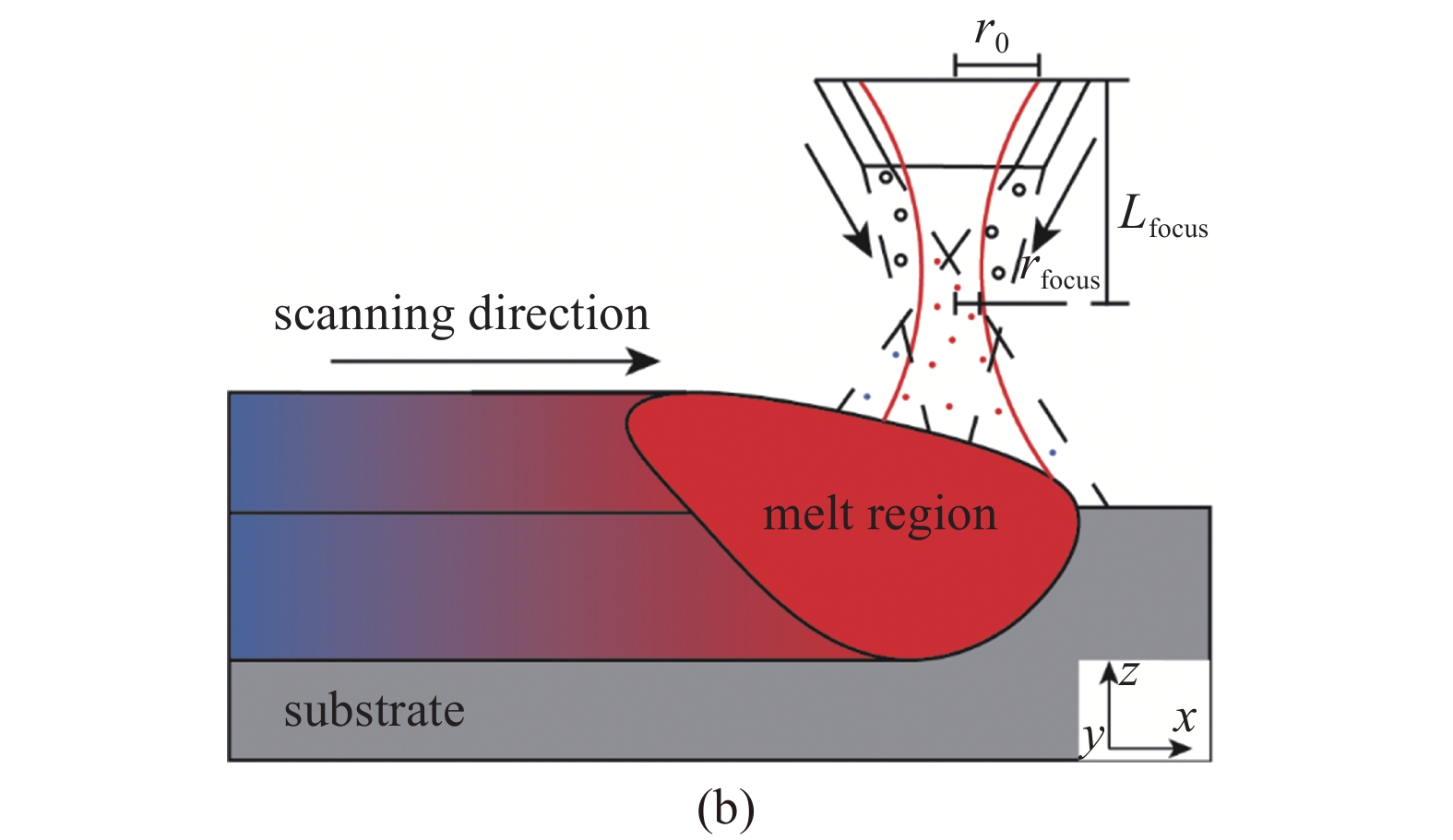
针对激光直接能量沉积增材制造技术, 本文建立了考虑了激光-粉末-熔池交互过程的高保真多物理场模型, 如图1所示. 其中, 全局坐标系以激光扫描方向为x轴正向, 建造方向为z轴正向, 垂直于xz平面的方向为y轴正向; 高保真多物理场模型包括3部分: 激光高斯面热源模型、粉末颗粒的拉格朗日质点模型、金属熔池的热流耦合模型, 具体如下.



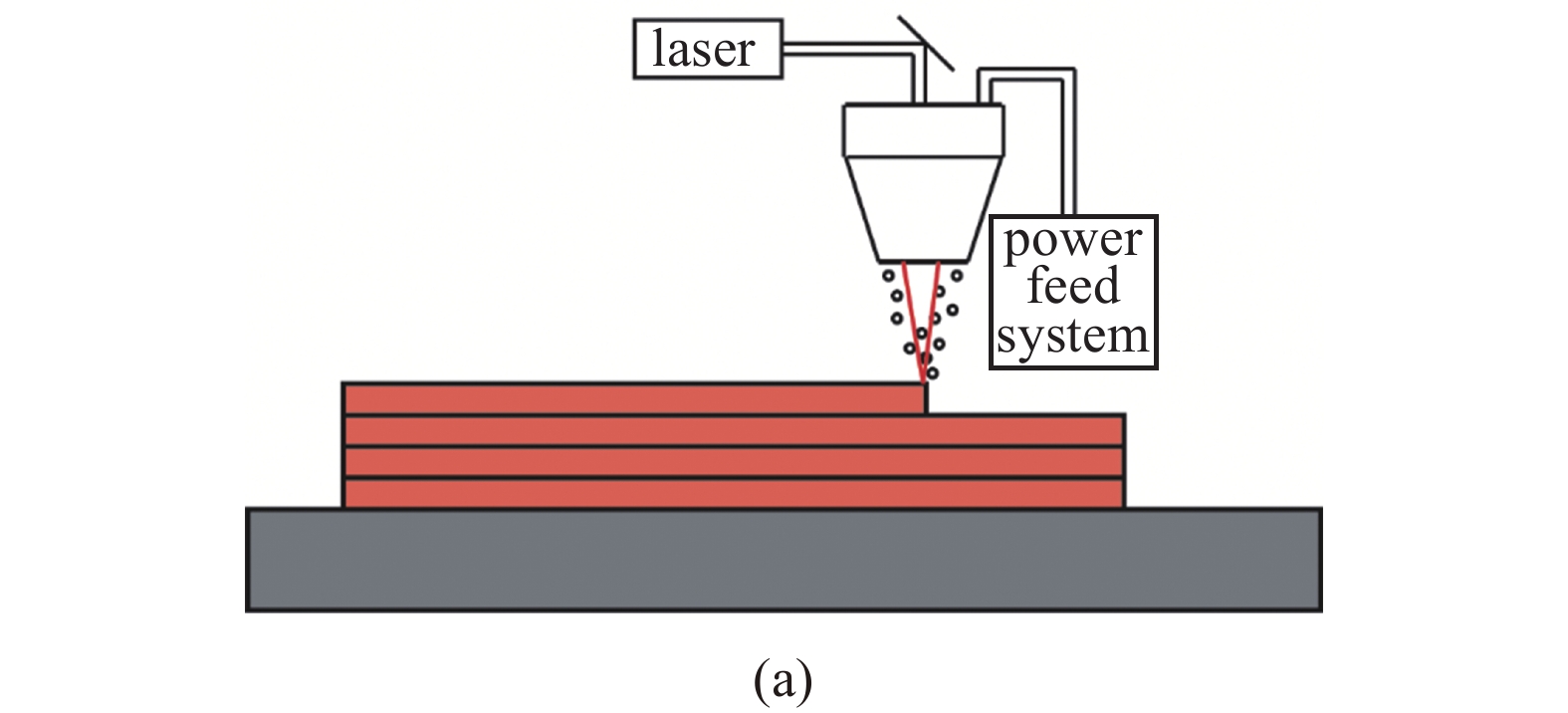onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-1-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
(a)激光DED成形原理; (b)高保真多物理场模型



Figure
1.
(a) Schematic diagram of laser DED. (b) High fidelity multi-physics model



下载:
全尺寸图片
幻灯片



1.1
激光高斯面热源模型


为简化计算, 本文假设激光能量在光束横截面上服从高斯分布, 如图1(b)所示. 不考虑粉末遮蔽的情况下, 激光照射范围内的热流密度$ {q_l}(x,y,z) $采用下式计算







$$ {q_l}(x,y,z) = frac{{2P}}{{{text{π}} {r^2}(z)}}{exp{left{ { - frac{{2left[ {{{left( {x - {x_0} - vt}
ight)}^2} + {{left( {y - {y_0}}
ight)}^2}}
ight]}}{{{text{π}} {r^2}(z)}}}
ight}}} $$
(1)

其中, $P$为热源功率, $ ({x_0},{y_0},{z_0}) $为激光中心初始坐标, $v$表示激光沿扫描方向的移动速度. $r(z)$为激光下方不同z位置处光束横截面半径, 如下







$$ r(z) = {r_{{text{focus}}}} + frac{{left| {z - {z_{{text{focus}}}}}
ight|}}{{{l_{text{focus} }}}}({r_0} - {r_{{text{focus}}}}) $$
(2)

其中, $ {r_0} $与$ {r_{{text{focus}}}} $分别为激光半径与激光焦平面半径, $ {z_{{text{focus}}}} $为激光焦平面的坐标, $ {l_{text{focus} }} $为激光焦距.


1.2
粉末颗粒的拉格朗日质点模型


激光-粉末-熔池的交互问题极其复杂, 且具有较强的随机性. 本文采用如下假设建立粉末与激光以及粉末与熔池交互作用的拉格朗日质点模型.

(1)粉末为实心球体, 在粉末源中均匀分布;

(2)粉末以给定的速度在空中飞行, 略去粉末颗粒之间的相互作用;

(3)粉末颗粒受激光照射面为上半球面, 彼此不存在能量遮蔽情形, 略去其与外界环境的对流换热;

(4)粉末若处于熔化状态并处于液体中, 则完全被吸收, 否则独立存在.

粉末-激光交互拉格朗日质点模型的基本思想是, 通过积分粉末颗粒空中飞行轨迹上所获得的温升获得粉末撞击熔池或熔覆层表面前的温度. 粉末在给定喷嘴处均匀生成, 以给定速度下落并经过激光作用区域, 落入待加工表面. 在该模型中, 采用时间步长$ Delta t $对粉末空中飞行总耗时${t_f}$进行离散, 并根据当前粉末颗粒位置结合式(1)和式(2)计算每个时间步的温升; 飞行总耗时则由粉末喷嘴口到粉末沉积表面竖直方向距离$Delta h$, 以及粉末z方向速度${v_z}$决定. 生成相同粉末数的激光作用时间${t_p}$由送粉速率$ {V_f} $和喷嘴同时喷出粉末颗粒总数$ {n_p} $确定







$$ {t_f} = frac{{Delta h}}{{{v_z}}} $$
(3)







$$ {t_p} = frac{{{n_p}}}{{{V_f}}}{m_p} $$
(4)

由式(1)和式(2)可知, 第i个时间步, 粉末颗粒p的温度值为$ T_p^i = T_p^{i - 1} + Delta T_p^i $. 其中, $ Delta T_p^i $为当前步温升, 计算如下







$$ Delta T_p^i = left{ {begin{array}{*{20}{l}} {dfrac{1}{{{m_p}{c_p}}}{eta _p}{A_p}{q_l}(x_p^i ,y_p^i,z_p^i)Delta t}{text{,}}&{T_p^i leqslant {T_s}{text{ or }}T_p^{i - 1} geqslant {T_l}} {dfrac{{{T_l} - {T_s}}}{{{m_p}Delta H}}left[{eta _p}{A_p}{q_l}(x_p^i ,y_p^i,z_p^i)Delta t - {m_p}{c_p}({T_s} - T_p^{i{-}1}) + {m_p}Delta Hdfrac{{{T_s} - T_p^{i{-}1}}}{{{T_l} - {T_s}}}
ight],}&{T_p^{i{-}1} leqslant {T_s}{text{ and }}{T_s} < T_p^i leqslant {T_l}} {dfrac{{{T_l} - {T_s}}}{{{m_p}Delta H}}{eta _p}{A_p}{q_l}(x_p^i ,y_p^i,z_p^i)Delta t}{text{,}}&{{T_s} < T_p^{i{-}1} < {T_l}{text{ and }}{T_s} < T_p^i leqslant {T_l}} {dfrac{1}{{{m_p}{c_p}}}left[{eta _p}{A_p}{q_l}(x_p^i ,y_p^i,z_p^i)Delta t - {m_p}Delta Hdfrac{{{T_l} - T_p^{i{-}1}}}{{{T_l} - {T_s}}} + {m_p}{c_p}({T_l} - T_p^{i{-}1})
ight],}&{{T_s} < T_p^{i{-}1} < {T_l}{text{ and }}T_p^i > {T_l}} end{array}}
ight. $$
(5)

其中, ${m_p}$为粉末颗粒质量, ${A_p} = 2{text{π}} r_p^2$为粉末受激光加热的面积, $ {r_p} $为粉末颗粒半径, ${eta _p}$为粉末的激光能量吸收率, $ (x_p^i ,y_p^i,z_p^i) $则由粉末颗初始位置、粉末颗粒速度和当前时间确定, 并根据粉末坐标与激光中心的相对距离, 确定对应位置热流密度$ {q_l}(x_p^i ,y_p^i,z_p^i) $. $ {T_s} $和$ {T_l} $分别为材料的固相线和液相线温度, $ Delta H $为固液相变焓值.

进一步, 本文采用粉末空中飞行时吸收激光能量与基板表面吸收激光能量之比度量粉末的遮蔽效应[28]. 依据粉末飞行时间${t_f}$与激光作用时间${t_p}$的大小关系, 粉末吸收能量计算为







$$ EP approx left{ {begin{array}{*{20}{l}} {displaystylesumlimits_{p = 1}^{{N_p}} {left[ {sumlimits_{i = 1}^{{t_f}/Delta t} {{eta _p}{A_p}{q_l}(x_p^i ,y_p^i,z_p^i)Delta t} }
ight],} }&{{t_p} geqslant {t_f}} {dfrac{{{t_{fp}}}}{{{t_f}}}displaystylesumlimits_{p = 1}^{{N_p}} {left[ {displaystylesumlimits_{i = 1}^{{t_f}/Delta t} {{eta _p}{A_p}{q_l}(x_p^i ,y_p^i,z_p^i)Delta t} }
ight],} }&{{t_p} < {t_f}} end{array}}
ight. $$
(6)

其中, $ {t_{fp}} $表示${t_f}$及${t_p}$的最小整数倍. 相应的, 激光总输入能量为$EL = P{t_p}$或$ EL = P{t_{fp}} $. 根据粉末吸收能量, 基板上表面吸收的能量为







$$ EM = eta left(EL - frac{1}{{{eta _p}}}EP
ight) $$
(7)

由式(6)则可计算基板上表面的等效激光吸收率为${eta ^{text{*}}} = dfrac{eta }{{{eta _p}}}left({eta _p} - dfrac{{EP}}{{EL}}
ight)$. 本文定义$ EP/EM $为粉末基材能量吸收比.

粉末落入熔池或基板表面, 其处理方式为: 若粉末颗粒温度达液相线温度, 则将其动量、体积、温度映射到其所在的流体网格单元上, 并将该粉末颗粒进行删除; 若粉末颗粒未熔化, 则保留该粉末并将其按非弹性碰撞处理, 并将其粘附于所在单元.


1.3
金属熔池的热流耦合模型


本文不考虑材料凝固区域的热应力/应变问题以及保护气体和粉末载气对熔池的影响, 假设金属熔池内液体的流动可视作不可压牛顿流体, 材料凝固区域则可视作高黏性系数无流速的液体区域. 因此, 该热?流耦合问题的控制方程采用欧拉描述, 包括连续性方程、动量守恒方程和能量守恒方程以及相应的热?流边界条件和初始条件, 具体如下[29-30].

连续性方程







$$ nabla cdot {boldsymbol{u}} = dot m $$
(8)

动量守恒方程







$$ begin{split} &frac{{partial
ho {boldsymbol{u}}}}{{partial t}} + nabla cdot left( {
ho {boldsymbol{uu}}}
ight) = - nabla p + &qquad nabla cdot (mu nabla {boldsymbol{u}}) +
ho {boldsymbol{g}} - {K_0}frac{{{{(1 - {f_l})}^2}}}{{f_l^3 + B}}{boldsymbol{u}} + {{boldsymbol{p}}_p} end{split} $$
(9)

能量守恒方程







$$ begin{split} &frac{{partial
ho h}}{{partial t}} + nabla cdot left( {
ho {boldsymbol{u}}h}
ight) = nabla cdot left(frac{k}{{{c_p}}}nabla h
ight) - &qquadfrac{{partial (
ho Delta H)}}{{partial t}} - nabla cdot left( {
ho {boldsymbol{u}}Delta H}
ight) + s end{split} $$
(10)

其中, $ {boldsymbol{u}} $为流体速度, $ dot m $表示熔池有效捕获的粉末质量, $
ho $为流体密度, $t$为时间, $p$为压力, $ mu $为流体黏性系数, $ {boldsymbol{g}} $为重力加速度, $ {K_0} $表示熔池在多孔介质中流动的拖曳力系数, $ {f_l} $代表液体体积分数, B为避免分母为0而设置的小数, $ {{boldsymbol{p}}_p} $为有效捕获的粉末所提供的动量, $h$为焓值, $k$, $c$分别为材料热传导系数和比热容, $ s $为体热源, 具体表示由被熔池有效捕获粉末而带来的能量输入以及熔池与未熔粉末发生的热量交换. 本文中, $ dot m $, $ {{boldsymbol{p}}_p} $和$ s $采用下式计算







$$ dot m = {n^ * }{m_p}/{V_{{text{cell}}}}qquad $$
(11)







$$ {{boldsymbol{p}}_p} = {n^ * }{m_p}{{boldsymbol{v}}_p}/{V_{{text{cell}}}} quad$$
(12)







$$ s = dot n{c_p}{m_p}Delta {T_p}/{V_{{text{cell}}}} $$
(13)

其中, $ dot n $为单位时间内在某一控制体积内与流体发生热量交换的粉末数量, $ {n^ * } $为$ dot n $内实际有效的粉末捕获量, $ {c_p} $代表粉末材料比热容, $ {m_p} $代表粉末的质量, $ Delta {T_p} $代表粉末的温度变化量, $ {V_{{text{cell}}}} $代表粉末所在单元的体积.

对于边界条件, 动量守恒方程在金属液体自由表面上的边界条件为







$$ {boldsymbol{f}} = sigma {boldsymbol{n}}kappa + frac{{{
m{d}}sigma }}{{{
m{d}}T}}left[ {nabla T - {boldsymbol{n}}({boldsymbol{n}} cdot nabla T)}
ight] $$
(14)

式中, $ sigma $为金属液体的表面张力系数, $ dfrac{{{
m{d}}sigma }}{{{
m{d}}T}} $表示表面张力随温度变化系数, $ {boldsymbol{n}} $和$ kappa $分别代表金属熔池自由表面的法向量与曲率. 能量守恒方程在熔覆层上表面的热流边界条件为







$$ - kfrac{{partial T}}{{partial n}} = {h_c}(T - {T_infty }) - {q_{{text{source}}}} $$
(15)

其中, $ {h_c} $为对流换热系数, $ {T_infty } $为参考环境温度(取值为293 K), ${q_{{
m{source}}}} = {eta ^ * }{q_l}(x,y,z)$为激光高斯面热源. 对于初始条件, 计算域内材料初始速度为0, 初始温度为293 K.

对于金属熔池的自由表面, 本文采用VOF进行重构. 其中, 单元流体体积分数$ phi $的演化方程为







$$ frac{{partial phi }}{{partial t}} + frac{partial }{{partial {x_i}}}(phi {u_i}) = 0 $$
(16)

当$ phi $处于0 ~ 1之间时会被判断为自由表面单元.


1.4
计算方法


上述多物理场模型通过FLOW-3D v12.0软件进行建模求解, 采用拉格朗日质点跟踪方法计算粉末-激光交互过程, 采用瞬态FVM并结合VOF计算粉末与熔池相互作用、熔池自由表面形状演化和熔覆层沉积过程, 时间积分算法采用显式时间积分.


2.
实验方法和数值模型设置


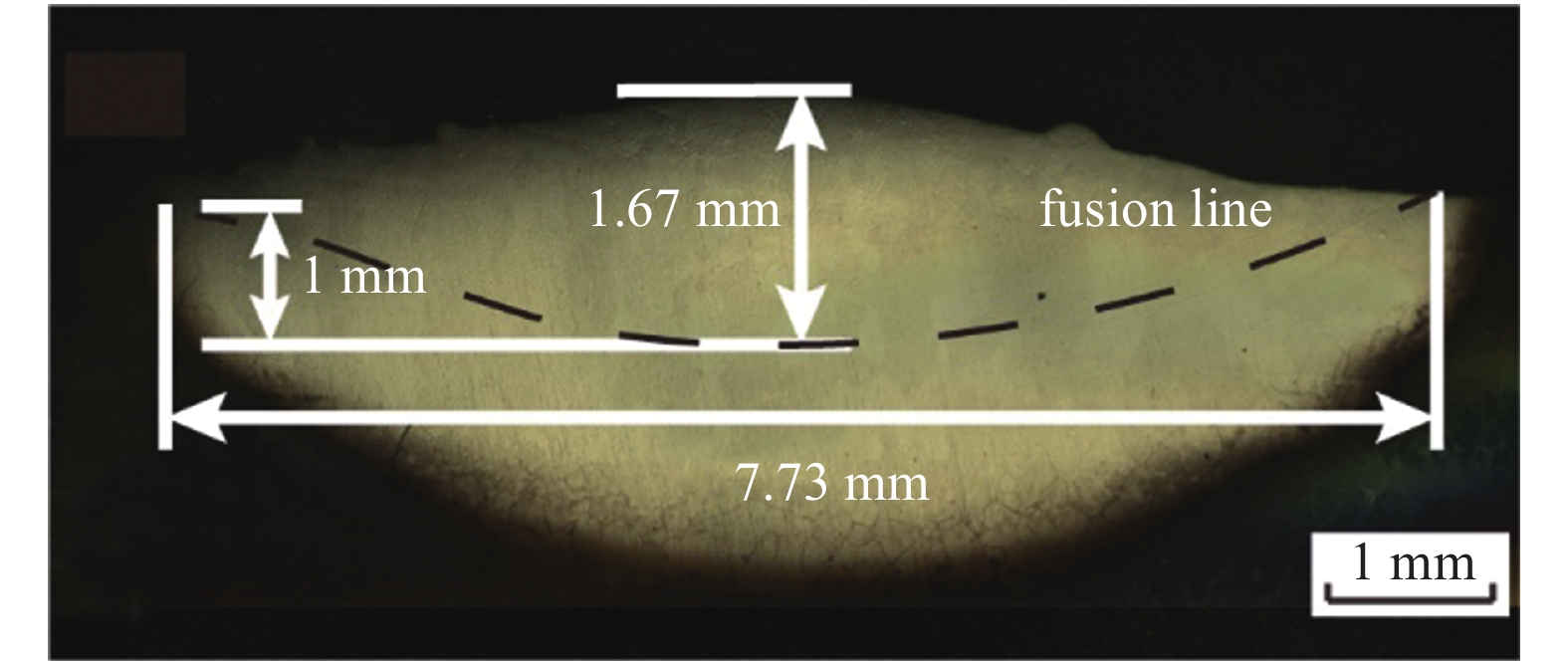
本文采用北京航空航天大学自主研发的LMD-V型同轴送粉激光直接能量沉积设备制备单道熔覆试样. 该系统配备有YLS-10000型光纤激光器(最大输出功率10 kW)、一套BSF-2同轴送粉装置、一套Fagor-8055四轴数控机床和一套自主研发的动态密封气氛保护装置; 其粉末汇聚平面与激光焦平面位置相同且相对固定, 采用氩气作为保护气氛并且保护腔内氧含量低于80 ppm. 本工作选用粒径为70 ~ 250 μm的TC17钛合金粉末, 采用如表1所示工艺参数, 在TC17钛合金基板开展单道加工; 熔覆成形后取熔覆层稳定段, 沿垂直于扫描方向切取熔覆试样, 研磨抛光之后进行镶样、腐蚀, 最后采用电镜观察试样以获得熔覆层和熔池的形貌尺寸, 如图2所示.




表
1
工艺参数



Table
1.
Process parameters



table_type1 ">
ParametersUnitsValue
$P$ $ {
m{kW}} $		 6
$v$ ${
m{mm} }/min$		 1000
$ {V_f} $ $ {text{g}}/{text{s}} $ 0.33
$ {r_0} $ $ {
m{cm}} $		 0.3
${r_{{
m{focus}}} }$		 $ {
m{cm}} $		 0.2
${l_{{
m{focus}}} }$		 $ {
m{cm}} $		 1
${z_{{
m{focus}}} }$		 $ {
m{cm}} $		 0.5





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
同轴送粉激光直接能量沉积TC17单道扫描横截面视图, 其中黑色虚线为熔合线



Figure
2.
Cross section view of the single track of TC17 by coaxial powder feeding laser directional energy deposition, where the black dashed line is the fusion line



下载:
全尺寸图片
幻灯片


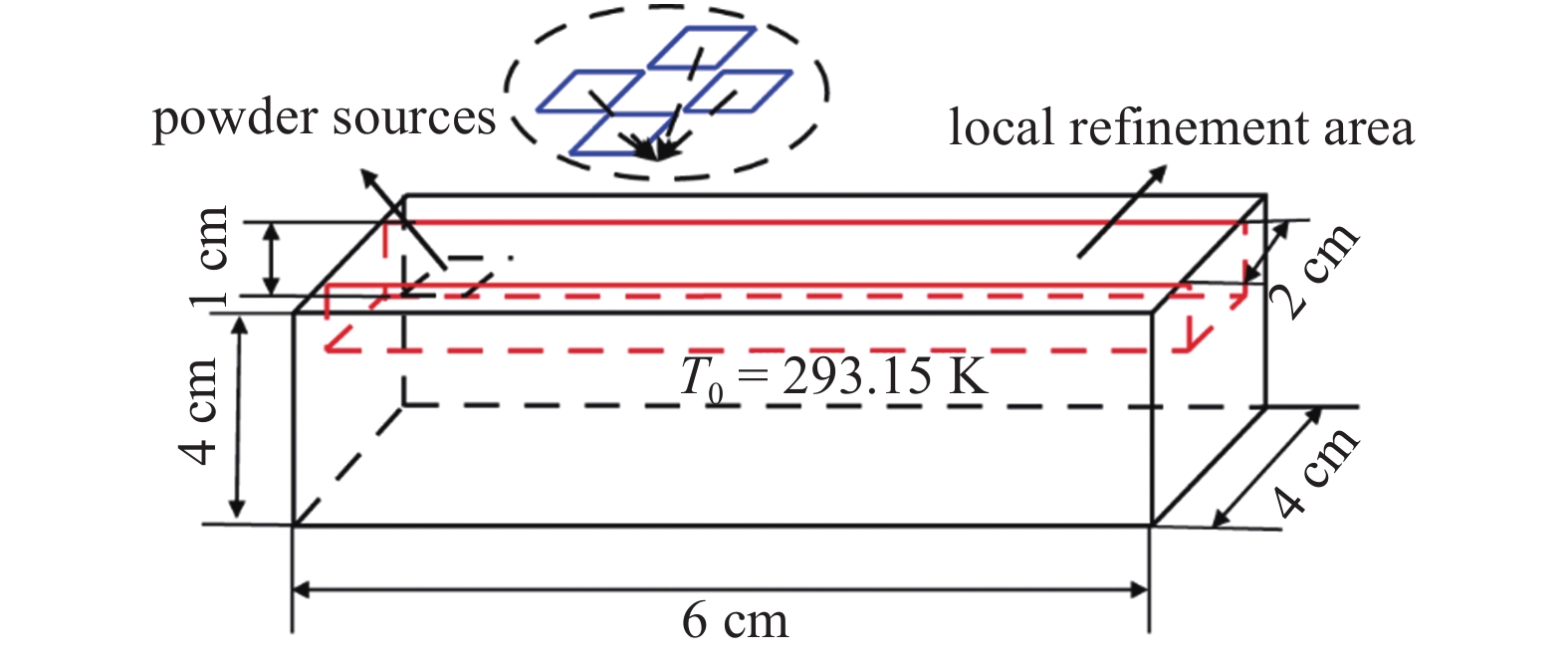
针对上述实验工况, 数值模型计算域沿X, Y, Z , 3个方向取值为$ 6;{
m{cm}} times 4;{
m{cm}} times 4 ;{
m{cm}} $, 如图3所示. 采用局部加密规则化网格离散计算区域; 经网格收敛性分析表明, 局部熔覆层区域$ 6;{
m{cm}} times 2;{
m{cm}} times 1 ;{
m{cm}} $内采用尺寸为0.025 cm单元离散, 其他区域材料采用尺寸为0.05 cm单元离散可以较好的平衡计算精度与计算效率的需求. 4个粉末源分别以平行于扫描方向(X轴)以及垂直于扫描方向(Y轴)两两排布, 并在每个粉末源的范围内随机生成不同粒径的粉末粒子, 对应粒径的粉末数量按高斯分布形式分布. 依据实验设置, 于粉末生成区域随机生成粉末颗粒, 其粉末直径符合高斯分布. 粉末颗粒生成后沿45°入射角, 以565.6 cm/s的恒定速度运动至加工表面. 下文称此为四喷嘴侧向送粉模式. 全计算域网格边界均设为连续性边界条件, 所采用的材料物性参数是通过TC17的合金组分[31], 结合理论模型及参数手册确定, 具体参数如表2所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
三维数值模型



Figure
3.
3D numerical model



下载:
全尺寸图片
幻灯片





表
2
TC17热物性参数



Table
2.
Thermal properties of TC17



table_type1 ">
PropertiesUnitsValue
$ {T_l} $ $ {
m{K}} $		 1960
$ {T_s} $ $ {
m{K}} $		 1770
$
ho $		 $ {
m{g}}/{
m{c}}{{
m{m}}^3} $		 4.69
$ k $ $ {
m{W}}/({
m{m}} cdot {
m{K}}) $		 6.5
$ c $ $ {
m{J}}/({
m{kg}} cdot {
m{K}}) $		 523
$ sigma $ $ {text{N/m}} $ 1.65
$dfrac{ { {
m{d} }sigma } }{ { {
m{d} }T} }$		 $ {
m{N}}/({
m{m}} cdot {
m{K}}) $		 2.4$ times {10^{-4}} $
$ Delta H $ $ {
m{J}}/{
m{kg}} $		 3.03$ times {10^5} $
$ {h_c} $ $ {
m{W}}/({{
m{m}}^2} cdot {
m{K}}) $		 10
$ eta $ ? 0.3
$ {eta _p} $ ? 0.7





下载:
导出CSV
|显示表格



3.
结果分析与讨论



3.1
模型验证


首先通过单道熔覆层横截面实验结果与数值模拟结果对比以验证本文所建立的多物理场模型. 在粉末吸收能量的计算中粉末在空中的飞行时间${t_f}$为0.001 s, 生成的粉末数为1764, 并根据送粉速率确定激光作用时间${t_p}$. 图4(a)为四向送粉模式下熔覆层形成过程的数值模拟结果, 其中基板及熔覆层上方的球体为粉末颗粒, 箭头表示熔池内流场. 计算表明当达到3 s时, 熔池已达稳定状态. 图4(b)为熔池稳定状态时的等温线分布, 其中黑色方框及标有数字的黑色线分别为粉末实际作用区域与粉末落入熔池前的等温线分布, 表明熔池温度分布与粉末温度分布有差异, 从而落入熔池的粉末颗粒将对熔池的温度场和流场产生影响. 图4(c)为稳定状态时单道熔覆层横截面数值模拟结果, 图中“melt region”表示该单元材料的熔化程度, 当且仅当该参数为1时表示材料全部熔化并成为熔池的一部分, 相应区域边缘则构成液相线熔池边界. 与图2的实验结果相比, 两者在基板上方熔覆层高度、熔池宽度与深度方面相吻合, 表明数值模拟结果与实验结果一致性良好.



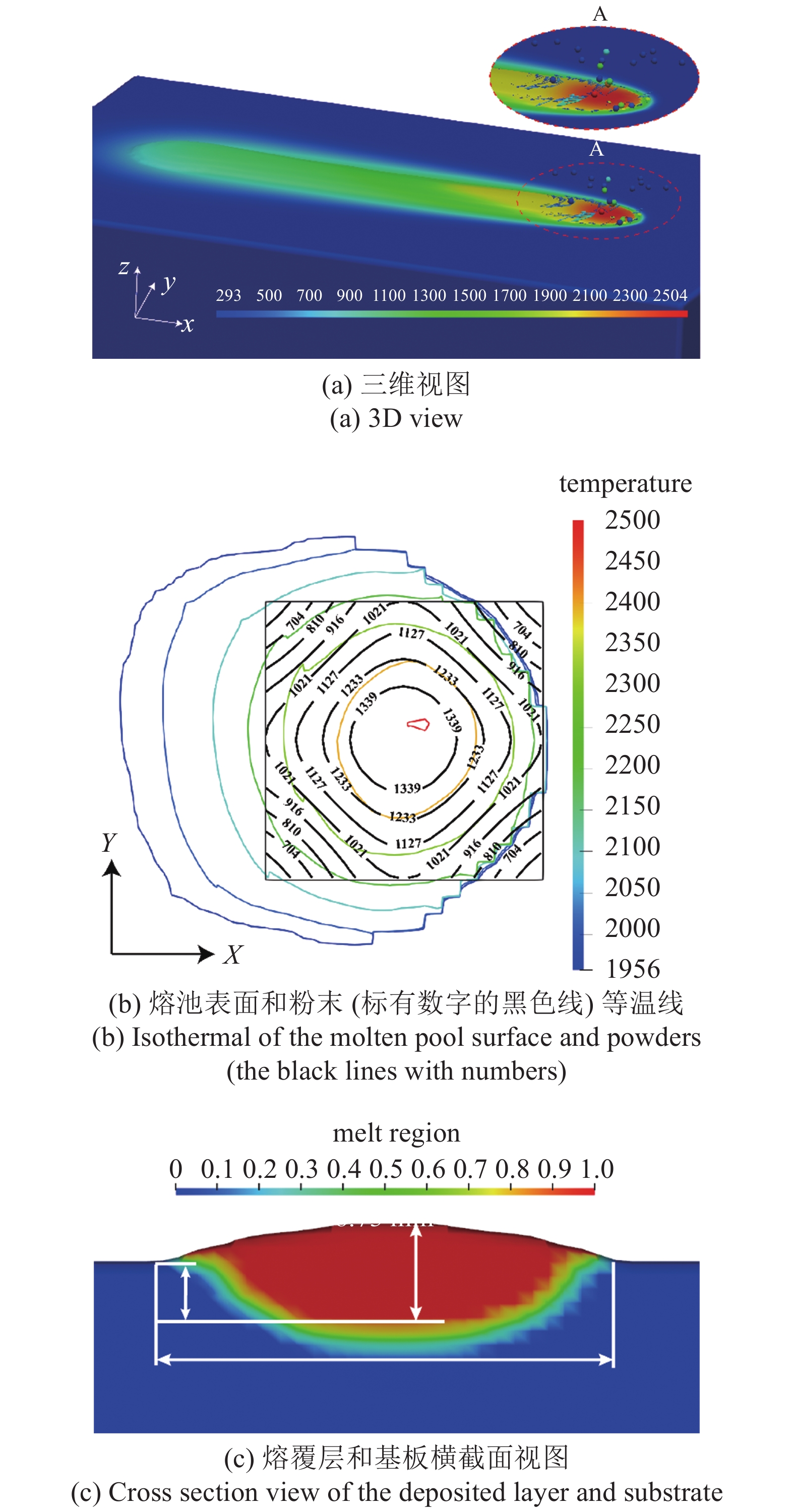onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
TC17合金单道扫描数值模拟结果



Figure
4.
Numerical results of TC17 single track



下载:
全尺寸图片
幻灯片



3.2
工艺参数对熔覆层形貌的影响分析


以3.1节实验工况的工艺参数为基准, 采用本文多物理场数值模型进一步研究激光功率、送粉速率和激光移动速度对熔池尺寸形貌的影响趋势, 并分析其成形尺寸的物理机理. 故通过固定所研究工艺参数外其余参数, 设计了3组数值算例.

图5展示的是不同激光功率(4 kW, 6 kW, 8 kW)下的数值模拟计算结果. 其中, 图5(a)列出了激光功率对于熔覆层尺寸及熔池峰值温度的影响, 表明激光功率越大熔覆层及熔池的尺寸越大, 且熔池峰值温度越高. 这是由于热输入增加使得熔化的材料更多、熔池温升更高、粉末熔化量更大, 并可由图5(b)证明. 考虑到粉末落入熔池对于其温度场的扰动, 熔池的峰值温度采用的是任意8个时刻下熔池的峰值温度, 并经平均后获得. 图5(b)为从X轴两侧喷嘴喷出的粉末落入熔池前沿Y轴分布的温度分布, 表明在相同的路径与激光作用时间下, 离散粉末温度随激光功率增加而显著升高, 同时基于式(6)和式(7)计算可得不同激光功率参数下的粉末基材能量吸收比均为0.13. 熔池获得的热量随之增加, 从而熔池尺寸越大. 图5(c)为激光功率8 kW时熔覆层横截面, 其熔覆层高度与熔池深度相较于基准算例均有所增加.



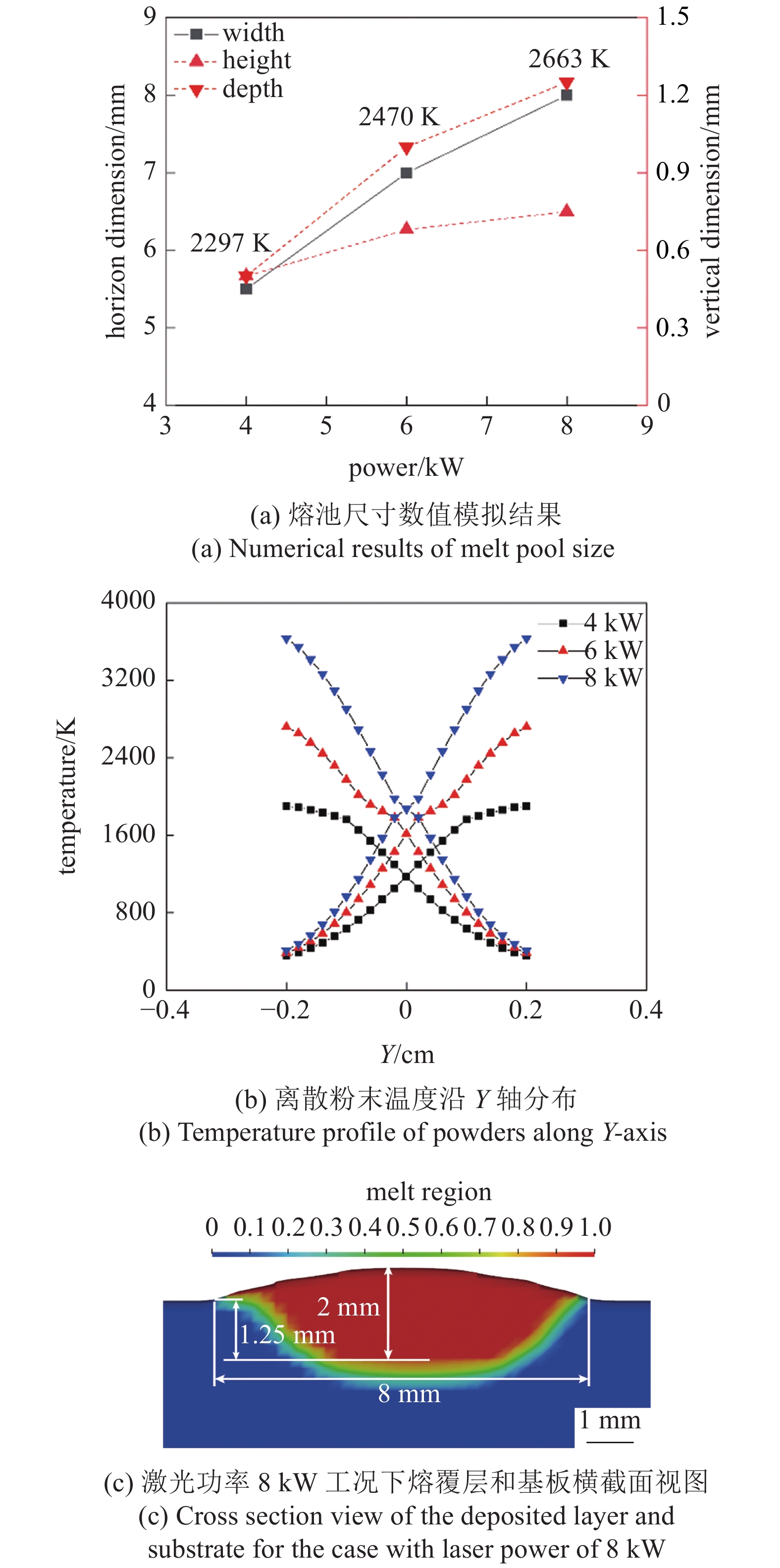onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同激光功率工况下的数值模拟结果



Figure
5.
Numerical results for the cases with different laser powers



下载:
全尺寸图片
幻灯片


图6为不同送粉速率(0.17 g/s, 0.33 g/s, 0.67 g/s)下数值模拟计算结果. 图6(a)显示, 熔覆层高度、宽度与送粉速率正相关, 但熔池深度则负相关, 并且熔池峰值温度也随之降低, 说明更多的粉末与熔池发生热量的交换, 也证明落入熔池前的粉末温度会影响熔池的温度场. 随着送粉速率增加, 图6(b)表明粉末落入熔池前的温升并无显著变化, 图6(c)则显示激光能量吸收比值$ EP/EM $随之显著增加. 结合图6(b)以及图6(c)可知, 粉末整体上获得的能量占比随送粉速率变大而增加, 使得更多被激光加热的粉末被熔池捕获, 增加了熔覆层的高度和宽度; $ EP/EM $越大表明粉末对激光的遮蔽效应越强, 使得熔池直接获得激光热量相对变少而使得基板熔深变浅. 因此, 在给定其他工艺参数情况下, 调整送粉速率可提高激光能量使用效率和成形效率. 图6(d)为送粉速率0.67 g/s时熔覆层横截面, 其熔覆层高度已大于基板下方熔池的深度, 与图4(c)和图5(c)显著不同. 同时, 由于更多的粉末与熔池发生热量交换, 导致熔池峰值温度变小. 此外, 由于所采用激光-粉末交互模型的局限性, 图6(b)预测$ EP/EM $与送粉速率的关系仅在粉末间遮蔽效应可忽略的工艺参数窗口范围内成立.



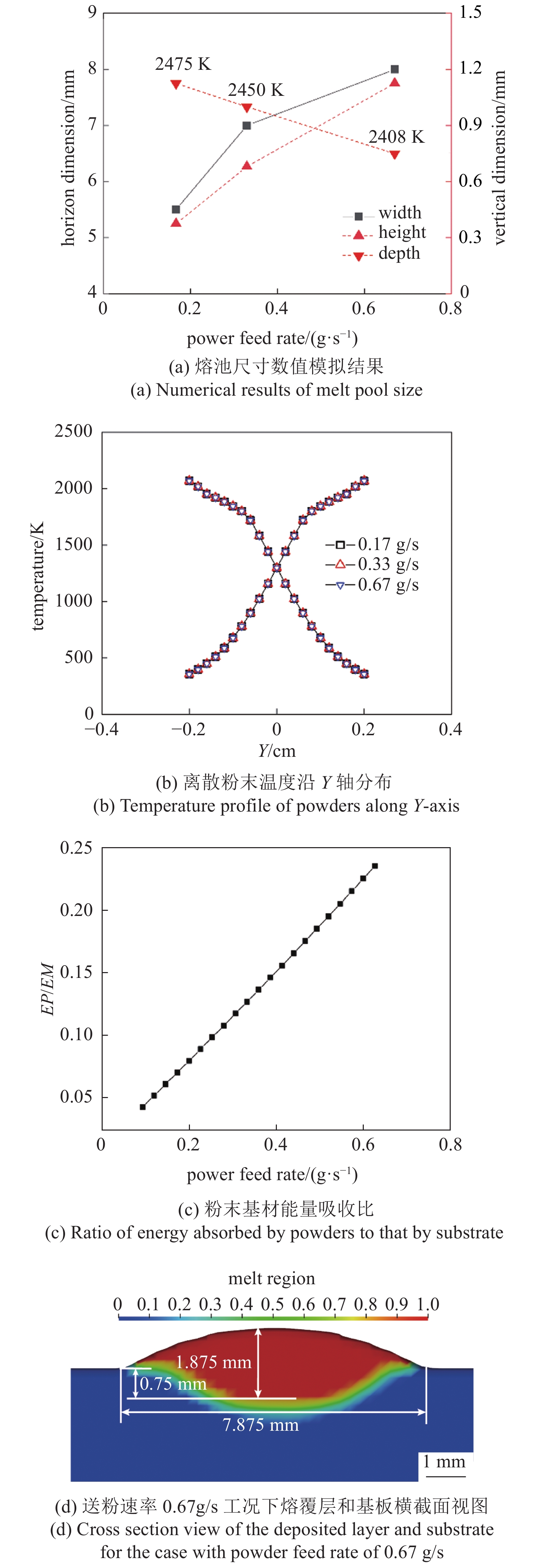onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
不同送粉速率工况下数值模拟结果



Figure
6.
Numerical results for the cases with different powder feed rates



下载:
全尺寸图片
幻灯片


此外, 不同激光移动速度下(500 mm/min, 1000 mm/min, 2000 mm/min, 2300 mm/min, 3000 mm/min)的数值模拟结果如图7所示. 图7(a)表明, 激光移动速度越大熔池尺寸及熔覆层尺寸均逐渐减小, 但熔池的峰值温度却呈现先减小后增大再减少的变化趋势. 依据本文激光-粉末交互模型的假设, 激光移动速度不影响粉末加热时间与粉末路径, 以及粉末温度分布与粉末基材能量吸收比. 因此, 熔覆层形貌及基板熔深主要是由于激光的线能量输入变小和单位长度上的粉末输入量变小所致. 其峰值温度变化则与粉末、基板的能量交换有一定的关系. 由图5(b)及图6(b)可知, 落入熔池中心的粉末由于其温度低于熔池温度及液相线温度则在进入熔池后与之发生急剧热交换. 伴随着激光移动速度的增大, 单位长度上热输入减小, 熔池宽度减小, 在达到某一激光移动速度后, 继续增加该工艺参数会使得越来越多的粉末落在熔池边缘或远离熔池边缘的位置, 粉末无法进入熔池并与其发生热量交换, 被基板吸收的能量可以更多地储存在基板内部, 使得峰值温度上升. 当粉末影响几乎可以忽略不计后, 整个扫描过程开始倾向于纯基板扫描, 峰值温度随着热输入量的减小再次发生下降(扫描速度为3500 mm/min工况下的峰值温度为2693 K). 图7(b)为扫描速度为2000 mm/min时的熔覆层横截面, 其熔池尺寸相比于图5(c)显著变小.



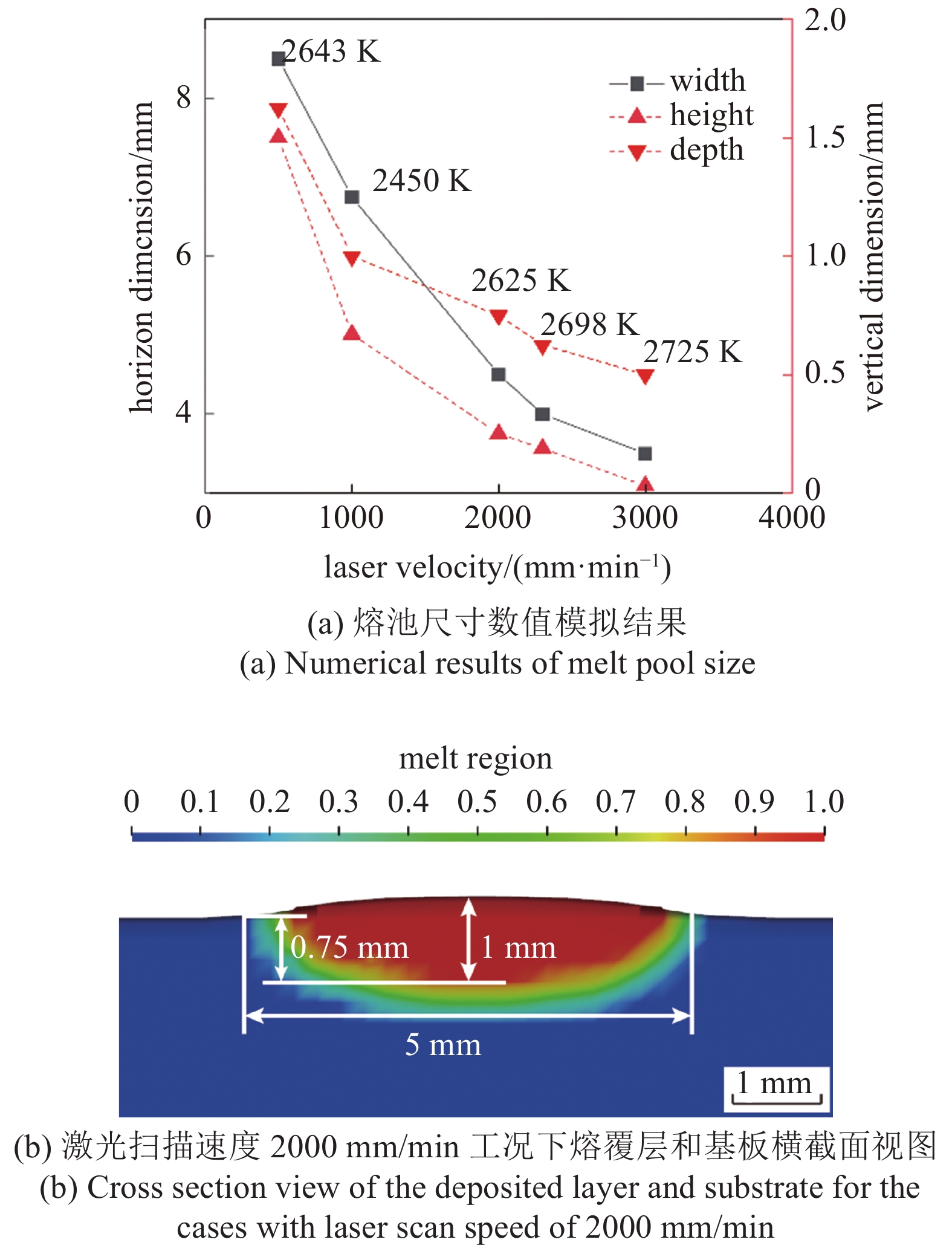onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
不同激光扫描速度工况下的数值模拟结果



Figure
7.
Numerical results for the cases with different laser scan speeds



下载:
全尺寸图片
幻灯片



3.3
给定工艺参数下的粉末温度影响机制


由3.2节可知, 粉末落入熔池前的温度和粉末基材能量吸收比也是影响熔覆层形貌尺寸的重要因素. 为进一步研究其与熔覆层形貌尺寸的关系, 本节在固定基准工艺参数的基础上, 通过调整粉末的运动速度和送粉模式以实现粉末温度的调控并开展相应的数值模拟.

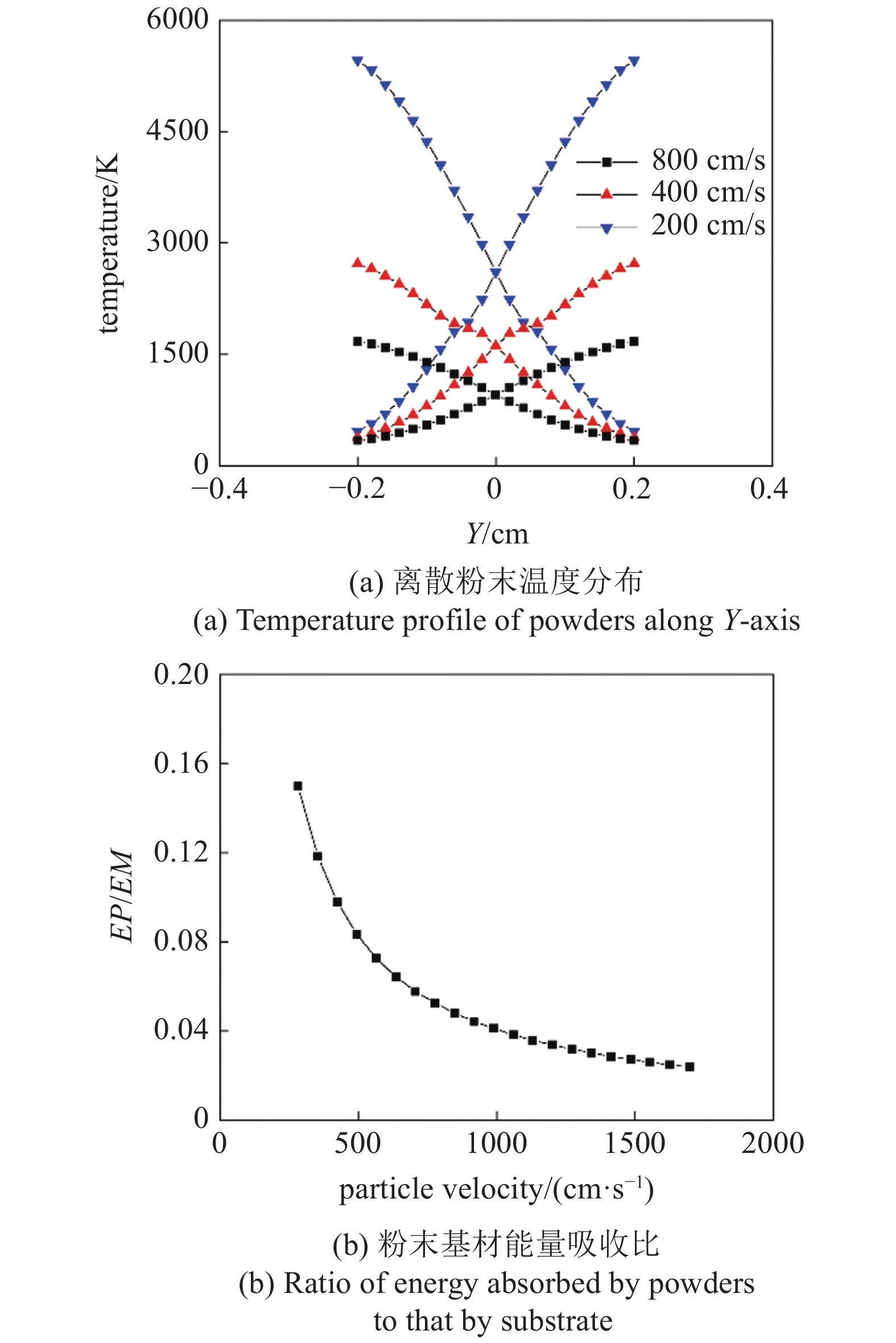
图8为四向送粉模式下不同粉末速度工况的粉末温度分布和粉末基板能量吸收比结果. 其中, 图8(a)为3种粉末速度(Z分量依次为800 cm/s, 400 cm/s, 200 cm/s)下粉末在未进入熔池前的落点平面处沿Y轴的温度分布, 表明粉末速度越大粉末峰值温度越低、空中熔化的粉末数量越少、粉末与熔池的温差越大. 这是因为粉末速度越大则粉末基板能量吸收比呈单调非线性减小, 粉末获得的能量越少, 如图8(b)所示. 此外, 由于激光粉末交互模型中未考虑粉末的汽化, 故图8(a)中部分粉末的温度大于材料的沸点.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
不同粉末Z向速度工况下计算结果



Figure
8.
Numerical results for the cases with different powder velocities along Z direction



下载:
全尺寸图片
幻灯片


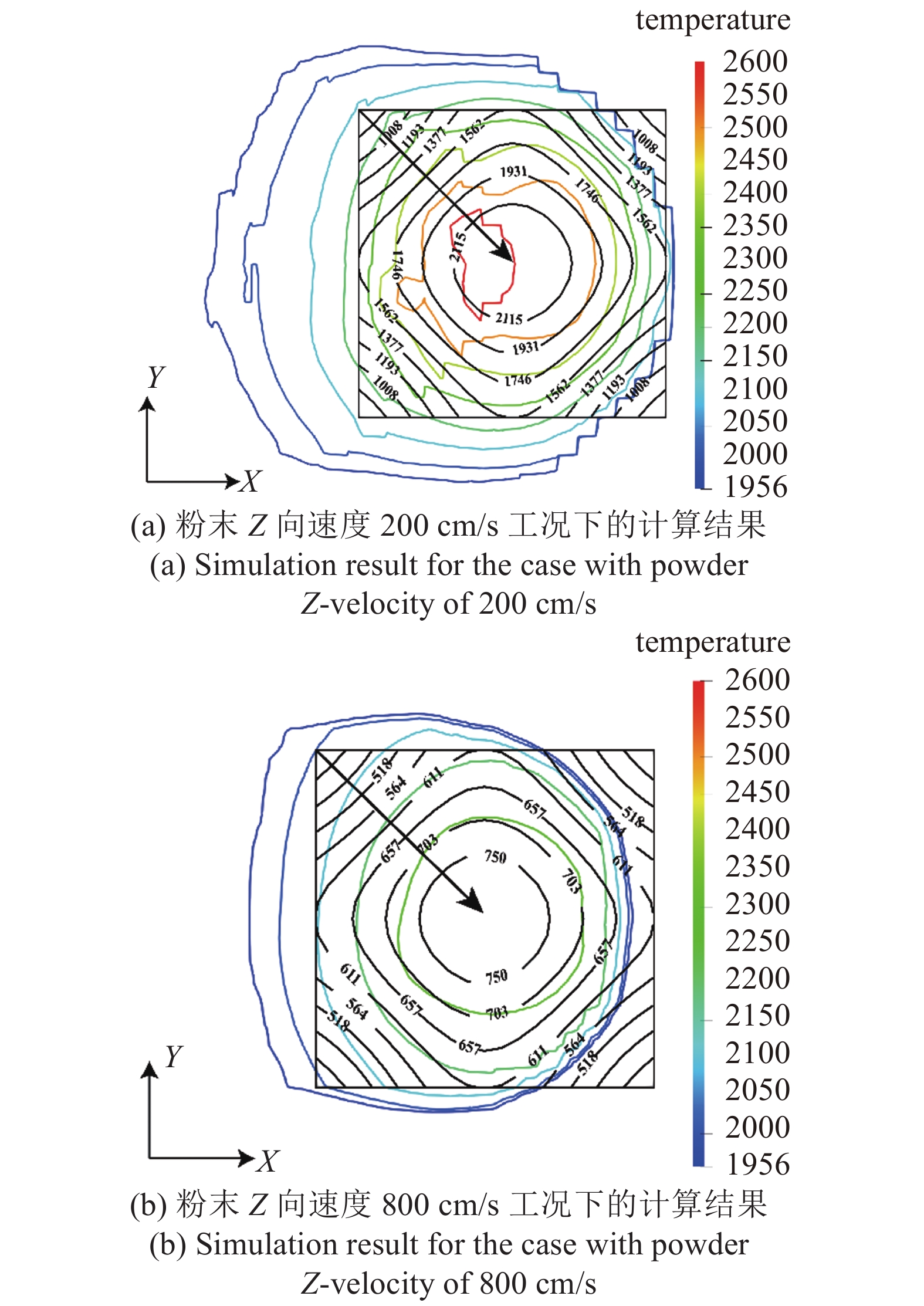
表4列出了图8(a)中3种工况的熔覆层尺寸、熔池最大流速以及熔池峰值温度数值模拟结果. 结果显示, 粉末速度越大则基板上方熔覆层的尺寸越小、粉末的实际捕获率减少, 表明虽然粉末基板能量吸收比变小, 但是熔池尺寸并没有因基板吸收更多的热量而变大. 这是由于基板在熔化落入其中的固态粉末颗粒的同时, 也在通过热传导进行散热, 所吸收能量并不能完全用于熔化粉末. 同时, 由于与落入熔池的粉末进行热量传递, 熔池峰值温度随着粉末速度的增大而不断降低, 熔池最大流速也相应变小, 如图9所示. 其中, 图9(a)与图9(b)分别代表粉末速度Z分量为200 cm/s与800 cm/s的熔池等温线数值模拟结果, 方框内部为粉末达到落点平面的温度分布等温线. 通过对比可以发现, 粉末与落点处的温差大于500 K, 因此通过热传导降低熔池峰值温度和温度梯度, 使得Marangoni效应变弱从而降低熔池流体速度. 将表4与图5(a)不同激光功率下熔池的峰值温度与熔池尺寸对比则可知, 粉末速度对熔池的影响与激光功率的影响趋势相反但影响程度相当. 此外, 相比于激光功率, 粉末速度对基板下方的熔池深度影响较弱, 如表4所示. 这是熔池对流传热减弱和落入粉末吸热相互竞争的结果. 综上可得, 粉末速度通过粉末温度分布及粉末基材能量吸收比比例从热量传递和熔池流动两个方面对熔覆层尺寸有着重要的影响, 两者呈负相关.




表
4
不同Z向粉末速度工况下熔池模拟结果



Table
4.
Simulation results of melt pool for the cases with different powder velocities along Z direction



table_type2 ">
Powder Z-velocity/(cm·s?1)Width/mmHeight/mmDepth/mmMax-velocity/(cm·s?1)Peak temperature/K
20070.81119.122690
4006.750.68116.222450
8005.50.5114.42350





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同粉末Z向速度工况下粉末(标有数值的黑色线)与熔池等温线对比



Figure
9.
Comparison of isotherm for powders (the black line with values) and melt pool for the cases with different powder velocitiesalong Z direction



下载:
全尺寸图片
幻灯片


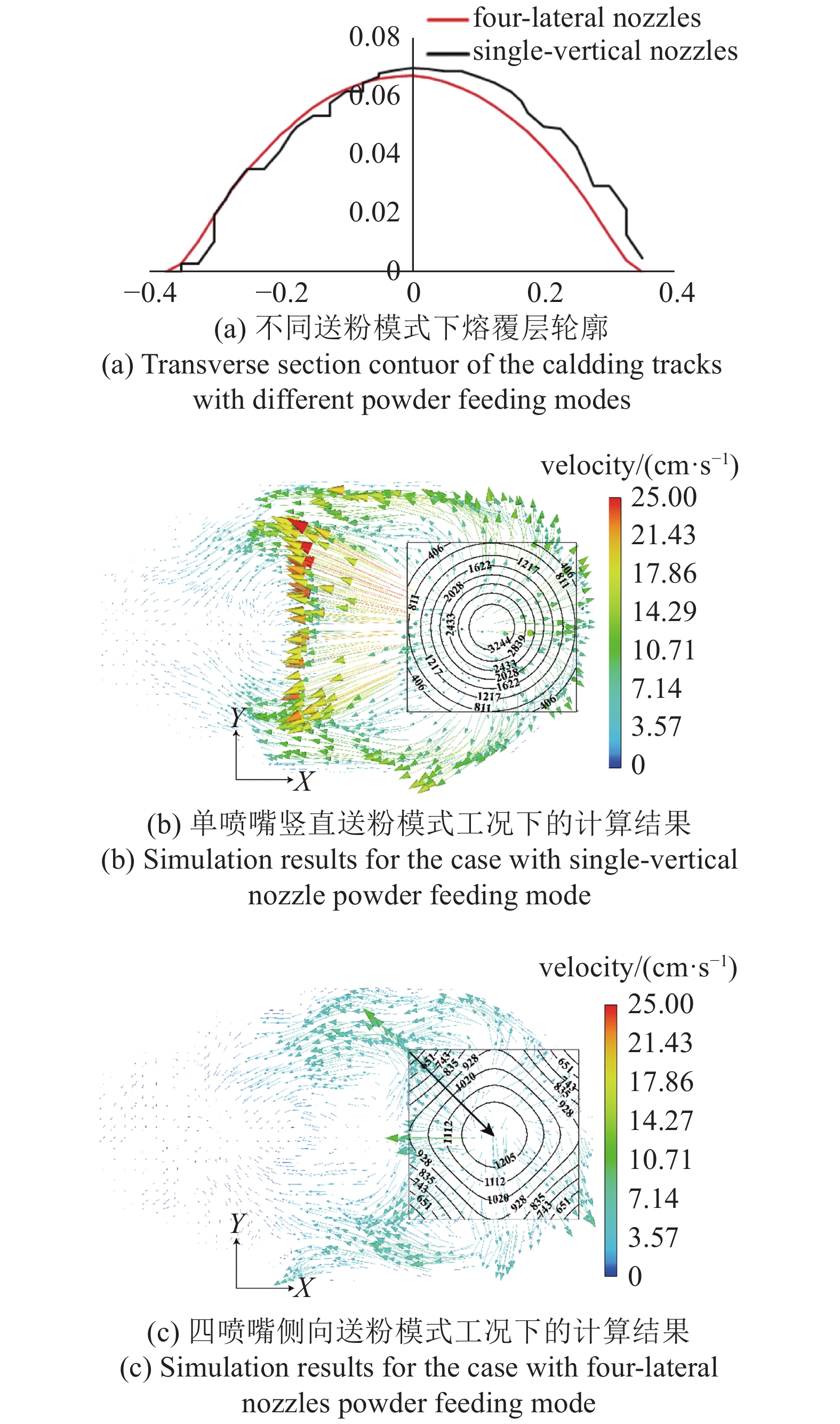
表5和图10为单喷嘴竖直送粉和四喷嘴侧向送粉模式且保持其他参数设置一致下的数值模拟结果对比. 其中, 粉末Z方向速度均为400 cm/s, 粉末基材能量吸收比分别为 16.7% 和 14.2%. 单喷嘴竖直送粉模式下熔覆层尺寸略大于四喷嘴侧向送粉模式下的结果, 如表5所示, 所得熔覆层横截面的轮廓线则如图10(a)所示. 结果表明, 单喷嘴竖直送粉模式获得的熔覆层体积更大, 但表面较为粗糙. 这是由于不同送粉模式下, 粉末落入熔池时的温度分布差异较大, 如图10(b)和图10(c)所示. 其中, 箭头表示熔池的流场, 方框中黑色带数字线为粉末落入熔池前的等温线. 与四喷嘴侧向送粉模式下粉末温度分布形式不同, 单喷嘴竖直送粉模式下粉末达到落点平面的温度分布以同心圆形式排布, 与激光热流密度高斯分布形式一致, 也因此其粉末峰值温度相对较高, 进而导致熔池峰值温度较高(如表5所示). 粉末温度分布形式不同也将导致熔池流场不同, 一定程度上决定了与熔池交汇处的流动方向. 单喷嘴竖直送粉模式下, 粉末温度梯度方向呈径向分布, 其最大值约为15000 K/cm; 而四喷嘴侧向送粉模式下, 粉末最大温度梯度约为3535 K/cm, 其方向则如图10(c)中的箭头所示. 粉末落入熔池后将一定程度上影响熔池表面的温度梯度分布, 进而通过Marangoni效应影响熔池的流场. 因此, 在粉末与熔池交汇的平面内, 单喷嘴竖直送粉模式导致熔池流动方向更倾向于径向分布, 而四喷嘴侧向送粉模式导致熔池流动方向主要为侧后方, 对应于粉末的温度梯度分布. 同时, 粉末的温度梯度大则熔池的流速更快, 如表5所示. 此外, 对于单喷嘴竖直送粉模式, 虽然粉末温度分布沿X轴的正、负方向温度梯度相同, 但由于熔池尾部流体运动空间大于熔池前端, 故熔池后端流体相较于熔池前端与侧面流体的速度更大.

综上可知, 在给定热输入下, 粉末基材能量吸收比例越高则熔覆层尺寸越大, 同时, 粉末温度越高则熔池的峰值温度越高, 粉末的温度梯度越大则熔池的流速越大, 并且粉末的最大温度梯度方向一定程度上决定了熔池上表面流场, 进而可影响熔覆层表面粗糙度.




表
5
不同送粉模式下熔池模拟结果



Table
5.
Simulation results of the melt pool for the cases with different powder feeding modes



table_type2 ">
Powder feeding modeWidth/mmHeight/mmDepth/mmMax-velocity/(cm·s?1)Peak temperature/K
single-vertical nozzle70.7125.212920
four-lateral nozzles6.750.68116.222450





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-420-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
不同送粉模式工况下熔池流场、温度场, 其中标有数值的黑色线为粉末等温线



Figure
10.
Flow field and temperature field of the melt pool with different powder feeding modes, where the black lines with values are the isotherm of the powders



下载:
全尺寸图片
幻灯片



4.
结论


针对同轴送粉激光定向能量沉积增材制造技术, 本文建立了激光-粉末-熔池交互的高保真多物理场模型. 其中, 将激光等效处理为高斯面热源, 采用拉格朗日质点法计算粉末空中飞行时的温升以及对激光遮蔽效应, 采用有限体积法和流体体积法模拟粉末-熔池交互及熔池自由液面演化过程以获得沉积层的形貌尺寸, 并通过单道熔覆层横截面实验结果进行了验证. 采用该模型, 对不同工艺参数和送粉方式下的单道扫描工况进行了数值模拟, 获得了粉末落入熔池前的温度分布及粉末基板能量吸收比值, 分析了熔池形貌的演化规律及其内在的物理机理, 得到如下主要结论.

(1)工艺参数对于熔覆层形貌的影响规律及机理: 在本文所研究的工艺参数窗口范围内, 激光功率越大, 熔覆层宽、高及基板熔深越大, 其原因是热输入增大, 导致粉末空中的温升增大以及熔池熔化粉末能力提升; 送粉速率越大, 熔覆层宽、高增大但基板熔深减小, 其原因在于粉末基板能量吸收比增加, 导致粉末熔化量上升, 有利于提高激光能量的利用率; 激光移动速度越大, 熔覆层宽高及基板熔深均减小, 归因于线能量输入与单位长度上粉末数量同时降低.

(2)在数值模拟中, 粉末落入加工表面前的温度分布对于熔覆层形貌和熔池流场的影响不可忽略: 在给定的工艺参数激光功率、扫描速度和送粉速率下, 粉末速度越大熔覆层尺寸越小, 其根本原因为粉末温度降低、粉末基板能量吸收比减小; 给定其他工艺参数单在不同的送粉模式下, 竖直单口送粉较侧向四口送粉获得的粉末温度更高、基板能量吸收比偏大, 则获得的熔覆层尺寸更大, 同时由于前者粉末温度场分布与后者显著不同, 导致相应的熔池流场迥异, 进而可影响熔覆层的表面质量.

(3)为提高成形效率并改善熔覆层表面质量, 在给定的激光功率、送粉速率、激光移动速度等基础工艺参数外, 还可通过调整粉末速度及送粉模式以进一步优化工艺参数窗口.

本文建立的激光-粉末-熔池交互的高保真多物理场模型, 能够考虑依赖于飞行路径的粉末空中温升, 可揭示其对熔池流场及熔覆层形貌的影响, 有助于理解同轴送粉激光定向能量沉积的工艺机理, 从而可辅助控形工艺参数优化.


致谢


感谢沈淑馨为本文实验开展和样件处理所提供的帮助.

相关话题/激光 计算 工艺 熔池 成形
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 增材制造微结构演化及疲劳分散性计算
    引言增材制造通过不断添加材料来完成零件的加工成型,满足了工业对零件形状、功能、材料的更高要求,成为当前材料加工技术发展的前沿方向.与传统制造工艺相比,增材制造在成形原理、材料形态、制件性能上发生了根本改变,具有材料浪费少、加工工序少、加工周期短、零件结构设计自由、易于实现形状复杂零部件快速成型等优点 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 面向增材制造的熔池凝固组织演变的相场研究
    引言激光增材制造技术因制造柔性高、周期短、材料局限小等优点,极适合复杂整体构件的制造与高附值零件的快速修复,在航空航天、能源动力等领域具有广阔的应用前景[1-3].然而,金属粉末在高能激光束的辐照下快速熔化与冷却.熔池内部涉及许多瞬态及冶金过程,特别是糊状区的非平衡快速凝固过程对枝晶组织生长和晶粒演 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 激光冲击下CoCrFeMnNi高熵合金微观塑性变形的分子动力学模拟
    引言激光冲击强化技术利用激光穿过约束层,作用于烧蚀层产生大量等离子体,等离子体继续吸收激光能量发生爆炸从而产生冲击波作用于金属表面.当冲击波峰值压力大于材料的屈服强度时,激光冲击使材料发生超高应变率(>106s?1)的塑性变形,造成材料表面出现残余压应力分布并且发生表面晶粒细化[1-3].与传统的机 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 增材制造中滚筒铺粉工艺参数对尼龙粉体铺展性的影响研究
    引言基于粉床的增材制造(additivemanufacturing,AM)技术在工业上被广泛应用[1-2],铺粉工艺是该增材制造技术的关键工序之一[3-4],铺展出平整均匀的高密度粉床是制备优良性能零件的前提条件.在薄层粉末(粉层厚度通常在200μm以下)的铺展过程中,由于微米级颗粒的粘附团聚和堵塞 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一种新的玻尔兹曼方程可计算模型构造与分析
    引言近年来,随着对临近空间战略意义认识的加深,各航空航天大国发展了众多临近空间飞行器.为满足长航时、大载荷、高超声速巡航等需求,这类临近空间飞行器通常整体尺寸较大,各部件间差异显著,飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象,传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 页岩凝析气藏相平衡的快速准确计算方法
    引言随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注,天然气作为一种相对较为清洁的能源得到了广泛的重视[1].近年来在非常规油气藏勘探和开发技术上的迅猛发展,使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2].中国 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.