引 言
激光增材制造技术因制造柔性高、周期短、材料局限小等优点, 极适合复杂整体构件的制造与高附值零件的快速修复, 在航空航天、能源动力等领域具有广阔的应用前景[1-3]. 然而, 金属粉末在高能激光束的辐照下快速熔化与冷却. 熔池内部涉及许多瞬态及冶金过程, 特别是糊状区的非平衡快速凝固过程对枝晶组织生长和晶粒演变起着关键作用, 最终影响材料的显微组织和服役性能[4]. 因此, 为了实现激光增材制造构件显微组织和力学性能的调控, 必须深入认知熔池的凝固行为和凝固组织演变规律.
目前, ****们开展了许多实验, 一方面研究工艺参数(激光功率、扫描速率、扫描策略、光束模式等)对熔池形貌的影响[5-7], 如熔池深宽比、稀释率、熔池模式等; 另一方面研究工艺参数对显微组织及力学性能的影响[8-10], 如晶粒尺寸、凝固模式、抗腐蚀等. 然而, 上述研究重点关注激光增材制造工艺与熔池形貌及力学性能映射关系, 极少重视凝固过程.
近年来, 随着监测技术的发展, 报道了许多研究熔池凝固过程的方法. 如利用红外测温[11]、高速摄像[12]和同步辐射X?射线成像技术[13-15]监测熔池表面的温度[11]及冷却速率、熔体流体流速[13]、固?液界面推进速度[15]等. 尽管实验监测手段越来越先进, 但目前仅能阐明宏观熔池的热?动力学机理, 微观尺度上仍难以追踪凝固组织的形成过程和揭示晶粒演变规律[16]. 因此, 单一的实验法还难以实现激光增材制造过程显微组织形成过程的完整描述. 与此同时, 实验的经济和时间成本也极高. 随着计算机技术的日益进步, 数值模拟技术逐步成为帮助人们理解材料的凝固行为, 有效率地进行工艺参数选取的有利工具[17].
目前, 针对增材制造过程的数值模拟, 国内外****开展了大量研究. Zhang等[16]通过多尺度模拟, 研究了凝固速率与枝晶臂间距的关系, 发现随着凝固速率的上升, 枝晶臂间距呈现下降趋势. Ghost等[18]通过模拟提取了凝固界面前沿的溶质分布变化情况, 发现随着凝固速率的上升, 枝晶尖端的溶质偏析显著下降. 上述研究主要建立了熔池凝固行为(温度梯度、凝固速率、冷却速度)与组织特征(枝晶臂间距、溶质分布、尖端过冷)的关系, 从而对成形件的性能指标进行简单判定. 但大都局限于单一取向晶粒的模拟[19-22], 而在增材制造过程中, 熔池的凝固受到多晶基板的作用, 往往是多晶粒间相互竞争的结果.
针对上述问题, 研究人员对晶粒间的竞争过程开展了深入的研究[23-24]. Wang等[25]利用温度场得到的温度梯度
目前针对熔池全域模拟的研究鲜有报道. Acharya等[27]将计算流体动力学与相场法结合, 定性研究了熔覆过程中横、纵截面的枝晶生长过程. 但在该****的研究中仅考虑了枝晶生长方向并预设了熔覆层尺寸, 忽略了工艺参数对熔池形貌以及凝固组织演化的影响.
通过上述文献的分析, 目前对于激光增材制造过程的数值模拟, 主要受限于狭小的模拟区域, 局限于熔池局部区域和单一取向晶粒开展模拟, 缺乏对熔池全域凝固组织演化的深入认识. 因此, 本文以激光直接能量沉积inconel 718合金为研究对象, 采用实验和多尺度模拟相结合的方法, 建立熔池全域的凝固组织演化模型. 为了解决模拟区域的问题, 采用信号传递接口编程 (message?passing interface,?MPI) 并行方法提高计算速率, 最终实现对熔池横、纵截面多晶粒竞争生长过程的模拟, 揭示凝固组织的生长行为. 本文的模拟结果有助于厘清激光增材制造热物理、化学、冶金过程, 为熔池内凝固组织的预测和调控提供理论指导.
1.
多尺度模型及实验
1.1
宏观传热传质模型
本文主要基于能量守恒、质量守恒、动量守恒定律开发激光增材制造宏观瞬态传热传质模型[21, 28], 为凝固组织的预测提供必要的热力学信息. 构建过程如下所示.
质量守恒方程
$$frac{partial ho }{partial t}+nabla cdot left( ho {boldsymbol{u}} ight)=0 $$  | (1) |
基于牛顿定律, 在
$$ frac{partial left( ho u ight)}{partial t}+nabla cdot left( ho {boldsymbol{u}}u ight)=nabla cdot left(mu nabla u ight)-{e}_{x}cdot {F}_{{mathrm{G}}/{mathrm{L}}}partial phi -frac{partial p}{partial x}-frac{mu }{K}u $$  | (2) |
$$ frac{partial left( ho v ight)}{partial t}+nabla cdot left( ho {boldsymbol{u}}v ight)=nabla cdot left(mu nabla v ight)-{e}_{y}cdot {F}_{{mathrm{G}}/{mathrm{L}}}partial phi -frac{partial p}{partial y}-frac{mu }{K}v $$  | (3) |
$$ begin{split} &frac{partial left( ho w ight)}{partial t}+nabla cdot left( ho {boldsymbol{u}}w ight)=nabla cdot left(mu nabla w ight)-&qquad{e}_{z}cdot {F}_{{mathrm{G}}/{mathrm{L}}}partial phi -frac{partial p}{partial z}-frac{mu }{K}w+ ho gbar{alpha }left(T-{T}_{r} ight)end{split} $$  | (4) |
能量守恒方程
$$ begin{split} &frac{partial left( ho {C}_{P}T ight)}{partial t}+{boldsymbol{u}}cdot nabla left( ho {C}_{P}T ight)=&qquadnabla cdot left(knabla T ight)-frac{partial left( ho {f}_{s}mathcal{L} ight)}{partial t}+frac{partial left( ho {f}_{s}Delta {bar{C}}_{P}T ight)}{partial t}end{split} $$  | (5) |
式(1) ~ 式(5)中,
ho $
ho }_{l} $
水平集方法被用来追踪熔池的气?液界面[28]. 激光束与金属粉末都假定为高斯分布. 熔池上表面主要有因吸收激光束及粉末加热带来的能量输入和熔体蒸发、热辐射导致的能量耗散[21]. 具体可表示为
$$ {q}'={q}_{text{G/L}}left(r,l ight){A}_{a}{left|{ m{cos}}{theta }_{l} ight|}^{0.2}+{q}_{p}-sigma epsilonleft({T}^{4}-{T}_{r}^{4} ight)-{ ho }_{l}{L}_{v}{J}_{e} $$  | (6) |
其中
1.2
多相场模型
通过传热传质模型的构建, 可以获取无量纲过冷作为枝晶生长的驱动力, 进而实现枝晶生长及溶质分布的计算. 本文的多相场模型是基于Karma[29]和Echebarria等[30]的连续相场法建立起来的. 由金兹堡-朗道理论可知, 二元合金的总自由能可表示为
$$ Fleft(varphi,c,T ight)={int }_{v}^{}left[frac{sigma }{2}{sum }_{i}{left|{nabla }{varphi }_{i} ight|}^{2}+{f}_{sl}left(varphi,c,T ight) ight]{ m{d}}V $$  | (7) |
式中,
ight) $
$$ begin{split}&left[1-left(1-k ight)U ight]{{a}^{2}_{s}left(widehat{n} ight)}frac{partial {varphi }_{i}}{partial t}= {{boldsymbol{nabla }} }cdot left[{{a}^{2}_{s}left(widehat{n} ight)}{{boldsymbol{nabla}} }{varphi }_{i} ight]-&qquadlambda {left(1-{{varphi }_{i}}^{2} ight)}^{2}left(U+theta ight)+{varphi }_{i}-{{varphi }_{i}}^{3}+ &qquad{partial }_{x}left[{left|{{boldsymbol{nabla}} }{varphi }_{i} ight|}^{2}{a}_{s}left(widehat{n} ight)frac{partial {a}_{s}left(widehat{n} ight)}{partial left({partial }_{x}{varphi }_{i} ight)} ight]+{partial }_{y}left[{left|{{boldsymbol{nabla}} }{varphi }_{i} ight|}^{2}{a}_{s}left(widehat{n} ight)frac{partial {a}_{s}left(widehat{n} ight)}{partial left({partial }_{y}{varphi }_{i} ight)} ight] end{split} $$  | (8) |
$$begin{split}& left(frac{1+k}{2}-frac{1-k}{2}sumlimits _{i=1}^{n}{varphi }_{i} ight)frac{partial U}{partial t}= &qquad{{boldsymbol{nabla}} }cdot left[tilde {D}left(frac{1-displaystylesumlimits _{i=1}^{n}{varphi }_{i}}{2} ight){{boldsymbol{nabla}} }U+{{J}}_{at} ight]+ &qquadfrac{1}{2}frac{partial displaystylesumlimits _{i=1}^{n}{varphi }_{i}}{partial t}left[1+left(1-k ight)U ight] end{split}$$  | (9) |
式中,
$$ U=Biggl[{22}frac{2ck/{c}_{mathrm{infty }}}{left(1+k ight)-left(1-k ight)displaystylesum _{i=1}^{n}{varphi }_{i}}-1Bigggr]{22}Biggl/{20} left(1-k ight) $$  | (10) |
式中,
$$ theta =kleft(T-{T}_{0} ight)/left[left|m ight|{c}_{mathrm{infty }}left(1-k ight) ight] $$  | (11) |
ight)$
$$ {a}_{s}left(widehat{n} ight)=1+varepsilon mathrm{cos}[4left(mathrm{alpha }+{theta }_{i} ight) ]$$  | (12) |
式中,
$$ {{{boldsymbol{J}}}}_{at}=frac{left[1+left(1-k ight)U ight]}{2sqrt{2}}frac{partial displaystylesum _{i=1}^{n}{varphi }_{i}}{partial t}frac{{nabla }{varphi }_{i}}{left|{nabla }{varphi }_{i} ight|} $$  | (13) |
在Inconel 718 合金凝固中, 后期富含Nb元素的区域会析出脆性Laves相, 而Laves相会显著降低构件的综合力学性能. 基于这一事实, 本文把多元的Inconel 718 合金简化为Ni-Nb二元合金处理[21, 32-34], 关于模型更详尽的阐述请参考文献[21, 32].
1.3
实验过程
在湖南大学HCX60激光复合制造系统上开展直接能量沉积Inconel 718合金实验. 通过正交实验, 优化后的工艺参数如表1所示. 打印态的试样经过线切割加工、镶嵌、磨抛、腐蚀等金相制样规范流程后备金相显微镜观察. 腐蚀液成分为1∶1∶1的蒸馏水、双氧水、盐酸的混合液.
表
1
激光直接能量沉积Inconel 718工艺参数
Table
1.
The processing parameters for DED-L of Inconel 718
table_type1 ">
| Processing parameters | Value |
| laser power, P/W | 600 |
| laser scan speed, V/(mm·s?1) | 6 |
| laser beam diameter, dL/mm | 1 |
| powder feed rate, F/(g·min?1) | 9 |
| shielding gas (Ar), sg/(L·min?1) | 6 |
| delivering gas (Ar), ng/(L·min?1) | 15 |
| defocus distance, n/mm | +19 |
下载: 导出CSV
|显示表格
1.4
数值求解过程
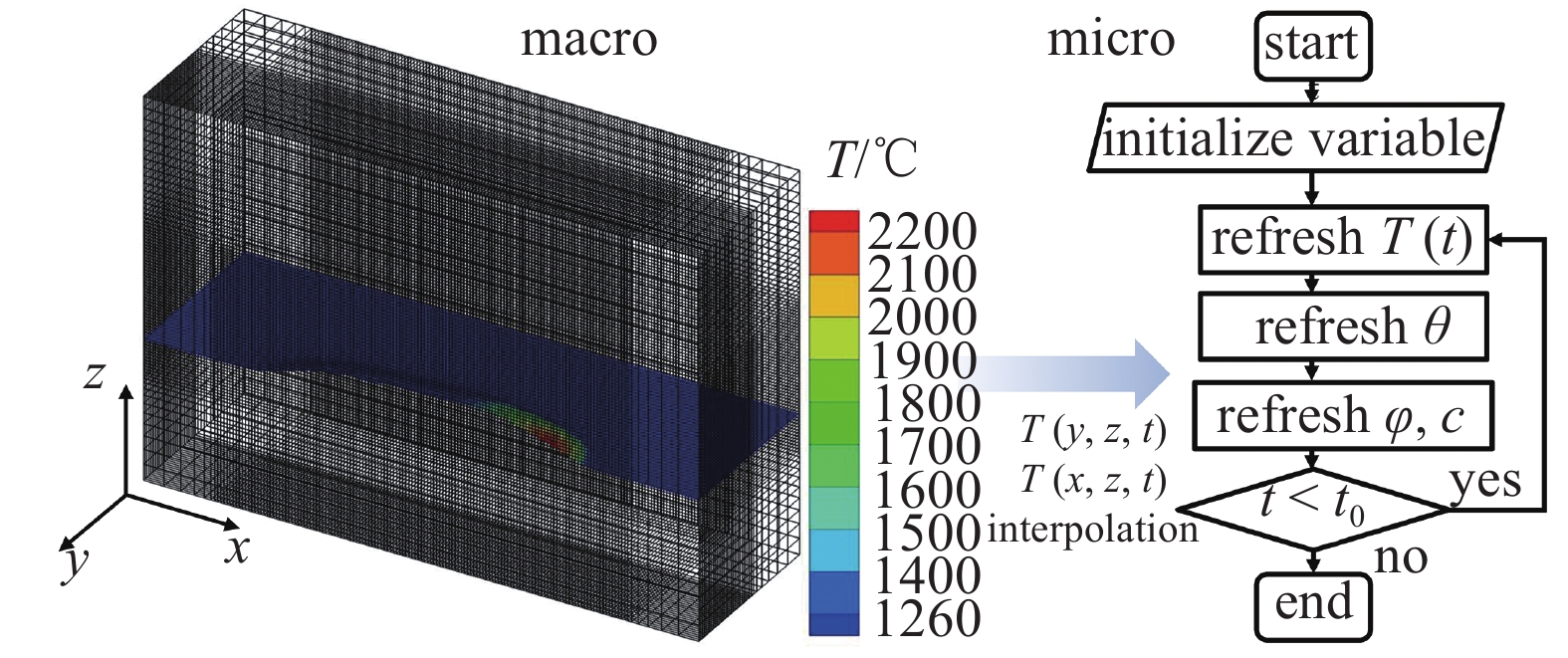
利用Fortran语言编写程序在戴尔服务器(12核24线程, 主频2.1 HGz, 内存64 GB, 存储18 TB)上实现多尺度模型的数值计算. 通过传热传质模型求解熔池形貌、温度及流场分布, 对得到的横截面(y-z平面)和纵截面(x-z平面)温度场进行无量纲处理, 获得无量纲温度
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
宏?微观模拟框架图
Figure
1.
Macro and micro simulation framework diagram
下载: 全尺寸图片
幻灯片
就宏观传热传质模拟而言, 采用有限体积法离散, 在保证精度的前提下, 为了节省计算资源, 采用非均匀网格划分, 对激光加载和熔覆层区域设置密网格, 其他区域设置疏网格(图1), 密网格的空间步长为0.05 mm, 疏网格的步长为0.3 mm. 就多相场模拟而言, 采用均匀网格划分, 空间步长约为0.058 μm. Inconel 718合金的物性参数如表2所示.
表
2
Inconel 718合金物性参数[21]
Table
2.
Physical property parameters for Inconel 718 alloy[21]
table_type1 ">
| Variables | Value |
| liquidus temperature[21], $ {T}_{l} $/K | 1609 |
| solidus temperature[21], $ {T}_{m} $/K | 1533 |
| dendsity, $ ho $/(kg·m?3) | 8190 |
| partition coefficient[33], $ k $ | 0.48 |
| alloy composition, $ {c}_{infty } $/wt% | 5.08 |
| Gibbs?Thomson coefficient[33], $ varGamma $/(K·m) | 3.65 × 10?7 |
| anisotropy[33], $ varepsilon $ | 0.02 |
| liquidus slope[33], $ m $/(K·wt%) | ?10.5 |
| thermal conductivity of solid, $ {k}_{s} $/(J·m?1·s?1·K?1) | 11.4 |
| thermal conductivity of liquid, $ {k}_{l} $/(J·m?1·s?1·K?1) | 28.3 |
| specific heat, $ {c}_{p} $/(J·kg?1·K?1) | 435/720 |
| latent heat[33], $ L $/(J·kg?1) | 2.95 × 105 |
| chemical capillary length[33], $ {d}_{0} $/m | 6.4 × 10?9 |
| liquid diffusion coefficient[33], $ {D}_{L} $/(m2·s?1) | 3 × 10?9 |
| laser absorption rate[21], $ {A}_{alpha } $ | 0.26 |
下载: 导出CSV
|显示表格
选取熔覆层的中部为主要研究截面以避免开光和关光瞬间造成的熔池波动. 此时熔池的横、纵截面形貌均倾向于准稳态. 通过将该平面从开始凝固(
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
横截面温度场数据拟合和插值过程示意图
Figure
2.
The schematic diagram of temperature field data fitting and interpolation process
下载: 全尺寸图片
幻灯片
由于经数值处理后的宏观温度场实时输给多相场模型, 微观上没有涉及传热的计算. 因此在多相场模型中没有考虑潜热的释放对凝固影响. 忽略凝固潜热, 会降低尖端过冷, 从而减小枝晶尖端生长速率. 然而, 控制枝晶生长的溶质扩散长度比热扩散长度要小约3个数量级, 潜热对微观凝固过程影响较小.
1.5
模拟的效率优化
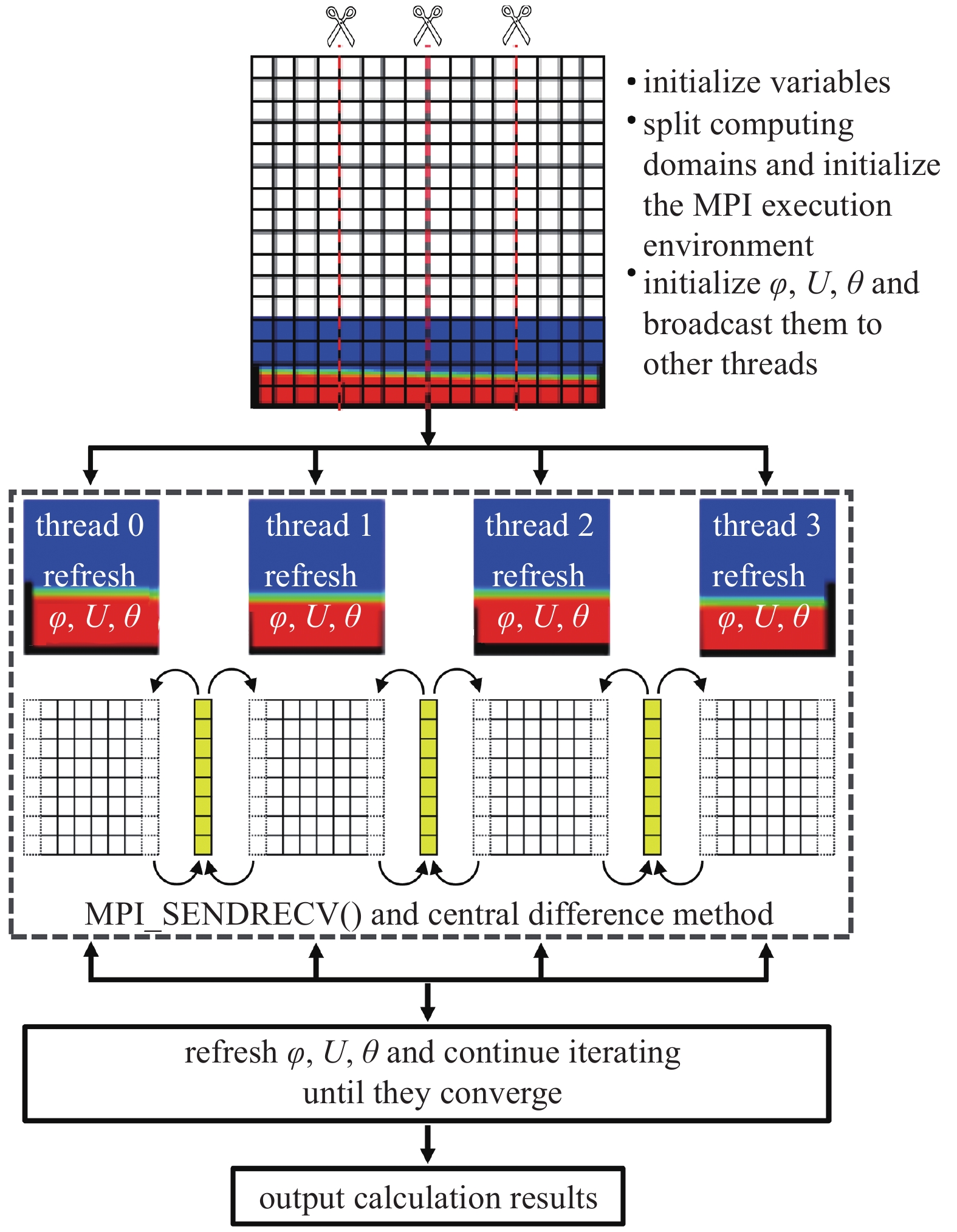
为了解决计算量巨大带来的模拟区域狭小问题, 本工作采用MPI并行工具对多相场模拟进行优化[35]. 如图3所示, 首先主线程初始化变量, 等分割计算域, 初始化
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
MPI并行计算工作原理
Figure
3.
The MPI parallel computing principle
下载: 全尺寸图片
幻灯片
同时, 为了深入分析MPI并行工具对于模拟带来的影响, 本文研究了计算效率与并行线程的关系, 并对结果可靠性进行了验证, 结果可见图4. 如图4(a)所示, 展示了MPI并行计算时间与线程数的关系, 可以发现随着MPI投入计算线程数量的增加, 耗时迅速由原串行计算的460 min下降到4线程的210 min. 随后, 计算耗费的时间趋于稳定, 12线程下耗费时间为236 min, 相比于4线程的情况, 耗时略微上升, 但仍然优先原串行计算. 这是因为随着线程的增加, 各局部计算区域之间的通信时间增加造成的.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
MPI工具的计算效率和结果可靠性分析
Figure
4.
The analysis of MPI computational efficiency and result reliability
下载: 全尺寸图片
幻灯片
另外, 分别从串行计算和并行计算的结果中提取了一次枝晶臂间距(primary dendrite arm spacing, PDAS), 研究了线程数量对PDAS结果的影响, 结果如图4(b)所示. 发现模拟得到的PDAS在4.25 ~ 5.0μm范围内波动, 且根据误差棒发现, 波动的幅度都十分近似. 由于, 在序参量初始化时设定了一个随机扰动的固/液界面以模拟凝固前期的热涨落现象, 这种因随机扰动造成的波动影响较小. 因此, 选取效率最优的4线程开展后续并行计算工作.
此外, 对比了MPI并行和串行程序情况下的PDAS和尖端半径随冷却速度的变化规律, 如图4(c) ~ 图4(d)所示. 不管是并行程序还是串行程序, 冷却速度与PDAS以及尖端半径都呈幂指数关系, 而且标度律非常接近. 由此论证了MPI并行计算的可靠性. 综上所述, 以线程数为4的MPI并行程序开展后续的熔池全域模拟工作, 可以提升计算效率约2.5倍.
2.
模拟结果与讨论
本节中首先对温度场模拟结果和实验结果进行分析, 验证了宏观模型的准确性. 然后开展熔池横、纵截面的多晶粒竞争生长模拟, 研究熔池全域凝固组织的动态演化过程.
2.1
熔池形貌模拟结果
基于前面激光直接能量沉积实验开展对应的宏观模拟, 发现随着开光时间的推移, 熔池中心温度上升, 且热影响区逐渐变大, 熔覆层的沉积高度也随之增加, 凝固界面后沿形貌逐渐由扁平的抛物线形向着半圆形转变, 当开光时间到达600 ms时, 熔池凝固界面趋于准稳态. 因此, 选取熔池中部x=3.6 mm (600 ms × 6 mm/s), y=0 mm (中心面) 的平面在600 ms时刻下进行横、纵截面实验与模拟结果的对比.
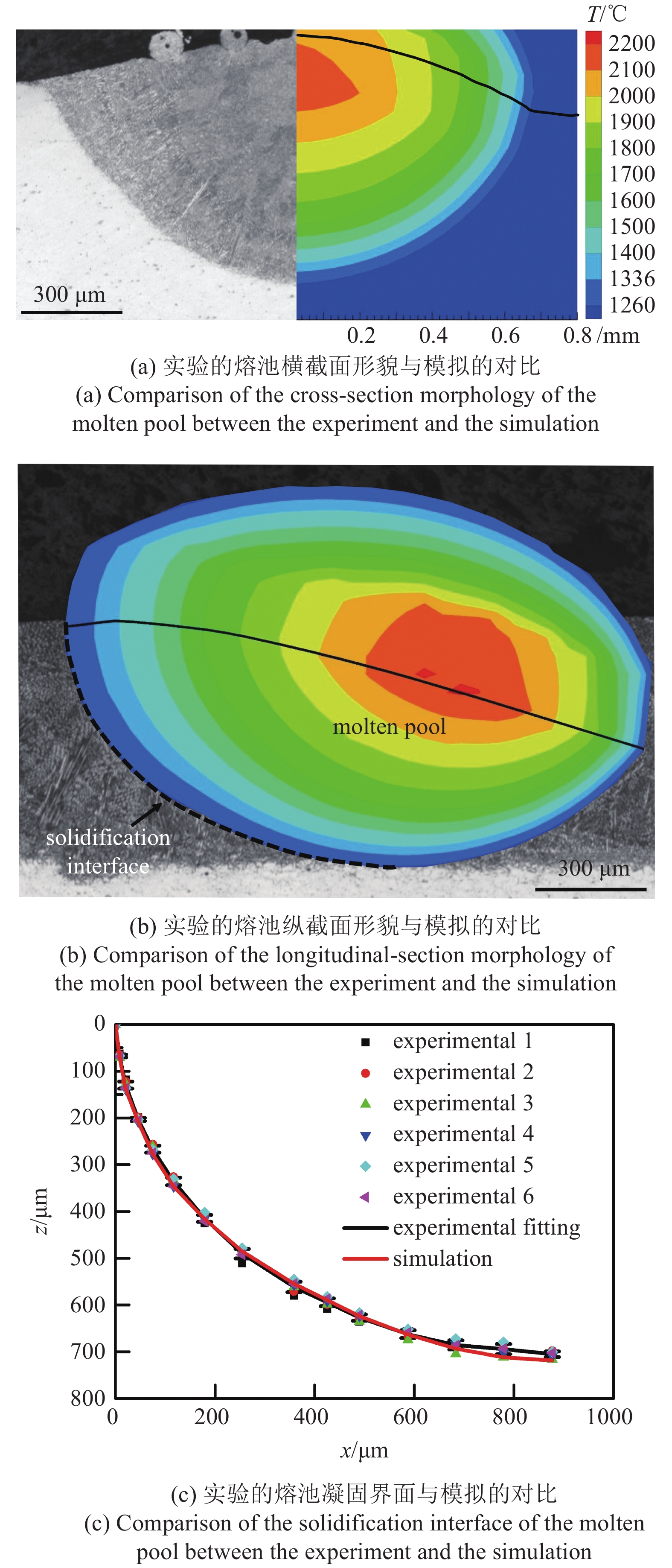
如图5(a)所示, 给出了实验的熔池横截面轮廓与模拟的对比. 在模拟中, 熔池的固/液界面由固相等温线(
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
实验的熔池形貌与模拟的对比
Figure
5.
Comparison of the molten pool morphology between the experiment and the simulation
下载: 全尺寸图片
幻灯片
此外, 对比了熔池纵截面的凝固界面变化趋势, 如图5(b)所示. 在激光增材制造实验中, 通过开光500 ms, 关光20 ms, 使金相组织中的熔池凝固界面清晰显示. 从图中可以发现模拟中的固相线温度等温线和实验凝固界面十分吻合. 进一步在金相图中随机提取了6组熔池凝固界面曲线, 拟合为实验凝固界面, 并与模拟的熔池固/液界面进行了对比, 见图5(c), 发现实验结果与模拟的熔池凝固界面十分接近. 综上所述, 可以得出本文的传热传质模型是可靠的. 根据1.3节所述的方法将温度场演变输入给多相场模型, 深入地开展镍基高温合金凝固组织演化研究.
2.2
熔池横截面凝固组织演化
为了减少计算资源, 考虑到熔池的对称性, 计算区域限制为熔池横截面区域的一半, 并采用零通量的边界条件. 此外, 由文献[36]的模拟结果阐明, 在激光增材制造过程中, 高的温度梯度会形成相对狭小的糊状区, 从而阻止了糊状区内新核的形成. 另外, 相比于铝合金等其他材料, 镍基合金的溶质配分系数高(0.48), 使得凝固前沿的偏析相对较小, 从而减轻了固/液界面处的成分过冷, 促使凝固前沿形核的概率进一步降低. 所以, 镍基合金的凝固过程主要由基板晶粒的外延生长所主导.
图6展示了熔池内部横截面凝固组织的动态演化过程. 在模拟的初始化过程中, 以气液界面确定熔池上表面, 以固相线确定熔池下表面, 在熔池的底部凝固界面即T=1260 °C的等温线上, 等间距随机布置0°, 20°, 40°, 60°的初始晶粒核点, 研究底部晶粒的外延生长过程.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
激光增材制造Inconel 718横截面凝固组织动态演化过程
Figure
6.
Dynamic evolution process of solidification microstructure in cross-section of molten pool for laser additive manufacturing Inconel 718
下载: 全尺寸图片
幻灯片
由图6(a)可知, 在凝固初始阶段(0 ~ 16 ms), 由于凝固速率较低, 凝固组织的生长也较缓慢, 凝固组织以顺着凝固界面生长为主, 使得各个晶粒间相互接触, 共同以平面晶的稳态形式向着凝固界面的法向进行生长. 在16 ~ 32 ms过程中, 即如图6(b)所示, 随着凝固的持续进行, 各个晶粒内部通过凝固前沿不断向液相排出Nb元素, 进而Nb元素会聚集在固/液界面前沿形成富铌层, 使得界面处的成分过冷迅速增大, 导致在晶界位置首先出现平面晶的失稳, 并逐步扩散至远离晶界位置, 随着凝固的推移, 会由原先微小的凸起转变为明显的枝晶形貌, 从而出现平面晶到枝晶的转变. 在32 ~ 90 ms过程中, 如图6(c)所示, 由于各晶粒的结晶学方向差异和表面能的各向异性, 各枝晶列表现为激烈的竞争生长. 在熔池底部, 由于等温线较为平缓, 温度梯度的方向接近于竖直方向, 因此, 可以发现取向角为0°的红色晶粒和20°的黄色晶粒在该区域占优生长, 并逐步淘汰相邻的黄色晶粒以及绿色晶粒. 而在熔池的顶部, 由于在该位置温度梯度的方向更接近于45°, 同时, 取向角为40°的绿色晶粒和取向角为60°的蓝色晶粒也更接近于温度梯度的方向. 因此, 可以发现取向角为0°的红色晶粒在熔池顶部区域逐步淘汰. 如图6(d)所示, 在128 ms左右时刻, 熔池即将完全凝固, 可以明显地发现, 熔池底部主要以取向角较小的红色晶粒和黄色晶粒为主, 熔池顶部主要以取向角度较大的绿色晶粒和蓝色晶粒为主. 综上所述, 可以得出, 在外延生长过程中, 横截面的凝固组织演化主要受温度梯度方向的影响. 当晶粒的结晶学方向接近于其凝固界面的温度梯度方向时, 该晶粒将在竞争过程中处于优势地位, 并逐步淘汰远离温度梯度方向生长的劣势晶粒.
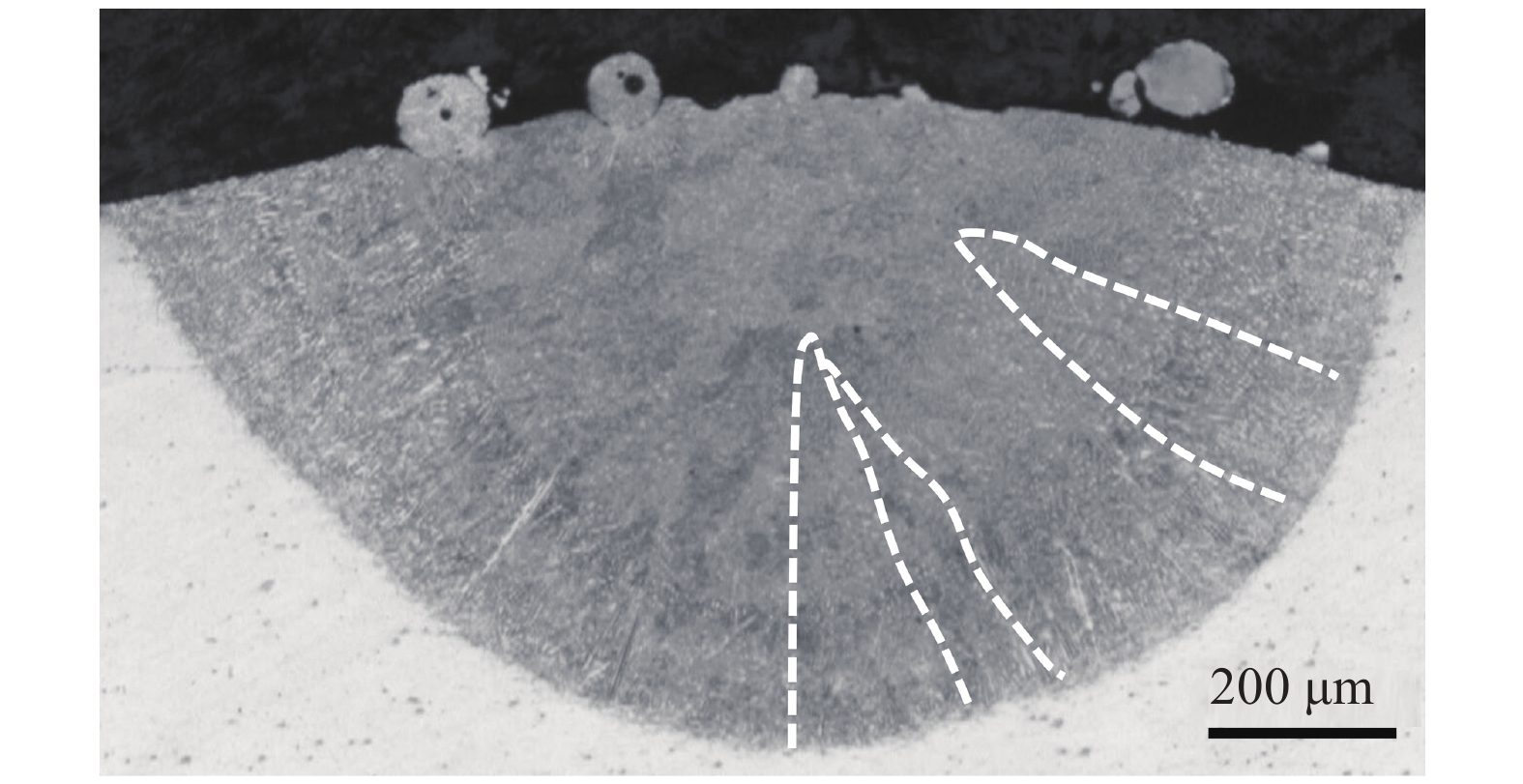
如图7所示, 展示了熔池横截面显微组织的金相图, 图中白色虚线描述了晶粒轮廓. 从中可以发现, 在熔池底部晶粒主要呈竖直生长, 在熔池顶部晶粒主要呈现枝晶的倾斜生长. 此外还发现了熔池中心区域呈现等轴生长, 这可能是由于熔池内形核增加, 抑制了晶粒的外延生长, 从而产生了柱状晶到等轴晶的转变(columnar to equiaxed, CET). 然而, 因难以直接评估凝固过程的形核过冷和形核密度, 在目前的模拟工作中, 开展形核对CET的定量研究十分困难. 对于多层熔覆和块体增材制造而言, 层间存在重熔现象, 使得在后一层的打印过程中, 前一层熔池顶部的等轴晶粒会率先熔化消失. 因此, 仍能延续前一层晶粒的外延生长. 通过模拟和实验的对比, 可以发现, 凝固组织演变受到温度梯度方向的影响, 在熔池底部呈现竖直生长, 在顶部呈现倾斜生长. 这与模拟的熔池横截面晶粒演变趋势一致.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
横截面的金相组织图
Figure
7.
Metallographic diagram of cross-section
下载: 全尺寸图片
幻灯片
2.3
熔池纵截面凝固组织演化
本节讨论了激光增材制造Inconel 718熔池纵截面的凝固组织动态演化过程, 如图8所示. 与横截面的结果类似, 在纵截面的模拟过程中, 同样包括了平面晶的生长、失稳转变为枝晶以及竞争生长的过程. 如图8(a)所示, 在凝固初始阶段, 熔池顶部的凝固组织生长明显快于底部, 可以发现, 熔池顶部已呈现明显的枝晶竞争生长状态, 而熔池底部仍保持着平面晶的生长状态. 该现象的产生是因熔池固/液界面各处的凝固条件不同造成的. 由文献[21]可知, 在固相线上, 熔池顶部的凝固速率大于熔池底部, 同理, 熔池顶部的等温线推进也会相应地快于熔池底部.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
激光增材制造Inconel 718纵截面凝固组织动态演化过程
Figure
8.
Dynamic evolution process of solidification microstructure in longitudinal-section of molten pool for laser additive manufacturing Inconel 718
下载: 全尺寸图片
幻灯片
在激光增材制造单道单层单向扫描的沉积过程中, 熔池中下部的凝固组织以40°的绿色晶粒和60°的蓝色晶粒为主, 如图8(b)所示. 这是因为在单向扫描过程中, 熔池的主要温度梯度方向与扫描方向有大约60°的夹角[37]. 此时, 取向角为40°和60°的晶粒为优势晶粒, 并随着凝固的进行, 不断地通过侧枝的生成挤压0°和20°晶粒的生长; 而在熔池的上部区域, 由于受到温度梯度方向和扫描方向的共同作用, 40°和60°的晶粒不再在竞争中占有优势. 因此, 各个晶粒都沿着扫描方向推进, 本文的模拟结果很好地支持了Wei等[38]的观点.
此外, 在图8(b)中可以发现取向角为0°的红色晶粒1出现了较为明显的晶粒弯曲生长现象. 这与Tan等[39]报道的实验结果类似. 该现象背后的实质是结晶学的择优取向. Inconel 718合金具有面心立方的晶体结构, 因此对于取向角为0°的晶粒而言, 竖直的0°方向和水平的90°方向都是其择优生长方向. 因为红色晶粒1的初始凝固位置位于熔池中下部, 此时0°的结晶学方向与温度梯度方向夹角较小, 因此, 红色晶粒倾向于竖直方向生长. 随着凝固界面的推移, 红色晶粒1不断生长, 晶粒前沿的温度梯度方向发生改变. 在凝固过程的某一时刻, 其红色晶粒的凝固界面位置处的温度梯度方向与90°的结晶学方向的夹角更小, 导致红色晶粒倾向于水平生长. 由于凝固界面的推进, 在温度梯度方向和择优取向的共同作用下, 晶粒生长方向从原先的竖直方向转变至水平方向, 最终导致了渐变弯曲晶粒的形成. 而对于同为0°取向的晶粒2而言, 由于其初生位置在熔池顶部, 因此, 从凝固开始到晶粒2淘汰的整个过程中, 始终为90°的结晶学方向与温度梯度方向夹角更小, 使得晶粒2保持着水平方向生长的状态, 同时受到相邻晶粒间的竞争, 晶粒2呈现典型的“上三角”形貌. 综上所述, 温度梯度方向的变化导致了渐变弯曲晶粒的形成, 相邻晶粒间的竞争行为决定了晶粒淘汰的形貌特征.
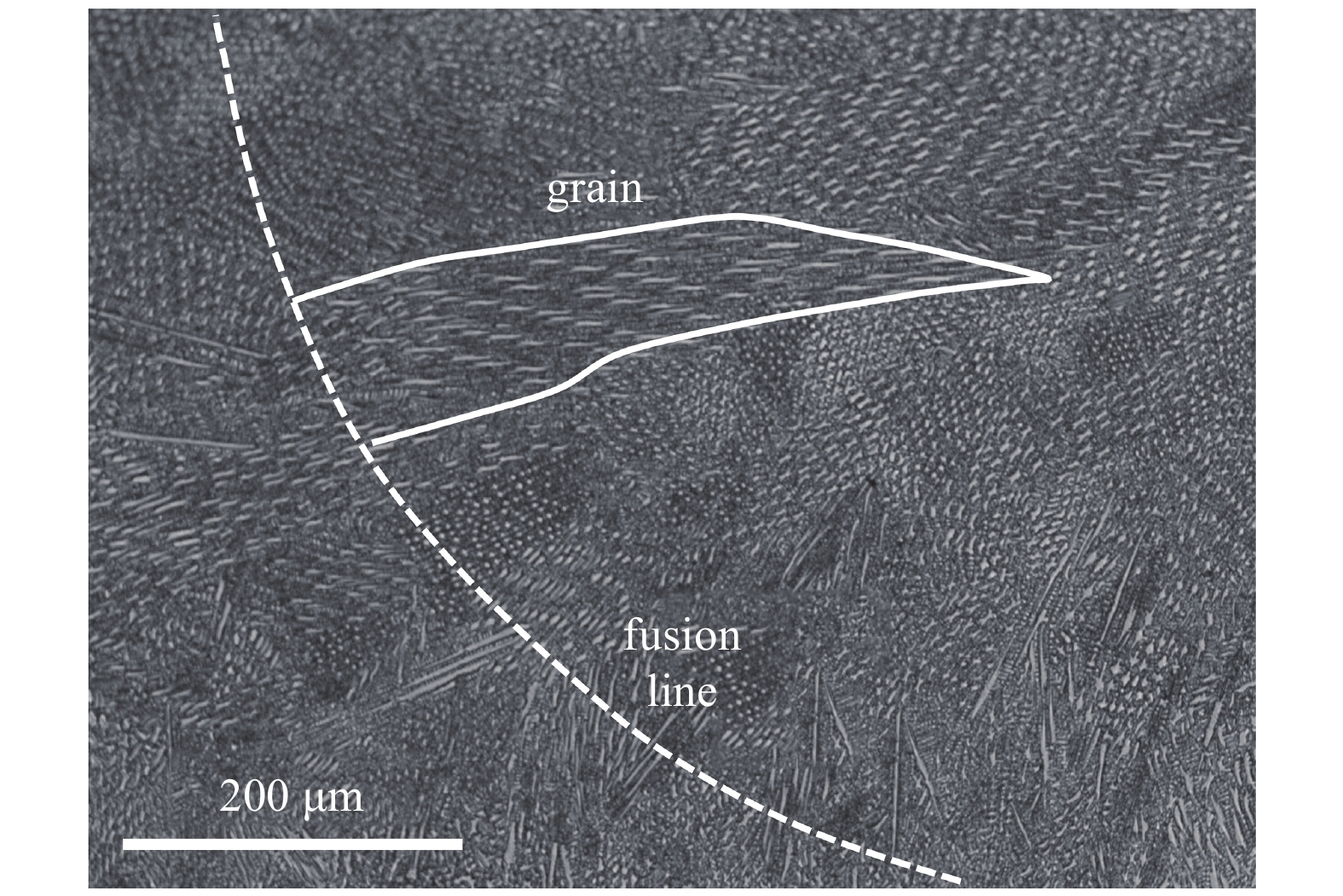
图9给出了熔池纵截面显微组织的金相图, 其中白色虚线为熔池的凝固界面. 从图中可以发现, 在熔池顶部区域, 出现晶粒(白色实线)倾向于水平方向生长, 晶粒形貌与模拟中的晶粒2非常相似, 呈“上三角”形态. 即在热流方向与晶体择优取向共同作用下, 经长时间的竞争生长后, 劣势晶粒被逐渐淘汰.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-364-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
纵截面的金相组织图
Figure
9.
Metallographic diagram of longitudinal-section
下载: 全尺寸图片
幻灯片
3.
结论
本文以激光增材制造Inconel 718为研究对象, 构建了宏观传热传质与多相场耦合的多尺度数学模型. 为了解决模拟区域受限的问题, 通过MPI并行计算工具优化模拟效率, 使得计算速度提升2.5倍. 实验和模拟研究了熔池形貌、横截面凝固组织、纵截面凝固组织等特征, 主要的结论总结如下:
(1) 通过对温度场在时间域和空间域的数值处理, 解决了宏观热行为与微观温度场演变的时空耦合, 构建了金属激光增材制造的多尺度数学模型;
(2) 熔池形貌在开关约600 ms后达到准稳态. 模拟的熔池尺寸、凝固界面与实验结果吻合较好. 模拟和实验研究表明, 熔池凝固界面形态是影响晶粒演变的重要因素;
(3) 对于横截面的凝固组织, 熔池中心主要体现为晶粒的外延生长, 凝固过程主要受温度梯度方向的驱使. 当晶粒的结晶学方向接近于其凝固界面的温度梯度方向时, 该晶粒将在竞争过程中处于优势地位, 并逐步淘汰远离温度梯度反向生长的劣势晶粒;
(4) 对于纵截面的凝固组织, 晶粒的生长表现出弯曲生长以及“上三角”的晶粒特征. 其可归因于温度梯度方向和相邻晶粒间的竞争行为. 温度梯度方向的变化导致了晶粒渐变弯曲, 相邻晶粒间的竞争行为通过枝晶列的生成与淘汰决定了晶粒的形貌特征.
