引 言
增材制造通过不断添加材料来完成零件的加工成型, 满足了工业对零件形状、功能、材料的更高要求, 成为当前材料加工技术发展的前沿方向. 与传统制造工艺相比, 增材制造在成形原理、材料形态、制件性能上发生了根本改变, 具有材料浪费少、加工工序少、加工周期短、零件结构设计自由、易于实现形状复杂零部件快速成型等优点, 被认为是能够深刻影响未来的战略前沿技术[1-3].
增材制造零部件在航空航天、医疗仪器、轨道交通等战略新兴产业领域内作为承载结构件应用时, 其力学性能至关重要. 而增材制造零部件的力学性能又与增材制造工艺产生的微结构紧密相关, 增材制造工艺参数、微结构及其演化、力学性能之间的关联规律, 显得尤为重要. 然而在实际生产过程中, 增材制造所涉及的物理过程极其复杂, 一次成功制造零部件的概率较低. 影响增材制造工艺的因素很多, 包括粉末的物理性质、激光参数、扫描速度、粉床厚度和扫描策略等, 若采用传统的实验试错法去优化微结构和力学性能, 将极大增加产品的制造周期和生产成本. 采用数值模拟来优化增材制造工艺参数及其导致的微结构和力学性能, 可以弥补实验试错法的不足[4-7]. 以微结构演化和力学性能为核心的数值模拟, 已成为加快增材制造材料与产品研发、降低生产成本、提升增材制造产能的重要手段.
在增材制造微结构演化模拟方面, 目前常用的方法有相场法、元胞自动机法和动力学蒙特卡洛法等. 对于相场方法, 大多数研究采用顺序耦合策略, 即先求出温度的时空变化, 然后将其作为输入参数导入相场模拟. 比如Sahoo和Chou[8]以温度梯度和凝固速度为输入参数, 采用等温相场模型计算了增材制造中微观尺度的枝晶形貌变化; Liu等[9]将预先得到的温度信息输入到非等温相场模拟, 在介观尺度研究了金属增材制造过程中的晶粒生长问题; Yan等[10]将粉末尺度热?流模型的温度结果输入到三维相场模拟, 计算了增材制造过程中晶粒形核、生长和粗化的微结构演化历程. 最近, Lu等[11]直接在粉末尺度考虑了含激光热源的热传导方程与相场演化方程的耦合, 并综合考虑了气/液/固相、粉末熔化、熔体凝固和晶粒生长过程; Yang等[12-16]进一步发展了热?熔体?微结构耦合的非等温相场模型, 可揭示增材制造中局部温度剧烈变化和极大温度梯度造成的微结构演化特征.
元胞自动机法也被广泛应用于金属增材制造的微结构演化. Lian等[17]基于MPI技术开展了金属增材制造三维元胞自动机算法的并行化研究, 预测了选区电子束熔融工艺Ti-6Al-4V合金的凝固初生相, 并进一步建立了外延式生长成核模型[18]. 魏雷等[19]采用元胞自动机模拟了激光立体成形过程中温度场分布、熔池形貌和凝固微观组织. 元胞自动机法也可与其他方法耦合, 比如Lian等[18]和Yan等[20]等将热流耦合模型与元胞自动机法进行顺序耦合, Rai等[21-22]将热流耦合模型的格子玻尔兹曼方法与元胞自动机法进行了弱耦合.
最近, Wang等[23]采用有限体积法和离散元法相结合的方法模拟了Ti-6Al-4V合金粉末颗粒的沉积, 可复现金属增材制造球化、局部熔化、未融合等现象, 预测增材制造产品的内部缺陷. 美国劳伦斯利弗莫尔国家实验室的金属增材制造研究组[24]也开发了ALE3D程序, 开展了粉末尺度的高保真热?流?固耦合及微结构演化的数值模拟.
在增材制造微结构力学性能计算方面, 目前主流方法是晶体塑性有限元. 比如Ahmadi等[25]采用晶体塑性有限元计算了SLM不锈钢微结构的力学性能, 计算结果与实验吻合较好; Yan等[20]基于晶体塑性自洽聚类分析方法, 采用疲劳指示参数计算了材料微结构决定的疲劳性能; 张昭等[26]针对同轴送粉激光熔覆增材制造, 采用考虑粒子数量的热源模型和Monte Carlo算法获得了双相钛合金微观结构, 并进一步采用晶体塑性有限元预测了所得微结构的力学性能; Liu等[27]为了提高晶体塑性模型的计算效率, 采用了基于快速傅里叶变换的弹黏塑性模型, 计算了含双相的钛合金微结构的力学行为.
在增材制造的工艺参数?微结构?力学性能关联计算方面, 主要是将多种模型和算法按顺序耦合进行计算. 比如Yan等[20]首先采用粉末铺展和热-流模型计算了不同工艺参数下的温度演化和孔洞形成, 然后将这些信息传递给元胞自动机模型计算晶粒结构, 进一步将含有晶粒和孔洞的结构信息传递至降阶的细观力学模型计算力学性能; 类似地, Liu等[27]首先在宏观尺度采用有限元计算了热响应, 然后将热历史信息输入到温度相关的晶粒生长相场模型计算晶粒形貌演化, 最后基于快速傅里叶变换的弹粘塑性模型计算了所得到微结构的力学性能. 最近, DebRoy等[28]和Smith等[29]针对金属增材制造过程参数、结构与性能之间的关联, 在实验和计算方面均做了详细综述.
本文为了预测增材制造中工艺参数?微结构?力学性能之间的关联规律, 实现粉床铺设、微结构演化和力学性能计算, 提出了集成离散元、相场模拟、晶体塑性有限元和极值概率理论的计算方法, 研究了激光扫描速度对微结构演化、屈服应力和疲劳分散性的影响, 以期为增材制造零部件力学性能的优化提供数值模拟方法.
1.
计算框架及模型
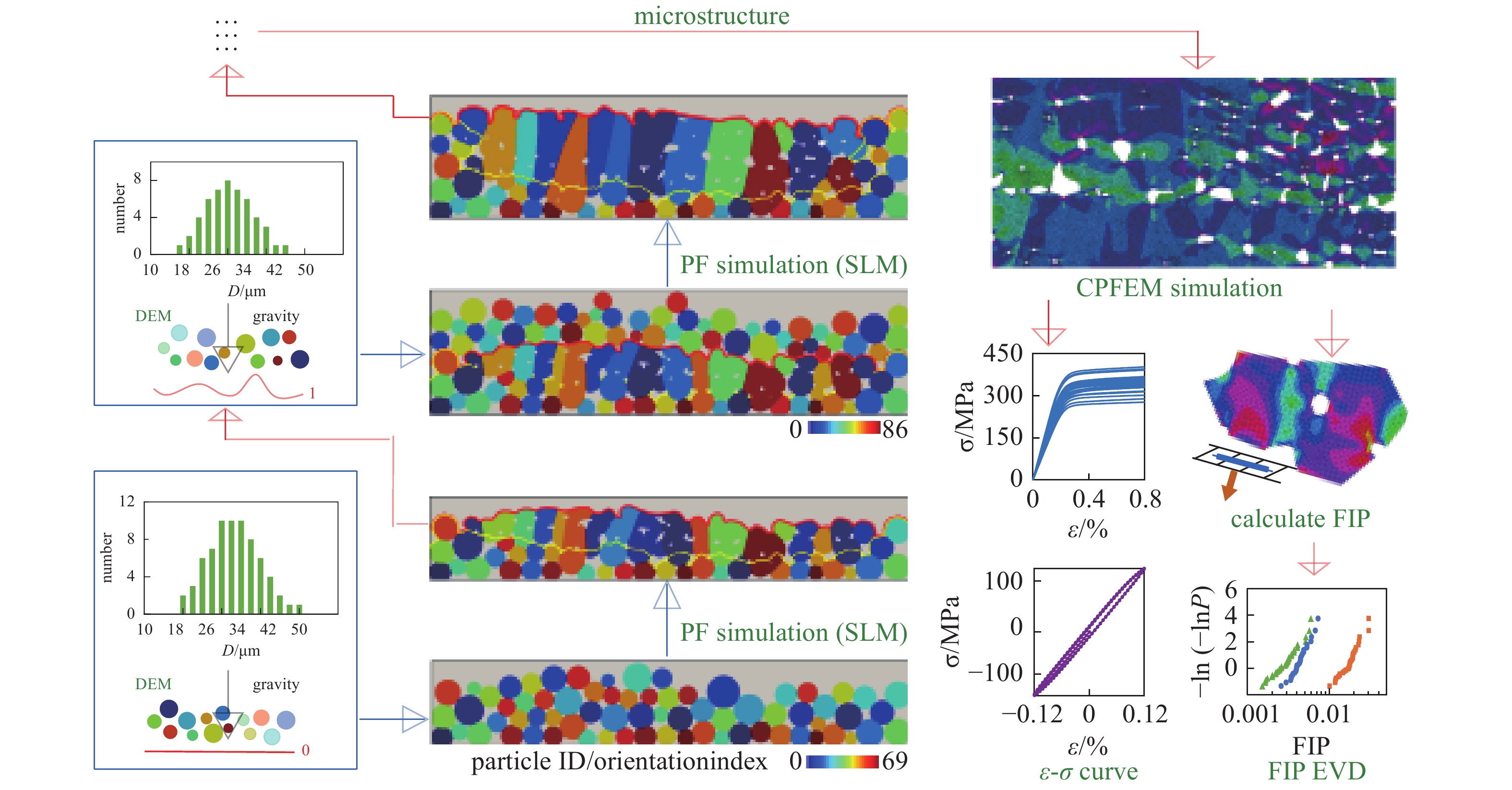
本文采用的计算框架及流程如图1所示, 具体包括: (1) 采用离散元方法(DEM)[30]生成粉末颗粒具有特定分布规律的粉床, 粉末颗粒在重力作用下自由沉降, 第一层以水平线为基板生成粉床, 后续粉床生成以上一层已凝固表面形貌(一般为曲线/面)为基板; (2) 以粉床为基础, 采用非等温相场模拟计算增材制造微结构演化, 包括粉末熔化、热传导、熔体流动、气泡/孔洞演化、凝固、晶界迁移、晶粒生长和粗化等; (3) 采用晶体塑性有限元计算增材制造所得微结构的应力?应变响应, 并对晶粒取向进行随机取样, 计算有限个多晶微结构的力学响应, 再统计平均求得屈服强度; (4) 计算有限个多晶微结构在不同应变幅下的循环应力?应变曲线及疲劳指示参数(fatigue indicator parameter, FIP), 并确定每个晶粒中最大的体积平均FIP, 表征晶粒受到的裂纹萌生驱动力; (5) 采用极值概率理论统计分析FIP, 确定不同载荷作用下的FIP极值概率分布规律, 进而分析疲劳性能的分散性.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-389-1.jpg'" class="figure_img
figure_type2 ccc " id="Figure1" />
图
1
用于增材制造微结构演化及疲劳分散性预测的集成离散元、相场模拟、晶体塑性有限元和极值概率理论的计算框架示意图(DEM: 离散元; PF: 相场; CPFEM: 晶体塑性有限元; FIP: 疲劳指示参数; EVD: 极值分布)
Figure
1.
Computational framework integrating discrete element method, phase-field simulation, crystal plasticity finite element method, and extreme value statistics for the prediction of evolution and fatigue dispersity of microstructures by additive manufacturing (DEM: discrete element method; PF: phase field; CPFEM: crystal plasticity finite element method; FIP: fatigue indicator parameter; EVD: extreme value distribution)
下载: 全尺寸图片
幻灯片
1.1
非等温相场模型
针对增材制造过程中高能集中热束作用产生的极大温度梯度和非平衡过程, 本文采用作者前期发展的增材制造非等温相场模型[13], 全面考虑热传导、熔池流体动力学和微结构演化三者之间的耦合. 描述微结构演化的相场模型采用以下序参量:
ho $
ho = 1$
ho = 0$
ho - phi $
ho - phi = 1$
$$ begin{split} &varTheta = intlimits_varOmega left[ {f_{{text{ht}}}}(T) + {f_{{text{loc}}}}(T, ho,phi,{ {eta _i}} ) + hat p{Sigma _g} + ight. [-2pt]&qquadleft.{f_{text{g}}}(T,nabla ho,nabla phi,{ nabla {eta _i}} ) ight]{text{d}}varOmega end{split} $$  | (1) |
其中
根据式(1)的能量泛函可推导出该非等温相场模型的主要控制方程. 控制序参量
$$ frac{{{text{D}}phi }}{{{text{D}}t}} = - {L_phi }frac{{delta varTheta }}{{delta phi }} $$  | (2) |
控制序参量
$$ frac{{{text{D}}{eta _i}}}{{{text{D}}t}} = - {L_eta }frac{{delta varTheta }}{{delta {eta _i}}} $$  | (3) |
控制序参量
ho $
$$ frac{{{text{D}} ho }}{{{text{D}}t}} = nabla cdot left[ {{boldsymbol{M}} cdot nabla frac{{delta varTheta }}{{delta ho }} + {{boldsymbol{M}}_{{text{th}}}} cdot left( {frac{{delta varTheta }}{{delta ho }}frac{{nabla T}}{T}} ight)} ight] $$  | (4) |
其中
控制温度
$$ begin{split} &{c_r}frac{{{text{D}}T}}{{{text{D}}t}} + frac{{partial e}}{{partial ho }}frac{{{text{D}} ho }}{{{text{D}}t}} + frac{{partial e}}{{partial phi }}frac{{{text{D}}phi }}{{{text{D}}t}} + sumlimits_i {frac{{partial e}}{{partial {eta _i}}}frac{{{text{D}}{eta _i}}}{{{text{D}}t}}} = &qquadnabla cdot ({boldsymbol{k}} cdot nabla T) +{boldsymbol{ sigma}}:nabla {boldsymbol{u}} + {q_v} end{split} $$  | (5) |
式(5)中
熔池流动速度场的控制方程为
$$ nabla cdot {boldsymbol{u}} = 0 $$  | (6) |
$$ wp frac{{{text{D}}{boldsymbol{u}}}}{{{text{D}}t}} = - nabla p + upsilon {nabla ^2}{boldsymbol{u}} - nabla cdot {{boldsymbol{sigma}} _k} + {boldsymbol{b}} $$  | (7) |
其中
式(2) ~ 式(7)采用有限元方法求解, 在开源代码MOOSE (multiphysics object-oriented simulation environment)[31]框架下编写有限元程序, 并采用PETSc和MPI实现并行计算.
1.2
晶体塑性模型
采用晶体塑性模型计算增材制造微结构的力学性能, 本文仅对该模型做简要概述. 根据有限变形条件下的乘法分解, 总变形梯度张量
$$ {dot{boldsymbol{ F}}^{text{p}}} cdot {{boldsymbol{F}}^{{text{p}} - 1}} = sumlimits_alpha {{{dot gamma }^{(alpha )}}} {{boldsymbol{s}}^{(alpha )}}{{boldsymbol{m}}^{(alpha )}} $$  | (8) |
其中单位矢量
ho _0}/
ho {boldsymbol{sigma}} cdot {{boldsymbol{s}}^{*(alpha )}} $
$$ {dot gamma ^{(alpha )}} = {dot a^{(alpha )}}frac{{{tau ^{(alpha )}}}}{{{g^{(alpha )}}}}{left| {frac{{{tau ^{(alpha )}}}}{{{g^{(alpha )}}}}} ight|^{n - 1}} $$  | (9) |
其中
ho _0} $
ho $
$$ {dot g^{(alpha )}} = sumlimits_beta {{h_{alpha beta }}{{dot gamma }^{(beta )}}} $$  | (10) |
其中
$$ {h_{alpha beta }} = {h_0}{{{ m{sech}}} ^2}left{left| {frac{{{h_0}gamma }}{{{tau _s} - {tau _0}}}} ight|left[ {q + (1 - q){delta _{alpha beta }}} ight] ight} $$  | (11) |
$$ gamma = sumlimits_alpha {int_0^t {left| {{{dot gamma }^{(alpha )}}(chi )} ight|} } {text{d}}chi $$  | (12) |
其中
1.3
疲劳指示参数计算
疲劳指示参数(FIP)是表征疲劳裂纹萌生驱动力的替代指标, FIP值越大所对应于的裂纹萌生驱动力也越大. 早期Fatemi和Socie[33]期望将多个晶粒内的疲劳裂纹萌生寿命(含裂纹形成和扩展)关联到几百微米尺度的寿命, 提出了基于临界平面的以剪切应变主导裂纹萌生的FIP. McDowell和Berard[34]发现该FIP可将微裂纹扩展速率与弹塑性断裂力学的
$$ {{FI}}{{{P}}_alpha } = frac{{Delta {gamma ^alpha }}}{2}left( {1 + {k_e}frac{{sigma _n^alpha }}{{{sigma _y}}}} ight) $$  | (13) |
其中
本文采用最后一个加载循环当中的
1.4
极值统计分析
微结构中疲劳裂纹的萌生一般发生在裂纹萌生驱动力最大的区域, 也即需要确定体积平均FIP的极大值. 为了研究增材制造微结构疲劳分散性, 采用极值概率理论对体积平均FIP极大值进行统计分析. FIP极值作为当前微结构中裂纹萌生的最大驱动力, 其概率分布特征将对应于疲劳的分散性, 两者具有关联.
对于增材制造得到的多晶微结构, 假设其晶粒取向服从均匀分布, 随机生成
$$ P(y) = {F_Y}(y) = exp left[ { - exp left( { - frac{{y - {u_0}}}{{{beta _0}}}} ight)} ight] $$  | (14) |
其中
$$ P({y_j}) = {F_Y}({y_j}) = frac{{j - 0.3}}{{N + 0.4}} $$  | (15) |
其中
$$ - ln ( - ln P) = frac{{y - {u_0}}}{{{beta _0}}} $$  | (16) |
将每个多晶微结构的体积平均FIP的极大值数据点按式(16)进行拟合, 可获得疲劳分散性结果.
2.
增材制造微结构演化
采用1.1节中的热?熔体?微结构耦合的非等温相场模型, 对选区激光熔化增材制造的微结构演化进行了详细计算研究, 激光功率P0固定为400 W, 激光扫描速度v设为0.5, 1.0, 1.5, 2.0 m/s, 选取金属材料为316L不锈钢. 非等温相场模拟在二维区域内进行, 316L不锈钢粉床x方向长度为600 μm, 粉末颗粒的平均粒径约为28 μm, 第一层粉末厚约为100 μm, 后续逐层铺粉的粉末层厚约为40 μm, 二维区域的底部假设为稳态导热换热的基板, 其余边界均允许对流散热, 基板、预热以及环境温度均设置为680 K.
图2给出了激光扫描速度v = 2 m/s下316L不锈钢粉末逐层选区激光熔化过程的典型微观结构演化, 其中可直接观察到熔池中的熔体流动以及气孔的运动. 粉末颗粒首先在激光辐照下发生快速熔化, 形成流动的熔池, 在重力作用下, 初始颗粒表面高低不平所形成的凸起熔体会向下流动, 引发表面和气孔附近的平展流. 颗粒间的间隙也以气孔的形式出现在熔池中, 成为增材制造微结构中孔隙的重要来源, 如图2(d)和图2(e)中的圆圈4所示. 当熔体凝固而气孔尚来不及从熔体表面逃逸出去时, 气孔会残留在微结构内部, 形成明显的孔洞缺陷, 如图2(a)的圆圈1和图2(e)的圆圈4所示. 若在熔体凝固前, 气孔能运动至熔体表面并逃逸出去, 则气孔不会在微结构内形成孔洞缺陷, 如图2(b)的圆圈2和图2(c)的圆圈3所示. 计算结果表明, 当激光扫描速度较大时, 熔池存在时间短且凝固发生快, 导致气孔难以逸出, 形成较多孔洞缺陷. 熔池的凝固伴随着晶体外延生长, 以减小晶界能, 如图2(b)中的箭头所示. 已凝固晶粒受到后续激光扫描的热影响, 会发生烧结现象, 晶粒粗化, 如图2(d)的圆圈5和图2(e)的圆圈6所示. 因此, 本文的非等温相场模型能够模拟增材制造中包括熔化、凝固、晶粒生长/粗化、熔池流动、气孔运动、晶界迁移和孔洞生成等在内的微结构演化全过程.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-389-2.jpg'" class="figure_img
figure_type2 ccc " id="Figure2" />
图
2
逐层选区激光熔化增材制造过程的微结构演化(v = 2 m/s)
Figure
2.
Microstructure evolution during layer-by-layer selective laser melting (v = 2 m/s)
下载: 全尺寸图片
幻灯片
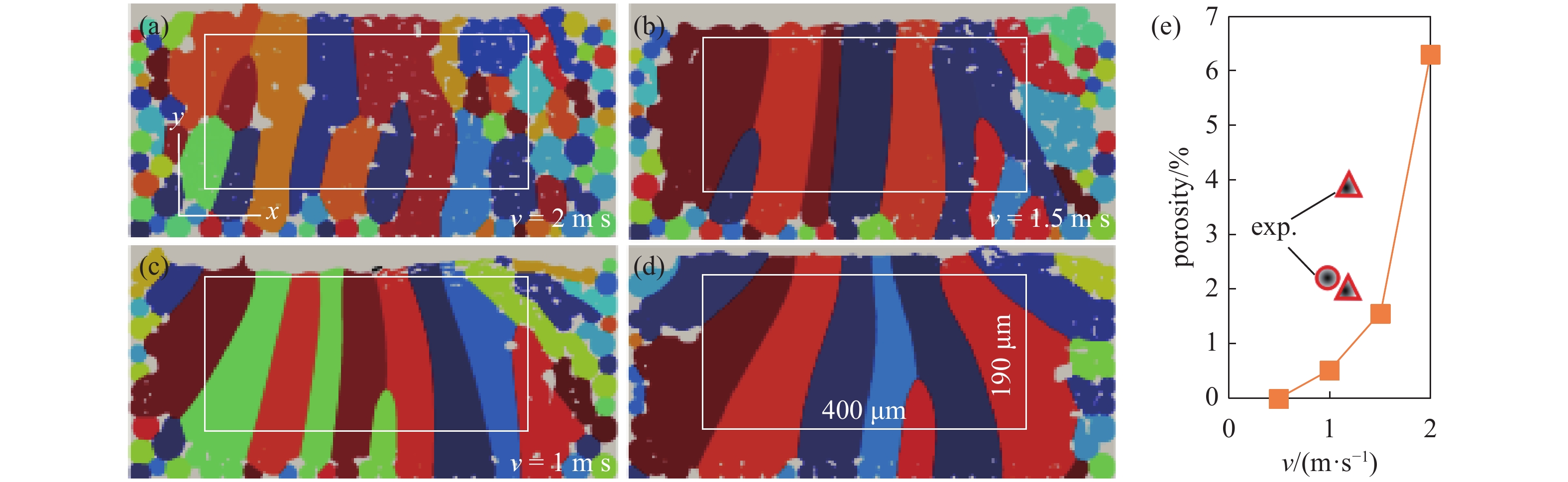
选区激光熔化五层粉末所获得的最终微结构如图3(a) ~ 图3(d)所示. 容易看出, 当激光扫描速度从2 m/s降至0.5 m/s时, 孔洞缺陷和晶粒数量显著减少, 在发生完全熔化的中间区域部分, 形成了明显的柱状晶结构. 对中间长400 μm、高190 μm的区域进行孔隙率计算(图3(e)), 发现2 m/s和1 m/s的激光扫描速度分别产生6.3%和0.52%的孔隙率, 而0.5 m/s的激光扫描速度可形成无孔隙的完美柱状晶微结构. 文献报道的选区激光熔化316L不锈钢的孔隙率实验结果表明, 功率90 W和扫描速度1 m/s得到的孔隙率约2.3%[44], 而功率160 W和扫描速度1.2 m/s得到的孔隙率为2% ~ 3.8%[45], 因此本文计算的孔隙率数值在实验结果范围之内.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-389-3.jpg'" class="figure_img
figure_type2 ccc " id="Figure3" />
图
3
选区激光熔化增材制造微结构及其孔隙率: (a) v = 2 m/s; (b) v = 1.5 m/s; (c) v = 1 m/s; (d) v = 0.5 m/s; (e) 图(a) ~ 图(d)中矩形区域(400 μm × 190 μm)的孔隙率, 其中圆形(90 W, 1 m/s)[44]和三角形(160 W, 1.2 m/s)[45]标记为实验结果
Figure
3.
Microstructure and porosity obtained by selective laser melting: (a) v = 2 m/s; (b) v = 1.5 m/s; (c) v = 1 m/s; (d) v = 0.5 m/s; (e) porosity of the rectangular region (400 μm × 190 μm) in (a)-(d), with the circle (90 W, 1 m/s)[44] and triangle (160 W, 1.2 m/s)[45] markers indicating the experimental results
下载: 全尺寸图片
幻灯片
3.
增材制造微结构力学性能及疲劳分散性
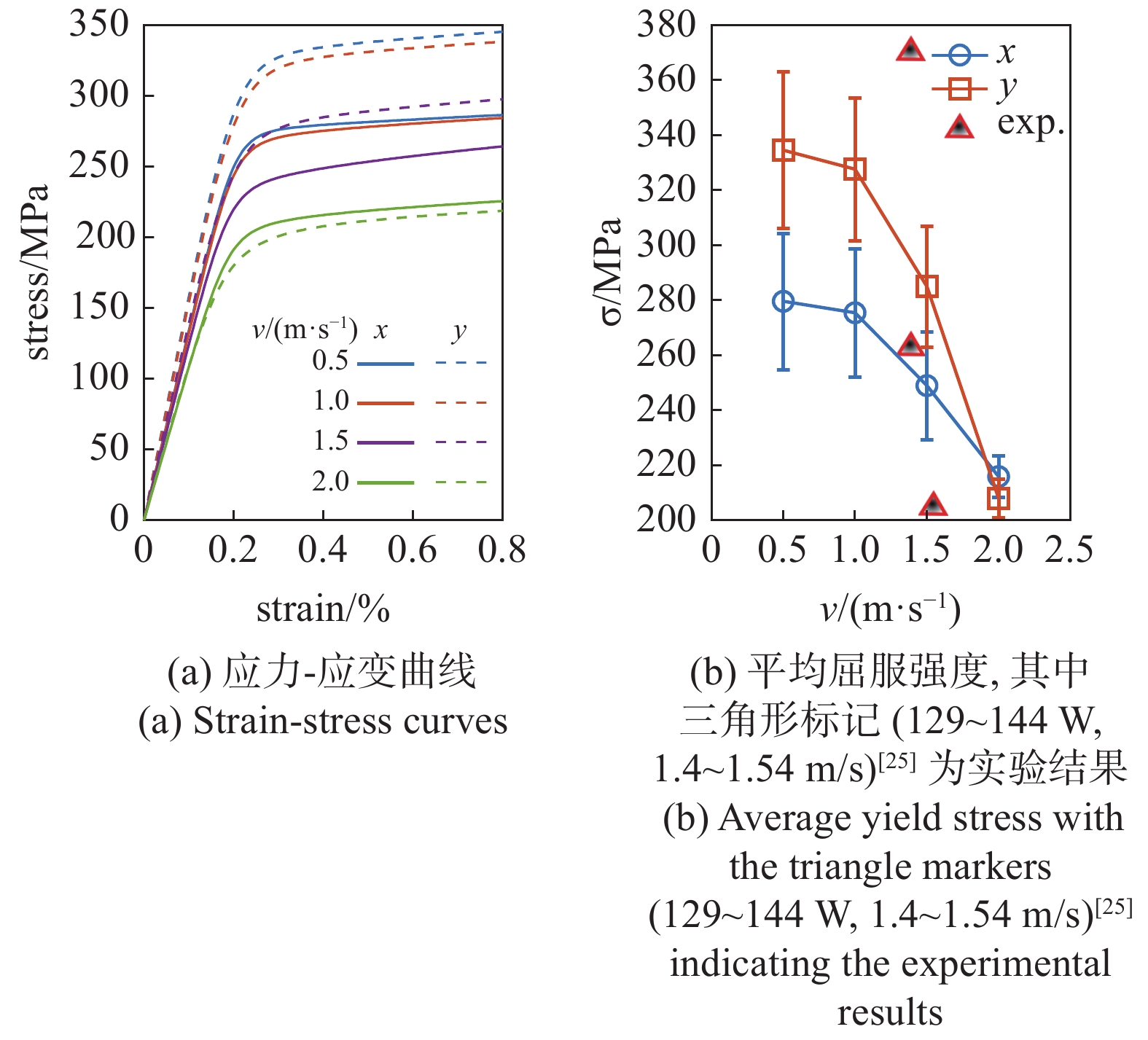
为了评定增材制造微结构的力学性能, 采用晶体塑性有限元对图3(a) ~ 图3(d)中400 μm × 190 μm的矩形区域进行了沿x和y方向的平面应变拉伸模拟. 增材制造模拟中存在明显的晶粒外延生长行为, 故第一层粉床凝固形成的晶粒的取向, 对整个微结构的晶粒取向分布影响甚大. 本文考虑第一层凝固生成晶粒的取向存在随机性, 将微结构中所有晶粒取向按均匀分布来设置, 共设30组分布, 也即每个微结构的力学行为计算30次, 统计平均后的计算结果如图4所示. 可以看出, 应力?应变曲线(图4(a))和屈服强度(图4(b))呈现明显的各向异性. 当激光扫描速度较低(v = 0.5 ~ 1.5 m/s)时, y方向的杨氏模量和屈服强度明显大于x方向的, 这是因为此时孔隙率较低, 沿y方向的柱状晶形貌成为各向异性的主要控制因素. 当激光扫描速度较高(v = 2 m/s)时, y方向和x方向的应力?应变曲线和屈服强度差别不大, 且屈服强度的分散性也小, 这是因为此时孔隙率较高, y方向柱状晶不连续, 决定微结构力学行为的主要因素是孔隙的应力集中, 晶向分布是次要影响因素. 文献实验报道的选区激光熔化316L不锈钢的屈服强度存在较大分散性, 比如Ahmadi等[25]采用功率129 ~ 144 W和扫描速度1.4 ~ 1.54 m/s得到的屈服强度为219 ~ 373 MPa, 而Kumar等[44]采用功率90 W和扫描速度1 m/s得到的屈服强度高达430 ~ 511 MPa. Shrestha等[46]采用功率350 W和扫描速度1 m/s得到的屈服强度为495 ~ 545 MPa. 本文计算的屈服强度低于文献实验值, 其原因可能与晶粒尺寸和晶体塑性模型参数相关. 文献实验得到的晶粒尺寸为1 μm[44]和28 ~ 33 μm[46], 远小于本文得到的晶粒尺寸, 故本文的相场模型及参数有待进一步改进.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-389-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
选区激光熔化增材制造微结构力学性能
Figure
4.
Mechanical property of microstructure from selective laser melting
下载: 全尺寸图片
幻灯片
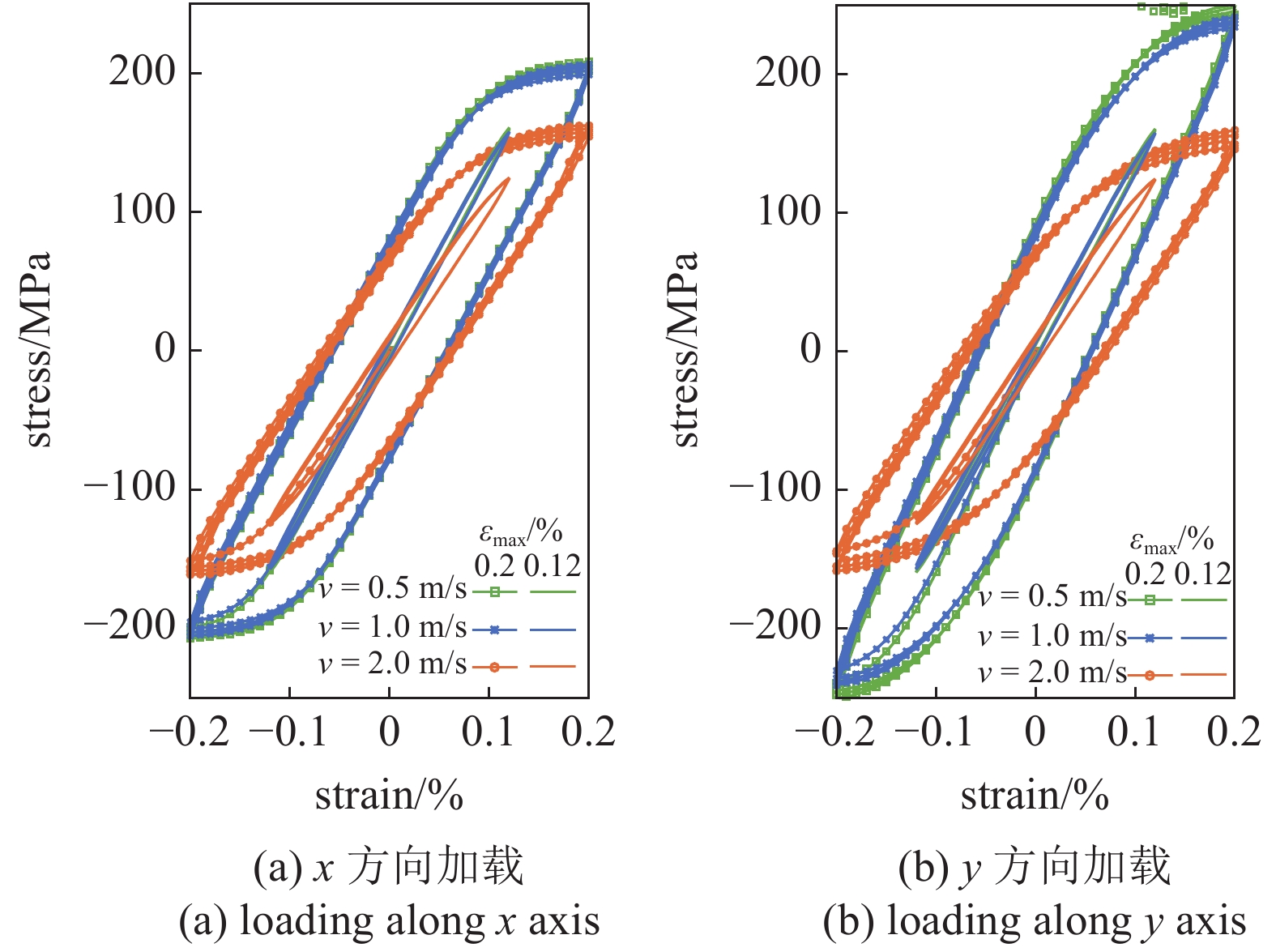
为了计算FIP, 首先计算了不同应变幅下微结构的循坏应力?应变曲线, 应变比为
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-389-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
不同应变幅(εmax)下选区激光熔化增材制造微结构的循环应力-应变曲线
Figure
5.
Macroscopic stress-strain cyclic response of microstructure from selective laser melting
下载: 全尺寸图片
幻灯片
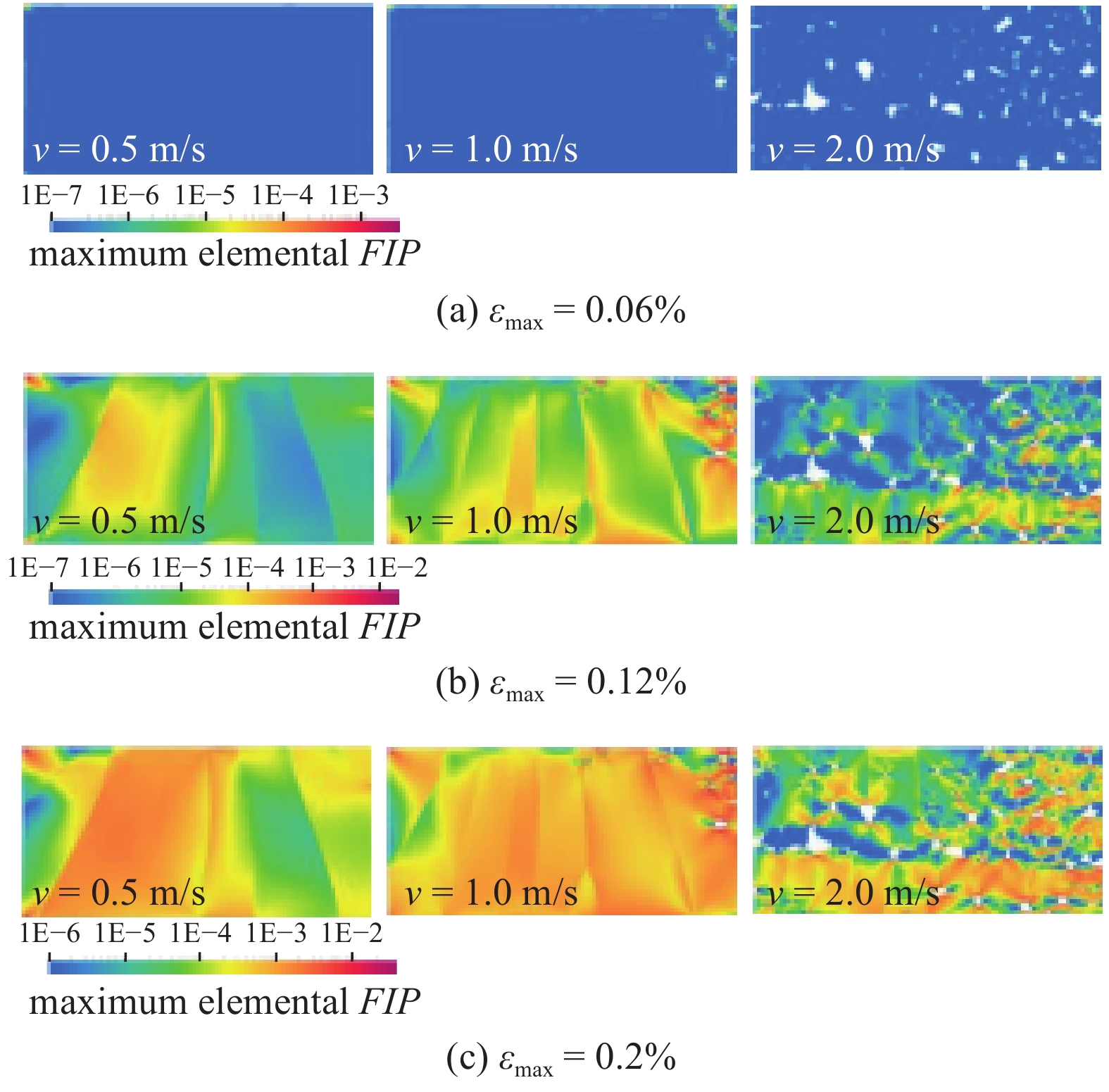
图6给出了每个有限元网格FIP最大值的分布, 可以发现当应变幅从0.06%增加至0.12%时, FIP最大值增加了一个数量级. 当应变幅为0.06%时(图6(a)), 大部分区域的FIP值在1 × 10?6以下, 仅孔洞边缘的FIP大于1 × 10?4; 当应变幅为0.12%时(图6(b)), 少量晶粒内部的FIP值大于10?4, 孔洞边缘的FIP达到1 × 10?2; 当应变幅为0.2%时(图6(c)), 大量晶粒内部的FIP值大于1 × 10?4, 孔洞边缘的FIP达到3 × 10?2. 疲劳裂纹最有可能在较高FIP的部位萌生, 因此在应变幅较大且孔洞缺陷较多的情况下, 疲劳裂纹萌生的驱动力也越大, 相应的疲劳寿命也会降低.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-389-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
x方向不同应变幅(εmax)下单元FIP分布
Figure
6.
Variation of elemental FIPs throughout the sample under different strain magnitude (εmax) along x axis
下载: 全尺寸图片
幻灯片
为了分析微结构疲劳性能的分散性, 需对表征疲劳裂纹萌生驱动力的FIP极值进行统计分析. 与前述类似, 每种应变幅和激光扫描速度的情形均计算30组多晶微结构(
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-389-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
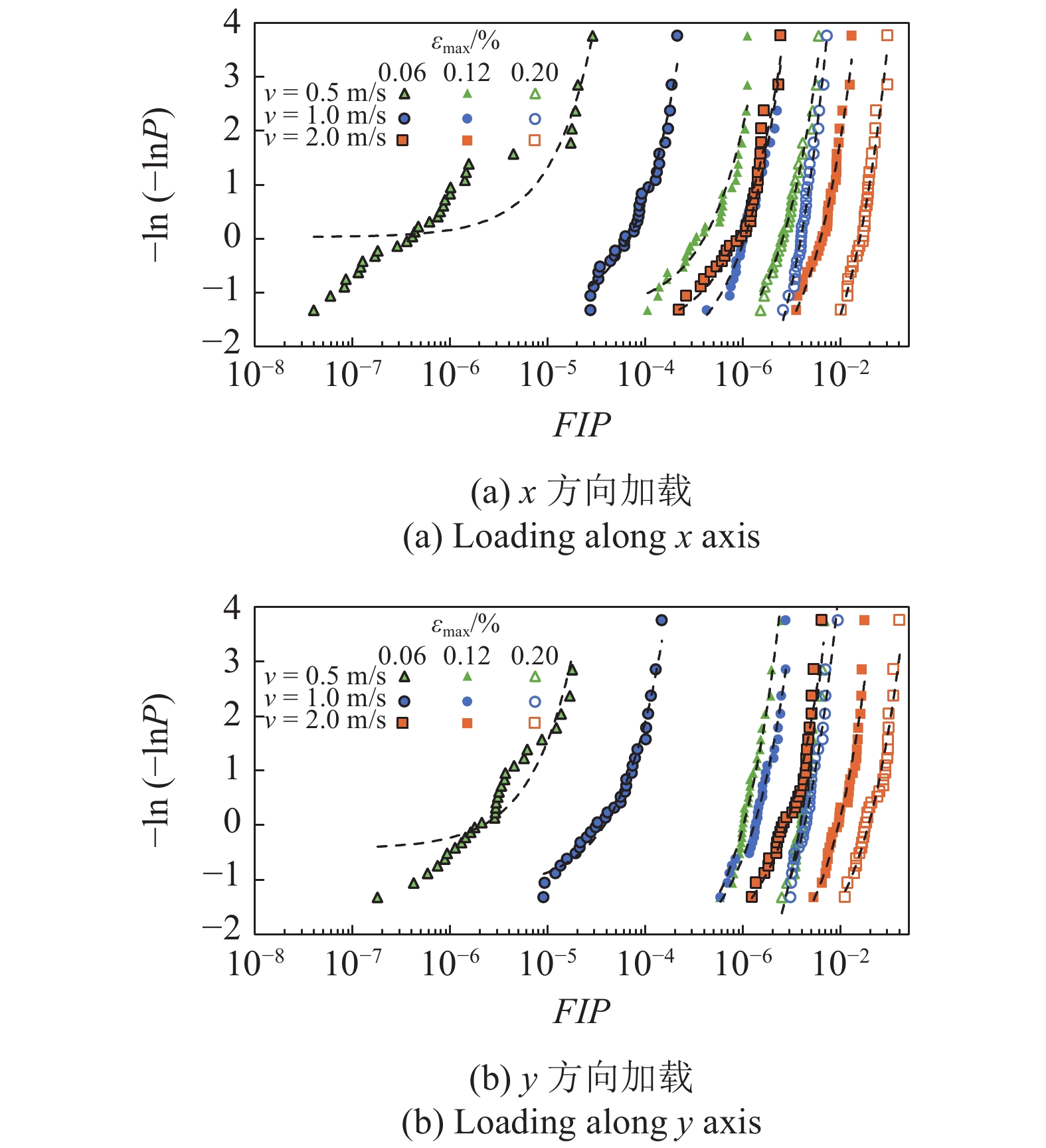
7
体积平均FIP极值概率分布及其Gumbel函数拟合
Figure
7.
Extreme value distributions of the volume averaged FIPs and their fit to the Gumbel distribution
下载: 全尺寸图片
幻灯片
随着应变幅增大和激光扫描速度增加(也即孔洞缺陷增多), Gumbel分布的匹配度不断上升, FIP极值分散性降低、量级跨度减小. 比如当应变幅增大到0.12%时, FIP极值所在区间的跨度下降至1个量级; 当应变幅继续增大到0.2%时, FIP极值分散度处于同一量级. 而在同一应变幅下, 不同激光扫描速度下的FIP极值所在区间跨度的量级相近, 但FIP极值分布随着激光扫描速度的增加而往右移动, 也即FIP极值有所升高, 裂纹萌生驱动力增大, 疲劳寿命降低. 因此, 应变幅是FIP极值区间跨度量级的主要决定因素, 而激光扫描速度是FIP极值大小的主要决定因素.
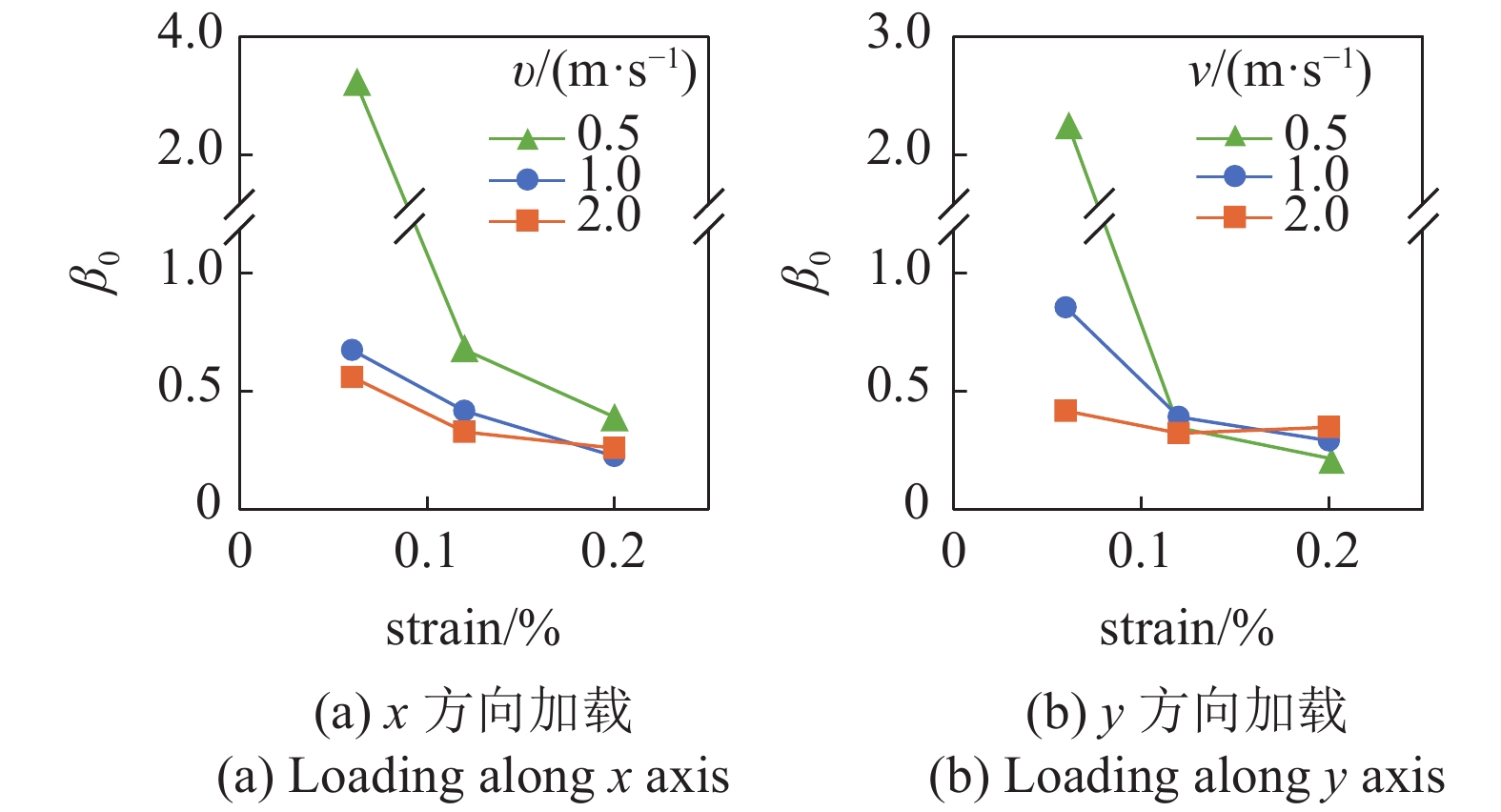
对比图7(a)和图7(b)可以看出, x和y方向加载时的FIP极值分散性相近, 但y方向加载时的FIP极值分布明显更为靠右, 也即FIP极值更大. 为了综合评估图7呈现的FIP分散性, 图8给出了拟合Gumbel分布得到的相对分散性参数
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-389-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
相对分散性参数(
Figure
8.
Relative dispersion parameter (
下载: 全尺寸图片
幻灯片
4.
结 论
(1) 集成离散元、非等温相场模拟、晶体塑性有限元和极值概率分析方法, 实现了增材制造中包括熔化、凝固、晶粒生长/粗化、熔池流动、气孔运动、孔洞生成等在内的微结构演化全过程的计算, 以及增材制造工艺参数对微结构力学性和疲劳分散性影响的计算.
(2) 增材制造微结构的宏观屈服强度
(3) 增材制造微结构在弹性应变幅范围内的FIP极值区间跨越1 ~ 3个量级, FIP分散性较大, 因而疲劳裂纹萌生对增材制造微结构更敏感, 疲劳寿命分散性也越大; 增加激光扫描速度可减小FIP相对分散性参数, 进而降低增材制造微结构疲劳分散性, 但会导致FIP极值升高, 对应增材制造微结构中更大的疲劳裂纹萌生驱动力和更短的疲劳寿命.
