引 言

与传统的铸造等减材制造技术相比, 增材制造技术有着设计灵活、制造周期短、制造复杂几何构型能力强等不可替代的优越性, 因此逐渐被广泛运用到航空航天精密器件、生物组织或义肢、梯度功能材料^[1]、印刷电子^[2], 甚至土木工程领域的大型构件的制造中, 且被认为是“第三次工业革命”的标志^[3]. 其中, 基于金属粉末的选区熔化技术和直接沉积技术是常用的两种打印金属构件的方式. 选区熔化技术在制造方向铺设金属粉末, 然后分块进行多道激光打印, 实现金属粉末熔化粘合及凝固. 按此循环往复, 沿着制造方向多次进行, 从而层层“打印”出构件的三维形貌. 而直接沉积技术, 则将粉末通过同轴喷口喷出, 使粉末汇聚在喷口下方时正好被激光击中、熔化. 汇聚点可在熔池上方或熔池中. 随着喷口的移动, 可以实现任意方位打印. 因此, 直接沉积技术可以被运用到精密或昂贵器件的修复中^[4].

激光直接沉积过程跨越粉末?熔道?构件从微观到宏观3个尺度, 且存在激光?热?相变?流体的多物理场耦合、粉末?粉末/粉末?熔体相互作用及高温高压等极端物理环境, 仅通过实验难以摸透其中的关键物理现象及机理^[5]. 因此, 数值模拟成为了研究直接沉积技术中熔池流动、匙孔及微气孔形成、熔道尺寸、空中熔池形成等现象的重要手段^[6]. 因直接沉积技术存在复杂的颗粒?流体相互作用及相变, 仅有少数****建立了初步的模拟框架. 例如Alimardani等^[7]通过人工控制粉末质量流量, 在三维宏观尺度模拟了多层的沉积过程. 模拟过程考虑了激光、材料、给粉量等多个因素, 获得了与实验相符的基板熔池温度场与熔池形态. 但颗粒的微观行为未在模型内体现, 因而该模拟框架不能捕获细节性的机理, 而适合大规模工程实际的研究. Katinas^[8]等利用不考虑撞击的拉格朗日点, 模拟了同轴送粉直接沉积技术中粉末的铺设过程. 粉末锥的形态、温度分布与实验吻合较好, 并且形成的熔池尺寸也与实验符合. 但是该模型没有考虑颗粒间的撞击和传热, 也无法模拟颗粒在熔化时形态的变化, 只能通过颗粒数量转化得到质量流量, 从而估计熔池的尺寸. Choi等^[9]通过液滴喷射的方式将已经熔化的颗粒注入计算域. 他的模型中还考虑了马兰格尼效应、相变、蒸发和熔融液滴的碰撞, 并研究了上述作用对熔池形貌演化的影响. 他们模拟所得到的平均表面粗糙度和实验较为符合. 但是, 他们的数值模拟是二维的, 与三维实际的粉末及熔池的空间分布有本质区别. 此外, 他们直接将熔融的颗粒射入计算域,而未考虑粉末在熔化前与空气和其他粉末的相互作用, 因此粉末进入熔池的形态未必符合真实物理情况. Wang等^[10]通过建立高精度数值模型, 结合试验验证, 研究了非线性送粉率、激光/粉末失焦和热积累对过度堆积、表面不平整等缺陷的影响. 同时他们还提出了减少这两类缺陷的有效方式. Ibarra-Medina和Pinkerton^[11]则耦合了计算流体力学与拉格朗日点, 重现了粉末在激光光斑下的沉积过程. 热传导、热辐射与强制对流也均被考虑计算, 模拟所得的温度分布和给粉量与实验符合较好. 但是他们的模拟框架未能考虑颗粒碰撞、熔化及熔池的形成.

上述模拟框架虽能较好地重现熔池的温度场与尺寸, 但是对于颗粒尺度的细节的捕获能力有限. 究其原因, 在以下两点: (1)工程实际问题中的颗粒流动的数值模拟, 因其庞大的计算量, 不能用细密网格解析颗粒边界的全解析即计算流体力学?离散元耦合(computational fluid dynamics-discrete element method耦合, CFD-DEM耦合)^[12]. 而在通过半理论半经验拖曳力模型计算的非解析CFD-DEM耦合中, 因需要合理重构背景流场的信息, 如背景速度、压力、颗粒体积分数、温度等, 背景的流体计算网格常常需要在3倍颗粒直径左右^[13-16], 因此无法刻画颗粒熔化后的形状. (2)缺乏有效的刚体颗粒、环境气体、熔融金属、凝固金属之间复杂相互作用的模拟框架.

近期发展的半解析CFD-DEM耦合技术可将网格加密至与颗粒尺寸相当甚至略小于颗粒. 再通过核函数重构出合适的背景流场, 以实现颗粒在与其尺寸相当的流体网格中的运动的数值模拟^[13]. 本文通过在半解析CFD-DEM引入流体体积分数法(volume of fluid, VOF), 处理自由液面和相变界面, 发展了半解析VOF-DEM (或半解析CFD-DEM-VOF)模拟框架, 可以模拟刚体颗粒达到熔点后的熔化, 以及未熔颗粒与熔池的相互作用, 并准确捕捉金属?环境气体的界面. 由此, 半解析VOF-DEM模拟框架实现了跨尺度的喷口?刚体颗粒?环境气体?熔体?凝固体之间复杂相互作用的数值模拟, 最大程度还原激光直接沉积技术打印构件过程中的种种物理现象.

1.
模型提法及控制方程

本文的模拟框架是基于传统非解析VOF-DEM耦合进行的, 并通过核函数重构颗粒背景流场发展半解析CFD-DEM耦合方法, 实现颗粒?流体间质量、动量、能量的相互作用的精准、高效计算. 其中, 环境气体与熔化、凝固的金属部分由基于有限体积元的VOF求解, 界面通过iso-Advector重构, 未熔化的刚体颗粒的运动用离散元求解. 具体控制方程如下.

1.1
基于VOF的场控制方程

VOF^[17]是基于二元论的思想, 将两种流体用0和1表示, 而界面则通过体积分数的权重表示, 例如体积分数$alpha = 0.5$, 则表示两种流体在该CFD网格中的流体总体积里各占一半. 而各物理量, 如密度$
ho $, 亦由体积分数加权估计得到: $
ho = alpha {
ho _1} + (1 - alpha ){
ho _2}$, 其中下标1, 2代表第一和第二相, 即${
ho _1}$和${
ho _2}$分别为第一相和第二相的密度, 下文中其他物理参数亦是如此. 求解量, 例如速度U, 温度T, 在VOF体系中不需要体积分数加权. 在本框架中, 两相流体分别为环境金属相(包括熔化和凝固的)和环境气体相, 其界面通过几何重构法iso-Advector^[18]进行重构. 对于这两项, 需要满足连续性方程为

$$ frac{partial }{partial t}left(varepsilon ho ight)+nabla cdot left(varepsilon ho {boldsymbol{U}} ight)=0 $$

(1)

其中t为时间, $varepsilon $为流体(包括环境气体、熔化和凝固的金属)体积分数. 因此$1 - varepsilon $则为离散元颗粒在流体网格中的体积分数, $alpha varepsilon $则是熔化和凝固金属在网格中的体积分数, 而$(1 - alpha )varepsilon $是环境气体的体积分数.

对于复杂颗粒流动, 通常使用Model A的非解析CFD-DEM耦合方式^[19], 其动量方程则为^[20-21]

$$begin{split} &frac{partial }{{partial t}}(varepsilon ho {boldsymbol{U}}) + varepsilon ho {boldsymbol{U}} cdot nabla {boldsymbol{U}} = nabla cdot [varepsilon mu (nabla {boldsymbol{U}} + {boldsymbol{U}}nabla )] + &qquadvarepsilon left[ { - nabla P + ho {boldsymbol{g}} + sigma kappa nabla alpha + frac{{{ m{d}}sigma }}{{{ m{d}}T}}({boldsymbol{I}} - {boldsymbol{n}} otimes {boldsymbol{n}}) cdot nabla T|nabla alpha |} ight] + &qquadvarepsilon Dc cdot frac{{{{left( {1 - {alpha _m}} ight)}^2}}}{{alpha _m^3 + Dcs}}{boldsymbol{U}} - {{boldsymbol{F}}_p}end{split}$$

(2)

其中$mu $为加权后的流体黏性系数, 本文所使用的均为层流模型. 对于湍流的情况, 可以通过解RANS模型求得等效湍流黏性系数, 叠加在物理流体黏性上, Dc和$D{c_s}$为达西系数, 该项用于模拟糊状区的速度突变, 其中${alpha _m}$为熔化体积分数, 且有${alpha _m} = dfrac{alpha }{2}Biggl{{16} 1 + {text{erf},}Biggl[{16} dfrac{4}{{{T_l} - {T_s}}}cdot $$ left(T - dfrac{{{T_l} + {T_s}}}{2}
ight) Biggl]{16} Biggl}{16}$, 这里的${T_l}$和${T_s}$分别为金属液相线与固相线^[20]. P为压力, g为重力加速度, $sigma $是表面张力系数, $kappa $是曲率: $kappa = - nabla cdot dfrac{{nabla alpha }}{{left| {nabla alpha }
ight|}} = - nabla cdot {boldsymbol{n}}$, 其中n为金属相的外法相方向. $dfrac{{{
m{d}}sigma }}{{{
m{d}}T}}$是表面张力系数随温度的线性变化率, I是单位矩阵, 该项是由于温度梯度导致的表面张力不平衡而形成的马兰格尼力, 往往在熔池形貌中有着决定性影响^[22]. ${{boldsymbol{F}}_p}$是颗粒对流体的作用力^[19]

$$ {{boldsymbol{F}}_p} = frac{1}{{{V_{{ m{cell}}}}}}sumlimits_{i = 1}^n {left( {{{boldsymbol{f}}_{{ m{drag}},i}} + {{boldsymbol{f}}_{{ m{Mag}},i}} + {{boldsymbol{f}}_{{ m{vm}},i}}} ight)} $$

(3)

即分别是i颗粒上的拖曳力、Magnus力、虚拟质量力在体积为${V_{{
m{cell}}}}$的流体网格上的平均, n为网格内的颗粒总数. 其中Magnus力与虚拟质量力有标准表达式, 具体可参见文献[23-26]. 拖曳力则采用的是Gidaspow模型^[27-28], ${boldsymbol{f}_{{
m{drag}},i}} = beta {V_i}left( {boldsymbol{bar U} - {boldsymbol{v}_i}}
ight)$, 其中$overline {boldsymbol{U}} $是颗粒的背景流场, 由核函数重构得到, 具体会在下节展示, ${V_i}$与${{boldsymbol{v}}_i}$则是颗粒i的体积与速度矢量, 系数$beta $可由下式计算

$$ beta = left{ begin{aligned} &{frac{{3varepsilon ho }}{{4{d_i}}}left| {{boldsymbol{bar U}} - {{boldsymbol{v}}_i}} ight|{C_d}{omega _d},qquadqquad;;;;{varepsilon > 0.74} } &{150frac{{left( {1 - varepsilon } ight)mu }}{{varepsilon {d_i}}} + 1.75frac{ ho }{{{d_i}}}left| {{boldsymbol{bar U}} - {{boldsymbol{v}}_i}} ight|,;; {varepsilon leqslant 0.74} } end{aligned} ight. $$

(4)

其中${d_i}$为颗粒的直径, ${C_d}$为拖曳力系数, ${omega _d}$的拟合公式可参见文献[29-30].

最后, 温度方程则写为^{[20, 31]}

$$ begin{split} &frac{partial }{{partial t}}( {varepsilon ho {C_p}T} ) + nabla cdot (varepsilon ho {C_p}T{{{boldsymbol{U}}}}) = nabla cdot (varepsilon knabla T) - &qquadLleft[frac{partial }{{partial t}}(varepsilon ho {alpha _m}) + nabla cdot (varepsilon ho {{{boldsymbol{U}}}}{alpha _m}) ight] - &qquadvarepsilon left| {nabla alpha } ight|left[ {{h_c}(T - {T_{{ m{ref}}}}) + {sigma _{{ m{sb}}}}({T^4} - T_{{ m{ref}}}^4) - {Q_l}} ight] + {Q_p},end{split} $$

(5)

其中${C_p}$和k为体积分数加权的比热容和热传导系数, 可根据温度非线性变化^[32], L为金属的潜热, ${h_c}$为强制对流热交换系数, ${T_{{
m{ref}}}}$为参考环境温度, ${sigma _{{
m{sb}}}}$为史蒂芬?波尔兹曼常数. ${Q_l}$为激光热源. 一般可用面热源或者体热源, 或其混合^[33], 一个常用的面热源表达式为

$$ {Q_l} = frac{{2eta {P_l}}}{{{text{π}} R_l^2}}exp left{ {frac{{ - 2[{{(x - {X_l}(t))}^2} + {{(y - {Y_l}(t))}^2}]}}{{R_l^2}}} ight} $$

(6)

其中$eta $为金属的激光吸收率, 可以设置为常数, 亦或是通过光线追踪法进行计算^[34]. ${P_l}$和${R_l}$分别为激光功率、半径, x和y为流体网格的平面坐标, ${X_l}$和${Y_l}$分别为激光轨迹. ${Q_p}$为颗粒热源, 考虑了颗粒与背景流体的强制对流换热和热辐射^[35-36]

$$ {Q_p} = - frac{1}{{{V_{{ m{cell}}}}}}sumlimits_{i = 1}^n {{S_i}left[ {eta {sigma _{sb}}left( {T_i^4 - {{bar T}^4}} ight) + {h_i}left( {{T_i} - bar T} ight)} ight]} $$

(7)

其中${S_i}$为颗粒的迎风面积, ${T_i}$和$overline T $分别为颗粒i的温度和其背景流体通过核函数插值得到温度. ${h_i}$是颗粒对背景流体的强制对流系数, 可通过颗粒Nu数估计: $ {h_i} = {{N{u_i}{k_f}} mathord{left/{vphantom {{N{u_i}{k_f}} {{d_i}}}}
ight.} {{d_i}}} $, 其中颗粒i的$N{u_{text{}{i}}}$可通过颗粒雷诺数$R{e_i}left( {{text{ = }}
ho {d_i}{{left| {{{boldsymbol{v}}_i}}
ight|}/ mu }}
ight)$和普朗特数Pr由下式估计^[37]

$$ N{u_i} = 2{text{ + }}left{ begin{aligned} &{0.6{varepsilon ^{3.5}}Re_i^{{1 mathord{left/{vphantom {1 2}}, ight.} 2}}P{r^{{1 mathord{left/{vphantom {1 3}} ight.} 3}}},quad{R{e_i} leqslant 200}} &{{varepsilon ^{3.5}}left( {0.5{Re} _i^{{1 mathord{left/{vphantom {1 2}} ight.} 2}} + 0.02Re_i^{0.8}} ight)P{r^{{1 mathord{left/{vphantom {1 3}} ight.} 3}}}} , &qquadqquad 200 < R{e_i} leqslant 1500 &{0.000~045{varepsilon ^{3.5}}Re_i^{1.8},quad{R{e_i} > 1500}}end{aligned} ight. $$

(8)

在较高的雷诺数的情况下, 往往需要考虑湍流效应. 此时还需要求解湍流的控制方程, 例如RANS模型中的湍动能、湍流耗散方程, 从而计算等效湍流黏性${mu _t}$和等效湍流热传导系数${k_t}$, 并分别叠加到方程式(2)和式(5)的物理黏性$;mu $、物理热传导系数k上. 具体控制方程和计算方法可参见文献[31, 38-39].

1.2
颗粒运动方程

颗粒运动采用牛顿第二定律计算, 控制方程为^[40-41]

$$ begin{split} &{m}_{i}frac{{ m{d}}{{boldsymbol{v}}}_{i}}{{ m{d}}t}={V}_{i}left[-overline{nabla P}- ho {boldsymbol{g}}+mu nabla cdot (overline{nabla {boldsymbol{U}}}+overline{{boldsymbol{U}}nabla }) ight]+&qquad {V}_{i}left[sigma kappa nabla alpha +frac{dsigma }{dT}left[nabla T-{boldsymbol{n}}({boldsymbol{n}}cdot nabla T) ight]left|nabla alpha ight| ight]+&qquad {m}_{i}{boldsymbol{g}}+{{boldsymbol{f}}}_{d,i}+{{boldsymbol{f}}}_{{ m{vm}},i}+{{boldsymbol{f}}}_{{ m{Mag}},i}+{displaystyle sum left({{boldsymbol{f}}}_{li,j}text+{{boldsymbol{f}}}_{ci,j} ight)}end{split} $$

(9)

方程右端依次为颗粒的压力梯度力、浮力、黏性力、经过气液表面时的表面张力与Marangoni力、颗粒自重、拖曳力、虚拟质量力、Magnus力, 求和符号内的分别为颗粒间或颗粒与壁面间的润滑力^[42]、碰撞力. 其中m_i为颗粒质量, 带上划线的物理量为核函数平均得到的背景量, 拖曳力、虚拟质量力、Magnus力如上节所述. 颗粒i和颗粒j间的润滑力表示为

$${{boldsymbol{f}}_{li,j}} = frac{3}{2}{text{π}} mu {left( {frac{{2{d_i}{d_j}}}{{{d_i} + {d_j}}}} ight)^2}frac{{{{boldsymbol{v}}_{n,ij}}}}{{{h_{ij}}}}$$

(10)

其中d_j是颗粒j的直径, 如相互作用发生在颗粒与壁面间, 则$ {d_j} = infty $, $ {h_{ij}} $是两颗粒表面最近距离, ${{boldsymbol{v}}_{n,ij}}$为两个颗粒的对心相对速度, 即${{boldsymbol{v}}_{n,ij}} = ( {{{boldsymbol{v}}_j} - {{boldsymbol{v}}_i}} ) cdot {{boldsymbol{e}}_{ij}}{{boldsymbol{e}}_{ij}}$, ${{{boldsymbol{v}}_j}} $是j颗粒的速度矢量, ${{boldsymbol{e}}_{ij}} $是颗粒j球心指向颗粒i球心的单位矢量: ${{boldsymbol{e}}_{ij}} = ( {{{boldsymbol{x}}_i} - {{boldsymbol{x}}_j}} )/| {( {{{boldsymbol{x}}_i} - {{boldsymbol{x}}_j}} )} |$, $ {{{boldsymbol{x}}_i}} $和$ {{{boldsymbol{x}}_j}} $为两颗粒的空间位置矢量.

撞击力则通过Hertz-Mindlin模型^[43]求得

$${{boldsymbol{f}}_{c,ij}} = left( {{k_n}{delta _{ij}}{{boldsymbol{e}}_{ij}} - {gamma _n}{{boldsymbol{v}}_{n,ij}}} ight) + left( {{k_t}{{boldsymbol{t}}_{ij}} - {gamma _t}{{boldsymbol{v}}_{t,ij}}} ight)$$

(11)

其中第一个括号为法向接触力, 第二个括号为切向接触力, $ k_n $, $ {gamma _n} $, $ {k_t} $, ${gamma _t} $为弹性常数, $ {delta _{ij}} $, $ {{boldsymbol{t}}_{ij}} $, $ {{boldsymbol{v}}_{t,ij}} $分别为两颗粒的重叠量、切向矢量和切向相对速度^{[26, 44-45]}. 颗粒的旋转则由

$${{boldsymbol{I}}_i} cdot frac{{{ m{d}}{{boldsymbol{omega }}_i}}}{{{ m{d}}t}} = sumlimits_j^m {frac{1}{2}} left( {{{boldsymbol{x}}_j} - {{boldsymbol{x}}_i}} ight) times left( {{k_t}{{boldsymbol{t}}_{ij}} - {gamma _t}{{boldsymbol{v}}_{t,ij}}} ight)$$

(12)

计算, 式中$ {{boldsymbol{I}}_i} $和${boldsymbol{omega }_i}$为颗粒的转动惯量和角速度.

颗粒的能量传递满足能量守恒

$$ begin{split} &{m}_{i}{C}_{p,i}frac{{ m{d}}{T}_{i}}{{ m{d}}t}={S}_{i}left[{h}_{i}left(overline{T}-{T}_{i} ight)+eta {sigma }_{sb}left({overline{T}}^{4}-{T}_{i}^{4} ight) ight]+&;;;; {S}_{i}left(eta {I}_{i}+{m}_{i}Lfrac{{ m{d}}{alpha }_{m,i}}{{ m{d}}t} ight)+{displaystyle sum _{j}^{}frac{4{k}_{i}{k}_{j}}{{k}_{i}+{k}_{j}}sqrt{{A}_{c,ij}}left({T}_{j}-{T}_{i} ight)}end{split} $$

(13)

方程右端依次考虑了颗粒表面与背景流场的换热、热辐射、激光热源、相变潜热以及最后一项: 相接触的颗粒间的热传导. 其中${C_{p,i}} $和$ k_i $是颗粒i的比热容和热传导系数($k_j $则是颗粒j的热传导系数), $ I_i $是激光热源辐照在颗粒上单位面积的功率^[46]

$${I_i} = frac{{2eta {P_l}}}{{{text{π}} R_l^2}}exp left{ {frac{{ - 2left[ {{{left( {{x_i} - {X_l}(t)} ight)}^2} + {{left( {{y_i} - {Y_l}(t)} ight)}^2}} ight]}}{{R_l^2}}} ight}$$

(14)

其中x_i及y_i是颗粒的平面坐标. $ {alpha _{m,i}}$是颗粒的熔化度

$${alpha _{m,i}} = frac{1}{2}left{ {1 + {mathop{ m erf}nolimits} left[ {frac{4}{{{T_l} - {T_s}}}left( {{T_i} - frac{{{T_l} + {T_s}}}{2}} ight)} ight]} ight}$$

(15)

${A_{c,ij}} $为相撞颗粒的接触面积, 可由弹性常数推导得到^[47-48].

1.3
VOF-DEM耦合技术

上述两节分别介绍了流体、颗粒的运动和温度的计算方法. 在计算过程中, 由于动量和能量存在复杂的耦合关系, 在计算颗粒和背景流体之间的动量、能量交换时, 需要用到两相的参数信息. 因此, 模拟框架分为3个模块, 基于有限体积元(finite volume method, FVM)的流体计算模块、基于离散元(DEM)的颗粒计算模块和信息交互模块. 该框架是基于成熟的、验证完备的开源代码CFDEM二次开发^[49-50]而成, 对于一步VOF-DEM耦合, 具体的执行过程如下.

(1)在FVM模块中, 为加速后续计算的收敛, 先进行动量预测.

(2)在DEM模块中判断颗粒是否熔化. 在本框架下, FVM网格的尺寸与颗粒直径相当, 甚至小于颗粒直径, 因此若颗粒熔化了, 则须将颗粒的温度、速度、体积分数映射到FVM网格上, 然后将DEM中对应的颗粒删除. 若颗粒未熔化, 判断颗粒是否与相邻颗粒或壁面碰撞, 如果有碰撞发生, 则按式(11)和式(12)右端计算碰撞产生力和力矩.

(3)界面模块从FVM中获得速度、温度和压力等信息, 从DEM中获得颗粒速度、温度、位置和直径等信息, 以计算拖曳力、压力梯度力、虚拟质量力、Magnus力、颗粒?流体热交换和热辐射等颗粒与流体间的动量、能量交换.

(4)将上一步计算所得到的颗粒?流体动量、能量交换代入流体的动量和能量方程, 即式(2)和式(5), 求解流体的速度与温度. 同时通过连续性方程求解VOF的体积分数场. 再通过PISO算法^[51]求解压力, 更新速度.

(5)根据温度更新熔化率和其他物理参数.

(6)将第(3)步计算所得到的颗粒?流体动量、能量交换以及第(2)步得到的碰撞力与力矩代入式(9)、式(12)和式(13), 更新颗粒的运动与温度.

将该流程整理为流程图, 如图1所示. 该流程同时计算了颗粒与流场、颗粒与颗粒/壁面之间动量与能量交换, 颗粒在激光作用下的熔化, 熔池的动力学演化及凝固, 大大弥补了以往模型模拟直接沉积技术真实物理状况的不足.



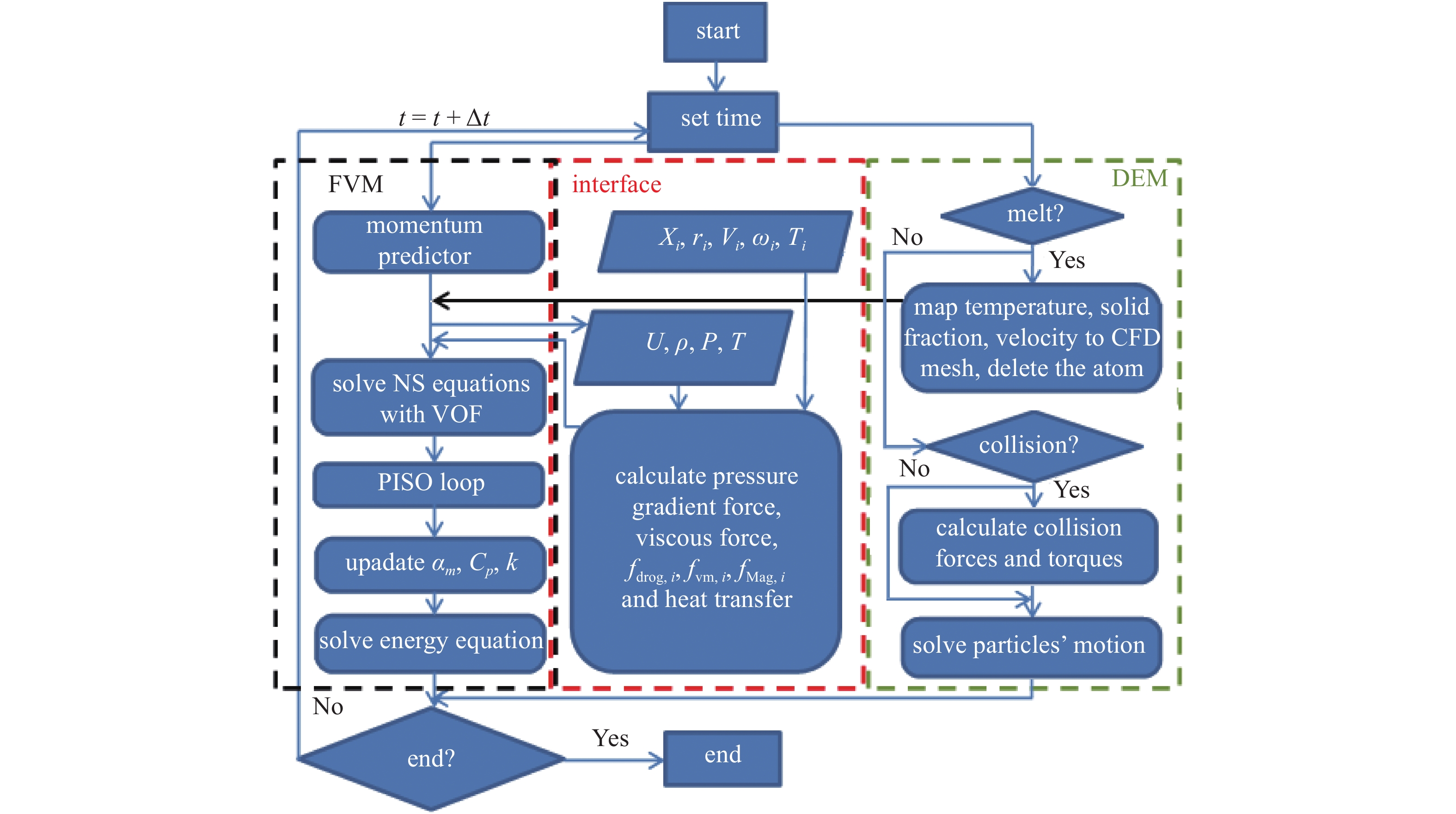onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure1" />



图
1
半解析VOF-DEM在直接沉积技术中运用的流程图



Figure
1.
Flow chart of implementation of the semi-resolved VOF-DEM in direct laser deposition



下载:
全尺寸图片
幻灯片

2.
半解析耦合技术在VOF-DEM中的运用

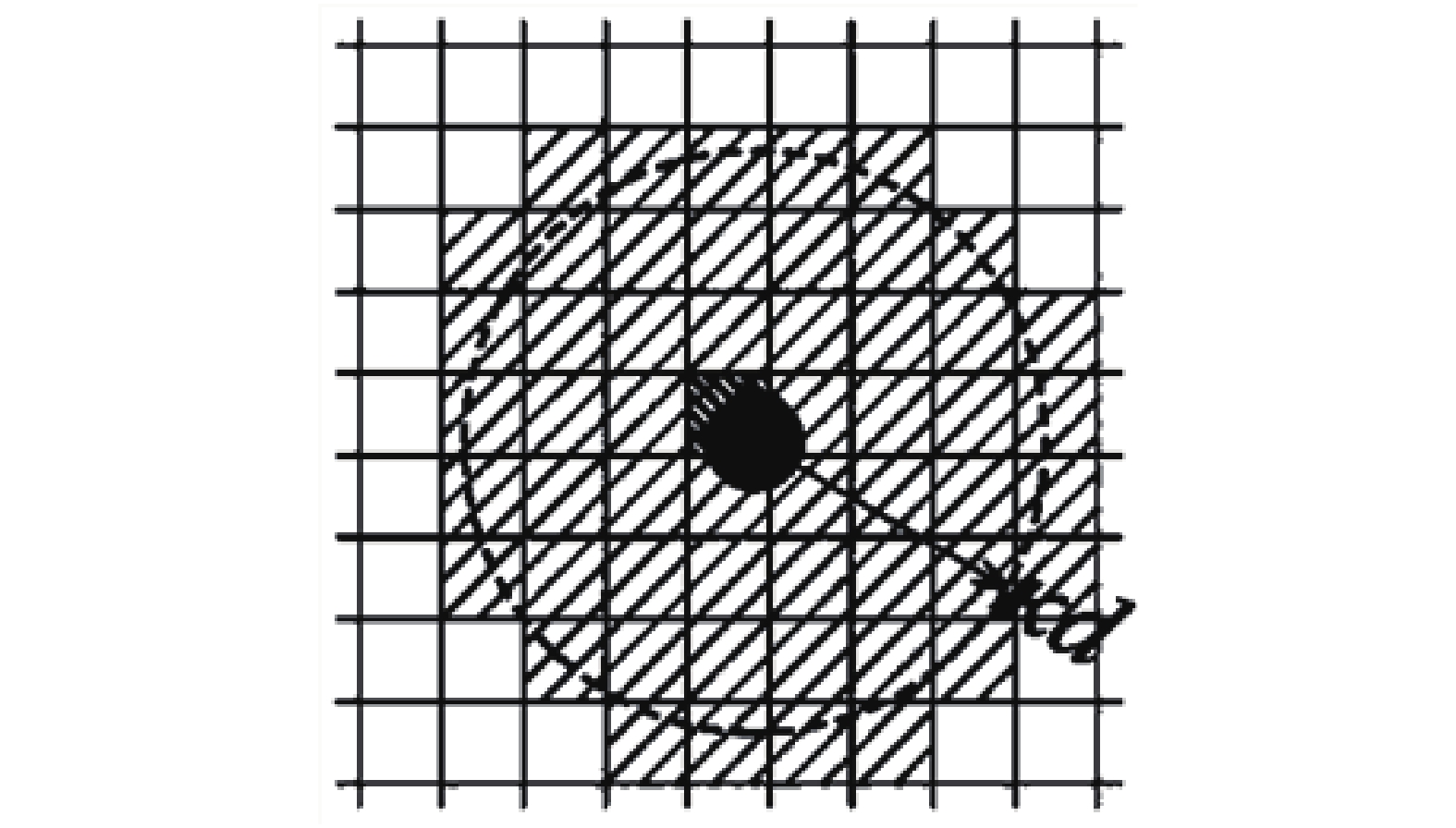
在上节的介绍中, 流体和颗粒间存在的复杂耦合现象均可用半理论半经验的公式模化. 在这些计算中, 即如式(4)、式(7) ~ 式(9)和式(13), 都存在背景量如背景压强, 背景黏性力, 亦或是颗粒与流体的相对物理量, 如相对速度、相对加速度、相对温度. 其中在计算相对物理量时, 颗粒的信息(如颗粒速度)是确定的, 而背景流场的信息(如流体速度)需要获取. 对于非解析CFD-DEM耦合而言, 背景量即为颗粒所在背景网格所存储的物理量. 因此使用细密网格时, 所获得的数据会严重受到颗粒的影响, 而不是真正的“背景”信息. 在本研究框架下, 因需要刻画出颗粒的熔化过程, 网格尺寸会与颗粒尺寸相当, 甚至少于颗粒尺寸, 此时则需引入核函数收集颗粒附近的流体信息, 近似背景流场(如图2).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
颗粒在光滑域内通过核函数重构背景流场



Figure
2.
Kernel function approximates the background information for a particle within its smoothing distance



下载:
全尺寸图片
幻灯片


具体的, 对于颗粒i所需要的网格上的背景物理量$ bar eta $, 如速度、加速度、温度和体积分数等, 有

$$bar eta = frac{{displaystylesumlimits_{J = 1}^N {{varepsilon _J}} {V_{{ m{cell}},J}}{eta _J}{k_{i,J}}left( {left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}} ight|} ight)}}{{displaystylesumlimits_{J = 1}^N {{varepsilon _J}} {V_{{{{ m{cell}} }},J}}{k_{i,J}}left( {left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}} ight|} ight)}}$$

(16)

其中N为颗粒光滑域内的流体网格总数, J为其中的某一个流体网格的编号, $ {{k_{i,J}}} $是以网格J到颗粒i之间距离${left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}}
ight|} $为自变量的核函数. 因背景量需要尽量剥离颗粒本身的影响, 故在核函数重构时, 还需附加流体体积分数作为权重($ {{varepsilon _J}} $). 而核函数一般选为较为光滑的且有一定物理意义的高斯函数, 也可选择光滑粒子动力学中常用的3次或5次样条函数^[52-53]. 本框架中, 使用高斯核函数^[13]

$${k_{i,J}}left( {left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}} ight|} ight) = exp left( { - frac{{{{left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}} ight|}^2}}}{{2{H_i}^2}}} ight)$$

(17)

其中$H_i $为颗粒i所带核函数的核宽, 且$ {H_i} = kappa {d_i}$, 通常$ kappa$为$ 1.5 $到$ 2 $, 以满足核心光滑域在颗粒直径3到4倍之间^{[13, 16, 54]}, 从而获得最佳精度. 因此, 例如求解拖曳力常用的相对速度, 可写为

$$ begin{split} &{boldsymbol{bar U}} - {{boldsymbol{v}}_i} = &;;;;;;frac{{displaystylesumlimits_{J = 1}^N {{varepsilon _J}{V_{{ m{cell}},J}}{{boldsymbol{U}}_J}exp left[ { - left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}} ight|{{^2} mathord{left/{vphantom {{^2} {(2{kappa ^2}d_i^2)}}} ight.} {(2{kappa ^2}d_i^2)}}} ight]} }}{{displaystylesumlimits_{J = 1}^N {{varepsilon _J}{V_{{ m{cell}},J}}exp left[ { - left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}} ight|{{^2} mathord{left/{vphantom {{^2} {left( {2{kappa ^2}d_i^2} ight)}}} ight.} {left( {2{kappa ^2}d_i^2} ight)}}} ight]} }} - {{boldsymbol{v}}_i} end{split} $$

(18)

但是特别地, 对于求解颗粒运动所需的压力梯度力与黏性力(方程(9)中), 因其本质是将颗粒表面的压力或黏性力的表面积分, 通过高斯定理转化为颗粒内部压力与黏性力的积分, 故在通过高斯核函数重构背景压强梯度和速度梯度时, 无需添加流体体积分数的权重

$${left. {bar eta } ight|_{ = nabla P,nabla {boldsymbol{U}}}} = frac{{displaystylesumlimits_{J = 1}^N {{V_{{ m{cell}},J}}} {eta _J}{k_{i,J}}left( {left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}} ight|} ight)}}{{displaystylesumlimits_{J = 1}^N {{V_{{ m{cell}},;J}}} {k_{i,J}}left( {left| {{{boldsymbol{r}}_i} - {{boldsymbol{r}}_J}} ight|} ight)}}$$

(19)

虽然高斯核函数有无穷大定义域, 但为减少搜索光滑域内网格信息的计算开销, 通常会对函数进行截断, 即有一定的搜索半径. 因网格位置信息为网格中心点的位置所确定, 避免出现网格仅部分在核宽范围内而未能检索到的情况, 搜索半径一般定为1.2至1.5倍的核宽.

因此, 通过结合半解析CFD-DEM和VOF, 发展了半解析VOF-DEM, 即半解析CFD-DEM-VOF模拟方法. 基于该方法的数值模拟框架可实现颗粒在与其尺寸相当甚至小于颗粒的尺寸的流体网格中进行计算, 并进一步模拟颗粒的熔化、融合等行为.

3.
基础算例验证与模型展示

对直接输粉技术中颗粒行为的观测非常困难, 难以通过实验观测验证模型框架的精度. 因此, 本文仅先对其子求解器进行标准算例的逐步验证. 首先, 对于仅有一种背景流体, 不带温度的最基本颗粒流动问题, 已对基于CFDEM^[55]开发的半解析CFD-DEM算法^[13]进行了验证. 结果证实, 半解析算法无论对简单的单颗粒运动, 亦或是多粒径颗粒床的统计学行为, 都有远超过非解析算法的精度, 而其计算量仍与非解析算法相当, 即远小于全解析CFD-DEM耦合的计算量^[13]. 后又将其运用于磨料高速气射流加工技术中, 发现半解析耦合框架在高雷诺数、窄管道中的颗粒流动问题中, 仍然相对于非解析耦合显示出与实验、理论解的高度吻合^[56]. 在该求解器基础上, 又将热流固耦合问题纳入半解析CFD-DEM框架中, 经过与实验对比验证, 结果表明半解析算法能够相较于非解析算法获得更好的颗粒及流场温度分布、颗粒空间分布, 能够捕捉到原本非解析模拟难以捕捉的现象, 如流体优势通道^[31].

因此基于以往的数项研究, 基本可以确定半解析CFD-DEM在气固或液固两相流中, 即使雷诺数高、壁面效应明显、颗粒尺寸分异且存在热传递, 也能获得相对于非解析更高的精度. 此外, 至于粉末增材制造中激光与金属的相互作用, 曾建立激光选区熔化的模拟框架, 并且数值模拟的结果与实验对比, 获得了较好的定性结果, 并能解释制造过程中的诸多机理^[20]. 因此本文主要验证半解析VOF-DEM方法在模拟自由液面方面的准确性(3.1节), 并简单验证激光与金属板相互作用下熔池的形貌(3.2节). 最后在3.3节中, 展示本文的半解析VOF-DEM热流固耦合框架在直接沉积技术中的运用.

3.1
半解析CFD-DEM-VOF耦合方法的算例验证

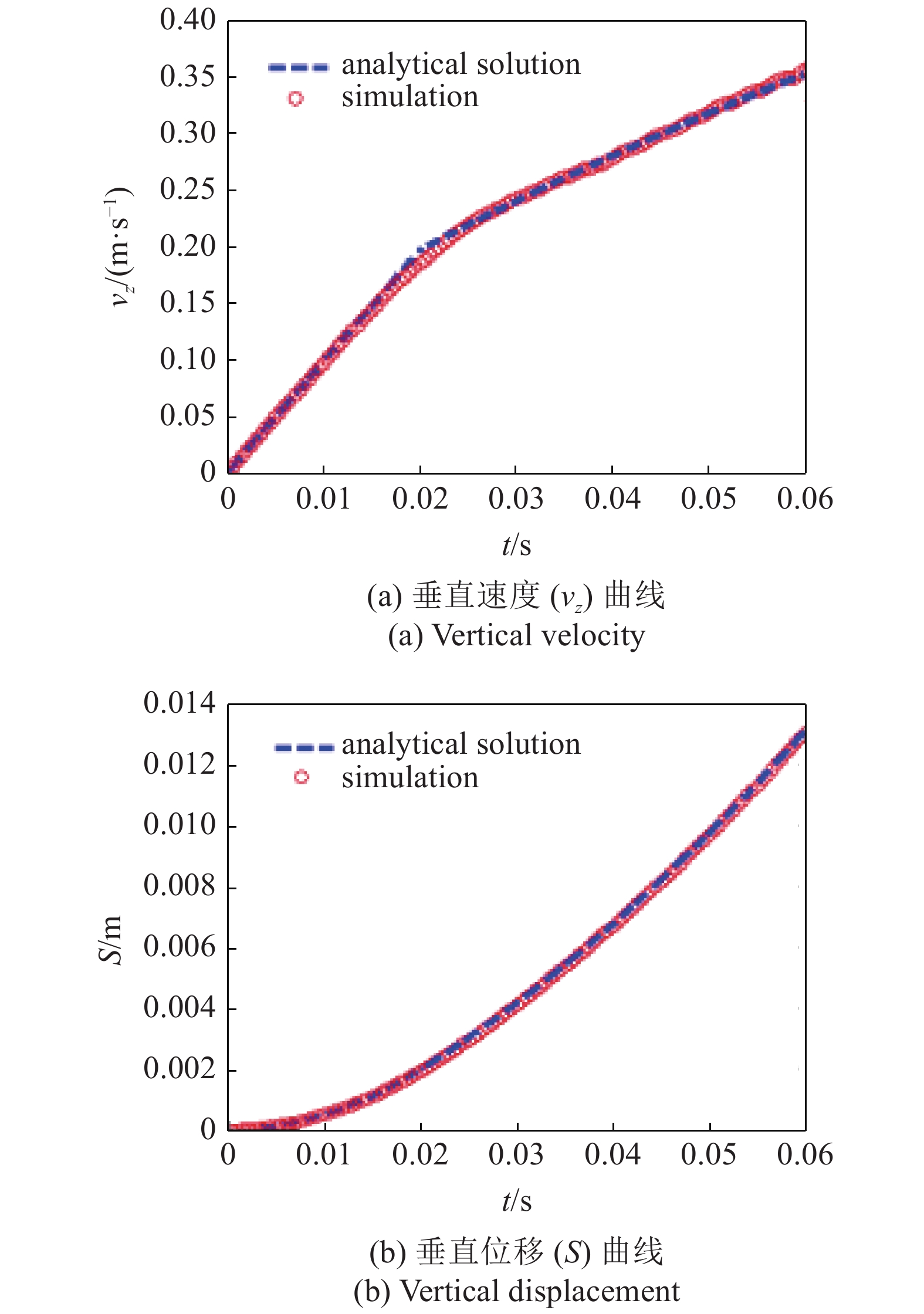
本节将所开发的半解析VOF-DEM耦合方法(不考虑热传导部分), 运用到两个标准算例(单颗粒入水、多颗粒溃坝)中, 以验证其准确性. 首先是单颗粒入水算例: 一个密度为2500 kg/m³, 半径为0.00135 m的颗粒悬挂于水面上的空气中, 距离水面0.02 m, 水深0.11 m. 该问题较为简单, 通过斯托克斯近似拖曳系数可以求得解析解. 运用相同的拖曳力模型, 也可在半解析VOF-DEM耦合方法中进行计算. 计算结果如图3所示: 颗粒运动的速度与垂直位移均与解析解符合, 且在气液界面, 颗粒的速度被光滑过度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
单颗粒入水的数值模拟结果与解析解相吻合



Figure
3.
Numerical results of a single particle entering water form air have good agreement with analytical result



下载:
全尺寸图片
幻灯片


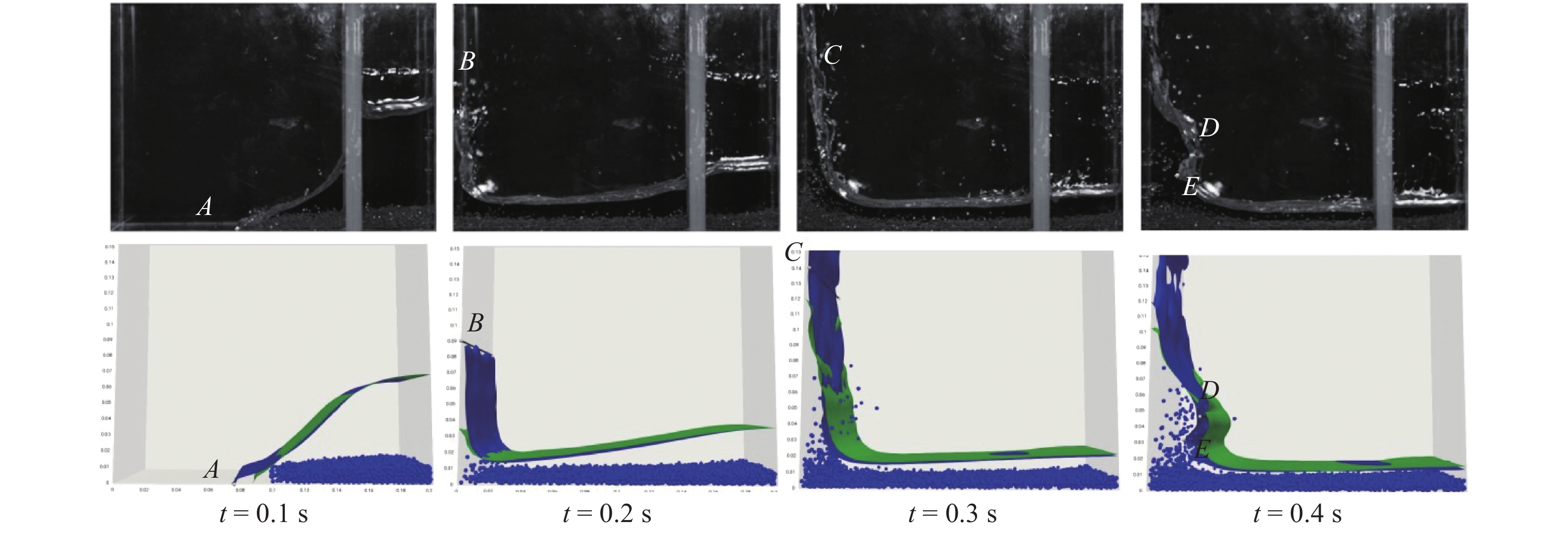
第二个标准算例为一个带固体颗粒的溃坝实验^[40]. 实验中水箱尺寸在3个方向分别为0.2 m, 0.1 m及(超过) 0.3 m, 计算域亦如此大. 水体初始在水箱的一侧, 尺寸为0.05 m, 0.1 m和0.1 m. 其中有3883个平均直径为2.7 mm的玻璃颗粒随机沉积在水体底部, 堆积高度约15 mm, 其他具体材料物性参数可参见文献[40]. 在本文的模拟中, 半解析VOF-DEM耦合方法耦合所使用的网格尺寸为颗粒直径的0.8倍, 对比目的所使用的非解析CFD-DEM网格尺寸是颗粒的3倍.

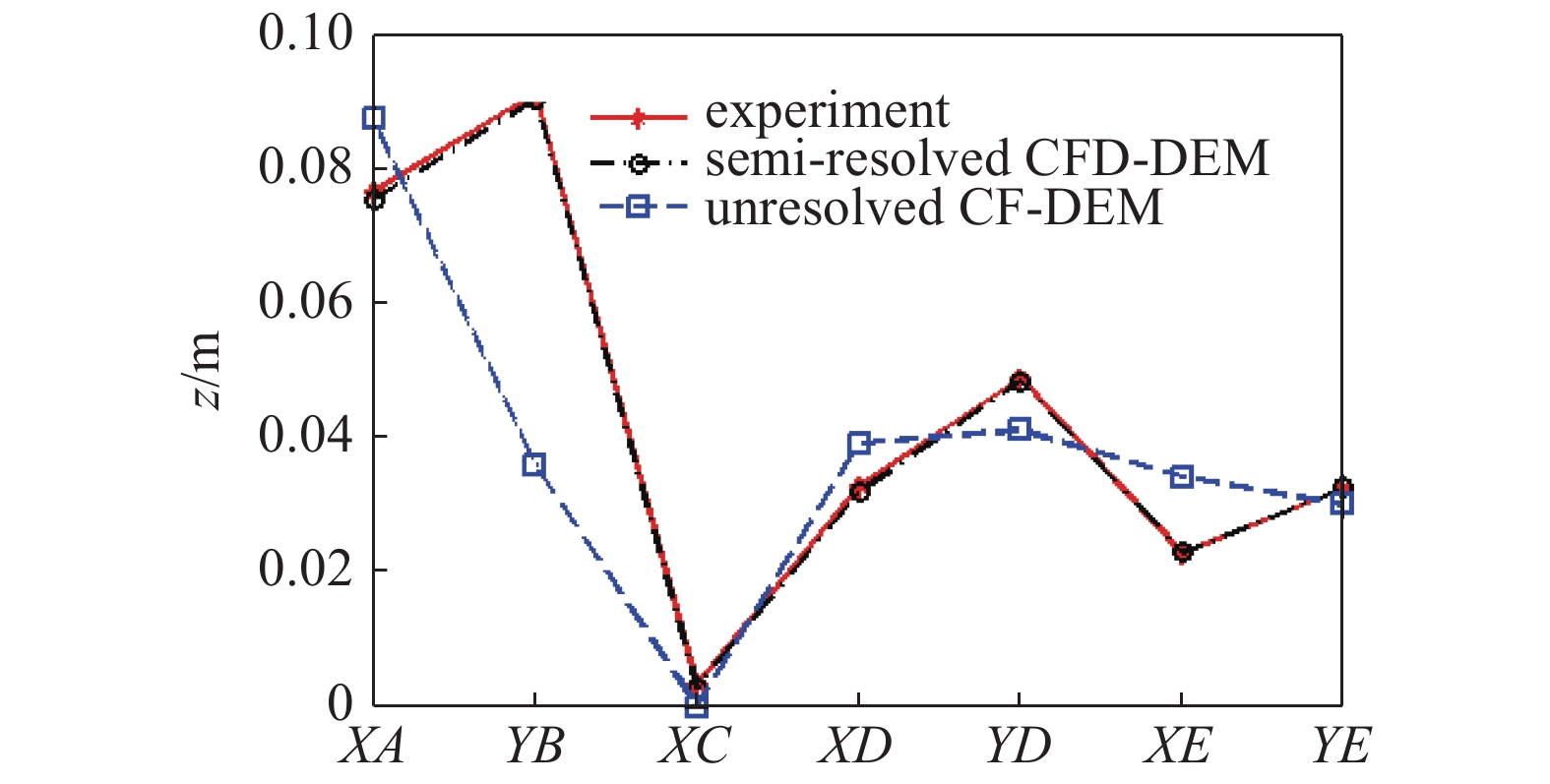
半解析VOF-DEM耦合方法的数值模拟结果(蓝色)与非解析耦合的结果(绿色)及实验在4个时刻的对比如图4所示: 可视化结果可见, 非解析模拟得到的流体前沿位移、冲击高度, 远不达实验所得数据, 而半解析的结果基本与实验吻合. 定量地看, 实验中设置了4个观测点^[57], 分别是在0.1 s时流体前沿A的横坐标, 0.2 s时流体冲击高度B的纵坐标, 0.3 s时指定冲击高度C点流体的厚度(横坐标), 0.4 s时流体回落的外凸点D与内凹点E的横纵坐标. 数值模拟结果与实验的定量对比如图5所示. 结果显示, 半解析VOF-DEM相较于非解析结果, 与实验有着极高的吻合度.

通过以上模拟, 及以往对单颗粒、喷动床、管道颗粒输运的验证^{[13, 31, 56]}, 基本可以确认, 半解析耦合策略无论在气?固、液?固两相, 亦或是气?液?固三相耦合中, 均表现远优于非解析模拟. 同时在高雷诺数、窄计算域、传热问题中也能出色得定性复现实验结果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
非解析、半解析耦合模拟结果与实验的对比



Figure
4.
Simulation results from unresolved and semi-resolved VOF-DEM versus experiment



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
流体前沿在4个时刻的位置: 实验与数值模拟的对比



Figure
5.
Flow frontier at four moments: experiments versus simulations



下载:
全尺寸图片
幻灯片

3.2
相变

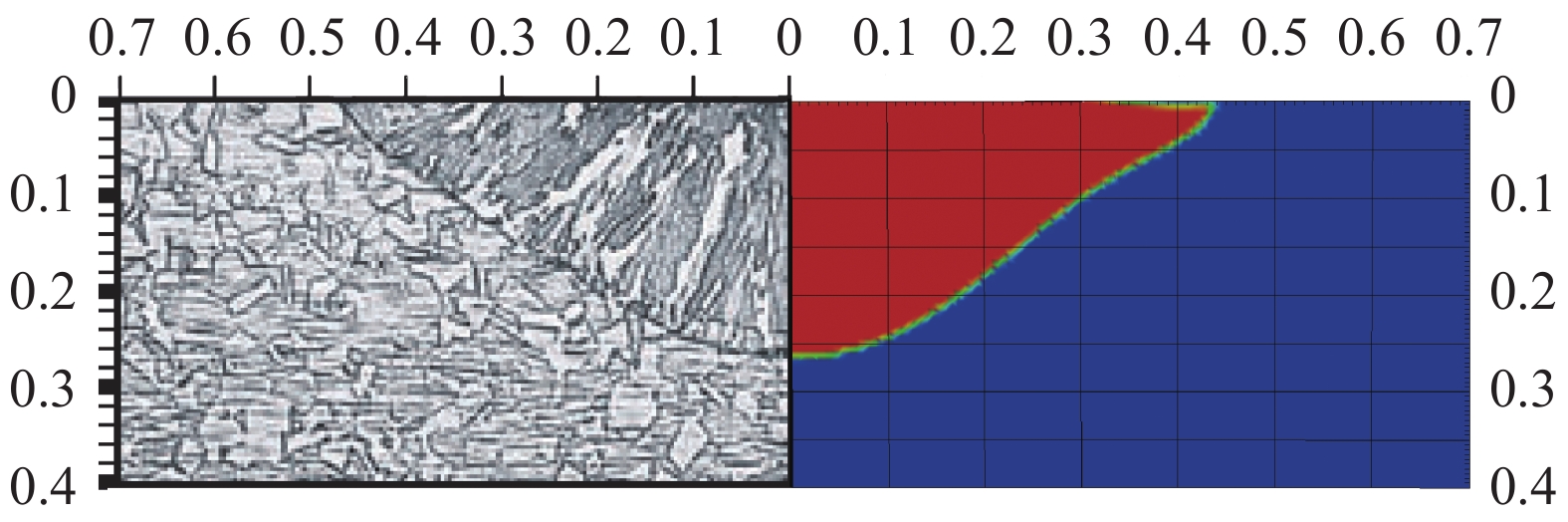
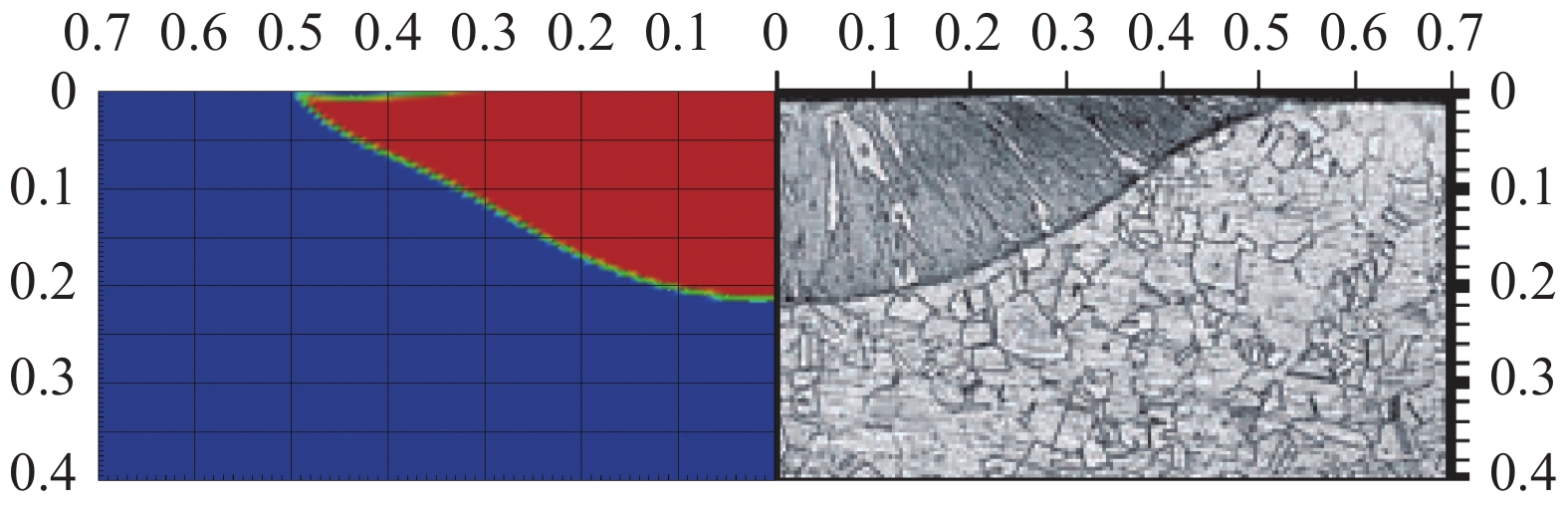
过去的研究, 已开发出耦合CFD-DEM及VOF的激光选区熔化技术^[20]. 其中铺粉及粉末熔化按次序进行, 因此不需要带传热的VOF-DEM耦合, 相对于本研究框架, 较为简单. 在上述研究中, 也对熔化部分的模拟器进行了基本验证, 结果显示该代码可以很好地模拟出粉床中各类空隙的产生过程、演变规律^[33], 熔道及深熔孔的形成^{[20, 33]}. 因此在本文中, 仅展示一个简单的点焊算例验证. He等^[58]利用功率为1967 W的激光, 半径分别控制为0.428 mm和0.57 mm, 对304不锈钢材料进行辐照, 分别形成两个熔池. 采用其热源模型^[58]对该问题进行了数值模拟, 模拟结果如图6和图7所示. 图中蓝色到红色的渐变即为${alpha _m} $从0 ~ 1的变化, 即红色为熔池, 所标注的数字分度值为0.1 mm. 结果可见, 开发的求解器可以很好得定量模拟出金属的相变和熔池的形成.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
数值模拟与实验对比, 激光半径为0.428 mm



Figure
6.
Numerical results versus experiment, with a laser radius of 0.428 mm



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
数值模拟与实验对比, 激光半径为0.57 mm



Figure
7.
Numerical results versus experiment, with a laser radius of 0.57 mm



下载:
全尺寸图片
幻灯片

3.3
直接沉积技术的数值模拟

在以往的研究中, 半解析耦合已分别在气固/液?固、带热传导、带自由液面的气?液?固等不同问题的颗粒流动中运用, 并展现出了出色的精度^{[13, 31, 56]}. 同时激光与粉床的相互作用的求解器, 也有了基本的验证^{[20, 33]}. 因此, 相信基于所开发的半解析VOF-DEM耦合方法, 可以应用于模拟激光直接沉积过程, 对其中的诸多重要物理现象进行复现, 并解释其中的机理.

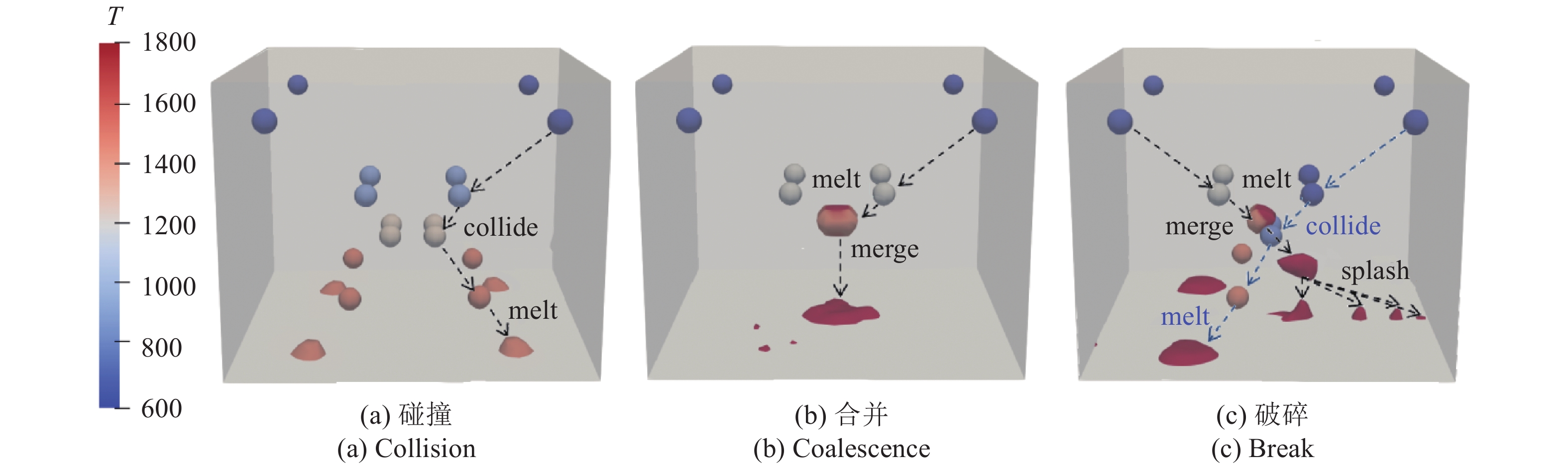
本文将分别展示直接输粉技术中少数颗粒相遇时的不同情形, 和熔道的形成过程. 首先, 设计一个算例, 算例计算域为1.4 mm×1.4 mm×1.1 mm, 4个直径为96 μm的高温合金Inconel718颗粒分别设置在4个角落, 并距离三侧壁面均50 μm. 颗粒初始速度汇向计算域中心, x和y轴的速度分量大小均为0.3 m/s, 垂直方向为0.9 m/s, 方向向下. 颗粒密度8380 kg/m³, 碰撞恢复系数0.9, 初始温度为573 K, 熔点1580 K, 比热650 J/(kg·K), 激光吸收率为0.51. 激光半径为27 μm. 以上情况基本接近预热的高温合金粉末(材料物性参数可参见文献[33, 59])在喷口下汇聚的真实情况, 故所展示的各类颗粒行为, 可供相关研究参考.

设计了3个算例, 分别重现了激光直接沉积技术中的3类典型颗粒相互作用. 第一个算例, 激光功率设计得较低, ${P_l} = 300;{
m{W}} $, 因此, 颗粒的相互碰撞发生在熔化之前, 对熔化的行为没有影响. 如图8(a)所示, 颗粒或熔体的温度初始为800 K, 在高斯激光热源的辐照下, 不断升温. 在发生碰撞后, 基本遵守动量守恒, 4个颗粒的水平速度分量分别被反弹至相反方向. 在颗粒分开后才被加热达到熔点, 故在基板上形成了4滩熔迹. 颗粒在熔化前后的空间轨迹由黑色虚线表示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
直接沉积技术中3种典型颗粒相互作用



Figure
8.
Three featured particle-particle interactions in laser direct deposition



下载:
全尺寸图片
幻灯片


如图8(b)所示的是第2个算例, 其中$ {P_l} = $$ 300;{
m{W}} $. 因激光功率较高, 在颗粒相互碰撞之前颗粒已经熔化. 当4个熔体相互接触时, 由于4个球动量相当, 且表面张力远大于惯性力(Ca = 0.0038), 它们将融为一体, 形成空中熔池, 在碰撞点垂直下落.

在第3个算例中, $ {P_l} = 300;{
m{W}} $, 但右侧的两个颗粒的比热被提高至1390 J/(kg·K), 以推迟其熔化. 在这个算例中, 左侧两个颗粒在汇聚前已经熔化. 熔化后, 因熔体具有流动性, 受到空气阻力影响, 熔体不能维持球形, 在迎风面积方向增大, 变为扁扁的饼形. 因此, 两个熔体在到达预定的刚体接触点前(计算域中央), 便已经接触(饼形的半径大于颗粒原半径). 因巨大的表面张力, 瞬间融合. 也因所受阻力较其是球体时更大, 左侧的两个颗粒(熔体)比右侧的两个颗粒更晚到达计算域中央, 其轨迹如图8(c)黑线所示. 但融合后的熔体在与右侧两个未熔化颗粒撞击后, 从未熔化的两个颗粒之间穿出, 并破碎溅落到基板上. 而未熔颗粒继续沿原方向行进, 其轨迹如图8(c)蓝线所示, 在而后的加温过程中, 他们也分别熔化, 形成两摊熔迹.

以上便是在直接输粉技术中常见的3种颗粒相互作用的形态. 由数值模拟可知, 在一定的输粉速率下, 如果激光功率不够, 如算例一, 粉末会在汇聚点以下的环状区域内熔化, 难以形成较深且稳定的熔池; 反之, 如果激光功率过高, 颗粒会过早熔化而因巨大的阻力变为扁平状, 易于破碎; 同时, 如果颗粒粒径分异较大, 可能在聚焦点同时存在熔化和未熔化的颗粒, 他们相互作用也容易导致已形成的空中熔池破碎.

而后, 进行了真实工况下全尺度情景的模拟. 其中喷口轮廓与铅垂的夹角为26°, 喷口在出口处内外径分别为5 mm, 6 mm, 平均直径为0.1 mm的高温合金Inconel718颗粒以1 m/s的速度从喷口入射, 流量为0.416 g/s. 激光束$ {P_l} = 1600;{
m{W}}$, $ {R_l} = $$ 0.45;{
m{mm}} $. 基板水平移动速度为y方向?0.4 m/s (向左). CFD网格尺寸为颗粒直径的0.8倍, 固体壁面通过stl网格设置. 其模拟结果如图9所示. 图中左侧为整个计算域的实际模拟尺度, 包括喷口、粉末、熔道和基板. 具体放大到右侧, 则可以看到金属颗粒在被加热到液相线后, 发生熔化. 在这个过程中, 颗粒被从离散元刚体单元转化为VOF中的金属相体积分数. 随着熔体向中心聚拢, 来自各径向的熔融颗粒凝并在一起, 形成更大的熔体垂直下落至基板. 随着基板或喷口的移动, 逐渐形成熔道. 此外, 图中还可见熔道表面微有皱褶, 皱褶方向与激光行进方向相反, 该现象亦与实际相符.



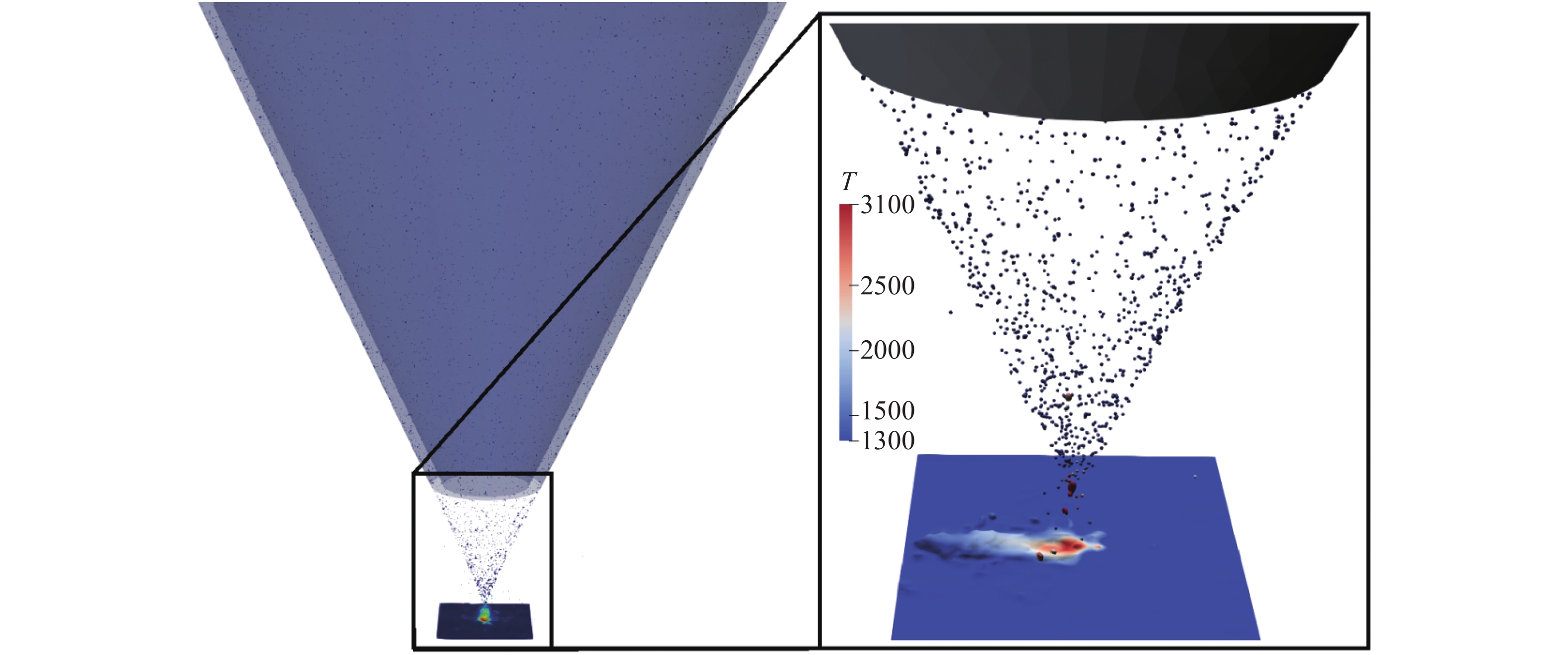onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-9.jpg'"
class="figure_img
figure_type2 ccc " id="Figure9" />



图
9
实际工况下激光直接沉积过程的数值模拟



Figure
9.
Simulation of Laser Direct Deposition process under actual working conditions



下载:
全尺寸图片
幻灯片


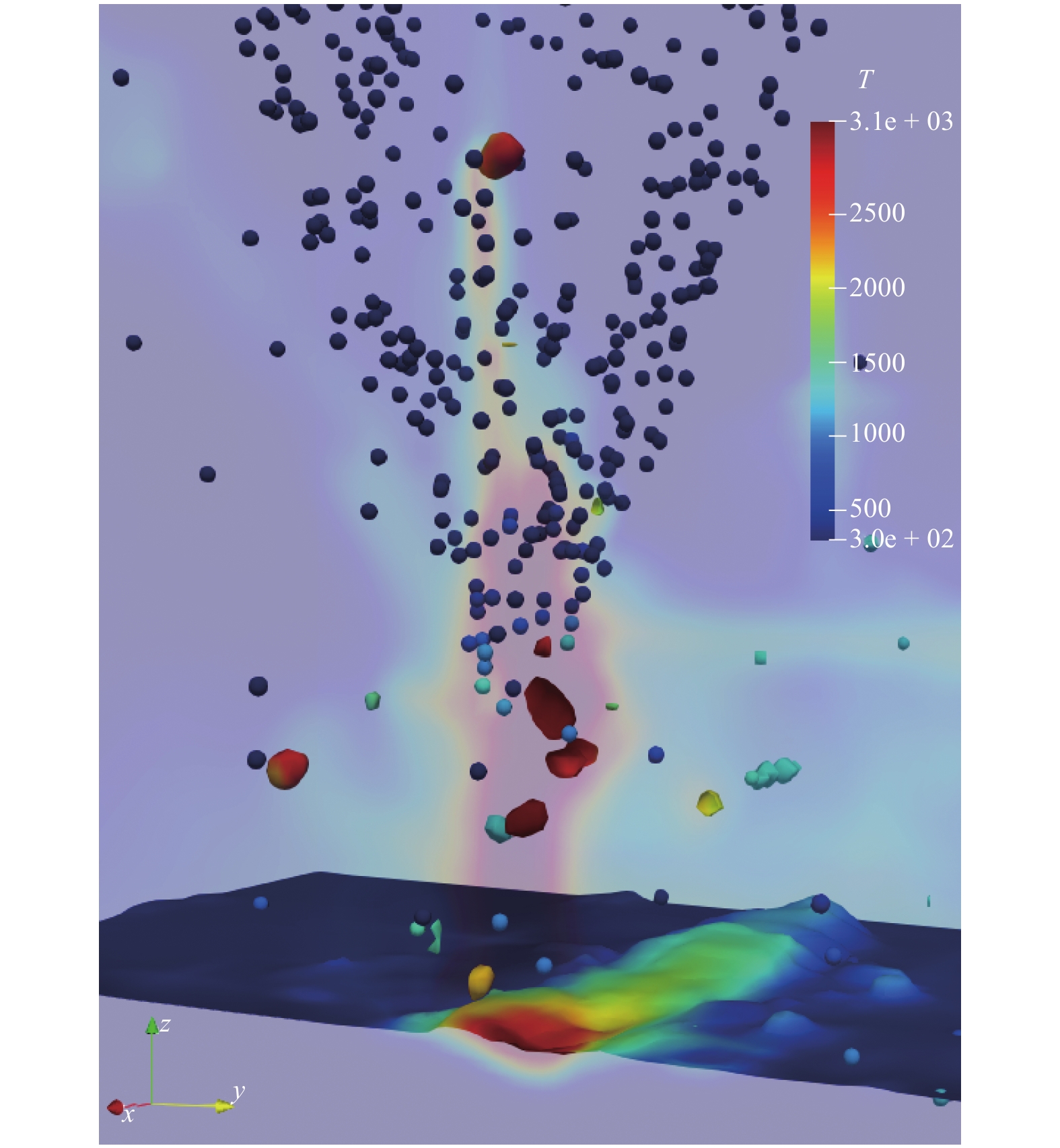
再继续放大至空中熔池(融合后的大块熔体), 如图10所示, 可见激光直接沉积技术中典型的几种状态, 如因刚体碰撞而弹出粉末汇聚点而未来得及熔化的颗粒、在汇聚点熔化形成空中熔池的颗粒、熔化颗粒与刚体颗粒粘结、因与未熔颗粒碰撞而破碎的熔体, 正如图8所示情形. 此外, 巨大熔体落至基板上的熔池后, 还会发生溅射. 由于存在喷嘴和基板直接的相对运动, 溅射方向倾向于激光扫描相背方向.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-361-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
熔道的形成



Figure
10.
Formation of molten track



下载:
全尺寸图片
幻灯片


由此可见, 开发的带传热传质的半解析VOF-DEM (或称半解析CFD-DEM-VOF)耦合方法, 可以很好地定性描述激光直接沉积技术中存在的种种现象, 为其中的机理提供解释, 有望成为未来模拟研究激光直接沉积的重要工具.

4.
总结与展望

本文通过在基于核函数重构背景流场的半解析CFD-DEM引入VOF技术, 发展了可以同时考虑含热、刚体颗粒的运动、相变和自由液面及相变界面的半解析VOF-DEM数值模拟框架. 该模拟框架可以将含自由液面的流体网格缩小至颗粒尺寸, 甚至小于颗粒尺寸, 从而大大提高了数值模拟的精度. 通过一系列验证后, 将其成功用于激光直接沉积技术的跨尺度数值模拟. 由于网格小于颗粒尺寸, 模型可以描述颗粒的熔化行为.

本文的主要结论与贡献, 可归纳如下:

(1)将半解析CFD-DEM的耦合策略运用到VOF-DEM后, 发展了半解析VOF-DEM耦合方法. 该方法可降低流体网格的尺寸. 再通过iso-advector重构VOF中气液两相的界面, 数值模拟的精度得到了大大提高.

(2)半解析VOF-DEM耦合框架考虑了相变、激光模型等热力学模型, 首次实现了符合真实物理的全尺度激光直接沉积技术数值模拟.

(3)该模型框架首次实现了直接沉积技术中颗粒间的碰撞、融合、破碎、粘结, 熔体飞溅等现象的同步模拟, 为解释其中机理提供了有力工具.

然而, 由于同时存在复杂的跨尺度、多物理场、多元颗粒体系、相变和高雷诺数的耦合模拟, 目前本框架的精度还有提高的空间. 在本文中, 我们先首次提出该框架, 并定性复现了激光直接沉积过程中的诸多复杂现象. 在未来的工作中, 我们还将不断优化模型提高精度. 此外, 该模型未来不仅有望为激光直接沉积技术提供重要的数值模拟技术支撑, 对其他涉及相变的复杂颗粒体系, 例如飞机结冰^[60-63]、天然气水合物开采^[64]等, 也有巨大的运用前景.

致谢

本研究得到了国家重点研发计划( 2018YFB0704000)与国家自然科学基金( 12032002)的支持. 涉及的所有计算均在北京并行科技有限公司所提供的广州天河二号超级计算机上进行.