引 言

分数阶微积分第一次被数学家Hospital与Leibnitz提出, 至今已有300多年历史. 起初, 分数阶微积分因其缺乏应用背景在早期工程研究中并未得到广泛关注. 1832年, Liouville首次将分数阶微积分用于解决一些实际问题. 此后, 众多****在分数阶微积分的定义、性质和计算方法等方面展开了详细的探讨^[1-6]. 在这个过程中, 分数阶微积分也由数学理论研究逐步走向工程应用^[7-11].

在控制工程领域, 分数阶微积分主要用来影响系统的闭环控制特性, 从而提高系统控制效果和鲁棒性. 如薛定宇和赵春娜^[12]提出了一种分数阶PID控制器的设计方法, 具体演示了分数阶控制器对系统优良的控制效果. 常宇健等^[13]则针对含分数阶阻尼的悬架模型进行了主动控制研究. 在动力学方面, 分数阶微积分主要集中用于描述黏弹特性材料的本构关系, 以此来提高此类非线性系统振动特性研究的准确性. 如Cao等^[14]采用数值积分法, 结合相图、庞加莱截面图、分岔图等分析了分数阶阻尼对系统动力学性能的影响. 申永军等^[15]通过对含分数阶线性单自由度振子的动力学分析, 首次提出等效线性阻尼和等效线性刚度概念. 申永军等^[16-17]利用平均法得到分数阶van der Pol振子的一次近似解, 比较了分数阶与整数阶系统并分析了分数阶微分项对系统动力特性的影响. 由上述研究可知, 相比整数阶模型, 分数阶模型的物理意义更清晰, 更能准确描述实际系统.

Mathieu方程作为一种周期系数线性微分方程, 因其本身复杂的动力学特性, 在动力学领域得到了广泛的应用^[18-20], 经常被用来处理一些参数共振现象. 如Qian等^[21]研究了在参数激励和强迫激励作用下的斜拉桥拉索的非线性动力学问题, 利用多尺度方法分析了1/2参激共振下的动力学响应. 黄建亮等^[22]对van der Pol-Mathieu方程的动力学特性进行了研究, 应用改进的谐波平衡法精确计算出了方程的准周期响应. 温少芳^[23]研究了分数阶参激系统的动力学特性, 分析了分数阶微分项对系统稳定性边界以及幅频响应的影响. 同时, 随着众多****对Mathieu方程的深入研究, 促使其形式也得到了丰富拓展. Kovacic等^[24]对Mathieu方程的推广型作了全面概述, 包含拟周期系数和椭圆系数等多种形式的Mathieu方程. 其中, 拟周期系数Mathieu方程通常被应用于一些特殊的动力系统, 如Galeotti和Toni^[25]提出的含双频激励时变刚度的高速列车受电弓非线性模型. Huan等^[26]研究了高速列车受电弓-悬链线组合系统中低频和高频参数激励对系统响应的影响等. Rand等^[27-28]则针对拟周期Mathieu方程不同共振状态的稳定区域进行了深入研究.

综上所述, 在含有黏弹性器件的参激系统(如弓网系统)中, 分数阶模型较整数阶模型对系统描述更加准确. 因此, 本文在拟周期Mathieu方程中引入分数阶微积分理论, 建立了分数阶拟周期Mathieu方程, 利用摄动法求得了方程过渡曲线的近似解析解, 通过数值方法在系统稳定图中分析了分数阶微分项参数对方程稳定区域大小和过渡曲线位置的影响, 并验证了分数阶微分项同时含有阻尼和刚度特性的特点.

1.
分数阶拟周期Mathieu方程

1.1
摄动分析

本文研究的分数阶拟周期Mathieu方程如下所示

$$ begin{split} & ddot uleft( t ight) + 2zeta dot uleft( t ight) + left{ {delta + varepsilon left[ {cos t + cos left( {omega {kern 1pt} t} ight)} ight]} ight}uleft( t ight) + hfill &qquad {K_1}{{ m{D}}^p} {uleft( t ight)} = 0 hfill end{split} $$

(1)

其中, $ omega $是无理数; $ varepsilon $为小参数, 满足$ left| varepsilon
ight| ll 1 $; $ 2zeta $和$ delta + varepsilon left[ {cos t + cos left( {omega {kern 1 pt} t}
ight)}
ight] $分别为线性阻尼和时变刚度; ${{
m{D}}^p}left[ {uleft( t
ight)}
ight]$为$ uleft( t
ight) $关于$ t $的$ ,p $阶导数$ left( {0 leqslant p leqslant 1}
ight) $; $ {K_1} $为分数阶微分项系数$ left( {{K_1} > 0}
ight) $.

关于分数阶微积分的定义有多种, 这里采用Caputo型分数阶微积分定义

$$ {{ m{D}}^p}left[ {uleft( t ight)} ight] = frac{1}{{Gammaleft({1 - p} ight)}}int_0^t {frac{{u'left( s ight)}}{{{{left( {t - s} ight)}^p}}}} {text{d}}{kern 1pt} s $$

(2)

式中$ Gamma $为Gamma函数, 具有$Gamma (z + 1) = zGamma (z)$的特性.

为了确定方程稳态周期解的过渡曲线, 引入$ zeta = $$ varepsilon mu ,,;mu = Oleft( 1
ight),;{K_1} = varepsilon k,,,;k = Oleft( 1
ight) $, 式(1)变换为

$$ begin{split} & ddot uleft( t ight) + 2varepsilon mu dot uleft( t ight) + left{ {delta + varepsilon left[ {cos t + cos left( {omega {kern 1pt} t} ight)} ight]} ight}uleft( t ight) + hfill & quad varepsilon k{{ m{D}}^p} {uleft( t ight)} = 0 hfill end{split} $$

(3)

利用摄动法, 假设式(3)的解满足

$$ uleft( {t,varepsilon } ight) = {u_0}left( t ight) + varepsilon {u_1}left( t ight) + {varepsilon ^2}{u_2}left( t ight) + cdots $$

(4)

过渡曲线在$ delta - omega $平面内具有如下形式

$$ delta left( {omega ,;varepsilon } ight) = {delta _0} + varepsilon {kern 1pt} {delta _1}left( omega ight) + {varepsilon ^2}{delta _2}left( omega ight) + cdots $$

(5)

将式(4)和式(5)代入式(3), 比较$varepsilon $的同次幂得到

$$ Oleft( {{varepsilon ^0}} ight):{kern 1pt} ;{kern 1pt} {ddot u_0} + {delta _0}{u_0} = 0tag{6a} $$

$$ begin{split} & Oleft( {{varepsilon ^1}} ight):{kern 1pt} {kern 1pt} ;{{ddot u}_1} + {delta _0}{u_1} = - {delta _1}{u_0} - [cos t + hfill & quad quad quad quad quad cos (omega t)]{u_0} - 2mu {{dot u}_0} - k{ m{D}}_{}^p{kern 1pt} {u_0} hfill end{split}tag{6b} $$

$$ begin{split} & Oleft( {{varepsilon ^2}} ight):{kern 1pt} ;{{ddot u}_2} + {delta _0}{u_2} = - {delta _1}{u_1} - {delta _2}{u_0} - [cos t + hfill & quad quad quad quad quad cos (omega t)]{u_1} - 2mu {{dot u}_1} - k{ m{D}}_{}^p{kern 1pt} {u_1} hfill end{split} tag{6c}$$

由式(6a)解得

$$ {u_0} = A{{text{e}}^{{text{i}}sqrt {{delta _0}} {kern 1pt} t}} + cc $$

(7)

其中$ cc $代表前面各项的共轭, 后不赘述. 由于$ omega $是无理的, 拟周期Mathieu方程稳态周期解的过渡曲线在$ delta - omega $平面上是从$ {delta _0} = dfrac{1}{4}{left( {alpha + beta omega }
ight)^2},alpha ,beta in mathbb{Z} $处产生^[29], 下面讨论方程在$ alpha =0, 1, ;beta =-1, 0, 1 $时的过渡曲线.

(1) ${delta _0} = 0$(即$ alpha =0, beta =0 $)

根据式(6a)解得

$$ {u_0} = c = { m{const}} .$$

(8)

式中$ c $是由初始条件确定的常量, 将其代入式(6b)得到

$$ {kern 1pt} {ddot u_1} = - {delta _1}c - left[ {cos t + cos (omega t)} ight]c $$

(9)

为了消除永年项需$ - {delta _1}c = 0 $, 所以有

$$ {delta _1} = 0 $$

(10)

则式(9)的特解为

$$ {u_1} = left[ {cos t + frac{{cos (omega t)}}{{{omega ^2}}}} ight]c $$

(11)

这里利用公式^[30]对分数阶微分项$ k{
m{D}}^p{u_1} $进行处理

$$ {{ m{D}}^p}{{text{e}}^{{text{i}}lambda t}} approx {({text{i}}lambda )^p}{{text{e}}^{{text{i}}lambda t}} $$

(12)

再结合欧拉公式得到

$$ begin{split} k{ m{D}}_{}^p{u_1} =& k{ m{D}}_{}^pleft{ {left[ {cos t + frac{{cos (omega t)}}{{{omega ^2}}}} ight]c} ight} hfill ;;quad quad =& frac{c}{2}{{text{i}}^p}kleft( {{{text{e}}^{{text{i}},t}} + frac{{{omega ^p}{{text{e}}^{{text{i}}omega t}}}}{{{omega ^2}}} + cc} ight) hfill end{split} $$

(13)

将式(8)、式(10)、式(11)和式(13)代入式(6c)得到

$$ begin{split} & {kern 1pt} {{ddot u}_2} = - c{delta _2} - frac{c}{2} - frac{c}{{2{omega ^2}}} - {text{i}}mu c{{text{e}}^{{text{i}},t}} - mu frac{{{text{i}}c{{text{e}}^{{text{i}}omega t,}}}}{omega } - hfill & qquad frac{1}{4}c{{text{e}}^{2{text{i}},t}} - frac{1}{4}c{{text{e}}^{{text{i}},(1 - omega ),t}} - frac{1}{4}c{{text{e}}^{{text{i}},(1 + omega ),t}} - frac{{c{{text{e}}^{2{text{i}}omega t}}}}{{4{omega ^2}}} - hfill & qquad frac{{c{{text{e}}^{{text{i}}(1 - omega ),t}}}}{{4{omega ^2}}} - frac{{c{{text{e}}^{{text{i}}(1 + omega ),t}}}}{{4{omega ^2}}} - frac{1}{2}{{text{i}}^p}c{{text{e}}^{{text{i}},t}}k - frac{{ck{{left( {{text{i}}omega } ight)}^p}{{text{e}}^{{text{i}}omega ,t}}}}{{2{omega ^2}}} + cc hfill end{split} $$

(14)

从上式得出消除永年项条件

$$ - c,{delta _2} - frac{c}{2} - frac{c}{{2{omega ^2}}} = 0 $$

即

$$ {delta _2} = - frac{1}{2}left( {1 + frac{1}{{{omega ^2}}}} ight) $$

(15)

此时式(14)的特解为

$$ begin{split} & {u_2} = frac{1}{{16}}c{{text{e}}^{2{text{i}}t}} + {text{i}}mu c{{text{e}}^{{text{i}}t}} + frac{{{text{i}}mu c{{text{e}}^{{text{i}}omega t}}}}{{{omega ^3}}} + frac{{c{{text{e}}^{{text{i}}left( { - 1 + omega } ight)t}}}}{{4{{left( { - 1 + omega } ight)}^2}}} + hfill &qquad frac{{c{{text{e}}^{{text{i}}left( {1 + omega } ight)t}}}}{{4{{left( {1 + omega } ight)}^2}}} + frac{{c{{text{e}}^{2{text{i}}omega t}}}}{{16{omega ^4}}} + frac{{c{{text{e}}^{{text{i}}left( { - 1 + omega } ight)t}}}}{{4{{left( { - 1 + omega } ight)}^2}{omega ^2}}} + hfill &qquad frac{{c{{text{e}}^{{text{i}}left( {1 + omega } ight)t}}}}{{4{{left( {1 + omega } ight)}^2}{omega ^2}}} + frac{{c{{text{e}}^{{text{i}}omega t}}k{{left( {{text{i}}omega } ight)}^p}}}{{2{omega ^4}}} + frac{c}{2}{{text{i}}^p}{{text{e}}^{{text{i}},t}}k + cc hfill end{split} $$

(16)

将式(10)和式(15)代入式(5)得到

$$ ,delta = - {varepsilon ^2}frac{1}{2}left( {1 + frac{1}{{{omega ^2}}}} ight) + Oleft( {{varepsilon ^3}} ight) $$

(17)

分析式(17)可以看出, 在$ {delta _0} = 0 $附近过渡曲线的二阶近似解与方程的分数阶微分项和阻尼都没有关系, 所以进行三阶近似计算

$$ begin{split} & Oleft( {{varepsilon ^3}} ight):quad {{ddot u}_3} + {delta _0}{u_3} = - {delta _3}{u_0} - {delta _2}{u_1} - {delta _1}{u_2} - hfill & quad quad quad quad quad ; left[ {cos t + cos (omega t)} ight]{u_2} - 2mu {{dot u}_2} - k{ m{D}}_{}^p{kern 1pt} {u_2} hfill end{split} $$

(18)

类似地, 将式(8)、式(10)、式(11)、式(15)和式(16)代入式(18)可得到消除永年项条件

$$ - c,{delta _3} - frac{{ckleft( {{omega ^4} + {omega ^p}} ight)}}{{2{omega ^4}}}cos left( {frac{{p{text{π }}}}{2}} ight) = 0 $$

即

$$ ,{delta _3} = - frac{{kleft( {{omega ^4} + {omega ^p}} ight)}}{{2{omega ^4}}}cos left( {frac{{p{text{π }}}}{2}} ight) $$

(19)

代入方程原参数得到$ {delta _0} = 0 $时过渡曲线的三阶近似解

$$ begin{split} ,delta = & - {varepsilon ^2}frac{1}{2}left( {1 + frac{1}{{{omega ^2}}}} ight) - {varepsilon ^2}frac{{{K_1}left( {{omega ^4} + {omega ^p}} ight)}}{{2{omega ^4}}}cos left( {frac{{p{text{π }}}}{2}} ight) +hfill & Oleft( {{varepsilon ^4}} ight) hfill end{split} $$

(20)

(2) ${delta _0} = dfrac{1}{4}{omega ^2}$(即$ alpha =0, beta =1 $)

由式(7)得到式(6a)的特解为

$$ {u_0} = A{{text{e}}^{frac{{text{i}}}{2}omega t}} + cc $$

(21)

对分数阶项$ k{
m{D}}_{}^p{u_0} $进行处理得到

$$ k{ m{D}}_{}^p{u_0} = k{ m{D}}_{}^pleft( {A{{text{e}}^{frac{{text{i}}}{2}omega ,t}} + cc} ight) = k{left( {frac{{text{i}}}{2}omega } ight)^p}A{{text{e}}^{frac{{text{i}}}{2}omega ,t}} + cc $$

(22)

将式(21)和式(22)代入式(6b)中得到

$$ begin{split} & {{ddot u}_1} + frac{1}{4}{omega ^2}{u_1} = {{text{e}}^{frac{{text{i}}}{2}omega ,t}}left[ { - {delta _1}A - {2^{ - p}}k{{left( {{text{i}}omega } ight)}^p}A - {text{i}}mu omega A - frac{1}{2}bar A} ight] hfill & quad - frac{1}{2}{{text{e}}^{frac{3}{2}{text{i}}omega ,t}}A - frac{1}{2}{{text{e}}^{{text{i}},t + frac{{text{i}}}{2}omega ,t}}A - frac{1}{2}{{text{e}}^{ - {text{i}},t + frac{{text{i}}}{2}omega ,t}}A + cc hfill end{split} $$

(23)

消除永年项条件为

$$ - {delta _1}A - {2^{ - p}}k{left( {{text{i}}omega } ight)^p}A - {text{i}}mu omega A - frac{1}{2}bar A = 0 $$

(24)

为了便于求解, 记$ A = dfrac{a}{2} - {text{i}}dfrac{b}{2} $, 求解式(24), 分离实部和虚部得

$$ left. begin{array}{l}left[ { - 1 - 2{delta _1} - 2dfrac{1}{{{2^p}}}{omega ^p}kcos left( {dfrac{{p{text{π }}{ m{ }}}}{2}} ight)} ight]a + qquad left[ { - 2omega mu - 2dfrac{1}{{{2^p}}}{omega ^p}ksin left( {dfrac{{p{text{π }}{ m{ }}}}{2}} ight)} ight]b = 0left[ { - 2omega mu - 2dfrac{1}{{{2^p}}}{omega ^p}ksin left( {dfrac{{p{text{π }}{ m{ }}}}{2}} ight)} ight]a + qquad left[ { - 1 + 2{delta _1} + 2dfrac{1}{{{2^p}}}{omega ^p}kcos left( {dfrac{{p{text{π }}{ m{ }}}}{2}} ight)} ight]b = 0end{array} ight} $$

(25)

该方程有非零解的条件是

$$ det left[ begin{array}{l} - 1 - 2{delta _1} - 2dfrac{1}{{{2^p}}}{omega ^p}kcos left( {dfrac{{p{text{π }}{ m{ }}}}{2}} ight) - 2omega mu - 2dfrac{1}{{{2^p}}}{omega ^p}ksin left( {dfrac{{p{text{π }}{ m{ }}}}{2}} ight) - 2omega mu - 2dfrac{1}{{{2^p}}}{omega ^p}ksin left( {dfrac{{p{text{π }}{ m{ }}}}{2}} ight) - 1 + 2{delta _1} + 2dfrac{1}{{{2^p}}}{omega ^p}kcos left( {dfrac{{p{text{π }}{ m{ }}}}{2}} ight)end{array} ight] = 0 $$

(26)

其中det为求解矩阵行列式. 计算得出

$$ ,{delta _1} = - frac{1}{{{2^p}}}{omega ^p}kcos left( {frac{{p{text{π }}}}{2}} ight) pm sqrt {frac{1}{4} - {{left[ {omega mu + frac{1}{{{2^p}}}{omega ^p}ksin left( {frac{{p{text{π }}}}{2}} ight)} ight]}^2}} $$

(27)

此时式(6b)的特解为

$$ begin{split} {u_1} =& frac{1}{{4{omega ^2}}}{{text{e}}^{frac{3}{2}{text{i}}omega t}}A - frac{1}{{2left( {omega - 1} ight)}}{{text{e}}^{ - {text{i}}{kern 1pt} t + frac{{text{i}}}{2}omega t}}A + hfill &frac{1}{{2left( {omega + 1} ight)}}{{text{e}}^{{text{i}}{kern 1pt} t + frac{{text{i}}}{2}omega t}}A + cc hfill end{split} $$

(28)

将式(21)、式(27)和式(28)代入式(6c)得

$$ begin{split} {{ddot u}_2} + frac{1}{4}{omega ^2}{u_2} &= left[ { - {delta _2}A + frac{A}{{4left( { - 1 + omega } ight)}} - frac{A}{{8{omega ^2}}} - } ight. hfill & left. {frac{A}{{4left( {1 + omega } ight)}}} ight]{{text{e}}^{frac{1}{2}{text{i}}omega t}} + cdots + cc hfill end{split} $$

(29)

为了消除永年项, 要求

$$ - {delta _2}A + frac{A}{{4left( { - 1 + omega } ight)}} - frac{A}{{8{omega ^2}}} - frac{A}{{4left( {1 + omega } ight)}} = 0 $$

从而得到

$$ {delta _2} = - frac{{1 + 3{omega ^2}}}{{8{omega ^2}left( {1 - omega } ight)left( {1 + omega } ight)}} $$

(30)

将式(27)和式(30)代入式(5), 代入原参数整理得到此时的两条过渡曲线

$$ begin{split} delta = &frac{1}{4}{omega ^2} - frac{{{K_1}}}{{{2^p}}}{omega ^p}cos left( {frac{{p{text{π }}}}{2}} ight) - {varepsilon ^2}frac{{1 + 3{omega ^2}}}{{8{omega ^2}left( {1 - omega } ight)left( {1 + omega } ight)}} pm hfill & sqrt {frac{{{varepsilon ^2}}}{4} - frac{{{omega ^2}}}{4}{{left[ {2zeta {kern 1pt} + frac{{{K_1}}}{{{2^{p - 1}}}}{omega ^{p - 1}}sin left( {frac{{p{text{π }}}}{2}} ight)} ight]}^2}} + Oleft( {{varepsilon ^3}} ight) hfill end{split} $$

(31)

根据上述类似的计算方法相应求出$ {delta _0} = dfrac{1}{4} $($alpha = 1$, $; beta = 0 $)时方程的过渡曲线为

$$ begin{split} delta = &frac{1}{4} - frac{{{K_1}}}{{{2^p}}}cos left( {frac{{p{text{π }}}}{2}} ight) - {varepsilon ^2}frac{{3 + {omega ^2}}}{{8left( {1 - {omega ^2}} ight)}} pm hfill & sqrt {frac{{{varepsilon ^2}}}{4} - frac{1}{4}{{left[ {2zeta + {K_1}frac{1}{{{2^{p - 1}}}}sin left( {frac{{p{text{π }}}}{2}} ight)} ight]}^2}} + Oleft( {{varepsilon ^3}} ight) hfill end{split} $$

(32)

$ {delta _0} = dfrac{1}{4}{left( {1 + omega }
ight)^2} $(即$alpha = 1,beta = 1$)时方程的过渡曲线为

$$ begin{split} & delta = frac{1}{4}{left( {1 + omega } ight)^2} + {varepsilon ^2}left[ {frac{1}{{2omega }} - frac{1}{{4left( {2 + omega } ight)}} - frac{1}{{4omega left( {1 + 2omega } ight)}}} ight] - hfill & quad frac{{{K_1}}}{{{2^p}}}{left( {1 + omega } ight)^p}cos left( {frac{{p{text{π }}}}{2}} ight) pm hfill & quad sqrt {frac{{{varepsilon ^2}}}{{4{omega ^2}}} - frac{1}{4}{{left( {1 + omega } ight)}^2}{{left[ {2zeta + frac{{{K_1}}}{{{2^{p - 1}}}}{{left( {1 + omega } ight)}^{p - 1}}sin left( {frac{{p{text{π }}}}{2}} ight)} ight]}^2}} + hfill & quad Oleft( {{varepsilon ^3}} ight) hfill end{split} $$

(33)

${delta _0} = dfrac{1}{4}{left( {1 - omega }
ight)^2}$(即$alpha = 1,beta = - 1$)时方程的过渡曲线为

$$ begin{split} & delta = frac{1}{4}{left( {1 - omega } ight)^2} + {varepsilon ^2}left[ { - frac{1}{{2omega }} - frac{1}{{4left( {2 - omega } ight)}} - frac{1}{{4omega left( {2omega - 1} ight)}}} ight] - hfill &quad frac{{{K_1}}}{{{2^p}}}{left( {1 - omega } ight)^p}cos left( {frac{{p{text{π }}}}{2}} ight) pm hfill & quad sqrt {frac{{{varepsilon ^2}}}{{4{omega ^2}}} - frac{1}{4}{{left( {1 - omega } ight)}^2}{{left[ {2zeta + frac{{{K_1}}}{{{2^{p - 1}}}}{{left( {1 - omega } ight)}^{p - 1}}sin left( {frac{{p{text{π }}}}{2}} ight)} ight]}^2}} + hfill &quad Oleft( {{varepsilon ^3}} ight) hfill end{split} $$

(34)

1.2
方程过渡曲线分析

选取一组参数$ zeta = 0.005 $, $ {K_1} = 0.005 $, $ p = 0.5 $, $ varepsilon = $$ 0.1 $, 利用式(20)和式(31) ~ 式(34)并略去式中高阶部分绘制解析结果的过渡曲线如图1所示.



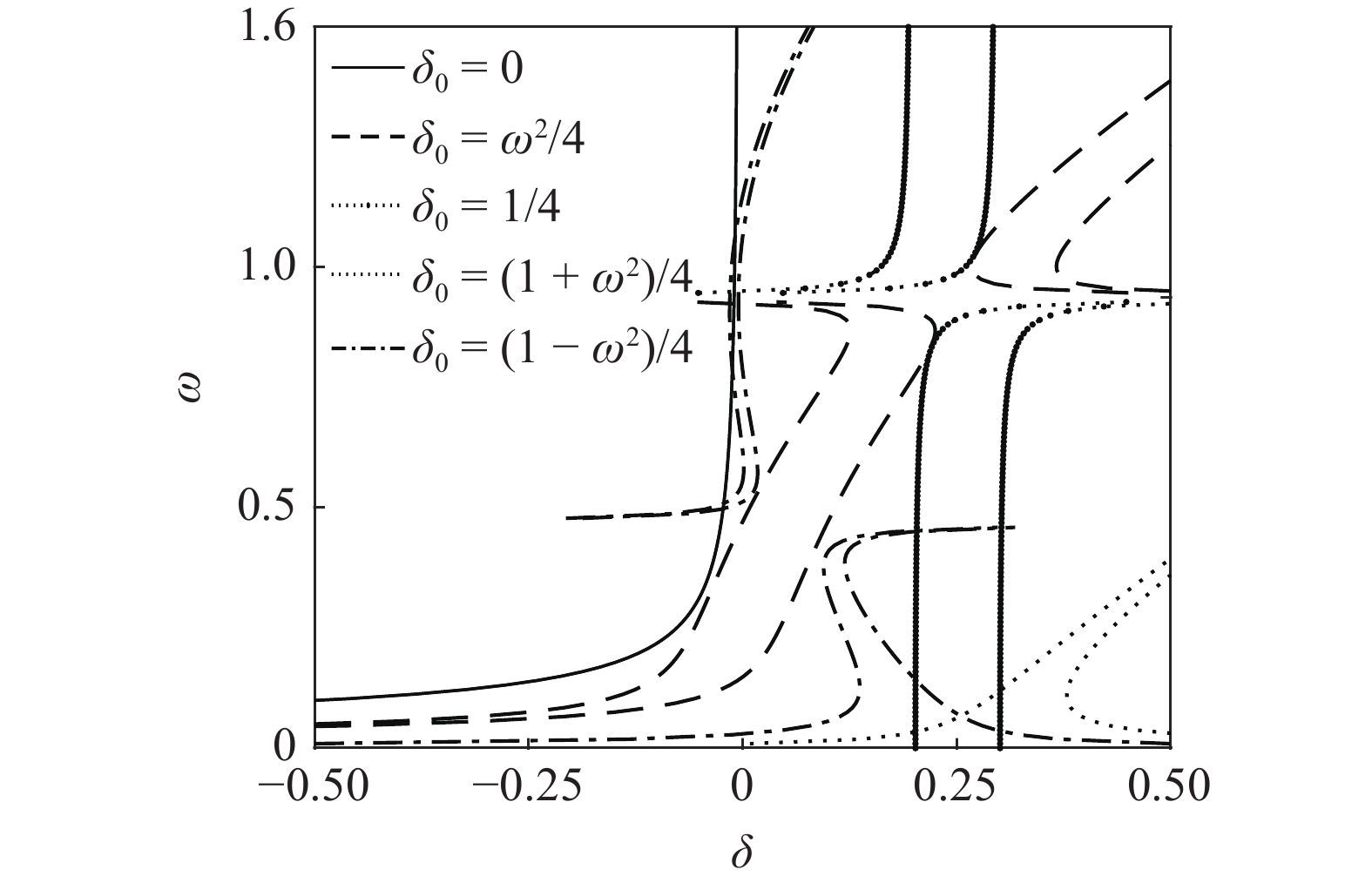onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-455-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
分数阶拟周期Mathieu方程的过渡曲线



Figure
1.
Transition curves of QP Mathieu equation with fractional-order derivative



下载:
全尺寸图片
幻灯片


对比不含分数阶微分项的Mathieu系统^[31-32], 通过定义等效线性阻尼$C(p)$和等效线性刚度$K(p)$的方法来分析分数阶微分项对拟周期Mathieu方程过渡曲线的影响. $ {delta _0} $在各情况下的等效线性阻尼和等效线性刚度如表1所示.




表
1
$ {delta _0} $在不同情况下的等效线性阻尼和等效线性刚度



Table
1.
Equivalent linear damping and equivalent linear stiffness of different $ {delta _0} $



table_type2 ">

	$ {delta _0} = 0 $	$ {delta _0} = dfrac{1}{4}{omega ^2} $	$ {delta _0} = dfrac{1}{4} $	$ {delta _0} = dfrac{1}{4}{left( {1 + omega } ight)^2} $	$ {delta _0} = dfrac{1}{4}{left( {1 - omega } ight)^2} $
$C(p)$	?	$ 2zeta {kern 1 pt} + dfrac{{{K_1}}}{{{2^{p - 1}}}}{omega ^{p - 1}}sin left( {dfrac{{p{text{π }}}}{2}} ight) $	$ 2zeta + {K_1}dfrac{1}{{{2^{p - 1}}}}sin left( {dfrac{{p{text{π }}}}{2}} ight) $	$ 2zeta + dfrac{{{K_1}}}{{{2^{p - 1}}}}{left( {1 + omega } ight)^{p - 1}}sin left( {dfrac{{p{text{π }}}}{2}} ight) $	$ 2zeta + dfrac{{{K_1}}}{{{2^{p - 1}}}}{left( {1 - omega } ight)^{p - 1}}sin left( {dfrac{{p{text{π }}}}{2}} ight); $
$K(p)$	$ delta + {varepsilon ^2}dfrac{{{K_1}left( {{omega ^4} + {omega ^p}} ight)}}{{2{omega ^4}}}cos left( {dfrac{{p{text{π }}}}{2}} ight) $	$ delta + dfrac{{{K_1}}}{{{2^p}}}{omega ^p}cos left( {dfrac{{p{text{π }}}}{2}} ight) $	$ delta + dfrac{{{K_1}}}{{{2^p}}}cos left( {dfrac{{p{text{π }}}}{2}} ight) $	$ delta + dfrac{{{K_1}}}{{{2^p}}}{left( {1 + omega } ight)^p}cos left( {dfrac{{p{text{π }}}}{2}} ight) $	$ delta + dfrac{{{K_1}}}{{{2^p}}}{left( {1 - omega } ight)^p}cos left( {dfrac{{p{text{π }}}}{2}} ight) $

下载:
导出CSV
|显示表格



通过表1, 得到方程等效阻尼和等效刚度的一般形式

$$ C(p) = 2zeta + {(sqrt {{delta _0}} )^{p - 1}}{K_1}sin left( {frac{{p{text{π }}}}{2}} ight);tag{35a} $$

$$ K(p) = delta + {(sqrt {{delta _0}} )^p}{K_1}cos left( {frac{{p{text{π }}}}{2}} ight) tag{35b}$$

分析上述5种情况下的结果可知, 在$ {delta _0} = 0 $时, 方程过渡曲线的二阶近似解与分数阶微分项无关, 分数阶微分项以等效线性阻尼和等效线性刚度的形式影响着过渡曲线的三阶近似解. 而在其他4种情况中, 分数阶微分项对方程二阶近似解均有影响, 并且它们的等效线性阻尼和等效线性刚度均可整理为一般形式(35). 通过分析式(35)发现, 分数阶微分项的系数${K_1}$和阶次$p$对方程过渡曲线有着重要影响: 当分数阶微分项系数$ {K_1} $逐渐增大时, 等效线性阻尼和等效线性刚度都会逐渐增大; 当分数阶阶次$ p $趋近于0时, 分数阶微分项几乎等于线性刚度; 而当$ p $趋近于1时, 分数阶微分项几乎等于线性阻尼.

另外, 通过对比式(31) ~ 式(34)发现方程过渡曲线表达式具有一定的相似性, 都是由$ {delta _0} $开始随着$ omega $的增大逐渐分裂成两条过渡曲线组成($ delta = {delta _0} + $$ E pm F $), 如方程在$ {delta _0} = dfrac{1}{4}{omega ^2} $时过渡曲线式(31). 根据这一特点, 可以定义此时两条过渡曲线之间的厚度(即非稳定区域厚度)为

$$ thickness approx 2sqrt {frac{{{varepsilon ^2}}}{4} - frac{{{omega ^2}}}{4}{{left[ {2zeta + {K_1}frac{1}{{{2^{p - 1}}}}{omega ^{p - 1}}sin left( {frac{{p{text{π }}}}{2}} ight)} ight]}^2}} $$

(36)

类似地, 在$ {delta _0} $为其他几种情况时也存在类似的式子来表示过渡曲线之间的厚度. 利用式(36)可以更加直观地显示分数阶微分项系数和阶次的变化对$ delta - omega $平面上非稳定性区域大小的影响.

2.
数值仿真

2.1
数值解和解析解的比较

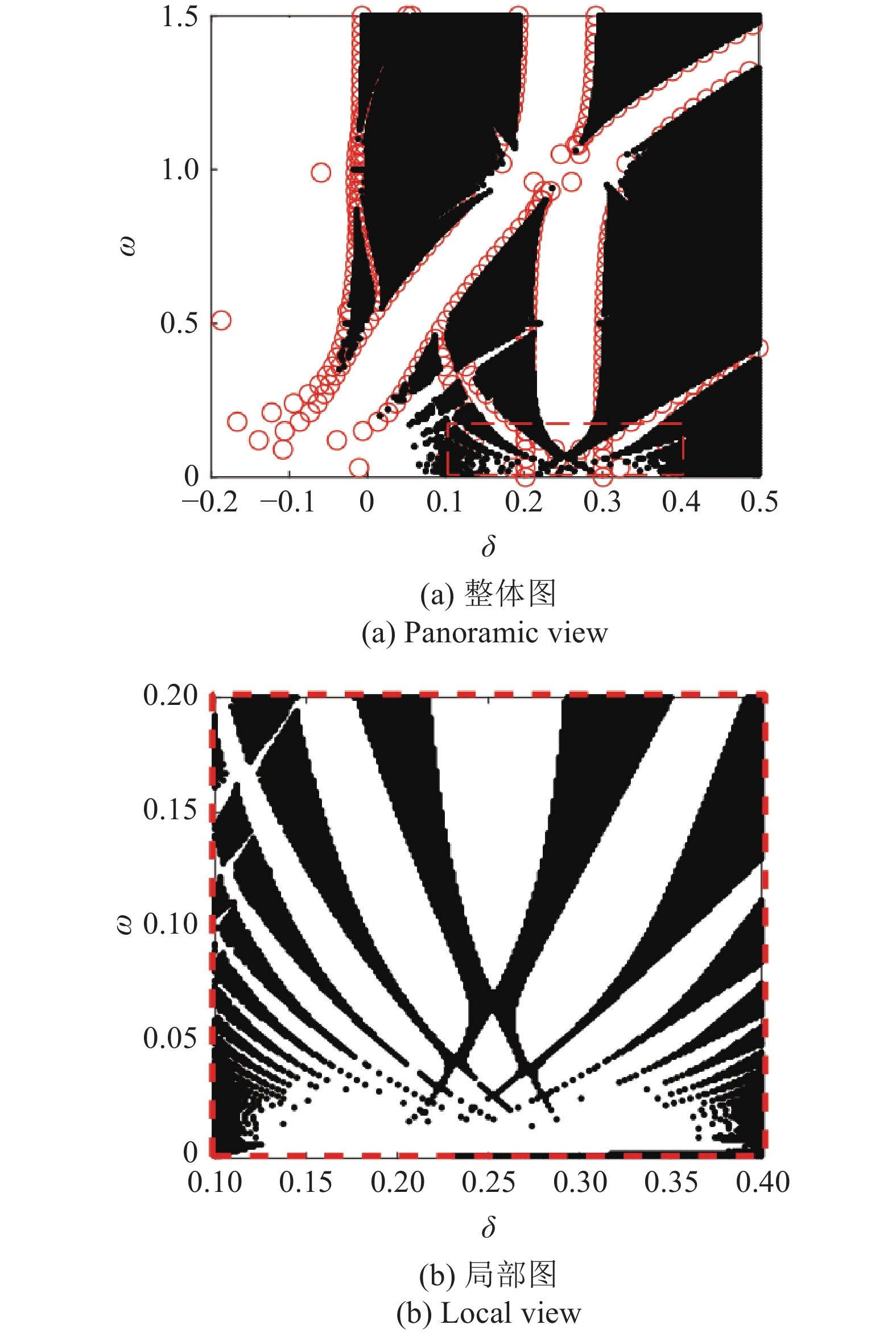
为了验证本文结果的正确性, 下面将上述过渡曲线的解析结果和数值结果进行对比. 利用文献[5]中介绍的数值方法研究方程(1), 该方法的近似公式为

$$ {{ m{D}}^p}u({t_l}) approx {h^{ - p}}sumlimits_{j = 0}^l {C_j^p} u({t_{l - j}}) $$

(37)

其中${t_l} = lh$为时间采样点, $h$为时间步长, $C_j^p$为分数阶二项式系数, 具有以下迭代关系

$$left. begin{array}{l} C_0^p = 1C_j^p = left( {1 - frac{{1 + p}}{j}} ight)C_{j - 1}^pend{array} ight} $$

(38)

将$ omega = 0 sim 1.5 $和$ delta = - 0.2 sim 0.5 $组成的$ delta - omega $平面内所有的点离散处理, 分别代入式(1)中对方程进行数值积分, 计算一段时间后根据方程响应的振幅变化情况判断各个参数点对应的稳定性, 以此来确定式(1)的稳定区和非稳定区分界线. 其中$ delta $选择间隔为0.002, $ omega $间隔为0.01, 计算时间为700 s, 计算步长选择0.001, 所得结果如图2所示. 仿真过程中参数取值为: $ zeta = 0.005 $, $ {K_1} = 0.005 $, $ p = 0.5 $, $ varepsilon = 0.1 $. 图中黑色的点代表数值解稳定点, 白色是非稳定区域, 白色和黑色的分界线是数值解的稳定性边界, 红圈代表方程过渡曲线的解析结果. 从图2中可以看到方程在$ {delta _0} = dfrac{1}{4}{omega ^2} $和$ {delta _0} = dfrac{1}{4} $附近形成了指状的非稳定区域, 且解析结果和数值结果的稳定性边界在主要区域吻合度较好, 证明了文中所述方法和结果具有较好的准确性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-455-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
数值解和解析解的方程过渡曲线



Figure
2.
Transition curves of numerical and analytical solutions



下载:
全尺寸图片
幻灯片

2.2
分数阶微分项对过渡曲线的影响

下面研究分数阶微分项参数对方程过渡曲线的影响. 首先选定参数$ varepsilon , {K}_{1} $和$zeta $, 当分数阶微分项阶次$p$分别选取0.1, 0.5和0.9时, 方程在$ {delta _0} = dfrac{1}{4}{omega ^2} $, $ {delta _0} = $$ dfrac{1}{4} $和$ {delta _0} = dfrac{1}{4}{(1 + omega )^2} $时的过渡曲线如图3所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-455-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
分数阶微分项阶次$ p $对过渡曲线的影响



Figure
3.
Effects of the fractional order$ p $on transition curves



下载:
全尺寸图片
幻灯片


从图3中可以看出, 当分数阶微分项阶次$ p $逐渐增大时, 由于等效线性刚度$K(p)$在逐渐减小, 因此方程的过渡曲线在向右移动; 同时, 等效线性阻尼$C(p)$在逐渐增大, 方程的非稳定区域在逐渐缩小. 说明分数阶阶次$p$不仅影响方程过渡曲线的位置, 而且还影响方程稳定区域的大小.

为了更好地区别分数阶微分项的阻尼和刚度特性, 分别取分数阶微分项阶次$p = 0.1,$$p = 0.5$和$p = $$ 0.9$, 观察不同阶次对方程过渡曲线的影响$ (varepsilon =0.1, $$ zeta = $$ 0.005,) $, 所得结果如图4 ~ 图6所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-455-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
$p = 0.1$时分数阶微分项系数${K_1}$对过渡曲线的影响



Figure
4.
Effects of the fractional coefficient$ {K_1} $on transition curves when$p = 0.1$



下载:
全尺寸图片
幻灯片


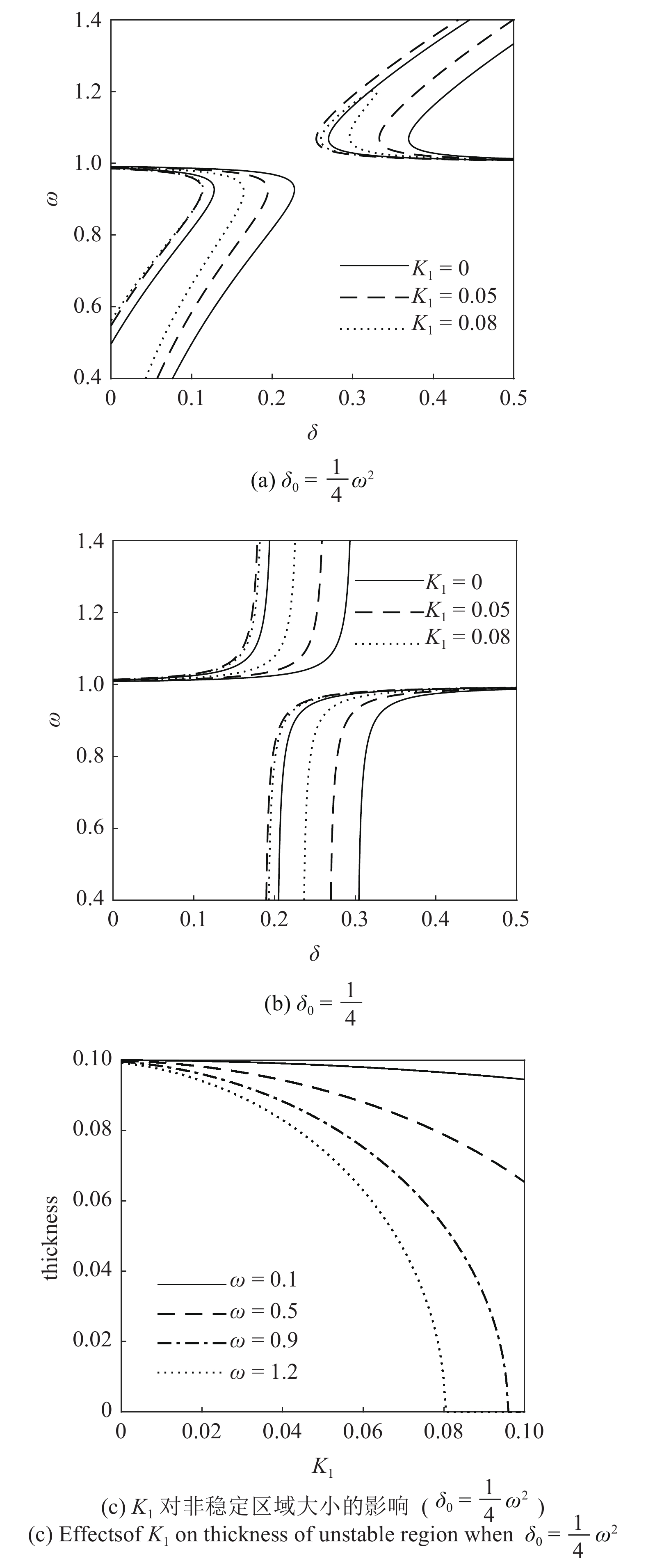
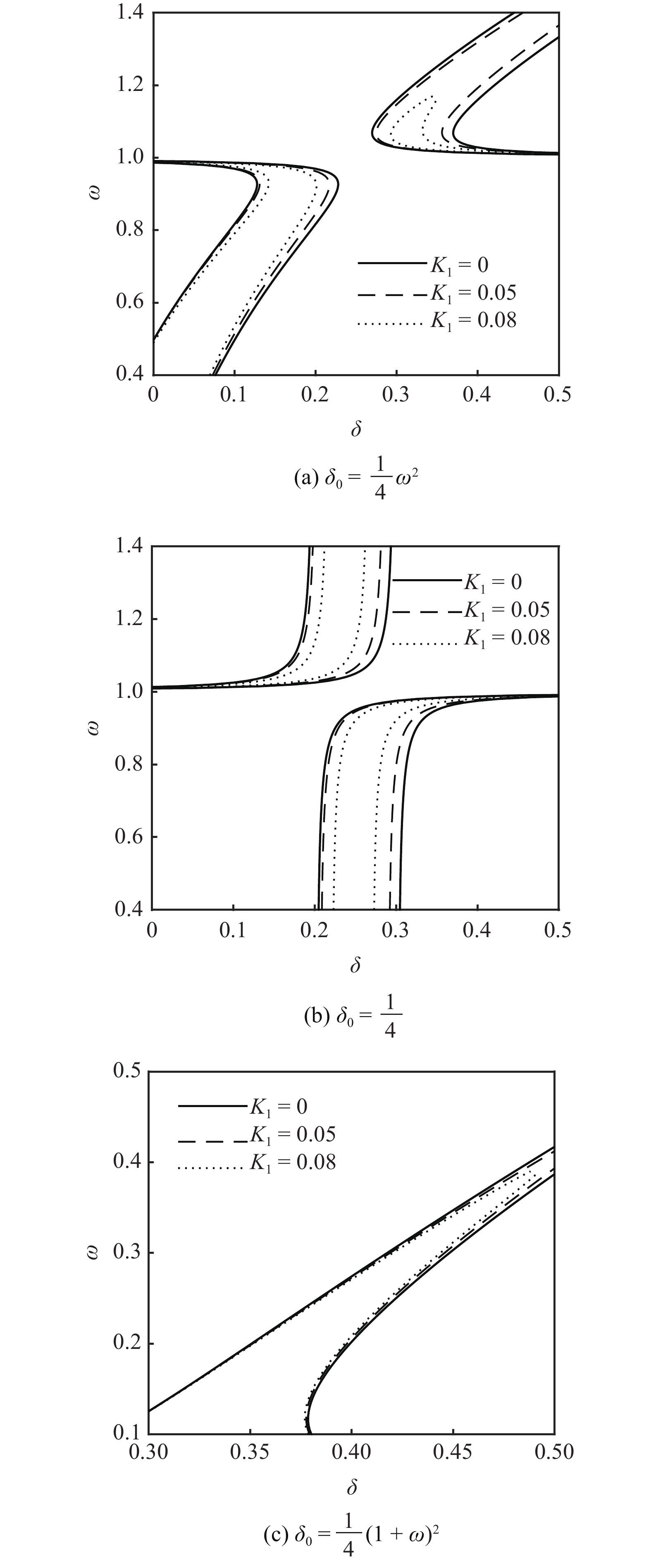
图4中给出了$p = 0.1$时方程过渡曲线随系数$ {K_1} $的变化情况. 可以发现, 当${K_1}$逐渐增大时, 由于等效线性刚度也在逐渐增大, 因此方程过渡曲线的位置发生了明显的左偏移; 但此时等效线性阻尼变化较小, 所以非稳定区域的面积未出现明显收缩. 说明$p = 0.1$时分数阶微分项呈现出较强的刚度特性, 而阻尼特性相对较弱.

当分数阶微分项阶次$p = 0.5$时, 如图5(a)和图5(b)显示, 随着分数阶微分项系数${K_1}$的逐渐增大, 此时等效线性刚度和等效线性阻尼都在增大, 方程过渡曲线不仅逐渐向左偏移, 同时曲线之间的厚度也在逐渐缩小. 利用式(36)观察${delta _0} = dfrac{1}{4}{omega ^2}$时非稳定区厚度随系数${K_1}$的变化情况, 从图5(c)看出, 随着系数${K_1}$的逐渐增大, 方程非稳定区面积在逐渐缩小, 并且当系数${K_1}$增大到一定程度, 发生了局部非稳定区域消失的现象. 说明当$p = 0.5$时, 分数阶微分项不仅具有明显的刚度特性还具有明显的阻尼特性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-455-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
$p = 0.5$时分数阶微分项系数对过渡曲线的影响



Figure
5.
Effects of the fractional coefficient on transition curves when$p = 0.5$



下载:
全尺寸图片
幻灯片


在图6中分析$p = 0.9$时不同分数阶微分项系数${K_1}$对过渡曲线的影响. 此外, 为了便于比较, 给出了$ p = $$ 0.5, {K}_{1}=0.001 $时线性阻尼系数$zeta $对方程过渡曲线的影响情况, 如图7所示. 由图6和图7可知, 随着系数$ {K_1} $和$zeta $逐渐增大, 方程的非稳定区域都发生了明显的收缩, 说明此时分数阶微分项呈现出较强的阻尼特性, 系数$ {K_1} $对系统的作用与线性阻尼系数$zeta $几乎相同.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-455-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
$p = 0.9$时分数阶微分项系数${K_1}$对过渡曲线的影响



Figure
6.
Effects of the fractional coefficient${K_1}$on transition curves when$p = 0.9$



下载:
全尺寸图片
幻灯片




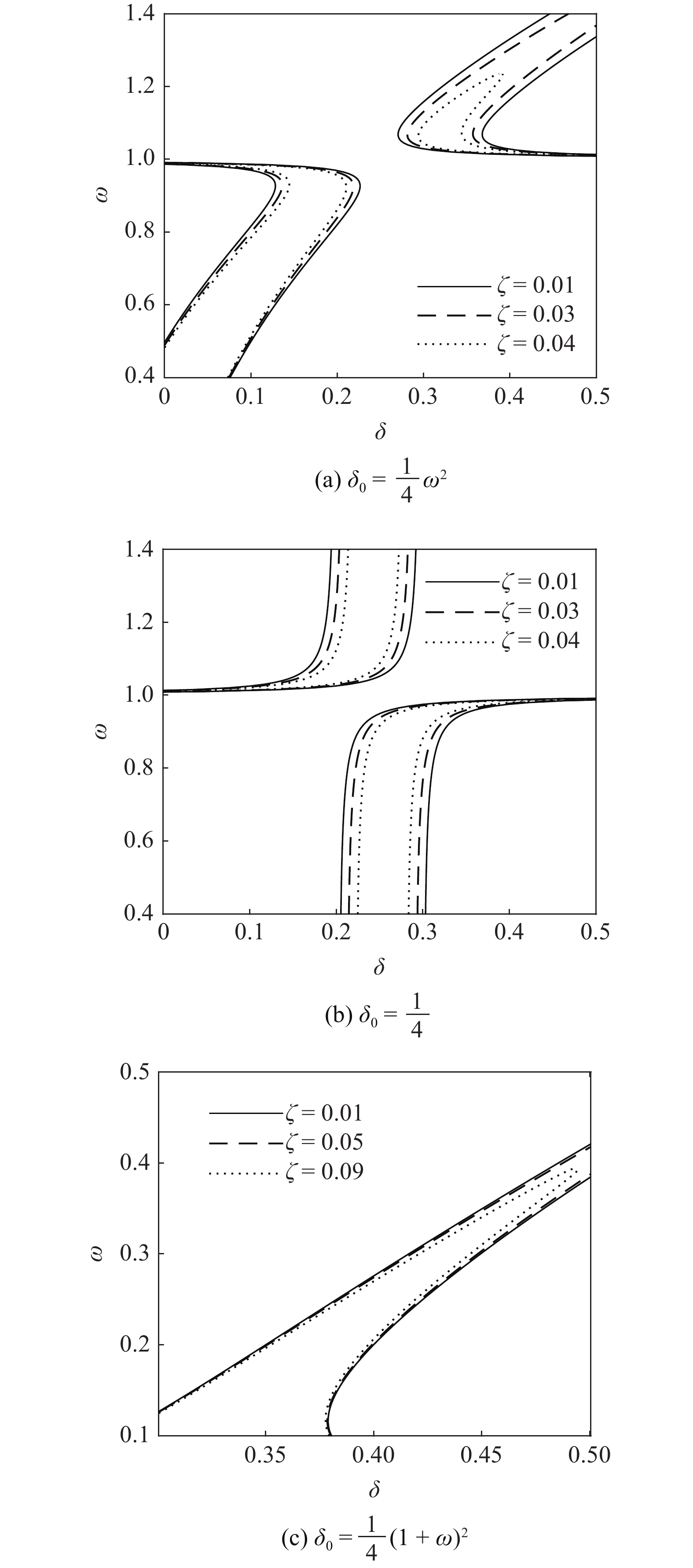onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-455-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
线性阻尼系数$zeta $对过渡曲线的影响



Figure
7.
The evolutions of the transition curves due to the change of$zeta $



下载:
全尺寸图片
幻灯片

3.
结 论

应用摄动法研究了分数阶拟周期Mathieu方程, 得到了方程在$delta - omega $平面内过渡曲线的近似表达式. 借助等效线性刚度和等效线性阻尼概念, 分别分析了不同分数阶微分项系数和阶次对方程过渡曲线的影响. 结果发现, 分数阶微分项同时具有刚度特性和阻尼特性, 选取不同的分数阶微分项阶次和系数可以使其呈现不同程度的刚度特性或阻尼特性, 方程稳定区域的大小和过渡曲线的位置也因此产生了不同程度的变化. 以上结果说明分数阶微分项对拟周期Mathieu方程的稳定特性有着重要的影响, 对此类系统的分析和稳定状态参数的选取有着重要的意义.