引 言

多次透射公式(multi-transmitting formula, MTF)是由廖振鹏等^[1-2]提出的一种基于离散参考点表示的局部人工边界条件^[3-4], 具有普适性、易实施和精度可控等优点. 近年来, MTF被广泛地应用于复杂地形场地^[5-7]、多种介质场地^[8-10]和大型结构^[11]的地震反应分析. 还有研究表明^[12-15], MTF与Clayton-Engquist边界^[16]和Higdon边界^[17]具有一定的包含关系, 并被应用于具有高精度特性的谱元法^[18-20]中. 高频振荡失稳^[21-23]和飘移失稳^[24-35]是MTF可能会出现的两种失稳现象, 本文将研究后者.

对飘移失稳的机理解释主要有两种: 一种观点^[24]认为将MTF与有限元法结合后, 用离散模型拟合连续介质产生的波场误差引发了失稳, 且失稳导致数值解将以$ {p^{N - 1}} $的形式增长^[24-25], 这里$ p $为计算步数, $ N $为MTF阶次; 另一种观点^[26-28]认为零频和零波数的MTF情形违背了用于判断双曲型微分方程初边值稳定性的GKS准则, 零频和零波数成分不断地从边界处进入波场从而产生了误差的累积.

基于第1种解释, 李小军等发展了实时降阶法^[24]和数值输入法^[29]等消飘方法. 实时降阶法认为一阶MTF不会发生失稳, 高阶MTF则可能发生失稳. 在应用高阶MTF的过程中, 通过判断失稳现象的发生将高阶MTF降为一阶MTF, 然后再适时调回高阶. 因此, 实时降阶法需要不断地进行失稳判断. 事实上, 杜修力等^[30]的研究表明一阶MTF也是可能发生失稳的, 只是在大多数情况下不易发生^[31]. 数值输入法则是建立边界计算区, 从而获得入射波离散数值解, 代替连续介质解析解作为波动的输入, 减少误差波场的产生. 基于第2种解释, 周正华和廖振鹏^[26]提出的主要消飘方法是对MTF添加消飘因子$ gamma $得到一种修正形式, 形式上表现为对MTF的各个时空外推节点项进行衰减. 该方法在物理概念上被理解为考虑了介质的几何扩散特性或增加了阻尼特征^[27]. 李小军和杨宇^[32]在MTF的基础上对边界附近的节点添加阻尼器或弹簧, 结合应力型人工边界来消除失稳, 本质上与添加消飘因子的方法类似. Zhang和Yu^[33]将一阶MTF与高阶MTF进行加权求和, 用来解决电磁波差分模拟中的高阶MTF飘移失稳问题. 在上述几种消飘方法中, 实时降阶法、数值输入法、附加黏弹性元件法和MTF加权求和法都增加了编程的复杂性, 并一定程度上降低了计算效率. 添加消飘因子的方法从形式上并没有过多地改变MTF的计算步骤, 非常容易实现. 然而添加消飘因子的方法对消飘因子$ gamma $的取值有较严苛的限制, 若$ gamma $取值太小, 消飘效果有限, 而当$ gamma $取值太大时, 则计算精度受到影响^[34]. 同时, MTF阶次越高, $ gamma $的取值也要求越大^[35]. 因此, 在对不同模型进行分析时, 传统的消飘因子添加方案需要根据经验不断地调试$ gamma $值, 难于掌握和使用. 值得注意的是, 消飘因子$ gamma $的存在必然会降低MTF的精度. 以一维波动问题为例, 当人工波速(MTF边界所使用的计算波速参数)取值等于视波速时, 除了离散舍入误差外, 一阶MTF本身不产生任何精度损失. 然而, 添加的消飘因子则先天性的对MTF进行了衰减, 使计算结果的幅值低于实际值. 由此导致的精度损失与$ gamma $取值的大小有关.

本文将采用消飘因子法的技术路径, 提出一种新的消飘因子修正MTF方案, 用于控制多次透射公式的飘移问题.该方法仅针对二阶及其以上各阶MTF的透射误差项进行修正, 而保持一次透射项不变, 从而在保有消飘因子法的消飘能力和高阶MTF适应不同人工波速能力的前提下提供了至少一阶MTF的精度保证. 在此基础上, 进一步将该方案推广至任意m阶MTF情形, 分别从反射系数和波动有限元数值算例的角度, 对基于不同$ gamma $取值的消飘方案的精度和消飘能力进行对比分析, 从而验证本文方法的可行性与适用性.

1.
MTF的小量修正形式

MTF是基于多次透射的概念建立起来的, 即假定所有外行波及其透射误差都是具有相同性质的外行单向波动, 它们都以相同的人工波速沿着法线方向从人工边界处透射出去. MTF的一般表达式写为

$$ u_0^{p + 1} = sumlimits_{j = 1}^N {{{left( { - 1} ight)}^{j + 1}}C_j^Nu_j^{p - j + 1}} $$

(1)

式中, N为透射阶次, $C_j^N$为二项式系数, $u_j^p$表示参考点j在t = p?t时刻的波场值, 由下式定义

$$ u_j^p = uleft( {pDelta t,; - j{c_a}Delta t} ight) $$

(2)

其中?t为时间步距, c_a为人工波速. 这里人工波速指的是MTF边界所使用的计算波速参数, 理论上它可以设定为任意值, 在实际计算中通常取为等于或略大于介质物理波速的某个值.

为了抑制MTF飘移失稳, 周正华和廖振鹏^{[26, 27]}提出了一种在MTF中直接添加带有几何扩散特性或阻尼特征的小量$ gamma $(本文称之为消飘因子)的措施, 即将MTF表达式(1)修正为如下形式

$$ u_0^{p + 1} = sumlimits_{j = 1}^N {{{left( { - 1} ight)}^{j + 1}}C_j^N cdot frac{{u_j^{p - j + 1}}}{{{{left( {1 + gamma } ight)}^j}}}} $$

(3)

这里消飘因子$ gamma $被规定为取值远小于1的正数, 因而其对有限元或有限差分模拟的波动分量只产生微小影响, 可以忽略不计^[2]. 本文中简称该措施为周?廖方案(Zhou-Liao’s method), 附录A给出了该方案在前4阶MTF情况下的具体表达式.

根据GKS准则, 添加消飘因子$ gamma $后的MTF防止了零频率和零波数的内行波进入计算区, 从而避免了边界节点的飘移失稳. 然而, 消飘因子$ gamma $的取值要求比较严格, 既不能过小亦不可太大: 若$ gamma $取值过小, 则抑制零频和零波数内行波穿过人工边界而进入计算域的效果不明显, 边界节点处位移依然可能会发生飘移失稳; 若$ gamma $取值较大, 由式(3)可知, 人工边界节点处的位移值将被大大压低, 这会严重地损失MTF模拟精度. 故$ gamma $值的确定需要平衡失稳抑制与精度损失这对矛盾, 具体实施时需要经过繁琐的试错和调试寻求比较合理的$ gamma $取值.

2.
MTF飘移失稳控制方案

一阶MTF不易发生飘移失稳现象, 但精度有限. 当人工波速偏离视波速越多, 其拟合波动的精度就越低. 此情形下可通过高阶MTF的方式提高模拟精度, 而高阶MTF通常又会带来失稳问题. 通过在MTF上添加小量的消飘因子能够有效地抑制MTF的飘移失稳, 从而保持人工波速与视波速不一致情况下使用高阶MTF时的稳定性. 观察式(3)可以发现, 这种消飘因子添加方案必然会降低所有阶次MTF的模拟精度, 如果控制不好将导致应用MTF模拟波动问题时失真.

事实上, 高阶MTF是对误差波再次实施透射的结果, 故仅针对误差波自身进行调整即可实现抑制失稳的目标, 从而将MTF精度损失尽可能控制在较小范围内. 考虑将一阶MTF表达为如下形式

$$ nabla u_0^{p + 1} = u_0^{p + 1} - u_1^p = 0 $$

(4)

如果定义

$$ {nabla ^N}u_0^{p + 1} = {nabla ^{(N - 1)}}u_0^{p + 1} - {nabla ^{(N - 1)}}u_1^p,quad {N geqslant 2} $$

(5)

则N阶MTF可以统一地写为

$$ {nabla ^N}u_0^{p + 1} = 0 $$

(6)

为实现抑制飘移失稳的目的, 将式(5)改写为

$$ {nabla ^N}u_0^{p + 1} = {nabla ^{(N - 1)}}u_0^{p + 1} - frac{{{nabla ^{(N - 1)}}u_1^p}}{{1 + gamma }},quad {N geqslant 2} $$

(7)

将式(7)代入式(6), 即得到MTF飘移失稳控制方案. 显然, 按照这种控制方案, 经过修正的前3阶MTF表示为

$$ u_0^{p + 1} = u_1^p,quad {N = 1} tag{8a}$$

$$ u_0^{p + 1} = u_1^p + frac{{nabla u_1^p}}{{1 + gamma }},quad {N = 2} tag{8b}$$

$$ u_0^{p + 1} = u_1^p + frac{{2nabla u_1^p}}{{1 + gamma }} - frac{{nabla u_2^{p - 1}}}{{{{left( {1 + gamma } ight)}^2}}},quad {N = 3} tag{8c} $$

如此修正MTF所形成的消飘方案是基于一阶MTF不易失稳这一前提. 容易发现, 该方案仅对透射误差项进行了衰减处理, 而一阶透射项保持不变, 因而至少能够保留一阶MTF的精度. 当N = 1时, 该方法实际上即转变为一阶MTF.

3.
反射系数

下面通过人工边界反射系数分析消飘因子$ gamma $对修正MTF精度的影响. 不失一般性, 这里使用文献[1]第4.2.3节所定义的反射系数. 令c_a = c (这里c代表物理波速), 当输入波为理想暂态波时, 一阶MTF的反射系数写为

$$ {R_0} = left| {1 - exp left[ {{ m{i}} cdot frac{{2{text{π}} Delta t}}{T}left( {cos theta - 1} ight)} ight]} ight| $$

(9)

式中, θ为入射平面波与人工边界法线的夹角, T为平面谐波的周期.

若定义

$$ R_f^N = {left| {1 - dfrac{{exp left[ {{ m{i}} cdot dfrac{{2{text{π}} Delta t}}{T}left( {cos theta - 1} ight)} ight]}}{{1 + gamma }}} ight|^N} $$

(10)

则按照本文方法, MTF反射系数可表达为

$$ R = {R_0} cdot R_f^{N - 1} $$

(11)

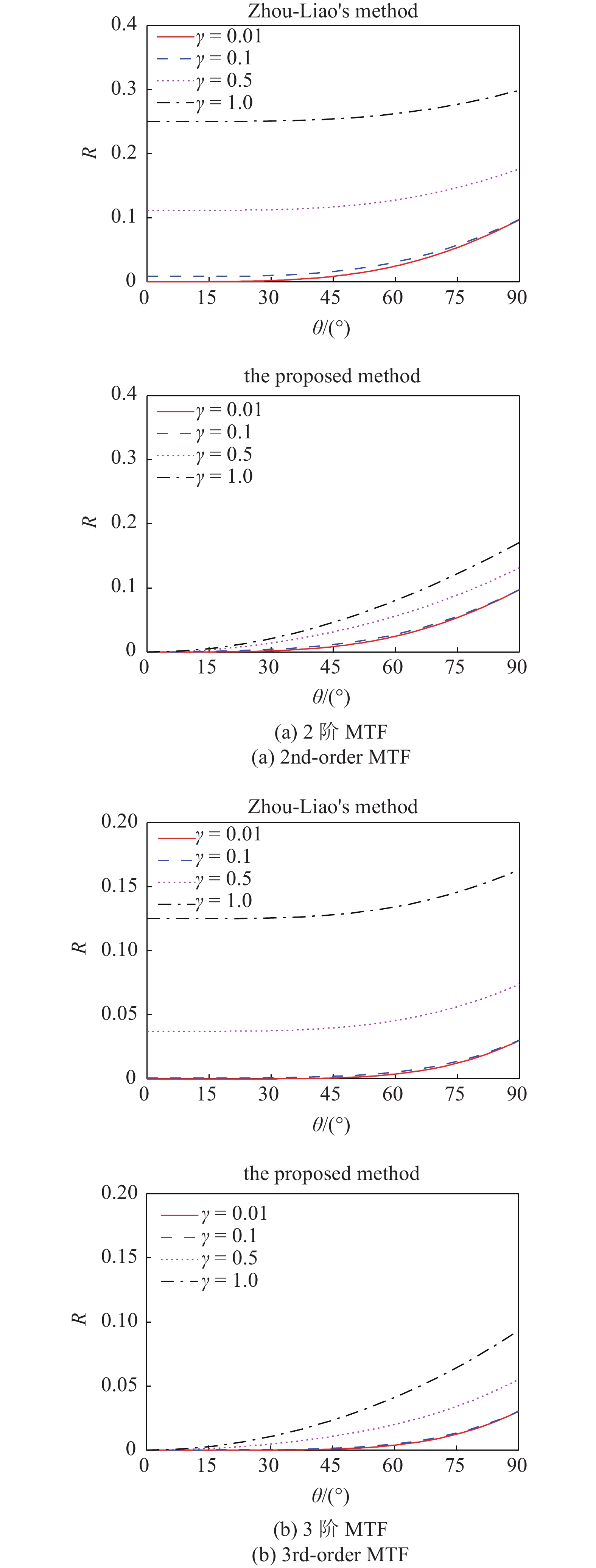
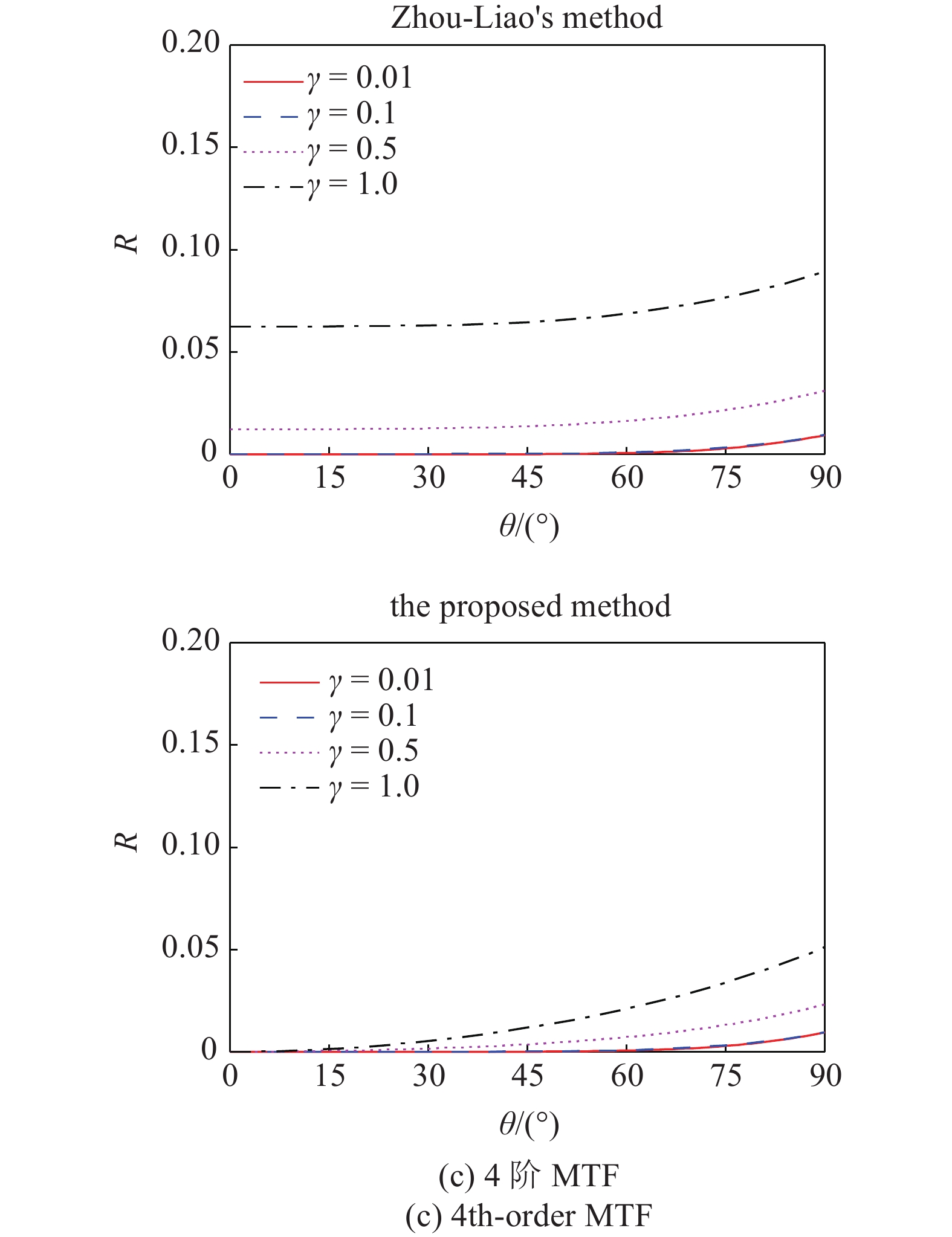
事实上, 式(10)给出的就是周?廖方案的边界反射系数表达式^[2]. 显然, 若取N = 1, 本文方法给出的MTF反射系数(见式(11))退化为式(9), 即一阶MTF反射系数, 这与本文方法在N = 1条件下即为一阶MTF的结论一致. 而形如式(10)的周?廖方案的MTF反射系数则不同, 为了比较, 图1示出了周?廖方案和本文方案在人工边界处的反射系数, 从中可以看出消飘因子$ gamma $对不同阶次MTF反射系数的影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-1-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1-1" />



1
边界反射系数比较(Δt/T = 1/20)



1.
Comparison of boundary reflection coefficients with respect to different $ gamma $ (Δt/T = 1/20)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
边界反射系数比较(Δt/T = 1/20) (续)



Figure
1.
Comparison of boundary reflection coefficients with respect to different $ gamma $ (Δt/T = 1/20) (continued)



下载:
全尺寸图片
幻灯片


分别比较图1(a)、图1(b)和图1(c), 可以发现, MTF阶次相同时, 本文方法的边界反射系数都明显低于周?廖方案的反射系数. 在入射角为0的情形下本文方法的反射系数保持为0, 而周?廖方案无法达到零反射系数. 从图1中还可知, 在本文方法中, 消飘因子$ gamma $取值增大时主要对中等和大角度透射波动的模拟精度造成影响, 而对波动能量比较集中的法向和小角度透射范围影响很小. 周?廖方案和本文方法的边界反射系数均随着消飘因子$ gamma $取值单调增大, 在$ gamma $取值较小时两种方案的反射系数差别很小, 但当$ gamma $取值较大时本文方法的反射系数明显要小得多. 因此, 本文方法能够适应更大的消飘因子取值范围(如1.0以内的正数)

由此可见, 对于引入$ gamma $带来的精度损失本文方法比周?廖方案要小. 比较同一种方案中的不同阶次MTF情况, 容易发现MTF的阶次越高则反射系数越低, 这符合高阶MTF的精度比低阶MTF精度高的特性.

下面从反射系数公式的角度来阐释本文方法反射系数低的原因. 一阶MTF方案、周?廖方案和本文方法的边界反射系数分别按照式(9)、式(10)和式(11)进行计算. 若分别以R₁, R₂和R₃表示θ = 0情形下上述3种方案的反射系数, 则有

$$ {R_1} = 0 $$

(12)

$$ {R_2} = {left| {frac{gamma }{{1 + gamma }}} ight|^N} $$

(13)

$$ {R_3} = 0 qquad$$

(14)

由于消飘因子$ gamma $为小值正数, 周?廖方案的反射系数R₂必定大于0, 即周?廖方案必定导致一定的精度损失. 由式(13)不难发现, 消飘因子$ gamma $取值越大, 周?廖方案的反射系数亦越大. 而一阶MTF方案则不受$ gamma $的影响, 在该情形下的反射系数R₁恒为0.本文方法建立在一阶MTF的基础上, 故该情形下的反射系数R₃同样恒为0, 即不会因为消飘因子$ gamma $的引入而产生精度损失.

当θ逐渐增大时, 人工波速c_a与边界上实际波 速的差值越大, MTF的精度越低, 反射系数也越大(见图1). 此时, 消飘因子$ gamma $取值越大, 周?廖方案和本文方案的反射系数整体上都有变大的趋势, 但本文方案的增长趋势较小, 而周?廖方案的增长趋势则十分显著. 这也是引入消飘因子$ gamma $后对本文方案的精度影响低于传统方案的原因.

值得指出, MTF在实际波动模拟中可以采用不同的插值方案^{[1,12,21,31,36]}来实现. Wang和Tang^[36]研究了MTF一种简洁直观的线性内插方案, 提出利用Taylor展开导出与之等效的微分方程形式, 进而导出理论反射系数的分析方法. 他们发现此时人工波速c_a的最优取值与介质物理波速c有所不同, 这表明插值方案对MTF的反射系数有重要影响. 廖振鹏^[1,21]以及邢浩洁等^[12,31]对这个问题亦做过一定探讨. 显然, 本文所提出的消飘因子修正MTF可以结合不同的插值方案对其反射系数进行进一步理论分析, 不过, 具体插值方案并不影响本文方法的适用性, 限于篇幅, 本文对此不做展开论述.

4.
数值算例

反射系数分析从解析解的角度客观地评估了各参数对计算精度的影响. 然而, 考虑到实际波场构成的复杂性以及有限元与人工边界相结合的特性, 对相关数值模型进行时域分析是必要的.

下面分别以初始波场输入的二维波源模型和平面波输入的二维散射模型为例, 检验本文方法的可靠性. 为便于分析比较, 输入波的类型皆为SH波. 将前述MTF人工边界方案施加到对应场地的有限元离散模型中, 并通过集中质量的显式时域有限元法^[1]计算出各种方案的波场值. 在本文数值算例中, MTF时空外推节点的位移由有限元节点位移用三点内插方法得到^[26], 详见附录B. 所有数值计算皆通过自编程序完成.

4.1
波源问题

图2为二维均匀介质模型, 分为半空间模型$ {varOmega _2} $和全空间模型$ {varOmega _3} $. 半空间模型$ {varOmega _2} $的左侧为前述各种方案对应的人工边界, 其余三侧为自由边界. 全空间模型$ {varOmega _3} $四边皆为自由边界. 图中, $ {varOmega _1} $为计算分析区域, 五角星位置为初始波场的中心位置, 圆点A(0, 0)为测点位置. 设定介质的物理波速为c = 1, 计算时间为2, 这将确保在计算时间内自由边界的反射波不会返回到分析区域$ {varOmega _1} $.

以初始波场输入的波源问题作为研究对象, 设定以(0.5, 0)为圆心, 半径为0.45的圆形扩散波场作为初始波场. 其表达式如下

$$ uleft( {0,;x,;y} ight) = exp left( { - 30{r^2}} ight),quad r leqslant 0.45 $$

(15)

式中, ${r^2} = {left( {x - 0.5}
ight)^2} + {y^2}$.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
二维波源问题模型



Figure
2.
Two-dimensional?model?of?wave?sourceproblem



下载:
全尺寸图片
幻灯片


由文献[13]可知, 圆形扩散波场的最短波长成分约为0.25. 为满足网格尺寸选取要求和时域积分稳定性条件, x和y方向的有限单元尺寸取为0.025, 时步长度取为0.01. 为便于进行二维波场的误差分析, 通过计算误差波场的弗罗贝尼乌斯(Frobenius)范数, 引入最大误差波场比值$Error({boldsymbol{U}})$的定义, 计算公式如下

$$ Error({boldsymbol{U}}) = frac{{max {{left( {sqrt {displaystylesumlimits_i {displaystylesumlimits_j {{{left| {left. {{{boldsymbol{U}}_{ij}}} ight|_{{varOmega _1}}^{{varOmega _2}} - left. {{{boldsymbol{U}}_{ij}}} ight|_{{varOmega _1}}^{{varOmega _3}}} ight|}^2}} } } } ight)}_{t = 2.0}}{kern 1pt} }}{{{{left( {sqrt {displaystylesumlimits_i {displaystylesumlimits_j {{{left| {left. {{{boldsymbol{U}}_{ij}}} ight|_{{varOmega _1}}^{{varOmega _3}}} ight|}^2}} } } } ight)}_{t = 0}}}} $$

(16)

式中, U为各个时刻波动位移的矩阵形式, i和j表示计算域内所有节点的编号和位移分量. 下标$ {varOmega _1} $表示计算节点的选取区域. 上标$ {varOmega _2} $和$ {varOmega _3} $分别表示计算对应的半空间模型和全空间模型. t为计算对应的时刻或时间范围. 误差波场为半空间模型$ {varOmega _2} $中计算域$ {varOmega _1} $的数值解减去全空间模型$ {varOmega _3} $中计算域$ {varOmega _1} $的精确解(即不受边界影响的大区域数值解), 可表示为$ Delta {varOmega _1} $.

经过大量的数值模拟发现, 当MTF为3阶时, 上述模型的边界节点发生了飘移现象. 针对3阶MTF的飘移失稳, 分别使用周?廖方法和本文方法对MTF人工边界进行修正. 图3为不同方案的人工边界情况下区域$ {varOmega _1} $的位移全波场快照和误差波场快照. 这里的人工波速取为物理波速(c_a = c). 其中, 图3(a)为未被修正过的3阶MTF人工边界, 图3(b)和图3(c)、图3(d)和图3(e)分别为消飘因子$gamma = 0.01$和$gamma = 0.1$时的周?廖方法与本文方法. 全波场($ {varOmega _1} $)快照的颜色标尺范围较大, 主要反应了波的传播过程. 误差波场($ Delta {varOmega _1} $)快照的颜色标尺范围较小, 便于比较不同方案的消飘效果和精度. 图4为上述不同方法情况下, 人工边界处测点A的位移时程图(测点A位移用u表示).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
不同方法情况下的全波场快照和误差波场快照 (c_a = c)



Figure
3.
Snapshots of full-field wave propagation and the error by using different methods (c_a = c)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同方法情况下测点A的位移



Figure
4.
Displacement at point A by using different methods



下载:
全尺寸图片
幻灯片


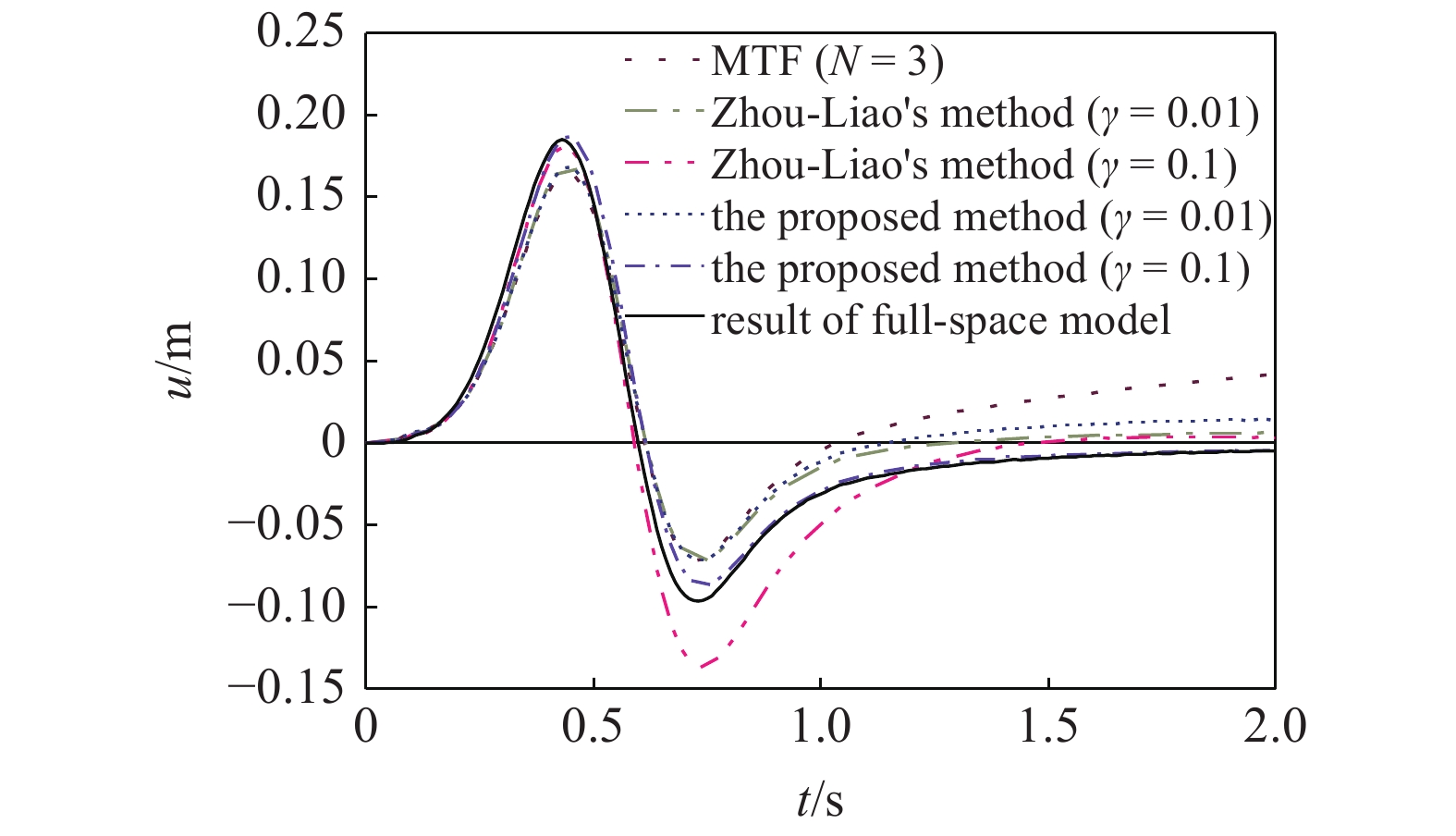
从图3和图4中不难看出, 3阶MTF情况下的波场位移从人工边界处测点A附近发生飘移; 不同的MTF修正方法都一定程度上消除了飘移失稳的趋势. 比较图3(b)~图3(d)中的全波场快照, 可以发现消飘因子$ gamma $越大, 两种MTF修正方法的消飘效果越好. 而比较图3中的误差波场和图4中t = 0.5~2.0之间的位移时程, 可以发现消飘因子$ gamma = 0.1 $时的本文方法在所有方案中最接近全空间模型的精确解. 此外, 当$ gamma = 0.1 $时, 周?廖方法下的测点A位移虽然在波峰处接近精确解, 但在波谷处比其他方案都远离精确解.

为了具体比较消飘因子$ gamma $对周?廖方法和本文方法精度的影响, 用式(16)中定义的最大误差波场比值$ Error({boldsymbol{U}}) $作为参考标准. 图5给出了不同人工波速情况下, 消飘因子$ gamma $对一阶MTF、3阶MTF、周?廖方法与本文方法波场精度的影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
人工波速对波场精度的影响



Figure
5.
The effect of artificial wave velocity on the accuracy of the wave field



下载:
全尺寸图片
幻灯片


当c_a = 0.5c时, 虽然3阶MTF在该情况下已经出现了飘移失稳的迹象, 但飘移趋势相对比较缓慢, 在计算时间内3阶MTF的最大误差波场比值小于一阶MTF, 表明3阶MTF的精度要高于一阶MTF; 当c_a ≥ c时, 3阶MTF受到飘移失稳的影响, 其最大误差波场比值大于一阶MTF, 即3阶MTF的精度反而低于一阶MTF. 由于周?廖方法与本文方法建立在3阶MTF的基础上, 当消飘因子$ gamma $极小时, 两种方案的精度与3阶MTF接近, 随着消飘因子的变大, 周?廖方法和本文方法的精度都得到提升. 当c_a ≤ 2c时, 两种MTF修正方法的测点位移值会随时间而逐步收敛为0, 解决了3阶MTF本身飘移失稳的问题. 当消飘因子$ gamma $增长到一定值时, 两种MTF修正方法的最大误差波场比值随$ gamma $的增长而变大. 其中, 周?廖方法的最大误差波场比值最终收敛至0.4左右, 而本文方法的最大误差波场比值则收敛为一阶MTF对应的值. 当c_a = 3c时, 3阶MTF方案、周?廖方法和本文方法都发生了较大的失稳, 只有当消飘因子$ gamma $接近1.0时, 两种MTF修正方法才可能收敛. 根据图5, 在不同的消飘因子和人工波速情况下, 本文方法的计算精度整体上要比周?廖方法高, 这一点与反射系数的分析结果一致.

4.2
散射问题

与波源问题不同, 散射问题需要考虑波场的输入问题. 同时, 散射问题需要将边界节点的全波场反应分解为入射波和散射波, 然后对散射波应用MTF人工边界, 使其离开不再回到计算域内.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
二维散射问题模型



Figure
6.
Two-dimensional?model?of?a?scatteringproblem



下载:
全尺寸图片
幻灯片


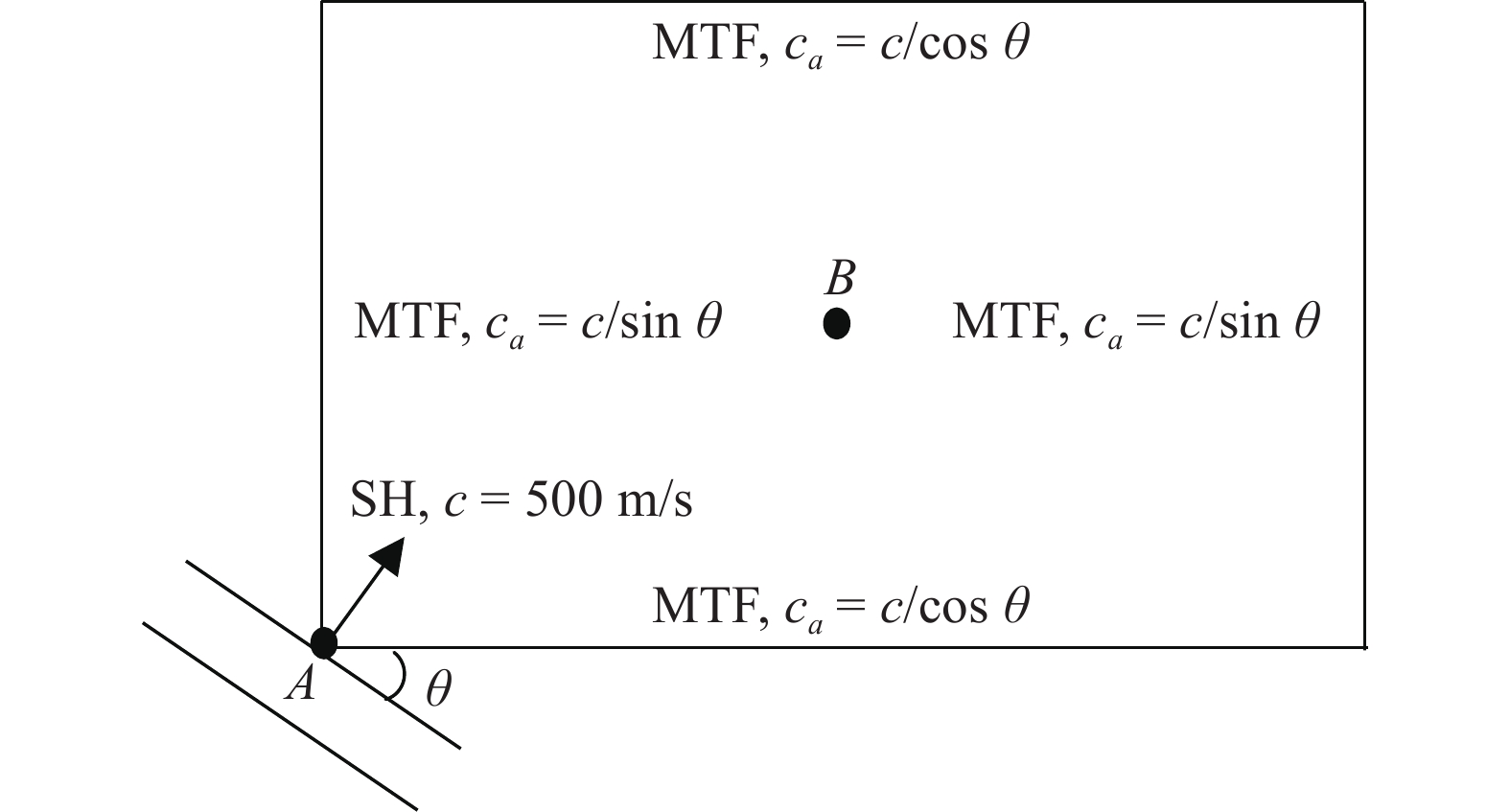
图6为SH平面波输入的散射问题模型. 模型为长300 m、宽150 m的矩形场地, 介质密度为ρ = 2500 kg?m^?3, 剪切波速为c = 500 m/s. 4个边界均为MTF人工边界, MTF的阶次为N = 4. 各个边界上MTF的人工波速取为对应边界的视波速. SH波从模型的左侧边界和底部边界斜入射进入波场, 入射角为θ = 30°. 入射波的波形为Ricker波, 中心频率取为f = 10 Hz^[15]. 有限单元网格的尺寸取为2 m, 时间步长取为0.001 s. 图中左侧底角的点A(0, 0)和模型中间的点B(150, 74)为观测点.

图7为采用不同MTF边界方案计算得到的波场快照图. 图中采用了两种不同尺度的颜色标尺. 对0.2 s, 0.4 s和0.8 s的波场快照采用尺度较大的颜色标尺, 便于观察波动传播过程. 由于波到达边界处的反射比较小, 对1.6 s和1.9 s的波场快照采用尺度较小的颜色标尺, 以便比较不同方案的效果.



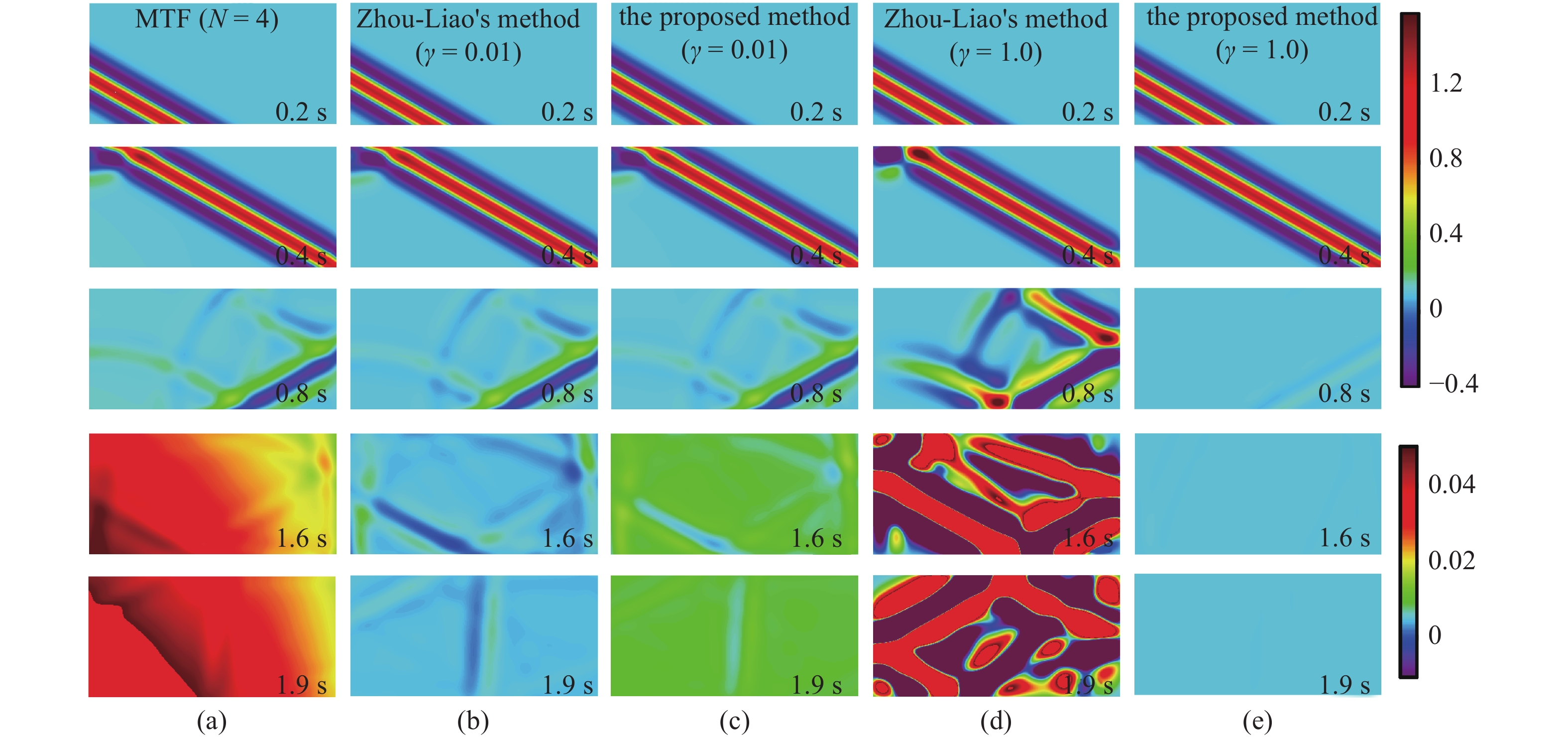onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
不同方法情况下的波场快照



Figure
7.
Snapshots of wave propagation by using different methods



下载:
全尺寸图片
幻灯片


图7(a)为未被修正过的4阶MTF, 从其1.6 s和1.9 s的波场快照看, 左侧人工边界和底部人工边界率先发生了比较明显的飘移失稳, 并且该失稳现象随着时间的进行而向内域蔓延. 图7(b)和图7(c)分别为消飘因子$ gamma = 0.01 $时的周?廖方法和本文方法, 从两图 1.6 s和1.9 s的波场快照看, 两种MTF修正方法都比较好的消除了4阶MTF的飘移失稳现象. 图7(d)为消飘因子$ gamma = 1.0 $时的周?廖方法, 从波场快照看, 残余波场的值较大, 其计算精度不高. 这是因为$ gamma $超过一定值后, 其值越大, 周?廖方法精度越低, 入射波到达边界后产生了较大的反射. 图7(e)为消飘因子$ gamma = 1.0 $时的本文方法, 从其0.8 s, 1.6 s和1.9 s的波场快照看, 该方案既消除了飘移失稳现象, 又保持了较高的计算精度. 这是因为本文方法的精度下限为一阶MTF, 且人工波速为视波速, 入射波到达边界后产生的反射较小.

图8为测点A和测点B在不同方法情况下的位移时程图及局部放大图(测点位移用u表示). 图8(b)和图8(d)分别为图8(a)和图8(c)中绿色矩形框处的局部放大图. 从图8(a)中可以明显看出, 4阶MTF对应的位移时程发生了明显的飘移失稳现象. 添加消飘因子的几种方案都较好的解决了飘移失稳, 但都存在一定的残余波场, 尤其是$ gamma = 1.0 $时的周?廖方法, 精度较差, 见图8(c). 在这几种消飘因子添加方案中, $ gamma = 1.0 $时的本文方法是残余波场幅值最小的, 精度最高, 见图8(b)和图8(d).



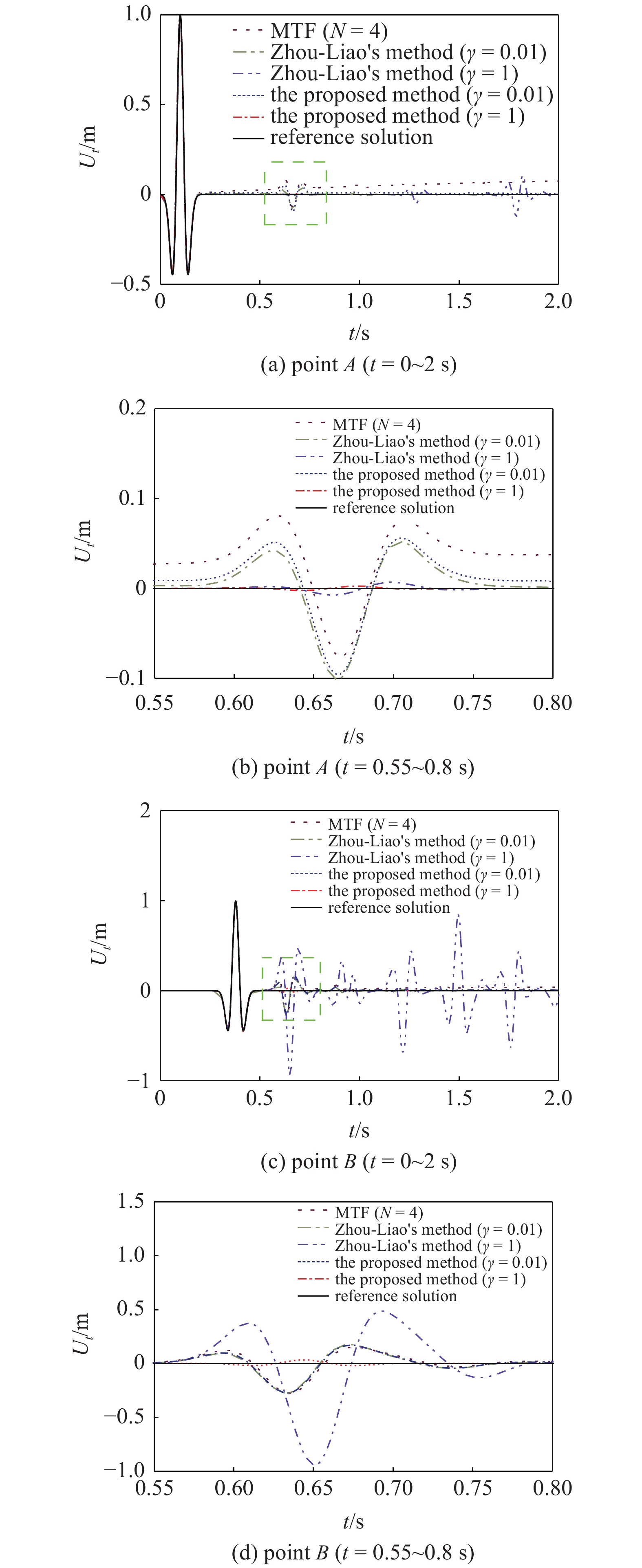onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
测点A和测点B的位移时程



Figure
8.
Displacement time histories at point A and point B



下载:
全尺寸图片
幻灯片


与前面波源问题相似, 这里以测点A和测点B在t = 0.5 s~2.0 s时间范围内的最大位移幅值|U|_max为参考标准, 来更具体的比较消飘因子$ gamma $对周?廖方法与本文方法计算精度的影响, 如图9所示. 从图9可以看出, 当消飘因子$ gamma $< 0.1时, 周?廖方法与本文方法的计算精度十分接近且几乎不随$ gamma $取值而改变; 当$ gamma $> 0.1时, 本文方法的误差随着$ gamma $的增大而逐渐降低为0, 而周?廖方法的误差整体上则随着$ gamma $的增大而迅速变大. 因此, 如果对计算精度有最低要求, 本文方法的消飘因子取值范围将明显大于周?廖方法. 这种情况下, 有别于周?廖方法在应用过程中对消飘因子$ gamma $取值需要不断地进行试错, 本文方法对消飘因子的选值更加方便与宽松.



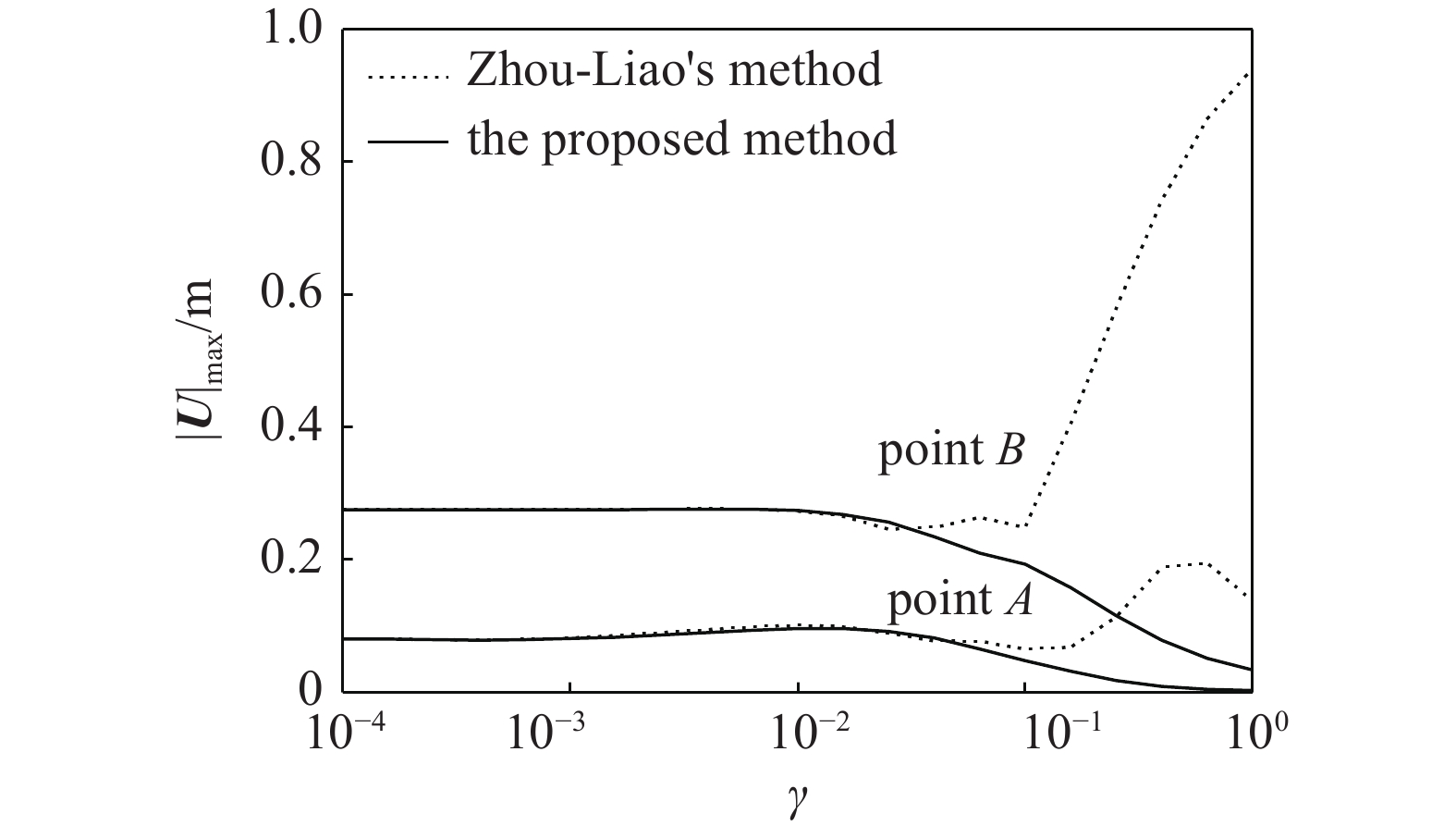onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
消飘因子$ gamma $对不同方法模拟波场精度的影响



Figure
9.
Influence of the drift-elimination factor $ gamma $ on the accuracy of simulated wave field by using different boundary methods



下载:
全尺寸图片
幻灯片


结合数值算例的结果与反射系数的分析, 可以发现, 两种方式都能反应出本文方法相对于传统方法的精度优势, 但精度的表现存在一定差异, 这主要是因为: (1) 理论反射系数基于稳态谐波导出, 而本文数值试验则是短持时的暂态波; (2) 反射系数是对每个特定频率ω (ω = 2πf = 2π/T)给出的, 而数值试验中的波动则具有多种频率成分; (3) 反射系数使用的是理想平面波, 具有特定的透射角度, 而数值试验中的波动以多种不同的角度射向边界, 且往往含有几何衰减、多波叠加等效应; (4) 离散网格具有数值频散效应, 会导致其中传播的波形发生变化, 对人工边界的反射特征造成一定影响.

依据应用本文方法的大量数值模拟经验, 对MTF的阶次N和消飘因子$ gamma $的取值有以下归纳: (1) MTF常用的阶次一般不超过3阶, 本文算例中使用高阶MTF (N = 4)是为了研究飘移失稳问题, 探讨消飘方法的效果; 此外, MTF并非只在高阶情况下才发生飘移失稳, 在有些情形下^{[2, 6, 26]}, 低阶MTF也可能出现飘移失稳; (2) 关于消飘因子$ gamma $的取值范围, 周?廖方法一般为0.001~0.05 ^{[1, 2, 6, 26, 35]}, 本文方法在同样精度情况下则为0.01~1.0, 取值范围更大; 对于飘移比较严重的问题, 本文方法对$ gamma $的取值可以大一些, 如0.5或接近1, 对于飘移比较轻微的问题, $ gamma $的取值则可以小一些, 如0.01左右.

5.
基于任意阶MTF的消飘通用形式

前面讨论的MTF飘移失稳控制方案是立足于一阶MTF上而建立起来的, 即保持一阶MTF不变, 而仅对二阶及其以上各阶MTF透射误差进行修正, 这样就在实现抑制飘移失稳的同时至少保留了一阶MTF的精度. 这种MTF飘移失稳控制方案的思路很容易推广至任意阶MTF情形. 如果认为前m阶MTF都能够保持稳定而不发生失稳, 则只需针对m+1阶及其以上的各阶MTF透射误差添加消飘因子, 即可达到抑制飘移失稳的目的. 考虑到m阶MTF可以表达为

$$ {nabla ^m}u_0^{p + 1} = {nabla ^{left( {m - 1} ight)}}u_0^{p + 1} - {nabla ^{left( {m - 1} ight)}}u_1^p = 0 $$

(17)

则只需将N阶MTF (N > m)修正为

$$ begin{gathered} {nabla ^N}u_0^{p + 1} = {nabla ^{(N - 1)}}u_0^{p + 1} - frac{{{nabla ^{(N - 1)}}u_1^p}}{{1 + gamma }} = 0 left( {N geqslant m + 1} ight) end{gathered} $$

(18)

此即为任意阶MTF飘移失稳控制的通用形式. 显然, 若取m = 1, 则式(18)与本文前面导出的MTF飘移失稳控制方案完全一致.

式(18)对应的边界反射系数可以统一地写为

$$ R = {left( {{R_0}} ight)^m} cdot R_f^{N - m} $$

(19)

不难发现, 当取m = 0时, 由式(19)给出的反射系数实际上就是周?廖方案的反射系数表达式. 下面证明周?廖方案是本文方法的一个特例.

如果定义记号

$$ {nabla ^0}u_0^{p + 1} = u_0^{p + 1} $$

(20)

则当m = 0时由式(17)立即得到

$$ u_0^{p + 1} = 0 $$

(21)

即边界点始终保持为0, 这表明零阶MTF实际上是固定边界条件. 在该情形下, 根据式(17)并利用式(18)容易导出各阶MTF如下

1阶: $u_0^{p + 1} = dfrac{1}{{1 + gamma }}u_1^p$

2阶: $u_0^{p + 1} = dfrac{2}{{1 + gamma }}u_1^p - dfrac{1}{{{{left( {1 + gamma }
ight)}^2}}}u_2^{p - 1}$

3阶: $u_0^{p + 1} = dfrac{3}{{1 + gamma }}u_1^p - dfrac{3}{{{{left( {1 + gamma }
ight)}^2}}}u_2^{p - 1} + dfrac{1}{{{{left( {1 + gamma }
ight)}^3}}}u_3^{p - 2}$

……

将上述各阶MTF写成通式, 有

$$ u_0^{p + 1} = sumlimits_{k = 1}^N {{{left( { - 1} ight)}^{k + 1}}C_k^N cdot frac{{u_k^{p - k + 1}}}{{{{left( {1 + gamma } ight)}^k}}}} $$

(22)

比较发现, 式(22)与式(3)完全相同, 即其实际上就是周?廖方案所给出的N阶MTF. 故无论从MTF表达式(式(22))还是边界反射系数(式(19))上看, 周?廖方案本质上只是本文方法取m = 0时的一个特例.

6.
结 论

多次透射公式(MTF)建立起来的人工边界条件有时存在飘移失稳问题. 本文将周正华和廖振鹏提出的抑制MTF飘移失稳的方案推广到一般情形, 发展了一种多次透射公式飘移问题的控制方法. 通过边界反射系数分析和数值试验, 对本文方法的精度和消飘效果进行了详细探讨, 得到主要研究结论如下.

(1) 本文方法能够十分有效地消除高阶MTF与有限元模型结合后出现的飘移失稳现象, 仅通过添加消飘因子的方式实现控制MTF飘移失稳的目标, 这对于MTF实施步骤及其编程基本不会产生额外负担.

(2) 本文的MTF飘移控制方案是在m阶MTF的基础上构建出来的, 仅针对(m+1)阶及其以上各阶MTF的透射误差项进行修正, 能够保证波动模拟结果至少保持m阶MTF精度(当取m = 1时即至少保有一阶MTF精度). 传统的周?廖方案本质上是本文方法的一个特例, 相当于取m = 0时的结果.

(3) 在本文方法中, 消飘因子$ gamma $取值增大时主要对中等和大角度透射波动的模拟精度造成影响, 而对波动能量比较集中的法向和小角度透射范围影响很小. 它能够适应更大的消飘因子取值范围(如1.0以内的正数), 且较传统方案能够在更高精度水平下实现对MTF飘移问题的有效控制.

(4) 当消飘因子取值趋向于无限大时, 由传统方案推算的边界运动趋近于零, 此情形相当于固定边界条件, 而本文方法则趋近于m阶MTF(实际应用时可只取为一阶MTF). 从原理上看, 本文方法融合了零频零波数情形下GKS准则所表述的消飘原理^{[26, 27]}和通常认为低阶MTF不易发生飘移失稳的经验观察^{[24, 33]}.

附录A$ ;$

周?廖方案修正MTF的前4阶表达式

$$ 1阶: u_0^{p + 1} = frac{1}{{1 + gamma }}u_1^p tag{A1}$$

$$ 2阶: u_0^{p + 1} = frac{2}{{1 + gamma }}u_1^p - frac{1}{{{{left( {1 + gamma } ight)}^2}}}u_2^{p - 1} tag{A2}$$

$$ 3阶: u_0^{p + 1} = frac{3}{{1 + gamma }}u_1^p - frac{3}{{{{left( {1 + gamma } ight)}^2}}}u_2^{p - 1} + frac{1}{{{{left( {1 + gamma } ight)}^3}}}u_3^{p - 2} tag{A3}$$

$$ begin{split} &4阶: u_0^{p + 1} = frac{4}{{1 + gamma }}u_1^p - frac{6}{{{{left( {1 + gamma } ight)}^2}}}u_2^{p - 1} + frac{4}{{{{left( {1 + gamma } ight)}^3}}}u_3^{p - 2} -&quad quad quad quad;;;; frac{1}{{{{left( {1 + gamma } ight)}^4}}}u_4^{p - 3} end{split}tag{A4}$$

附录B

本文MTF外推节点插值格式

MTF外推节点位移通过有限元节点位移的3点内插方式获得.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-435-B1.jpg'"
class="figure_img
figure_type1 bbb " id="FigureB1" />



B1
透射边界(MTF)示意图



B1.
Schematic diagram of multi-transmitting formula (MTF)



下载:
全尺寸图片
幻灯片


如图B1所示, 多次透射公式可以看成是基于时空节点信息的有限差分外推公式. 其形式如下

$$ u_0^{p + 1} = sumlimits_{j = 1}^N {{{( - 1)}^{j + 1}}C_j^N} u_j^{p + 1 - j} tag{B1}$$

以第一个时空外推节点$ u_1^p $为例(图中节点1a, 一次透射项), 令$ s = {c_a}Delta t/Delta x $, $ Delta x $为相邻的有限元网格节点之间的空间间距, 基于$ u_1^p $与同一时刻相邻3个有限元网格节点位移的空间插值关系, 有

$$ {u}_1^p = left[ {(2 - s)(1 - s){text{/}}2{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} s(2 - s){kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} s(s - 1){text{/}}2{kern 1pt} } ight] cdot {left[ {bar u_0^p{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} bar u_1^p{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} bar u_2^p} ight]^{text{T}}}tag{B2} $$

式中, $ bar u_i^p $表示编号为i的有限元网格节点在p时刻的位移.

同理, 令${s_j}{text{ = }}j{c_a}Delta t/Delta x$, 可求第j个外推时空节点的位移$ u_j^{p + 1 - j} $, 以矩阵形式表示如下

$$ begin{split}{u}_j^{p + 1 - j} = &left[ {(2 - {s_j})(1 - {s_j}){text{/}}2 qquad {s_j}(2 - {s_j})qquad {s_j}({s_j} - 1){text{/}}2} ight] cdot hfill &{left[ {bar u_0^{p + 1 - j} bar u_1^{p + 1 - j} bar u_2^{p + 1 - j}} ight]^{text{T}}} hfill = &{A_j} cdot {{bar U}^{p + 1 - j}} end{split} tag{B3}$$

式中, $ {bar U^{p + 1 - j}} $为($ p + 1 - j $)时刻边界附近3个有限元网格节点的位移数组, $ {A_j} $为用该位移数组拟合$ u_j^{p + 1 - j} $的插值系数数组. 需要注意的是, 基于3点空间插值的格式需要各个外推节点与边界的距离都不超过两个单元长度, 即$ {s_j} leqslant 2 $.

将式(B3)代入式(B1), 可得用有限元网格离散节点的位移表示的MTF形式, 即

$$ u_0^{p + 1} = sumlimits_{j = 1}^N {{{( - 1)}^{j + 1}}C_j^N} {A_j} cdot {bar U^{p + 1 - j}}tag{B4} $$