删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于反激变压器的压电振动能量双向操控技术

本站小编 Free考研考试/2022-01-01


引 言


压电材料所存在的正逆压电效应是应用最为广泛的一种机电耦合效应, 基于这两种效应能实现机械能与电能之间的相互转换[1]. 压电材料因其正压电效应, 即在外力作用下产生电荷的效应, 常被应用在传感和能量俘获等领域. 如刘客等[2]通过在螺栓球和杆件上外贴压电陶瓷片, 有效地实现了对螺栓球节点内部螺栓连接松紧状态的识别和监测. 曹东兴等[3]提出了一种新型流致振动附磁压电能量采集器, 其在低速流体激励下具有良好的俘能效果. Zhang等[4]、周生喜等[5]、Liu等[6]和王军雷等[7]也分别从压电元件本身、非线性压电振子结构、接口电路甚至风致振动角度研究了基于正压电效应的振动能量俘获技术, 以期在一些低功耗独立设备的自供电方面获得实际应用[8-10].

此外, 压电材料因其在外电场作用下材料产生变形的效应即逆压电效应, 常应用于驱动和振动控制等领域. 如刘赵淼等[11]设计了一种用于生成均匀微滴的压电驱动式微滴喷射装置, 通过压电材料带动柔性膜片振动, 将液体从喷嘴中喷出生成微滴. 唐冶等[12]利用压电材料对脉动旋转悬臂梁系统的振动进行控制, 分析了旋转机构中各项参数对主动控制系统稳定性的影响. 张顺琦等[13-14]设计了应用于压电悬臂梁振动主动控制的模糊逻辑控制器,优化了对压电智能结构进行振动抑制时针对高频周期扰动和随机扰动的抗干扰控制策略. Shen等[15]使用基于压电材料的主动式支杆阻尼器, 有效地抑制了风洞试验中支撑气动模型的悬臂支杆振动.

值得一提的是, 法国里昂国立应用科学院的Richard等[16]在2000年左右基于压电智能结构提出了一种同步开关阻尼(synchronized switch damping, SSD)电路, 采用半主动控制的思想在特定时候改变电路中同步开关的状态, 进而达到抑制结构振动的目的. 为进一步提高振动控制效果, 通过在SSD电路中串联电感利用LC振荡效应增加压电开路电压的SSDI (SSD based on inductor)技术随之被提了出来[17]. 在此基础上, 通过串联外加电压源的SSDV(SSD based on voltage)等更加先进的方法也被提出并获得了大量的跟踪研究[18-22]. 理论研究表明, 若外加电压源调节得当, 结构振动响应几乎可被完全抑制[23-24].

考虑到压电元件的正逆压电效应, 几乎在同一时刻, Guyomar等[25]就将SSDI技术拓宽应用到了振动能量收集领域, 该技术被命名为基于电感的同步开关回收(synchronized switch harvesting on inductor, SSHI)技术, 其中并联型SSHI即在SSDI的电路基础上增加了负载电路, 用于收集压电元件上产生的电荷能[26]. 为优化宽频条件下压电振动能量的收集效率, Wu等[27-28]在同步电荷提取技术[29]的基础上提出了一种利用反激变压器的优化型同步电荷提取(optimized synchronous electric charge extraction, OSECE)方法, OSECE电路中的反激变压器, 能够有效地隔离压电元件和负载阻抗, 在振动位移达到极值的时候, 首先闭合对应的同步开关将电荷能提取到变压器中, 再通过变压器转移至负载电路, 无须通过阻抗匹配即可获得较高的能量收集功率.

基于OSECE电路, 本文提出了一种能量逆向流动的操控方法, 即首先将外界电能存储至电路中的反激变压器中, 再通过控制同步开关将变压器中临时存储的电能注入至压电元件, 进而提高压电元件两端的开路电压, 最大化结构振动的抑制效果. 该方法被称为基于能量注入的SSD (SSD based on energy injection, SSDEI)技术. 由于SSDEI技术是通过反激变压器及对应的开关电路将外界电能注入至压电元件中的, 因此仅需调节注能开关控制信号的“占空比”即可实时调节外界输入的电能, 不仅具有明显的控制效果, 还大大简化了电路的实现难度, 提高了控制精度, 增强了控制系统的抗干扰能力.

为此, 本文首先介绍用于压电振动能量俘获的OSECE技术, 随后介绍了SSDEI技术的工作原理及经典机电耦合模型下SSDEI引入的振动阻尼比模型. 以工程中常见的悬臂梁结构为例搭建了振动控制实验平台, 通过实验验证了SSDEI的理论控制效果, 最后对实验结果进行全面的分析与讨论.


1.
基于反激变压器的压电能量双向操控原理



1.1
用于振动能量俘获OSECE技术


用于振动能量俘获的OSECE技术主要利用了正压电效应, 即将压电元件产生的电荷能提取并存储到电路中, 为后续微功率设备提供电能. OSECE的电路原理图如图1所示, 其中反激变压器具有两个原边绕组(L1和L2)与一个副边绕组(L3)并将电路分为两个部分, 连接压电材料的原边侧电路即为SSDI控制电路, 副边侧电路则为振动能量收集系统中的负载端.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
优化型同步电荷提取(OSECE)电路原理图



Figure
1.
Schematic circuit of the OSECE technique



下载:
全尺寸图片
幻灯片


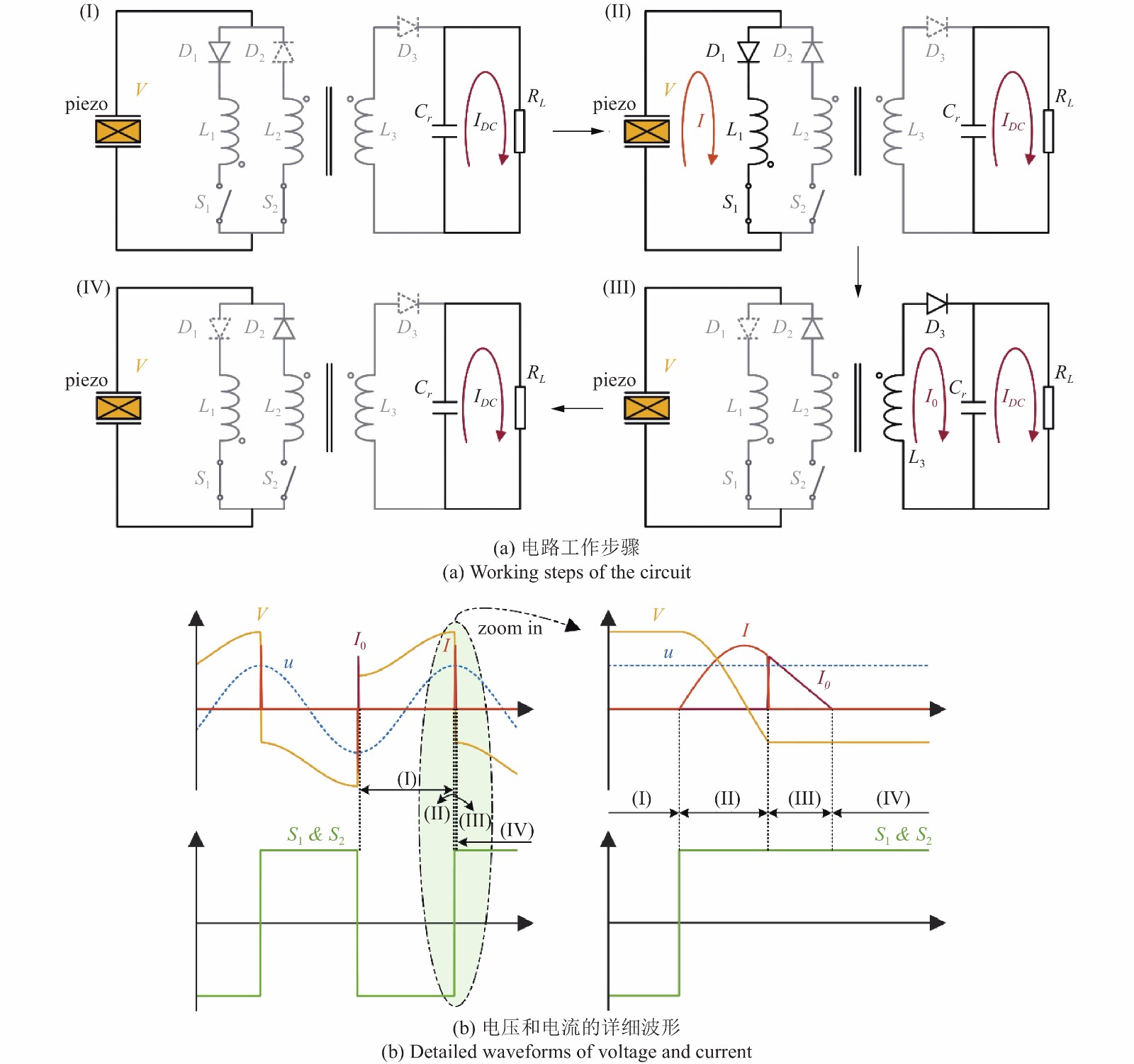
将OSECE电路在半个振动周期内的工作原理分为了如图2(a)所示的4个阶段, 详细的电流、电压及开关控制波形如图2(b)所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-2.jpg'"
class="figure_img
figure_type2 ccc " id="Figure2" />



图
2
优化型同步电荷提取(OSECE)技术的工作原理



Figure
2.
Operation principle of the OSECE approach



下载:
全尺寸图片
幻灯片


第1阶段如图2中(Ⅰ)所示, 结构振动位移从极小值开始增加, 压电元件此时因电压为正导致二极管D2截止而处于开路状态, 负载RL消耗的电能来自于电容Cr于上个周期储存的电能.

第2阶段如图2中(Ⅱ)所示, 当结构振动位移达到极大值时开关S1闭合且二极管D2导通使原边绕组L1与压电元件连接, 压电元件因其电容特性与原边绕组L1形成LC振荡, 并在这期间内向变压器内充入电能, 而此时副边绕组同名端电压为负导致该侧电路中二极管D3截止, 电容Cr继续为负载RL供电.

第3阶段如图2中(Ⅲ)所示, 假设LC振荡频率远大于结构振动频率, 此时结构振动位移仍认为处于极大值, 因为LC振荡使压电元件的电压翻转为负导致二极管D1截止, 压电元件开路且副边绕组同名端电压为正, 该侧电路中二极管D的导通使变压器储存的电能在该阶段内转移到CrRL负载电路, 直到电流为零开始第4阶段.

第4阶段如图2中(Ⅳ)所示, 此时结构振动位移从极大值开始减小, 压电元件电压仍为继续为负且随结构振动位移继续减小, 二极管D1仍处于截止状态, 直到位移达到最小值时. 该阶段亦可视为下半个振动周期的第1阶段.

通过上述描述可以发现, OSECE电路中的反激变压器起到了临时储能的“桥梁”作用, 不仅隔离了负载使得提取功率受其影响较小, 还因为电容Cr的存在, 在第2阶段反向“注入”了部分电能给压电元件(电流波形图(Ⅱ)阶段从极大值变小的原因), 从而提高了压电元件功率密度[30]. 那么, 能否利用OSECE电路并通过变换开关控制策略重点提高压电元件开路电压并将其用于结构振动抑制中成为了本文重点研究的问题.


1.2
用于振动能量抑制的SSDEI技术


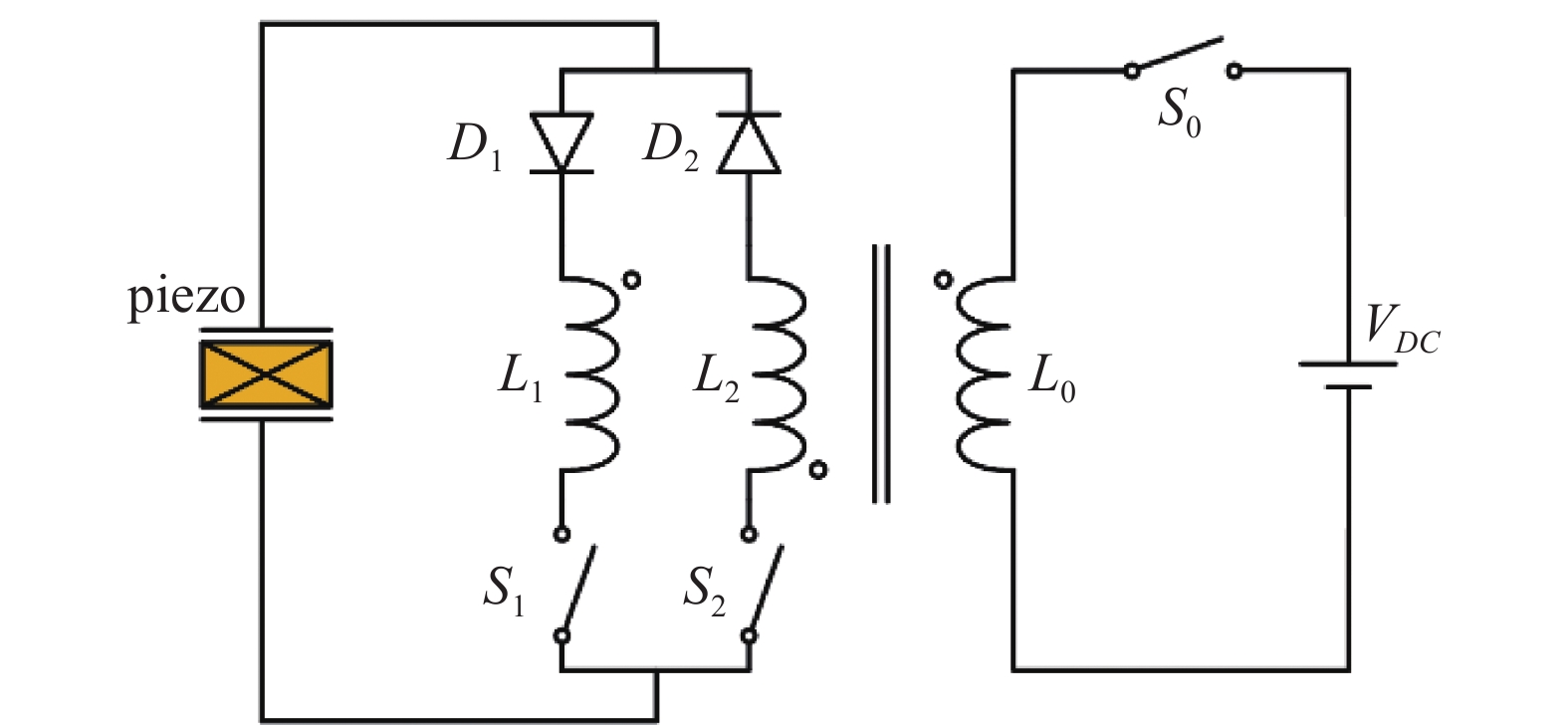
用于振动能量抑制的SSDEI技术主要利用了压电元件的逆压电效应, 即将外界电能“注入”至压电元件, 实现结构振动抑制的目的. SSDEI电路如图3所示, 可以发现该电路拓扑结构与OSECE电路非常相似, 具有一个原边绕组(L0)与两个副边绕组(L1和L2)的反激变压器将电路分为两个部分. 副边绕组侧电路同样为SSDI控制电路, 但是SSDEI方法会在同步开关(S1或S2)切换前, 控制原边绕组侧的注能开关S0提前闭合, 将电压源VDC提供的电能临时存储至变压器原边电感中, 一旦同步开关(S1或S2)发生切换, 提前注入至变压器的电能再次注入至压电元件, 获得了与SSDV类似的增大压电元件开路电压的效果, 极大地提高了结构振动控制效果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
基于能量注入的同步开关阻尼(SSDEI)电路



Figure
3.
Schematic circuit of the SSDEI technique



下载:
全尺寸图片
幻灯片


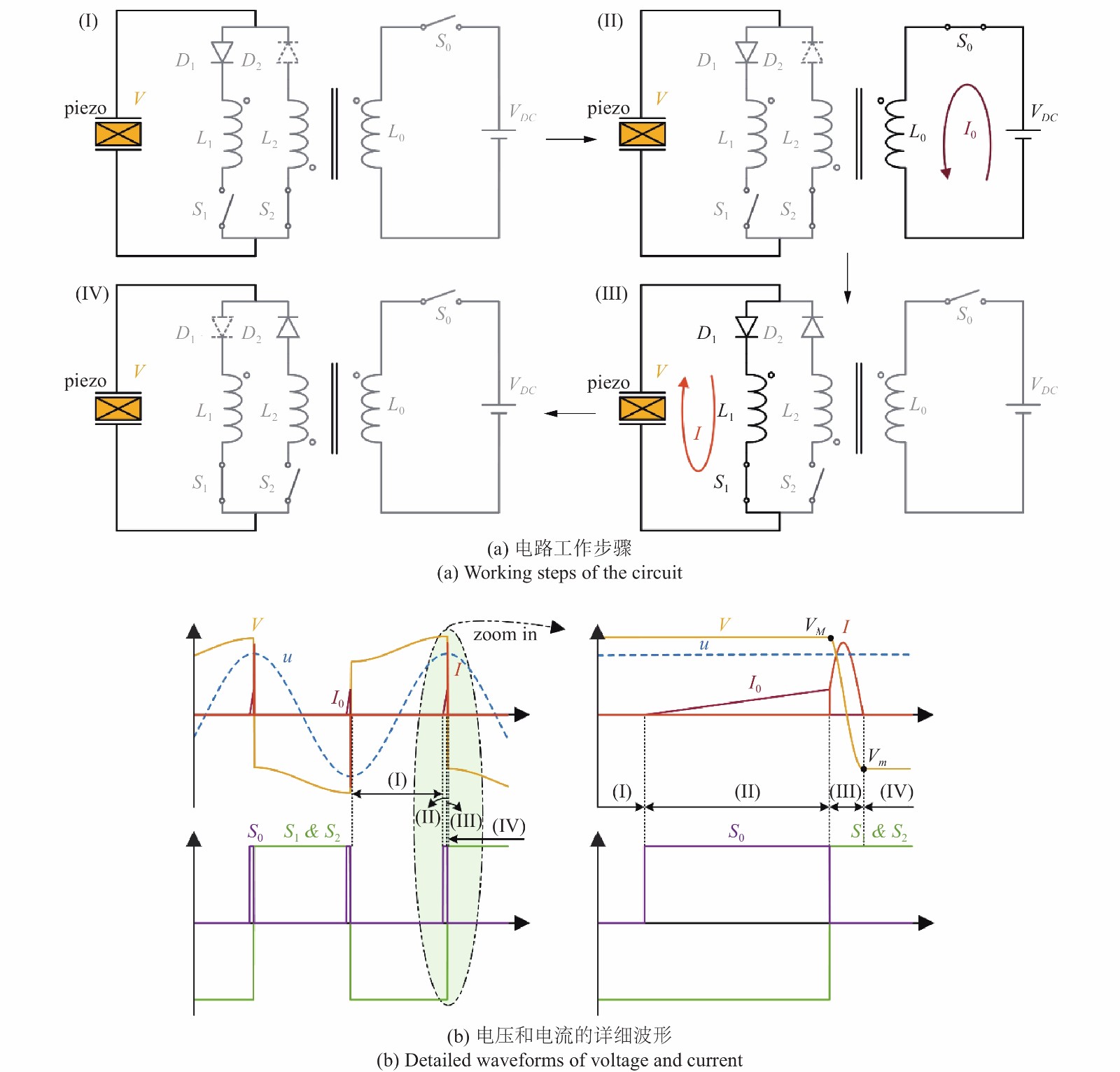
同样将SSDEI电路在结构半个振动周期内的工作原理分为了如图4(a)所示的4个阶段, 详细的电流、电压及开关控制波形如图4(b)所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
基于能量注入的同步开关阻尼(SSSEI)技术的工作原理



Figure
4.
Operation principle of the SSDEI approach



下载:
全尺寸图片
幻灯片


第1阶段如图4中(Ⅰ)所示, 开关S2闭合但是因为此时压电元件电压为正导致二极管D2截止, 开关S0以及开关S1断开, 所以此时压电元件处于开路状态且副边绕组侧电路不工作.

原边绕组侧的注能开关S0闭合后开始第2阶段, 如图4中(Ⅱ)所示, 此时压电元件仍处于开路状态, 电压源VDC与原边绕组电感L0连接并形成回路, 将一部分电能存储至L0中, 该过程可表示为







$$ {V_{DC}} = {L_0}frac{{{
m{d}}{I_0}}}{{{
m{d}}t}} $$
(1)

式中, VDC为外加电压源电压值, L0为原边绕组线圈电感值, I0为原边绕组侧回路电流.

第3阶段如图4中(Ⅲ)所示, 结构位移达到最大值时, 开关S1闭合, 开关S0和S2断开. 此时, 原边绕组侧电路断路, 并且二极管D1导通使副边绕组电感L1与压电元件连接形成LC振荡回路. 为便于计算, 假设变压器为线性的, 原边绕组与副边绕组间的耦合是理想的且3个线圈匝数比为1:1:1, 即3个接入电路的电感感值相等. 基于以上假设, 压电元件上的电荷q可由下式表达







$$ {L_1}ddot q + rdot q + frac{1}{{{C_p}}}q = 0 $$
(2)

式中, L1为副边绕组线圈电感值, r为振荡回路的等效电阻, Cp为压电元件的等效电容.

为方便计算, 定义τ为开关时间系数, 可为任意非负常数, 并将第2阶段的持续时间定义为L1Cp电路振荡周期的τ/2倍, 最后假设存入变压器的电能全部注入压电元件中, 可以计算出第2阶段结束时电流I0的大小, 即第3阶段开始时电流I的初始值, 因此方程(2)的初始条件可表示为







$$ left. begin{aligned} &dot qleft( 0
ight) = tau {text{π}} {V_{DC}}sqrt {frac{{{C_p}}}{{{L_1}}}} hfill &qleft( 0
ight) = - {C_p}{V_M} hfill end{aligned}
ight} $$
(3)

式中, VM为第2阶段结束时即第3阶段开始时压电元件的电压. 定义λ为SSDEI技术的电压翻转因子, 则有







$$ {V_m} = lambda {V_M} $$
(4)

式中, Vm为第3阶段结束时压电元件的电压. 与SSDI技术相似[17], VM与Vm的关系可表示为







$$ {V_M} = {V_m} + frac{{2alpha }}{{{C_p}}}{u_M} $$
(5)

式中, α为压电耦合结构的力因子, uM为结构的振动位移幅值. 根据式(2), 第3阶段期间的压电元件两端电压V与L1Cp回路电流I可表示为







$$ left. begin{gathered} I = dot q = tau {text{π}} {C_p}{omega _e}{V_{DC}}cos left( {{omega _e}t}
ight){{
m{e}}^{ - frac{{{omega _e}t}}{{2{Q_e}}}}} + hfill quad {text{ }}{C_p}{omega _e}{V_M}sin left( {{omega _e}t}
ight){{
m{e}}^{ - frac{{{omega _e}t}}{{2{Q_e}}}}} hfill V = frac{q}{{{C_p}}} = {V_M}cos left( {{omega _e}t}
ight){{
m{e}}^{ - frac{{{omega _e}t}}{{2{Q_e}}}}} - hfill quad {text{ }}left( {tau {text{π}} {V_{DC}} - frac{{{V_M}}}{{2{Q_e}}}}
ight)sin left( {{omega _e}t}
ight){{
m{e}}^{ - frac{{{omega _e}t}}{{2{Q_e}}}}} hfill end{gathered}
ight} $$
(6)

式中, Qe为振荡电路的品质因子, ωe为振荡电路的角频率, 其中时间t的取值范围为







$$ frac{{text{π}} }{2} leqslant {omega _e}t leqslant {text{π}} $$
(7)

当电流I为0时第3阶段结束, 如图4中(Ⅳ)所示, 此时电压V继续下降, 二极管D1截止使压电元件开路. 最后, 由式(4) ~式 (6)可以得到翻转因子λ与翻转相位ωet的表达式为







$$ left. begin{gathered} lambda {text{ = }} - left[ {{{tan }^2}left( {{omega _e}t}
ight) + frac{1}{{2{Q_e}}}tan left( {{omega _e}t}
ight) + 1}
ight]cos left( {{omega _e}t}
ight){{
m{e}}^{ - frac{{{omega _e}t}}{{2{Q_e}}}}} hfill tan left( {{omega _e}t}
ight) = - frac{{tau {text{π}} {V_{DC}}}}{{{V_M}}} hfill end{gathered}
ight} $$
(8)

SSDI技术中的翻转因子仅与振荡电路的品质因子Qe相关[17], 而根据式(8)可知, 在SSDEI技术中, 开关时间系数τ与外加电压源VDC的大小共同决定了注入能量的多少, 最终决定了翻转因子λ的大小: 注入能量越少则翻转相位越大, 翻转因子越小. 若τ等于零即没有注入能量, 则翻转相位等于π, 这时SSDEI的翻转因子与SSDI的翻转因子相等, 即此时SSDEI与SSDI技术等同.


1.3
基于SSDEI的振动控制模型


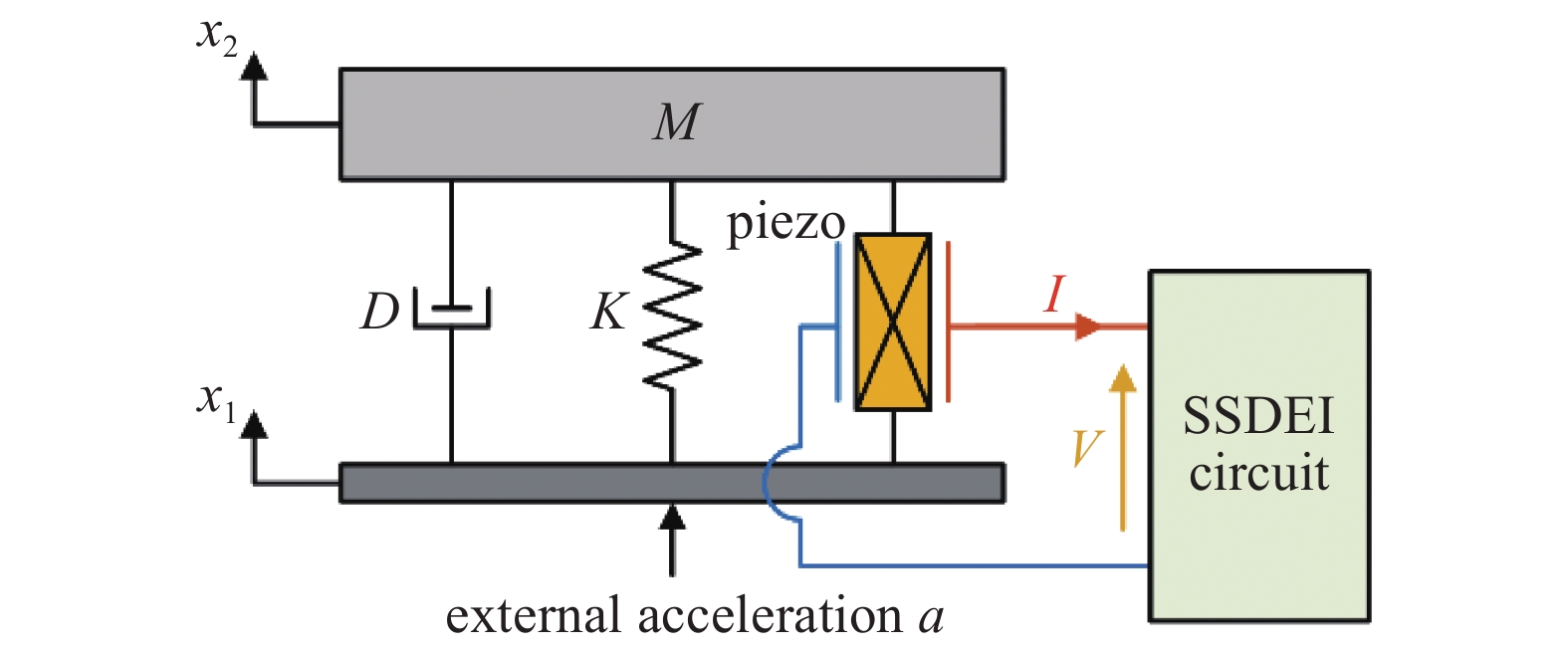
受控压电结构假设为粘贴了压电元件的简单悬臂梁, 该结构受到正弦激励并在一阶共振频率发生振动时, 其机电耦合模型可以用图5所示的单自由度弹簧质量阻尼系统进行描述.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
机电模型示意图



Figure
5.
Schematic representation of the electromechanical model



下载:
全尺寸图片
幻灯片


其中M为等效质量, D为等效阻尼, K为压电元件短路时机电耦合模型的等效刚度. x1是外部激励加速度a下的基座位移, x2为等效质量位移, V和I分别是压电元件输出的电压和电流. 可得该模型的动态平衡方程为







$$ Mddot u + Ddot u + Ku + {F_p} = F $$
(9)







$$left. begin{array}{l} u = {x_2} - {x_1} hfill F = Ma hfill end{array}
ight} $$
(10)

式中, u为基座与等效质量间的相对位移, F为提供外部激励加速度a的正弦激振力, Fp为压电元件通过逆压电效应产生的作用在结构上的力. 受控压电结构的机电耦合方程为







$$ {F_p} = alpha V $$
(11)







$$ I = alpha dot u - {C_p}dot V $$
(12)

综上, 结构和压电元件共同振动时的微分方程可表示为







$$ Mddot u + Ddot u + Ku + alpha V = F $$
(13)

上式两边同乘以速度$dot u$并对时间t积分得







$$ int {Fdot u,{
m{d}}t} {text{ = }}frac{1}{2}M{dot u^2} + frac{1}{2}K{u^2} + int {D{{dot u}^2};{
m{d}}t} + int {alpha Vdot u;{
m{d}}t} $$
(14)







$$ int {alpha Vdot u;{
m{d}}t} {text{ = }}frac{1}{2}{C_p}{V^2} + int {VI;{
m{d}}t} $$
(15)

由式(14)和式(15)可以看出, 系统的总能量分为了动能、弹性势能、机械损耗以及机电转换能, 机电转换能又分为储存在压电元件上的静电能和由SSDEI控制电路消耗以及注入的电能, 如表1所示.




表
1
系统中各能量的表达式



Table
1.
Energy terms definitions



table_type1 ">
Energy termDefinition
$displaystyleint {Fdot u;{
m{d}}t}$		provided energy
$dfrac{1}{2}M{dot u^2}$kinetic energy
$dfrac{1}{2}K{u^2}$potential elastic energy
$displaystyleint {D{ {dot u}^2};{
m{d}}t}$		mechanical losses
$displaystyleint {alpha Vdot u;{
m{d}}t}$		transferred energy
$dfrac{1}{2}{C_p}{V^2}$electrostatic energy
$displaystyleint {VI;{
m{d}}t}$		controlled energy by SSD





下载:
导出CSV
|显示表格



基于SSD技术的振动控制原理就是通过控制电路中开关的切换, 改变压电元件上电压的幅值和相位, 提高了机电转换的能量, 从而达到振动控制的效果. SSDEI技术在SSD技术的基础上通过向压电元件“注入”能量进一步增大了机电转换能从而提高了振动控制效果.

当压电元件处于开路状态时压电元件没有电流输出且输出电压与位移同相位, 此时机电转换能量为0即没有控制效果. 假设系统振动周期为T, 则在半个振动周期内即时间t0至t0 + T/2期间系统的总能量仅提供给机械能损耗.







$$ int_{{t_0}}^{{t_0} + frac{T}{2}} {Fdot u,{
m{d}}t} = int_{{t_0}}^{{t_0} + frac{T}{2}} {D{{dot u}^2},{
m{d}}t} $$
(16)

当振动发生在系统共振频率时, 可以假设结构位移保持正弦, 且当结构的黏性阻尼损耗很低时可以认为力F与速度$dot u$同相位, 基于以上假设, 压电元件开路时即在控制前的位移幅值为







$$ {u_M} = frac{{{F_M}}}{{Domega }} $$
(17)

式中, ω为共振角频率, FM和uM分别为力和位移的极值.

若考虑在SSDEI控制下的位移幅值$u_M' $, 则机电系统在时间t0至t0 + T/2的半个振动周期内系统总能量不仅提供给机械能损耗, 还有机电转换能







$$ int_{{t_0}}^{{t_0} + frac{T}{2}} {Fdot u,{
m{d}}t} = int_{{t_0}}^{{t_0} + frac{T}{2}} {D{{dot u}^2},{
m{d}}t} {text{ + }}frac{1}{2}{C_p}left( {V_M^2 - V_m^2}
ight) $$
(18)

将式(4)和式(5)代入上式即可得SSDEI控制下的位移幅值u'M







$$ {u'_M} = frac{{{F_M}}}{{ {Domega {text{ + }}dfrac{{4{alpha ^2}}}{{{text{π}} {C_p}}}dfrac{{1 + lambda }}{{1 - lambda }}} }} $$
(19)

若定义结构振动的阻尼公式为







$$ A = 20lg left( {frac{{{{u_M'}}}}{{{u_M}}}}
ight) $$
(20)

则将式(17)和式(19)代入上式(20)则可得SSDEI控制下的振动阻尼公式, 式中翻转因子λ的表达式如式(8)所示







$$ {A_{{
m{SSDEI}}}} = 20lg left( {frac{{Domega }}{{Domega + dfrac{{4{alpha ^2}}}{{{text{π}} {C_p}}}dfrac{{1 + lambda }}{{1 - lambda }}}}}
ight) $$
(21)


2.
SSDEI实验系统与实验结果分析



2.1
实验系统


本文以工程中常见的悬臂梁结构为例, 搭建了如图6所示的实验系统, 受控压电结构被夹持固定在激振器上的基座中, 其材料为65 Mn弹簧钢. 粘贴在悬臂梁根部的电压元件为Mide公司的PPA-1001产品. 实验选用东华检测技术公司的激振器(DH40200)和功率放大器(DH5872)为受控压电结构提供激振力, 并使用PCB Piezotronics公司的加速度传感器(TLD352A56)与KEYENCE公司的激光位移传感器(IL-100)分别测量悬臂梁根部基座的加速度与自由端的振动位移, 模拟信号的采集与处理以及SSDEI电路开关控制信号的生成都通过基于MATLAB/Simulink的Speedgoat实时控制系统完成.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-6.jpg'"
class="figure_img
figure_type2 ccc " id="Figure6" />



图
6
实验系统示意框图及装置图



Figure
6.
Schematic and the corresponding photos of the experimental setup



下载:
全尺寸图片
幻灯片


SSDEI电路中, 变压器的3个绕组电感L0和L1和L2均为22 mH, 两节串联的干电池作为VDC提供了3 V的直流电压, 开关S0和S1为N沟道金属氧化物半导体场效晶体管(MOSFET), 型号为IRF640, 开关S2为P沟道MOSFET, 型号为IRFP9240.


2.2
系统模型的参数识别


实际压电耦合结构的控制参数若直接通过压电元件、悬臂梁本身的结构尺寸和材料参数推导, 将会出现较大的误差. 本文通过对表2所示的关键参数进行测量, 利用如下公式, 计算得到了压电耦合控制系统所需的参数值, 如表3所示







$$left. begin{array}{l} {text{ }}alpha {text{ = }}beta {C_p},quad {text{ }}K = alpha beta dfrac{{f_s^2}}{{f_o^2 - f_s^2}} M = dfrac{K}{{4{{text{π}} ^2}f_s^2}},quad {text{ }}D = dfrac{{2{text{π}} M{f_o}}}{{{Q_m}}} end{array}
ight} $$
(22)




表
2
被控结构的实验测量参数



Table
2.
Measured parameters of the controlled structure



table_type1 ">
ParameterSymbolValue
short-circuit resonant frequency/Hzfs28.95
open-circuit resonant frequency/Hzfo29.06
open-circuit mechanical quality factorQm19
open-circuit piezoelectric voltage to the
beam free-end displacement ratio/(V·m?1)		β5900
clamped capacitance of the piezoelectric ceramic/nFCp100





下载:
导出CSV
|显示表格






表
3
计算模型所需参数值



Table
3.
Values of the parameters for calculated model



table_type1 ">
SymbolValue
α 5.9 × 10?4 N/V
K 457.2 N/m
M 13.8 g
D 0.133 N/(m·s?1)





下载:
导出CSV
|显示表格



2.3
结果与讨论


图7所示为SSDEI电路实际工作时压电元件的电压V与输出电流I, 原边绕组电流I0, S0, S1和S2的开关控制信号的实验波形与局部放大波形. 振动位移达到最大值之前, 注能开关S0被驱动闭合, 电压源VDC以将电能注入至变压器的原边绕组L0中, 此时流经L0的电流为I0. 振动位移达到最大值时注能开关S0因其控制信号下降至0 V而断开, 同步开关S1因其驱动控制信号达到10 V而闭合, 变压器中储存的能量通过副边线圈L1注入至压电元件, 此时流经L1的电流为I, 压电元件的电压因振荡以及注入的电能从VM翻转至Vm.



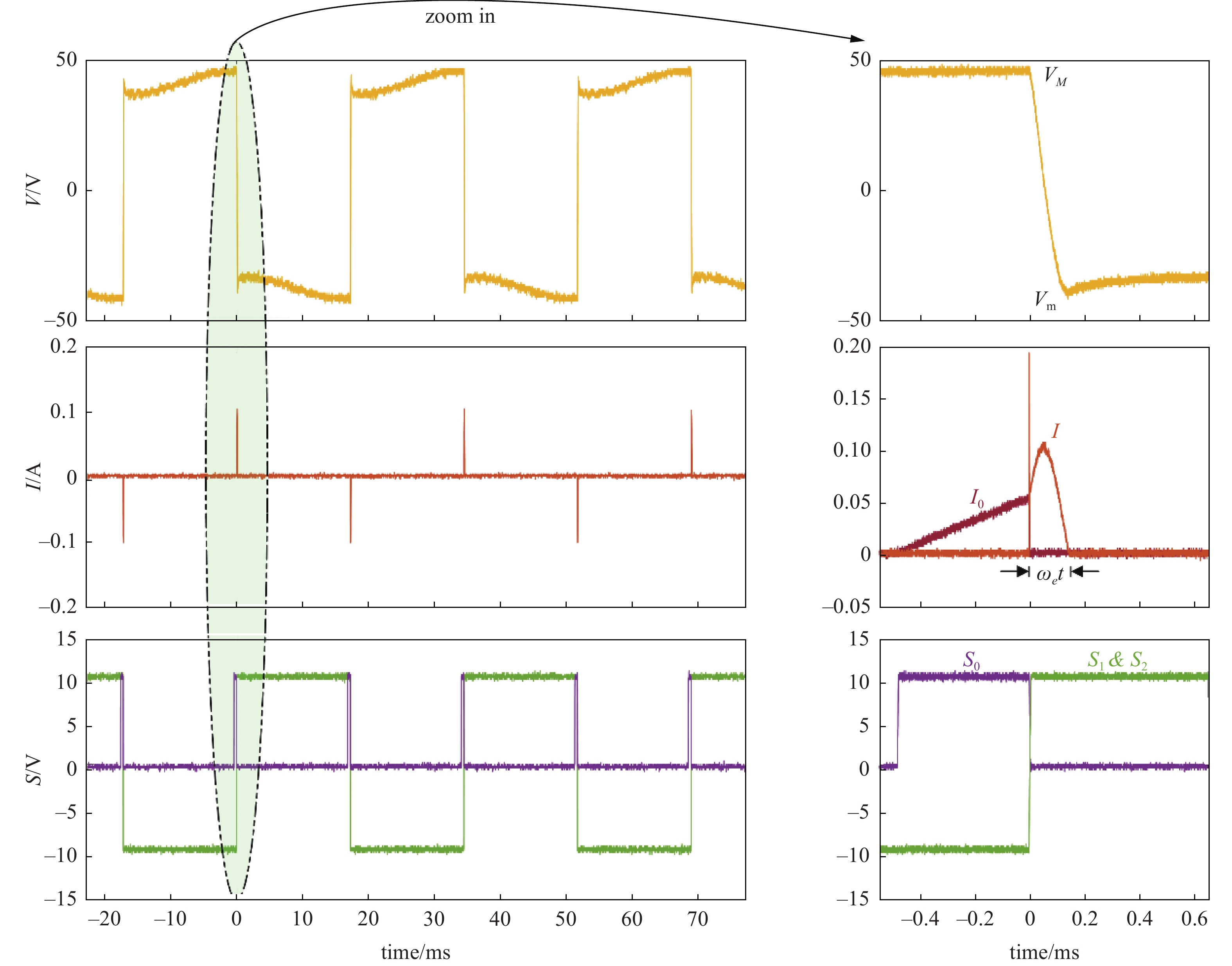onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
基于能量注入的同步开关阻尼(SSDEI)电路实验波形



Figure
7.
Experimental waveforms in the SSDEI circuit



下载:
全尺寸图片
幻灯片


值得说明的是, 理想情况下同步开关S1需要在注能开关S0断开的同时切换至闭合状态, 但是由于现实中开关驱动信号的上升沿与下降沿并不是瞬间完成的而存在时间延迟. 开关S0和开关S1的切换之间存在数个纳秒的时间差, 这段时间内会有电流从压电元件通过变压器流入原边侧电路中, 这导致了脉冲电流的出现, 但该过程仅有几个纳秒, 其带来的影响可忽略.

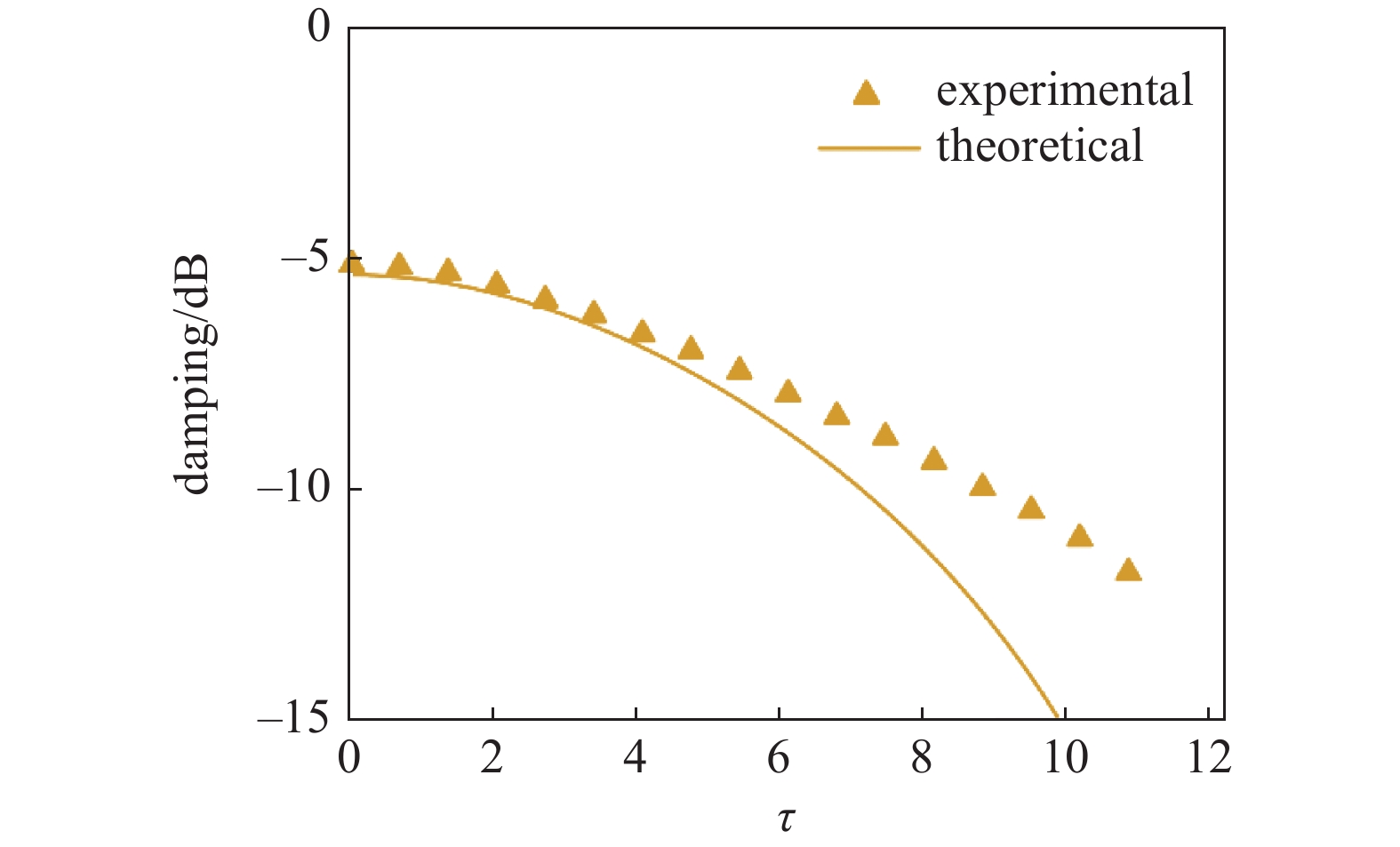
SSDEI技术的振动控制效果随注能开关S0闭合时间变化的关系如图8所示. 该实验中, 激励加速度a幅值为6.30 m/s2, 振荡电路品质因子Qe为3.65, 直流电压源VDC的电压为3 V.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
振动控制效果与τ的关系



Figure
8.
The relationship between vibration control effect and τ



下载:
全尺寸图片
幻灯片


图8中所示曲线为理论计算结果, 散点为实验测试结果. 可以看出SSDEI的振动控制效果会随注能开关S0闭合时间不同而变化且与系数τ成正相关. 但是相对于理论结果, 实验得到的结果偏小, 尤其是当τ偏大时, 实际的振动控制效果越小于计算所得. 出现该现象的主要原因是结构机械品质因子Qm的参数识别误差较大, 影响了计算结果, 另外也有变压器漏感损耗, 压电元件漏电流损耗等因素影响. 但总体来说, 该实验结果较好地验证了SSDEI理论模型, 且振动控制是有效的.

图9显示了在4种不同τ值下的电压波形与振动位移幅值, 本次实验中激励加速度a仍为6.30 m/s2且其他条件未改变. 可以更直观地看到电压在振动位移极值处翻转, 且随开关时间系数τ的增大电压的翻转因子逐渐增大并接近1, 且振动位移随τ的增大明显减小. 能量注入时间为1.6 ms (τ = 10.86)时的振动位移幅值1.08 mm , 仅为能量注入时间为0.4 ms (τ = 2.71)时振动位移幅值1.82 mm的59%.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-9.jpg'"
class="figure_img
figure_type2 ccc " id="Figure9" />



图
9
不同τ值下的振动位移与压电电压波形



Figure
9.
Vibration displacement and piezoelectric voltage waveform under different τ values



下载:
全尺寸图片
幻灯片


图10显示了SSDEI技术控制下的受控压电结构在其一阶共振频率29.06 Hz附近频率振动时的幅频响应, 包括理论计算结果与实验测试结果. 实验中的激振加速度a仍保持6.30 m/s2不变且其他实验条件不变. 可以看到理论与实验结果较为吻合, 实验中受控压电结构没有被控制时在共振频率下的梁端位移幅值为3.52 mm, 在SSDEI技术控制下的位移幅值显著减小: 能量注入时间为1.0 ms (τ = 6.79)时理论仿真的振动位移幅值为1.2 mm, 实验结果的位移幅值为1.38 mm. 能量注入时间越长即τ值越大位移幅值越小, 同样的, 当τ值较大时实际的控制效果不如理论计算的理想, 这与前文所述的规律相同, 但是可以明显看到, 在SSDEI技术的控制下, 压电结构在给定的频带内振动响应都降低了, 因此, SSDEI技术也具有对宽频振动控制的有利特性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-453-10.jpg'"
class="figure_img
figure_type2 ccc " id="Figure10" />



图
10
被控结构在不同控制条件下的幅频响应曲线



Figure
10.
Frequency amplitude responses of the controlled structure under the different control methods



下载:
全尺寸图片
幻灯片



3.
结 论


利用反激变压器可将压电元件产生的能量提取出来完成振动能量收集, 反之亦可通过反激变压器将外界电能注入压电元件进行振动抑制. 本文参考OSECE非线性能量提取电路并基于经典SSD技术原理提出了SSDEI振动半主动控制技术. 理论仿真与实验结果皆表明SSDEI技术具有良好的振动控制效果. 并且可以看出, 相较于经典的SSD技术, 新的SSDEI技术能够通过改变能量注入时间调整振动控制水平, 能有效提高振动控制效果的同时, 提高了控制系统的鲁棒性. 未来可深入研究能量注入时间与结构振动位移幅值之间的关系, 实现仅基于微控制器对开关控制信号的调节, 完全自适应地控制结构振动.

相关话题/控制 电路 结构 电压 技术
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 多次透射公式飘移问题的控制方法
    引言多次透射公式(multi-transmittingformula,MTF)是由廖振鹏等[1-2]提出的一种基于离散参考点表示的局部人工边界条件[3-4],具有普适性、易实施和精度可控等优点.近年来,MTF被广泛地应用于复杂地形场地[5-7]、多种介质场地[8-10]和大型结构[11]的地震反应分 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 动力吸振器复合非线性能量阱对线性镗杆系统的振动控制
    引言在机械零件中带孔零件占比为50%~80%[1],因此孔加工在金属切削加工中占有重要地位.孔加工约占金属切削总量的33%[2],而深孔加工是孔加工中的一个重要领域.镗杆在深孔加工中应用广泛,当镗杆的长度与直径比大于5时便容易发生颤振,从而导致零件的加工质量大幅下降[3-5].因此,对镗杆进行减振就 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 机器学习在力学模拟与控制中的应用专题序
    近几年来,随着高性能计算机和大数据科学的快速发展,机器学习方法在各个领域得到了越来越多的应用.力学学科在过去几十年积累了大量的数值模拟数据、实验测量数据和现场监测数据,这些大规模、高维度的数据蕴含了丰富的物理特征,但传统方法无法有效地处理这些庞大的数据群.机器学习方法可以从巨量的数据海洋中挖掘有用的 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工神经网络的非结构网格尺度控制方法
    引言网格生成是计算流体力学(computationalfluiddynamics,CFD)数值计算的第一步,也是未来CFD六大重要研究领域之一[1-2].在现代CFD应用过程中,自动生成复杂构型的高质量网格(包括网格自适应)依然是一个重大挑战性问题.自动化程度和网格质量是网格生成过程中最重要的两个问 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 水中开孔腔流激振荡控制实验研究
    引言空腔流激振荡是工程中常遇到的一类问题,它是指流体在流经开口结构时,边界层在开口前缘发生流动分离并形成不稳定的自由剪切层,在满足一定的流速和几何特征条件下,会引起剪切层发生稳定的自持振荡,产生很强的周期脉动压力,并通常引起高幅值纯音噪声辐射、附加阻力甚至是结构疲劳.以往对空腔流激振荡的研究主要集中 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • K<sub>0</sub>超固结结构性黏土的本构模型
    引言自然界存在的天然黏土通常是K0固结与结构性并存的状态[1-2],而K0固结又按照当前竖向应力是否大于先期固结压力而分为K0正常固结与K0超固结黏土.大量的室内试验以及现场测试表明,K0正常固结黏土由于初始固结为偏压固结,与等方向正常固结黏土相比,其在大主应力与先期固结压力一致的情况下,K0固结黏 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 倾斜吹吸控制下湍流边界层减阻的直接数值模拟
    引言湍流流动对流体质量、动量和能量的输运要远大于分子热运动产生的输运,湍流流动的控制(包括抑制和增强)是湍流研究领域的重要课题,如减阻控制等.湍流减阻控制研究能够在工程和国民经济领域发挥作用,如能够减少能量损失、减少环境污染、提高装置运行效率等.随着计算机水平的不断提高,数值模拟逐渐成为重要的湍流控 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 压电超构材料及其波动控制研究: 现状与展望
    引言超构材料或超材料(metamaterials)是将精心设计的基本单元通过一定的空间排列来实现普通材料所不具有的奇异或反常性能,如带隙、波导、负折射、负模量、负密度、超透镜、声学聚焦、声学隐身和拓扑态等[1-2],已成为一个多学科交叉的前沿研究领域.过去几十多年来陆续出现的左手材料[3]、光子晶体 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于核磁共振技术的非均质岩心中泡沫动态稳定性评价方法及应用
    引言由于储集层孔隙度与渗透率的差异,油藏表现出不同的非均质性[1].非均质油藏在开发过程中气窜或水窜问题突出,波及效率较低,严重影响了开发效果.泡沫有密度小、视黏度高的特点,在多孔介质中流动时会不断变形产生额外的阻力[2],大幅增加气体的表观黏度.研究表明,泡沫能够先进入高渗层,并随着流动堵塞高渗层 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.