引 言

存在于自然界中(如大肠杆菌^[1])或是人工合成的(如Janus粒子^[2])活性粒子(active particles)能够将其周围环境中各种形式的能量转化为空间运动的动能, 驱动自身运动并扰动周围流场. 包含大量活性粒子的悬浮液被称为活性流体(active fluids). 被动粒子(passive particles)则是指那些不能自发运动, 只能通过布朗运动和流体对流输运发生迁移的粒子. 由于活性粒子的自驱动性, 活性流体属于一种不遵循能量耗散定理的非平衡体系, 具有与被动流体(passive fluids)完全不同的物理特性, 例如生物湍流^[3]、相分离行为^[4]、超扩散现象^[5]和特殊流变行为^[6]等. 深入研究活性流体流变学不仅有助于理解生物物理学的基本过程、更好地控制微生物输运过程中生物膜的形成以及改善微流控设备中的混合过程, 更重要的是可以为当前新材料的开发提供设计帮助^[7-8]. 活性粒子一般为亚微米级或微米级^[9-10], 当前实验研究主要专注于宏观流变行为^[11-12], 而借助数值模拟的方法可以通过再现活性粒子的自驱动行为, 从介观尺度分析宏观流变行为的形成机理, 也能研究外部剪切流与活性粒子自驱动行为之间的耦合作用, 因此逐渐引起****们的关注.

活性粒子可以响应外部流场的剪切作用, 在活性流体中产生“润滑”作用, 使悬浮液的黏度下降, 甚至有可能使宏观黏度降至液相黏度之下^[13-16]. Sokolov和Aranson^[17]首次完成细菌悬浮液流变学的测试, 结果发现浓细菌悬浮液的黏度甚至低于未加入细菌的基液的黏度. Gachelin等^[18]利用Y型微通道实验研究了25 °C下大肠杆菌悬浮液的相对黏度与剪切速率之间的关系, 结果发现在低剪切速率(<10 s^?1)条件下, 大肠杆菌悬浮液的黏度低于液相黏度, 且随着剪切速率的增大, 悬浮液的相对黏度不断增大, 即出现剪切增稠现象, 在临界剪切速率20 s^?1处存在最大值; 当剪切速率大于临界剪切速率时又出现了剪切稀化现象.

为了揭示活性流体特殊流变行为的成因, 数值模拟的手段被广泛采用以研究活性粒子介尺度行为对体系宏观流变行为的影响. Saintillan和Shelley^[19]基于细长体理论创建了活性流体模型, 结果发现该体系具有集群运动的特性. Ezhilan和Saintillan^[20]建立了控制悬浮液中粒子速度、浓度和应力场的控制方程, 该控制方程适用于细菌悬浮液等一系列活性流体. Haines等^[21]建立活性流体的二维模型, 引入了粒子自驱动项, 模拟的结果与实验类似, 观察到了活性流体的黏度下降现象. 后来他们还将模型推广到三维^[22], 考虑了活性粒子的转向行为以及由于粒子形状不对称引起的随机扭矩的影响, 结果表明活性粒子的自驱动行为降低了有效黏度. Ryan等^[23]以偶极子的方式创建黏性流体中的稀释活性粒子体系, 不考虑粒子间的相互作用. 模拟结果表明, 随着活性粒子浓度的增加, 悬浮体系的黏度开始逐渐减小, 达到一个临界点后开始增加, 这一变化趋势与Sokolov和Aranson^[17]的实验结果一致; 然而, 这种直接忽略短程相互作用, 仅考虑粒子与流体的相互作用的方式可能导致模拟结果的偏差. Pagonabarraga和Llopis^[24]模拟库埃特流中偶极蠕动粒子悬浮液和无极蠕动粒子悬浮液的稳态剪切响应, 结果表明前者出现剪切稀化特性, 后者出现剪切增稠特性, 认为活性流体黏度下降是粒子内部的活性力与流体阻力竞争的结果, 然而并未直接给出黏度的结果, 并且模拟结果与流变学实验结果不一致.

过往的模拟研究为了简化计算, 通常会忽略一些影响因素, 例如粒子间作用力、活性粒子的转向运动和直行速度的变化等, 因此会出现和实验结果不一致的情况. 此外, 还存在不能发挥模拟计算单因素分析优势的问题, 仅考虑活性粒子体积分数的影响, 而忽略了粒子自驱动的影响. 本文基于粗粒化的布朗动力学方法^[25], 在布朗运动方程中添加直行运动项并耦合粒子转向运动, 建立可以描述活性粒子运动的活性布朗动力学控制方程; 在准二维模拟区域中建立活性流体模型, 使用反向非平衡法模拟计算活性流体体系的黏度; 考察活性粒子体积分数、直行速度和转向扩散系数对活性流体流变行为的影响规律, 并且分析活性粒子的涨落规律, 探究活性流体特殊流变行为的形成机理.

1.
模型的建立和求解

1.1
布朗运动方程的扩展

对于一个悬浮在液体中, 坐标为q, 质量为m, 动量为p的刚性球粒子, 其运动可用布朗运动方程描述

$$ left. begin{aligned}& dfrac{{{text{d}}{boldsymbol{q}}}}{{{text{d}}t}} = dfrac{{boldsymbol{p}}}{m} hfill & dfrac{{{text{d}}{boldsymbol{p}}}}{{{text{d}}t}} = {boldsymbol{f}} - nabla U({boldsymbol{q}}) + {{boldsymbol{xi}} }(t) end{aligned} ight}$$

(1)

其中, t是时间; ${boldsymbol{ f }}= - dfrac{alpha }{m}{boldsymbol{p}} $表示粒子受到的摩擦阻力, 由该悬浮粒子与周围溶剂分子摩擦产生(α表示斯托克斯系数, 对于球形粒子, 根据斯托克斯定律有α=6πηa, 其中η为流体黏度, a为粒子半径); $ {{boldsymbol{xi }}}(t){text{ = }}lambda {boldsymbol{R}}left( t
ight) $表示粒子与流体分子碰撞产生的随机力(λ=(2D_T)^1/2α表示阻尼系数, 其中直行扩散系数$ {D_T}{text{ = }}dfrac{{{k_{B}}T}}{{6{text{π}}eta a}} $, k_B是玻尔兹曼常数, T是体系的绝对温度; R是高斯随机噪声), 使粒子的运动轨迹杂乱无章, 随机力的均值是零, 满足高斯分布, 因此也称为高斯噪声项; 除此以外, 粒子还会受到势力$ - nabla U({boldsymbol{q}}) $, U是粒子之间的相互作用势. 本文使用Lennard-Jones (LJ)势函数描述粒子间相互作用势

$$ U(r) = 4varepsilon left[{left(frac{sigma }{r} ight)^{12}} - {left(frac{sigma }{r} ight)^6} ight] $$

(2)

其中, r为粒子间的距离; ε和σ表示势能参数, 与粒子的种类和性质有关. 式(2)中, ${left(dfrac{sigma }{r}
ight)^{12}}$为排斥项, ${left(dfrac{sigma }{r}
ight)^{text{6}}}$为吸引项. 粒子间距离越近, 排斥力力越大, 通过势力项$ - nabla U({boldsymbol{q}}) $即可反映粒子间碰撞的过程.

活性粒子为亚微米或微米尺寸, 其运动属于低雷诺数运动, 因此活性粒子受到的惯性力可以忽略不计. 将直行扩散系数D_T代入布朗运动方程中整理得

$$ frac{{{text{d}}{boldsymbol{q}}}}{{{text{d}}t}}(t) = - frac{{{D_T}}}{{{k_B}T}}nabla U({boldsymbol{q}}) + sqrt {{text{2}}{D_T}} {boldsymbol{R}}(t) $$

(3)

与被动粒子相比, 活性粒子在流体中运动时会将系统中其他形式能量转化为自身运动的动能. 因此, 除了流体分子对粒子的碰撞和摩擦作用以外, 活性粒子还在自驱动力的作用下产生一个直行速度U₀n (其中, n表示活性粒子自驱动的方向向量). 扩展后的布朗运动方程为

$$ frac{{{{ m{d}}} {boldsymbol{q}}(t)}}{{{{ m{d}}} t}} = - frac{{{D_T}}}{{{k_B}T}}nabla U({boldsymbol{q}}) + sqrt {{text{2}}{D_T}} {boldsymbol{R}}(t) + {U_0}{boldsymbol{n}} $$

(4)

除直行运动以外, 活性粒子的运动还包括转向运动. 描述活性粒子转向运动的方程如下

$$ frac{{{{ m{d}}boldsymbol psi} (t)}}{{{{ m{d}}} t}} = sqrt {2{D_R}} {boldsymbol{R}}(t) $$

(5)

其中, ψ是活性粒子自驱动方向角, dψ是矢量, 角速度ω=dψ/dt也是矢量; $ {D_{R}}{text{ = }}dfrac{{text{1}}}{{{tau _R}}}{text{ = }}dfrac{{{k_B}T}}{{8{{text{π}} }eta {a^3}}} $是活性粒子特征时间尺度τ_R的倒数, 表示粒子的转向扩散系数.

活性粒子自驱动方向是随机的, 活性粒子的实际运动是直行运动和转向运动的组合. 因此, 描述活性粒子运动的方程式为

$$ left. begin{aligned}&frac{{{{ m{d}}} {boldsymbol{q}}(t)}}{{{{ m{d}}} t}} = - frac{{{D_T}}}{{{k_B}T}}nabla U({boldsymbol{q}}) + sqrt {{text{2}}{D_T}} {boldsymbol{R}}(t) + {U_0}{boldsymbol{n}} hfill & frac{{{{ m{d}}boldsymbol psi} (t)}}{{{{ m{d}}} t}} = sqrt {2{D_R}} {boldsymbol{R}}(t) end{aligned} ight} $$

(6)

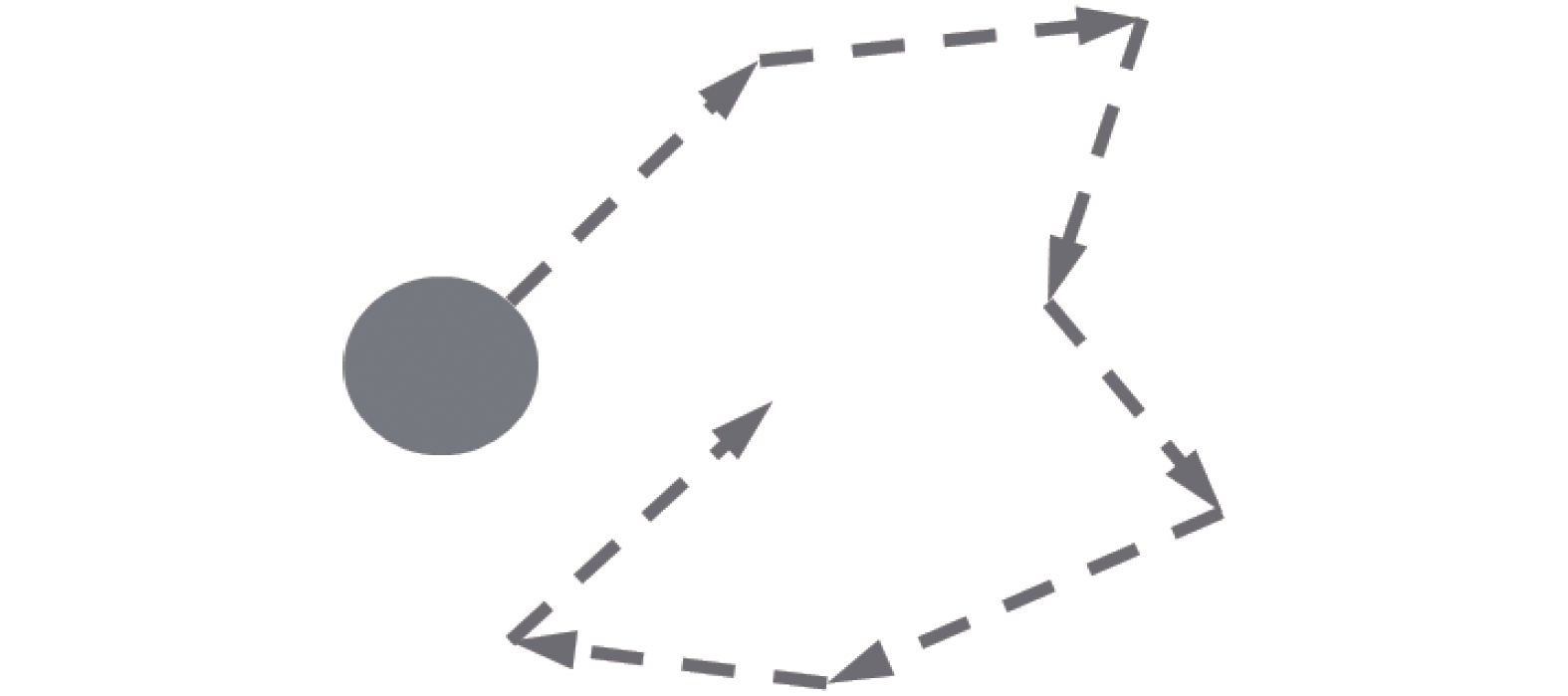
根据式(6)建立的数学模型, 单个活性粒子的运动轨迹如图1所示, 粒子从环境中获得能量后所呈现的运动形式用直行速度U₀和转向扩散系数D_R来描述.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
活性粒子运动示意图



Figure
1.
Schematic diagram of active particle locomotion



下载:
全尺寸图片
幻灯片

1.2
活性流体黏度的模拟计算

分子动力学模拟计算黏度的方法主要包括平衡分子动力学法(equilibrium molecular dynamics, EMD)^[26]和非平衡分子动力学法(non-equilibrium molecular dynamics, NEMD)^[27]. 其中, EMD法主要使用Green-Kubo关系^[28]确定流体黏度

$$ eta {text{ = }}frac{V}{{{k_B}T}}int_0^infty {leftlangle {{P_{alpha beta }}(t) cdot {P_{alpha beta }}(0)} ight angle } {text{d}}t $$

(7)

其中, V是系统的体积, P_αβ为应力张量的分量. 然而, 对于活性流体这样的非平衡体系, 使用NEMD法计算会得到更加准确的结果. NEMD法的思路是对流体施加一个剪切作用, 计算流体在剪切作用下的响应, 借助计算动量通量和速度梯度的比值确定流体的黏度^[29-30]. Müller-Plathe^[31]对NEMD法做出改进, 提出以非物理(unphysical)的方法在系统中施加动量通量. Müller-Plathe的思路是将模拟盒子沿指定方向划分为M层, 第1层在指定方向的下边缘, 第M层在指定方向的上边缘. 每N步交换模拟盒子中不同层的两个粒子的动量, 由于体系中每个粒子的质量相同, 相当于二者的动能也发生了交换. 随着模拟过程的进行, 可以在体系中产生一个剪切速率曲线来计算流体的黏度. 该方法也被称为反向非平衡分子动力学(reverse non-equilibrium molecular dynamics, rNEMD)法, 这是因为NEMD法是通过对体系施加剪切作用, 然后对应力张量的非对角元(正比于动量通量)进行统计计算, 而rNEMD法是先施加动量通量, 剪切速率曲线是流体响应的结果.

在布朗动力学的模拟过程中, 通过对流体速度场、特征剪切应力和特征剪切速率等物理量的统计计算, 就可以获得流体的黏度值. 为验证黏度计算方法的可靠性, 采用简单LJ流体进行测试, 其理论黏度η^*=1.0. 图2给出采用EMD法、NEMD法和rNEMD法模拟计算LJ流体黏度的结果. 从图2可以看出, EMD法计算的黏度随时间波动较大, 计算得到的黏度平均值为0.946; NEMD法计算得到的黏度平均值为1.18; 而使用反向非平衡的rNEMD法获得的被动流体黏度平均值为0.997, 更接近该流体的理论黏度值, 且相对于其他两种方法计算结果更加稳定, 可以快速准确地确定体系的黏度. 因此, 本文采用rNEMD法计算活性流体的黏度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
3种方法计算被动LJ流体的黏度随时间的变化关系



Figure
2.
Variation of viscosity of LJ passive fluid with time simulated by three schemes



下载:
全尺寸图片
幻灯片

1.3
模型的求解计算

本研究使用LAMMPS软件求解描述活性粒子运动的扩展布朗运动方程, 采用Velocity-Verlet算法, 粒子间作用势能选择LJ势函数, 运算时的物理量使用LJ单位, 边界处采用周期性边界条件. 本文为了考察活性粒子体积分数、直行速度和转向扩散系数对活性流体流变行为的影响规律, 确定模拟区域为0.5 mm × 0.5 mm × 0.1 mm的准二维模拟盒, 活性粒子被设置为刚性球体, 活性流体中粒子的体积分数φ分别为0.05%, 0.1%, 0.3%和0.5%, 活性粒子的直行速度U₀的大小分别为0 μm/s (无直行运动)、20 μm/s, 30 μm/s和40 μm/s, 活性粒子的转向行为由转向扩散系数D_R反映, 大小分别为0 s^?1 (无转向运动)、1.0 × 10^?4 s^?1、5.0 × 10^?4 s^?1和1.0 × 10^?3 s^?1.

通过求解描述活性粒子运动的扩展布朗运动方程, 可以得到体系中每个活性粒子的运动轨迹信息. 活性流体的非平衡特性和活性布朗动力学中的随机机制使得结果的准确性受到影响, 需要大量的重复统计以获取更为接近实际情况的结果. 因此, 本文每一种工况的模拟计算, 先运行5.0 × 10⁴τ (τ是体系特征时间)的时间进行弛豫, 然后运行2.0 × 10⁵τ的时间以获取所需的宏观物理信息, 计算中统计时间步长Δt=0.001τ. 使用大量独立轨迹的时间平均来获得系统平均, 这对于体系宏观物理量的计算是必要的.

1.4
模型的可靠性验证

被动流体是平衡体系, 高斯噪声的均值为零, 体系内粒子分布是均匀的, 只有在外部输入能量的情况下才会出现相变. 而活性流体属于非平衡体系, 无需外界输入能量, 通过粒子间的相互作用就可发生“相变”, 出现分离的“液相”和“气相”, 具体表现为粒子聚集, 并出现分布不均匀的情况. 图3给出活性流体和被动流体中粒子分布的对比. 从图3可以看出, 被动流体作为平衡体系, 粒子的运动遵从布朗运动方程, 长时间运动后仍呈现均匀分布状态(见图3(b)); 而活性流体是非平衡体系, 会自发地出现粒子聚集的“液相”区和粒子稀疏的“气相”区(见图3(c)), 再现非平衡体系的这一特征证明了本文提出的扩展布朗运动方程的正确性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
被动流体平衡体系和活性流体非平衡体系粒子分布的对比



Figure
3.
Comparison of particle distribution between equilibrium system of passive fluids and non-equilibrium system of active fluids



下载:
全尺寸图片
幻灯片


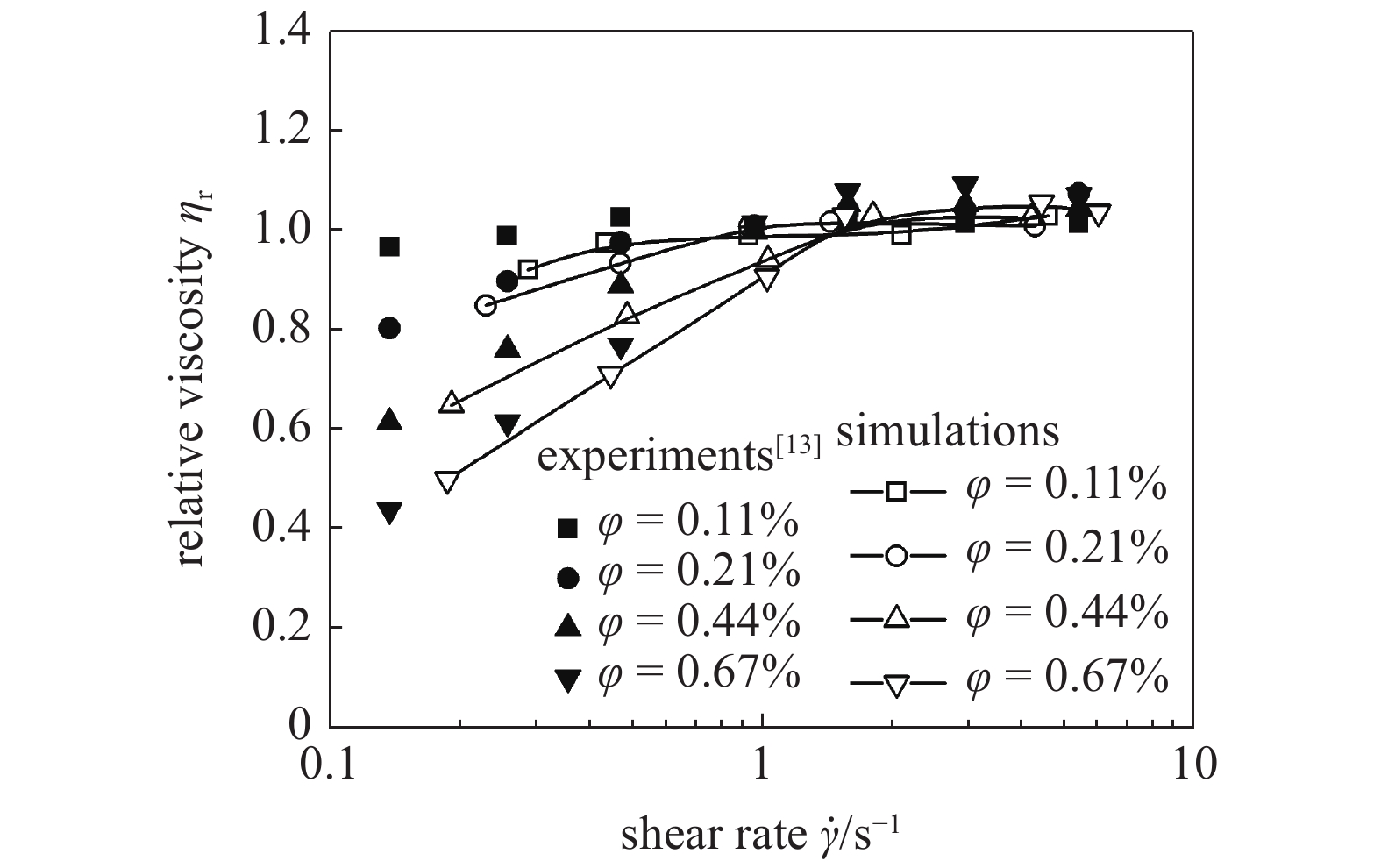
因易于配制、稳定性高和粒子自驱动机制简单等特点, 大肠杆菌悬浮液通常被作为典型的活性流体模型来研究活性流体所表现出的一些特殊的物理现象. 基于此, 大肠杆菌悬浮液的流变学实验测试结果被用来验证本文提出的数学模型和模拟计算方法的可靠性. 设不加入活性粒子的液相黏度为η₀, 加入活性粒子后体系的黏度为η, 定义体系的相对黏度为η_r=η/η₀. 图4给出使用rNEMD法计算的活性流体相对黏度结果与López等^[13]的实验结果的对比. 自驱动活性粒子的直行速度U₀和转向扩散率D均使用López等^[13]实验中测得的数据, 其中U₀=20 μm/s, D=13 μm²/s. 从图4可以看出, 在低剪切速率区域, 基于本文确定的活性流体模型及rNEMD法所得的结果与实验结果一致性良好. 与实验手段不同的是, 布朗动力学模拟的方法可以更容易地控制变量, 分析多因素对活性流体流变行为的影响规律.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
相对黏度随剪切速率变化的模拟结果和实验数据对比



Figure
4.
Comparison of simulated results and experimental data of relative viscosity of active fluids



下载:
全尺寸图片
幻灯片

2.
模拟结果与分析

2.1
活性流体流变行为的影响因素分析

图5给出不同体积分数活性流体的相对黏度η_r随剪切速率$ dot gamma $的变化. 活性粒子的自驱动速度U₀=40 μm/s, 转向扩散系数D_R=0.0001 s^?1. 从图5可以看出, 对于体积分数为0.05%的活性流体, 相对黏度随剪切速率增大没有明显改变; 而体积分数φ≥0.1%的活性流体呈现非牛顿流体特性, 流变曲线具有非单调性, 可以划分为3个区域, 具体包括: (1) 黏度下降区($ dot gamma $< ~ 10 s^?1), 低剪切速率区域内活性流体的相对黏度η_r<1, 即活性流体的黏度低于未加入活性粒子的流体黏度, 并且活性粒子的体积分数越高, 黏度下降越明显; (2) 过渡区( ~ 10 s^?1<$ dot gamma $< ~ 50 s^?1), 中剪切速率区域内活性流体的黏度出现先增大后减小的变化趋势, 并且存在一个临界剪切速率$ {dot gamma _{text{c}}} $, 此时活性流体的黏度最大, 临界剪切速率$ {dot gamma _{text{c}}} $出现在剪切速率$ dot gamma $=20 s^?1附近; (3) 牛顿区($ dot gamma $> ~ 50 s^?1), 高剪切速率区域内活性流体的相对黏度η_r ≈ 1, 可以被看作为牛顿流体. 活性流体的非单调流变学行为受到活性粒子自驱动行为和外部施加的剪切应力耦合作用的影响, 当剪切速率较小时, 活性粒子自驱动行为的贡献占主导, η_r < 1; 当剪切速率较大时, 外部施加的剪切应力的作用占主导, η_r ≈ 1; 当二者作用的大小相当时, 出现黏度变化的过渡区域, 黏度值小幅度增大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
活性粒子的体积分数对活性流体相对黏度的影响



Figure
5.
Effect of volume fraction of active fluid on relative viscosity of active particles



下载:
全尺寸图片
幻灯片


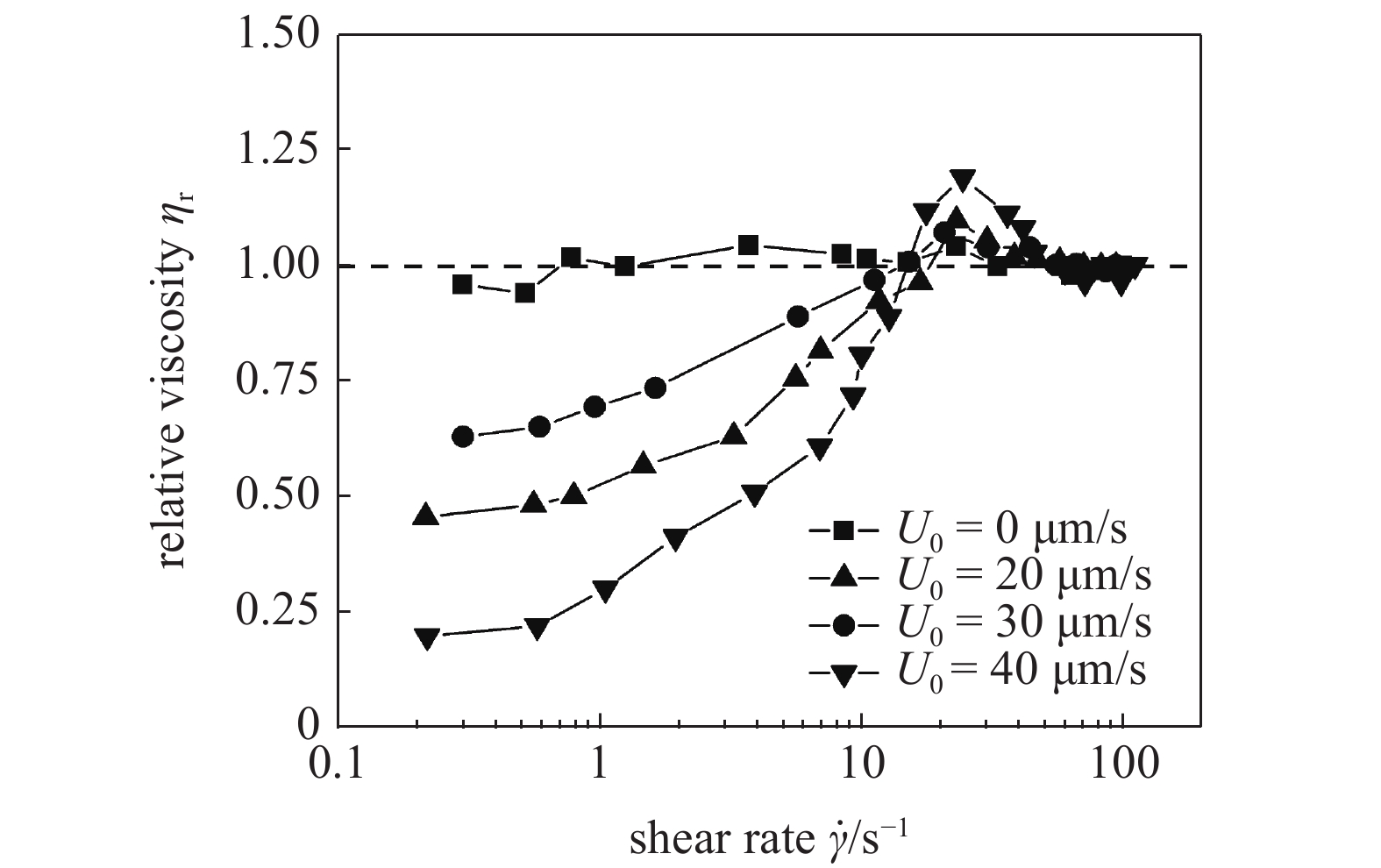
图6给出具有不同直行速度活性粒子的活性流体相对黏度随剪切速率的变化. 活性粒子的体积分数φ=0.5%, 活性粒子的转向扩散系数D_R = 0.0001 s^?1. 从图6可以看出, 对于活性粒子直行速度U₀ = 0 μm/s的活性流体, 相对黏度随剪切速率增大没有明显改变; 活性粒子的直行速度U₀的大小对低剪切区黏度的下降有显著贡献, U₀越大则在同一剪切速率下黏度下降的幅度越大; 而且活性流体在过渡区形成的先增稠后稀化现象也更显著, 证明活性粒子的直行运动对活性流体流变行为有重要影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
活性粒子直行速度对活性流体黏度的影响



Figure
6.
Effect of forward locomotion velocity of active particles on relative viscosity of active fluids



下载:
全尺寸图片
幻灯片


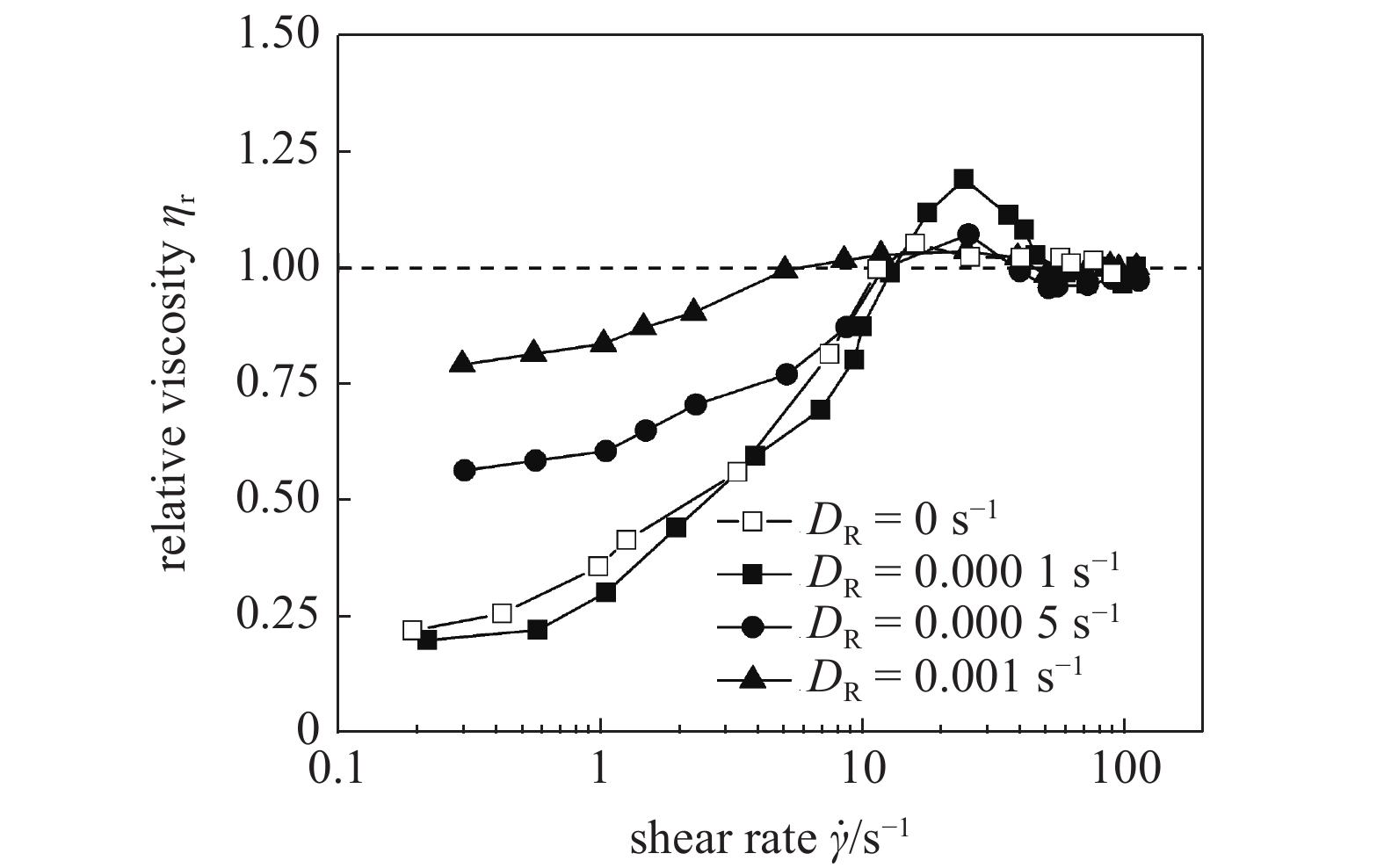
除了直行速度外, 控制其自驱动方向改变频率的转向扩散系数D_R同样是描述活性粒子自驱动行为的重要参数. 当D_R很大时, 活性粒子会在原地不断转向, 导致直行运动不明显; 当D_R较小时, 与直行运动耦合使粒子表现出一定的活性(同时具有明显的直行运动和转向运动); 当D_R为零时, 活性粒子无转向运动, 只存在直行运动. 图7给出具有不同转向扩散系数活性粒子组成的活性流体的相对黏度随剪切速率的变化. 活性粒子的体积分数φ = 0.5%, 活性粒子的直行速度U₀ = 40 μm/s. 从图7可以看出, 转向运动和直行运动的耦合作用是导致过渡区流变曲线非单调变化的主要原因(结合图6分析), 黏度下降区活性流体黏度下降的现象是由活性粒子直行运动所引起的. 究其原因是不发生转向运动的活性粒子仅具有直行运动能力, 其仍可通过活性粒子间相互碰撞作用形成一定规模的微集群运动, 造成低剪切速率区域内宏观黏度的下降; 由于形成的微结构稳定性较差, 剪切速率升高后也容易被破坏, 因此在中剪切速率区域没有观察到流变曲线非单调变化的现象. 从图7还可以看出, 若活性粒子存在转向运动, 低剪切速率区域活性流体黏度的下降幅度随D_R的增大而减小; 在过渡区, 先增稠后稀化的非单调流变学现象随着D_R的增大而减弱. 这些现象说明若活性粒子的运动方向改变地过于频繁, 会对活性流体的非牛顿流体行为有明显的抑制作用.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
活性粒子转向扩散系数对活性流体相对黏度的影响



Figure
7.
Effect of rotational diffusion coefficient of active particle on relative viscosity of active fluids



下载:
全尺寸图片
幻灯片

2.2
活性流体特殊流变行为的形成机理

悬浮液体系的宏观流变特性是由体系中的介观结构决定的, 通过考察不同剪切速率下活性粒子的聚集行为, 可以确定活性流体特殊流变学行为的形成机理. 活性粒子可自发形成直行运动和转向运动, 粒子间相互作用频繁, 容易形成聚集结构, 诱导集群运动. 图8给出活性粒子涨落计算方法示意图. 如图8所示, 观察区被等面积划分为若干区域, 对每个区域内粒子数量计数, 以每个区域内粒子涨落(标准差ρ)表征活性粒子的聚集程度. 标注差ρ的计算公式如下

$$ ho {text{ = }}sqrt {frac{{displaystylesumlimits_{i = 1}^n {{{left( {{x_i} - bar x} ight)}^2}} }}{n}} $$

(8)

其中, x_i为第i个区域中的活性粒子数, $bar x$为所有区域中活性粒子数的平均值, n是划分区域的个数.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
活性粒子涨落计算方法示意图



Figure
8.
Schematic of the calculation method for the fluctuation of active particles



下载:
全尺寸图片
幻灯片


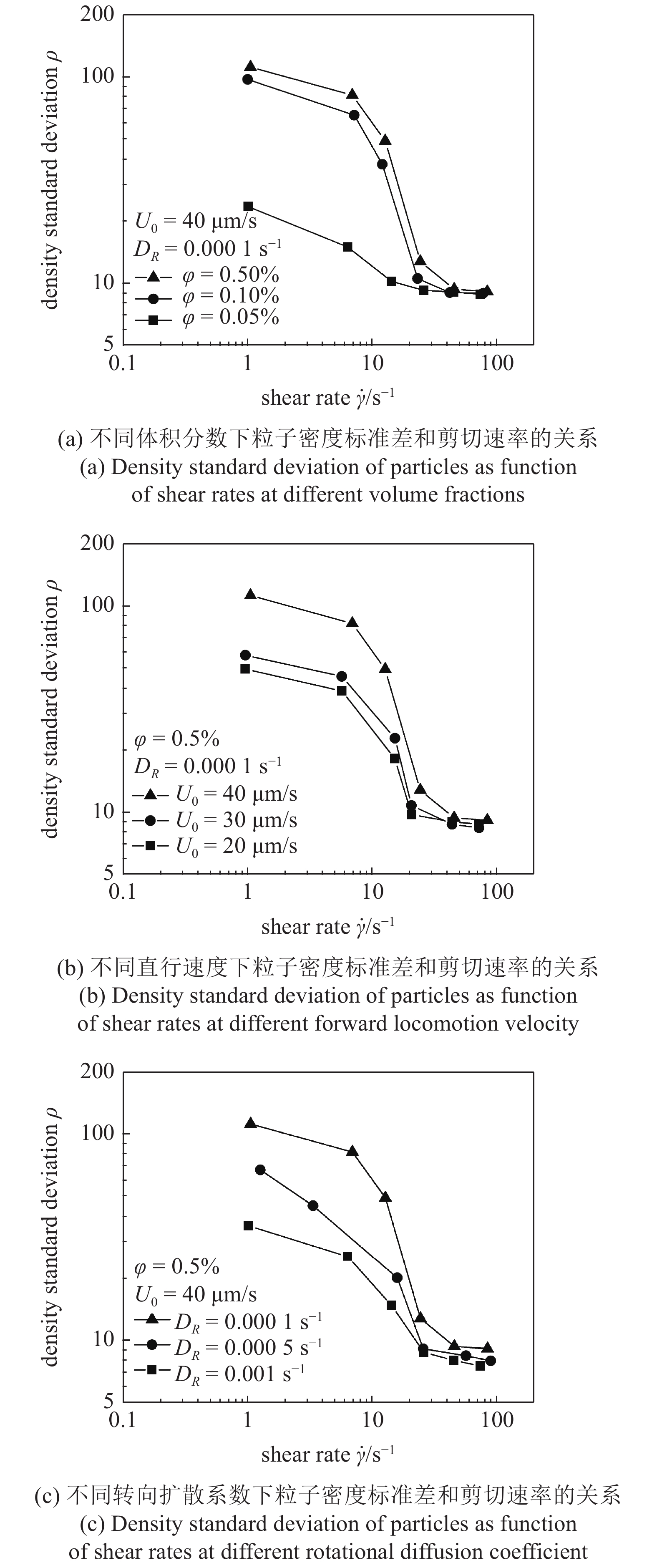
图9是不同工况下活性流体中粒子涨落随剪切速率的变化. 从图9可以看出, 活性粒子的涨落现象与活性粒子的体积分数、直行速度和转向扩散系数的大小直接相关; 活性粒子体积分数越高、直行速度越快和转向扩散系数越小, 活性粒子分布的标准差越大, 也就是涨落越显著. 从图9还可以看出, 随着外部施加剪切速率的不断增大, 在低剪切速率区域, 粒子分布的标准差缓慢减小; 在中剪切速率区域, 粒子分布的标准差急剧的下降; 而在高剪切速率区域, 粒子分布的标准差基本不发生改变. 3个剪切速率区域内的涨落情况与2.1节中活性流体的流变曲线划分为3个阶段具有一致性, 这说明活性流体特殊的流变行为与活性粒子的涨落密切相关. 在低剪切速率区域, 粒子自驱动形成的聚集结构产生的内部应力可以抵消部分外部剪切应力, 使得驱动活性流体达到一定剪切速率的剪切应力减小, 因此体系的相对黏度η_r < 1. 随着外部剪切速率的增大, 活性流体中的聚集结构产生的内部应力相比于外部剪切作用变小, 驱动活性流体达到一定剪切速率所需的剪切力增大, 宏观表现为剪切增稠行为, 介观表现为粒子分布标准差快速减小. 在高剪切速率区域, 活性粒子自发形成的聚集结构会被逐渐破坏, 宏观表现为剪切稀化行为, 介观表现为粒子分布标准差加速减小. 当外部施加的剪切作用足够大时, 活性流体中的聚集结构完全消失, 活性粒子的分布趋向于与被动粒子类似的随机分布, 此时体系可视为一般被动流体, 具有牛顿流体特性. 活性粒子的体积分数、自驱动直行速度和转向扩散系数均通过影响聚集结构的形成进而改变体系的宏观流变特性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-368-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
活性流体中粒子密度标准差与剪切速率的关系



Figure
9.
Density standard deviation of particles as function of shear rates in active fluids



下载:
全尺寸图片
幻灯片

3.
结 论

本文基于布朗动力学理论, 通过扩展布朗运动方程, 引入驱动项和随机旋转项再现活性粒子的直行和转向运动, 建立可以模拟活性粒子运动的数学模型. 采用反向非平衡分子动力学(rNEMD)法计算活性流体黏度, 考察了活性粒子体积分数、直行速度和转向扩散系数对活性流体流变行为的影响规律, 并分析活性粒子的涨落确定活性流体特殊流变行为的形成机理. 结论如下:

(1)建立的活性流体布朗动力学模型可以很好地描述活性粒子的直行和转向运动, 可以再现活性流体体系中粒子分布不均匀的非平衡特征, rNEMD法可以高效准确地计算体系的黏度.

(2)随着剪切速率的增大, 活性流体的流变曲线可划分为3个阶段. 在低剪切速率区域为黏度下降区, 活性流体的相对黏度η_r < 1; 中剪切速率区域为过渡区, 活性流体的相对黏度呈现先增大后减小的非单调变化; 高剪切速率区域为牛顿区, 活性流体的黏度与一般被动流体类似. 活性粒子的体积分数越大、活性粒子的直行速度越快, 非单调流变学行为越显著. 低剪切速率区域活性流体黏度下降是因为活性粒子直行运动存在引起的, 转向运动的存在是导致中剪切速率区域流变曲线非单调变化的主因, 活性粒子频繁改变运动方向会抑制活性流体的非牛顿特性.

(3)活性流体的宏观流变学特性和粒子的涨落直接相关. 活性粒子体积分数越高、直行速度越快和转向扩散系数越小, 活性流体中活性粒子越容易产生显著的涨落; 活性粒子的涨落越显著, 低剪切速率区域的黏度下降现象和中剪切速率区域的非单调流变学行为越明显. 随着外部剪切流场的增强, 活性粒子形成的局部聚集结构会被外部施加的剪切作用破坏, 并在中剪切速率区域流变曲线出现先增稠后稀化的非单调行为; 当剪切速率进一步增大时, 活性流体中粒子聚集结构被完全破坏, 体系可视为一般被动流体.