引 言

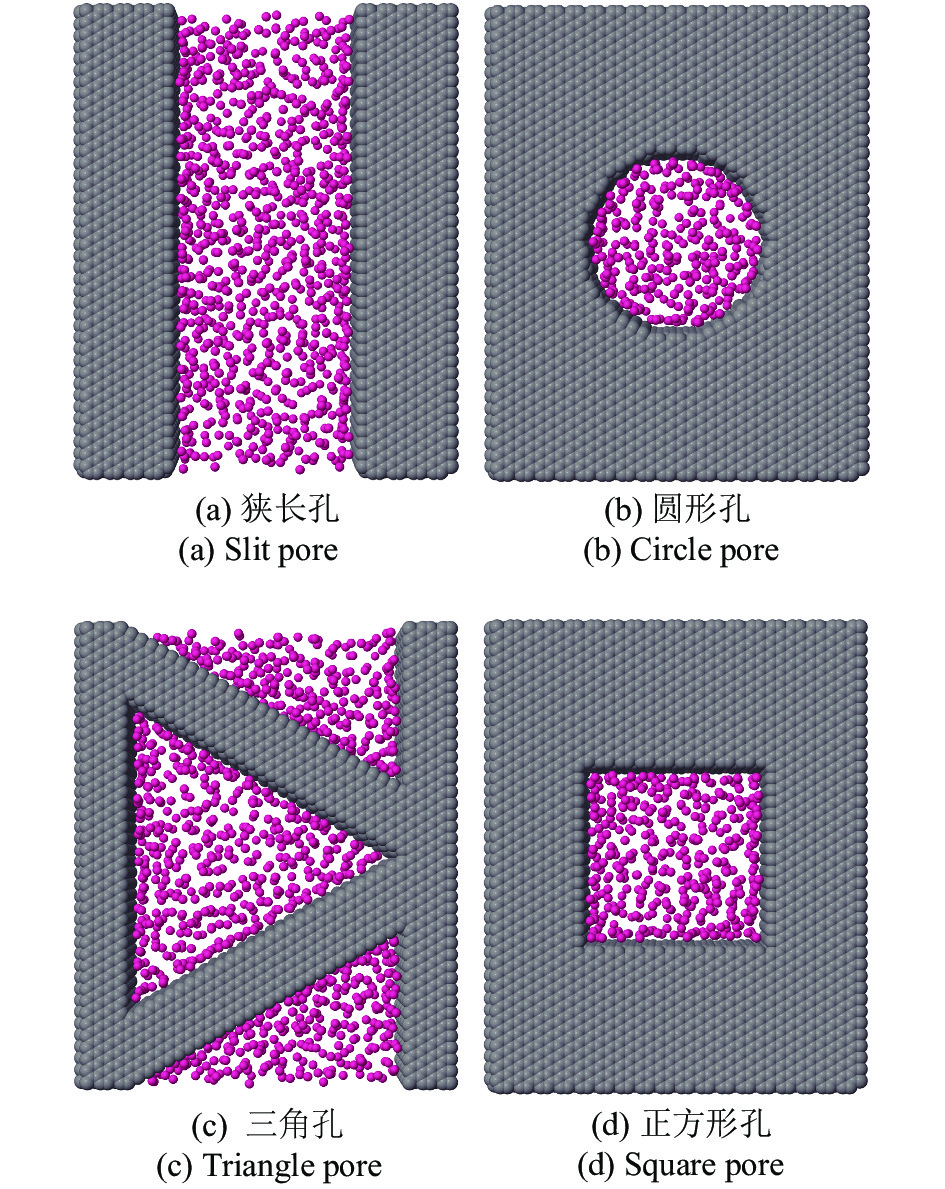
页岩气藏储层孔隙结构复杂, 孔隙尺寸跨度较大^[1-5]. 国际理论化学与应用化学联合会对孔隙尺寸分类定义^[6]如下: 孔隙尺寸在2 nm以下孔隙为微孔隙; 孔隙尺寸在2 ~ 50 nm之间的孔隙为介孔隙; 孔隙尺寸在50 nm以上孔隙为大孔隙. 2 ~ 50 nm之间的介孔占据了页岩孔隙绝大部分^[7-10]. 吸附气和自由气共存于有机质孔隙中^{[11, 12]}, 且吸附气含量占据总含气量20% ~ 85%^[13-15]. Rine等^[16]通过对美国主要页岩区块孔隙形状进行分析, 将页岩孔隙形状划分为圆形孔隙、三角形孔隙、正方形孔隙、狭长孔隙. Yang等^[17]通过四川龙马溪组页岩扫描电镜结果将页岩孔隙形状划分为长方形、椭圆形以及三角形. Afsharpoor等^[18]将页岩孔隙形状划分为4种孔隙形状包括圆形孔隙、正方形孔隙、三角形孔隙、狭长孔隙. 根据我国某区块页岩有机质扫描电镜成像结果, 与Afsharpoor等归纳的4种孔隙形状较为吻合(图1). 页岩气吸附规律研究是认识页岩气流动与赋存状态的基础. Ren等^[19]分析了不同孔隙压力(0.1 ~ 25 MPa), 有机质含量对气体绝对吸附以及过剩吸附的影响. Tang等^[20-21]测量了龙马溪页岩不同温度(273.15 ~ 373.15 K), 不同孔隙压力 (0.1 ~ 27 MPa)下气体绝对吸附以及过剩吸附曲线. Li等^[13]采用多点吸附模型分析了四川盆地寒武纪页岩高温高压下气体绝对吸附与过剩吸附规律. Wang等^[22]分析了四川盆地页岩岩心不同孔隙压力(0.1 ~ 17 MPa)、地层温度(305 ~ 315 K)、粒径大小下气体动态吸附过程. Pang等^[23]通过岩心吸附实验得到气体吸附解吸曲线, 进一步建立狭长孔内自由气和吸附气流动模型分析了岩心吸附参数对气体流动能力的影响. 岩心实验方法只能测量一定温度压力阶段下页岩岩心气体吸附和流动规律, 由于实验条件限制, 无法测量原始地层高温高压下的气体吸附和流动行为. 另一方面, 目前岩心实验方法难以揭示孔隙形状对气体吸附和流动规律的影响. 分子模拟方法被广泛应用于研究页岩纳米有机质孔隙内气体吸附规律^[10]. Mosher等^[8]和Jin等^[24-25]采用巨正则蒙特卡洛方法研究了不同孔隙压力下狭长孔隙内气体吸附规律. Guo等^[26]研究了高温高压下(温度373 K, 压力40 MPa)有机质狭长孔隙内气体吸附规律. Cracknell等^[27]建立了狭长孔隙和圆形孔隙模型研究了有机质内气体吸附规律. He等^[28]结合巨正则蒙特卡洛分子模拟方法和分子动力学模拟方法研究了有机质多孔介质内气体吸附和流动规律. Wu等^[29]基于理想气体吸附模型分析了圆形有机质孔隙内自由气流动和吸附气流动对气体渗透率的贡献. Akkutlu等^[30]基于分子动力学模拟结果分析了圆形孔隙内吸附气表面扩散对气体流动能力的贡献. Yin等^[31]结合分子模拟结果研究了单个纳米有机孔内页岩气的耦合输运机制, Qu等^[32]研究了有机质内自由气和吸附气的耦合扩散特性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
不同有机质孔隙形状高分辨率页岩扫描电镜图像



Figure
1.
High resolution shale SEM images (the different pore morphologies are marked on the SEM image)



下载:
全尺寸图片
幻灯片


综上所述, 目前页岩有机质纳米孔隙气体吸附与流动规律研究均存在尚未解决的问题. 从气体吸附角度, 岩心实验方法仅能对页岩低压下过剩吸附线进行测量, 实际气藏条件高压高温下气体绝对吸附与过剩吸附规律还不是很清楚, 现有理论模型未考虑有机质孔隙中不同孔隙形状对气体吸附规律的影响. 从气体流动角度, 吸附气表面扩散能力取决于孔隙形状以及页岩岩心表面吸附气浓度随压力的变化规律, 但岩心实验测量方法无法测量得到岩心固体壁面吸附层内气体浓度, 导致对不同孔隙形状下吸附气表面扩散能力认识不清楚. 为解决以上两个问题, 本文首先采用巨正则蒙特卡洛方法模拟气体在不同形状有机质孔隙吸附过程, 分析了吸附曲线以及气体浓度随孔隙尺寸、压力的变化, 研究了孔隙形状对气体吸附规律的影响规律. 在明确不同形状有机质孔隙内气体吸附规律基础上, 建立不同形状有机质孔隙内吸附气表面扩散数学模型和考虑气体滑脱的自由气流动模型, 分析了不同形状有机质孔隙中吸附气流动与自由气流动对气体流动能力的贡献, 揭示了实际生产过程中有机质孔隙形状、孔隙尺寸对页岩气流动的影响机制.

1.
基于巨正则蒙特卡洛方法的气体吸附模拟

1.1
巨正则蒙特卡洛方法原理

巨正则系统为体积(V)、温度(T)与化学势能(μ)皆为定值的系统集合^[33]. 系统的粒子数为可变化的参数. 产生巨正则系综的马尔可夫链过程涉及到三种不同的粒子随机移动: ①随机移动系统中的一个粒子; ②随机消除系统中的一个粒子; ③随机产生一个新的粒子. 采用梅特罗波利斯?黑斯廷斯?马尔科夫蒙特卡洛算法模拟上述三种随机移动^[34-35]. 每种随机过程接受或拒绝的概率相等. 粒子间势能形式采用12–6 Lennard?Jones (LJ)势能模型进行描述^[36], 见式(1). 本文基于光滑壁面假设, 采用刚性碳原子模型以及ABA构型^[37]构建4种不同孔隙形状的三维有机质孔隙: 狭长孔隙、圆形孔隙、三角形孔隙以及正方形, 边界条件设置为周期性边界. 通过每种孔隙中的最大内切圆来定义孔隙尺寸, 横向剖面见图2, 纵向剖面见图3, 模型孔隙半径设置范围1~ 8 nm.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
不同有机质孔隙模型横向剖面形状(孔隙半径2 nm)



Figure
2.
Visualization of constructed 3D carbon pores lateral cross sections (r = 2 nm)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
有机质孔隙模型纵向剖面(圆形孔隙为例, 孔隙半径2 nm)



Figure
3.
Visualization of constructed carbon pore longitudinal cross section, circle pore as an example, r = 2 nm



下载:
全尺寸图片
幻灯片

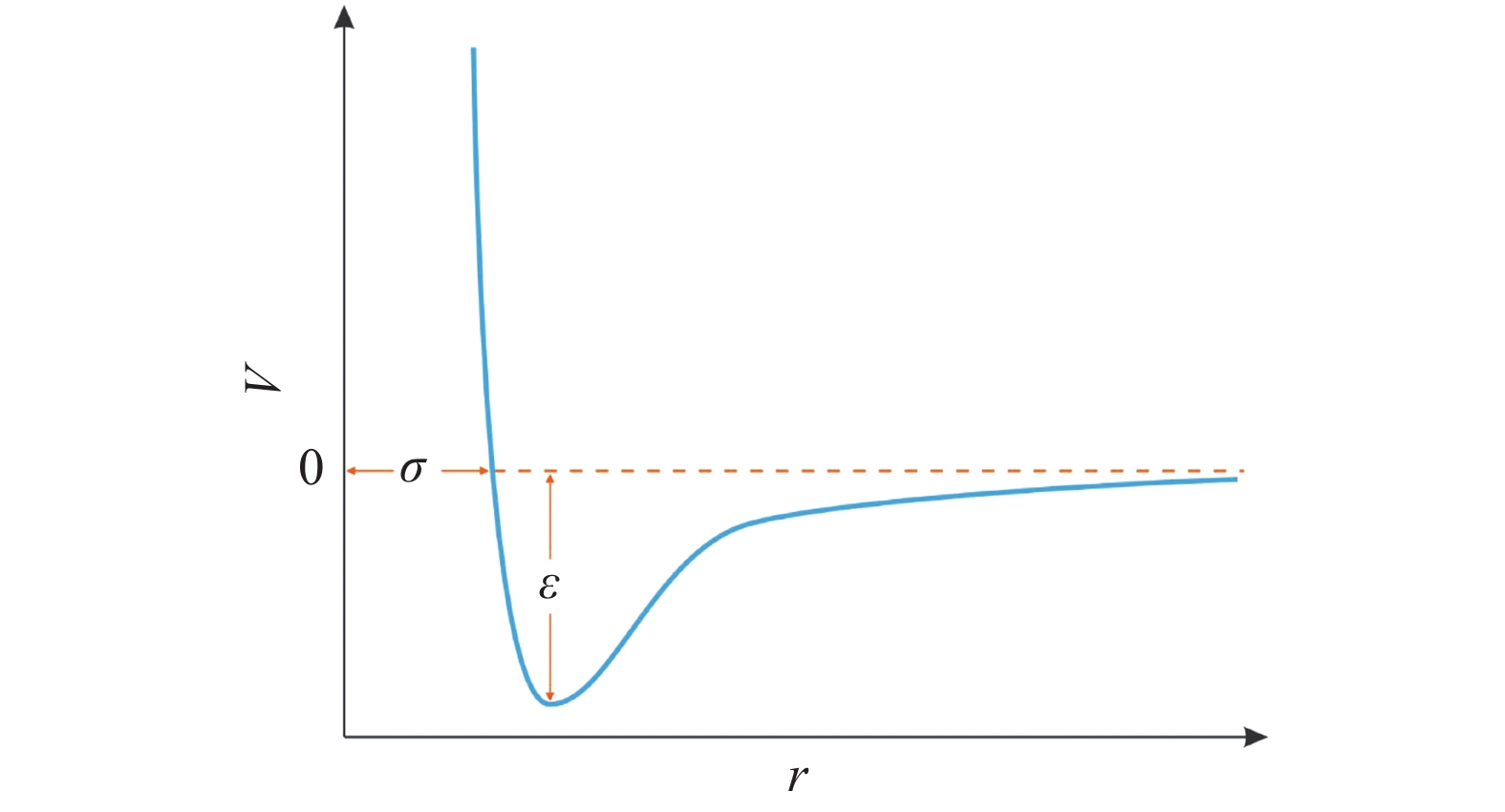
$$V(r) = 4varepsilon left[ {{{left( {frac{sigma }{{{r_{ m{m}}}}}} ight)}^{12}} - {{left( {frac{sigma }{{{r_{ m{m}}}}}} ight)}^6}} ight]$$

(1)

式中, r_m为原子对之间的距离, m; ε和σ为势能参数, 因原子的种类而异. ε物理意义为由势能最低点至势能为0的差, 其大小反应势能曲线的深度. σ大小反映原子间的平衡距离, 见图4. $r_{
m{m}}^{ - 12}$为排斥项, $r_{
m{m}}^{ - 6}$为吸引项. 当r_m很大时, LJ势能趋近于0, 表示当原子对距离很远时, 彼此间已无键结作用. 力场参数见表1^[38-39], 其中k_B为玻尔兹曼常量, 1.38064852 × 10^?23 m²·kg·s^?2·K^?1. 两种不同原子间LJ作用常数采用Lorentz–Berthelot规则进行计算^[34], 见式(2)和式(3)



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
LJ势能曲线示意图



Figure
4.
Illustration of LJ potential curve



下载:
全尺寸图片
幻灯片





表
1
力场参数



Table
1.
Force field potential parameters



table_type1 ">

Potential parameter	εff/kB/K	σff/nm
CH4	148	0.373
C	28	0.34

下载:
导出CSV
|显示表格

$${varepsilon _{ij}} = sqrt {{varepsilon _{ii}}{varepsilon _{jj}}} $$

(2)

$${sigma _{ij}} = frac{{{sigma _{ii}} + {sigma _{jj}}}}{2}$$

(3)

采用Steele 10-4-3势能模型描述气体分子与孔隙壁面的相互作用^{[40, 41]}

$${varphi _{{ m{sf}}}} = 2{text{π}} { ho _{ m{s}}}{varepsilon _{{ m{sf}}}}sigma _{{ m{sf}}}^2varDelta left{ {frac{2}{5}{{left( {frac{{{sigma _{{ m{sf}}}}}}{{textit{z}}}} ight)}^{10}} - {{left( {frac{{{sigma _{{ m{sf}}}}}}{{textit{z}}}} ight)}^4} - left[ {frac{{sigma _{{ m{sf}}}^4}}{{3varDelta {{left( {{textit{z}} + 0.61varDelta } ight)}^3}}}} ight]} ight}$$

(4)

式中Δ为孔隙壁面碳原子层间距离(0.335 nm), ρ_s为孔隙壁面碳原子个数密度(114 nm^?3), σ_sf和ε_sf为基于式(2)和式(3)计算得到的孔隙壁面与气体分子之间的势能作用参数. z为气体分子与最外层孔隙壁面中心的最短距离, m.

气体逸度计算采用Peng–Robinson状态方程进行计算^[42], 见式(5) ~ 式(9)

$$P = - frac{{RT}}{{{V_{ m{m}}} - b}} - frac{{aalpha }}{{V_{ m{m}}^2 + 2b{V_{ m{m}}} - {b^2}}}qquad;;$$

(5)

$$a = frac{{0.457;235{R^2}T_{ m{c}}^2}}{{{P_{ m{c}}}}}qquadqquadqquad;;;;;;$$

(6)

$$alpha = {{ {1 + kappa left[ {1 - {{left( {{T / {{T_{ m{c}}}}}} ight)}^{0.5}}} ight]} }^2}qquadqquad;;$$

(7)

$$b = frac{{0.077;796R{T_{ m{c}}}}}{{{P_{ m{c}}}}}qquadqquadqquadqquad$$

(8)

$$kappa = 0.374;64 + 1.542;26omega - 0.269;92{omega ^2}$$

(9)

式中, P为压力, MPa; R为理想气体常数, R = 8.314 × 10^?3 kPa·m³·K^?1; V_m为摩尔体积, m³/mol; T为温度, K; T_c为临界温度, P_c为临界压力, ω为偏心因子; 对于甲烷气体P_c = 4.6 MPa, T_c = 190.6 K, ω = 0.011. 设置温度400 K, 最高压力60 MPa, 模拟随机过程次数110百万步, 模拟得到的孔隙半径2 nm、压力60 MPa、温度400 K条件下气体分子分布见图5.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同形状有机质孔隙内气体分子分布(气体分子: 红色, 孔隙半径2 nm)



Figure
5.
Gas molecule distribution in different shapes of organic pore (gas molecule: red color, r = 2 nm)



下载:
全尺寸图片
幻灯片


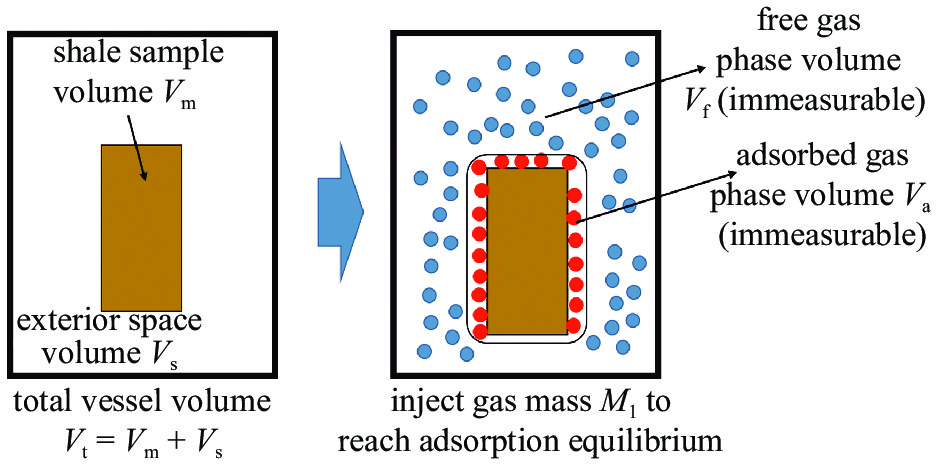
图6表示实验室等温吸附曲线测试原理示意图, 对于固定容积真空状态下的箱体, 注入质量为M₁的气体, 根据质量守恒原理可以得到式(10), 其中ρ_adsorbedV_a表示绝对吸附量, ρ_adsorbedV_a?ρ_freeV_a表示过剩吸附量. 由于吸附相体积V_a不可测量, 因此实验室条件下测量得到的气体吸附量为过剩吸附量ρ_adsorbedV_a?ρ_freeV_a, 并不是表征真实气体吸附量的绝对吸附量ρ_adsorbedV_a. 当压力很小时, 吸附相V_a非常小, ρ_freeV_a可忽略不计, 过剩吸附量可近似代替绝对吸附量, 但高压下由于ρ_free和V_a均增加, 因此实验室测量得到的过剩吸附量会远小于绝对吸附量



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
实验室等温吸附曲线测试原理示意图



Figure
6.
Illustration of laboratory measured isothermal gas adsorption curve



下载:
全尺寸图片
幻灯片

$$begin{split} {M_1} =& { ho _{{ m{free}}}}left( {{V_{ m{s}}} - {V_{ m{a}}}} ight) + { ho _{{ m{adsorbed}}}}{V_{ m{a}}} = & { m{ }} { ho _{{ m{free}}}}{V_{ m{s}}} + { ho _{{ m{adsorbed}}}}{V_{ m{a}}} - { ho _{{ m{free}}}}{V_{ m{a}}} end{split} $$

(10)

式中, ρ_free和ρ_adsorbed分别表示自由气密度和吸附气密度, kg/m³; V_s和V_a分别表示外部封闭空间体积和吸附相气体体积, m³.

过剩吸附量与绝对吸附量之间关系采用式(11)进行计算^[43]

$${n_{{ m{ex}}}} = {n_{{ m{abs}}}} - {V_{ m{g}}}{ ho _{ m{g}}}$$

(11)

式中, n_ex为过剩吸附量, mol/m³; n_abs为绝对吸附量, mol/m³; V_g为孔隙体积, m³. 根据上述孔隙半径范围, 1.2节主要对过剩吸附、绝对吸附以及吸附气赋存状态开展研究.

1.2
页岩不同形状有机质孔隙内气体吸附规律与赋存状态

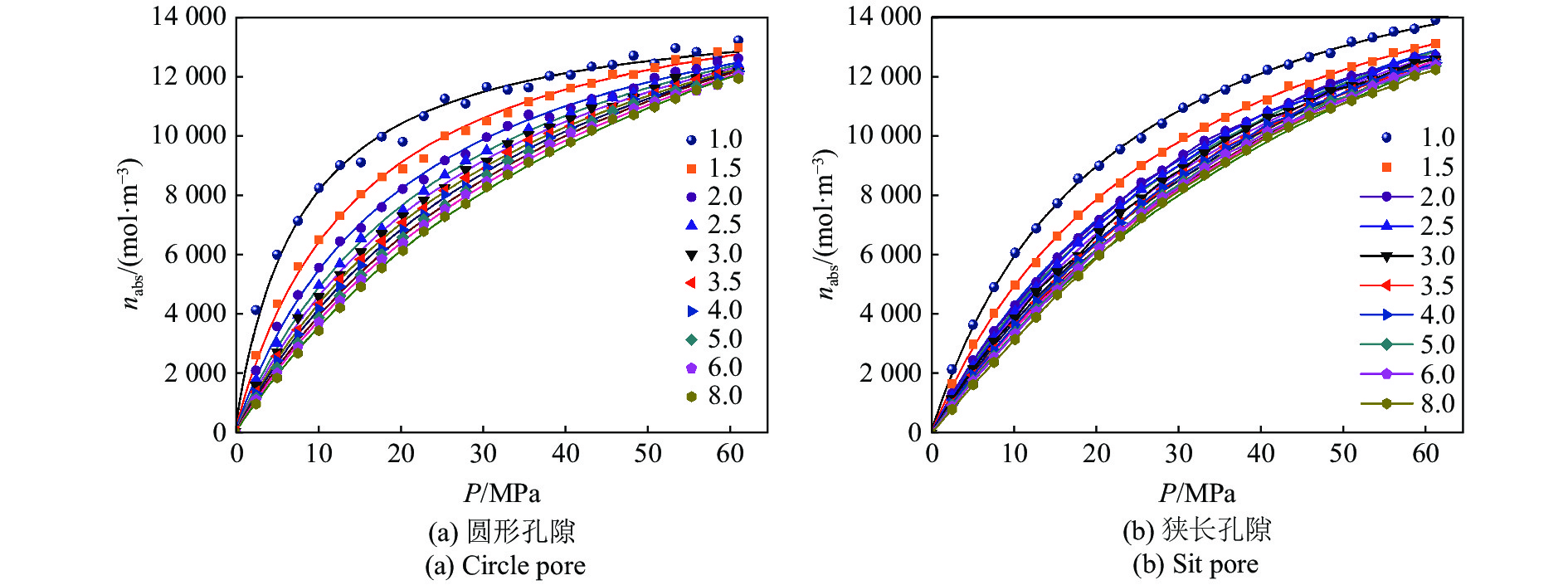
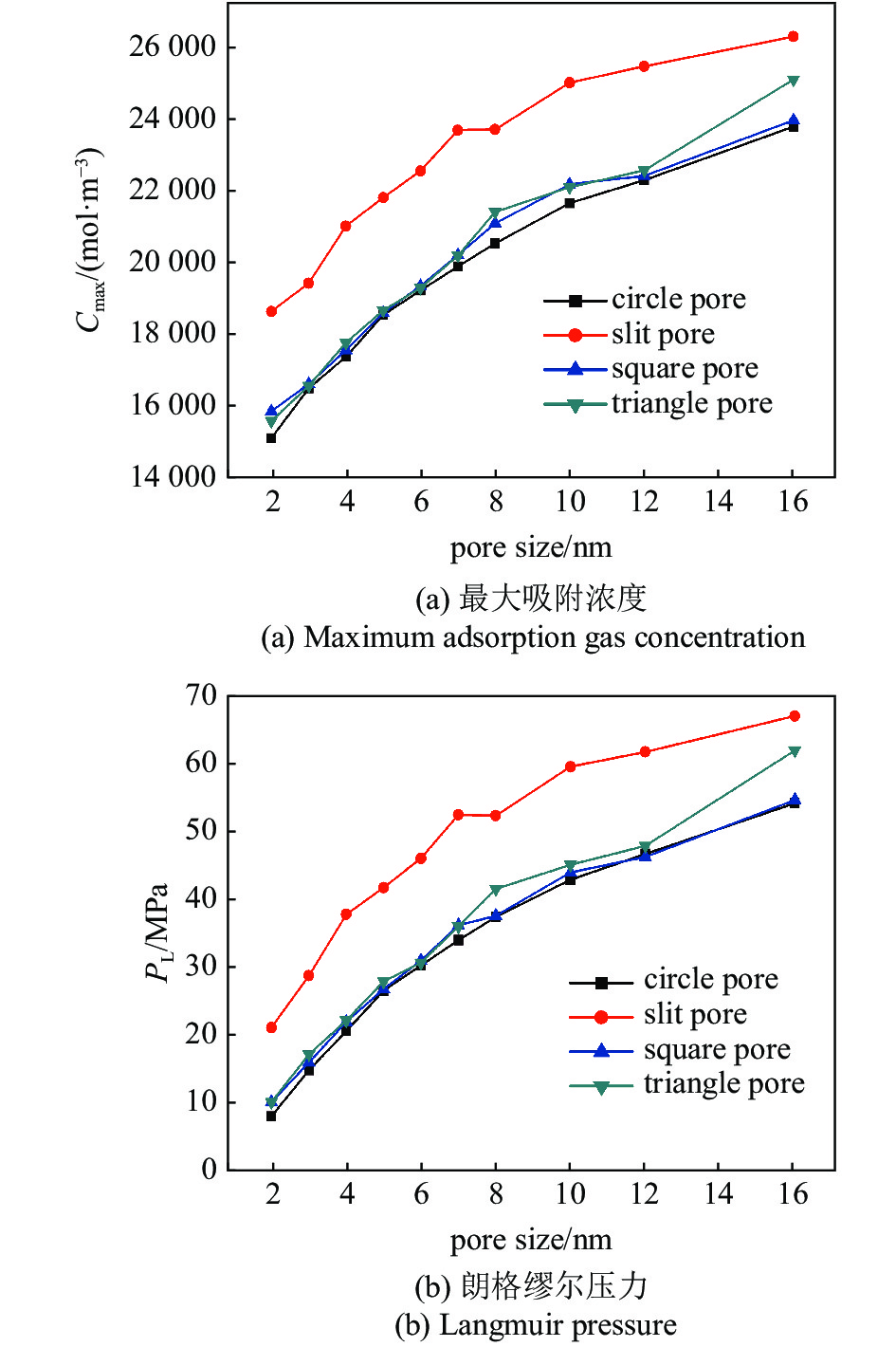
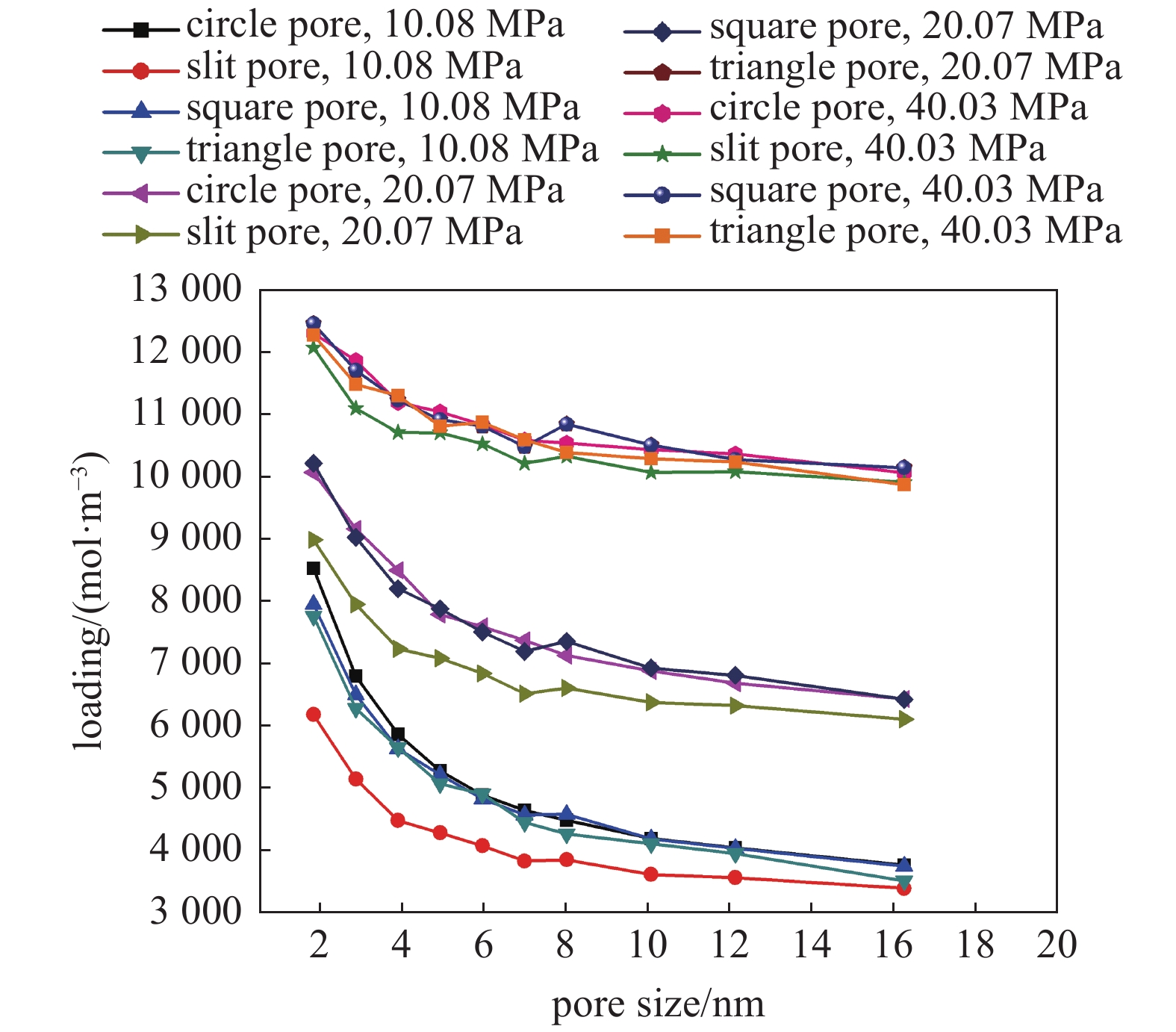
图7表示典型气藏高温高压条件下不同孔隙半径、孔隙形状中绝对吸附量变化以及相对应的Langmuir吸附模型拟合曲线(式(12)). 从图中可以看到气体吸附行为符合Langmuir单层吸附规律. 气体绝对吸附量随着孔隙压力的增加而增加, 60 MPa下1 nm ~ 8 nm孔隙半径范围内绝对吸附浓度在12000?14000 mol/m³之间. 随着孔隙半径的减小, 绝对吸附量显著增加. 图8表示最大吸附浓度和朗格缪尔压力均随着孔隙半径的增加而增大. 狭长孔最大吸附浓度和朗格缪尔压力最高, 其他三种孔隙类型差别不大, 这意味着页岩生产降压开采过程中狭长孔中的吸附气首先解吸. 图9表示典型气藏生产过程不同压力阶段下不同孔隙形状气体绝对吸附量随孔隙尺寸变化. 由于狭长孔朗格缪尔压力相比于其他三种孔隙较高, 因此实际气藏条件下狭长孔隙中气体浓度最低



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-7-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7-1" />



7
温度400 K下不同压力、孔隙半径(1 nm ~ 8 nm)下不同形状孔隙中绝对吸附量变化



7.
Absolute adsorption isotherms at 400 K in different structures of carbon pores with pore radii ranging from 1 nm to 8 nm



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
温度400 K下不同压力、孔隙半径(1 nm ~ 8 nm)下不同形状孔隙中绝对吸附量变化 (续)



Figure
7.
Absolute adsorption isotherms at 400 K in different structures of carbon pores with pore radii ranging from 1 nm to 8 nm (continued)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
朗格缪尔吸附参数随孔隙半径的变化



Figure
8.
Langmuir adsorption parameters variation with pore radius



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
典型气藏生产条件下不同孔隙形状气体绝对吸附量随孔隙尺寸变化



Figure
9.
Absolute adsorption concentration change with pore size in different pore structures at typical reservoir conditions



下载:
全尺寸图片
幻灯片

$$C = {C_{max }}frac{P}{{{P_{ m{L}}} + P}}$$

(12)

式中, C表示基于孔隙空间的气体浓度, mol/m³; P_L表示朗格缪尔压力, MPa; C_max为基于孔隙空间的最大气体浓度, mol/m³.

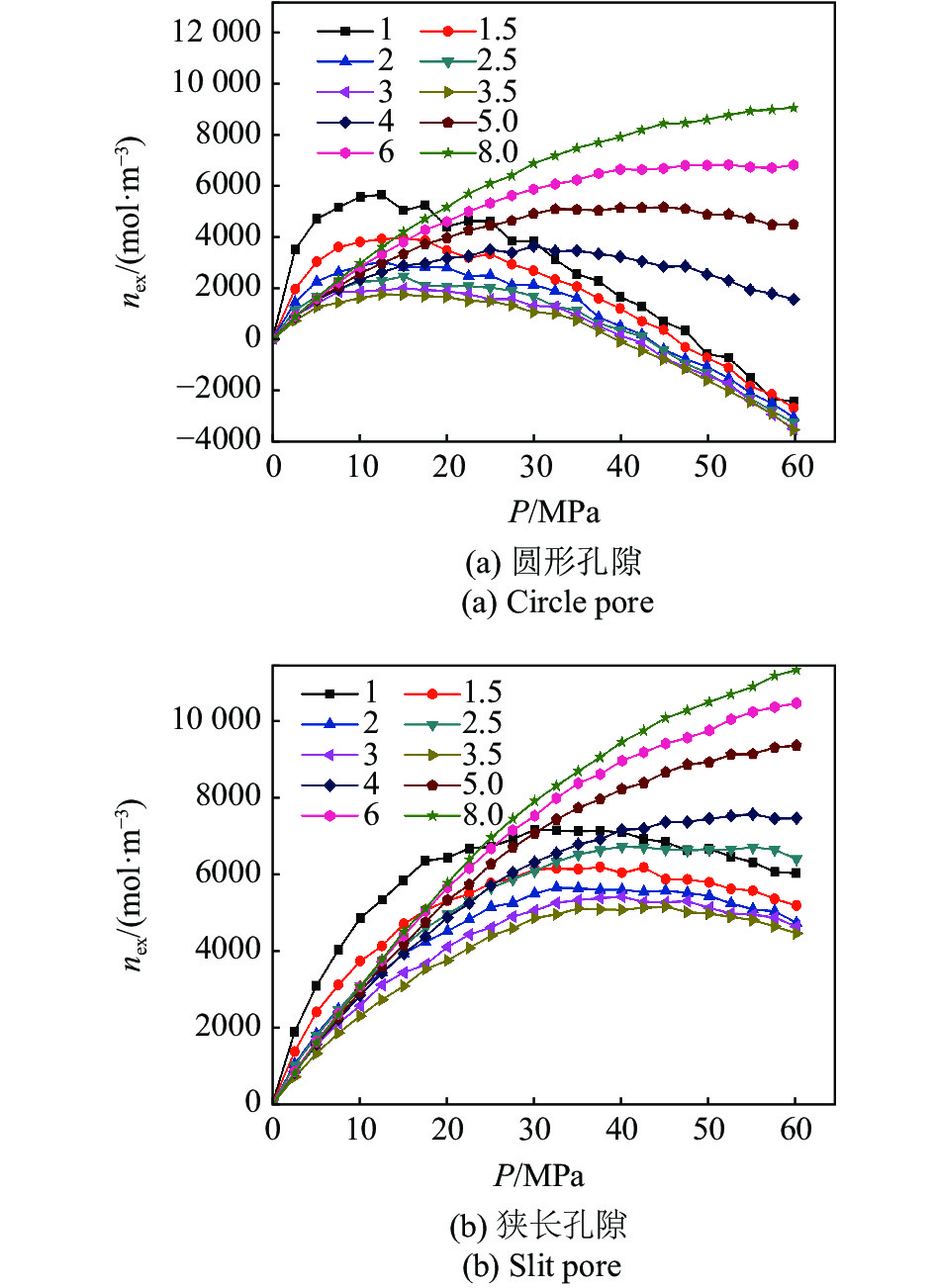
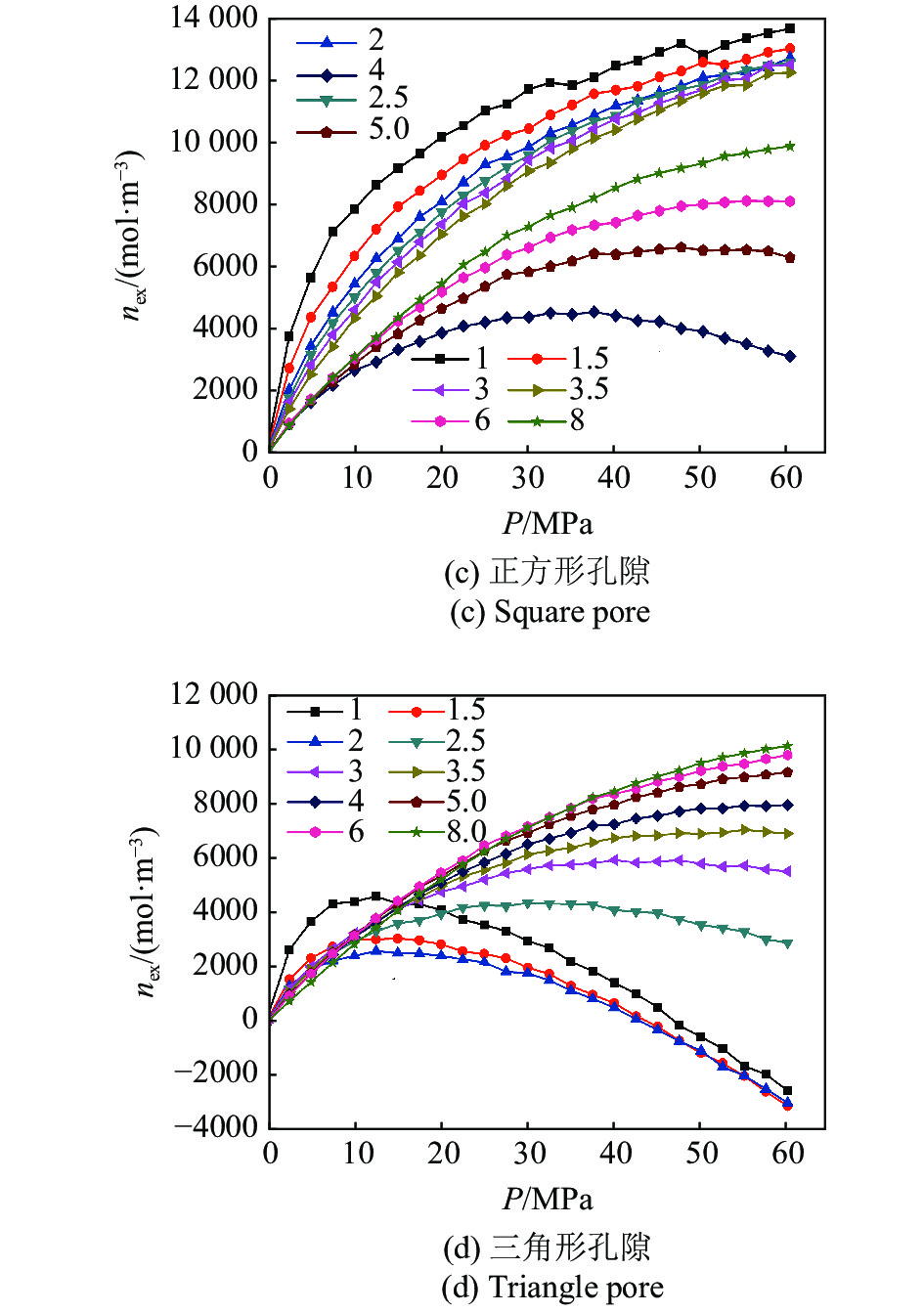
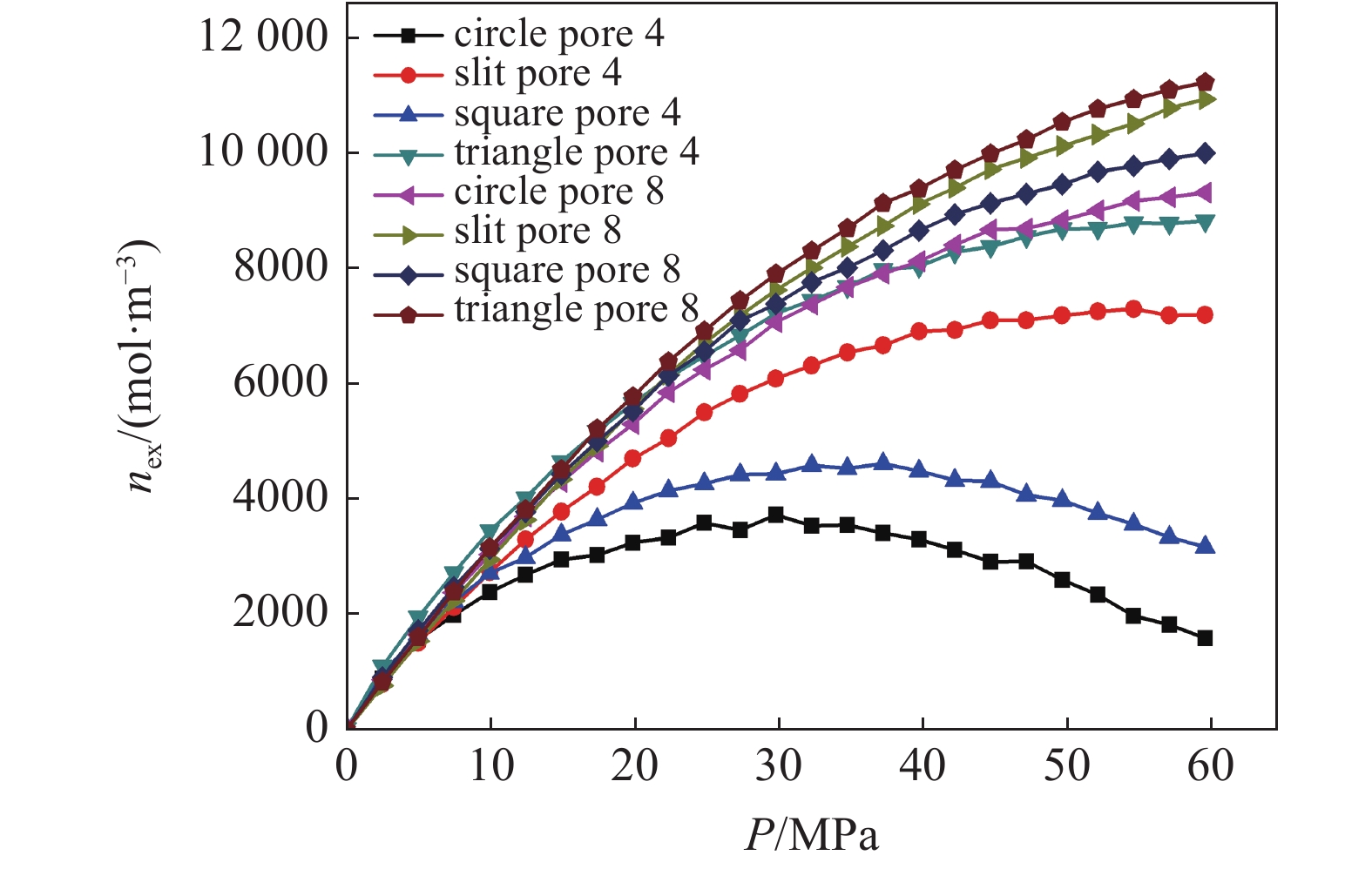
根据图7得到的Langmuir单层吸附规律, 气体在不同形状孔隙中吸附气和自由气赋存状态见图10. 根据图10中的吸附气赋存状态, 计算不同孔隙半径下不同孔隙形状对应的40 MPa下吸附层内气体浓度, 带入表征吸附层内气体浓度变化的Langmuir吸附模型(式(13)), 得到吸附层内最大气体浓度随孔隙半径的变化, 见图11. 从图11中可以发现, 圆形孔隙、狭长孔隙、正方形孔隙中吸附层内的最大气体吸附浓度均高于基于整个孔隙空间的最大气体吸附浓度, 但三角形孔隙中吸附层内的最大气体吸附浓度远低于基于整个孔隙空间的最大气体吸附浓度. 图12表示温度400 K下不同压力、孔隙半径下不同形状孔隙中过剩吸附浓度变化. 孔隙半径4 nm以下, 4种孔隙中过剩吸附浓度均随着孔隙压力先增加后减小. 孔隙以上4 nm以上, 4种孔隙中过剩吸附浓度均随着孔隙压力增加逐渐增加. 这意味着在一定程度上可根据实验室测量得到的过剩吸附曲线变化趋势来粗略估算实验岩样的孔隙尺寸范围. 图13表示典型介孔尺寸(r = 4 nm, 8 nm)情况下不同孔隙形状、孔隙半径下过剩吸附线. 从图中可以发现对于介孔尺寸, 不同孔隙形状中过剩吸附浓度大小顺序依次为三角形孔隙、狭长孔隙、正方形孔隙、圆形孔隙



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-10.jpg'"
class="figure_img
figure_type2 ccc " id="Figure10" />



图
10
孔隙半径1.5 nm、温度400 K、压力40 MPa下气体赋存状态. (a)(d)(g)(j)吸附气和自由气赋存状态, (b)(e)(h)(k)自由气赋存状态, (c)(f)(i)(l)吸附气赋存状态. 三角形孔隙以中心三角形孔隙分析



Figure
10.
Methane molecule distribution in different pore structures with pore radius 1.5 nm at 400 K, 40 MPa. (a)(d)(g)(j) Adsorbed gas and bulk gas total distribution, (b)(e)(h)(k) bulk gas distribution, (c)(f)(i)(l) adsorbed gas distribution. Triangle pore is studied using central triangle



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
温度400 K基于吸附层和基于孔隙整体空间最大吸附浓度随孔隙半径的变化



Figure
11.
Variation of maximum adsorption gas concentration based on total pore space and adsorption layer with pore radius at 400 K



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-12-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
温度400 K、孔隙半径1 nm~ 8 nm下不同压力、不同形状孔隙中过剩吸附浓度变化



Figure
12.
Excess adsorption isotherms at 400 K in different structures of carbon pores with pore radii ranging from 1 nm to 8 nm



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
温度400 K下不同孔隙形状、孔隙半径下过剩吸附线



Figure
13.
Excess adsorption isotherms at 400 K in different structures of carbon pores with different pore radii



下载:
全尺寸图片
幻灯片

$${C_{{ m{ads}}}} = {C_{{ m{amax}}}}frac{P}{{{P_{ m{L}}} + P}}$$

(13)

式中, C_ads表示气体吸附层内的气体浓度, mol/m³; C_amax为气体吸附层内的最大气体浓度, mol/m³.

2.
基于分子模拟结果的纳米有机质孔隙气体流动规律

2.1
有机质孔隙内气体流动机制

如图14所示, 有机质孔隙中吸附气和自由气在压差作用下同时流动, 吸附气以表面扩散的形式在孔隙壁面流动, 自由气流动形态取决于努森数大小(圆形孔隙为例, 式(14)^[44])



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
页岩气在有机质孔隙中的流动机制



Figure
14.
Gas transport mechanisms in organic pore



下载:
全尺寸图片
幻灯片

$$Kn = frac{delta }{{{r_{{ m{cir_eff}}}}}}$$

(14)

式中, Kn为努森数, 无因次; r_{cir_eff}为考虑吸附层厚度校正后的自由气有效流动半径, m; δ为平均分子自由程, m, 可表示为^[45]

$$delta = sqrt {frac{{{text{π}} ZRT}}{{2{M_w}}}} frac{{{mu _g}}}{P}$$

(15)

式中, Z为气体压缩因子, 无因次; M_w为气体摩尔质量, 0.01604 Kg/mol; μ_g为气体黏度, Pa·s, 采用Lee等提出的方法计算^[46-48]. 根据1.2节得到的Langmuir吸附规律, 吸附气在孔隙壁面的覆盖度可表示为^[45]

$$theta = frac{{{P / Z}}}{{{P_{ m{L}}} + {P / Z}}}$$

(16)

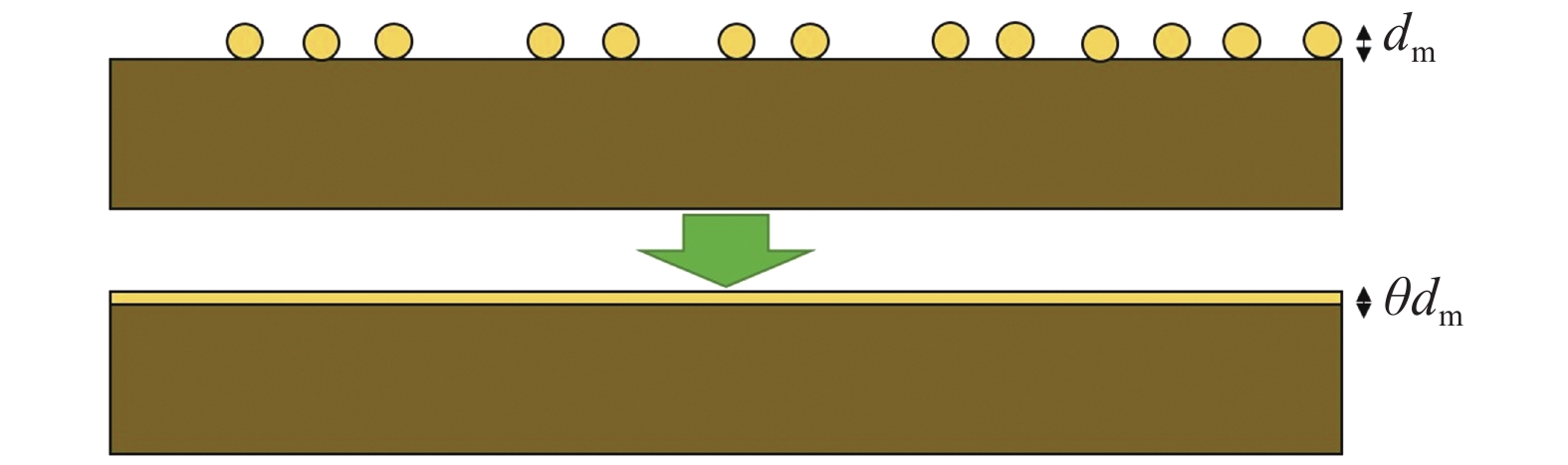
如图15所示可将孔隙壁面的吸附气等效为连续厚度的吸附层. 该吸附层厚度随气体吸附性质和孔隙压力发生变化, 考虑吸附气等效厚度后有机质圆形孔隙、正方形孔隙、狭长形孔隙、三角形孔隙中自由气流动半径/宽度可分别表示为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
有机质孔隙表面吸附层等效方法



Figure
15.
Equivalent adsorbed layer on organic pore surface



下载:
全尺寸图片
幻灯片

$${r_{{ m{cir_eff}}}} = r - {d_{ m{m}}}theta ;;;;;; ;;;$$

(17)

$${w_{{ m{eff}}}} = w - 2{d_{ m{m}}}theta ;;;;;;;;; $$

(18)

$${w_{{ m{slit_eff}}}} = {w_{{ m{slit}}}} - 2{d_{ m{m}}}theta $$

(19)

$${r_{{ m{tri_eff}}}} = {r_{{ m{tri}}}} - {d_{ m{m}}}theta ;;;;;;;;$$

(20)

式中, d_m为气体分子碰撞直径, 0.4 nm; w为正方形边长, m; r_tri为三角形孔隙内切圆半径, m.

2.2
不同形状有机质孔隙内自由气和吸附气流动规律

Beskok建立了针对于圆形孔隙内基于努森数的气体流量随压差变化关系的公式^[49], 如式(21)所示

$$q = {f_{_{{ m{cir}}}}}(K{n_{{ m{cir}}}})frac{{{text{π}} r_{{ m{cir_eff}}}^4}}{{8{mu _{ m{g}}}}}left( {frac{{Delta P}}{l}} ight)$$

(21)

式中, ΔP为单个孔隙两端压力降, Pa; l为单个孔隙长度, m; Kn_cir和f_cir(Kn_cir)可分别表示为

$$K{n_{{ m{cir}}}} = frac{delta }{{{r_{{ m{eff}}}}}}qquadqquadqquadqquadqquadqquad$$

(22)

$${f_{{ m{cir}}}}(K{n_{{ m{cir}}}}) = (1 + {alpha _{{ m{cir}}}}K{n_{{ m{cir}}}})left(1 + frac{{4K{n_{{ m{cir}}}}}}{{1 - beta K{n_{{ m{cir}}}}}} ight)$$

(23)

式中, β为滑移系数, 无因次; α_cir为无因次气体稀薄系数. 滑移系数取值?1, 最初仅被使用于滑脱流动阶段. Beskok与分子模拟数据对比验证, 滑移系数值?1可适用于全部Knudsen数流动阶段^[44]. 无因次气体稀薄系数α_cir可表示为

$${alpha _{{ m{cir}}}} = frac{{128}}{{15{{text{π}} ^2}}}{tan ^{ - 1}}(4.0K{n_{{ m{cir}}}}^{0.4})$$

(24)

同样正方形孔隙中气体流量随压差变化关系可表示为^[49]

$$q = 0.421;73frac{{w_{{ m{eff}}}^4}}{{12{mu _g}}}left( {frac{{Delta P}}{l}} ight){f_{{ m{squ}}}}(K{n_{{ m{squ}}}})$$

(25)

式中, w_eff为正方形自由气有效流动宽度, m; Kn_squ和f_squ(Kn_squ)可分别表示为

$$K{n_{{ m{squ}}}} = frac{delta }{{{w_{{ m{eff}}}}}}qquadqquadqquadqquadqquadqquad;;;$$

(26)

$${f_{{ m{squ}}}}(K{n_{{ m{squ}}}}) = left( {1 + {alpha _{{ m{duct}}}}K{n_{{ m{squ}}}}} ight)left( {1 + frac{{6K{n_{{ m{squ}}}}}}{{1 - beta K{n_{{ m{squ}}}}}}} ight)$$

(27)

式中, 正方形无因次气体稀薄系数α_duct可表示为

$${alpha _{{ m{duct}}}} = 1.704;2frac{2}{{text{π}} }{tan ^{ - 1}}(8Kn_{{ m{squ}}}^{0.5})$$

(28)

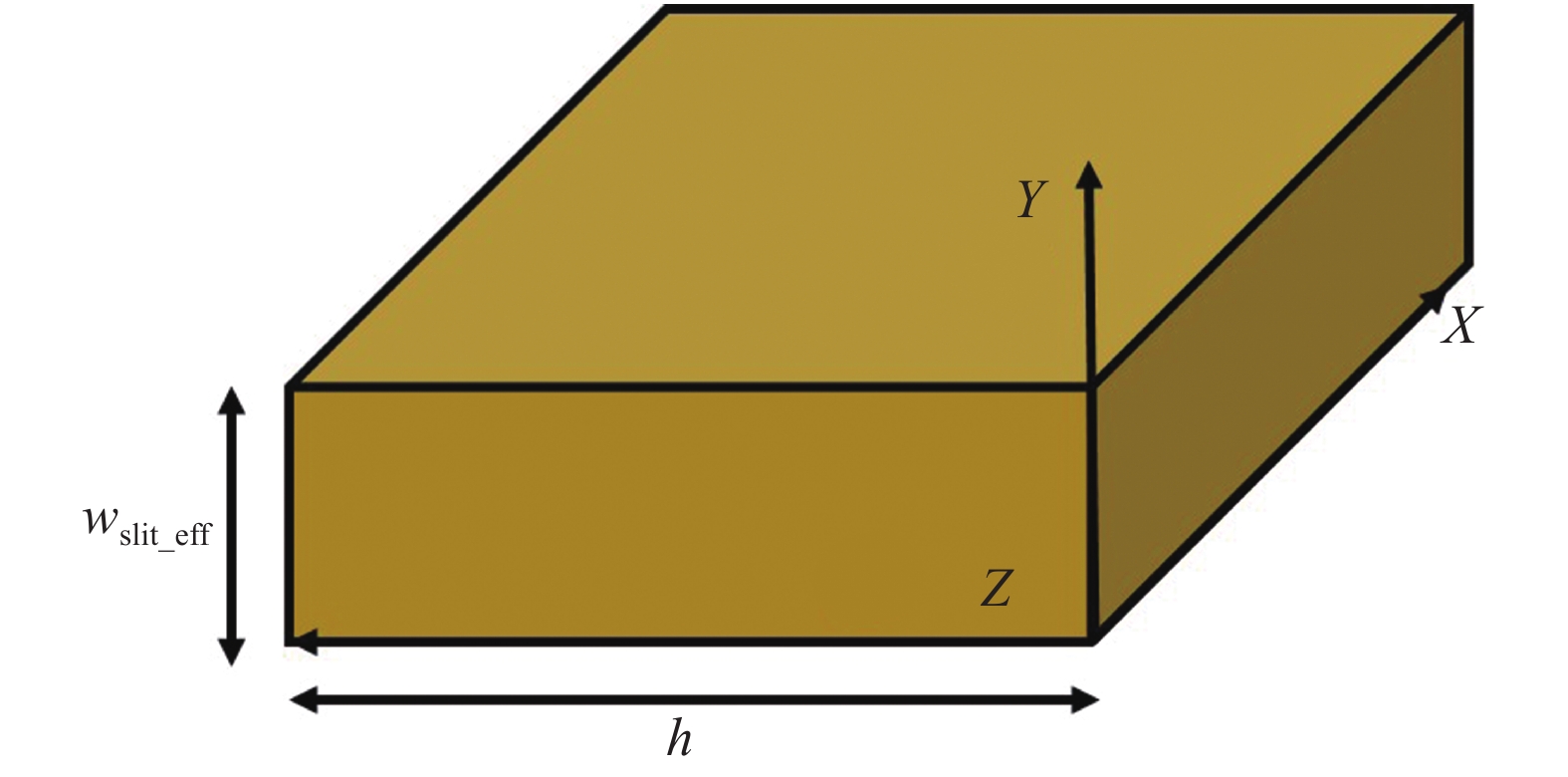
采用二阶滑移边界条件推导狭长孔隙内气体流量随压差变化关系, 考虑压力梯度沿X方向(图16), 控制方程可表示为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
狭长孔隙气体流动物理模型



Figure
16.
Physical model of gas flow in slit pore



下载:
全尺寸图片
幻灯片

$$ - frac{{{ m{d}}P}}{{{ m{d}}x}} + {mu _{ m{g}}}left( {frac{{{partial ^2}u}}{{partial {x^2}}} + frac{{{partial ^2}u}}{{partial {y^2}}}} ight) = 0$$

(29)

二阶滑移边界条件可表示为^[50]

$$begin{split} &&u = pm {A_1}lambda frac{{partial u}}{{partial y}} - {A_2}{lambda ^2}frac{{{partial ^2}u}}{{partial {y^2}}}end{split}$$

(30)

式中, A₁为1阶气体滑移系数, 无因次; A₂为2阶气体滑移系数, 无因次.

根据式(29)和式(30), 狭长孔气体流量随压差变化关系可表示为^[50]

$$q = frac{{w_{{ m{slit_eff}}}^3h}}{{12{mu _{ m{g}}}}}left( {frac{{Delta P}}{l}} ight)left( {1 + 6{A_1}K{n_{{ m{slit}}}} + 12{A_2}Kn_{{ m{slit}}}^2} ight)$$

(31)

$$K{n_{{ m{slit}}}} = frac{delta }{{{w_{{ m{slit_eff}}}}}}$$

(32)

式中, h为狭长孔z方向长度, m; w_{slit_eff}为y方向自由气有效流动宽度, m. Maure等^[50]测量了气体在滑移流和过渡流区域流量随压差的变化关系, 并给定了1阶气体滑移系数和2阶气体滑移系数的具体数值. 根据Maure等的实验分析结果, A₁给定为1.25, A₂给定为0.23. 根据达西公式, 狭长孔自由气渗透率可表示为

$${k_{{ m{slit}}}} = frac{{w_{{ m{slit_eff}}}^2}}{{12}}left( {1 + 6{A_1}K{n_{{ m{slit}}}} + 12{A_2}Kn_{{ m{slit}}}^2} ight)$$

(33)

式中, k_slit为狭长孔隙自由气渗透率, μm².

三角形孔隙中气体流量随压差变化的变化关系可表示为^[51]

$$q = 0.6frac{{A_{{ m{tri}}}^2G}}{{{mu _{ m{g}}}}}left( {frac{{Delta P}}{l}} ight)f(G,K{n_{{ m{tri}}}})$$

(34)

式中, A_tri为三角形孔隙截面面积, m²; G为形状因子, 无因次. 三角形孔隙截面面积可表示为

$${A_{{ m{tri}}}} = frac{{r_{{ m{tri_eff}}}^2}}{{tan {beta _1}}} + frac{{r_{{ m{tri_eff}}}^2}}{{tan {beta _2}}} + frac{{r_{{ m{tri_eff}}}^2}}{{tan {beta _3}}}$$

(35)

式中, r_tri为三角形内切圆半径, m; β₁, β₂, β₃分别为三角形三个角的各自半角, (°). 形状因子G可表示为

$$G = frac{{{A_{ m{p}}}}}{{P_{ m{e}}^2}}$$

(36)

式中, A_p为孔隙截面面积, m²; P_e为孔隙截面周长, m, f(G, Kn_tri)为与形状因子、努森数相关的函数, 可表示为^[52]

$$begin{split} {f_{{ m{tri}}}}(G,K{n_{ m{tri}}}) =& 1.033 + 0.623;3G + 5.472K{n_{ m{tri}}} - &25.98GK{n_{ m{tri}}} + 0.337;7Kn_{ m{tri}}^2{ m{ }} end{split} $$

(37)

将三角形孔隙中努森数Kn_tri定义为

$$K{n_{{ m{tri}}}} = frac{delta }{{{r_{{ m{tri_eff}}}}}}$$

(38)

根据式(21)、式(31)和式(34), 圆形孔隙、正方形孔隙、三角形孔隙中自由气渗透率可表示为

$${k_{{ m{cir}}}} = frac{{{f_{_{{ m{cir}}}}}(K{n_{{ m{cir}}}})r_{{ m{cir_eff}}}^2}}{8};;;;;;;;;;;;$$

(39)

$${k_{{ m{squ}}}} = 0.421;73{f_{{ m{squ}}}}(K{n_{{ m{squ}}}})frac{{w_{{ m{eff}}}^2}}{{12}}$$

(40)

$${k_{{ m{tri}}}} = 0.6{f_{{ m{tri}}}}(G,K{n_{{ m{tri}}}}){A_{{ m{tri}}}}G;;;;;;;$$

(41)

式中, k_cir, k_squ, k_tri分别为圆形孔隙、正方形孔隙、三角形孔隙自由气渗透率, μm².

吸附气通过表面扩散方式进行流动, 单位面积气体分子摩尔流量J_a可表示为^{[29, 53]}

$${J_{ m{a}}} = {D_{ m{s}}}frac{{{ m{d}}{C_{{ m{ads}}}}}}{{{ m{d}}x}}$$

(42)

式中, J_a, mol/(m²·s); D_s为表面扩散系数, m²/s; 吸附层内气体浓度C_ads可表示为

$${C_{{ m{ads}}}} = {C_{{ m{a}}max }}theta $$

(43)

式中, C_amax可通过1.2节分子模拟结果子吸附模拟结果得到. 根据式(42)、式(43)以及等效吸附层厚度d_mθ, 吸附层内气体分子摩尔流量J_A可表示为

$${J_{ m{A}}} = {D_{ m{s}}}{C_{{ m{a}}max }}frac{{{ m{d}}theta }}{{{ m{d}}P}}{P_{ m{e}}}{d_{ m{m}}}theta frac{{{ m{d}}P}}{{{ m{d}}x}}$$

(44)

式中, J_A, mol/s; dP/dx为给定流动方向压力梯度, MPa/m; 根据式(44), 吸附气体积流量V_A可表示为

$${V_{ m{A}}} = frac{{{M_{ m{w}}}}}{{{ ho _{ m{g}}}}}{D_{ m{s}}}{C_{{ m{a}}max }}frac{{{ m{d}}theta }}{{{ m{d}}P}}{P_{ m{e}}}{d_{ m{m}}}theta frac{{{ m{d}}P}}{{{ m{d}}x}}$$

(45)

式中, V_A, mol/s; 注意式(45)中ρ_g给定为自由气密度, 因此计算出的吸附气体积流量V_A为经过自由气密度折算后的体积流量, 这也与吸附气流出有机质孔隙后进入无机质后以自由气形式流动的物理现象相一致. 有机质孔隙表面吸附气覆盖度为0情况下气体表面扩散系数可通过Arrhenius公式表示为^[54]

$${D_{{ m{s0}}}} = {C_{{ m{ons}}}}{T^n}exp left( - frac{{ - {E_a}}}{{RT}} ight)$$

(46)

式中, C_ons为给定常数; n为给定数值, 通常取值为0, 0.5, 1; E_a为活化能, J/mol; 活化能E_a为等温吸附热ΔH的函数^[55,56], 根据Guo等^[57]实验结果, n值给定为0.5, C_ons值给定为8.29 × 10^?7, 活化能E_a表示为

$${E_{ m{a}}} = Delta {H^{0.8}}$$

(47)

式中ΔH, J/mol; 等温吸附热与孔隙表面吸附气覆盖度有关, 可表示为吸附气覆盖度的函数^[58]

$$Delta H = gamma theta + Delta H(0)$$

(48)

式中, γ为等温吸附热线性变化系数, J/mol; ΔH(0)为吸附气覆盖度为0情况下的等温吸附热. 式(46)中表面扩散系数在低压下计算得到, 与气体摩尔质量、温度、活化能、等温吸附热有关^[59]. 为了描述高压条件下吸附气覆盖度对表面扩散系数的影响, 采用Chen等^[60]提出的模型来计算高压下表面扩散系数

$${D_{ m s}} = {D_{{ m s}0}}dfrac{{(1 - theta ) + dfrac{kappa }{2}theta (2 - theta ) + left(1 - kappa ight)dfrac{kappa }{2}{theta ^2} {H(1 - kappa )} }}{{{{left(1 - theta + dfrac{kappa }{2}theta ight)}^2}}}$$

(49)

$$H(1 - kappa ) = left{ begin{array}{l} 1,;;;0 leqslant kappa < 1 0,;;;kappa geqslant 1 end{array} ight.$$

(50)

$$kappa = dfrac{{{kappa _{ m b}}}}{{{kappa _{ m m}}}}$$

(51)

式中, $kappa _{
m b}$为堵塞速度常数, 无因次; $kappa _{
m m}$为迁移速度常数, 无因次; $kappa $为堵塞速度常数与迁移速度常数比值, 无因次; H(1?$ kappa $)为Heaviside函数.

根据达西公式和式(45), 单个孔隙吸附气渗透率可表示为

$${k_{{ m{ads}}}} = frac{{{M_{ m{w}}}{mu _{ m{g}}}}}{{{ ho _{ m{g}}}{A_{ m{p}}}}}{D_{ m{s}}}{C_{{ m{a}}max }}frac{{{ m{d}}theta }}{{{ m{d}}P}}{P_{ m{e}}}{d_{ m{m}}}theta $$

(52)

对于不同形状的有机质孔隙, 渗透率可表示为

$${k_{{ m{cir_or}}}} = frac{{{f_{_{{ m{cir}}}}}(K{n_{{ m{cir}}}})r_{{ m{cir_eff}}}^2}}{8} + frac{{{M_{ m{w}}}{mu _{ m{g}}}}}{{{ ho _{ m{g}}}{A_{ m{p}}}}}{D_{ m{s}}}{C_{{ m{a}}max }}frac{{{ m{d}}theta }}{{{ m{d}}P}}{P_{ m{e}}}{d_{ m{m}}}theta ;;;;;;;;$$

(53)

$$begin{split} {k_{{ m{slit_or}}}} =& frac{{w_{{ m{slit_eff}}}^2}}{{12}}left( {1 + 6{A_1}K{n_{{ m{slit}}}} + 12{A_2}Kn_{s{ m{lit}}}^2} ight) +&frac{{{M_{ m{w}}}{mu _{ m{g}}}}}{{{ ho _{ m{g}}}{A_{ m{p}}}}}{D_{ m{s}}}{C_{{ m{a}}max }}frac{{{ m{d}}theta }}{{{ m{d}}P}}{P_{ m{e}}}{d_{ m{m}}}theta [-15pt]end{split};;;;;;;;;;;;;;;;;;;;$$

(54)

$${k_{{ m{squ_or}}}} !!=!!0.421;73 {f_{{ m{squ}}}}(K{n_{{ m{squ}}}})frac{{w_{{ m{eff}}}^2}}{{12}} !!+!! frac{{{M_{ m{w}}}{mu _{ m{g}}}}}{{{ ho _{ m{g}}}{A_{ m{p}}}}}{D_{ m{s}}}{C_{{ m{a}}max }}frac{{{ m{d}}theta }}{{{ m{d}}P}}{P_{ m{e}}}{d_{ m{m}}}theta $$

(55)

$${k_{{ m{tri_or}}}} =0.6 {f_{{ m{tri}}}}(G,K{n_{{ m{tri}}}}){A_{{ m{tri}}}}G + frac{{{M_{ m{w}}}{mu _{ m{g}}}}}{{{ ho _{ m{g}}}{A_{ m{p}}}}}{D_{ m{s}}}{C_{{ m{a}}max }}frac{{{ m{d}}theta }}{{{ m{d}}P}}{P_{ m{e}}}{d_{ m{m}}}theta ;;;$$

(56)

2.3
有机质孔隙内吸附气表面扩散对气体渗透率贡献

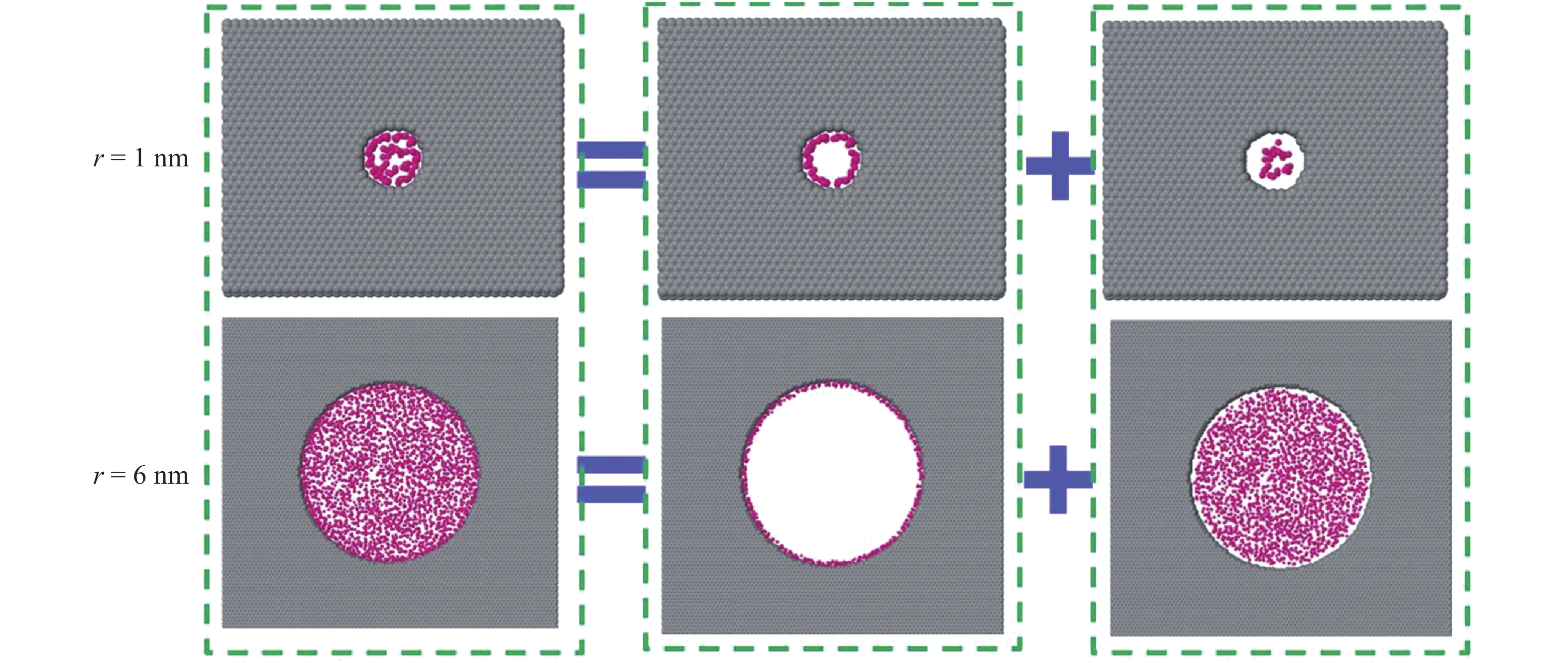
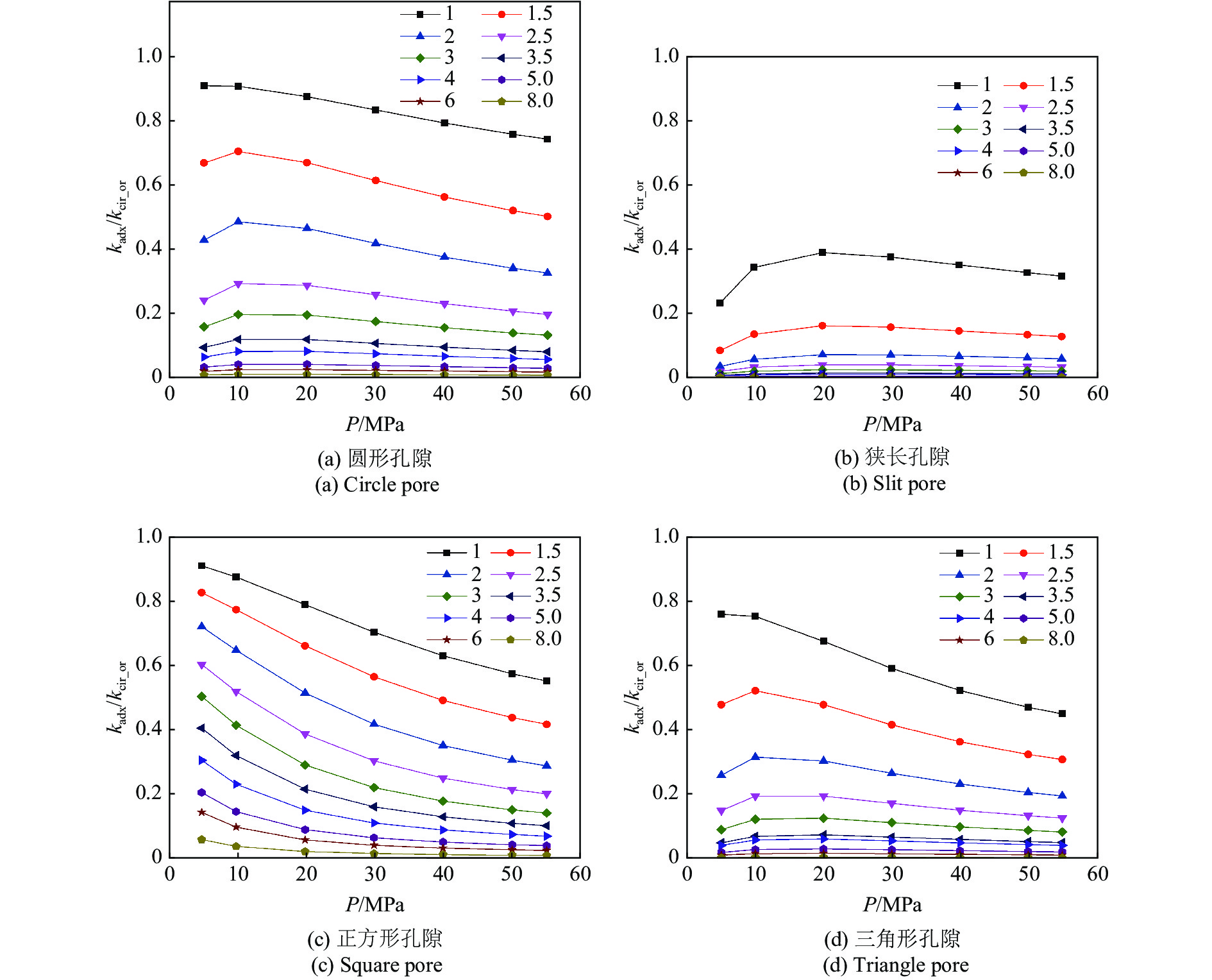
图17表示圆形孔隙40 MPa, 400 K下吸附气和自由气赋存状态随孔隙半径的变化, 从图中可以看出, 微孔隙中吸附气占据气体分子绝大部分, 表面扩散对气体渗透率的影响不能够被忽略, 介孔中吸附气占据气体分子很小一部分, 自由气对气体渗透率的贡献占据绝大比重. 为定量分析吸附气表面扩散对气体渗透率的贡献, 根据1.2节中的分子吸附模拟计算得到的不同孔径、孔隙形状下吸附层最大吸附浓度以及朗格缪尔压力, 结合式(53) ~ 式(56)计算不同孔径圆形孔隙、狭长孔隙、正方形孔隙、三角形孔隙中吸附气表面扩散对气体渗透率的贡献. 从图18中可以看出, 随着孔隙半径增加, 自由气流动对气体渗透率的贡献逐渐增加, 吸附气表面扩散对气体渗透率的贡献逐渐减小. 狭长孔隙内吸附气表面扩散能力相比于气体在其他三种孔隙中的表面扩散能力最弱(图18(b)). 孔隙半径5 nm以上时, 表面扩散对气体渗透率的影响可忽略, 孔隙半径1.5 nm以下时, 圆形孔隙、正方形孔隙、三角形孔隙中吸附气表面扩散贡献占据主导作用. 随着孔隙压力的减小, 由于式(52)中ρ_g减小, dθ/dp增加, 表面扩散对气体渗透率贡献随之增大, 但由于孔隙压力减小的同时努森数增大, 导致自由气流动能力增强, 因此考虑自由气渗透率和吸附气渗透率的相对比重, 部分孔隙形状中吸附气表面扩散贡献在低压下会出现先上升后下降的趋势(图18(a),(b),(d)).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-17.jpg'"
class="figure_img
figure_type2 ccc " id="Figure17" />



图
17
不同孔隙尺寸下吸附气和自由气赋存状态变化及其对气体渗透率影响(圆形孔隙为例, 40 MPa, 400 K)



Figure
17.
Adsorbed gas and bulk gas distributions at different pore radii and its influence on gas permeability (circle pore as an example, 40 MPa, 400 K)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-224-18.jpg'"
class="figure_img
figure_type2 ccc " id="Figure18" />



图
18
温度400 K, 不同孔隙半径、孔隙压力下吸附气表面扩散对气体渗透率贡献



Figure
18.
Contribution of surface diffusion on total gas permeability at different pore radii, pore pressure and 400 K



下载:
全尺寸图片
幻灯片

3.
结论

本文首先采用巨正则蒙特卡洛方法研究了气体在典型页岩纳米有机质孔隙中的吸附规律, 在分子吸附模拟结果基础上建立了考虑纳微尺度气体运移机制、赋存状态的纳米有机质孔隙气体流动数学模型, 分析了气体赋存状态、孔隙形状、孔隙尺寸对页岩气流动规律的影响, 主要结论如下:

(1)狭长孔隙内气体最大吸附浓度和朗格缪尔压力最高; 圆形孔隙、狭长孔隙、正方形孔隙中吸附层内最大气体吸附浓度均高于基于整个孔隙空间的最大气体吸附浓度, 三角形孔隙中吸附层内最大气体吸附浓度远低于基于整个孔隙空间的最大气体吸附浓度;

(2)孔隙半径越小, 绝对吸附浓度越高; 孔隙半径4 nm以下, 过剩吸附浓度均随着孔隙压力先增加后减小; 孔隙半径4 nm以上, 过剩吸附浓度均随着孔隙压力增加逐渐增加;

(3)狭长孔隙吸附气表面扩散能力最弱. 随着孔隙尺寸增加, 自由气流动对气体渗透率贡献逐渐增加. 孔隙半径5 nm以上时, 吸附气表面扩散对气体渗透率影响可忽略.

本文研究结果可进一步结合页岩扫描电镜图像孔隙尺寸、形状识别结果, 准确预测不同储层条件下页岩气流动能力.