引言

时间积分方法被广泛应用在瞬态响应的求解中. 根据递推公式的格式, 其可被划分为两类, 分别是显式方法和隐式方法. 比较而言, 显式方法效率高但条件稳定, 隐式方法效率低但多为无条件稳定. 对于非线性系统, 确定显式方法的时间步长具有挑战性. 因此, 本文致力于发展对线性和非线性系统都是无条件稳定的隐式方法.

对瞬态热传导问题, 广义梯形法则^[1]是一种较为流行的方法, 由它可衍生出Crank-Nicolson方法、Galerkin方法和后向差分方法(backward difference formula, BDF)等. 在这些方法中, 只有Crank-Nicolson方法具有二阶精度, 但其在高频段无法提供数值耗散, 从而会诱发出虚假的数值振荡. 一阶精确的BDF具有极强的数值耗散从而能迅速地过滤掉高频信息, 但其无法准确地保留重要的低频信息. 相比之下, Galerkin方法能够有效地平衡低频精度和高频耗散. 随着人们对精度、效率、耗散和稳定性的追求, 在过去的几十年中, 不断涌现出新的时间积分方法^[2-31].

除减小步长外, 提高算法阶次^[2-6]也是一种提高精度的有效手段. 针对一阶线性常微分方程, Fung借助加权残量法^[2]、最小二乘法^[3]和微分求积法^[4]构造出一系列具有任意高阶精度的无条件稳定时间积分方法, 但这些方法在求解过程中需要对系统矩阵进行扩维处理, 从而大幅增加计算量. 为了同时获得高精度和高效率, 一种精细积分方法^[7]被提出. 该方法利用Taylor级数来近似解析的传递矩阵, 利用分段线性技术处理外载荷. 此外, 该方法采用了2^m算法和增量矩阵存贮技术, 大幅提高了效率、减少了舍入误差. 虽然精细积分方法是条件稳定的, 但由于在计算中采用了极小步长, 因此条件稳定性并不影响其应用. 精细时间积分方法已被广泛地应用在热传导^[8-9]、双边值^[10-11]和结构动力学^[12-13]等问题中.

上面提到的优秀方法仅能求解线性问题, 下面回顾一下能够求解一般非线性瞬态热传导问题的方法^[14-31]. Runge-Kutta方法^[14-16]是具有无条件稳定的高阶格式. 但与单步方法相比, 多级结构使其计算量更高. 为了在不牺牲计算效率的前提下提高精度, 线性多步方法^[17-21]和多分步方法^[22-28]被提出. 一般来说, 线性多步方法是二阶精确的, 但其不能自启动. 与单步方法相比, 线性多步方法的使用略显繁琐. 多分步方法是自启动的, 但各个分步的有效刚度矩阵可能不同, 致使其计算量略高于单步方法. 瞬态热传导问题普遍存在于航空航天、土木和冶金等领域中, 构造一种具有无条件稳定性且能够灵活处理该类问题的高精度、高效率时间积分方法是必要的. 在这种背景下, 本文提出了一种能处理一般瞬态热传导问题的无条件稳定单步时间积分方法, 其具备二阶精度、高频耗散和自启动特性. 利用拉格朗日插值函数分别近似温度场及其一阶导数场, 并利用加权残量法建立二者之间的关系. 理论分析和数值测试均显示出了本文方法在精度、耗散和稳定性方面的优势.

1.
算法描述

瞬态热传导问题的非线性控制方程^[32]可以写为

$$left. begin{array}{l} {boldsymbol{C}}left( {boldsymbol{T}} ight){dot{boldsymbol T}} + {boldsymbol{K}}left( {boldsymbol{T}} ight){boldsymbol{T}} = {boldsymbol{Q}} {boldsymbol{T}}left( 0 ight) = {{boldsymbol{T}}_0} end{array} ight}$$

(1)

式中, C和K分别是N × N的热容矩阵和热传导矩阵, T和Q分别是N × 1的温度列向量和外部施加的热源列向量. 当C和K是与温度T无关的定常矩阵时, 式(1)退化为线性方程, 即

$$left. begin{array}{l} {boldsymbol{Cdot T}} + {boldsymbol{KT}} = {boldsymbol{Q}} {boldsymbol{T}}left( 0 ight) = {{boldsymbol{T}}_0} end{array} ight}$$

(2)

为求解式(1)和式(2)中给出的瞬态热传导问题, 本文首先把待求的时间域[0, t_Total]等间距地划分为n个时间单元, 各离散点为0 = t₀ < t₁ < ··· < t_k < ··· < t_n-1 < t_n = t_Total, 其中t_k = kΔt (k = 1, 2, ···, n), Δt = t_Total /n为时间单元长度. 在任一时间单元t∈[t_k, t_k + Δt]中, 温度场及其一阶导数场被近似为

$$left. begin{array}{l} {dot{boldsymbol T}}left( t ight) = {psi _0}left( t ight){{{dot{boldsymbol T}}}_0} + {psi _1}left( t ight){{{dot{boldsymbol T}}}_1} + {psi _2}left( t ight){{{dot{boldsymbol T}}}_2} {boldsymbol{T}}left( t ight) = {psi _0}left( t ight){{boldsymbol{T}}_0} + {psi _1}left( t ight){{boldsymbol{T}}_1} + {psi _2}left( t ight){{boldsymbol{T}}_2} end{array} ight}$$

(3)

式中, ψ_j(t)是与第j个节点关联的拉格朗日插值函数, T_j和${{dot{boldsymbol T}}_j}$分别描述了与第j个节点关联的温度及其一阶导数. 拉格朗日插值函数的定义为

$${psi _j}left( t ight) = prodlimits_{k = 0 atopleft( {k ne j} ight) }^2 {frac{{tau - {tau _k}}}{{{tau _j} - {tau _k}}}} $$

(4)

其中, τ = (t ? t_k)/Δt, ${tau _j} $用来确定第j个节点的位置即t_j = t_k + τ_jΔt. 在本文方法中, τ₀ = 0, τ₁ = 0.5, τ₂ = 1. 在式(3)中, 利用拉格朗日函数作为基函数分别独立得到了T和${dot{boldsymbol T}}$, 因此二者之间不存在关系${dot{boldsymbol T}}$ = dT/dt. 下面利用加权残量法来建立T和${dot{boldsymbol T}}$之间的关系. 定义如下加权残量r(t)

$$begin{split} {boldsymbol{r}}left( t ight) =& {{psi _0}left( t ight){{{dot{boldsymbol T}}}_0} + {psi _1}left( t ight){{{dot{boldsymbol T}}}_1} + {psi _2}left( t ight){{{dot{boldsymbol T}}}_2}} - &left( {{{dot psi }_0}left( t ight){{boldsymbol{T}}_0} + {{dot psi }_1}left( t ight){{boldsymbol{T}}_1} + {{dot psi }_2}left( t ight){{boldsymbol{T}}_2}} ight) end{split} $$

(5)

对于解析方法, 上述残量在任意时刻均为0. 为了最小化r(t), 本文方法要求

$$int_0^{Delta t} {wleft( t ight)frac{{{{ m{d}}^{i - 1}}{boldsymbol{r}}left( t ight)}}{{{ m{d}}{t^{i - 1}}}}} { m{d}}t = {boldsymbol{0}},;; {i = 1,2} $$

(6)

式中, w(t)为权函数. 将式(5)代入式(6)可得

$$int_0^{Delta t} {wleft( t ight)left( {sumlimits_{j = 0}^2 {frac{{{{ m{d}}^{i - 1}}{psi _j}left( t ight)}}{{{ m{d}}{t^{i - 1}}}}} {{{dot{boldsymbol T}}}_j} - sumlimits_{j = 0}^2 {frac{{{{ m{d}}^i}{psi _j}left( t ight)}}{{{ m{d}}{t^i}}}{{boldsymbol{T}}_j}} } ight)} { m{d}}t = {boldsymbol{0}}$$

(7)

选用不同的权函数w(t), 可以获得不同数值特性的时间积分方法. 但这种方式很难设计出具有无条件稳定和理想耗散的方法, 为此本文没有直接使用权函数w(t), 而是利用如下参数θ_k来控制算法的性能.

$${theta _k} = frac{{displaystyleint_0^{Delta t} {wleft( t ight){t^k}} { m{d}}t}}{{Delta {t^k}displaystyleint_0^{Delta t} {wleft( t ight)} { m{d}}t}},;; {k = 1,2} $$

(8)

将式(4)和式(8)代入式(7)整理可得

$$left. begin{array}{l} {{{dot{boldsymbol T}}}_{{t_{k + {1 / 2}}}}} = {alpha _{11}}{{boldsymbol{T}}_{{t_{k + {1 / 2}}}}} + {alpha _{12}}{{boldsymbol{T}}_{{t_{k + 1}}}} + {beta _1}{{boldsymbol{T}}_{{t_k}}} + {eta _1}{{{dot{boldsymbol T}}}_{{t_k}}} {{{dot{boldsymbol T}}}_{{t_{k + 1}}}} = {alpha _{21}}{{boldsymbol{T}}_{{t_{k + {1 / 2}}}}} + {alpha _{22}}{{boldsymbol{T}}_{{t_{k + 1}}}} + {beta _2}{{boldsymbol{T}}_{{t_k}}} + {eta _2}{{{dot{boldsymbol T}}}_{{t_k}}} end{array} ight}$$

(9)

式中

$$begin{split} &{boldsymbol{alpha }}{ m{ = }}left[ {begin{array}{*{20}{c}} {{alpha _{11}}}&{{alpha _{12}}} {{alpha _{21}}}&{{alpha _{22}}} end{array}} ight]{ m{ = }}frac{1}{{4Delta tleft( {2theta _1^2 - theta _2^{}} ight)}}cdot&left[ {begin{array}{*{20}{c}} { - 4left( {8theta _1^2 - 4theta _1^{} - 4theta _2^{} + 1} ight)}&{ {16theta _1^2 - 4theta _1^{} - 8theta _2^{} + 1} } { - 16left( {4theta _1^2 - 2theta _1^{} - 2theta _2^{} + 1} ight)}&{4left( {8theta _1^2 - 2theta _1^{} - 4theta _2^{} + 1} ight)} end{array}} ight]end{split}$$

(10)

$${boldsymbol{beta }}{ m{ = }}left[ {begin{array}{*{20}{c}} {{beta _1}} {{beta _2}} end{array}} ight]{ m{ = }}frac{1}{{4Delta tleft( {2theta _1^2 - theta _2^{}} ight)}}left[ {begin{array}{*{20}{c}} { {16theta _1^2 - 12theta _1^{} - 8theta _2^{} + 3} } {4left( {8theta _1^2 - 6theta _1^{} - 4theta _2^{} + 3} ight)} end{array}} ight]$$

(11)

$${boldsymbol{eta }}{ m{ = }}left[ {begin{array}{*{20}{c}} {{eta _1}} {{eta _2}} end{array}} ight]{ m{ = }}frac{1}{{4left( {2theta _1^2 - theta _2^{}} ight)}}left[ {begin{array}{*{20}{c}} { {8theta _1^2 - 4theta _1^{} - 4theta _2^{} + 1} } {4left( {2theta _1^2 - 2theta _1^{} - theta _2^{} + 1} ight)} end{array}} ight]$$

(12)

本文方法的数值性能仅由参数θ₁和θ₂控制, 在之后的章节中, 它们将按所希望的性能要求进行设计.

2.
改进Hughes理论

经典Hughes^[33]理论可用来评估已有时间积分方法在非线性瞬态热传导系统中的稳定性特性. 为了能够设计出对该类非线性问题无条件稳定的新方法, 本文对经典Hughes理论进行了改进.

多自由度线性系统(2)可以借助${boldsymbol{T}}=displaystylesumlimits_i^N {{T^i}{varphi ^i}}$解耦为N个关于温度坐标Tⁱ的方程${dot T^i}$ + λⁱTⁱ = rⁱ, 其中λ为由(K?λC)φ = 0得到的热特征值, φ为热特征向量. 因此, 大多数已有时间积分方法的理论分析是基于如下线性模型^[32]

$$dot T + lambda T = r$$

(13)

但大量的数值实验表明对线性系统无条件稳定的方法对非线性系统可能是失效的. 在用时间积分方法求解非线性方程(1)时, 由于不同时刻的C和K是不同的, 因此利用线性化方法得到的不同时刻的热特征值和特征向量是不同的. 为了能够考虑非线性系统的这个特征, Hughes^[33]建立了如下模型

$${dot T_{{t_{k + 1}}}} + {lambda _{{t_{k + 1}}}}{T_{{t_{k + 1}}}} = {r_{{t_{k + 1}}}}$$

(14)

其中${lambda _{{t_{k + 1}}}}$为t_k+1 = t_k + Δt = (k + 1)Δt时刻的热特征值. 若系统是线性的, 则${lambda _{{t_{k + 1}}}}$不随时间变化, 恒为常数, 即${lambda _{{t_{k + 1}}}}$ = λ, 此时模型(14)退化为经典线性模型(13). 将时间积分方法的递推公式代入模型(14)可推出时变的传递因子A. 若|A| ≤ 1, 则时间积分方法对单自由度非线性系统是无条件稳定的. 对于非线性多自由度系统, 对其控制方程(1)在不同时刻分别解耦时, 同一阶次的φ在不同时刻是不同的. 不同时刻的温度坐标和特征向量的顺序是根据对应时刻特征值λ的从小向大的顺序依次排列的. 值得指出的是, 由模型(14)推出的稳定性条件对单自由度非线性系统是充分且必要的, 而对多自由度非线性系统是必要但不充分的. 借助方程(14), Hughes^[33]详细分析了广义梯形法则在非线性瞬态热传导系统中的稳定性. 广义梯形法则^[32]的递推公式为

$${T_{{t_{k + 1}}}}{ m{ = }}{T_{{t_k}}} + Delta tleft[ {left( {1 - alpha } ight){{dot T}_{{t_k}}} + alpha {{dot T}_{{t_{k + 1}}}}} ight]$$

(15)

将式(15)代入式(14)中可得传递因子为

$$A = frac{{1 - {lambda _{{t_k}}}Delta tleft( {1 - alpha } ight)}}{{1 + {lambda _{{t_{k + 1}}}}Delta talpha }}$$

(16)

将式(16)代入|A| ≤ 1中可得

$$left. begin{array}{l}alpha = 0:Delta t leqslant 2/{lambda _{{t_k}}}alpha in left( {0,1} ight):;;;;;;{ m{stable}},;;{lambda _{{t_{k + 1}}}} geqslant dfrac{{left( {1 - alpha } ight)}}{alpha }{lambda _{{t_k}}};;;;;;Delta t leqslant dfrac{2}{{left( {1 - alpha } ight){lambda _{{t_k}}} - alpha {lambda _{{t_{k + 1}}}}}},;;{lambda _{{t_{k + 1}}}} < dfrac{{left( {1 - alpha } ight)}}{alpha }{lambda _{{t_k}}}alpha = 1:{ m{stable}}end{array} ight} $$

(17)

从式(17)中可以发现, 在广义梯形法则中只有BDF (α = 1)对非线性系统是无条件稳定的, 而对线性系统无条件稳定的Crank-Nicolson方法(α = 1/2)对非线性系统则是条件稳定的. 另外, 注意到对于显式方法(α = 0), 失稳原因是时间步长尺寸Δt不够小, 而隐式方法(0 < α $leqslant$ 1)失稳的原因与热特征值λ演化规律相关. 为了能够借助Hughes理论设计出对非线性瞬态热传导系统是无条件稳定的隐式时间积分方法, 本文在Hughes理论中引入一个用来刻画λ演化规律的函数, 其定义为

$${delta _t} = frac{{{lambda _t}}}{{{lambda _{{t_k}}}}},t in left[ {{t_k},{t_k} + Delta t} ight]$$

(18)

函数δ_t可以刻画λ在一个时间单元内[t_k, t_k + Δt]的变化情况. 将函数δ_t代入模型(14)可得改进的模型为

$${dot T_{{t_{k + 1}}}} + {delta _{{t_{k + 1}}}}{lambda _{{t_k}}}{T_{{t_{k + 1}}}} = {r_{{t_{k + 1}}}}$$

(19)

利用改进的模型(19)得到的广义梯形法则的稳定条件为

$$left( { - {delta _{{t_{k + 1}}}}alpha - alpha + 1} ight){lambda _{{t_k}}}Delta t leqslant 2,;;{ m{ }}{delta _{{t_{k + 1}}}} = frac{{{lambda _{{t_{k + 1}}}}}}{{{lambda _{{t_k}}}}} in left( {0, + infty } ight)$$

(20)

比较式(20)和式(17)可以发现, 由改进模型得到的稳定性条件与Hughes理论得到的结果完全一致, 从而说明改进理论在稳定性分析方面与Hughes理论是等价的. 下面以广义梯形法则的稳定性条件(20)为例, 简述如何利用改进Hughes理论设计无条件稳定方法. 从式(20)可以看出, 当(?${delta _{{t_{k + 1}}}}$α-α + 1) $leqslant $ 0成立时, 不等式(20)恒成立. 为了消除正的${delta _{{t_{k + 1}}}}$对稳定性的影响, α的取值区间应为α $geqslant$ 1. 当α $geqslant $ 1时, 广义梯形法则是无条件稳定的, 其中α = 1对应的是BDF. 这种通过消除${delta _{{t_{k + 1}}}}$对稳定性影响的方法可以用来设计无条件稳定方法, 并被用于本文方法的参数设计中. Hughes理论原模型(14)虽然可以用于分析方法的稳定性, 但难以用于设计无条件稳定方法.

3.
算法设计与分析

将本文方法的递推公式(9)代入式(19)可得递推关系为

$${T_{{t_{k + 1}}}} = A{T_{{t_k}}} + L$$

(21)

其中, 时变的传递因子A和载荷算子L分别为

$$A = frac{{{varOmega }_{}^2{g_2} + {varOmega }{g_1} + 2}}{{{varOmega }_{}^2{h_2} + {varOmega }{h_1} + 2}}quad;$$

(22)

$$L = - Delta tfrac{{{varOmega }{{bar g}_2} + {{bar g}_1}}}{{{varOmega }_{}^2{h_2} + {varOmega }{h_1} + 2}}$$

(23)

式中, Ω = ${lambda _{{t_k}}}$Δt, 函数g_i, ${bar g_i}$和h_i (i = 1,2)为

$$begin{split} {g_1} = &1 - 4theta _1^{} - 4theta _2^{} + 8theta _1^2 + &quad{delta _{{t_{k + {1 / 2}}}}}left( { - 3 + 6theta _1^{} + 4theta _2^{} - 8theta _1^2} ight) end{split}tag{24a};;;;;;;;;;;, $$

$${g_2} = {delta _{{t_{k + {1 / 2}}}}}left( {1 + 2theta _1^2 - 2theta _1^{} - theta _2^{}} ight)tag{24b} ;;;;;;;;;;;;$$

$$begin{split} {{bar g}_1} = &left( {{r_{{t_k}}} + {r_{{t_{k + 1}}}}} ight)left( {1 - 4theta _1^{} - 4theta _2^{} + 8theta _1^2} ight) - &quad 4{r_{{t_{k + {1 / 2}}}}}left( {1 - 2theta _1^{} - 2theta _2^{} + 4theta _1^2} ight) end{split} tag{24c};;;;;;,$$

$$begin{split} {bar g_2} =& {delta _{{t_{k + {1 / 2}}}}}{r_{{t_k}}}left( {1 - 2theta _1^{} - theta _2^{} + 2theta _1^2} ight) +&quad{delta _{{t_{k + {1 / 2}}}}}{r_{{t_{k + 1}}}}left( {theta _2^{} - 2theta _1^2} ight)end{split}tag{24d};;;;;;;;,,,,,,,$$

$$begin{split} {h_1} =& left( {{delta _{{t_{k + {1 / 2}}}}} - {delta _{{t_{k + 1}}}}} ight)left( {1 + 8theta _1^2} ight) - &quad2{delta _{{t_{k + {1 / 2}}}}}left( {theta _1^{} + 2theta _2^{}} ight) + 4{delta _{{t_{k + 1}}}}left( {theta _1^{} + theta _2^{}} ight) end{split} tag{24e},,$$

$${h_2} = {delta _{{t_{k + {1 / 2}}}}}{delta _{{t_{k + 1}}}}left( {2theta _1^2 - theta _2^{}} ight)tag{24f};;;;;;;;;;;;;;;;;;;;,,,,$$

其中${delta _{{t_{k + {1 / 2}}}}}$ = ${lambda _{{t_{k + {1 / 2}}}}}$/${lambda _{{t_k}}}$, ${delta _{{t_{k + 1}}}}$ = ${lambda _{{t_{k + 1}}}}$/${lambda _{{t_k}}}$, t_k+1/2 = t_k + Δt/2 = (k + 1/2)Δt.

首先考虑本文方法的高频耗散特性. 若一个无条件稳定时间积分方法的传递因子满足A|_Ω→∞ = 0, 则其被认为是L型耗散方法. 为了能够快速过滤掉高频振荡, L型耗散是被期望的, 为此要求

$${left. A ight|_{{varOmega } to infty }}{ m{ = }}0 Rightarrow {g_2}{ m{ = 0}}$$

(25)

从而可以建立θ₁和θ₂的约束关系为

$$theta _2^{} = 2theta _1^2 - 2theta _1^{} + 1$$

(26)

进而式(22)中的传递因子A和式(23)中的载荷算子L分别被更新为

$$begin{split}A = &left{varOmega left[ {{delta _{{t_{k + 1/2}}}}left( {1 - 2theta _1^{}} ight) - left( {3 - 4theta _1^{}} ight)} ight] + 2 ight}Big/left{varOmega _{}^2{delta _{{t_{k + 1/2}}}}{delta _{{t_{k + 1}}}} ight.cdot&;;;;;;;;left.left( {2theta _1^{} !-! 1} ight) + varOmega left[ {{delta _{{t_{k + 1}}}}left( {3 - 4theta _1^{}} ight) + 3{delta _{{t_{k + 1/2}}}}left( {2theta _1^{} - 1} ight)} ight] !+! 2 ight}end{split}$$

(27)

$$begin{split}L = &Delta t;left{ {varOmega {delta _{{t_{k + 1/2}}}}{r_{{t_{k + 1}}}}left( {2{theta _1} - 1} ight) + left[ {3{r_{{t_k}}} - 4{r_{{t_{k + 1/2}}}} + 3{r_{{t_{k + 1}}}} - } ight.} ight.&quadleft. {left. {4{theta _1}left( {{r_{{t_k}}} - 2{r_{{t_{k + 1/2}}}} + {r_{{t_{k + 1}}}}} ight)} ight]} ight}/left{{varOmega _{}^2{delta _{{t_{k + 1/2}}}}{delta _{{t_{k + 1}}}}left( {2{theta _1} - 1} ight) + } ight.&quadleft. {varOmega left[ {{delta _{{t_{k + 1}}}}left( {3 - 4theta _1^{}} ight) + 3{delta _{{t_{k + 1/2}}}}left( {2theta _1^{} - 1} ight)} ight] + 2} ight}[-12pt]end{split}$$

(28)

下面讨论本文方法的稳定性. 这里假设1/2 $leqslant$ θ₁ $leqslant $ 3/4, 从而使得式(27)中的传递因子A的分母恒为正值, 进而不等式|A| $leqslant $ 1可等价表示为

$$ begin{split}&0leqslant {varOmega }_{}^{2}{delta }_{{t}_{k+1/2}}{delta }_{{t}_{k+1}}left(2{theta }_{1}^{}-1 ight)+2varOmega {delta }_{{t}_{k+1/2}}left(2{theta }_{1}^{}-1 ight)+4+&qquadunderset{{text{不稳定因素}}}{underbrace{varOmega left({delta }_{{t}_{k+1}}-1 ight)left(3-4{theta }_{1}^{} ight)}}end{split}$$

(29)

式中, Ω∈[0, +∞), ${delta _{{t_{k + {1 / 2}}}}}$∈(0, +∞), ${delta _{{t_{k + 1}}}}$∈(0, +∞). 从式(29)中可以观察到, 当0 < ${delta _{{t_{k + 1}}}}$ < 1时, 算法有可能失稳. 为了消除这个不稳定因素, 令θ₁ = 3/4. 另外可以注意到, 对于线性系统(${delta _{{t_{k + {1 / 2}}}}}$ ≡ ${delta _{{t_{k + 1}}}}$ ≡ 1), 不等式(29)是恒成立的. 再次说明造成隐式方法对非线性问题失稳的原因与热特征值的时变性有关. 至此, 两个自由参数θ₁和θ₂确定完成, 它们使得本文方法具有无条件稳定性和L型耗散.

最后, 利用局部截断误差σ^[32]来分析本文方法的精度阶次. 局部误差定义为

$$sigma = {{left( {{T_{{t_{k + 1}}}} - A{T_{{t_k}}} - L} ight)} / {Delta t}}$$

(30)

将式(27)和式(28)代入上式整理可得

$$sigma = {s_0}Oleft( {Delta {t^0}} ight) + {s_1}Oleft( {Delta t} ight) + {s_2}Oleft( {Delta {t^2}} ight)$$

(31)

式中

$$begin{split} {s_0} = &4left( {{{dot T}_{{t_k}}} + {delta _{{t_{k + {1 / 2}}}}}{lambda _{{t_k}}}{T_{{t_k}}} - {r_{{t_k}}}} ight) + {varOmega }left[ left( {3{delta _{{t_{k + {1 / 2}}}}} - 2} ight){{dot T}_{{t_k}}} + ight. &left. {delta _{{t_{k + {1 / 2}}}}}{delta _{{t_{k + 1}}}}{lambda _{{t_k}}}{T_{{t_k}}} - {delta _{{t_{k + {1 / 2}}}}}{r_{{t_k}}} ight] end{split} tag{32a}$$

$${s_1} = frac{1}{2}{varOmega }left[ {left( {3{delta _{{t_{k + {1 / 2}}}}} - 1} ight){{ddot T}_{{t_k}}} + 2{delta _{{t_{k + {1 / 2}}}}}{delta _{{t_{k + 1}}}}{lambda _{{t_k}}}{{dot T}_{{t_k}}} - 2{delta _{{t_{k + {1 / 2}}}}}{{dot r}_{{t_k}}}} ight]tag{32b}$$

$${s_2} = frac{1}{8}{delta _{{t_{k + {1 / 2}}}}}{varOmega }left( {3{{dddot T}_{{t_k}}} + 4{delta _{{t_{k + 1}}}}{lambda _{{t_k}}}{{ddot T}_{{t_k}}} - 4{{ddot r}_{{t_k}}}} ight)tag{32c}$$

可以看到对线性系统(${delta _{{t_{k + {1 / 2}}}}}$ ≡ ${delta _{{t_{k + 1}}}}$ ≡ 1), s₀ = s₁ = 0, 故本文方法具有严格的二阶精度. 对于非线性系统, 当${delta _{{t_{k + {1 / 2}}}}}$和${delta _{{t_{k + 1}}}}$均趋近于1时, s₀和s₁则趋于0, 此时本文方法是近似二阶精确的.

为便于读者使用, 下面给出本文方法对线性系统(2)的求解流程. 求解过程中涉及t_k+1/2和t_k+1两个时刻的平衡方程, 即

$$left. begin{array}{l} {boldsymbol{C}}{{{dot{boldsymbol T}}}_{{t_{k + {1 / 2}}}}} + {boldsymbol{K}}{{boldsymbol{T}}_{{t_{k + {1 / 2}}}}} = {boldsymbol{Q}}left( {{t_{k + {1 / 2}}}} ight) {boldsymbol{C}}{{{dot{boldsymbol T}}}_{{t_{k + 1}}}} + {boldsymbol{K}}{{boldsymbol{T}}_{{t_{k + 1}}}} = {boldsymbol{Q}}left( {{t_{k + 1}}} ight) end{array} ight}$$

(33)

首先将递推公式(9)代入平衡方程(33)中可解出t_k+1和t_k+1/2两个时刻的温度, 即

$$begin{split}{{boldsymbol{T}}_{{t_{k + 1}}}}{ m{ = }}&{left( {{alpha _{12}}{boldsymbol{C}} - {{boldsymbol{C}}_4}} ight)^{ - 1}}left[ {left( {{{boldsymbol{Q}}_{{t_{k + 1/2}}}} - {{boldsymbol{C}}_5}{{boldsymbol{Q}}_{{t_{k + 1}}}}} ight) + } ight.&quadleft. {left( {{{boldsymbol{beta}} _2}{{boldsymbol{C}}_5} - {{boldsymbol{beta}} _1}} ight){boldsymbol{C}}{{boldsymbol{T}}_{{t_k}}} + left( {{{boldsymbol{eta}} _2}{{boldsymbol{C}}_5} - {eta _1}} ight){boldsymbol{C}}{{mathop Tlimits^. }_{{t_k}}}} ight]end{split};;;$$

(34)

$${{boldsymbol{T}}_{{t_{k + {1 / 2}}}}}{ m{ = }}{{boldsymbol{C}}_1}left( {{{boldsymbol{Q}}_{{t_{k + 1}}}} - {{boldsymbol{C}}_3}{{boldsymbol{T}}_{{t_{k + 1}}}} - {beta _2}{boldsymbol{C}}{{boldsymbol{T}}_{{t_k}}} - {eta _2}{boldsymbol{C}}{{{dot{boldsymbol T}}}_{{t_k}}}} ight)$$

(35)

式中

$$left. begin{array}{l} {{boldsymbol{C}}_1} = {left( {{alpha _{21}}{boldsymbol{C}}} ight)^{ - 1}},{{boldsymbol{C}}_2} = left( {{alpha _{11}}{boldsymbol{C}} + {boldsymbol{K}}} ight),{{boldsymbol{C}}_3} = left( {{alpha _{22}}{boldsymbol{C}} + {boldsymbol{K}}} ight){{boldsymbol{C}}_4} = {{boldsymbol{C}}_2}{{boldsymbol{C}}_1}{{boldsymbol{C}}_3},{{boldsymbol{C}}_5} = {{boldsymbol{C}}_2}{{boldsymbol{C}}_1} end{array} ight} $$

(36)

将求得的${{boldsymbol{T}}_{{t_{k + 1}}}}$和${{boldsymbol{T}}_{{t_{k + {1 / 2}}}}}$回代到式(9)即可得到${{dot{boldsymbol T}}_{{t_{k + 1}}}}$和${{dot{boldsymbol T}}_{{t_{k + {1 / 2}}}}}$, 从而获得所有未知的变量信息. 计算步骤如下:

第1步　准备工作:

(1) 构造热容矩阵C, 热传导矩阵K, 热源向量Q.

(2) 初始化T₀和${{dot{boldsymbol T}}_0}$.

(3) 选择步长Δt和计算算法参数:

　　θ₂, α₁₁, α₁₂, α₂₁, α₂₂, β₁, β₂, η₁, η₂.

(4) 构造系数矩阵:

$$begin{array}{l} {{boldsymbol{C}}_1} = {left( {{alpha _{21}}{boldsymbol{C}}} ight)^{ - 1}},{{boldsymbol{C}}_2} = left( {{alpha _{11}}{boldsymbol{C}} + {boldsymbol{K}}} ight),{{boldsymbol{C}}_3} = left( {{alpha _{22}}{boldsymbol{C}} + {boldsymbol{K}}} ight), {{boldsymbol{C}}_4} = {{boldsymbol{C}}_2}{{boldsymbol{C}}_1}{{boldsymbol{C}}_3},{{boldsymbol{C}}_5} = {{boldsymbol{C}}_2}{{boldsymbol{C}}_1} end{array} $$

(5) 构造有效刚度矩阵${{overset{frown}{boldsymbol{ K}}}}$: ${{overset{frown}{boldsymbol{ K}}}} = left( {{alpha _{12}}{boldsymbol{C}} - {{boldsymbol{C}}_4}}
ight)$.

第2步　迭代运算:

(1) 计算t_k +Δt时刻的有效载荷向量:

$${{overset{frown}{boldsymbol{ Q}}}} = left( {{{boldsymbol{Q}}_{{t_{k + {1 / 2}}}}} - {{boldsymbol{C}}_5}{{boldsymbol{Q}}_{{t_{k + 1}}}}} ight) + left( {{beta _2}{{boldsymbol{C}}_5} - {beta _1}} ight){boldsymbol{C}}{{boldsymbol{T}}_{{t_k}}} + left( {{eta _2}{{boldsymbol{C}}_5} - {eta _1}} ight){boldsymbol{C}}{{dot{boldsymbol T}}_{{t_k}}}$$

(2) 求解t_k+1和t_k+1/2时刻的温度:

$${{boldsymbol{T}}_{{t_{k + 1}}}} !!=!! {{{overset{frown}{boldsymbol{ K}}}}^{ - 1}}{{overset{frown}{boldsymbol{ Q}}}},; {{boldsymbol{T}}_{{t_{k + {1 / 2}}}}}!! =!! {{boldsymbol{C}}_1}left( {{{boldsymbol{Q}}_{{t_{k + 1}}}} - {{boldsymbol{C}}_3}{{boldsymbol{T}}_{{t_{k + 1}}}} - {beta _2}{boldsymbol{C}}{{boldsymbol{T}}_{{t_k}}} - {eta _2}{boldsymbol{C}}{{{dot{boldsymbol T}}}_{{t_k}}}} ight)$$

(3) 求解t_k +Δt时刻温度的一次导数:

$${{dot{boldsymbol T}}_{{t_{k + 1}}}}{ m{ = }}{alpha _{21}}{{boldsymbol{T}}_{{t_{k + {1 / 2}}}}} + {alpha _{22}}{{boldsymbol{T}}_{{t_{k + 1}}}} + {beta _2}{{boldsymbol{T}}_{{t_k}}} + {eta _2}{{dot{boldsymbol T}}_{{t_k}}}$$

对非线性系统(1), 利用递推公式(9)、平衡方程(33)和Newton迭代法, 可求解出未知变量${{boldsymbol{T}}_{{t_{k + 1}}}}$, ${{boldsymbol{T}}_{{t_{k + {1 / 2}}}}}$和${{dot{boldsymbol T}}_{{t_{k + 1}}}}$.

4.
数值性能

本节对本文方法的无条件稳定性、L型耗散和二阶精度进行数值验证和讨论.

4.1
传递因子

图1(a)给出了本文方法和一些现有方法在线性系统中的传递因子^[32]曲线, 其中解析传递因子的表达式为A_exact = exp(?λΔt). 与Crank-Nicolson方法和Galerkin方法相比, 本文方法具有高频耗散优势. 与BDF相比, 本文方法有低频精度优势. 图1(b)给出了本文方法在非线性系统下的传递因子曲线, 可以看到对任意${delta _{{t_{k + {1 / 2}}}}}$和${delta _{{t_{k + 1}}}}$的组合, 在不同Ω值下|A| $leqslant $ 1始终成立, 并且几乎无数值振荡区. 随着Ω值增加, A逐渐趋于0, 说明本文方法对非线性问题具备较强的高频耗散能力.



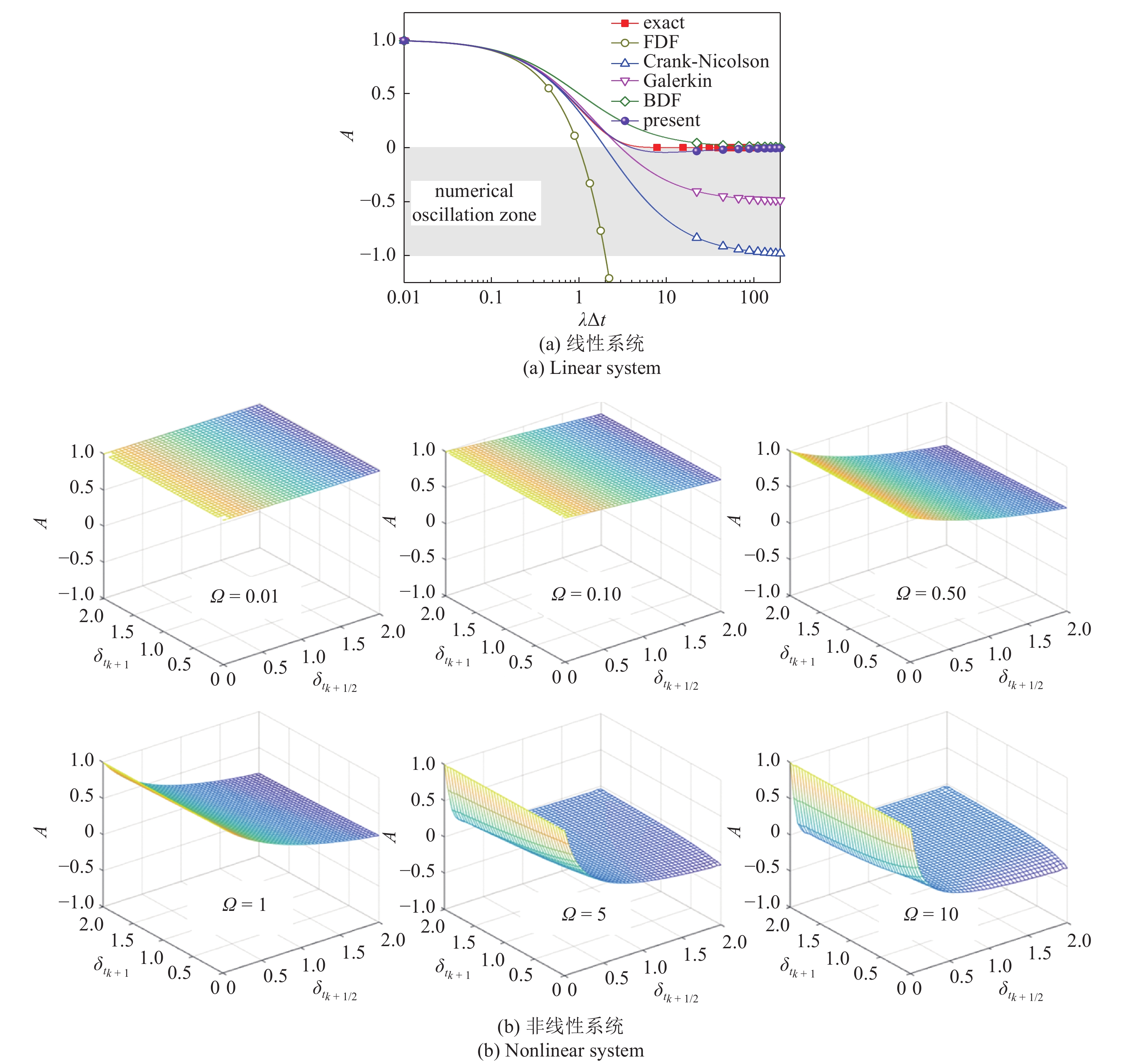onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure1" />



图
1
传递因子



Figure
1.
Amplification factor



下载:
全尺寸图片
幻灯片

4.2
收敛率

收敛率可检测时间积分方法的精度阶次, 其定义为在指定时刻物理量的相对误差随步长减小而减小的速率. 先测试线性系统^[34], 考虑如下方程

$$ dot{T}+T=10mathrm{cos}left(0.1t ight),;{T}_{0}=100$$

(37)

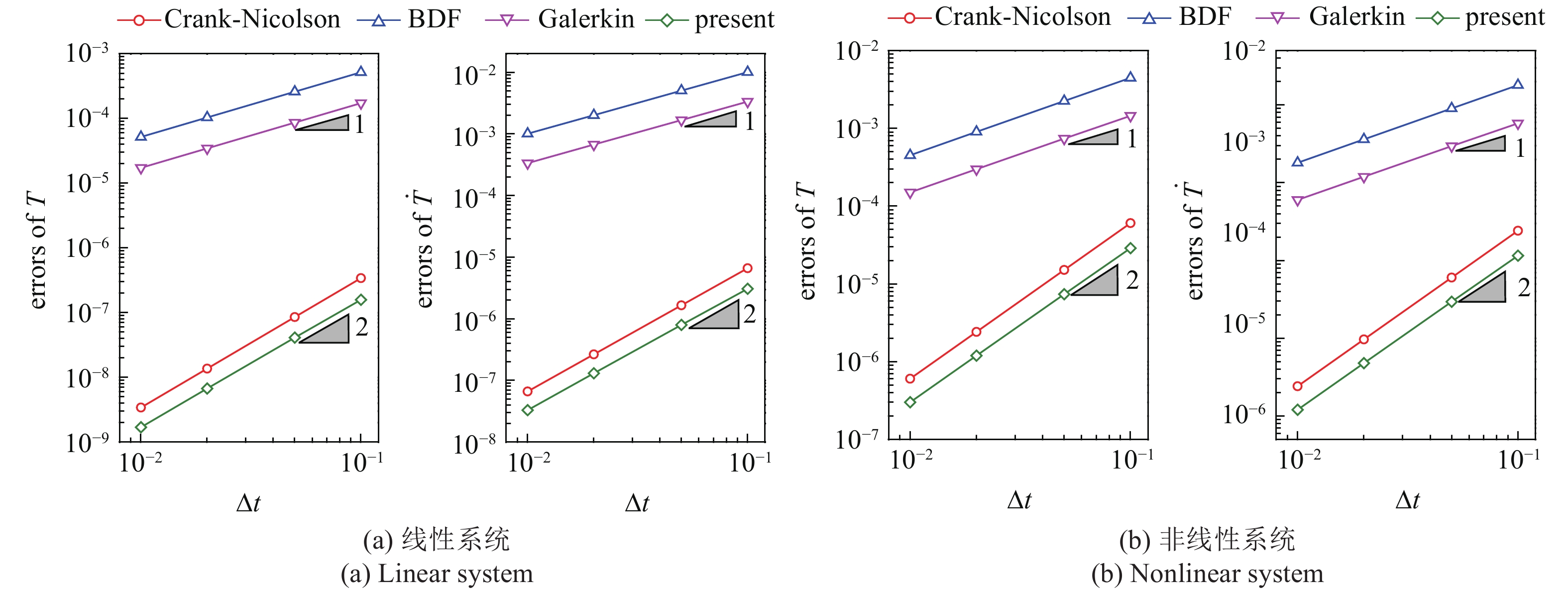
图2(a)给出了t = 100时的相对误差, 可以看出本文方法与Crank-Nicolson方法具有相同的斜率. 从而说明对线性系统, 本文方法具有严格的二阶精度. 再测试非线性系统^[34], 考虑如下方程



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-2.jpg'"
class="figure_img
figure_type2 ccc " id="Figure2" />



图
2
收敛率



Figure
2.
Convergence rate



下载:
全尺寸图片
幻灯片

$$ dot{T}+sigma {T}^{4}=0,;{T}_{0}=200,sigma =3.629{ m{e}}^{-8}$$

(38)

该问题的解析解为T(t) = T₀/(3σT₀³t + 1)^1/3. 图2(b)给出了t = 10的相对误差, 可以看出对非线性问题, 本文方法也能够达到二阶精度, 此时s₀和s₁趋于0.

5.
数值测试

本节利用3个算例来测试本文方法在不同类型瞬态热传导问题中的性能. 本文方法的求解过程中涉及t_k+1和t_k+1/2两个时刻的平衡方程, 而广义梯形法则仅求解t_k+1时刻平衡方程. 为保证精度比较在相同计算量下执行, 在所有的算例中, 本文方法的时间步长取为单步方法的两倍. 在本节, 除广义梯形法则外, 具有二阶精确和L型耗散的BDF2方法^[21]也被考虑, 由于其不具备自启动特性, 本文采用Crank-Nicolson方法作为启动算法. 此外, 所有问题的参考解均由使用小步长的Crank-Nicolson方法得到.

5.1
矩形功能梯度板中的二维热传导问题

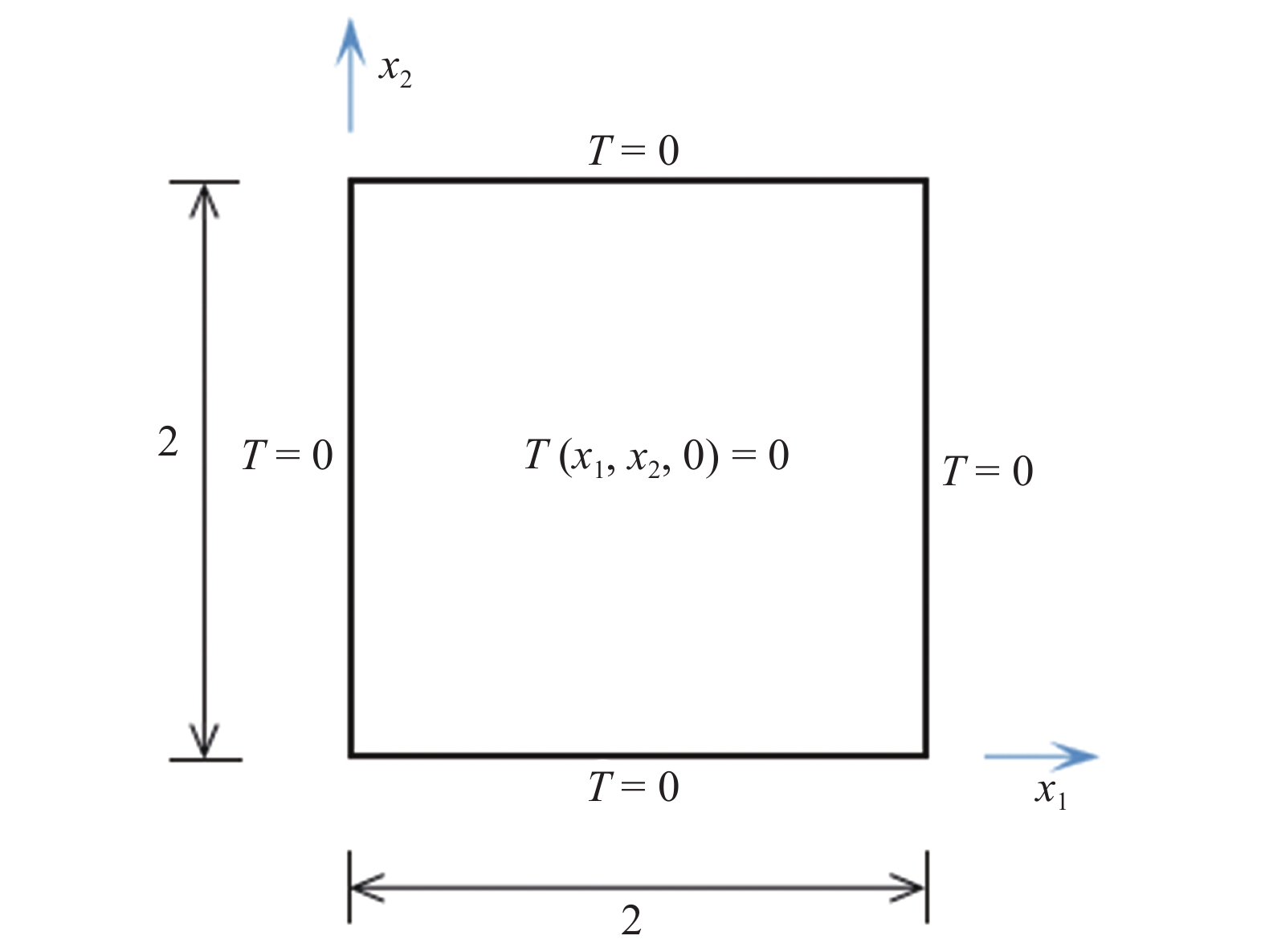
考虑一个功能梯度板中的二维热传导问题^[35], 如图3所知, 假设导热系数k_x1 = k_x2 = 1 + (x₁ ? 1)² + (x₂ ? 1)², 密度ρ = 1, 比热容c_v = 1. 整个域内施加单位初始温度, 所有边界施加T = 0的温度场. 该矩形域利用20 × 20个4结点矩形单元进行空间离散, 广义梯形法则采用步长Δt = 0.01.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
算例1的几何尺寸和边界条件



Figure
3.
Geometry and boundary conditions for Ex.1



下载:
全尺寸图片
幻灯片


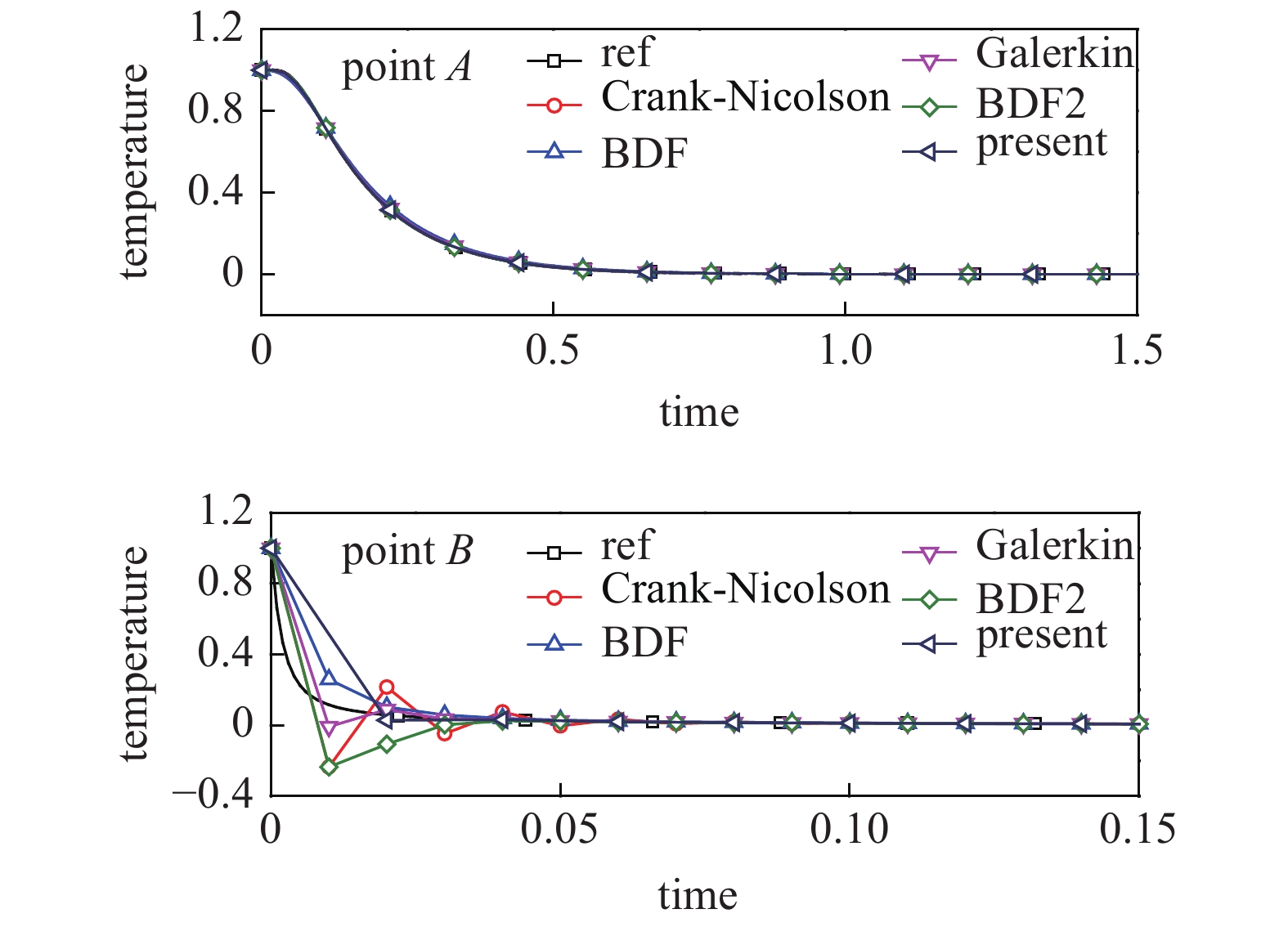
图4给出了中点A(1,1)和角点B(1.9,1.9)的温度?时间曲线. 可以看到在中点A处, 所有方法均与参考解吻合得较好, 但在边界点B处, Crank-Nicolson方法存在明显的数值振荡.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
点A和点B的温度?时间曲线



Figure
4.
Temperatures of point A and point B versus time



下载:
全尺寸图片
幻灯片


为了进一步比较这些方法在域内的精度表现, 图5提供了所有方法在t = 0.1时刻温度误差的分布结果, 可以看出本文方法不会像Crank-Nicolson方法一样在边界处产生剧烈的数值振荡, 且在所有方法中, 本文方法的域内精度最高. BDF和Galerkin方法虽然没有数值振荡, 但域内精度不令人满意.



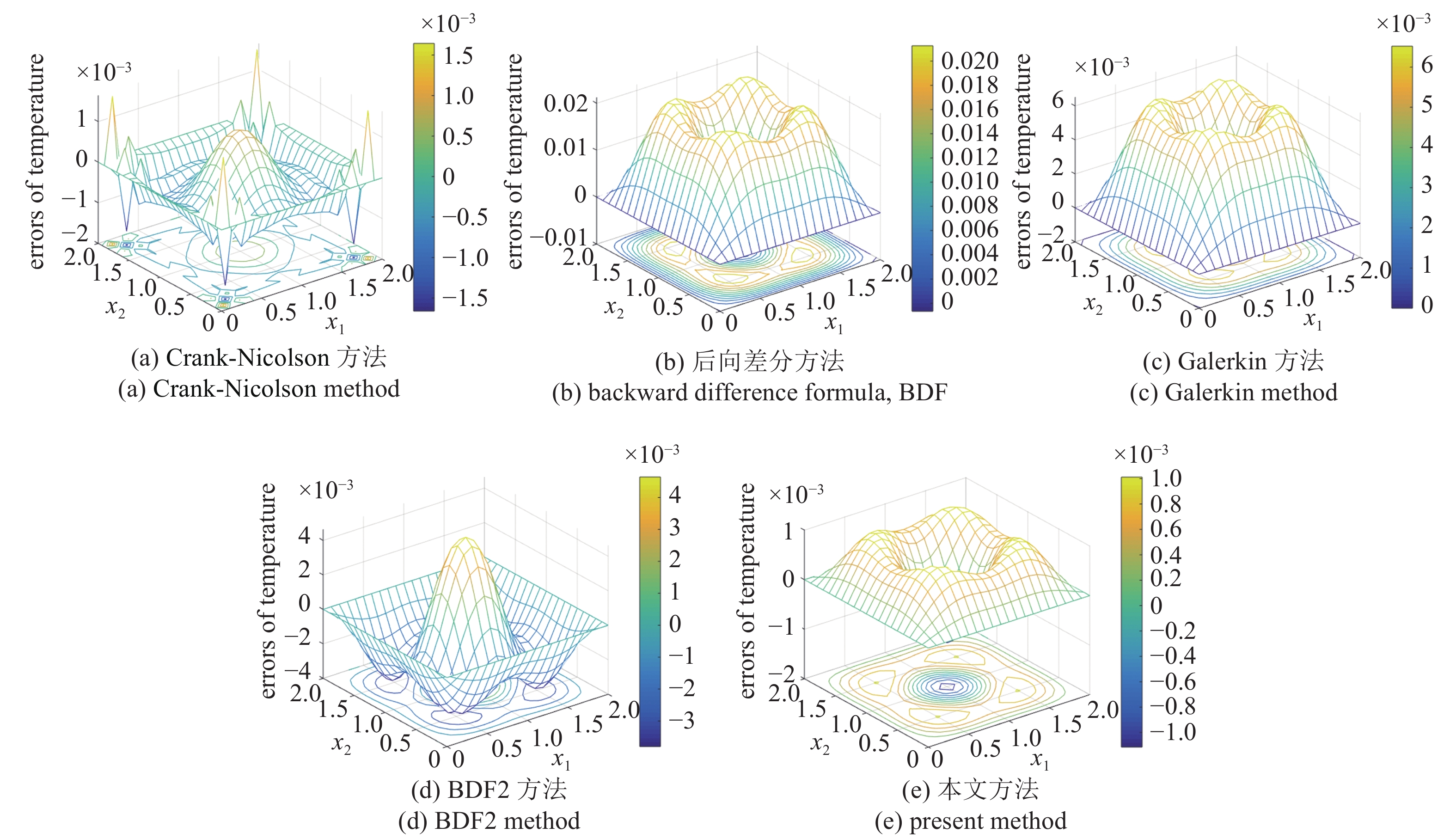onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-5.jpg'"
class="figure_img
figure_type2 ccc " id="Figure5" />



图
5
温度误差分布(t = 0.1)



Figure
5.
Errors of temperature at t = 0.1



下载:
全尺寸图片
幻灯片

5.2
一维非线性热传导问题

考虑一个材料参数与温度有关的一维杆^[36], 杆长l假设为1, 材料参数为k = γT² + βT + η (γ, β, η∈R)和ρc_v = 1. 在杆的两端施加T = 0的温度场, 域内施加单位初始温度. 利用20个两结点单元对杆进行空间离散.

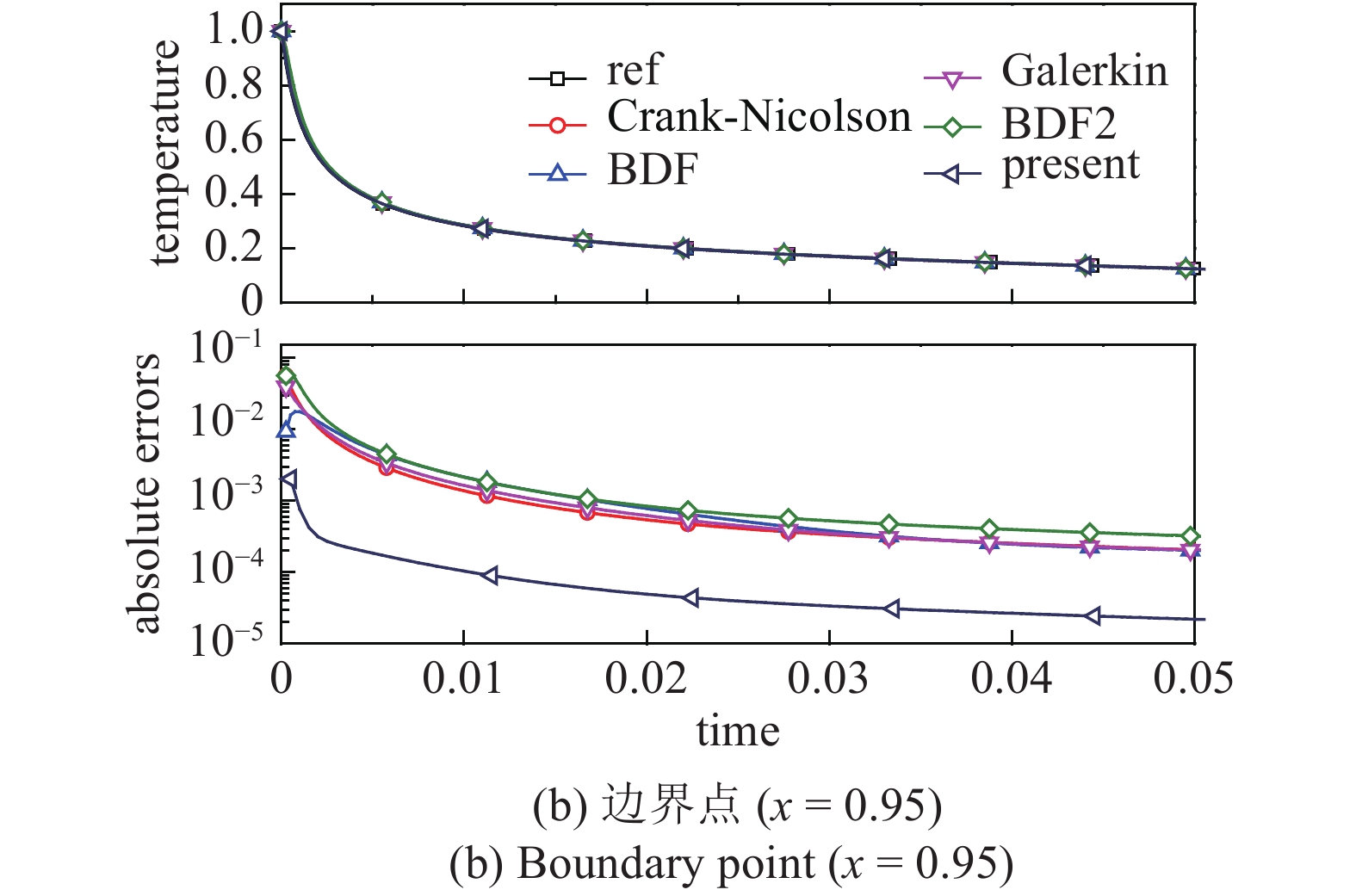
首先考虑γ = 0, β = η = 1的情况, 广义梯形法则的Δt =0.000 25. 图6给出了中点处(x = 0.5)和边界处(x = 0.95)的温度?时间曲线, 可以看到本文提出的方法展示出明显的精度优势.



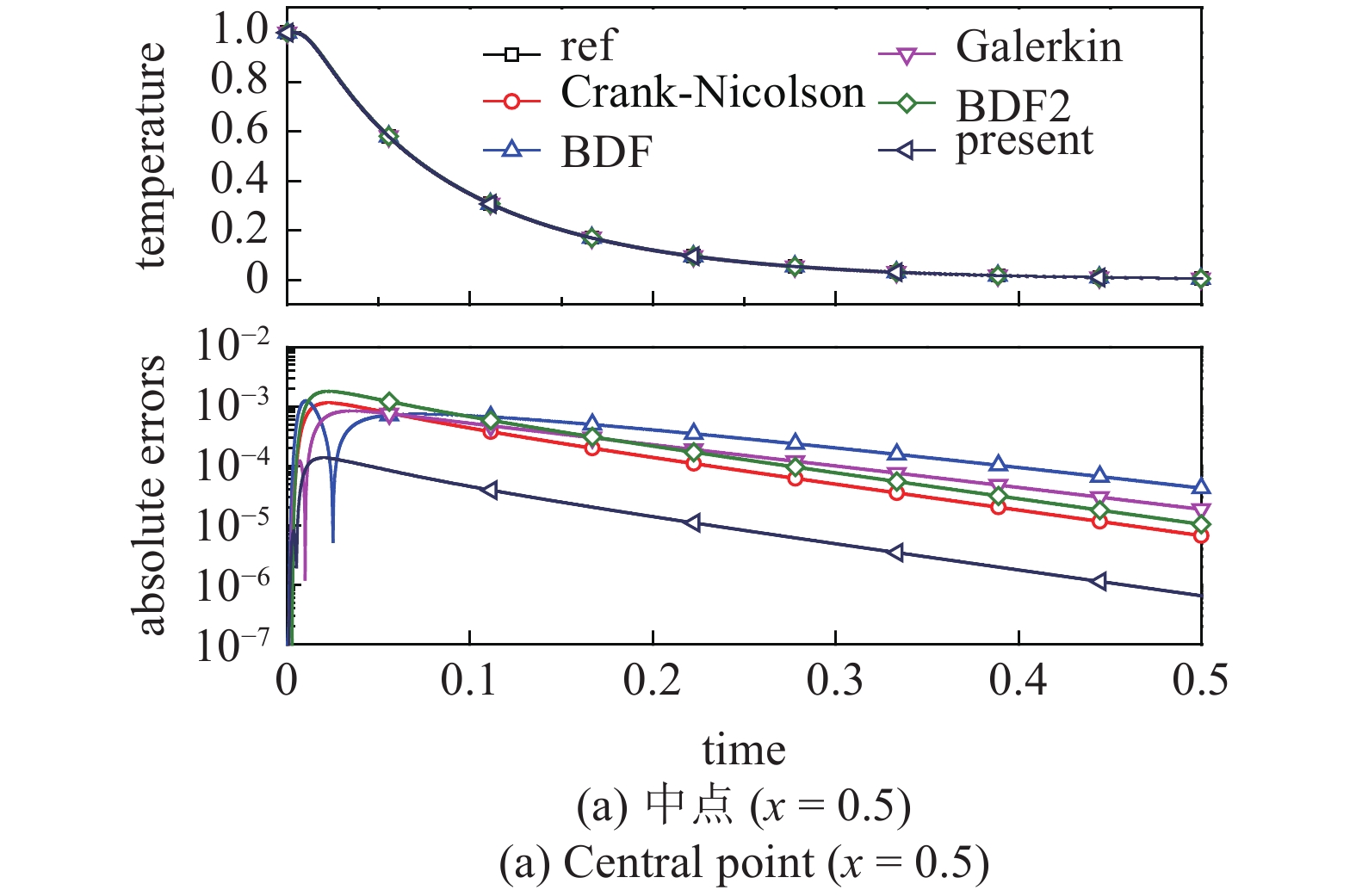onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-6-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6-1" />



6
温度?时间曲线(γ = 0, β = η = 1)



6.
Temperature-time history



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
温度?时间曲线(γ = 0, β = η = 1) (续)



Figure
6.
Temperature-time history (continued)



下载:
全尺寸图片
幻灯片


为了展示本文方法的稳定性优势, 另一种情况β = 100, γ = η = 1被考虑. 此时广义梯形法则的Δt = 0.005. 从图7可以看到Crank-Nicolson方法在计算一段时间后就失去了稳定性, 而本文方法不仅没有失去稳定性, 且在所有收敛的方法中具有最高的精度.



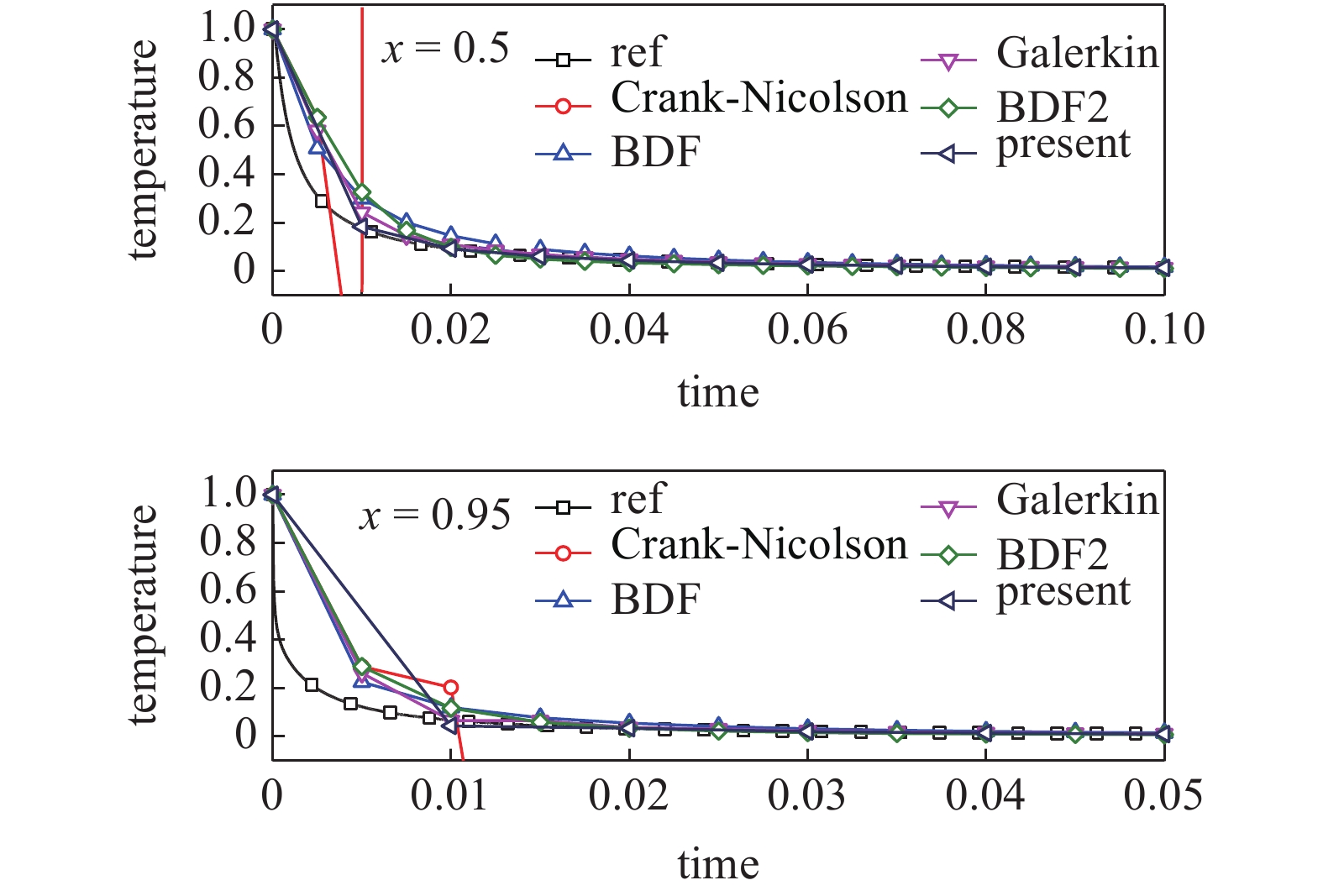onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
温度?时间曲线(β = 100, γ = η = 1)



Figure
7.
Temperature-time history



下载:
全尺寸图片
幻灯片

5.3
具有外部热源的二维热传导问题

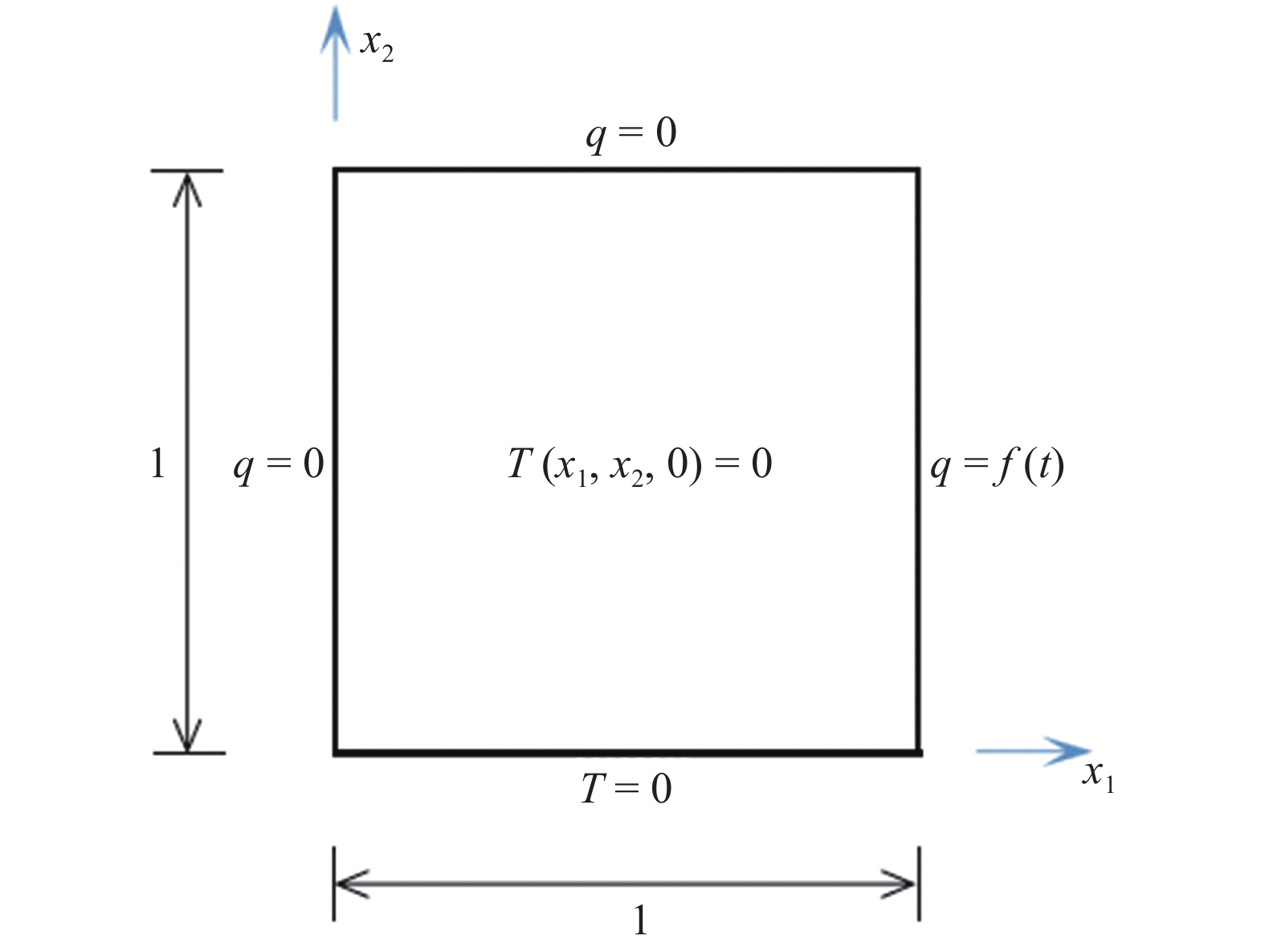
考虑一均质矩形板^[9], 如图8所示, 外部热源f(t) = cos(10t)从右边界持续不断地向域内输入, 底部边界施加T = 0的温度场, 其余边界为绝热状态. 利用50 × 50个4结点矩形单元进行划分, 广义梯形法则的Δt =0.005.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
算例3的几何尺寸和边界条件



Figure
8.
Geometry and boundary conditions for Ex.3



下载:
全尺寸图片
幻灯片


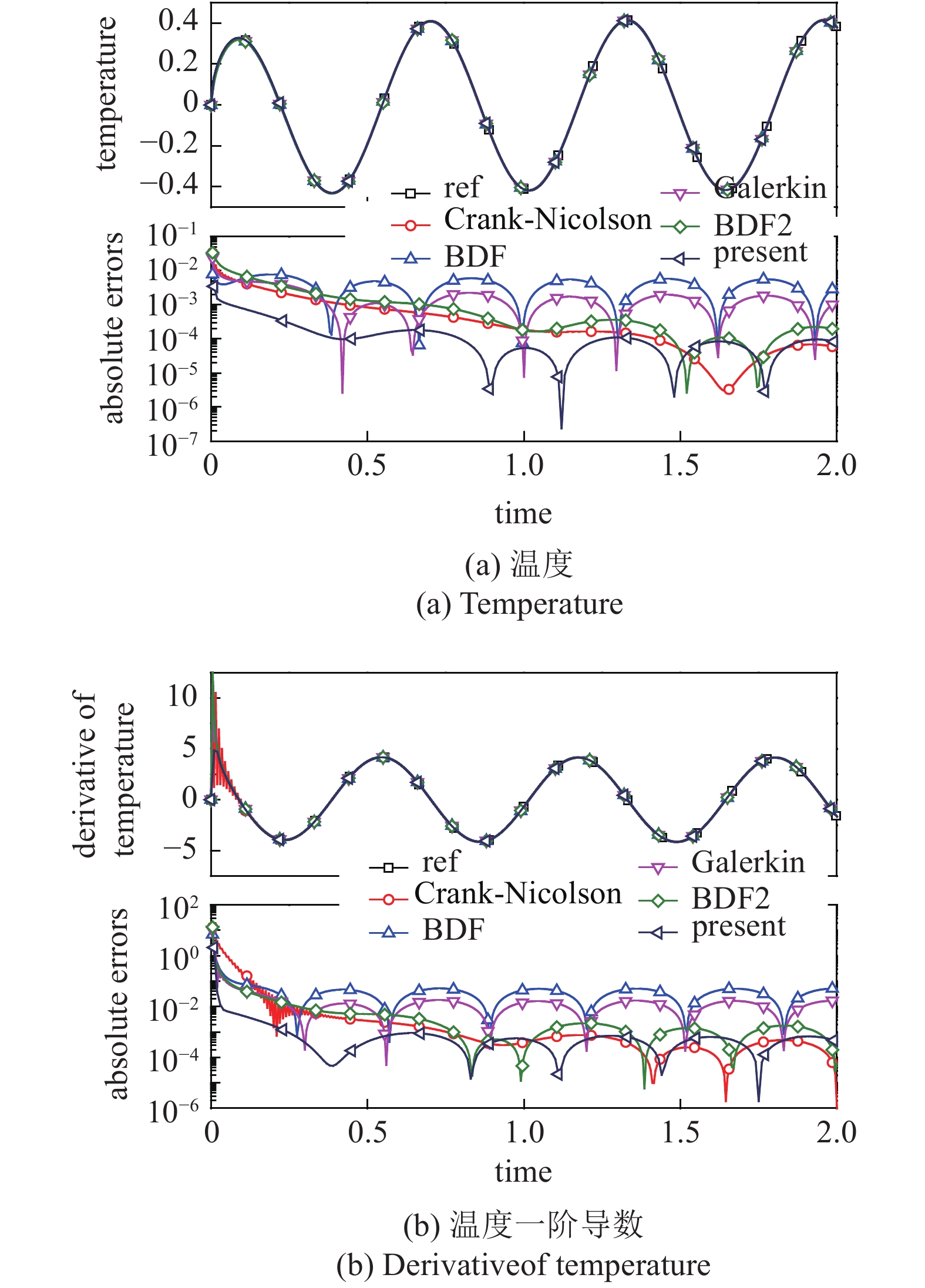
图9给出了点A(0.98, 0.98)处的温度和温度一阶导数的结果, 从绝对误差的数值上可以看出: 本文方法要比二阶Crank-Nicolson方法和BDF2更加精确. 总体来说, 这3种二阶精度算法的精度明显优于一阶精度的Galerkin方法和BDF.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-140-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
点A处温度和其一阶导数与时间的关系曲线



Figure
9.
Temperature and its derivative -time histories of point A



下载:
全尺寸图片
幻灯片

6.
结论

本文提出了一种适用于求解一般瞬态热传导问题的无条件稳定单步时间积分方法. 该方法具有无条件稳定性、二阶精度、L型数值耗散和自启动特性. 需要强调的是, 与大多数现有时间积分方法不同, 本文方法对线性和非线性瞬态热传导问题均是无条件稳定的.

线性和非线性数值比较结果表明, 与著名的二阶Crank-Nicolson方法相比, 在计算量相同的前提下, 本文方法具有更理想的精度和稳定性, 并且不会在高频段诱发出虚假的数值振荡. 与具有L型耗散的二阶BDF2相比, 本文方法具有更高的精度且无需其他算法来启动计算.

鉴于本文方法具有优秀的数值性能和易执行性, 故推荐其用于一般瞬态热传导问题的求解.