, 邵素娟山东理工大学 交通与车辆工程学院,淄博 255000
The research of time delay vibration control with time - varying parameters
LiShuai, ZhouJilei, RenChuanbo中图分类号:O032.8
文献标识码:A
通讯作者:
收稿日期:2017-05-31
接受日期:2017-11-16
网络出版日期:2018-02-20
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (712KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
动力吸振器减振机理已经在理论研究和实际工程中被广泛应用。为了克服传统被动吸振器减振频域小,只能对特定频率的激励取得有效减振控制的缺陷,寻找能够有效改善动力吸振器减振性能的主动控制力一直是振动主动控制技术的主要研究方向。闫立勋等[1]为了扩大吸振器的工作频带,设计了一种自适应主动共振吸振器,并提出了一种变步长、双寻优的控制算法,提高了吸振器的减振控制效果。钱小勇和胡海岩[2]为了扩展吸振器的工作带宽,提出一种实时调节弹性元件的半主动吸振器,并给出了吸振器的控制策略。在动力吸振器减振机理的研究过程中,研究者们发现时滞现象在振动系统中是广泛存在甚至是不可避免的。起初,因时滞的存在会使得振动系统失稳或使其振动非线性化,所以时滞动力学问题的研究主要集中在对时滞的辨识和补偿上。随着振动主动控制技术的发展,越来越多的研究表明,时滞反馈也可以作为主动控制项在振动的主动控制技术中被有效利用。Olgac[3]最早提出了利用基于吸振器质量块位移的时滞反馈控制结构来吸收主系统的振动能量的概念,并取得了显著的效果。为了进一步验证时滞控制的减振效果,又设计出能够在固定双频下完全抑制主系统振动的双频时滞动力吸振器[4]。随后,Olgac等人[5,6]又研究了实时可调谐吸振器减振机理,分别引入位移和速度时滞状态反馈,其可随频率变化调节时滞反馈量,从而最大限度的减小了主系统的振动响应。
近些年来,时滞减振控制技术取得了进一步的发展。Shin与Kim等[7]从理论上对气动隔振板的时滞减振控制技术进行了研究,并取得了很好的实验效果。Nayfeh等[8]在对悬臂梁的时滞减振控制上也取得了非常好的实验效果。在工程领域,申永军、赵永香、田佳雨等[9]对一类采用有限相对位移控制的含时滞单自由度半主动悬架系统进行了动力学分析,研究了被动悬架系统并且和半主动悬架系统进行了比较,证实了半主动悬架系统的优越性。赵艳影、徐鉴[10]采用多尺度法研究了时滞非线性动力吸振器对主系统的减振性能。陈龙祥、蔡国平研究了柔性梁旋转运动[11]与受迫振动[12]的时滞主动控制。除此之外,时滞对振动非线性的影响[13]和状态反馈问题[14]也是工程领域时滞控制问题的研究重点。随着主动控制技术的兴起,阻尼的时滞补偿方法 [15]、时滞吸振器的减振频宽[16]、稳定性[17]及参数优化[18]成为了近些年来的研究热点。
目前,时滞减振控制理论的研究大多还是集中于吸振器[19,20]与隔振器[21,22,23],通过对比加入时滞控制前后时滞动力吸振器的减振控制效果来[24,25]突出时滞减振控制的优越性。时滞参数为定值的时滞动力吸振器对谐波激励有着出色的减振控制效果,但对随机激励的减振控制效果并不明显,具体表现为时滞动力吸振器对随机激励的减振控制效果与被动吸振器几乎相同。针对上述问题,本文提出了一种时变参数时滞减振控制方法,通过使时变优化得到的多组时滞控制参数以一定周期循环作用于振动控制过程的方法来提高时滞动力吸振器对随机激励的减振控制效果,进一步改善了时滞动力吸振器的减振性能,为结构时滞减振控制提供了一种新的途径。
1 时滞动力吸振器
1.1 时滞动力吸振器模型
在实际工程中,动力吸振器的形态和结构是复杂多变的,为了便于研究,需要根据所研究的问题对研究对象进行合理简化。时滞动力吸振器模型通常由质量块、弹簧、阻尼元件和时滞反馈控制力构成,通过调节时滞反馈控制力中的时滞增益系数和时滞反馈量来使时滞动力吸振器达到最佳的减振控制效果。在此前时滞动力吸振器的研究中,时滞参数一般为定值,即定值参数时滞动力吸振器。本文以二自由度动力吸振器减振系统为例,建立了二自由度时滞动力吸振器减振系统的力学模型。模型如图1所示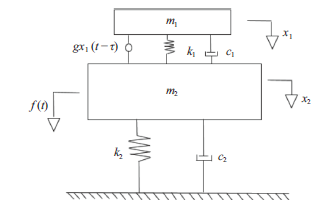
显示原图|下载原图ZIP|生成PPT图1含时滞反馈控制的二自由度减振系统
-->Fig.1Two-degree-of-freedom damping system with time-delay feedback control
-->
图中,m1为时滞动力吸振器质量, c1和k1分别为时滞动力吸振器弹簧的刚度系数和阻尼元件的阻尼系数,x1为时滞动力吸振器质量m1的位移;m2为主系统质量,k2与c2分别为主系统弹簧的刚度系数和阻尼元件的阻尼系数,x2为主系统质量m2的位移。图1中,f(t)为直接作用于主系统上的外界激励,激励形式未定;g为时滞增益系数,τ为时滞反馈量。系统模型的动力学方程为
$\left\{ \begin{matrix}\begin{align}{m_{1}}\overset{..}{\mathop{{x_{1}}}}+{c_{1}}\overset{.}{\mathop{x_{1}}}-\overset{.}{\mathop{x_{2}}})+{k_{1}}\left({x_{1}}-{x_{2}} \right)+u=0 \\{{m}_{2}}\overset{.,}{\mathop{{{x}_{2}}}}\,+{{c}_{1}}\overset{.}{\mathop{{{x}_{2}}}}\,-\overset{.}{\mathop{{{x}_{1}}}}\,)+{{k}_{1}}\left( {{x}_{2}}-{{x}_{1}} \right)+{{c}_{2}}\overset{}{\mathop{{{x}_{2}}}}+ \\{{k}_{2}}\overset{}{\mathop{{{x}_{2}}}}\,-u=f\left( t \right) \\\end{align} \\\end{matrix} \right.$ (1)
其中,u为时滞反馈控制力,其方程形式为
$u=g{{x}_{1}}\left( t-\tau \right)$ (2)
当方程(2)中g=0时, u=0,此时时滞反馈控制力消失,时滞动力吸振器变为被动吸振器。
本文选取的系统参数值如表1所示
Table.1
表1
表1系统参数
Table.1System parameters
| subscript | m/kg | c/ (N·m·s-1) | k/( N·m-1) |
|---|---|---|---|
| 1 | 0.1 | 0.1 | 10 |
| 2 | 1 | 2 | 100 |
新窗口打开
1.2 时变时滞参数的确定
本文将时滞反馈控制力中的时滞增益系数由定值形式g变为时间函数形式g(t),以此在优化环节中得到一些列对应不同时间点的优化结果。时滞增益系数由定值形式g变为时间函数形式g(t)后,系统动力学方程(1)变为$\left\{ \begin{matrix}\begin{align}{{m}_{1}}\overset{..}{\mathop{x_{1}}}+{c_{1}}(\overset{.}{\mathop{x_{1}}}-\overset{.}{\mathop{x_{2}}})+{k_{1}}\left( {x_{1}}-{x_{2}} \right)+g\left( t \right){{x}_{1}}\left( t-\tau \right)=0 \\{{m}_{2}}\overset{..}{\mathop{{{x}_{2}}}}\,+{{c}_{1}}(\overset{.}{\mathop{{{x}_{2}}}}-\overset{.}{\mathop{{{x}_{1}}}})+{{k}_{1}}\left( {{x}_{2}}-{{x}_{1}} \right)+{{c}_{2}}\overset{}{\mathop{{{x}_{2}}}}+{{k}_{2}}{{x}_{2}}-g\left( t \right){{x}_{1}}\left( t-\tau \right)=f\left( t \right) \\\end{align} \\\end{matrix} \right.$ (3)
首先设方程(3)中作用于主系统上的激励f(t)为谐波激励f(t)=sin(ωt),其中ω为主系统振动频域响应的峰值频率,其值为ω=ωn(1-2ζ2)1/2=9.9rad/s,其中, ζ=c2/2(k2m2)1/2, ωn =(k2/m2)1/2=10rad/s, ωn为主系统的固有频率。
因时滞增益函数g(t)的方程形式不确定,而优化算法只能对定值形式的目标参数进行优化计算,本文选择将g(t)在一系列时间点tk上进行Taylor级数展开,将时滞增益函数g(t)构造为时间点上的定值形式。g(t)的Taylor级数展开式为
$\begin{align}g\left( t \right)=g\left( {{t}_{k}} \right)+\frac{g{{\left( {{t}_{k}} \right)}^{'}}}{1!}\left( t-{{t}_{k}} \right)+ \frac{g{{\left( {{t}_{k}} \right)}^{''}}}{2!}{{\left( t-{{t}_{k}} \right)}^{2}}+\frac{g{{\left( {{t}_{k}} \right)}^{'''}}}{3!}{{\left( t-{{t}_{k}} \right)}^{3}} +\ldots +\frac{g{{\left( {{t}_{k}} \right)}^{n}}}{n!}{{\left( t-{{t}_{k}} \right)}^{n}}+{{R}_{n}}\left( t \right) \\\end{align}$ (4)
由于公式(4)中的Taylor级数展开时间区间较小,因此本文只取时滞增益函数g(t)的 Taylor级数展开式的前两项,其中tk为Taylor级数展开式(4)的展开时间点。为建立主系统振动频域响应函数,需要对方程(3)进行拉普拉斯变换得到系统的特征方程。若将公式(4)代入方程(3)进行拉普拉斯变换,由于s域微分定理,在变换过程中会出现无法消除的冗余微分项$\frac{dx\left( s \right)}{ds}$,因此无法在连续的时间区间对方程(3)进行拉普拉斯变。为了避免出现冗余微分项,本文选择对方程(3)所在的连续时间区间进行离散,将时滞增益函数g(t)在离散时间区间上进行Taylor级数展开。
首先将方程(3)所在的时间区间由连续时间区间离散为由k个长度相等的时间区间T组成的离散时间区间,其中k=t/T,t为方程(3)所在的连续时间区间长度。然后再将每个时间区间T离散为n个相等的时间区间ΔT,其中n=T/ΔT。最后取Taylor级数展开式(4)中的展开时间点tk为第k个时间区间T的起始时间点。由此可得每个时间区间T内的系统动力学方程为
$\left \{ \begin{matrix}\begin{align}{{m}_{1}}\overset{..}{\mathop{{{x}_{1}}}}\,({{t}_{a}})+{{c}_{1}}[\overset{.}{\mathop{{{x}_{1}}}}\,({{t}_{a}})-\overset{.}{\mathop{{{x}_{2}}}}\,({{t}_{a}})]+{{k}_{1}}[{{x}_{1}}\left( {{t}_{a}} \right)-{{x}_{2}}\left( {{t}_{a}} \right)]+g\left( {{t}_{a}} \right){{x}_{1}}\left( {{t}_{a}}-\tau \right)=0 \\{{m}_{1}}\overset{..}{\mathop{{{x}_{2}}}}\,({{t}_{a}})+{{c}_{1}}[\overset{.}{\mathop{{{x}_{2}}}}\,({{t}_{a}})-\overset{.}{\mathop{{{x}_{1}}}}\,({{t}_{a}})]+{{k}_{1}}[{{x}_{2}}\left( {{t}_{a}} \right)-{{x}_{1}}\left( {{t}_{a}} \right)]+{{c}_{2}}\overset{.}{\mathop{{{x}_{2}}}}\,({{t}_{a}})+{{k}_{2}}{{x}_{2}}\left( {{t}_{a}} \right)-g\left( {{t}_{a}} \right){{x}_{1}}\left( {{t}_{a}}-\tau \right)=f\left( {{t}_{a}} \right) \\\end{align} \\\end{matrix} \right.$ (5)
其中,ta为各时间区间T内第a个时间区间ΔT的末端,且ta=aΔT,1≦a≦n。
当将方程(5)变换为状态方程形式,并运用精细积分法[26,27,28]对其进行计算时,在时间区间T内,精细积分法计算方程(5)的方程形式为$$
$\begin{align} {{\mathbf{y}}_{a}}=\exp \left( \mathbf{A}t \right){{\mathbf{y}}_{a-1}}+ \underset{{{t}_{a-1}}}{\overset{{{t}_{a}}}{\mathop \int }}\,\exp \left[ \mathbf{A}\left( {{t}_{a}}-s \right) \right]\mathbf{B}{{\mathbf{y}}_{a-1}}\left( s-\tau \right)\text{d}s +\underset{{{t}_{a-1}}}{\overset{{{t}_{a}}}{\mathop \int }}\,\exp \left[ \mathbf{A}\left( {{t}_{a}}-s \right) \right]f\left( s \right)\text{d}s \\ \end{align}$ (6)
方程(6)中, ya、A、B 与ya-1(s-τ)分别为
${{\mathbf{y}}_{a}}={{\left[ \begin{matrix} {{{\dot{x}}}_{1}}({{t}_{a}}) & {{{\dot{x}}}_{2}}({{t}_{a}}) & {{x}_{1}}({{t}_{a}}) & {{x}_{2}}({{t}_{a}}) \\ \end{matrix} \right]}^{\text{T}}}$ (7a)
${{\mathbf{y}}_{a-1}}(s-\tau )={{\left[ \begin{matrix} 0 & 0 & g{{x}_{1}}(s-\tau ) & 0 \\ \end{matrix} \right]}^{\text{T}}}$ (7b)
$\mathbf{A}=\left[ \begin{matrix}-\frac{{{c}_{1}}}{{{m}_{1}}} & \frac{{{c}_{1}}}{{{m}_{1}}} & -\frac{{{k}_{1}}}{{{m}_{1}}} & \frac{{{k}_{1}}}{{{m}_{1}}} \\\frac{{{c}_{2}}}{{{m}_{2}}} & \frac{-2{{c}_{1}}}{{{m}_{2}}} & \frac{{{k}_{2}}}{{{m}_{2}}} & \frac{2{{k}_{2}}}{{{m}_{2}}} \\ 1 & 0 & 0 & 0 \\ \text{0} & \text{1} & 0 & 0 \\\end{matrix} \right]$ (7c)
$\mathbf{B}=\left[ \begin{matrix} 0 & 0 & \frac{-1}{{{m}_{1}}} & 0 \\ 0 & 0 & \frac{1}{{{m}_{2}}} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{matrix} \right]$ (7d)
当a=1时,ta-1=t0=0,ya-1=y0。其中, ${{\mathbf{y}}_{0}}={{\left[ \begin{matrix} {{{\dot{x}}}_{1}}({{t}_{0}}) & {{{\dot{x}}}_{2}}({{t}_{0}}) & {{x}_{1}}({{t}_{0}}) & {{x}_{2}}({{t}_{0}}) \\ \end{matrix} \right]}^{\text{T}}}$,为方程(6)当前计算时间区间T的初始条件。
在方程(6)中,时滞增益函数g(ta)的Taylor级数展开形式变为
$g\left( {{t}_{a}} \right)={{g}_{0}}+\left( {{g}_{a}}-{{g}_{0}} \right)a$ (8)
其中,g0、ga分别为Taylor级数展开式中t0与ta处的时滞增益项。当a由1变换到n时,g(ta)即为时间区间T内时间点ta处的时滞增益。因 a=1时方程(8)中g0项会消失,方程的形式发生改变,因此判定a=1处的优化结果无效,令该时间点处的优化结果等于与之相邻的a=2处的优化结果。同时,令t=0处的时滞增益系数与时滞反馈量等于a=100处的优化结果。
在时间区间T内的时间点ta处对系统动力学方程组进行拉普拉斯变换得该时间点处的系统特征方程为
$\left[ \begin{matrix} {{A}_{11}} & {{A}_{12}} \\ {{A}_{21}} & {{A}_{22}} \\ \end{matrix} \right]\left[ \begin{matrix} {{X}_{1}}\left( s \right) \\ {{X}_{2}}\left( s \right) \\ \end{matrix} \right]=\left[ \begin{matrix} 0 \\ F\left( s \right) \\ \end{matrix} \right]$ (9)
其中,s=ωi
$\begin{align} \begin{array}{*{35}{l}} {{A}_{11}}={{m}_{\text{1}}}{{s}^{\text{2}}}+{{c}_{1}}s+{{k}_{1}}+\left[ {{g}_{0}}+\left( {{g}_{a}}-{{g}_{0}} \right)a \right]{{e}^{-\tau s}} \\ {{A}_{12}}=-{{c}_{1}}s-{{k}_{1}} \\ {{A}_{21}}=-{{c}_{\text{1}}}s-{{k}_{\text{1}}}-\left[ {{g}_{0}}+\left( {{g}_{a}}-{{g}_{0}} \right)a \right]{{e}^{-\tau s}} \\ {{A}_{22}}={{m}_{2}}{{s}^{\text{2}}}+\left( {{c}_{1}}+{{c}_{2}} \right)s+\left( {{k}_{1}}+{{k}_{2}} \right)~~~ \\ \end{array} \\ \end{align}$ (10)
由方程(10)可得
$\frac{{{X}_{1}}}{F(s)}=\frac{{{A}_{1\text{2}}}}{{{A}_{11}}{{A}_{22}}-{{A}_{12}}{{A}_{21}}}$ (11)
$\frac{{{X}_{\text{2}}}}{F(s)}=\frac{{{A}_{1\text{1}}}}{{{A}_{11}}{{A}_{22}}-{{A}_{12}}{{A}_{21}}}$ (12)
由方程(11)可得主系统振动位移、振动速度、振动加速度的频域响应函数分别为
${{\left| {{H}_{1}}(\omega ) \right|}_{{{X}_{2}}}}=\left| \frac{{{X}_{2}}}{F(s)} \right|=\left| \frac{{{A}_{11}}}{{{A}_{11}}{{A}_{22}}-{{A}_{12}}{{A}_{21}}} \right|$ (13)
${{\left| {{H}_{2}}(\omega ) \right|}_{\overset{.}{\mathop{{{X}_{2}}}}\,}}=\left| \frac{\overset{.}{\mathop{{{X}_{2}}}}\,}{F(s)} \right|=~\left| \frac{s{{A}_{12}}}{{{A}_{11}}{{A}_{22}}-{{A}_{12}}{{A}_{21}}} \right|$ (14)
${{\left| {{H}_{3}}(\omega ) \right|}_{\overset{..}{\mathop{{{X}_{2}}}}\,}}=\left| \frac{\overset{..}{\mathop{{{X}_{2}}}}\,}{F(s)} \right|=~\left| \frac{{{s}^{2}}{{A}_{12}}}{{{A}_{11}}{{A}_{22}}-{{A}_{12}}{{A}_{21}}} \right|$ (15)
取上述主系统振动频域响应函数之和作为优化目标函数J
$\begin{align} & J=~{{\left| {{H}_{1}}(\omega ) \right|}_{{{X}_{2}}}}+{{\left| {{H}_{2}}(\omega ) \right|}_{\overset{.}{\mathop{{{X}_{2}}}}\,}}+{{\left| {{H}_{3}}(\omega ) \right|}_{\overset{..}{\mathop{{{X}_{2}}}}\,}} \\ & Subject\begin{matrix} {} & to & 0 \\ \end{matrix}<\tau \le 20 \\ \end{align}$ (16)
当对目标函数(16)进行优化计算时,随着a由1到n的变化,可得到每个时间区间T内各个时间点ta处时滞τ与时滞增益系数g的优化结果。在实际运算过程中发现若n的值过大,优化计算过程中会出现明显的累积误差。因此,经反复计算试验,本文选取n=100。在系统特征方程根s=ωi中,特征方程根虚部ω与激励频率相等,即s=9.9i。为了在仿真计算过程中使精细积分法的计算时间步长ΔT与时滞优化结果τ的精度相对应,本文选取ΔT=0.0001s,时滞增益函数的Taylor级数展开时间区间为T=nΔT =0.01s。设置优化目标函数(16)中g0、ga、τ优化初始点均为0.1,计算步长为0.02,精度为0.0001。经优化计算得时间区间T内时变时滞参数的优化结果如图2、图3所示。
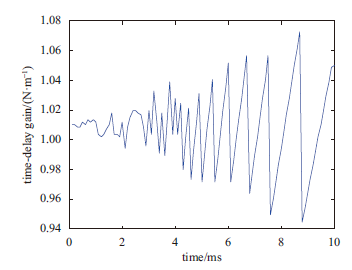
显示原图|下载原图ZIP|生成PPT图2时滞增益优化结果
-->Fig.2The optimization results of Time-delay gain
-->
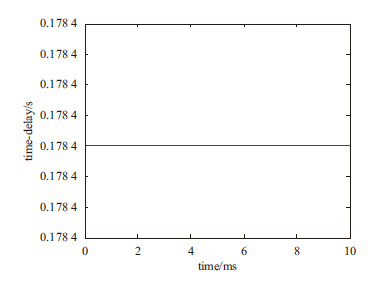
显示原图|下载原图ZIP|生成PPT图3时滞值优化结果
-->Fig.3The optimization results of time-delay
-->
由图2、图3可看出,因时滞增益在优化目标函数(16)中为时间函数形式,所以其优化结果在时域上为一条随时间的变化而起伏的曲线。相比之下,时滞在优化目标函数(16)中为定值形式,因此其优化结果为定值。
将目标函数(16)中的时滞增益由时间函数形式g(ta)变为定值形式g,运用同样的方法进行优化计算可得定值时滞参数的优化结果为
$g=1.0408\text{N}/\text{m},\tau =0.1576\text{s}$ (17)
2 系统稳定性分析
为了确保整个系统的稳定,需要对系统进行稳定性分析,以确保优化所得时滞参数符合系统稳定条件。由系统的动力学方程,可以列出系统的特征方程多项式为
$G(s)=A(s)+g{{e}^{-\tau s}}P(s)=0$ (18)
其中$A(s)=({{m}_{1}}{{s}^{2}}+{{c}_{1}}s+{{k}_{1}})P(s)+{{m}_{1}}{{s}^{2}}({{c}_{1}}s+{{k}_{1}})$ $P\left( s \right)={{m}_{2}}{{s}_{2}}+{{c}_{2}}s+{{k}_{2}}$ (19)
在系统特征方程(18)中,时滞增益与时滞的关系为
$\left| g \right|=(\left| A \right|/\left| P \right|){{e}^{\tau b}}$ (20)
其中b为特征方程根s的实部
$b=\Re (s)$ (21)
且有
$\angle P-\angle A=(2k+1) \pi +\tau \omega g>0$ (22a)
$\angle P-\angle A=2k \pi +\tau \omega \begin{matrix} {} & {} \\ \end{matrix}g<0$ (22b)
其中,k=0,±1, ±2, ±3…
当特征方程根s为纯虚根s=ωi时,方程(20)变为
${{\left| g \right|}_{s={{\omega }_{\text{c}}}i}}=\left| A \right|/\left| P \right|$ (23)
本文通过寻找特征方程根实部与时滞增益g 的导数关系探究了时滞增益g对复平面上系统特征方程根轨迹的影响。经计算,当时滞τ与穿越频率ωc均为正数时,有
$\Re {{(\text{d}s/\text{d}g)}_{s={{\omega }_{\text{c}}}\text{i}}}>0\begin{matrix} , & g>0 \\ \end{matrix}$ (24a)
$\Re {{(\text{d}s/\text{d}g)}_{s={{\omega }_{\text{c}}}\text{i}}}<0\begin{matrix} , & g<0 \\
\end{matrix}$ (24b)
根据系统稳定性理论,若系统稳定,则系统特征方程根在复平面上位于虚轴的左侧。由式(24)可知,在时滞确定的情况下,当时滞增益大于零时,时滞增益的增大会使得系统特征方程根在复平面上向右移动,若时滞增益不断增大,系统特征方程根最终会自左向右穿过虚轴进入不稳定区域;而当时滞增益小于零时,时滞增益的减小会使得系统特征方程根在复平面上向右移动,若时滞增益不断减小,系统特征方程根最终会自左向右穿过虚轴进入不稳定区域。在式(24)中,ωc为系统特征根轨迹在复平面上穿越虚轴时的虚坐标,称为穿越频率。
对于确定的时滞τ与穿越频率ωc,由式(23)可计算得出其对应的使系统特征方程根位于虚轴,即系统处于临界稳定状态时的临界时滞增增益gc(τ(ωc))。因此,对于确定的时滞τ与穿越频率ωc,若要使得系统稳定,时滞增益所必须满足的条件为
$g<{{g}_{\text{c}}}(\tau ({{\omega }_{\text{c}}}))\begin{matrix} , & g>0 \\ \end{matrix}$ (25a)
$g>{{g}_{\text{c}}}(\tau ({{\omega }_{\text{c}}}))\begin{matrix} , & g<0 \\ \end{matrix}$ (25b)
由方程 (22)可知,对于确定的时滞τ,当k取不同的值时,其对应的穿越频率也不相同,这也就意味着时滞τ对应有多个临界时滞增益。为了保证系统稳定,应确保在时滞确定的情况下,时滞增益不会使系统的特征方程根进入不稳定区域。因此,时滞系统的稳定条件为：在时滞确定的情况下,若时滞增益大于零,则时滞增益应小于时滞所对应的所有系统临界时滞增益中的最小值gcmin(τ(ωc));若时滞增益小于零,则时滞增益应大于时滞所对应的所有系统临界时滞增益中的最大值gcmax(τ(ωc))。由式(24)、(25)可得出时滞振动系统的稳定条件为
$g<{{g}_{\text{c}\min }}(\tau ({{\omega }_{\text{c}}}))\begin{matrix} , & g>0 \\ \end{matrix}$ (26a)
$g>{{g}_{\text{c}\max }}(\tau ({{\omega }_{\text{c}}}))\begin{matrix} , & g<0 \\ \end{matrix}$ (26b)
利用上述系统稳定性分析方法进行计算可得时变时滞参数所对应的系统稳定条件为
$g<2.3419\text{N}/\text{m}\begin{matrix} , & g>0 \\ \end{matrix}$ (27a)
$g>-0.2384\text{N}/\text{m}\begin{matrix} , & g<0 \\ \end{matrix}$ (27b)
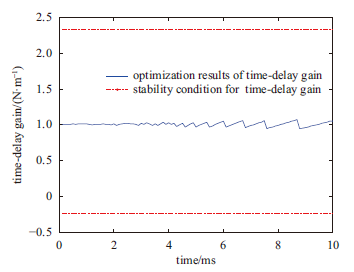
通过系统稳定条件(27)与图2中时滞增益优化结果得时变时滞参数的系统稳定性分析结果如图4所示
显示原图|下载原图ZIP|生成PPT图4系统稳定性分析结果
-->Fig.4System stability analysis results
-->
由图4可知,图2中的时滞增益优化结果均符合系统稳定条件(27),由此可以判定,时变时滞参数符合系统稳定条件。
对式(17)中的定值时滞参数优化结果运用同样的稳定性分析方法进行计算分析可得定值时滞参数所对应的系统稳定条件为
$g<1.1512\text{N}/\text{m}\begin{matrix} , & g>0 \\ \end{matrix}$ (28a)
$g>-0.2400\text{N}/\text{m}\begin{matrix} , & g<0 \\ \end{matrix}$ (28b)
通过对比系统稳定条件(27)、(28)可以看出时变时滞参数所对应的时滞增益稳定区间大于定值时滞参数对应的时滞增益稳定区间。说明相比于定值参数时滞动力吸振器,时变参数时滞动力吸振器的时滞增益稳定调节区间更大,控制的鲁棒性也更好。
3 仿真分析与验证
3.1 谐波激励下的仿真分析
将时变时滞参数代入方程(6)中,以ΔT为计算时间步长,时滞增益函数g(t)的Taylor级数展开时间区间T为时变时滞参数的循环作用周期,对谐波激励f(t)=sin(ωt)作用下主系统振动响应进行仿真运算,可得在时变参数时滞动力吸振器控制下主系统振动的时域仿真结果。同时将g=0N/m与定值时滞参数(17)代入系统动力学方程(1)中进行运算,可分别得到在被动吸振器和定值参数时滞动力吸振器控制下主系统振动的时域仿真结果。方程(1)的计算初始条件与方程(6)在第一个时间区间T的计算初始条件均为${{\mathbf{y}}_{0}}={{\left[ \begin{matrix} \text{0} & \text{0} & \text{0} & \text{0} \\ \end{matrix} \right]}^{\text{T}}}$ (29)
经仿真运算得主系统振动的时域仿真结果为
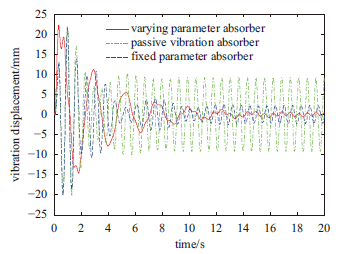显示原图|下载原图ZIP|生成PPT图5系主系统振动位移
-->Fig.5Vibration displacement of primary system
-->
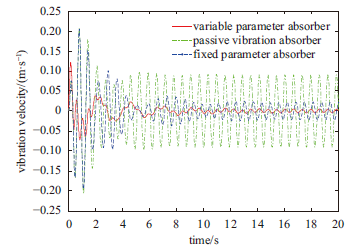显示原图|下载原图ZIP|生成PPT图6主系统振动速度
-->Fig.6Vibration velocity of primary system
-->
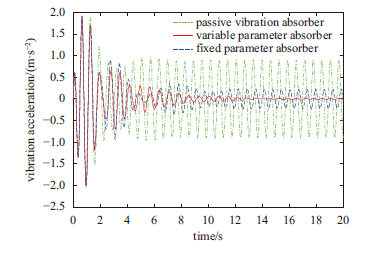显示原图|下载原图ZIP|生成PPT图7主系统振动加速度
-->Fig.7Vibration acceleration of primary system
-->
由主系统振动的时域仿真结果可知,对于谐波激励,定值参数时滞动力吸振器取得了比于被动吸振器更好的减振控制效果,而时变参数时滞动力吸振器取得了比定值参数时滞动力吸振器更加显著的减振控制效果。在时变参数时滞动力吸振器控制下,主系统的振动趋于稳定后,其振动位移、振动速度与振动加速度均出现了大幅下降。由仿真计算结果可得,相比于被动吸振器,在定值参数时滞动力吸振器的控制下,主系统的振动趋于稳定后,其振动位移、振动速度与振动加速度的均方根值分别减少了72.9%、73.4%、73.8%;在时变参数时滞动力吸振器的控制下,主系统的振动趋于稳定后,其振动位移、振动速度与振动加速度的均方根值分别减少了92.59%、92.14%、95.15%。由以上分析数据可知,对于谐波激励,时变参数时滞动力吸振器可以取得比被动吸振器与定值参数时滞动力吸振器更好的减振控制效果。
3.2 随机激励下的优化仿真分析
由图5、图6、图7的分析结果可知,对于谐波激励,时变参数时滞动力吸振器取得了比定值参数时滞动力吸振器更好的减振控制效果。为了进一步探究时变参数时滞动力吸振器的减振性能,本文将系统方程(3)中的外界激励由谐波激励f(t)=sin(ωt)变为随机激励,以此来探究时变参数时滞动力吸振器对随机激励的减振控制效果。本文选取功率为10dBM的高斯白噪声作为随机激励的激励形式,以主系统的振动位移、振动速度与振动加速度为控制对象,对随机激励下时变参数时滞动力吸振器的减振性能进行了探究。因高斯白噪声为宽频激励,所以本文选取主系统振动位移、振动速度与振动加速度频域响应函数的平方和在无限宽频域上的积分作为优化目标函数J
$\begin{align}& J=~\int\limits_{0}^{\infty }{{{\left| {{H}_{1}}(f) \right|}^{\text{2}}}_{{{X}_{2}}}+{{\left| {{H}_{2}}(f) \right|}^{\text{2}}}_{\overset{.}{\mathop{{{X}_{2}}}}\,}+{{\left| {{H}_{3}}(f) \right|}^{\text{2}}}_{\overset{..}{\mathop{{{X}_{2}}}}\,}}\text{d}f \\& Subject\begin{matrix}{} & to & 0 \\\end{matrix}<\tau \le 20 \\\end{align}$ (30)
当时滞增益为时间函数形式时,运用前文中优化计算目标函数(16)的方法对目标函数(30)进行优化计算可得随机激励下时变时滞参数的优化结果如图8、图9所示
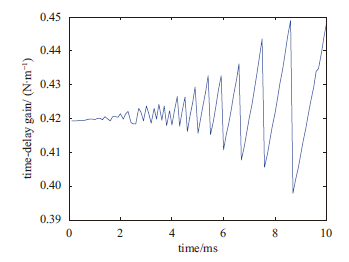显示原图|下载原图ZIP|生成PPT图8时滞增益优化结果
-->Fig.8The optimization results of Time-delay gain
-->
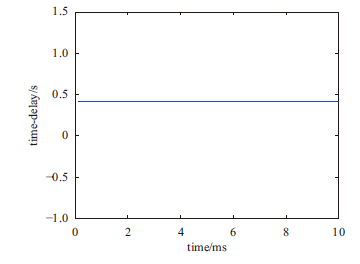
显示原图|下载原图ZIP|生成PPT图9时滞优化结果
-->Fig.9The optimization results of Time-delay
-->
将目标函数(30)中的时滞增益由函数形式变为定值形式,可得随机激励下定值时滞参数的优化结果为
x$g=1.3616\text{N}/\text{m}\tau =0.2488\text{s}$ (31)
由图8、图9可知,随机激励下时变时滞参数优化结果中的时滞增益优化结果随时间变化的趋势与谐波激励下时滞增益优化结果相似,且时滞增益优化结果在时域上同样为一条随时间变化而波动的曲线,时滞优化结果同样为一定值τ=0.4136s。由前文中的系统稳定性分析方法计算可得随机激励下时变时滞参数所对应的系统稳定条件为
$g<7.1429\text{N}/\text{m}\begin{matrix} , & g>0 \\ \end{matrix}$ (32a)
$g>-3.8216\text{N}/\text{m}\begin{matrix} , & g<0 \\ \end{matrix}$ (32b)
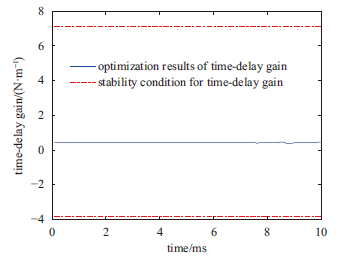
由此可得时变时滞参数的系统稳定性分析结果如图10所示
显示原图|下载原图ZIP|生成PPT图10系统稳定性分析结果
-->Fig.10System stability analysis results
-->
由图10可知,在随机激励下优化所得的时滞增益均符合系统稳定条件(32),由此可以判定在随机激励下所得的时变时滞参数符合系统稳定条件。
对式(31)中的时滞参数优化结果运用同样的方法进行计算分析可得随机激励下定值时滞参数所对应的系统稳定条件为
$g<2.4196\text{N}/\text{m}\begin{matrix} , & g>0 \\\end{matrix}$ (33a)
$g>-3.3672\text{N}/\text{m}\begin{matrix} , & g<0 \\\end{matrix}$ (33b)
通过对比系统稳定条件(32)与(33)可以看出在随机激励下,时变时滞参数所对应的时滞增益稳定区间同样大于定值时滞参数对应的时滞增益稳定区间。说明在随机激励下,时变参数时滞动力吸振器的时滞增益稳定调节区间同样更大,控制鲁棒性也更好。
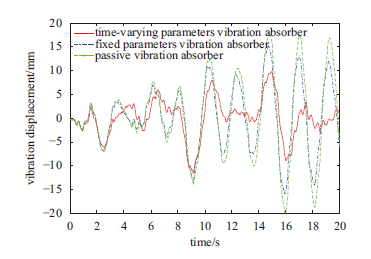
将时变时滞参数、定值时滞参数与g=0N/m代入方程(6)中进行运算可分别得到在变参数时滞动力吸振器、定参数时滞动力吸振器与被动吸振器控制下主系统振动的时域仿真结果。仿真计算的初始条件与谐波激励下仿真计算的初始条件相同。经计算得主系统振动的时域仿真结果如图11、图12、图13所示
显示原图|下载原图ZIP|生成PPT图11主系统振动位移
-->Fig.11Vibration displacement of primary system
-->
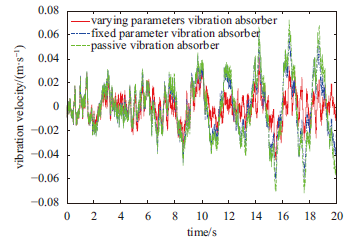
显示原图|下载原图ZIP|生成PPT图12主系统振动速度
-->Fig.12Vibration velocity of primary system
-->
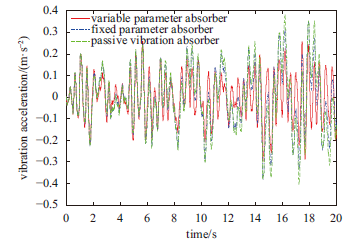
显示原图|下载原图ZIP|生成PPT图13主系统振动加速度
-->Fig.13Vibration acceleration of primary system
-->
由图11、图12和图13可以看出,对于随机激励,时变参数时滞动力吸振器同样取得了比定值参数时滞动力吸振器和被动吸振器更好的减振控制效果。经分析得,相比于被动吸振器,在定值参数时滞动力吸振器的控制下,主系统振动的最大瞬态位移降低了6.5%,振动位移的均方根值减少了20.8%,最大瞬时速率降低了1%,振动速度的均方根值减少了24.6%,最大瞬时加速度降低了33.1%,振动加速度的均方根值减少了36.1%;在时变参数时滞动力吸振器的控制下,主系统振动的最大瞬态位移降低了32.8%,振动位移的均方根值减少了31%,最大瞬时速率降低了26.8%,振动速度的均方根值减少了26.1%,最大瞬时加速度降低了46.7%,振动加速度的均方根值减少了48.3%。由以上分析数据可知,对于随机激励,时变参数时滞动力吸振器同样取得了比定值参数时滞动力吸振器更好的减振控制效果,这一点在对主系统的最大瞬态振动位移与最大瞬态振动速率的控制上表现得尤为明显。
由仿真分析结果可知,无论作用于主系统上的激励是谐波激励还是随机激励,时变参数时滞动力吸振器均取得了比定值参数时滞动力吸振器更好的减振控制效果。在时变参数时滞动力吸振器的控制下,主系统的振动位移、速度和加速度均比在定值参数时滞动力吸振器控制下时有明显的减少。说明多组时滞控制参数以一定周期循环作用于振动控制过程的方法能够进一步改善时滞动力吸振器的减振性能,时变参数时滞减振控制方法取得了显著的效果,这与本文的目标一致。
4 结论
本文主要研究了利用时变时滞参数提高时滞动力吸振器对随机激励的减振控制效果,以此改善时滞动力吸振器的减振性能的问题。文章提出了一种新的时变参数时滞减振控制方法,通过使时变优化所得的多组时滞控制参数以一定时间周期循环作用于振动控制过程的方法有效地控制了主系统的振动响应,并得到以下结论：1)时变参数时滞动力吸振器无论对谐波激励还是对随机激励,均能取得比定值参数时滞动力吸振器更好的减振控制效果。2）相比于定值参数时滞动力吸振器,时变参数时滞动力吸振器的时滞增益稳定调节区间更大,控制的鲁棒性也更好;3) 通过使时变优化所得的时变时滞参数以一定时间周期循环作用于振动控制过程的方法可以有效地改善时滞动力吸振器的减振性能。后续将致力于其他时滞反馈形式的时变参数时滞减振控制研究,如速度反馈,加速度反馈等。The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . . |
| [3] | . |
| [4] | . |
| [5] | |
| [6] | [J]. |
| [7] | . |
| [8] | ( |
| [9] | . . |
| [10] | [J]. [J]. |
| [11] | [J]. [J]. |
| [12] | [J]. [J]. |
| [13] | [J]. . |
| [14] | . . |
| [15] | [J]. |
| [16] | . |
| [17] | [J]. |
| [18] | [J]. |
| [19] | [ [C]. |
| [20] | [J]. [J]. |
| [21] | [J]. [J]. |
| [22] | [J]. [J]. |
| [23] | . . |
| [24] | [J]. [J]. |
| [25] | [J]. [J]. |
| [26] | [J]. [J]. |
| [27] | [J]. [J]. |
| [28] | [J]. [J]. |
