叶子飘
1 , 于冯
2 , 3 , 安婷
1 , 王复标
1 , 康华靖
, 2 , 3 , 4 , * 1 井冈山大学数理学院, 江西吉安 343009 2 温州市农业科学研究院, 浙江温州 325006 3 温州市农林渔生态系统增汇减排重点实验室, 浙江温州 325006 4 浙江省浙南作物育种重点实验室, 浙江温州 325006 Investigation on CO2 -response model of stomatal conductance for plants Zi-Piao YE
1 , Feng YU
2 , 3 , Ting AN
1 , Fu-Biao WANG
1 , Hua-Jing KANG
, 2 , 3 , 4 , * 1 College of Math and Physics, Jinggangshan University, Ji’an, Jiangxi 343009, China 2 Wenzhou Academy of Agricultural Sciences, Wenzhou, Zhejiang 325006, China 3 Wenzhou Key Laboratory of Adding Carbon Sinks and Reducing Carbon Emissions of Agriculture, Forestry and Fishery Ecosystem, Wenzhou, Zhejiang 325006, China 4 Southern Zhejiang Key Laboratory of Crop Breeding of Zhejiang Provence, Wenzhou, Zhejiang 325006, China 通讯作者: *
kanghuajing@126.com 编委: 于强
责任编辑: 李敏
收稿日期: 2020-10-9
接受日期: 2021-01-16
网络出版日期: 2021-04-20
基金资助: 国家自然科学基金 (31960054 )国家自然科学基金 (31560069 )
Corresponding authors: *
kanghuajing@126.com Received: 2020-10-9
Accepted: 2021-01-16
Online: 2021-04-20
Fund supported: National Natural Science Foundation of China (31960054 )National Natural Science Foundation of China (31560069 )
摘要 构建一个普适性的植物叶片气孔导度(
g s )对CO
2 浓度响应(
g s -
C a )的模型, 对定量研究植物叶片
g s 对CO
2 浓度的响应变化尤为必要。该研究运用便携式光合仪(LI-6400)测量了大豆(
Glycine max )和小麦(
Triticum aestivum )光合作用对CO
2 的响应曲线(
A n -
C a ), 在比较传统的Michaelis-Menten模型(M-M模型)和叶子飘构建的CO
2 响应模型拟合大豆和小麦
A n -
C a 效果的基础上, 构建了
g s -
C a 响应新模型。然后用新构建的模型拟合大豆和小麦的
g s -
C a 曲线, 并将拟合结果与传统模型的拟合结果, 以及与其对应的观测数据进行比较, 以判断所构建模型是否合理。结果显示: 叶子飘构建的
A n -
C a 模型可较好地拟合大豆和小麦的
A n -
C a 曲线, 确定系数(
R 2 )均高达0.999。M-M模型拟合大豆和小麦的
A n -
C a 曲线时的
R 2 虽然也较高, 但在较高CO
2 浓度时的拟合曲线偏离观测曲线。因此, 基于叶子飘的
A n -
C a 模型构建
g s -
C a 模型更为可行。新构建的
g s -
C a 模型可较好地拟合大豆和小麦的
g s -
C a 曲线,
R 2 分别为0.995和0.994, 而且还可以直接给出最大气孔导度(
g s-max )、最小气孔导度(
g s-min ), 以及与
g s-min 相对应的CO
2 浓度值(
C s-min )。拟合得到大豆和小麦的
g s-max 分别为0.686和0.481 mol·m
-2 ·s
-1 , 与其对应的观测值(分别为0.666和0.471 mol·m
-2 ·s
-1 )之间均不存在显著差异; 同样, 拟合得到的大豆和小麦的
g s-min 分别为0.271和0.297 mol·m
-2 ·s
-1 , 与其对应的观测值(分别为0.279和0.293 mol·m
-2 ·s
-1 )之间也均不存在显著差异; 此外, 新构建的
g s -
C a 模型给出大豆和小麦的
C s-min 值分别为741.45和1 112.43 μmol·mol
-1 , 与其对应的观测值(732.78和1 200.34 μmol·mol
-1 )也不存在显著差异。由此可见, 该研究新构建的
g s -
C a 模型可作为定量研究植物叶片气孔导度对CO
2 浓度变化的有效数学工具。
关键词: 气孔导度 ;
CO2 响应模型 ;
CO2 浓度 ;
光合作用 Abstract Aims To quantify the responses of stomatal conductance (
g s ) to CO
2 concentration (
g s -
C a ) under current and future climate conditions, it is necessary to build a generally applicable model suitable for simulating this process at plant leaf levels.
Methods The response curves (
A n -
C a ) of photosynthesis of soybean (
Glycine max ) and wheat (
Triticum aestivum ) to CO
2 were fitted using data collected from a portable photosynthetic apparatus (LI-6400). Based on the comparison between the traditional Michaelis-Menten model (M-M model) and the CO
2 response model developed by Ye, a new
g s -
C a response model was proposed. Then, the measured
g s -
C a curves of soybean and wheat were fitted with the new model. The model results were compared with those of the traditional model and the corresponding observation data to judge the rationality of the model.
Important findings The
A n -
C a model developed by Ye could fit well the
A n -
C a curve of soybean and wheat, and the coefficient of determination (
R 2 ) is as high as 0.999. Although the
R 2 values of M-M model fitting the
A n -
C a curves of soybean and wheat were also high, the fitting curves deviated from the observation at higher CO
2 concentrations. Meanwhile, M-M model greatly overestimated the maximum photosynthetic rate and could not estimate the saturation CO
2 concentrations. Therefore, it was more feasible to develop
g s -
C a model based on the
A n -
C a model of Ye. The new model of
g s -
C a could fit well the
g s -
C a curves of soybean and wheat, and the
R 2 were 0.995 and 0.994, respectively. Moreover, the maximum stomatal conductance (
g s-max ), the minimum stomatal conductance (
g s-min ) and the CO
2 concentration corresponding to
g s-min (
C s-min ) could also be generated directly.
g s-max of soybean and wheat fitted by the
g s -
C a model was 0.686 and 0.481 mol·m
-2 ·s
-1 , respectively, and there was no significant difference between the fitted values and corresponding observation values (0.666 and 0.471 mol·m
-2 ·s
-1 , respectively). The new model of
g s -
C a could also obtain the minimum
g s (
g s-min ) of soybean and wheat (0.271 and 0.297 mol·m
-2 ·s
-1 , respectively), and there was also no significant difference between the fitted values and corresponding observation values (0.279 and 0.293 mol·m
-2 ·s
-1 , respectively). In addition, the new model of
g s -
C a generated the
C s-min values of 741.45 and 1 112.43 μmol·mol
-1 for soybean and wheat, respectively, and also showed no significant difference from the observed value (732.78 and 1 200.34 μmol·mol
-1 , respectively). Consequently, the
g s -
C a model developed in this paper can be used as an effective mathematical tool to quantitatively study the effect of stomatal conductance on CO
2 concentration.
Keywords: stomatal conductance ;
CO2 response model ;
CO2 concentration ;
photosynthesis PDF (444KB) 元数据 多维度评价 相关文章 导出 EndNote |
Ris |
Bibtex 收藏本文 引用本文 叶子飘, 于冯, 安婷, 王复标, 康华靖. 植物气孔导度对CO
2 响应模型的构建. 植物生态学报, 2021, 45(4): 420-428. DOI:
10.17521/cjpe.2020.0326 YE Zi-Piao, YU Feng, AN Ting, WANG Fu-Biao, KANG Hua-Jing.
Investigation on CO2 -response model of stomatal conductance for plants .
Chinese Journal of Plant Ecology , 2021, 45(4): 420-428. DOI:
10.17521/cjpe.2020.0326 未来大气CO
2 浓度上升、温度升高与水资源短缺将威胁着人类的生存环境并极大地影响着全球的粮食安全(
Drakea et al ., 2017 ;
刘英等, 2018 )。提高作物的水分利用效率是减少单位水量的消耗以产生更多碳同化量的重要途径。气孔作为高等植物与外界环境进行水汽和CO
2 气体交换的主要通道(
王建林等, 2012 ), 它在调节植物的碳同化、蒸腾作用, 以及调控土壤、植物和大气连续体系统中水循环与碳循环等方面具有重要的作用, 直接决定生态系统的水热平衡过程(
Bonan, 2008 )。
多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究。目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 )。此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 )。
大气CO
2 浓度对植物的光合来说是极为重要的环境因子。已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 )。但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律。为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势。然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 )。
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异。由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道。这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利。而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 )。因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要。
本文的研究目的主要为: (1)基于
叶子飘(2010) 构建的光合作用对CO
2 响应模型构建
g s 对CO
2 的响应模型; (2)测量大豆(
Glycine max )和小麦(
Triticum aestivum )在光合有效辐射强度(
PAR )为2 000 μmol·m
-2 ·s
-1 时的气体交换数据, 即光合作用对CO
2 的响应曲线(
A n -
C a ), 然后用传统的Michaelis-Menten模型(M-M模型)(
Harley et al ., 1992 )和近年来
叶子飘(2010) 构建的CO
2 的响应模型(简称叶模型)拟合这些
A n -
C a 曲线, 比较两种模型的拟合效果; (3)用构建的
g s 对
C a 的响应模型拟合测量曲线, 并将拟合结果与
王建林(2009) 构建模型的拟合结果以及观测数据进行比较, 以判断所构建模型是否合理。
1 材料和方法 1.1 气孔导度对CO2 响应模型的构建 1.1.1 新模型的构建
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应曲线(
A n -
C )模型为:
(1) $A_{\mathrm{n}}=\alpha \frac{1-\beta C}{1+\gamma C} C-R_{\mathrm{p}}$ 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率。因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i )。并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数。该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 )。公式(1)称为叶子飘模型(叶模型)。
Farquhar等(1980) 根据Rubisco酶动力学反应和核酮糖-1,5-双磷酸(RuBP)再生反应化学计量学而提出的C
3 植物的光合生化模型认为, 光合作用的关键酶是核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco), 其活性受叶肉细胞
C i 和氧气浓度(
O i )决定, 而植物的光合作用又可改变叶肉细胞的CO
2 浓度并最终驱动气孔运动。由此分析并结合CO
2 浓度为0 μmol·mol
-1 时植物叶片
g s 为最大值的实验事实, 同时基于公式(1)可以较好地描述植物叶片
A n 对CO
2 的响应曲线, 我们推测植物叶片
g s 对CO
2 的响应模型的表达式可以表示为,
(2) $g_{\mathrm{s}}=g_{\mathrm{s}-\mathrm{max}}-\alpha_{\mathrm{i}} \frac{1-\beta_{\mathrm{i}} C}{1+\gamma_{\mathrm{i}} C}C $ 式中,
α i 为
g s 对CO
2 的响应(
g s -
C )曲线的初始斜率;
β i 和
γ i 为系数;
g s-max 为最大气孔导度。由公式(2)可知, 当CO
2 浓度等于0 μmol·mol
-1 时,
g s 就等于
g s-max 。同样, 公式(2)既可以描述植物叶片的
g s 对大气CO
2 浓度的响应曲线(
g s -
C a ), 也可以用于描述
g s 对胞间CO
2 浓度的响应曲线(
g s -
C i )。公式(2)简称为气孔导度对CO
2 响应新模型(新模型)。
由于公式(2)是一个有极点的函数, 因此, 可以由式(2)得到与最小
g s (
g s-min )相对应的CO
2 浓度(
C m ), 即
(3) $C_{\mathrm{m}}=\frac{\sqrt{\left(\beta_{\mathrm{i}}+\gamma_{\mathrm{i}}\right) / \beta_{\mathrm{i}}}-1}{\gamma_{\mathrm{i}}}$ 把公式(3)代入公式(2), 那么
g s-min 可以由下式得到, 即
(4) $g_{\mathrm{s}-\mathrm{mim}}=g_{\mathrm{s}-\max }-\alpha_{\mathrm{i}}\left(\frac{\sqrt{\beta_{1}+\gamma_{\mathrm{i}}}-\sqrt{\beta_{1}}}{\gamma_{\mathrm{i}}}\right)^{2}$ 1.1.2 现有模型介绍
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述Rubisco酶活性限制的子模型得到气孔导度与变量
C a 之间的关系为:
(5) $g_{\mathrm{s}}=\frac{g_{\mathrm{s}-\operatorname{nax}}}{1+C / C_{\mathrm{s} 0}}$ 式中,
g s-max 称为最大气孔导度;
C s0 为常数。同样地, 公式(5)既可以描述植物叶片的
g s 对大气CO
2 浓度的响应曲线(
g s -
C a ), 也可以用于研究
g s 对胞间CO
2 浓度的响应曲线(
g s -
C i )。此外, 从公式(5)可知,
g s 随CO
2 浓度的增加而非线性下降。公式(5)简称为气孔导度对CO
2 响应的经验模型(经验模型)。
1.2 材料培养及数据测量 以大豆和小麦为供试材料。小麦播种于2012年10月, 大豆种植于2013年6月17日, 大田常规管理。小麦和大豆的气体交换数据分别于2013年5月2-3日和2013年8月1-2日的晴天进行。小麦处于盛花期, 大豆处于旺盛营养生长期。随机选长势较为一致的健壮植株, 小麦以其旗叶作为测量对象, 大豆则以自上而下第4复叶的顶叶作为测量对象。此时所选叶片已完全展开, 叶色深绿, 叶形饱满。利用便携式光合仪(LI-6400-40, LI-COR, Lincoln, USA)于9:00- 11:30进行数据测量。数据测量前进行开机预热及各项检查。采用开放式气路, 流速为400 μmol·s
-1 。测量期间外界温度较为稳定, 小麦和大豆的叶室温度分别稳定在29.33和37.12 ℃左右。空气相对湿度控制在45%-70%, 光合有效辐射强度(
PAR )设置为2 000 μmol·m
-2 ·s
-1 , 应用CO
2 注入系统提供不同的外界CO
2 浓度: 1 600 (大豆测量未设置该梯度)、1 400、1 200、1 000、800、600、380、200、150、100、80、50和0 μmol·mol
-1 。应用自动测量程序(Flr
A n -
C a curve)进行数据测量。每次程序记录最小等待时间为2 min, 最大等待时间为3 min, 数据记录前仪器均自动进行参比室和样品室之间的匹配。
1.3 数据处理 CO
2 补偿点的观测值是用内插法得到。其他光合参数则是利用“光合模型拟合软件(PMSS)” (
http://photosynthetic.sinaapp.com/calc.html )中有关模型对
A n -
C a 和g
s -
C a 曲线进行拟合, 并获得相应的光合参数。数据分析均取5个重复(平均值±标准误,
n = 5), 用SPSS 18.5对拟合结果与观测值之间进行方差分析。用Origin 8.5作图, 最后用Adobe Illustrator CS 5进行图形处理。此外, 文中用确定系数(
R 2 = 1
- SSE/SST, 其中
SST 和
SSE 分别为平方总和与误差平方和)表示模型拟合与观测点的符合程度。
2 结果和分析 2.1 光合作用对CO2 的响应 图1 为大豆和小麦的
A n -
C a 曲线。由
图1 可知, 在低CO
2 浓度(≤400 μmol·mol
-1 )时, 大豆和小麦的
A n 随
C a 的增加而快速上升, 之后
A n 随
C a 的增加而缓慢递增直到饱和, 出现磷酸丙糖利用(
TPU )的限制阶段。由
图1 还可知, 叶模型可较好地拟合大豆和小麦的
A n -
C a 曲线,
R 2 分别高达0.999 8和0.999 9。此外, 从
图1 也可知, 虽然用M-M模型拟合大豆和小麦的
A n -
C a 曲线时的
R 2 也较高, 但在较高CO
2 浓度时的拟合曲线偏离观测曲线。
图1 新窗口打开 |
下载原图ZIP |
生成PPT 图1大豆(A)和小麦(B)光合作用对大气CO2 浓度的响应曲线(平均值±标准误,n = 5)。 Fig. 1CO2 -response curves of photosynthesis for air CO2 concentrations for soybean (A) and wheat (B)(mean ± SE, n = 5). A n , net photosynthetic rate; C a , air CO2 concentration. 表1 给出了用公式(1)和M-M模型分别拟合大豆和小麦的
A n -
C a 曲线得到的主要光合参数。由
表1 数据可知, 公式(1)可较好地拟合大豆和小麦的
A n -
C a 曲线, 确定系数分别为0.999 8和0.999 9。由公式(1)拟合大豆的
A n -
C a 曲线得到的各个光合参数与其对应的观测值之间均不存在显著差异(
p > 0.05)(
表1 )。而由M-M模型拟合大豆和小麦的
A n -
C a 曲线得到的
A nmax 和
R p 与其对应的观测值之间均存在显著差异(
p < 0.05)。由M-M模型拟合大豆和小麦得到的
A nmax 值甚至比其观测值分别高估了91.25%和86.75%。由此可知, 基于公式(1), 即由叶模型构建
g s 对
C a 的响应模型是可行的。
Table 1 表1 表1 用叶模型和M-M模型拟合大豆和小麦叶片的
A n -
C a 曲线得到光合参数及与其对应的观测数据(平均值±标准误,
n = 5)
Table 1
Observed data and results fitted by Ye model and M-M model for A n -C a curves of soybean and wheat (mean ± SE, n = 5) 参数 物种 Species 大豆 Soybean 小麦 Wheat 叶模型 M-M模型 观测值 叶模型 M-M模型 观测值 初始斜率 α 0.101 ± 0.019 b 0.128 ± 0.014 a - 0.101 ± 0.001 b 0.132 ± 0.001 a - 最大羧化速率A nmax (mol·m-2 ·s-1 ) 48.61 ± 5.52 b 93.71 ± 17.67 a 49.00 ± 4.33 b 68.13 ± 1.62 b 127.03 ± 4.42 a 68.02 ± 1.45 b 饱和CO2 浓度C i,TPU (μmol·mol-1 ) 1 328.28 ± 79.07 a - 1 332.72 ± 66.52 a 1 596.73 ± 31.88 a - 1 599.46 ± 0.25 a CO2 补偿点 Γ (μmol·mol-1 ) 66.32 ± 4.04 a 66.02 ± 4.48 a 70.32 ± 2.33 a 63.82 ± 1.59 b 64.91 ± 1.26 a 65.18 ± 1.13 ab 光下呼吸速率R p (μmol·m-2 ·s-1 ) 6.22 ± 0.62 b 7.58 ± 0.19 a 5.39 ± 0.32 b 6.29 ± 0.22 b 8.06 ± 0.15 a 6.22 ± 0.26 b 确定系数 R 2 0.999 8 0.996 3 - 0.999 9 0.995 3 -
数值右上角的不同小写字母表示每个作物两个模型估算值与观测值之间差异显著(p < 0.05)。 Values followed by the different lowercase letters are significantly different among fitted values by two model for P n -C a curves and observed values for each species at 0.05 level. α, initial slope; A nmax , the maximum rate of carboxylation; C i,TPU , saturation CO2 concentration; Γ, CO2 compensation point; R p , photorespiratory rate; R 2 , determination coefficient. 新窗口打开 |
下载CSV 2.2 气孔导度对大气CO2 浓度响应 用新模型和经验模型拟合大豆和小麦的
g s -
C a 曲线(
图2 ), 对于大豆的
g s -
C a 曲线(
图2 A)而言,
g s 先随CO
2 浓度升高而下降, 当CO
2 浓度为800 μmol·mol
-1 时
g s 最小, 之后
g s 随CO
2 浓度的升高而增加; 对于小麦的
g s -
C a 曲线(
图2 B)而言,
g s 随CO
2 浓度升高而下降, 当CO
2 浓度大于1 000 μmol·mol
-1 后
g s 基本保持稳定。由此可知, 新构建的
g s -
C a 模型,即新模型可以很好地拟合大豆和小麦的
g s -
C a 曲线,
R 2 分别为0.995 1和0.994 1。而经验模型只可较好地拟合小麦的
g s -
C a 曲线(
图2 B),
R 2 为0.984 2, 但拟合大豆的
g s -
C a 曲线的效果较差, 不能真实地反映大豆的
g s 对
C a 的变化趋势,
R 2 仅为0.727 3 (
图2 A)。
图2 新窗口打开 |
下载原图ZIP |
生成PPT 图2大豆(A)和小麦(B)叶片的气孔导度对大气CO2 浓度的响应曲线(平均值±标准误,n = 5)。 Fig. 2CO2 -response curves of stomatal conductance for air CO2 concentrations for soybean (A) and wheat (B)(mean ± SE, n = 5). C a , air CO2 concentration;g s , stomatal conductance. 表2 给出了用新模型和经验模型分别拟合大豆和小麦的
g s -
C a 曲线得到的主要参数。由
表2 可知, 由新模型和经验模型拟合大豆
g s -
C a 曲线得到的
g s-max 分别为0.686和0.615 mol·m
-2 ·s
-1 ; 拟合小麦
g s -
C a 曲线得到的
g s-max , 分别为0.481和0.438 mol·m
-2 ·s
-1 , 与其对应的观测值(大豆和小麦分别为0.666和0.471 mol·m
-2 ·s
-1 )之间均不存在显著差异(
p > 0.05)。
Table 2 表2 表2 由新模型和经验模型拟合大豆和小麦叶片的
g s -
C a 曲线得到参数及与它们对应的观测数据(平均值±标准误,
n = 5)
Table 2
Observed data and results fitted by new model and empirical model for g s -C a curves of soybean and wheat (mean ± SE, n = 5) 参数 物种 Species 大豆 Soybean 小麦 Wheat 新模型 经验模型 观测值 新模型 经验模型 观测值 初始斜率 α i (1.42 ± 0.68) × 10 -3 - - (7.22 ± 1.43) × 10 -4 - - 系数 β i (mol·mol-1 ) (6.14 ± 0.33) × 10 -4 - - (2.34 ± 0.73) × 10 -4 - - 系数 γ i (mol·mol-1 ) (7.02 ± 0.68) × 10 -4 - - (2.08 ± 0.35) × 10 -3 - - 最大气孔导度 g s-max (mol·m-2 ·s-1 ) 0.686 ± 0.154 a 0.615 ± 0.161 a 0.666 ± 0.151 a 0.481 ± 0.023 a 0.438 ± 0.013 a 0.471 ± 0.023 a 常数 C s0 (mol·mol-1 ) - 6 725.12 ± 3 765.30 - - 2 781.66 ± 792.63 - 最小气孔导度 g s-min (mol·m-2 ·s-1 ) 0.271 ± 0.062 a - 0.279 ± 0.066 a 0.297 ± 0.018 a - 0.293 ± 0.020 a CO2 浓度 C s-min (μmol·mol-1 ) 741.45 ± 143.22 a - 732.78 ± 133.14 a 1 112.43 ± 149.31 a - 1 200.34 ± 200.38 a 确定系数 R 2 0.995 1 0.727 3 - 0.994 1 0.984 2 -
数值右上角的不同小写字母表示每个作物两个模型估算值与观测值之间差异显著(p < 0.05)。 Values followed by the different lowercase letters are significantly different among fitted values by two model for g s -C a curves and observed values for each species at 0.05 level. α i , initial slope; β i , γ i , coefficient; g s - max , the maximum stomatal condunctance; C s0 , constant; g s-min , the minimum stomatal condunctance; C s-min , CO2 concentration corresponding to g s-min ; R 2 , determination coefficient. 新窗口打开 |
下载CSV 此外, 由新模型拟合大豆和小麦的
g s -
C a 曲线还可以得到它们的
g s-min (分别为0.271和0.297 mol·m
-2 ·s
-1 )以及其相对应的最低CO
2 浓度(
C s-min )(分别为741.45和1 112.43 μmol·mol
-1 ), 且
C s-min 与其对应的观测值之间同样也无显著差异(
p > 0.05)(
表2 )。而由经验模型拟合大豆和小麦的
g s -
C a 曲线得到的
C s0 分别为6 725.12和2 781.66 μmol·mol
-1 , 该值远超过所设置的CO
2 浓度, 目前尚不清楚该参数的生物学意义。
3 讨论和结论 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 )。当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 )。Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 )。BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 )。然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400。此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I )。要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型。
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近。
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果。
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 )。鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型。
大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 )。在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B )。而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%。同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应。但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势。同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚。因此, 该模型存在一定的局限性。其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论。
此外, 还有****发现, 植物叶片的气孔导度对
C a 的响应并非单纯的非线性下降, 还存在其他的变化趋势(
Yu et al ., 2004 ;
李菲等, 2018 ;
Batkeet al ., 2020 )。比如,
Batke等(2020) 研究了
Sambucus racemosa 、
Populus tremula 和
Populus tremuloides 3种植物气孔导度对CO
2 浓度的响应问题, 发现这些植物既存在气孔导度随CO
2 浓度的增加而下降的情况, 也存在气孔导度随CO
2 浓度的增加先下降后上升的情况。对于后者, 尚不能用经验模型描述其气孔对CO
2 浓度响应的变化趋势。与经验模型相比较, 新模型不仅可以很好地拟合大豆和小麦的气孔导度对CO
2 浓度的变化趋势, 而且还可以估算其最大气孔导度、最小气孔导度以及相对应的CO
2 浓度等参数。同时, 模型中各个参数具有明确的生物学意义。因此, 新模型可以真实地反应大豆和小麦的气孔导度对CO
2 的响应变化趋势。
总之, 新构建的气孔导度对CO
2 浓度响应的模型不仅可以很好地拟合大豆和小麦叶片的气孔导度对CO
2 浓度的响应曲线, 而且还可以直接准确地得到大豆和小麦的最大气孔导度、最小气孔导度以及与最小气孔导度相对应的CO
2 浓度, 且得到的这些参数与观测值非常接近。因此, 本研究新构建的
g s -
C a 模型可作为定量研究植物叶片气孔导度对CO
2 浓度变化的有效数学工具。
致谢 感谢温州市重点科技创新团队项目(C20150008)资助。
[1] Allen LH Kakani VG Vu JCV Boote KJ 2011 ). Elevated CO2 increases water use efficiency by sustaining photosynthesis of water-limited maize andSorghum. Journal of Plant Physiology, 168,1909 -1918 . [本文引用: 1] [2] Ball JT Woodrow IE Berry JA 1987 ). A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions //Biggens J. Progress in Photosynthesis Research Martinus Nijhoff Publishers,Dordrecht . 221 -224 . [本文引用: 5] [3] Batke SP Yiotis C Elliott-Kingston C Holohan A McElwain J 2020 ). Plant responses to decadal scale increments in atmospheric CO2 concentration: comparing two stomatal conductance sampling methodsPlanta, 251, 52 . DOI: https://www.plant-ecology.com/article/2021/1005-264X/10.1007/s00425-020-03343-z . URL [本文引用: 2] [4] Bonan GB 2008 ). Forests and climate change: forcings, feedbacks, and the climate benefits of forestsScience, 320, 1444 -1449 . DOI:
10.1126/science.1155121 URL [本文引用: 2] [5] Buckley TN Mott KA 2013 ). Modelling stomatal conductance in response to environmental factorsPlant, Cell & Environment, 36, 1691 -1699 . [本文引用: 1] [6] Cheng XF Zhang FY Chai SX 2010 ). Stomatal response of spring wheat and related affecting factors under different irrigation treatmentsChinese Journal of Applied Ecology, 21, 36 -40 . [本文引用: 1] [ 成雪峰 , 张凤云 , 柴守玺 ( 2010 ). 春小麦对不同灌水处理的气孔反应及其影响因子应用生态学报 , 21, 36 -40 .] [本文引用: 1] [7] Ding LK Kan F Li L Yue N Zhou LL Wei GX 2019 ). Response model of maize to light and CO2 concentration in semi-arid area of central Gansu Province Jiangsu Agricultural Sciences, 47, 86 -91 . [本文引用: 2] [ 丁林凯 , 阚飞 , 李玲 , 岳宁 , 周琳琳 , 魏国孝 ( 2019 ). 陇中半干旱区玉米对光和CO2 浓度的响应模型江苏农业科学 , 47, 86 -91 .] [本文引用: 2] [8] Drake JE Power SA Duursma RA Medlyn BE Aspinwall MJ Choat B Creek D Eamus D Maier C Pfautsch S Smith RA Tjoelker MG Tissue DT 2017 ). Stomatal and non-stomatal limitations of photosynthesis for four tree species under drought: a comparison of model formulationsAgricultural and Forest Meteorology, 247, 454 -466 . DOI:
10.1016/j.agrformet.2017.08.026 URL [本文引用: 2] [9] Farquhar GD Caemmerer S Berry JA 1980 ). A biochemical model of photosynthetic CO2 assimilation in leaves of C3 speciesPlanta, 149, 78 -90 . DOI:
10.1007/BF00386231 PMID:
24306196 [本文引用: 6] Various aspects of the biochemistry of photosynthetic carbon assimilation in C3 plants are integrated into a form compatible with studies of gas exchange in leaves. These aspects include the kinetic properties of ribulose bisphosphate carboxylase-oxygenase; the requirements of the photosynthetic carbon reduction and photorespiratory carbon oxidation cycles for reduced pyridine nucleotides; the dependence of electron transport on photon flux and the presence of a temperature dependent upper limit to electron transport. The measurements of gas exchange with which the model outputs may be compared include those of the temperature and partial pressure of CO2(p(CO2)) dependencies of quantum yield, the variation of compensation point with temperature and partial pressure of O2(p(O2)), the dependence of net CO2 assimilation rate on p(CO2) and irradiance, and the influence of p(CO2) and irradiance on the temperature dependence of assimilation rate.
[10] Flexas J Díaz-Espejo A Conesa MA Coopman RE Douthe C Gago J Gallé A Galmés J Medrano H Ribas-Carbo M Tomàs M Niinemets Ü 2016 ). Mesophyll conductance to CO2 and Rubisco as targets for improving intrinsic water use efficiency in C3 plantsPlant, Cell & Environment, 39, 965 -982 . [本文引用: 2] [11] Gao GL Feng Q Liu XD Li W 2020 ). Simulating the leaf stomatal conductance of the desert riparianTamarix ramosissima Ledeb. based on three empirical models. Acta Ecologica Sinica, 3486 -3494 . [本文引用: 3] [ 高冠龙 , 冯起 , 刘贤德 , 李伟 ( 2020 ). 三种经验模型模拟荒漠河岸柽柳叶片气孔导度生态学报 , 40, 3486 -3494 .] [本文引用: 3] [12] Guo BH Wang RS Xiao HJ 2018 ). Response of leaf water potential and stomatal conductance of sea-buckthorn to water stress during seedling stageJournal of Nuclear Agricultural Sciences, 32, 609 -616 . [本文引用: 1] [ 郭冰寒 , 王若水 , 肖辉杰 ( 2018 ). 沙棘苗期叶水势与气孔导度对水分胁迫的响应核农学报 , 32, 609 -616 .] [本文引用: 1] [13] Guo FY Ha R Ma YP Cao B 2019 ). Effects of elevated CO2 concentration on photosynthesis characteristics and biomass allocation of Lycium barbarum seedlings. Acta Botanica Boreali-Occidentalia Sinica, 302 -309 . [本文引用: 1] [ 郭芳芸 , 哈蓉 , 马亚平 , 曹兵 ( 2019 ). CO2 浓度升高对宁夏枸杞苗木光合特性及生物量分配影响西北植物学报 , 39, 302 -309 .] [本文引用: 1] [14] Guo RP Lin ZH Mo XG Yang CL 2010 ). Responses of crop yield and water use efficiency to climate change in the North China PlainAgricultural Water Management, 97, 1185 -1194 . DOI:
10.1016/j.agwat.2009.07.006 URL [本文引用: 1] [15] Harley PC Thomas RB Reynolds JF Strain BR 1992 ). Modelling photosynthesis of cotton grown in elevated CO2 Plant, Cell & Environment, 15, 271 -282 . [本文引用: 1] [16] Jarvis PG 1976 ). The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the fieldPhilosophical Transactions of the Royal Society of London B, Biological Sciences, 273, 593 -610 . DOI:
10.1098/rstb.1976.0035 URL [本文引用: 4] [17] Köhler IH MacDonald AJ Schnyder H 2016 ). Last-century increases in intrinsic water-use efficiency of grassland communities have occurred over a wide range of vegetation composition, nutrient inputs, and soil pHPlant Physiology, 170, 881 -890 . DOI:
10.1104/pp.15.01472 PMID:
26620525 [本文引用: 1] Last-century climate change has led to variable increases of the intrinsic water-use efficiency (Wi; the ratio of net CO2 assimilation to stomatal conductance for water vapor) of trees and C3 grassland ecosystems, but the causes of the variability are not well understood. Here, we address putative drivers underlying variable Wi responses in a wide range of grassland communities. Wi was estimated from carbon isotope discrimination in archived herbage samples from 16 contrasting fertilizer treatments in the Park Grass Experiment, Rothamsted, England, for the 1915 to 1929 and 1995 to 2009 periods. Changes in Wi were analyzed in relation to nitrogen input, soil pH, species richness, and functional group composition. Treatments included liming as well as phosphorus and potassium additions with or without ammonium or nitrate fertilizer applications at three levels. Wi increased between 11% and 25% (P < 0.001) in the different treatments between the two periods. None of the fertilizers had a direct effect on the change of Wi (ΔWi). However, soil pH (P < 0.05), species richness (P < 0.01), and percentage grass content (P < 0.01) were significantly related to ΔWi. Grass-dominated, species-poor plots on acidic soils showed the largest ΔWi (+14.7 μmol mol(-1)). The ΔWi response of these acidic plots was probably related to drought effects resulting from aluminum toxicity on root growth. Our results from the Park Grass Experiment show that Wi in grassland communities consistently increased over a wide range of nutrient inputs, soil pH, and plant community compositions during the last century. © 2016 American Society of Plant Biologists. All Rights Reserved.
[18] Leuning R 1990 ). Modelling stomatal behavior and photosynthesis of Eucalyptus grandis Australian Journal of Plant Physiology, 159 -175 . [本文引用: 4] [19] Leuning R 1995 ). A critical appraisal of a combined stomatal- photosynthesis model for C3 plantsPlant, Cell & Environment, 18, 339 -355 . [本文引用: 4] [20] Li F Liu L Zhang H Wang QT Guo LL Hao LH Zhang XX Cao X Liang WJ Zheng YP 2018 ). Effects of CO2 concentrations on stomatal traits and gas exchange in leaves of soybean Acta Agronomica Sinica, 44, 1212 -1220 . DOI:
10.3724/SP.J.1006.2018.01212 URL [本文引用: 2] [ 李菲 , 刘亮 , 张浩 , 王清涛 , 郭丽丽 , 郝立华 , 张茜茜 , 曹旭 , 梁伟佳 , 郑云普 ( 2018 ). CO2 浓度对大豆叶片气孔特征和气体交换参数的影响作物学报 , 44, 1212 -1220 .] [本文引用: 2] [21] Li LX Liu JM Huang XL Wang JC Luo C Liu JJ Xiong X 2017 ). Response characteristic of Cinnamomum migao seedling’s photosynthesis to CO2 in different conditions of nitrogen Journal of Northeast Agricultural University, 29 -36 . [本文引用: 1] [ 李丽霞 , 刘济明 , 黄小龙 , 王军才 , 骆畅 , 柳嘉佳 , 熊雪 ( 2017 ). 不同氮素条件米槁幼苗光合作用对CO2 响应特征东北农业大学学报 , 48, 29 -36 .] [本文引用: 1] [22] Li YX Lou YS Zhang FC 2011 ). Comparison of stomatal conductance models for winter wheatChinese Journal of Agrometeorology, 32, 106 -110 . [本文引用: 1] [ 李永秀 , 娄运生 , 张富存 ( 2011 ). 冬小麦气孔导度模型的比较中国农业气象 , 32, 106 -110 .] [本文引用: 1] [23] Liu Y Lei SG Cheng LS Cheng W Bian ZF 2018 ). Effects of soil water content on stomatal conductance, transpiration, and photosynthetic rate of Caragana korshinskii under the influence of coal mining subsidence Acta Ecologica Sinica, 3069 -3077 . [本文引用: 1] [ 刘英 , 雷少刚 , 程林森 , 程伟 , 卞正富 ( 2018 ). 采煤塌陷影响下土壤含水量变化对柠条气孔导度、蒸腾与光合作用速率的影响生态学报 , 38, 3069 -3077 .] [本文引用: 1] [24] Medlyn BE Duursma RA Eamus D Ellsworth DS Prentice IC Barton CVM Crous KY Angelis PDE Freeman M Wingate L 2011 ). Reconciling the optimal and empirical approaches to modelling stomatal conductanceGlobal Change Biology, 17, 2134 -2144 . DOI:
10.1111/gcb.2011.17.issue-6 URL [本文引用: 3] [25] Miner GL Bauerle WL 2017 ). Seasonal variability of the parameters of the Ball-Berry model of stomatal conductance in maize (Zea mays L.) and sunflower (Helianthus annuus L.) under well-watered and water-stressed conditionsPlant, Cell & Environment, 1874 -1886 . [本文引用: 1] [26] Ren B Li J Tong XJ Mu YM Meng P Zhang JS 2018 ). Simulation on photosynthetic-CO2 response of Quercus variabilis and Robinia pseudoacacia in the southern foot of the Taihang Mountain, China Chinese Journal of Applied Ecology, 1 -10 . DOI:
10.13287/j.1001-9332.201801.003 PMID:
29692006 [本文引用: 1] In this study, leaf photosynthetic CO-response curves of Quercus variabilis and Robinia pseudoacacia were measured using a Li-6400XT photosynthetic measurement system in the southern foot of the Taihang Mountain, China. The rectangular hyperbola model (RH), nonrectangular hyperbola model (NRH) andYe model (YZP) were used to fit photosynthetic-CO response curves and compare photosynthetic parameters, including the maximum net photosynthetic rate (A), the initial carboxylation rate (η), light respiration rate (R), CO compensation point (CCP) and CO saturation point (CSP). Compared with the NRH and YZP models, A, η, R and CCP obtained by the RH model were higher, and were 59.8%, 128.6%, 133.4% and 19.8% higher than the measured values. The accuracy of the RH model was lower and its relative error was higher than that of the NRH and YZP models.Compared with the RH and YZP models, A fitted by the NRH model was higher, and was 11.1% higher than the measured value. η, R and CCP fitted by the NRH model were closer to the measured values. CO saturation phenomenon of photosynthesis could be simulated by the YZP model, and A and CSP were fitted well. A, R and CCP in the shaded leaves of Q. variabilis were 31.3%, 5.2% and 14.3% lower than those in the sunlit leaves. A, R and CCP in shaded leaves of R. pseudoacacia were 23.5%, 11.0% and 5.4% more than those in the sunlit leaves. η in the shaded leaves of Q. variabilis and R. pseudoacacia were 6.9% and 7.0% higher than those in the sunlit leaves, respectively. R and CCP of R. pseudoacacia leaves had linear relationships with temperature (T) and photosynthetic active radiation (PAR), and η had a significant relationship with stomatal conductance (g). η of Q. variabilis leaves was linearly correlated with PAR and g, and CCP was affected by T and relative humidity. A of Q. variabilis leaves had significant positive linear relationships with RH and g.
[ 任博 , 李俊 , 同小娟 , 母艳梅 , 孟平 , 张劲松 ( 2018 ). 太行山南麓栓皮栎和刺槐光合作用-CO2 响应模拟应用生态学报 , 29, 1 -10 .] PMID:
29692006 [本文引用: 1] [27] Su WH Zhang GF 2002 ). The effect of soil and air temperature on photosynthesis and transpiration of Primula sinopurpurea Acta Botanica Boreali-Occidentalia Sinica, 824 -830 . [本文引用: 1] [ 苏文华 , 张光飞 ( 2002 ). 土壤温度与气温对紫花雪山报春光合作用和蒸腾作用的影响西北植物学报 , 22, 824 -830 .] [本文引用: 1] [28] Tang XL Cao YH Zhou BZ Zhou Y Gu LH 2017 ). Comparison of light response modeling of photosynthesis in Castanopsis sclerophylla leaves under different CO2 concentrations Chinese Journal of Ecology, 2060 -2067 . [本文引用: 1] [ 唐星林 , 曹永慧 , 周本智 , 周燕 , 顾连宏 ( 2017 ). 不同CO2 浓度下苦槠(Castanopsis sclerophylla )叶片光合光响应模型模拟比较生态学杂志 , 36, 2060 -2067 .] [本文引用: 1] [29] Tao FL Hayashi Y Zhang Z Sakamoto T Yokozawa M 2008 ). Global warming, rice production and water use in China: developing a probabilistic assessmentAgricultural and Forest Meteorology, 148, 94 -110 . DOI:
10.1016/j.agrformet.2007.09.012 URL [本文引用: 1] [30] Tuzet A Perrier A Leuning R 2003 ). A coupled model of stomatal conductance, photosynthesis and transpirationPlant, Cell & Environment, 26, 1097 -1116 . [本文引用: 3] [31] Wang HZ Han L Xu YL Niu JL 2015 ). Model analysis of the stomatal conductance response to light in Populus pruinosa at different temperatures in the Taklimakan desert Ecology and Environmental Sciences, 741 -748 . [本文引用: 2] [ 王海珍 , 韩路 , 徐雅丽 , 牛建龙 ( 2015 ). 不同温度下灰胡杨叶片气孔导度对光强响应的模型分析生态环境学报 , 24, 741 -748 .] [本文引用: 2] [32] Wang JL 2009 ). Response of photosynthetic rate and stomatal conductance of oat to light intensity and CO2 concentration and its modeling Acta Agriculturae Boreali-Sinica, 24, 134 -137 . [本文引用: 5] [ 王建林 ( 2009 ). 燕麦叶片光合速率、气孔导度对光强和CO2 的响应与模拟华北农学报 , 24, 134 -137 .] [本文引用: 5] [33] Wang JL Wen XF 2010 ). Modeling the response of stomatal conductance to variable CO2 concentration and its physiological mechanism Acta Ecologica Sinica, 30, 4815 -4820 . [本文引用: 6] [ 王建林 , 温学发 ( 2010 ). 气孔导度对CO2 浓度变化的模拟及其生理机制生态学报 , 30, 4815 -4820 .] [本文引用: 6] [34] Wang JL Wen XF Zhao FH Fang QX Yang XM 2012 ). Effects of doubled CO2 concentration on leaf photosynthesis, transpiration and water use efficiency of eight crop species Chinese Journal of Plant Ecology, 36, 438 -446 . DOI:
10.3724/SP.J.1258.2012.00438 URL [本文引用: 1] [ 王建林 , 温学发 , 赵风华 , 房全孝 , 杨新民 ( 2012 ). CO2 浓度倍增对8种作物叶片光合作用、蒸腾作用和水分利用效率的影响植物生态学报 , 36, 438 -446 .] [本文引用: 1] [35] Wang QL Zhou GS 2018 ). Comparisons between common stomatal conductance models under progressive drought in spring maizeActa Ecologica Sinica, 38, 6846 -6856 . [本文引用: 1] [ 王秋玲 , 周广胜 ( 2018 ). 春玉米持续干旱过程中常用气孔导度模型的比较研究生态学报 , 38, 6846 -6856 .] [本文引用: 1] [36] Xing HL Zhou WB Hao WP Li L Wang C Ma HY Wang YS 2020 ). Inhibition of nitrogen increasing on maize growth under water stressChinese Journal of Agrometeorology, 41, 240 -252 . [本文引用: 1] [ 邢换丽 , 周文彬 , 郝卫平 , 李丽 , 王超 , 马海洋 , 王耀生 ( 2020 ). 水分胁迫下氮素增加对玉米生长的抑制作用中国农业气象 , 41, 240 -252 .] [本文引用: 1] [37] Ye ZP 2007 ). A new model for relationship between irradiance and the rate of photosynthesis in Oryza sativaPhotosynthetica, 45, 637 -640 . DOI:
10.1007/s11099-007-0110-5 URL [本文引用: 1] [38] Ye ZP 2010 ). A review on modeling of responses of photosynthesis to light and CO2 Chinese Journal of Plant Ecology, 34, 727 -740 . [本文引用: 5] [ 叶子飘 ( 2010 ). 光合作用对光和CO2 响应模型的研究进展植物生态学报 , 34, 727 -740 .] [本文引用: 5] [39] Ye ZP Yu Q 2008 ). A coupled model of stomatal conductance and photosynthesis for winter wheatPhotosynthetica, 46, 637 -640 . DOI:
10.1007/s11099-008-0110-0 URL [本文引用: 1] [40] Ye ZP Yu Q 2009a ). Mechanism model of stomatal conductanceChinese Journal of Plant Ecology, 33, 772 -782 . [本文引用: 2] [ 叶子飘 , 于强 ( 2009a ). 植物气孔导度的机理模型植物生态学报 , 33, 772 -782 .] [本文引用: 2] [41] Ye ZP Yu Q 2009b ). A comparison of response curves of winter wheat photosynthesis to flag leaf intercellular and air CO2 concentrations Chinese Journal of Ecology, 28, 2233 -2238 . [本文引用: 2] [ 叶子飘 , 于强 ( 2009b ). 光合作用对胞间和大气CO2 响应曲线的比较生态学杂志 , 28, 2233 -2238 .] [本文引用: 2] [42] Yu Q Zhang YQ Liu YF Shi PL 2004 ). Simulation of the stomatal conductance of winter wheat in response to light, temperature and CO2 changesAnnals of Botany, 93, 435 -441 . DOI:
10.1093/aob/mch023 URL [本文引用: 3] [43] Zheng FY Peng SL 2003 ). Responses of plant stomatal conductance to elevated CO2 at different scales Chinese Journal of Ecology, 22, 26 -30 . [本文引用: 1] [ 郑凤英 , 彭少麟 ( 2003 ). 不同尺度上植物叶气孔导度对升高CO2 的响应生态学杂志 , 22, 26 -30 .] [本文引用: 1] [44] Zhong C Zhu Y 2013 ). Response of stomatal conductance to light in tobacco plantsChinese Journal of Eco- Agriculture, 21, 966 -972 . DOI:
10.3724/SP.J.1011.2013.00966 URL [本文引用: 2] [ 钟楚 , 朱勇 ( 2013 ). 烟草气孔导度对光强的响应中国生态农业学报 , 21, 966 -972 .] [本文引用: 2] Elevated CO
2 increases water use efficiency by sustaining photosynthesis of water-limited maize and
1
2011
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions //Biggens J.
Progress in Photosynthesis Research 5
1987
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
... 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
Plant responses to decadal scale increments in atmospheric CO
2 concentration: comparing two stomatal conductance sampling methods
2
2020
... 此外, 还有****发现, 植物叶片的气孔导度对
C a 的响应并非单纯的非线性下降, 还存在其他的变化趋势(
Yu et al ., 2004 ;
李菲等, 2018 ;
Batkeet al ., 2020 ).比如,
Batke等(2020) 研究了
Sambucus racemosa 、
Populus tremula 和
Populus tremuloides 3种植物气孔导度对CO
2 浓度的响应问题, 发现这些植物既存在气孔导度随CO
2 浓度的增加而下降的情况, 也存在气孔导度随CO
2 浓度的增加先下降后上升的情况.对于后者, 尚不能用经验模型描述其气孔对CO
2 浓度响应的变化趋势.与经验模型相比较, 新模型不仅可以很好地拟合大豆和小麦的气孔导度对CO
2 浓度的变化趋势, 而且还可以估算其最大气孔导度、最小气孔导度以及相对应的CO
2 浓度等参数.同时, 模型中各个参数具有明确的生物学意义.因此, 新模型可以真实地反应大豆和小麦的气孔导度对CO
2 的响应变化趋势. ...
... ).比如,
Batke等(2020) 研究了
Sambucus racemosa 、
Populus tremula 和
Populus tremuloides 3种植物气孔导度对CO
2 浓度的响应问题, 发现这些植物既存在气孔导度随CO
2 浓度的增加而下降的情况, 也存在气孔导度随CO
2 浓度的增加先下降后上升的情况.对于后者, 尚不能用经验模型描述其气孔对CO
2 浓度响应的变化趋势.与经验模型相比较, 新模型不仅可以很好地拟合大豆和小麦的气孔导度对CO
2 浓度的变化趋势, 而且还可以估算其最大气孔导度、最小气孔导度以及相对应的CO
2 浓度等参数.同时, 模型中各个参数具有明确的生物学意义.因此, 新模型可以真实地反应大豆和小麦的气孔导度对CO
2 的响应变化趋势. ...
Forests and climate change: forcings, feedbacks, and the climate benefits of forests
2
2008
... 未来大气CO
2 浓度上升、温度升高与水资源短缺将威胁着人类的生存环境并极大地影响着全球的粮食安全(
Drakea et al ., 2017 ;
刘英等, 2018 ).提高作物的水分利用效率是减少单位水量的消耗以产生更多碳同化量的重要途径.气孔作为高等植物与外界环境进行水汽和CO
2 气体交换的主要通道(
王建林等, 2012 ), 它在调节植物的碳同化、蒸腾作用, 以及调控土壤、植物和大气连续体系统中水循环与碳循环等方面具有重要的作用, 直接决定生态系统的水热平衡过程(
Bonan, 2008 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
Modelling stomatal conductance in response to environmental factors
1
2013
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
春小麦对不同灌水处理的气孔反应及其影响因子
1
2010
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
春小麦对不同灌水处理的气孔反应及其影响因子
1
2010
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
陇中半干旱区玉米对光和CO
2 浓度的响应模型
2
2019
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
陇中半干旱区玉米对光和CO
2 浓度的响应模型
2
2019
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
Stomatal and non-stomatal limitations of photosynthesis for four tree species under drought: a comparison of model formulations
2
2017
... 未来大气CO
2 浓度上升、温度升高与水资源短缺将威胁着人类的生存环境并极大地影响着全球的粮食安全(
Drakea et al ., 2017 ;
刘英等, 2018 ).提高作物的水分利用效率是减少单位水量的消耗以产生更多碳同化量的重要途径.气孔作为高等植物与外界环境进行水汽和CO
2 气体交换的主要通道(
王建林等, 2012 ), 它在调节植物的碳同化、蒸腾作用, 以及调控土壤、植物和大气连续体系统中水循环与碳循环等方面具有重要的作用, 直接决定生态系统的水热平衡过程(
Bonan, 2008 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
A biochemical model of photosynthetic CO
2 assimilation in leaves of C
3 species
6
1980
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
...
Farquhar等(1980) 根据Rubisco酶动力学反应和核酮糖-1,5-双磷酸(RuBP)再生反应化学计量学而提出的C
3 植物的光合生化模型认为, 光合作用的关键酶是核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco), 其活性受叶肉细胞
C i 和氧气浓度(
O i )决定, 而植物的光合作用又可改变叶肉细胞的CO
2 浓度并最终驱动气孔运动.由此分析并结合CO
2 浓度为0 μmol·mol
-1 时植物叶片
g s 为最大值的实验事实, 同时基于公式(1)可以较好地描述植物叶片
A n 对CO
2 的响应曲线, 我们推测植物叶片
g s 对CO
2 的响应模型的表达式可以表示为, ...
...
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述Rubisco酶活性限制的子模型得到气孔导度与变量
C a 之间的关系为: ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
... 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
Mesophyll conductance to CO
2 and Rubisco as targets for improving intrinsic water use efficiency in C
3 plants
2
2016
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
三种经验模型模拟荒漠河岸柽柳叶片气孔导度
3
2020
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
... ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
三种经验模型模拟荒漠河岸柽柳叶片气孔导度
3
2020
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
... ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
沙棘苗期叶水势与气孔导度对水分胁迫的响应
1
2018
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
沙棘苗期叶水势与气孔导度对水分胁迫的响应
1
2018
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
CO
2 浓度升高对宁夏枸杞苗木光合特性及生物量分配影响
1
2019
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
CO
2 浓度升高对宁夏枸杞苗木光合特性及生物量分配影响
1
2019
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
Responses of crop yield and water use efficiency to climate change in the North China Plain
1
2010
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
Modelling photosynthesis of cotton grown in elevated CO
2 1
1992
... 本文的研究目的主要为: (1)基于
叶子飘(2010) 构建的光合作用对CO
2 响应模型构建
g s 对CO
2 的响应模型; (2)测量大豆(
Glycine max )和小麦(
Triticum aestivum )在光合有效辐射强度(
PAR )为2 000 μmol·m
-2 ·s
-1 时的气体交换数据, 即光合作用对CO
2 的响应曲线(
A n -
C a ), 然后用传统的Michaelis-Menten模型(M-M模型)(
Harley et al ., 1992 )和近年来
叶子飘(2010) 构建的CO
2 的响应模型(简称叶模型)拟合这些
A n -
C a 曲线, 比较两种模型的拟合效果; (3)用构建的
g s 对
C a 的响应模型拟合测量曲线, 并将拟合结果与
王建林(2009) 构建模型的拟合结果以及观测数据进行比较, 以判断所构建模型是否合理. ...
The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field
4
1976
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
Last-century increases in intrinsic water-use efficiency of grassland communities have occurred over a wide range of vegetation composition, nutrient inputs, and soil pH
1
2016
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
Modelling stomatal behavior and photosynthesis of
Eucalyptus grandis 4
1990
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
A critical appraisal of a combined stomatal- photosynthesis model for C
3 plants
4
1995
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
CO
2 浓度对大豆叶片气孔特征和气体交换参数的影响
2
2018
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 此外, 还有****发现, 植物叶片的气孔导度对
C a 的响应并非单纯的非线性下降, 还存在其他的变化趋势(
Yu et al ., 2004 ;
李菲等, 2018 ;
Batkeet al ., 2020 ).比如,
Batke等(2020) 研究了
Sambucus racemosa 、
Populus tremula 和
Populus tremuloides 3种植物气孔导度对CO
2 浓度的响应问题, 发现这些植物既存在气孔导度随CO
2 浓度的增加而下降的情况, 也存在气孔导度随CO
2 浓度的增加先下降后上升的情况.对于后者, 尚不能用经验模型描述其气孔对CO
2 浓度响应的变化趋势.与经验模型相比较, 新模型不仅可以很好地拟合大豆和小麦的气孔导度对CO
2 浓度的变化趋势, 而且还可以估算其最大气孔导度、最小气孔导度以及相对应的CO
2 浓度等参数.同时, 模型中各个参数具有明确的生物学意义.因此, 新模型可以真实地反应大豆和小麦的气孔导度对CO
2 的响应变化趋势. ...
CO
2 浓度对大豆叶片气孔特征和气体交换参数的影响
2
2018
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 此外, 还有****发现, 植物叶片的气孔导度对
C a 的响应并非单纯的非线性下降, 还存在其他的变化趋势(
Yu et al ., 2004 ;
李菲等, 2018 ;
Batkeet al ., 2020 ).比如,
Batke等(2020) 研究了
Sambucus racemosa 、
Populus tremula 和
Populus tremuloides 3种植物气孔导度对CO
2 浓度的响应问题, 发现这些植物既存在气孔导度随CO
2 浓度的增加而下降的情况, 也存在气孔导度随CO
2 浓度的增加先下降后上升的情况.对于后者, 尚不能用经验模型描述其气孔对CO
2 浓度响应的变化趋势.与经验模型相比较, 新模型不仅可以很好地拟合大豆和小麦的气孔导度对CO
2 浓度的变化趋势, 而且还可以估算其最大气孔导度、最小气孔导度以及相对应的CO
2 浓度等参数.同时, 模型中各个参数具有明确的生物学意义.因此, 新模型可以真实地反应大豆和小麦的气孔导度对CO
2 的响应变化趋势. ...
不同氮素条件米槁幼苗光合作用对CO
2 响应特征
1
2017
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
不同氮素条件米槁幼苗光合作用对CO
2 响应特征
1
2017
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
冬小麦气孔导度模型的比较
1
2011
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
冬小麦气孔导度模型的比较
1
2011
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
采煤塌陷影响下土壤含水量变化对柠条气孔导度、蒸腾与光合作用速率的影响
1
2018
... 未来大气CO
2 浓度上升、温度升高与水资源短缺将威胁着人类的生存环境并极大地影响着全球的粮食安全(
Drakea et al ., 2017 ;
刘英等, 2018 ).提高作物的水分利用效率是减少单位水量的消耗以产生更多碳同化量的重要途径.气孔作为高等植物与外界环境进行水汽和CO
2 气体交换的主要通道(
王建林等, 2012 ), 它在调节植物的碳同化、蒸腾作用, 以及调控土壤、植物和大气连续体系统中水循环与碳循环等方面具有重要的作用, 直接决定生态系统的水热平衡过程(
Bonan, 2008 ). ...
采煤塌陷影响下土壤含水量变化对柠条气孔导度、蒸腾与光合作用速率的影响
1
2018
... 未来大气CO
2 浓度上升、温度升高与水资源短缺将威胁着人类的生存环境并极大地影响着全球的粮食安全(
Drakea et al ., 2017 ;
刘英等, 2018 ).提高作物的水分利用效率是减少单位水量的消耗以产生更多碳同化量的重要途径.气孔作为高等植物与外界环境进行水汽和CO
2 气体交换的主要通道(
王建林等, 2012 ), 它在调节植物的碳同化、蒸腾作用, 以及调控土壤、植物和大气连续体系统中水循环与碳循环等方面具有重要的作用, 直接决定生态系统的水热平衡过程(
Bonan, 2008 ). ...
Reconciling the optimal and empirical approaches to modelling stomatal conductance
3
2011
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
Seasonal variability of the parameters of the Ball-Berry model of stomatal conductance in maize (
Zea mays L.) and sunflower (
Helianthus annuus L.) under well-watered and water-stressed conditions
1
2017
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
太行山南麓栓皮栎和刺槐光合作用-CO
2 响应模拟
1
2018
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
太行山南麓栓皮栎和刺槐光合作用-CO
2 响应模拟
1
2018
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
土壤温度与气温对紫花雪山报春光合作用和蒸腾作用的影响
1
2002
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
土壤温度与气温对紫花雪山报春光合作用和蒸腾作用的影响
1
2002
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
不同CO
2 浓度下苦槠(
Castanopsis sclerophylla )叶片光合光响应模型模拟比较
1
2017
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
不同CO
2 浓度下苦槠(
Castanopsis sclerophylla )叶片光合光响应模型模拟比较
1
2017
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
Global warming, rice production and water use in China: developing a probabilistic assessment
1
2008
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
A coupled model of stomatal conductance, photosynthesis and transpiration
3
2003
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
不同温度下灰胡杨叶片气孔导度对光强响应的模型分析
2
2015
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
不同温度下灰胡杨叶片气孔导度对光强响应的模型分析
2
2015
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
燕麦叶片光合速率、气孔导度对光强和CO
2 的响应与模拟
5
2009
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 本文的研究目的主要为: (1)基于
叶子飘(2010) 构建的光合作用对CO
2 响应模型构建
g s 对CO
2 的响应模型; (2)测量大豆(
Glycine max )和小麦(
Triticum aestivum )在光合有效辐射强度(
PAR )为2 000 μmol·m
-2 ·s
-1 时的气体交换数据, 即光合作用对CO
2 的响应曲线(
A n -
C a ), 然后用传统的Michaelis-Menten模型(M-M模型)(
Harley et al ., 1992 )和近年来
叶子飘(2010) 构建的CO
2 的响应模型(简称叶模型)拟合这些
A n -
C a 曲线, 比较两种模型的拟合效果; (3)用构建的
g s 对
C a 的响应模型拟合测量曲线, 并将拟合结果与
王建林(2009) 构建模型的拟合结果以及观测数据进行比较, 以判断所构建模型是否合理. ...
...
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述Rubisco酶活性限制的子模型得到气孔导度与变量
C a 之间的关系为: ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
燕麦叶片光合速率、气孔导度对光强和CO
2 的响应与模拟
5
2009
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 本文的研究目的主要为: (1)基于
叶子飘(2010) 构建的光合作用对CO
2 响应模型构建
g s 对CO
2 的响应模型; (2)测量大豆(
Glycine max )和小麦(
Triticum aestivum )在光合有效辐射强度(
PAR )为2 000 μmol·m
-2 ·s
-1 时的气体交换数据, 即光合作用对CO
2 的响应曲线(
A n -
C a ), 然后用传统的Michaelis-Menten模型(M-M模型)(
Harley et al ., 1992 )和近年来
叶子飘(2010) 构建的CO
2 的响应模型(简称叶模型)拟合这些
A n -
C a 曲线, 比较两种模型的拟合效果; (3)用构建的
g s 对
C a 的响应模型拟合测量曲线, 并将拟合结果与
王建林(2009) 构建模型的拟合结果以及观测数据进行比较, 以判断所构建模型是否合理. ...
...
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述Rubisco酶活性限制的子模型得到气孔导度与变量
C a 之间的关系为: ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
气孔导度对CO
2 浓度变化的模拟及其生理机制
6
2010
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
...
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述Rubisco酶活性限制的子模型得到气孔导度与变量
C a 之间的关系为: ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
... ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
气孔导度对CO
2 浓度变化的模拟及其生理机制
6
2010
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
...
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述Rubisco酶活性限制的子模型得到气孔导度与变量
C a 之间的关系为: ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
... ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
CO
2 浓度倍增对8种作物叶片光合作用、蒸腾作用和水分利用效率的影响
1
2012
... 未来大气CO
2 浓度上升、温度升高与水资源短缺将威胁着人类的生存环境并极大地影响着全球的粮食安全(
Drakea et al ., 2017 ;
刘英等, 2018 ).提高作物的水分利用效率是减少单位水量的消耗以产生更多碳同化量的重要途径.气孔作为高等植物与外界环境进行水汽和CO
2 气体交换的主要通道(
王建林等, 2012 ), 它在调节植物的碳同化、蒸腾作用, 以及调控土壤、植物和大气连续体系统中水循环与碳循环等方面具有重要的作用, 直接决定生态系统的水热平衡过程(
Bonan, 2008 ). ...
CO
2 浓度倍增对8种作物叶片光合作用、蒸腾作用和水分利用效率的影响
1
2012
... 未来大气CO
2 浓度上升、温度升高与水资源短缺将威胁着人类的生存环境并极大地影响着全球的粮食安全(
Drakea et al ., 2017 ;
刘英等, 2018 ).提高作物的水分利用效率是减少单位水量的消耗以产生更多碳同化量的重要途径.气孔作为高等植物与外界环境进行水汽和CO
2 气体交换的主要通道(
王建林等, 2012 ), 它在调节植物的碳同化、蒸腾作用, 以及调控土壤、植物和大气连续体系统中水循环与碳循环等方面具有重要的作用, 直接决定生态系统的水热平衡过程(
Bonan, 2008 ). ...
春玉米持续干旱过程中常用气孔导度模型的比较研究
1
2018
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
春玉米持续干旱过程中常用气孔导度模型的比较研究
1
2018
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
水分胁迫下氮素增加对玉米生长的抑制作用
1
2020
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
水分胁迫下氮素增加对玉米生长的抑制作用
1
2020
... 式中,
α 为
A n -
C 曲线的初始斜率;
C 为CO
2 浓度, 它既可以表示大气CO
2 浓度(
C a ), 也可以表示为胞间CO
2 浓度(
C i );
β 和
γ 分别称为加氧和羧化系数;
R p 是CO
2 浓度为0 μmol·mol
-1 时植物叶片的光下呼吸速率.因此, 公式(1)既可以描述植物叶片光合作用对大气CO
2 浓度的响应曲线(
A n -
C a ), 也可以用于描述光合作用对胞间CO
2 浓度的响应曲线(
A n -
C i ).并由此可以得到植物叶片的最大羧化速率(
A nmax )、饱和CO
2 浓度(
C i,TPU )、CO
2 补偿点(
Γ )和
R p 等光合参数.该模型发表后获得广泛引用和应用, 且拟合得到的光合参数与观测值均较为接近(
李丽霞等, 2017 ;
任博等, 2018 ;
丁林凯等, 2019 ;
郭芳芸等, 2019 ;
邢换丽等, 2020 ).公式(1)称为叶子飘模型(叶模型). ...
A new model for relationship between irradiance and the rate of photosynthesis in Oryza sativa
1
2007
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
光合作用对光和CO
2 响应模型的研究进展
5
2010
... 本文的研究目的主要为: (1)基于
叶子飘(2010) 构建的光合作用对CO
2 响应模型构建
g s 对CO
2 的响应模型; (2)测量大豆(
Glycine max )和小麦(
Triticum aestivum )在光合有效辐射强度(
PAR )为2 000 μmol·m
-2 ·s
-1 时的气体交换数据, 即光合作用对CO
2 的响应曲线(
A n -
C a ), 然后用传统的Michaelis-Menten模型(M-M模型)(
Harley et al ., 1992 )和近年来
叶子飘(2010) 构建的CO
2 的响应模型(简称叶模型)拟合这些
A n -
C a 曲线, 比较两种模型的拟合效果; (3)用构建的
g s 对
C a 的响应模型拟合测量曲线, 并将拟合结果与
王建林(2009) 构建模型的拟合结果以及观测数据进行比较, 以判断所构建模型是否合理. ...
... )和近年来
叶子飘(2010) 构建的CO
2 的响应模型(简称叶模型)拟合这些
A n -
C a 曲线, 比较两种模型的拟合效果; (3)用构建的
g s 对
C a 的响应模型拟合测量曲线, 并将拟合结果与
王建林(2009) 构建模型的拟合结果以及观测数据进行比较, 以判断所构建模型是否合理. ...
...
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应曲线(
A n -
C )模型为: ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
... 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
光合作用对光和CO
2 响应模型的研究进展
5
2010
... 本文的研究目的主要为: (1)基于
叶子飘(2010) 构建的光合作用对CO
2 响应模型构建
g s 对CO
2 的响应模型; (2)测量大豆(
Glycine max )和小麦(
Triticum aestivum )在光合有效辐射强度(
PAR )为2 000 μmol·m
-2 ·s
-1 时的气体交换数据, 即光合作用对CO
2 的响应曲线(
A n -
C a ), 然后用传统的Michaelis-Menten模型(M-M模型)(
Harley et al ., 1992 )和近年来
叶子飘(2010) 构建的CO
2 的响应模型(简称叶模型)拟合这些
A n -
C a 曲线, 比较两种模型的拟合效果; (3)用构建的
g s 对
C a 的响应模型拟合测量曲线, 并将拟合结果与
王建林(2009) 构建模型的拟合结果以及观测数据进行比较, 以判断所构建模型是否合理. ...
... )和近年来
叶子飘(2010) 构建的CO
2 的响应模型(简称叶模型)拟合这些
A n -
C a 曲线, 比较两种模型的拟合效果; (3)用构建的
g s 对
C a 的响应模型拟合测量曲线, 并将拟合结果与
王建林(2009) 构建模型的拟合结果以及观测数据进行比较, 以判断所构建模型是否合理. ...
...
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应曲线(
A n -
C )模型为: ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
... 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
A coupled model of stomatal conductance and photosynthesis for winter wheat
1
2008
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
植物气孔导度的机理模型
2
2009a
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
植物气孔导度的机理模型
2
2009a
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
光合作用对胞间和大气CO
2 响应曲线的比较
2
2009b
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
光合作用对胞间和大气CO
2 响应曲线的比较
2
2009b
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
Simulation of the stomatal conductance of winter wheat in response to light, temperature and CO
2 changes
3
2004
... 大气CO
2 浓度对植物的光合来说是极为重要的环境因子.已有的气孔导度模型往往仅将
C a 作为常量讨论
g s 与
A n 和其他环境因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ).但这些模型不能用于研究植物叶片
g s 对
C a 的响应规律.为了探究
g s 对
C a 的响应关系, 国内****
王建林(2009) 、
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述核酮糖-1,5-双磷酸羧化酶/加氧酶(Rubisco)活性限制子模型得到
g s 与变量
C a 之间存在非线性下降的关系, 该模型可以较好地拟合
g s 随
C a 增加而下降的趋势.然而, 也有实验数据表明植物叶片的
g s 随CO
2 浓度的增加先下降到达最小值, 之后又随CO
2 浓度的增加而上升(
Yuet al ., 2004 ;
李菲等, 2018 ).
g s 这种变化趋势与
王建林(2009) 、
王建林和温学发(2010) 所给出的模型所描述的响应曲线存在较大的差异.由此可见, 迄今为止尚无一个普适性的气孔导度模型能够准确地描述植物叶片
g s 对
C a 或胞间CO
2 浓度(
C i )响应曲线的文献报道.这对深入研究未来CO
2 浓度升高对植物叶片气孔导度的影响极为不利.而未来干旱和CO
2 浓度升高等全球气候变化正在通过影响气孔导度进而影响着植物的光合作用和气体交换(
Taoet al ., 2008 ;
Guo et al ., 2010 ;
Allenet al ., 2011 ;
Köhleret al ., 2016 ).因此, 构建一个合理的植物叶片气孔导度对CO
2 响应模型, 对定量研究植物叶片的气孔导度对CO
2 浓度响应的变化规律尤为必要. ...
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
... 此外, 还有****发现, 植物叶片的气孔导度对
C a 的响应并非单纯的非线性下降, 还存在其他的变化趋势(
Yu et al ., 2004 ;
李菲等, 2018 ;
Batkeet al ., 2020 ).比如,
Batke等(2020) 研究了
Sambucus racemosa 、
Populus tremula 和
Populus tremuloides 3种植物气孔导度对CO
2 浓度的响应问题, 发现这些植物既存在气孔导度随CO
2 浓度的增加而下降的情况, 也存在气孔导度随CO
2 浓度的增加先下降后上升的情况.对于后者, 尚不能用经验模型描述其气孔对CO
2 浓度响应的变化趋势.与经验模型相比较, 新模型不仅可以很好地拟合大豆和小麦的气孔导度对CO
2 浓度的变化趋势, 而且还可以估算其最大气孔导度、最小气孔导度以及相对应的CO
2 浓度等参数.同时, 模型中各个参数具有明确的生物学意义.因此, 新模型可以真实地反应大豆和小麦的气孔导度对CO
2 的响应变化趋势. ...
不同尺度上植物叶气孔导度对升高CO
2 的响应
1
2003
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
不同尺度上植物叶气孔导度对升高CO
2 的响应
1
2003
... 大量的研究结果表明, 较低浓度CO
2 促使气孔张开, 而较高浓度的则能诱导气孔关闭, 即高CO
2 浓度可降低植物叶片的
g s , 但
g s 对高CO
2 浓度的响应同光合作用一样随植物种类的不同和环境条件的不同而变化(
郑凤英和彭少麟, 2003 ).在本研究中, 大豆和小麦的
g s 随CO
2 浓度的升高而下降, 大豆的
g s 到最小值之后大豆的气孔导度随CO
2 浓度的升高有较大的上升(
图2A ), 而小麦在气孔导度出现最小值之后略有增加(
图2B ).而
王建林(2009) 用其构建的模型拟合燕麦(
Avena sativa )的
g s -
C a 曲线, 其拟合结果表明, CO
2 浓度越高, 气孔导度越小, 且其气孔导度随CO
2 浓度的升高而一直下降, 但其模型拟合得到的最大气孔导度是观测值的57.33%.同时,
王建林和温学发(2010) 利用
Farquhar等(1980) 生化模型中描述的Rubisco酶活性限制子模型得到气孔导度与变量
C a 之间的关系, 并用此模型研究了9种植物叶片的气孔导度对CO
2 浓度的响应.但在CO
2 浓度大于500 μmol·mol
-1 左右时, 由该模型拟合羊草(
Leymus chinensis )、玉米(
Zea mays )和柑橘(
Citrus reticulata ) 3种植物叶片的气孔导度与观测点偏差较大(
王建林和温学发, 2010 ), 不能真实反映这3种植物
g s -
C a 曲线的变化趋势.同时, 该模型给出的9种植物
C s0 值从最小的182 μmol·mol
-1 到最大的985 μmol·mol
-1 , 为何
C s0 有这么大的差异则尚不清楚.因此, 该模型存在一定的局限性.其原因是
Farquhar等(1980) 生化模型认为Rubisco酶活性满足M-M模型, 而已有的实验结果表明, M-M模型远远高估植物的最大光合能力(
Yu et al ., 2004 ;
叶子飘和于强, 2009b ;
唐星林等, 2017 ;
丁林凯等, 2019 ), 本实验结果(
表1 )也验证了这个结论. ...
烟草气孔导度对光强的响应
2
2013
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
烟草气孔导度对光强的响应
2
2013
... 多年来, 构建气孔导度(
g s )与环境因子间的响应关系模型一直被国内外****关注, 并围绕气孔运动的机理开展了大量研究.目前建立了一系列经验或半经验模型, 主要有
Jarvis (1976) 建立的经验型阶乘模型(Jarvis模型)、
Ball等(1987) 建立的半经验模型(BWB模型)、Ball-Berry-Leuning模型(BBL模型) (
Leuning, 1990 ,
1995 )、Tuzet-Perrier-Leuning模型(Tuzet模型)(
Tuzet et al ., 2003 )、
Medlyn等(2011) 的优化模型以及
叶子飘和于强(2009a) 构建的机理模型等, 其中国内****主要用Jarvis模型和BWB模型或BBL模型研究植物的
g s 对环境因素的响应(
成雪峰等, 2010 ;
李永秀等, 2011 ;
郭冰寒等, 2018 ;
王秋玲和周广胜, 2018 ;
高冠龙等, 2020 ); 国外****则主要是用Medlyn的优化模型和Tuzet模型研究植物的
g s 对环境因素的响应(
Buckley & Mott, 2013 ;
Flexas et al ., 2016 ;
Miner & Bauerle, 2017 ).此外, 当CO
2 浓度确定时, 除Jarvis模型外, 其他模型主要研究
g s 与净光合速率(
A n )或光强、叶面大气相对湿度、大气CO
2 浓度(
C a )、水汽压亏缺和叶水势函数等环境因子中的一个或多个因子之间的关系(
Jarvis, 1976 ;
Ball et al ., 1987 ;
Leuning, 1990 ,
1995 ;
Tuzet et al ., 2003 ;
叶子飘和于强, 2009a ;
Medlyn et al ., 2011 ;
钟楚和朱勇, 2013 ;
王海珍等, 2015 ). ...
... 气孔导度的开放程度直接影响植物的蒸腾速率和光合作用(
苏文华和张光飞 , 2002;
Bonan, 2008 ;
Drakea et al ., 2017 ), 且在控制水分平衡中起关键作用(
Flexas et al ., 2016 ).当前, 被学术界广泛用于估算气孔导度对环境因子响应的模型只有两类: 即Jarvis模型(
Jarvis, 1976 )和BWB模型(
Ball et al ., 1987 )以及BWB的修正模型(BBL模型)(
Leuning, 1990 ,
1995 ).Jarvis模型是一个连乘型的经验模型, 被认为仅仅是数学上的拟合, 且拟合程度不高(
高冠龙等, 2020 ), 同时具有较大的不确定性(
王建林和温学发, 2010 ).BWB模型则是在实验数据的基础构建的半机理模型, 给出了气孔导度与净光合速率、相对湿度以及叶表面CO
2 浓度之间的关系(
Ball et al ., 1987 ).然而,
高冠龙等(2020) 用3个模型(Jarvis模型、BWB模型和BBL模型)拟合2015和2016年柽柳(
Tamarix ramosissima )叶片的气孔导度时发现, 拟合曲线与观测点之间差异较大, 如用BBL模型拟合其响应曲线则给出的确定系数仅有0.603和0.400.此外, 由该模型的数学表达式可知, 该模型无法直接拟合气孔导度对光的响应曲线(
g s -
I ).要获得植物叶片的
g s-max 以及与
g s-max 相对应的饱和光强就必须把模型耦合到其他光响应模型.
Ye和Yu (2008) 把该模型耦合到由
Ye (2007) 构建的光合作用对光响应新模型后可较好地拟合冬小麦的
g s -
I 曲线, 且可以得到冬小麦的
g s-max 、饱和光强与其对应的观测值非常接近.
钟楚和朱勇(2013) 以及
王海珍等(2015) 利用该耦合模型分别拟合了烟草(
Nicotiana tabacum )和灰胡杨(
Populus pruinosa )叶片的
g s -
I 曲线, 也得到类似的结果.
叶子飘(2010) 构建的植物叶片
A n 对CO
2 的响应模型, 可较好地拟合大豆和小麦的
A n -
C a 曲线, 拟合得到的主要光合参数与其对应的观测值高度一致(
表1 ).鉴于此, 为了构建
g s -
C a 模型, 本文借鉴了
Farquhar等(1980) 的生化模型中的思路, 在
叶子飘(2010) 构建的光合作用对CO
2 响应模型基础上构建了植物叶片的气孔导度对CO
2 浓度的响应模型. ...
 ,2,3,4,*
,2,3,4,* ,2,3,4,*
,2,3,4,*

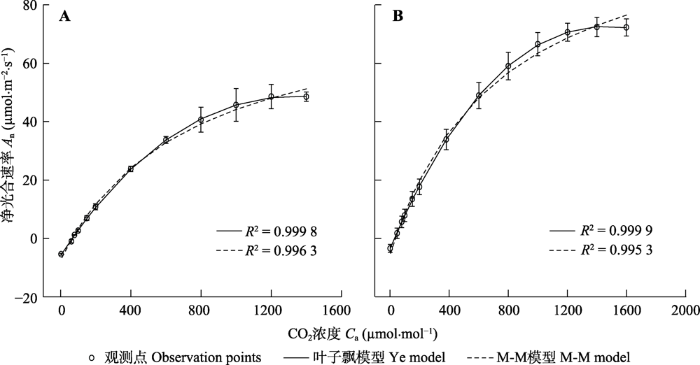 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT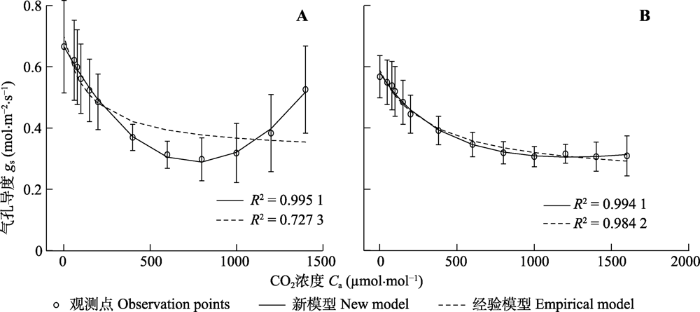 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT


