HTML
--> --> -->Comparing these various precipitation retrieval algorithms, in general, there are three common major features that a conventional precipitation retrieval algorithm should follow. First, the algorithm retrieves precipitation intensity using the contrast of brightness temperature (TB) from hydrometeors and the radiatively cool ocean. Secondly, the algorithm is associated with statistical approaches. For example, a study by Ferraro and Marks (1995) proposed both linear and nonlinear regression methods to retrieve instantaneous rain rates from SSMI observations. Sanò et al. (2015) proposed an algorithm based on neural networks for precipitation rate estimation from AMSU/MHS observations. Lastly, the algorithm requires historical precipitation datasets from measurements of spaceborne radars, ground radar networks or cloud-resolving model output. Widely used spaceborne radars include the Tropical Rainfall Measuring Mission’s (TRMM) Precipitation Radar (PR) (Surussavadee and Staelin, 2010; Kummerow et al., 2015), the Global Precipitation Measurement’s (GPM) Dual-Frequency Radar (DPR) and CloudSat profiling radar (Kidd et al., 2016).
The two principal physical mechanisms that permit the measurement of rain with microwave radiometers are emission and scattering. Precipitation retrievals derived from channels under 89 GHz are emission-based, where liquid precipitation causes TB to increase over a radiometrically cold background. Because channels above 89 GHz can hardly “see” through the atmosphere to the surface when precipitation occurs, the precipitation algorithms are scattering-based, where precipitation, especially that above freezing level, causes brightness temperature to decrease over a radiometrically warm or cold background (Wilheit, 1986; Spencer et al., 1989). While other temperature and humidity absorption bands between 89 and 190 GHz have been well-investigated based on satellite observations, the 118 GHz oxygen absorption line has not been in full use because none of these spaceborne instruments employs the 118 GHz channels. To augment existing retrieval algorithms, this study proposes to use TB depression caused by scattering associated with precipitation-sized ice particles to retrieve indirectly related surface rainfall information. The channels used in this study are between 89 and 190 GHz, of which some are near the 118 GHz oxygen absorption line.
The China Meteorological Administration’s (CMA) Fengyun-3C (FY-3C) MicroWave Humidity Sounder-2 (MWHS-2) is characterized by 15 microwave channels ranging in frequency from 89 to 190 GHz. In addition to carrying more traditional channels around 89, 150 and 183 GHz, the MWHS-2 carries eight temperature sounding channels near 118 Gz (Dong et al., 2009; Zhang et al., 2012). It is the first space-borne instrument carrying the 118 GHz channels, and expected to provide new information for not only temperature sounding but also for precipitation retrievals (Bauer and Mugnai, 2003; He and Chen, 2019).
This study builds upon the work from Chen and Bennartz (2020) that investigated the sensitivities of TBs at channels between 89 and 190 GHz to ice scattering caused by precipitation-sized ice particles using MWHS-2 observations. Based on the findings from this work, we will continue using the MWHS-2 observations and focus on the channels that were discovered to show sensitivities to ice scattering in varying degrees for rainfall retrieval algorithm development. This study will provide new perspectives for other instruments that have frequency coverage at 118 and 183 GHz, such as NASA’s Time-Resolved Observations of Precipitation structure and storm Intensity with a Constellation of Smallsats (TROPICS) and EUMETSAT’s Microwave Imager (MWI) (Holmlund et al., 2017; Blackwell et al., 2018; Mattioli et al., 2019).
The remainder of this paper is structured as follows. The instruments and dataset used, as well as the method of preprocessing the data, are described in section 2. In section 3 we present the bias correction process for the MWHS-2 observations, and the responses of TB and scattering-induced TB depression to rainfall. Next, we describe three precipitation retrieval algorithms and evaluate the rain rates produced by each algorithm by comparing them against other well-established rainfall products in section 4. Finally, the conclusions are presented in section 5.
| Channel number | Frequency (GHz) | Polarization at nadir used in RTTOV |
| 1 | 89 | H |
| 2 | 118.75 ± 0.08 | V |
| 3 | 118.75 ± 0.2 | V |
| 4 | 118.75 ± 0.3 | V |
| 5 | 118.75 ± 0.8 | V |
| 6 | 118.75 ± 1.1 | V |
| 7 | 118.75 ± 2.5 | V |
| 8 | 118.75 ± 3.0 | V |
| 9 | 118.75 ± 5.0 | V |
| 10 | 150 | H |
| 11 | 183.31 ± 1.0 | V |
| 12 | 183.31 ± 1.8 | V |
| 13 | 183.31 ± 3.0 | V |
| 14 | 183.31 ± 4.5 | V |
| 15 | 183.31 ± 7.0 | V |
Table1. MWHS-2 channel frequencies and polarization at nadir used in RTTOV
The GPM core spacecraft hosts two instruments: the DPR and the GPM Microwave Imager (GMI) (Hou et al., 2014). The GPM operates in a circular orbit at an altitude of 407 km and inclination of 65°. This orbit was chosen because it can ensure sufficient overlap with sun-synchronous satellites, such as FY-3C, for cross-calibration and covering a large portion of Earth’s surface with minimal repetition of ground track. It also allows for the gathering of samples at latitudes where most precipitation occurs in terms of absolute amount at various times of the day. The DPR instrument combines a Ku- and Ka-band precipitation radar capable of making accurate rainfall measurements from the ground to 19 km in altitude. The surface rain rates retrieved from the DPR were collocated with the MWHS-2 observations to produce matchups for investigating the implicit relationships in between at various channels including the newly added 118 GHz channels. The DPR rainfall retrieval was obtained from the GPM 2BCMB product provided by the NASA Precipitation Processing System archived at the NASA GES DISC (
MWHS-2 observations and DPR profiles were projected into each 0.25° latitude × 0.25° longitude grid with their maximum time difference being 15 minutes. This process was applied to oceans only due to the more complicated simulation of the surface emissivity over land. To eliminate the impact of the high zenith angles and the low spatial resolution of MWHS-2 at the outer edge of each scan, the ten outermost scan positions (five on each side) were excluded from the collocated dataset. Eventually, a total of over 1.5 million samples were achieved for the year of 2017.
To validate the developed rainfall retrieval algorithms, two different precipitation products were used as benchmarks. The first consists of rain rates in the aforementioned GPM 2BCMB product. The other source of rain rate data is the Global Precipitation Climatology Project (GPCP) formed by the World Climate Research Program in 1986 (WCRP 1986) to exploit the capabilities of satellite-borne instruments along with gauges for producing monthly and finer temporal resolution global precipitation in the long term (Adler et al., 2003). It has three products on different scales: 2.5° × 2.5°, 1° × 1°, and pentad (5 days). In this study, the GPCP monthly global precipitation data on 2.5° × 2.5° scales for the year 2016 were used. The GPCP data were provided by NOAA/OAR/ESRL PSL, Boulder, Colorado, USA, from their website at https://psl.noaa.gov/.
3.1. Bias correction and radiative transfer simulation
It is important to ensure that the MWHS-2 TBs are bias-free before we use them for further analysis. Chen and Bennartz (2020) proposed a bias-correction method based on the idea that the mode of the histogram of the TB differences corresponds to the observations affected by precipitation at a minimum level, and therefore this mode can be regarded as an estimate of the bias. We applied this method by first calculating the differences between observed and simulated TBs for each MWHS-2 channel. We then calculated the mode of the histograms of TB differences per channel and per scan position. The resulting bias-correction values were subtracted from observations to produce bias-free observed TBs.The TIROS Operational Vertical Sounder Radiative Transfer (RTTOV, Version 12.2) Model (Saunders et al., 2007; Saunders et al., 2018; Hocking et al., 2019) was used to simulate clear-sky background TBs for all the 15 channels of MWHS-2. The ERA-Interim data from the European Centre for Medium-Range Weather Forecasts (ECMWF) provided the 6-hourly surface and vertically resolved moisture and temperature field products (Dee et al., 2011). This dataset was obtained from the National Center for Atmospheric Research (downloaded from
2
3.2. Brightness temperature response to rainfall
We define the scattering-induced brightness temperature depression (ΔTB) as the difference between bias-corrected microwave observations, TBobs, and simulated clear-sky background brightness temperatures, TBsim:Chen and Bennartz (2020) investigated the relation between ΔTB of the individual MWHS-2 channels to the presence of hydrometeors and concluded that the oxygen and water vapor sounding channels exhibit a strong dependency on how close each channel is to the center of its corresponding absorption line. It was also found that the actual scattering intensity of ice particles monotonically increases with frequency. Based on these findings, we first examine the relation between the hydrometeor water path and the surface rain rate. Figure 1 shows a strong linear relationship between the two, which indicates that the surface rain rate is highly associated with the quantity of hydrometeors in a vertical column. This reinforces the implicit yet virtual relationship between the surface rain rates and scattering-induced ΔTB, which forms the basis of the subsequent rainfall retrieval algorithm development.
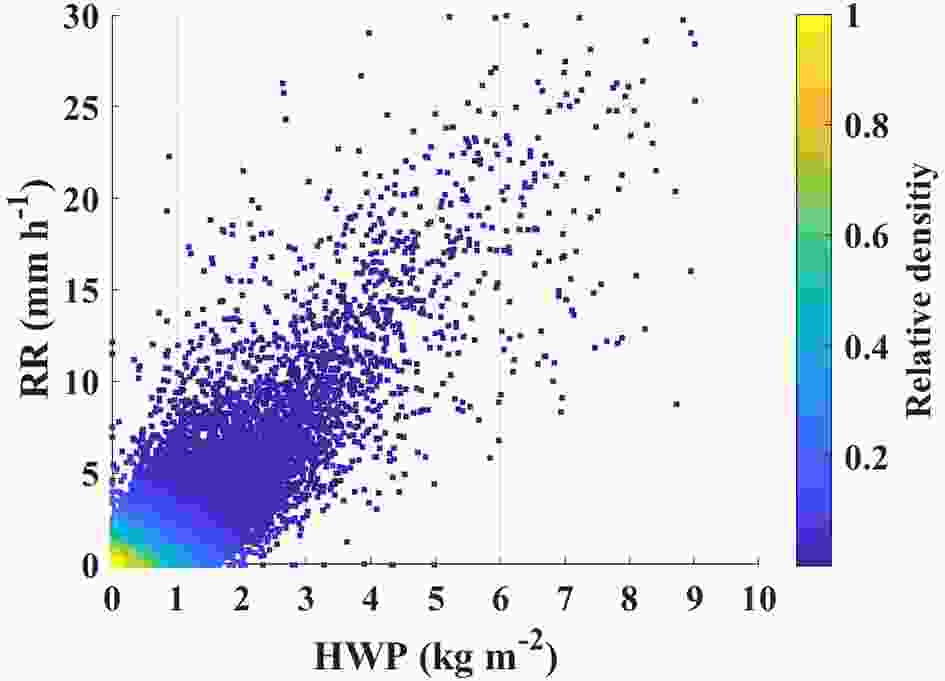Figure1. Linear relationship between hydrometeor water path (HWP) and surface rain rate (RR).Next, we explore the pattern of rain rates derived from the DPR in terms of variations in ΔTB and TBobs. Figure 2 presents the two-dimensional rainfall distribution relative to the TBobs and ΔTB for all 15 MWHS-2 channels. The highest-peaking channels 2–4 only exhibit slight deviations of ΔTB from zero. Because of their insensitivity to ice particle scattering, channels 2–4 will be excluded in subsequent analysis. Channel 5 presents the weakest sensitivity among the rest channels (channels 1, 5–15) and therefore this channel is non-essential for deriving the rainfall retrieval algorithms. In this study, we will include channel 5 in only one of the three algorithms that will be described in section 4.
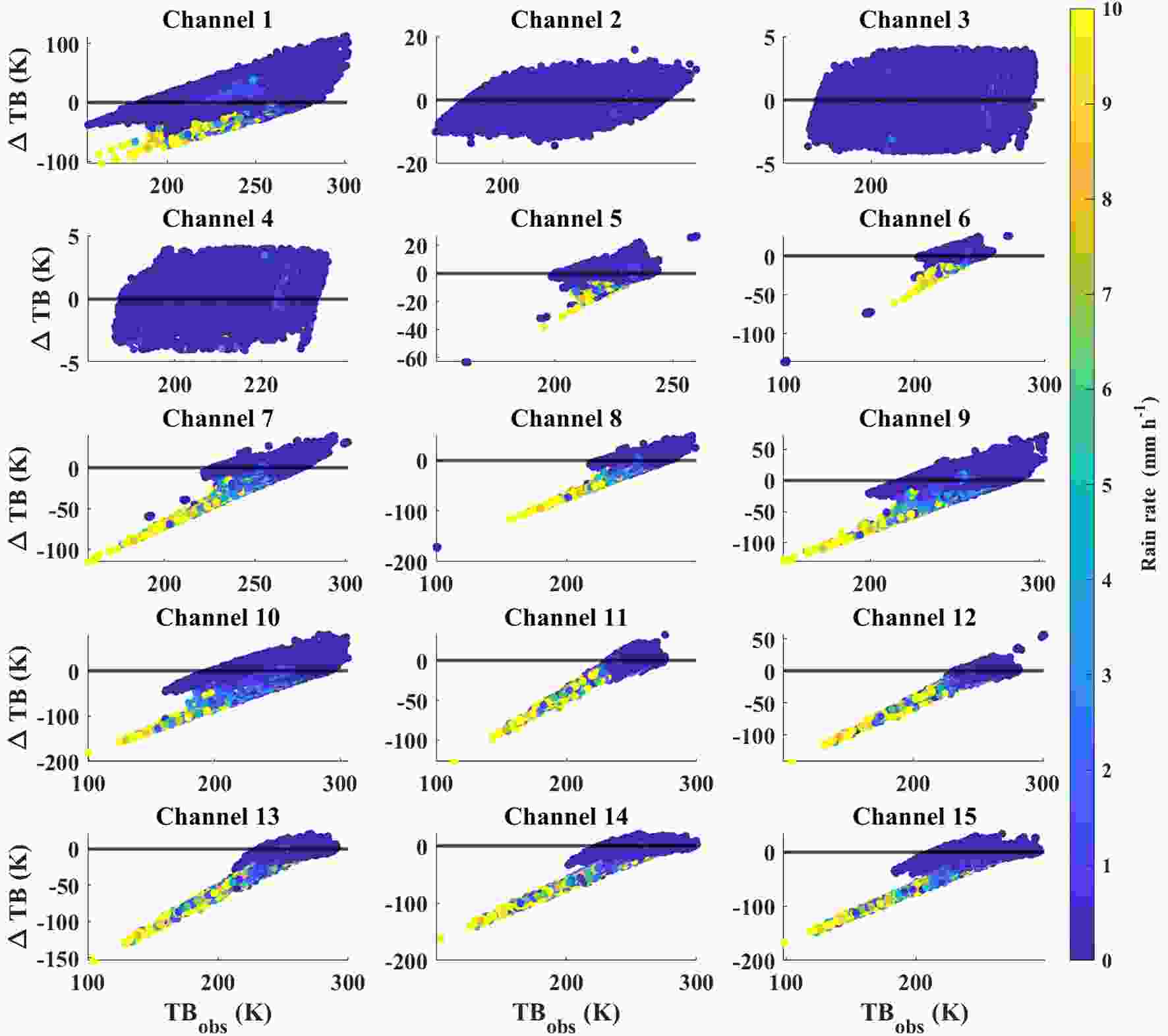Figure2. Two-dimensional rain rate distributions of TBobs and ΔTB for all 15 channels of MWHS-2 and for all collocated data. Note the different scales of both the x- and y-axis.For all the 12 channels, heavier rainfall occurs at colder TBobs and larger negative ΔTBs, while warm TBobs and near-zero ΔTB are mostly accompanied by near-zero rain rates. The latter highlights that a perfect radiative transfer model with a perfect clear-sky input would produce near-zero values in ΔTB for all cloud-free conditions regardless of how warm the TBobs is. Also noticeable is that, in several channels, including channels 7–10 and 14–15, the rainfall distribution shows a bifurcation between those data following the horizontal zero line and those for which ΔTB decreases approximately linearly with decreasing TBobs. Among the two groups of data, given the same TBobs the latter occurs with larger negative ΔTB and heavier rainfall, and the former is mostly with much smaller negative (or near zero) ΔTB and very light (or near-zero) rainfall. In other words, scattering reduces the amount of radiation and results in large negative ΔTB, which provides more substantial information than the TBobs regarding the measurement of rainfall.
The large positive ΔTB in each of channels 1 and 7–10 represents an emission signal caused by liquid clouds and rain to different extents, with the largest of over 100 K in channel 1. For cases of little or no ice as scatterers in the atmosphere, this will allow us to still be able to retrieve rainfall using these channels based on their emission signals.
4.1. Multilinear regression
34.1.1. Algorithm description
Based on the above analysis, we develop four different multilinear regression (MLR) models for each of the 44 scan positions using different sets of channels of MWHS-2. ΔTBs of different combinations of channels and rain rates are considered as independent and response variables, respectively, to model their relationships. Because dry snow can scatter significantly like the precipitation ice particles, the signal can be misinterpreted as rainfall. To avoid this issue, the retrieval methods in this study are limited to the tropics and midlatitudes between 35°N and 35°S. The channel sets of the four models are: (1) channels 1, 6–15; (2) channels 1, 10–15; (3) channels 1 and 10; (4) channel 1 only. Therefore, for each set of channels, we have built 44 different MLR sub-models for 88 symmetrical scan beams of MWHS-2 (five scan beams on each side are removed for the purpose of quality control). The regression performances in terms of the correlation coefficient (R), mean absolute error (MAE) and root-mean-square error (RMSE) for each of the models are presented in Table 2. Model 1 performs better than the other models in terms of R and RMSE. The MAEs of Models 1, 3 and 4 are the same and slightly lower than that of Model 2. The better performance of Model 1 indicates that the addition of the lower peaking channels near 118 GHz, channels 6–9, is necessary to improve rainfall retrieval.| Model | R | MAE (mm h?1) | RMSE (mm h?1) | MWHS-2 channels | Channel selection |
| 1 | 0.64 | 0.23 | 0.69 | 1, 6–15 | 89 GHz and 150 GHz window channels and 118 GHz and 183 GHz sounding channels |
| 2 | 0.61 | 0.22 | 0.71 | 1, 10–15 | Excluding 118 GHz sounding channels |
| 3 | 0.59 | 0.23 | 0.73 | 1 and 10 | Only 89 GHz and 150 GHz |
| 4 | 0.57 | 0.23 | 0.74 | 10 | Only 150 GHz |
Table2. Performance metrics summary of RR regression models. Reported are the correlation coefficient (R), the mean absolute error (MAE) and the root-mean-square error (RMSE) for all four retrieval models. All regressions were performed on the precipitation-induced brightness temperature depressions ΔTBs. Coefficients for each model were derived individually for each scan position.
3
4.1.2. Algorithm evaluation
We further apply the regression coefficients derived from Model 1 in the above analysis to another full year (2016) of MWHS-2 observations over oceans between 35°N and 35°S. The resulting rain rates are compared with the DPR-derived rain rates as well as with the GPCP gridded rain rates. All comparisons are performed on an annual-averaged 2.5° × 2.5° grid that is also used by the GPCP. We note that comparisons between DPR- and MWHS-2-derived annual means are not entirely independent as DPR values are also chosen for training the MWHS-2 regression retrievals, although a different year was used for the collocated dataset that underlies the training.Figure 3 shows scatterplots of annual mean surface rain rates for all four MWHS-2 retrievals against the DPR and GPCP, respectively. The following conclusions can be drawn from these scatterplots:
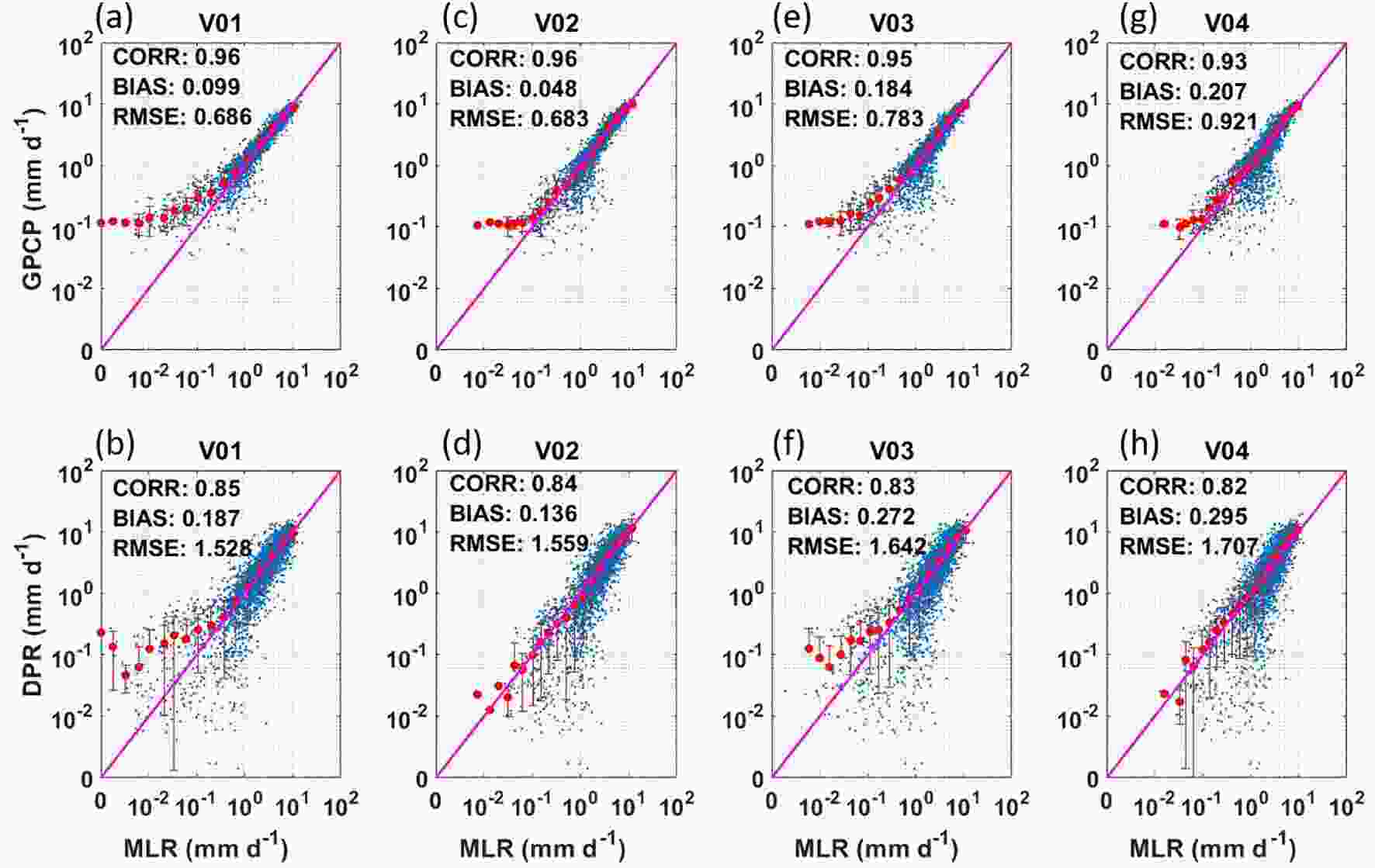Figure3. Scatterplots of annual mean 2.5° × 2.5° gridded rain from GPCP [y-axis of (a, c, e, g)] and DPR [y-axis of (b, d, f, h)] compared against the four different retrievals from MWHS-2 over oceans between 35°N and 35°S.(1) The scatterplots provided in Fig. 3 show generally strong correlations (R > 0.82 in all cases) between the DPR-derived annual mean rain rates and all four retrieval versions of MWHS-2. A degradation can be observed, however, both in terms of RMSE and in terms of the linear relation between the two quantities (see red lines in Fig. 3). Going from V01 to V04, the regression uses fewer channels (Table 2), and the relation between MWHS-2-derived retrievals and DPR-derived retrievals deviates more strongly from the 1:1 line. It thus appears that all four bands (89, 118, 150, and 183 GHz) provide independent information that contributes to improved rain rate retrievals.
(2) When comparing MWHS-2 to GPCP, one can see that the scatter between the two different datasets is significantly smaller than the scatter between DPR and MWHS-2 partly because the data density for DPR is lower (only 25 independent beams per scan, as opposed to 88 for MWHS-2). This increased noise in DPR gridded estimates will also be observed in the following analysis.
(3) The correlation between the GPCP and MWHS-2 exceeds 0.93 for all four versions of the retrievals. Similar to the comparison between DPR and MWHS-2, the inclusion of more bands (V01) illustrates a greater sensitivity than the MWHS-2 retrievals with fewer bands (e.g., V04).
In particular, the MWHS-2 V01 retrievals compare well against the GPCP, with the regression curve (red line) falling nearly on the 1:1 line and a correlation of 0.96, whereas a slight underestimation occurs at light rainfall (< 0.3 mm d?1).
A comparison of the spatial distribution of the annual mean surface rain rates between MWHS2, GPCP and DPR (Fig. 4) yields the following key points:
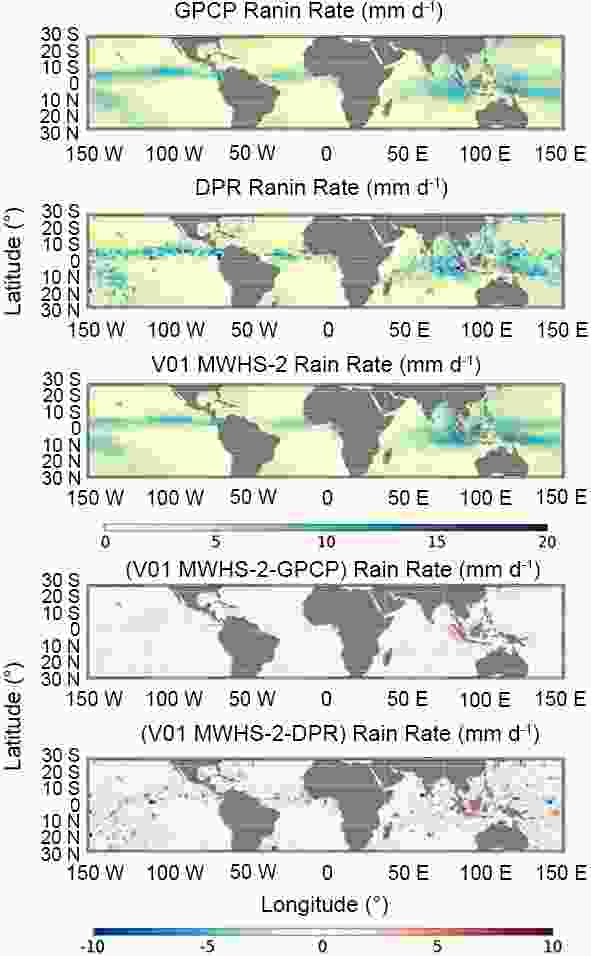Figure4. Comparison of monthly mean surface rain rates between MWHS-2 (V01 regression only), DPR and GPCP. The upper three plots show the annual mean surface rain rates. The lower two plots show MWHS-2 minus GPCP and DPR, respecively.(1) The spatial distribution of both MWHS-2 and GPCP reflects well the major areas of deep convection in the tropics. Differences between DPR and MWHS-2 appear to show an overestimation by MWHS-2 near Indonesia and an underestimation in areas such as the central Pacific ITCZ. Interestingly, this behavior differs from that observed in the ice water path derived from MWHS-2 observations (for brevity, not shown here), indicating that the relation between the ice water path and surface rain rates itself differs in these two areas. This result could conceivably be caused by higher aerosol loading near Indonesia, which would, compared to cleaner air, lead to reduced surface rain rates for given hydrometeor water paths. Such a mechanism over Indonesia was first described by Rosenfeld (1999). The DPR-derived rain rates are noisier than the MWHS-2 derived rain rates, which supports the above explanation that the lower DPR data density is at least partly responsible for the increased scatter.
(2) Comparing GPCP and MWHS-2, the scatter is generally lower, with a similar overestimation over Indonesia and a few other coastal regions. The central Pacific ITCZ also shows slight underestimation that is evident in the comparisons with the DPR.
The comparison illustrated here suggests that the high-frequency microwave channels between 89 GHz and 183 GHz can successfully be used to derive rain rates. These channels can also be used for precipitation retrieval with the caveat that the retrieval relies on the indirect scattering signature of ice particles higher up in the atmosphere that are not directly linked to surface precipitation. Thus, if the relation between the ice water path and surface rain rates itself changes, the surface rain rate retrievals will be adversely affected, as shown above in the case of Indonesia. In addition, the algorithm used to perform the regression based on scan positions has the advantage of eliminating the concern that different footprints of a cross-track radiometer have different local zenith angles.
Based on the above analysis, channels 1 and 6–15 are selected for our study going forward (channel 5 will be carried for some cases, but its impact is negligible because of its high peaking weighting function).
2
4.2. Range searches and nearest neighbor searches
34.2.1. Description of algorithms
A K-Dimensional tree (or k-d tree, where k is the dimensionality of the search space) is a hierarchal structure built by partitioning the data recursively along the dimension of maximum variance. At each iteration, the variance of each column is computed and the data is split into two parts on the column with maximum variance. It is a very useful structure, especially for searches involving a multi-dimensional search key, e.g., range searches and nearest neighbor searches (Bentley, 1980). As a simple example, assume that k = 2 and one needs to build a 2D tree which is also regarded as a generalization of a binary search tree. The idea is to build a binary search tree with points in the nodes using the x- and y-coordinates of the points as keys in strictly alternating sequence. Stating with the x-coordinate at the root, if the point to be inserted has a smaller x-coordinate than the point at the root, it goes left; otherwise it goes right. At the next level, the insertion is switched to the other coordinate (y-coordinate). If the point to be inserted has a smaller y-coordinate than the point in the node, it goes left, otherwise it goes right. The coordinate is then switched again and so on and so forth, until the insertion of the last point.For the purpose of rainfall retrieval, we use 12 channels (channels 1 and 5–15) of MWHS-2 observations and radiative transfer simulations as well as matched rain rates derived directly from the DPR to build a 12-dimensional tree. We first divide the ~1.5 million collocated data for the full year of 2017 into two sub-datasets: 70% for training and 30% for testing. Each sub-dataset included the ΔTBs of channels 1 and 5–15 from MWHS-2 observations and radiative transfer simulations. To address the slant path impact on the MWHS-2 observations, we further stratify the training dataset into four subsets uniformly based on the relative airmass [1 / cos(θ)] that is calculated from the zenith angle (θ) of MWHS-2. Considering the training subset i (i = 1, 2, 3 or 4) has ni points, the k-d tree algorithm partitions this ni-by-12 dataset by recursively splitting the ni points in 12-dimensional space into a binary tree known as a model object, which is a convenient way of storing information of the grown tree. Four individual k-d trees (model objects) are then created and passed to the subsequent process of searching neighbors.
Next, two different search mechanisms are adopted to estimate the rain rates from MWHS-2 observations based on the four k-d trees built earlier:
(1) Range searches (RS): Given a range (hypersphere radius) of r Kelvin and a point in the query data (testing data), we search for all points in the model object that are within a Euclidean distance r Kelvin from that query point and consider them as neighbors. The indices of these neighboring points are then used to map the corresponding DPR rain rates in the training data. This will allow us to obtain a set of neighboring rain rate estimates for each query point. The average value over this neighboring set represents the estimated k-d rain rate, henceforth called the RS rain rate. Excluding the zero rain rates, the rest of the neighboring rain rates, which are precipitation cases, are averaged to represent the conditional rain rate. An advantage of this method is that the percentage of non-zero rain rates over this neighboring set provides an estimation of the probability of precipitation.
(2) Nearest neighbor searches (NNS): Given a point in the query data, we find the point in the k-d tree that is nearest to that query point in terms of the Euclidean distance. The index of the nearest neighbor then enables the mapping of the corresponding DPR rain rate in the training data. This mapping then yields the nearest neighboring rain rate, which serves as another way of representing the estimated k-d rain rate of that query point, henceforth called the KD NN rain rate. Compared to RS, NNS can be done efficiently by using the tree’s properties to quickly eliminate large portions of the search space, especially in a study such as the present one that deals with high dimensional data (12 dimensions).
For both the RS and NNS method, we use the zenith angles in the testing data to determine which k-d tree out of the four should be used for searching neighbors. For RS, we set the radius to be proportional to the MWHS-2 noise equivalent temperature (NEΔT), as the following equation shows:
The NEΔT of MWH-2 is initially set to be 1 K and k is the dimension of the query dataset (here, 12). For points found to be without neighbors within the initial radius, we extend the search to a larger hypersphere by continuously increasing the NEΔT with increments of 1 K until the maximum value of 5 K was reached. As such, more than 98% of the points are found with at least one neighbor. The NNS is concluded once the first neighbor is found with the search range within up to 5 K.
The statistics of the RS rain rates compared to the DPR rain rates for testing data per scan position are shown in Fig. 5. These statistics include the mean bias, standard deviation of the bias, and MAE. Despite different slant paths at various scan positions, the rain rate estimates are very stable across the same scanline. The largest deviation from the DPR rain rates is about 0.04 mm h?1 and the largest MAE is less than 0.1 mm h?1.
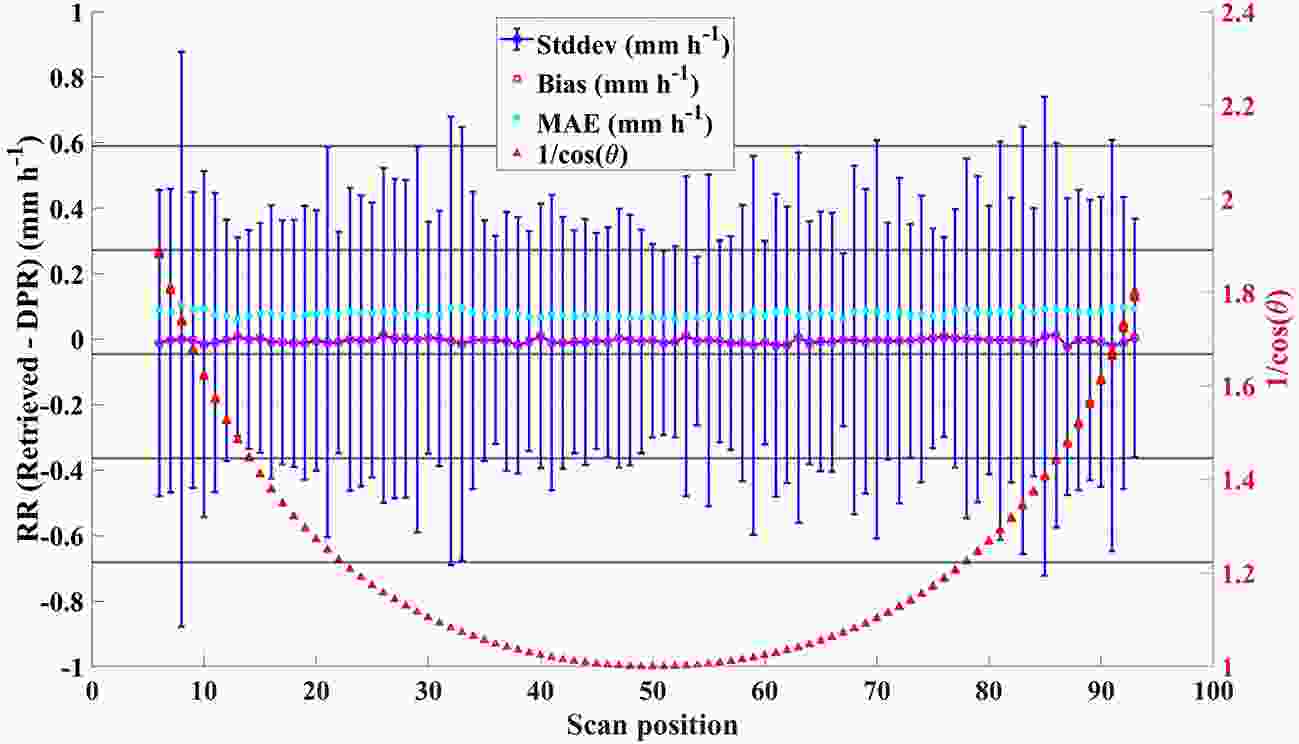Figure5. Statistics of retrieved rain rates compared to DPR rain rates, for testing data from MWHS-2 by searching neighbors within a fixed hypersphere radius per scan position. The statistics include bias (magenta dots), mean absolute error (MAE, mint-green dots) and standard deviation of the bias (blue line). The brick-red dots are for relative airmass, which is used to stratify the training data when creating the four k-d trees and to determine which k-d tree is used in neighbor-searching for testing data.3
4.2.2. Evaluation of algorithms
Like the procedure for validating the MLR method, we apply the created k-d trees to the MWHS-2 observations for the year 2016 to retrieve the rain rates based on either RS or NNS. An example of the rain rate retrievals with the unit of mm h?1 using the RS method for the day of 15 July 2016 is shown in Fig. 6a. The corresponding probability of precipitation is also shown, in Fig. 6b, in which the tropical regions with deep convection generally have a higher chance of precipitation. RS rain rates and probabilities of precipitation, as well as their bin-averaged values, are projected on a double logarithmic scale in Fig. 6c. Note that the probability of precipitation cannot be averaged and therefore we take the mode of the probabilities within each bin to represent the probability of precipitation of a given bin. The probability of precipitation derived from RS is correlated well with the rain rate retrieval. This precipitation probability provides us with an uncertainty estimate associated with each measurement and it allows us to evaluate whether or not the observed scene is raining at all. Classical retrieval algorithms only provide rain rates.
Figure6. Spatial distribution of (a) rain rate retrieval and (b) proability of precipitation, and (c) scatterplot of (a) versus (b) on double logarithmic scale (blut dota) with their bin average (x-axis, RS rain rate) or mode (y-axis, probability of precipitatin, red dots), from MWHS-2 observations on 15 July 2016.After applying the created k-d trees to the MWHS-2 observation, we then gridded RS rain rates and NNS rain rates to compare them with those from DPR and GPCP. Hereafter, the analysis is based on the annual mean gridded rain rates with the unit of mm d?1. Figures 7a and b show the scatterplots of annual RS rain rates against GPCP and DPR rain rates, respectively. The correlation coefficient between RS rain rates and GPCP rain rates is more than 0.96. It is worth noting that the scatter between the RS rain rates and GPCP rain rates is significantly smaller than the scatter between those from RS and DPR. This confirms the results observed in the MLR models. This again is mostly caused by the lower data density of DPR, which has only 25 independent beams per scan, as opposed to 88 for MWHS-2. The gridded rain rates are also stratified logarithmically based on RS rain rates. These averaged rain rates are also illustrated over the scatterplots in Fig. 7, in which the red dots and lines represent averages and standard deviations of rain rates of the y-axis. In other words, the average and standard deviation are of either GPCP rain rates or DPR rain rates. In both subplots, the yellow dots fall on the 1:1 lines with slight overestimation over the light precipitation range (< 0.4 mm d?1), which means that the RS rain rate retrievals are in exceptional agreement with the rain rates from GPCP and DPR. The results of NNS are substantially equivalent to those of RS shown by Fig. 7c, where the correlation coefficient is 1, and both the bias and RMSE are extremely low. This demonstrates that these constructed k-d trees tend to be robust to noise and invariant to the spatial heterogeneity of rainfall. Moreover, this allows for the selection of NNS over RS in scenarios requiring lower computation costs and disregarding the probability of precipitation.
Figure7. Scatterplots of annual mean 2.5° × 2.5° gridded rain rates from GPCP [y-axis, (a)] and DPR [y-axis, (b)] compared against rain rate retrievals by RS from MWHS-2 with units of mm d?1, on logarithmic scale. (c) Comparison of rain rate retrievals between RS and NNS. Red dots and red lines are averages and standard deviations of either GPCP rain rates or DPR rain rates by subsetting RS rain rates logarithmically.Because of the above analysis, we leave out the results of NNS and only show the spatial distributions of the rain rates from RS compared with those from GPCP and DPR in Fig. 8. Similar to that of MLR compared against GPCP and DPR, the spatial distributions of RS rain rates also reflect the major areas of deep convection in the tropics well. However, the overestimation near Indonesia is less than that using the MLR method. Comparing the RS rain rates and DPR-derived rain rates, the latter are noisier than the former, which further confirms the previous inference that the lower DPR data density is at least partly responsible for the less congruent retrievals.
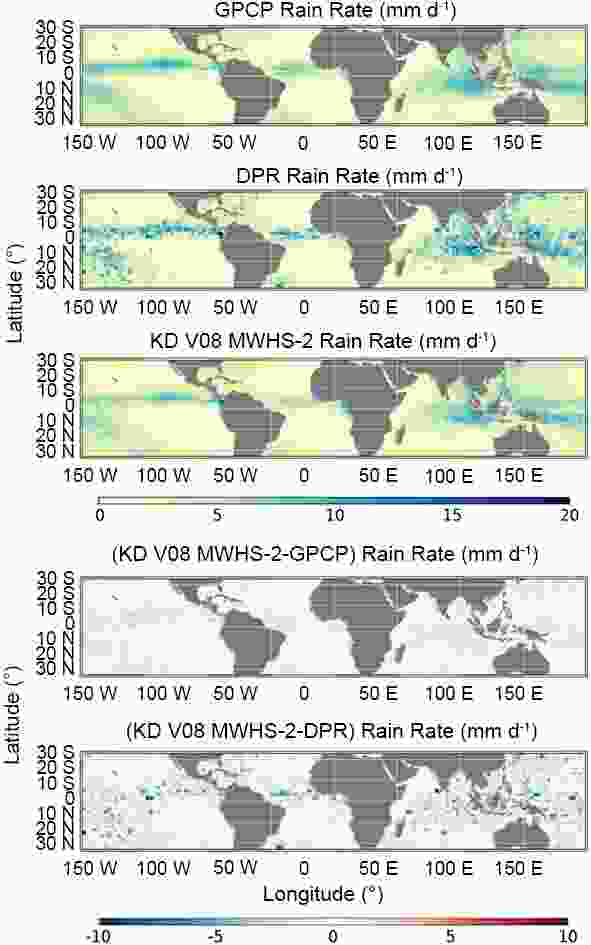Figure8. Spatial distirubtion of annual mean 2.5° × 2.5° gridded rain rates from MWHS-2 by RS compared against the rain rates from DPR and GPCP with units of mm d?1.All three algorithms generally show good agreement with the GPCP rain rates, with correlation coefficients of 0.96 and maximum averaged bias less than 5%. While the averaged bias of the MLR rain rates is slightly lower than that of RS or NNS, a slight underestimation exists in MLR at light rainfall (< 0.3 mm d?1). The results of RS and NNS based on k-d trees are in extremely high agreement in terms of the correlation coefficient, bias and RMSE, which makes them almost interchangeable. Yet, NNS can be carried out more efficiently than RS by using the tree properties to quickly eliminate large portions of the search space. In addition, RS is the only algorithm of the three that allows for the derivation of probability of precipitation, which is an important measure in weather forecasts.
Compared to the consistency between rain rates from the MWHS-2 observations and those from GPCP (R = 0.96 for all three algorithms), the comparisons with DPR produce slightly lower correlation coefficients of 0.84 (for MLR) and 0.85 (for RRS and NSS). Their biases increase by up to ~3%. The reason for this degraded correlation between monthly mean gridded FY-3C data and DPR likely lies in the relatively low data density of DPR, caused by its narrow swath. This causes the DPR statistics for each 2.5° × 2.5° box to be noisier simply because each box holds fewer individual measurements compared to either GPCP or our own gridded results from MWHS-2. This increased noise in DPR gridded estimates is readily apparent in the global maps shown in Fig. 8 (DPR being the second panel from the top).
These rainfall retrieval algorithms are developed based on scan positions of MWHS-2 observations, which helps eliminate the concern that different footprints of a cross-track radiometer have different local zenith angles. In addition, a unique feature of RS is that it provides probability of precipitation apart from the instantaneous rain rate estimates. The probability of precipitation provides us with an uncertainty estimate associated with each rain rate retrieval, which allows us to evaluate whether or not the observed scene is raining at all. Classical rainfall retrieval algorithms do not provide this property.
The results from the validation process suggest that the high-frequency microwave channels between 89 GHz and 190 GHz can successfully be used for measurement of rainfall. The developed algorithms can be used in conjunction to improve upon what could be accomplished with only one method alone. Moreover, this study serves as proof of concept for developing rain rate estimation algorithms using satellite observations from FY-3C/MWHS-2, which for the first time carries 118 GHz channels. This holds significance for other future sensors carrying these bands, such as NASA’s TROPICS mission and EUMETSAT’s MWI, both of which will contribute to near-global high temporal and spatial resolution microwave measurements at various high frequencies, including 118 and 183 GHz.
Acknowledgements. This work was supported by a NASA grant (Grant No. NNX17AJ09G) to Vanderbilt University. The authors thank the NASA Precipitation Processing System (PPS) for providing the GPM 2BCMB data and the China Meteorological Administration/National Satellite Meteorological Center (CMA/NSMC) for providing the MWHS-2 L1B data for this research. The authors further acknowledge and support the help of EUMETSAT and the UK Met Office for providing and maintaining RTTOV.
