HTML
--> --> -->Previous studies have focused on the development of PBL schemes and their impacts on the simulations of boundary layer structures under various atmospheric conditions (Shin and Hong, 2011; Efstathiou et al., 2013; Dong et al., 2019). Generally, there are two categories for the PBL schemes in the WRF model based on their turbulence closure assumptions. The first category is the nonlocal closure, such as the Yonsei University (YSU) (Hong et al., 2006) and the Asymmetric Convection Model 2 (ACM2) (Pleim, 2007, b) schemes. These conventional nonlocal closure PBL schemes determine the nonlocal SGS transport through a mass-flux term (Pleim, 2007a, b) or a gradient-adjustment gamma term (Hong et al., 2006) and adopt multiple vertical levels to simulate the effect of larger eddies in the convective boundary layers (Stensrud, 2007). They are typically characterized by overly vigorous vertical mixing and tend to simulate deep, dry and warm boundary layers (Coniglio et al., 2013; Burlingame et al., 2017). The second is local closure, such as the 1.5-order Bougeault?Lacarrere (Bougeault and Lacarrere, 1989), Mellor?Yamada?Janic (MYJ) (Janji?, 1994) and Mellor?Yamada Nakanishi Niino (MYNN) Level 2.5 and 3.0 (Mellor and Yamada, 1982; Nakanishi and Niino, 2006, 2009; Olson et al., 2019) schemes. These are generally turbulent kinetic energy (TKE) closure schemes and adopt only adjacent vertical levels to estimate the turbulent fluxes through a full range of atmospheric turbulent regimes. These local closure schemes, such as MYNN and MYJ, more likely simulate shallow, cool and moist boundary layers due to relatively weak vertical mixing (Burlingame et al., 2017). However, controversy still exists regarding their application under convectively unstable conditions. For instance, Shin and Hong (2011) concluded that nonlocal closure PBL schemes such as YSU and ACM2 are favorable in unstable conditions, while Burlingame et al. (2017) suggested that local closure PBL schemes such as MYJ and the Quasi-normal Scale Elimination (QNSE) scheme (Sukoriansky et al., 2005) show advantages over nonlocal closure schemes in detecting convection initiation.
Many studies have likewise demonstrated the model sensitivity to the choice of PBL scheme in the simulation of heavy precipitation related to tropical cyclones (Dong et al., 2019) and severe midlatitude convections (Shin and Hong, 2011; Efstathiou et al., 2013). For instance, Wang et al. (2013) reported that the YSU scheme predicted the intensity, track and associated precipitation more realistically for a weak typhoon [Muifa (2011)] than the MRF (Medium-Range Forecast) scheme. However, Liu et al. (2017) argued that the MYJ scheme generated a better simulation of the rapid intensification process of Hurricane Katrina (2005) offshore, before its landfall, than the YSU scheme. Dong et al. (2019) showed that the YSU and MYNN2.5 schemes outperformed the MYJ and QNSE schemes in reproducing the precipitation after the landfall of Typhoon Fitow (2013). For severe convection and heavy precipitation in the midlatitudes, Efstathiou et al. (2013) suggested that the YSU scheme produces enhanced vertical mixing and moisture transport, and more realistically simulates the strong convection and intense precipitation over the Chalkidiki peninsula in northern Greece. However, Srinivas et al. (2018) examined an extreme heavy rainfall event in December over India and found that, in the 1-km cloud-resolving grid, the MYNN2.5 scheme showed advantages over the YSU and MYJ schemes in simulating the strong convection and associated heavy rainfall. Therefore, large uncertainty still exists with respect to the effects of PBL schemes on heavy rainfall predictions. In particular, as the model resolution is increased to explicitly represent cumulus convection, the effects of PBL schemes become as important as those of the microphysics parameterizations (Braun and Tao, 2000; Li and Pu, 2008). Therefore, this study attempts to explore the sensitivity of PBL schemes in high-resolution WRF simulations based on an extreme rainfall event over Shanghai and its nearby area on 25 May 2018. This event involved the interaction of multi-scale systems from the synoptic circulation, mesoscale low-level jet (LLJ) and low-level shear line to local convective activities, which provides a great test bed for examining the boundary layer processes and their interaction with the large-scale environment and mesoscale convections.
The objectives of this study are twofold: (1) to investigate the different sensitivities of PBL schemes in extreme rainfall simulations over the mesoscale (15-, 9-km) and high-resolution (1-km) grids with different means of treating convection; and (2) to identify the model differences and explore the underlying mechanisms that affect the interaction of boundary layer processes with the large-scale forcings and convection development.
The rest of the paper is organized as follows: Section 2 briefly describes the extreme rainfall event in Shanghai. Section 3 describes the design of the WRF model experiments and their physics settings, as well as the three PBL parameterization schemes (YSU, MYJ, MYNN2.5) used in this study. Section 4 compares the spatiotemporal characteristics of heavy rainfall simulations using the different PBLs over varying grid spacings. Section 5 focuses on exploring the physical mechanisms for model differences using the three PBL schemes in the inner 1-km grid simulations. Section 6 summarizes our conclusions.
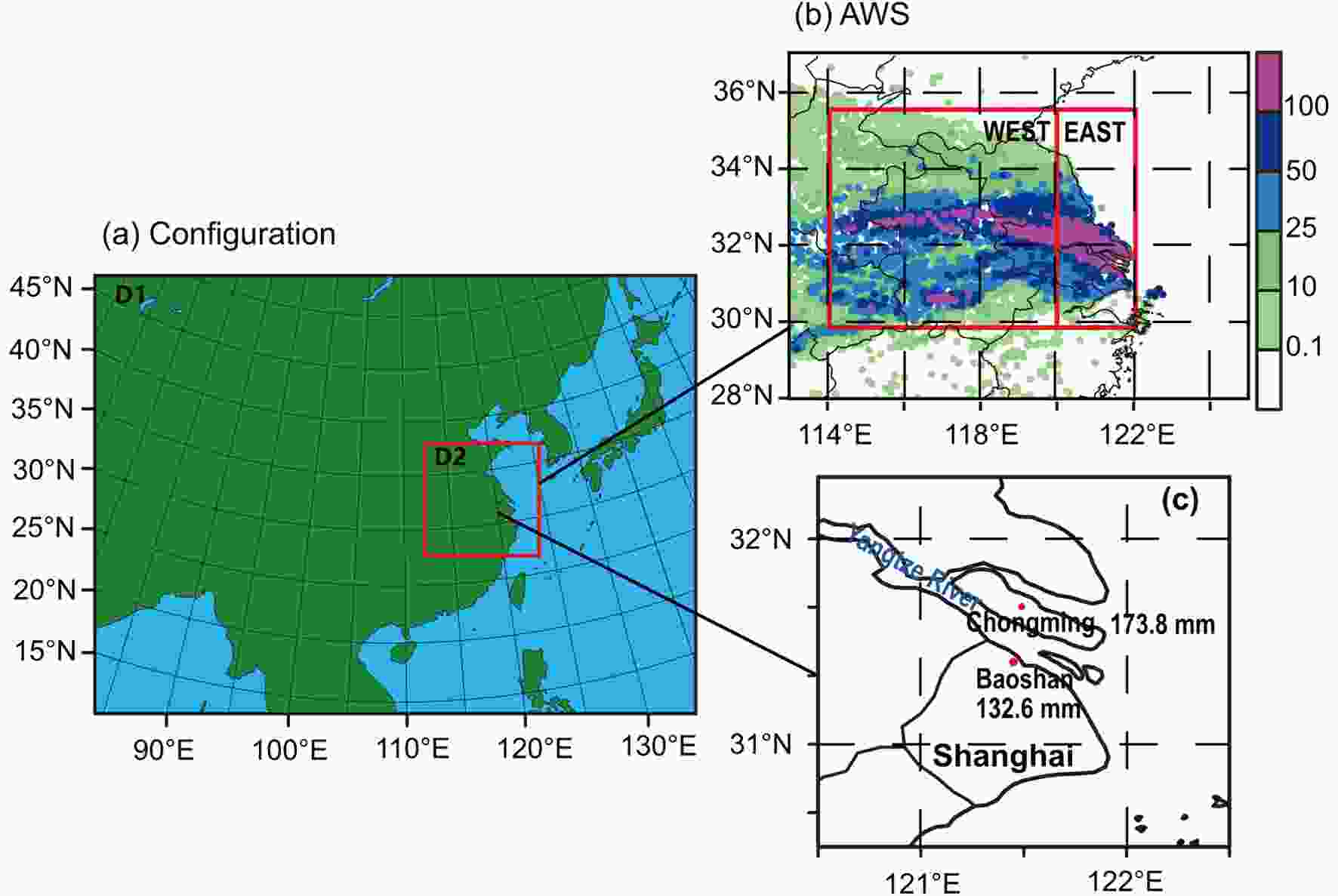Figure1. (a) WRF experiment domain configurations. (b) Geographic distribution of the observed 24-h accumulated rainfall amounts on 25 May 2018 from AWSs. (c) Location of Shanghai.To determine the dividing line, we fully examined the observed hourly variations of extreme rainfall over the stations within the core rainband. As shown in Fig. 2, the coastal stations east of 120°E basically had three rainfall peaks, whereas the stations in the western inland area had two peaks without the early-morning secondary one. The core rainband had three rainfall peaks, with the primary peak at 1200 LST and two secondary peaks at 0700 LST and 1800 LST, respectively. The primary and late-afternoon peaks were contributed by both the east and west parts, while the early-morning peak was primarily attributable to the east part. This implies that the extreme rainfall in these two subregions was caused by different precipitation systems or mechanisms, which will be further analyzed below.
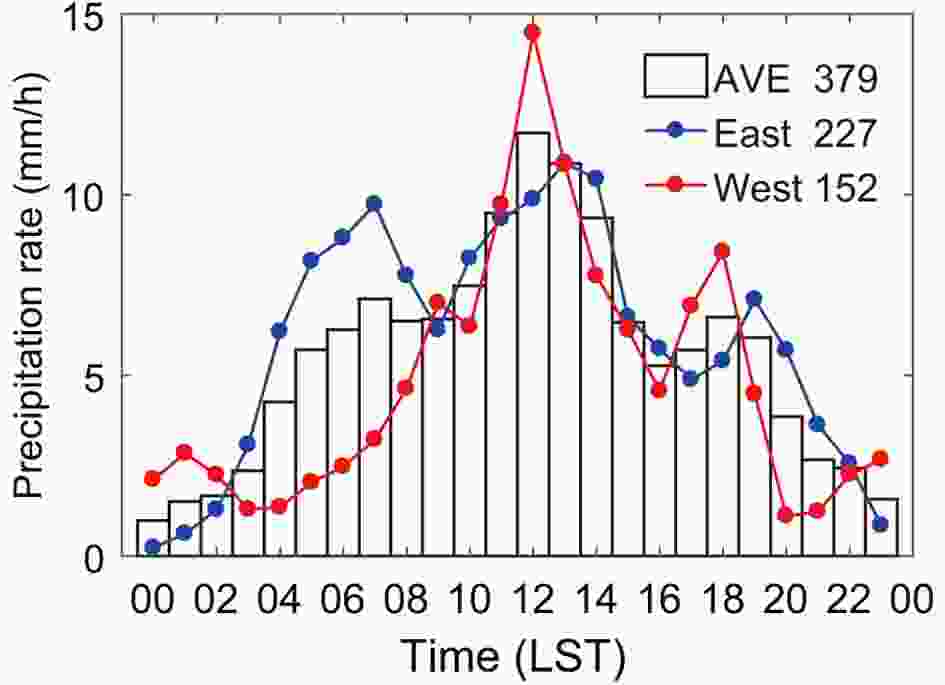Figure2. Hourly variation of AWS-observed precipitation on 25 May averaged over the core rainband (AVE 379) and averaged over the two typical regions in Fig. 1b: East region (East 227) and West region (West 152) (units: mm h?1).Figure 3 presents the evolution of three-hourly AWS accumulated rainfall and wind fields, moisture convergence, as well as geopotential heights at 850 hPa from the National Centers for Environmental Prediction (NCEP) Final (FNL) Operational Global Analysis data at 1° grids at 0800 LST, 1400 LST and 2000 LST 25 May, and 0200 LST 26 May. Hereafter, the LLJ is defined by wind speeds greater than 12 m s?1 at 850 hPa. At 0800 LST, the southwesterly LLJ was strong and transported a great amount of water vapor to the Anhui?Shanghai region, producing intense moisture convergence and a heavy rainfall center with the presence of a low-level warm shear line along the east coast region. A warm shear line is a discontinuous line between southerly and easterly winds with the cyclonic shear in the lower troposphere (Yan and Yao, 2019). This explains the early-morning rainfall peak in the east rainband. Thereafter, the LLJ gradually weakened due to its diurnal variation (Bonner and Paegle, 1970), but the moisture convergence and uplifting motion associated with the low-level warm shear lines were still conducive to the development of mesoscale convection in the east coastal region. At the same time, a shortwave trough at 500 hPa was propagating eastward (figure not shown), and the low-pressure vortex at 850 hPa ahead of the trough began to affect the west rainband. The strong convergence at the back of the low vortex intensified the uplifting motion and mesoscale convection, resulting in the primary rainfall peak at 1200 LST for the west rainband. At 1400 LST, the LLJ and associated low-level moisture convergence decreased, and then, up until 2000 LST, the nocturnal LLJ intensity began to increase but its northern terminus moved south, and the moisture convergence and rainfall at the back of low vortex were intensified. Therefore, the diurnal variation of the LLJ and associated moisture advection contributed more to the secondary peaks in the early morning (0700 LST) and late afternoon (1800 LST), and the strong uplifting motion caused by the low-level warm shear line (east rainband) and the convergence at the back of the low 850-hPa vortex (west rainband) made significant contributions to the development and maintenance of mesoscale convection and heavy precipitation at 1200 LST.
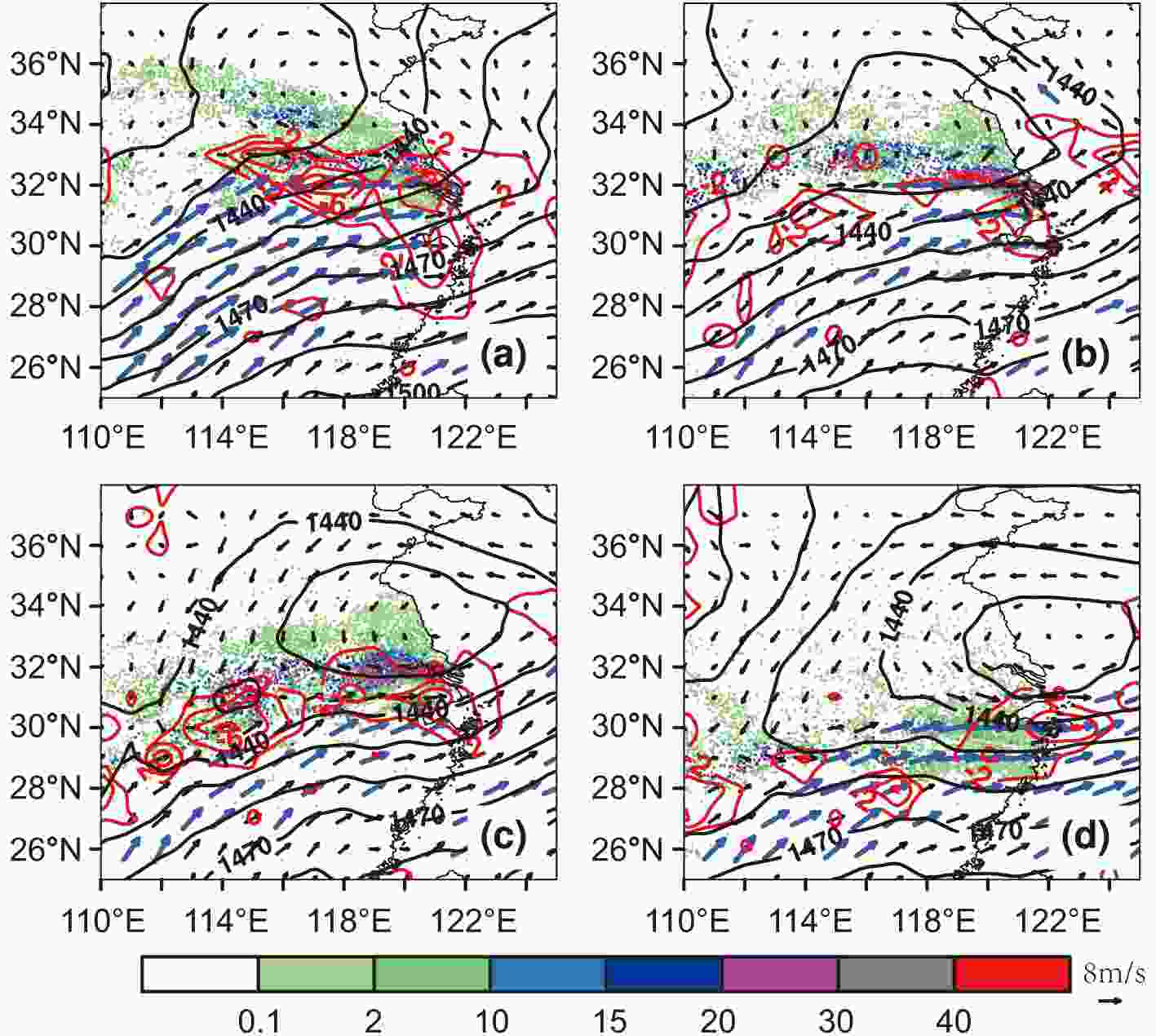Figure3. Geopotential height (black solid contours; units: gpm), wind field (black vectors), LLJ (wind speed 
Liang et al. (2019) put forward a pragmatic and effective approach in precipitation forecasting to avoid the challenge in representing convection across the gray zone. The convective gray zone refers to the model grid spacing around 1?10 km, where parameterized and resolved convective clouds could exist simultaneously. In the gray zone, many widely used cumulus parameterization assumptions become invalid and it is difficult to realistically represent the convection (Yano et al., 2010). Liang et al. (2019) found that double-nesting simulations using the WRF model with a large grid ratio (15:1 or 9:1) outperformed the traditional triple nesting with a middle (3- or 5-km) grid in forecasting the extreme rainfall of Jiangsu province. In particular, the outer grid using the KF scheme (Kain, 2004) to parameterize cumuli at 15 km with explicitly resolving convection at 1 km produced the best forecast of hourly rainfall variation. Therefore, we followed the same double-nesting experiments using the KF cumulus scheme in the outer coarse (15- and 9-km) grids and explicitly resolving convection at the inner 1-km grid. Our focus, however, is to examine the PBL effects on the prediction of extreme rainfall.
Three PBL schemes were used and the related diffusion equations and eddy diffusivity coefficient computations are listed in Table 1. These schemes are all based on the K-gradient transport theory, which determines the turbulent flux by multiplying the eddy moment or heat diffusivity coefficient with the vertical gradient of grid-mean variables. Their main differences are the closure assumptions used to define the eddy diffusivity coefficient and the non-local effect for the energy exchange between model layers. The YSU scheme is a first-order closure scheme that determines the K-profile in the mixed layer by introducing the PBL height [Eq. (3)] but depends on the mixing length and Richardson number above the entrainment zone [Eqs. (1) and (2)]. A counter gradient transport term [Eq. (7)] related to surface buoyancy flux is included for the nonlocal effect, especially for unstable boundary layers (Hong et al., 2006). As higher-order schemes, both MYNN (which hereafter refers to MYNN 2.5 in WRFv3.9.1.1) and MYJ (Janji?, 1994) are based on TKE closure to parameterize the eddy diffusivity but without considering the nonlocal effect in the unstable layer. They differ in the diagnostic equations for dimensionless stability function (S) and turbulent length scale (
| PBL parameterization schemes | |||
| YSU | MYNN | MYJ | |
| Reference(s) | Hong et al. (2006) | Mellor and Yamada (1982); Nakanishi and Niino (2004); Olson et al. (2019) | Janji?, 1994 |
| Eddy diffusivity coefficient | ${K}_{{\rm{m}},t\_\mathrm{l}\mathrm{o}\mathrm{c} }={l}^{2}{f}_{{\rm{m}},t}\left(\mathrm{R}\mathrm{i}\mathrm{g}\right)\left(\dfrac{\partial U}{\partial \mathrm{z} }\right)$ (1) $\mathrm{R}\mathrm{i}\mathrm{g}=\dfrac{\mathrm{g}\left[\theta-\theta_{\mathrm{s} }\right]\left(h-{Z}_{\mathrm{m}\mathrm{i}\mathrm{x} }\right)}{\theta {\left[U\left(h\right)-U\left({Z}_{\mathrm{m}\mathrm{i}\mathrm{x} }\right)\right]}^{2} }$ (2) ${K}_{{\rm{m}}}=k{w}_{s}z{\left(1-\dfrac{z}{h}\right)}^{P}$ (3) | ${K}_{{\rm{h,m}}}=lq{S}_{{\rm{h,m}}}$ (4) | $ K=Slq $ (5) |
| Diffusion equation | $ \dfrac{\partial C}{\partial t}=\dfrac{\partial }{\partial \mathrm{z}}\left[{K}_{c}\left(\dfrac{\partial C}{\partial z}-{\gamma }_{c}\right)-{\left(\overline{{w}'{c}'}\right)}_{h}{\left(\dfrac{z}{h}\right)}^{3}\right] $ (6) ${\gamma }_{c}= {b}\dfrac{ {\left(\overline{ {w}'{c}'}\right)}_{0} }{ {w}_{s}h}$ (7) | $ \dfrac{\left(\dfrac{{q}^{2}}{2}\right)}{\partial t}=\dfrac{\partial }{\partial z}\left[lqS\dfrac{\partial \left(\dfrac{{q}^{2}}{2}\right)}{\partial z}\right]+{P}_{\mathrm{s}}+{P}_{\mathrm{b}}+D $ (8) | |
| Description of variables | ${K}_{{\rm{m}},t\_\mathrm{l}\mathrm{o}\mathrm{c} }$ denotes the diffusivity coefficient used above the entrainment zone; ${K}_{{\rm{m}}}$ denotes the momentum eddy diffusivity in the mixed-layer; Kc denotes the eddy diffusivity; Z is the height from the surface and h is the height of the PBL; C denotes the prognostic variables for wind fields (u, v, w), water vapor (q) and potential temperature ($ \theta $); $ {w}'{c}' $ denotes the flux for prognostic variables (u, v, q, $ \theta $); b is a constant of proportionality; ${\gamma }_{{\rm{c}}}$ is a local gradient correction item. | ${S}_{{\rm{h,m}}}$ is a dimensionless stability item that is a function of the Richardson number (Rig); ${K}_{{\rm{h,m}}}$ denotes the heat, water vapor and momentum eddy diffusivity; $ l $ denotes the turbulent length; ${ {q}^{2} }/{2}$ denotes the TKE; Ps denotes the TKE induced by wind shear; Pb denotes the TKE induced by buoyancy; D denotes the dissipation of TKE. | $ S $ is a dimensionless stability item that is a function of the Richardson number (Rig); K denotes the eddy diffusivity. |
Table1. Diffusion equations and vertical diffusivity coefficient computations for the three PBL parameterization schemes used in the model experiments.
Table 2 summarizes the configurations for two groups of double-nesting simulations. The mesoscale grids (15 and 9 km) used KF-parameterized convection, while the 1-km grid used fully explicit convection (EC). All experiments were initialized at 0800 LST 24 May 2018, and integrated for 48 h up to 0800 LST 26 May 2018. For convenience, D1 and D2 are denoted as the outer and inner domains, respectively. Nesting grid configurations are denoted directly by the grid spacing in km in sequential order. For example, 15-1 km denotes a double nesting configuration between D1 at 15 km and D2 at 1 km. The model results were bilinearly interpolated to the AWS stations to facilitate the comparison.
| Outer domain [D1] | Inner domain [D2] | ||||
| 15 km | 9 km | 15-1 km | 9-1 km | ||
| CUP | KF | KF | EC | EC | |
| PBL | YSU/MYJ/MYNN | YSU/MYJ/MYNN | YSU/MYJ/MYNN | YSU/MYJ/MYNN | |
| Grid cells | 407 × 297 | 677 × 494 | 1156 × 1141 | 1153 × 1135 | |
Table2. Two groups of model experiments using different configurations of grid nesting and PBL parameterization schemes as well as convection treatments. 15-1 km and 9-1 km denote the experiments in 1-km grid nested with the 15 km- and 9 km-grid, respectively.
The evaluation methods include pattern correlations (COR; Barnston, 1992), root-mean-square errors (RMSE; Barnston, 1992), threat score (TS; Wilks, 2011), and bias score (BS; Wilks, 2011) for different precipitation intensity thresholds (i.e., 0.1, 10, 25, 50, 100 mm, representing light, moderate, large, heavy, and extreme rain respectively). Larger COR and smaller RMSE indicate a better forecast of the spatial pattern of rainfall amount. The TS is also called the Critical Success Index, and a larger TS indicates higher predictive skill (perfect = 1) for the corresponding precipitation intensity. The bias score (Bias) denotes the frequency of rainfall forecasts compared with observations, and BS = 1 indicates an ideal prediction of the relative area size of corresponding precipitation intensity. The equations of COR, RMSE, TS, and BS are as follows:
where “
| Rainfall Event | Forecast | |
| yes | no | |
| yes | a | c |
| no | b | d |
Table3. Four categories of the occurrence/non-occurrence for a rain event at each threshold. Four categories of hit (a), miss (b), false alarm (c) and correct non-rain forecast (d) are used to refer to the occurrence/non-occurrence of a rain event at each threshold.
2
4.1. 24-h accumulated precipitation
Figure 4 compares the 24-h accumulated precipitation from 0000 LST 25 May to 2300 LST 25 May using different grid spacing (15 km, 9 km, 1 km) and PBL schemes (YSU, MYJ, and MYNN). For the D1 15-km grid, all PBL schemes failed to capture the location of the observed rain band and the extreme rainfall amount was largely underestimated. As grid spacing was reduced to 9 km, these dry biases for all PBL schemes were reduced, but this still underestimated the west rainband and overestimated the coverage of the east rainband. The model differences between these three PBL schemes were not significant, implying that the extreme rainfall simulations at coarser grids are not sensitive to the choice of PBL scheme. In the inner D2 1-km grid simulations, the model biases in the outer coarser grids were greatly reduced and the simulation of rainfall structure was refined, but the differences in using the three PBL schemes became more significant. Specifically, using the YSU scheme in 1-km grids generally underestimated the east rainband nearby the Yangtze River Delta. The general pattern of the core rainband was better represented in the experiments using the MYJ and MYNN schemes, but the former produced a rainband that deviated too far north.
Figure4. Spatial distributions of 24-h accumulated rainfall on 25 May 2018 simulated by WRF in D1 (15 km, 9 km) and D2 1-km grids with three different PBL schemes (YSU, MYJ and MYNN) (units: mm).Figure 5 further compares the TS and BS statistics for different daily rainfall intensity thresholds, as well as COR and RMSE for all 5207 stations in the inner 1-km grid from all the double-nesting simulations. In all the 1-km grid simulations, TS scores for light rain were generally higher than those for moderate?heavy rain. This is similar to the study of Liang et al. (2019), in which the WRF model using the KF cumulus parameterization scheme at 15- and 9-km grids produced higher TSs for light?moderate rain but lower scores for all other categories in a monthly prediction over Jiangsu Province. Thus, we speculate that this might be because the WRF model has limitations in representing physical (microphysics, PBL, etc.) and dynamic processes, leading to lower skill in predicting the convective cells than the general rainfall patterns. More importantly, the three PBL schemes showed notable differences in predicting the intensity of extreme rainfall and the size of its relative area. For instance, in the double nesting of 9-1 km simulations, the MYNN scheme was superior in predicting the intensity and relative area of extreme rainfall, with the highest TS and more realistic BS value; while the YSU scheme only performed better in predicting the intensity of light rain, and even performed worse in predicting the intensity and relative area of extreme rainfall, with the lowest TS and BS values. Using the MYJ scheme showed advantages in predicting the moderate rain, with the highest TS and a more realistic BS (close to 1), but had medium predictive skill for the intensity and area of extreme rainfall. Furthermore, double nesting of 9-1 km performed slightly better than 15-1 km in predicting the entire precipitation distribution, with systematically higher COR and lower RMSE.
Figure5. The (a) TS, (b) BS and (c) COR/RMSE for all 5207 stations with parameterized PBLs (YSU, MYJ and MYNN) for the inner D2 grids.Therefore, among all the double-nesting simulations, using MYNN in the 1-km grid nested with the 9-km grid produced the best predictive skill for the entire precipitation distribution, intensity, and size of the core rainband. This can be demonstrated by the largest COR for all the stations, as well as TS and BS (0.68, 0.34, 0.93), for the extreme rainfall threshold compared to YSU (0.63. 0.12, 0.40) and MYJ (0.76, 0.24, 0.60).
2
4.2. Hourly rainfall variations
Figure 6 compares the hourly variations of observed and simulated rainfall averages over the two subregions (Fig. 1b) and the entire core rainband in the inner 1-km grid as well as the outer D1 coarser grids (15 and 9 km). In observations, the rainfall amount was gradually increasing from 0000 LST and reached an early-morning peak at around 0700 LST. The primary rainfall peak occurred at around 1200 LST and then weakened up until 1600 LST, after which the rainfall increased again followed by a late-afternoon secondary peak at 1800 LST due to the intensification of the nocturnal LLJ and the mesoscale convective systems (Fig. 2). In the outer 15-km or 9-km grid (Figs. 6a and b), all three simulations systematically underestimated the primary and secondary rainfall peaks. The YSU scheme showed slight advantages over the MYNN and MYJ schemes in capturing the peak time as well as the intensity, while the MYJ scheme had the worst performance by producing a 1-h earlier peak with the lowest intensity.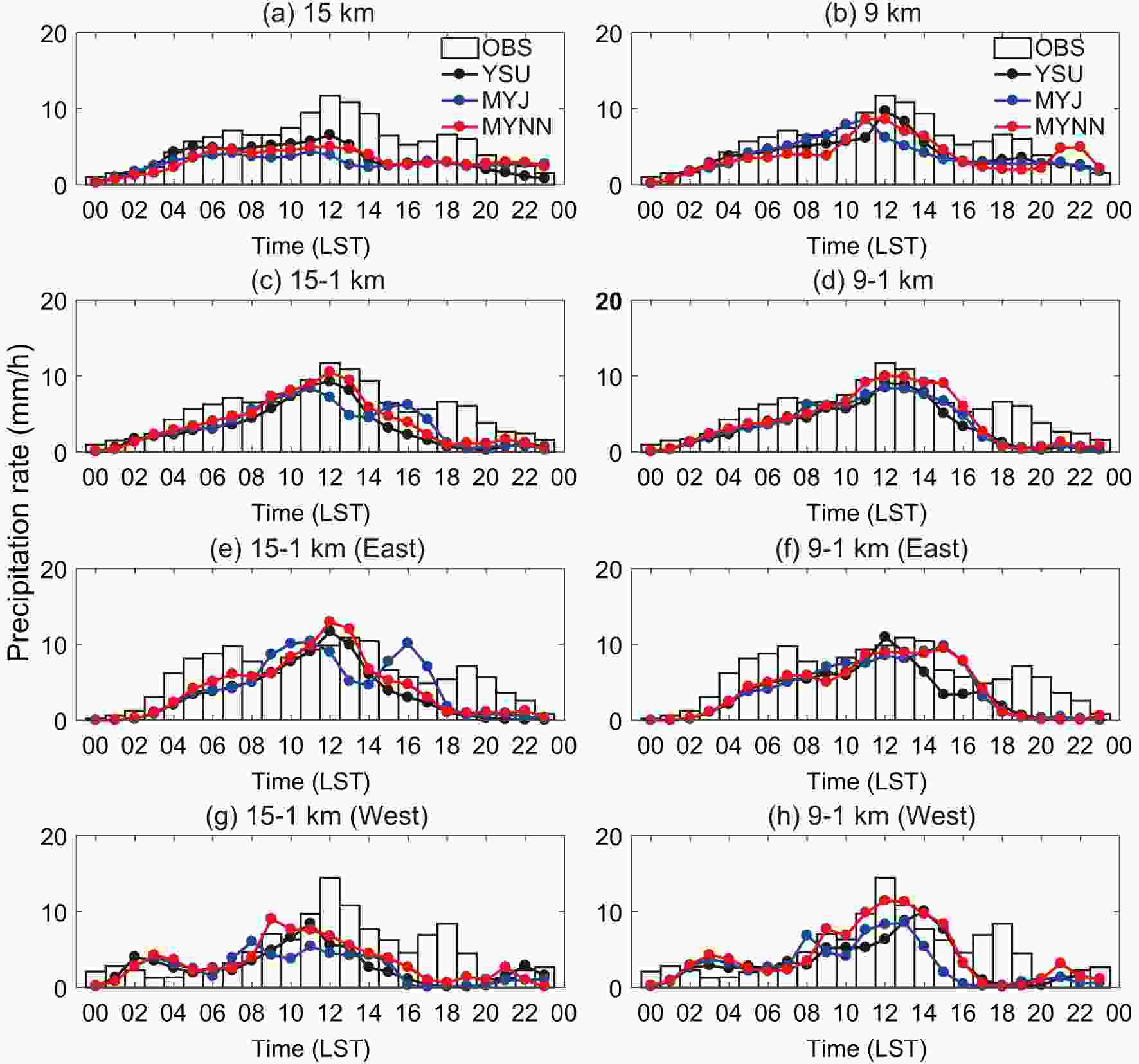
Figure6. Hourly variations of observed (OBS) and simulated rainfall averages over the (a?d) core rainband and (e?h) two subregions [(e, f) East; (g, h) West] on 25 May 2018 by the WRF model using three different PBL schemes (units: mm h?1).In the inner 1-km grid nested with the outer 15-km or 9-km grid (Figs. 6c and d), consistent advantages existed for the MYNN scheme over the other schemes in capturing the primary rainfall peak and intensity. The YSU scheme was capable of capturing the primary rainfall peak time, but with lower intensity than that of the MYNN scheme. However, using the MYJ scheme would still produce a 1-h earlier rainfall peak with the lowest intensity in the double nesting of 15-1 km, which was improved in the double nesting of 9-1 km.
By analyzing the hourly rainfall simulations over two subregions, we found that using the MYNN scheme in the double nesting of 9-1 km also reproduced the primary rainfall peaks well over both subregions (Figs. 6f and h). However, using the MYNN scheme in double nesting of 15-1 km would overestimate the peak intensity over the east rainband (Fig. 6e), also producing an earlier and weaker peak over the west rainband (Fig. 6g) compared to the observations. Furthermore, the largely underestimated rainfall peaks simulated by the MYJ scheme for both 15-1 km and 9-1 km were all mainly due to the dry biases over the west rainband. Therefore, we will focus on the double nesting of 9-1 km using the MYNN scheme, and explore the possible causes for its superiority in simulating the primary rainfall peak intensity. The analyses mainly include the PBL effects on the boundary layer structure, convective thermodynamic, and large-scale forcing variations.
5.1. Simulations of boundary layer structure
Figure 7 compares the time?height sections of vertical eddy transport of equivalent potential temperature and water vapor mixing ratio. They are averaged over the core rainband from the double nesting of 9-1 km using the three PBL schemes. The simulated vertical transport of heat and water vapor in the boundary layer all gradually became stronger from the early morning to noon, corresponding to the time when the primary rainfall peak occurred. The major difference existed with the vertical transport and mixing process at the top of the boundary layer between the nonlocal (YSU) and local (MYNN & MYJ) PBL schemes. The YSU scheme includes the nonlocal effect with the counter gradient transport and produced stronger vertical mixing below 2000 m than that of the local MYNN scheme before 1200 LST. The MYJ scheme showed intermediate vertical mixing between the YSU and MYNN schemes, as supported by Srinivas et al. (2018). This would cause differences in the vertical distribution of heat and water vapor from the boundary layer to the lower troposphere, and thus affect the stability of the atmosphere as well as the development of convection and precipitation, which will be discussed as follows. It is noteworthy that there was high vertical equivalent potential temperature and moisture transport at 2000 LST in the experiment with the MYNN scheme, which may explain the high precipitation at 2100 LST shown in Fig. 6.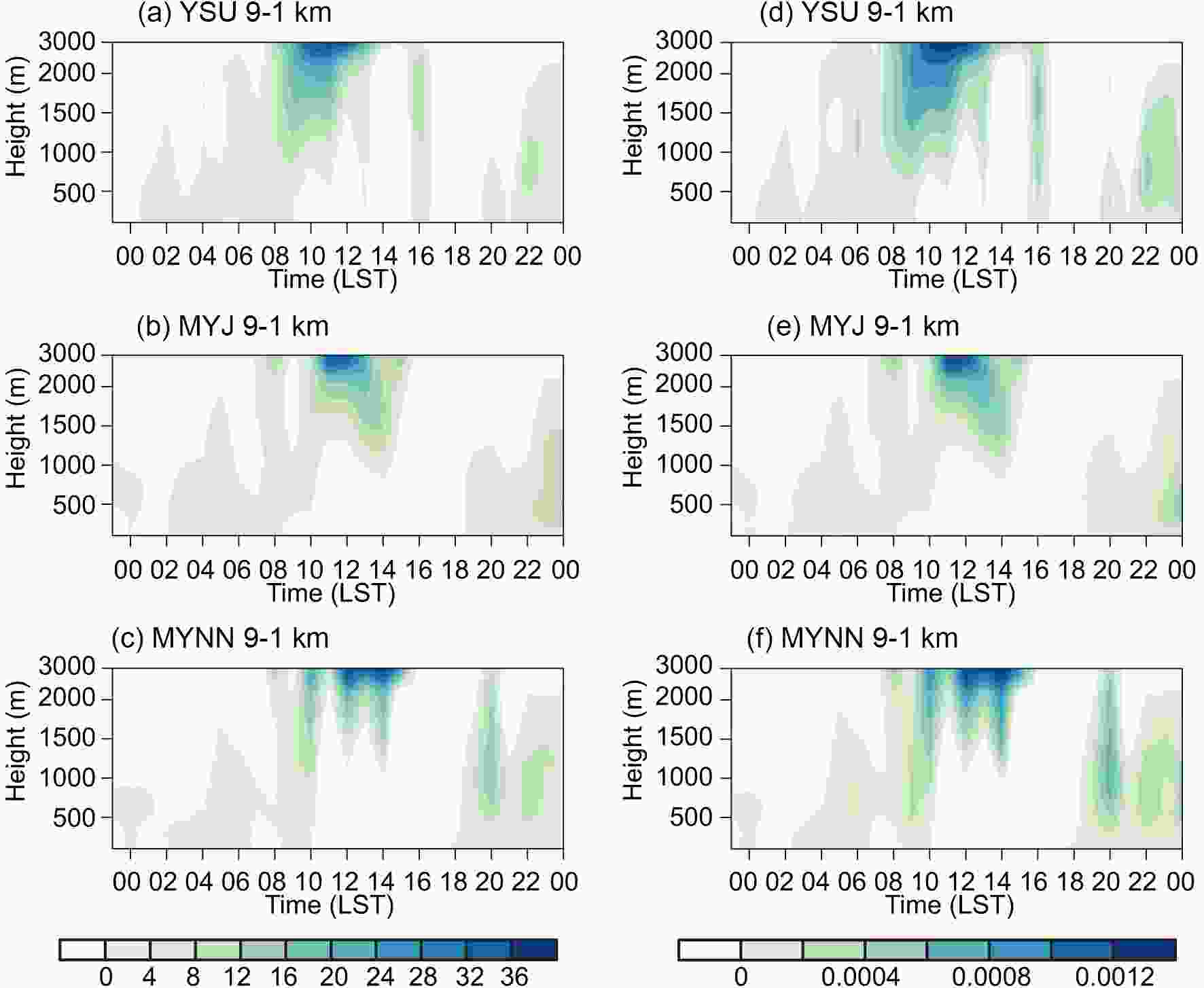
Figure7. Time?height cross sections of the vertical eddy transport of (a?c) equivalent potential temperature (unit: K s?1) and (d?f) water vapor [units: kg (cm hPa s)?1] averaged over the core rainband on 25 May in the inner 1-km grids (9-1) simulations using YSU, MYJ and MYNN.Figure 8 compares the hourly variation of vertical distributions of equivalent potential temperature, water vapor mixing ratio, horizontal wind speed, and vertical velocity averaged over the core rainband from the surface to the lower troposphere. The vertical profiles of these corresponding variables at 1200 LST in Fig. 9 are also combined to discuss the different effects of the PBL schemes. For the thermal structures, the three PBL schemes all produced an inversion layer near the surface and the depth was decreasing from the early morning till noon, but the local MYNN scheme produced the shallowest inversion layer at 1200 LST around 1000 m compared to the nonlocal YSU scheme (1200 m) or the local MYJ scheme (1300 m) (Fig. 9a). Meanwhile, they all produced a warm layer in the middle-upper boundary layer, resulting in an unstable layer above. For the water vapor distribution, the three PBL schemes showed relatively little difference, but the water vapor was still more evenly distributed within the inversion layer (< 1000 m) during morning till noon in the nonlocal YSU scheme. The local MYJ and MYNN schemes both showed a more concentrated water vapor center in the bottom layer, but the MYJ scheme produced slightly higher water vapor mixing ratios from the top of the boundary layer to the middle troposphere at 1200 LST (Fig. 9b). For the wind structure, the local MYNN scheme produced stronger horizontal wind speed and upward motion than the nonlocal YSU scheme from the lower troposphere to the upper levels. The wind fields simulated by the MYJ scheme were strong at the lower troposphere; however, they rapidly reduced from the lower troposphere to upper levels (Figs. 9c and d). However, the nonlocal YSU scheme produced the lowest wind speed from the low-level troposphere (2500 m; 13.60 m s?1) to upper levels (6000 m; 17.42 m s?1) owing to its strongest vertical mixing at the top of the unstable boundary layer (Figs. 7a and d).
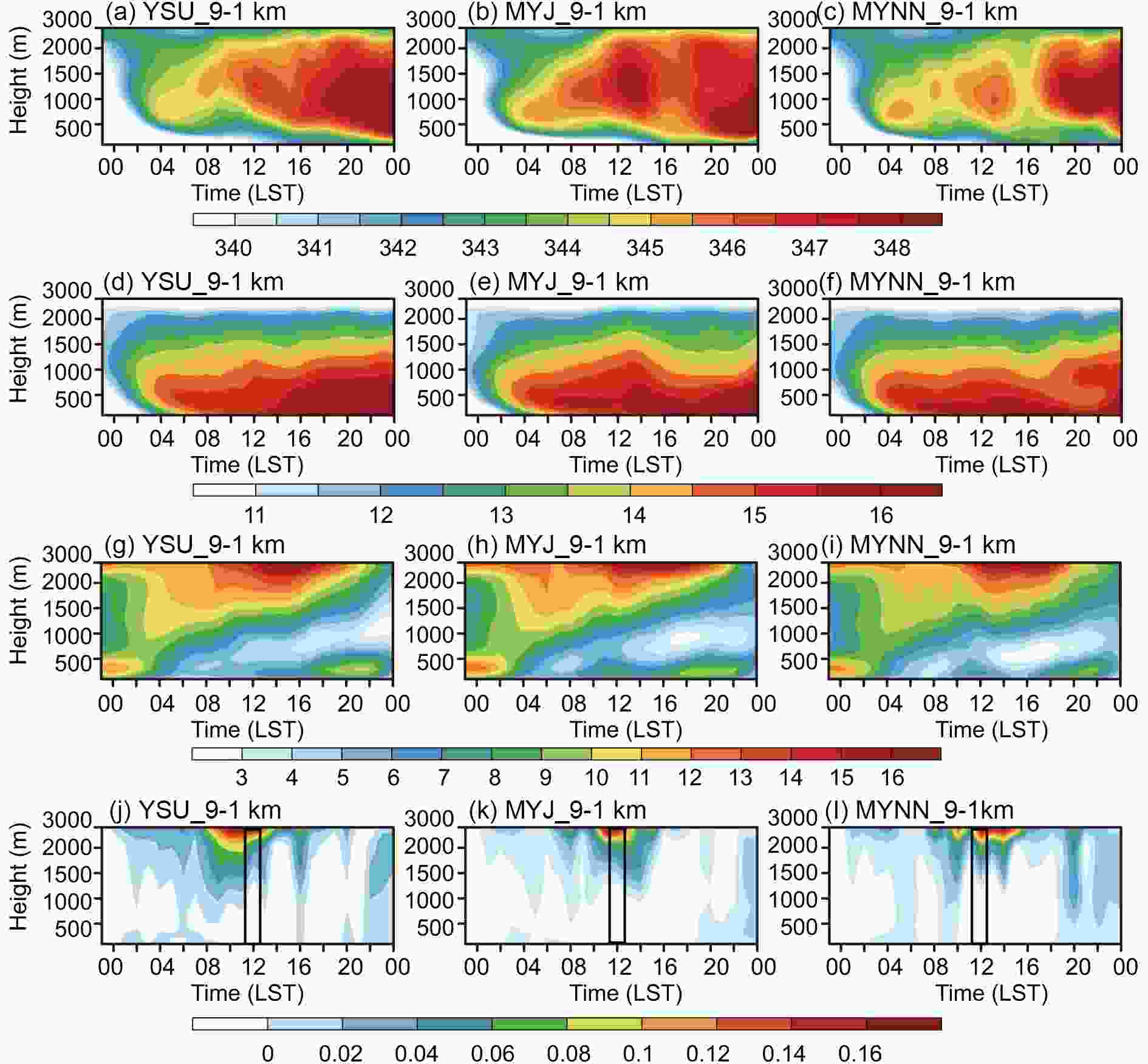Figure8. Time?height sections of the (a?c) equivalent potential temperature (units: K), (d?f) water vapor mixing ratio (units: g kg?1), (g?i) horizontal wind speed (unit: m s?1), and (j?l) vertical velocity (units: m s?1) averaged over the core rainband 1-km grids (9-1) using YSU, MYJ and MYNN.
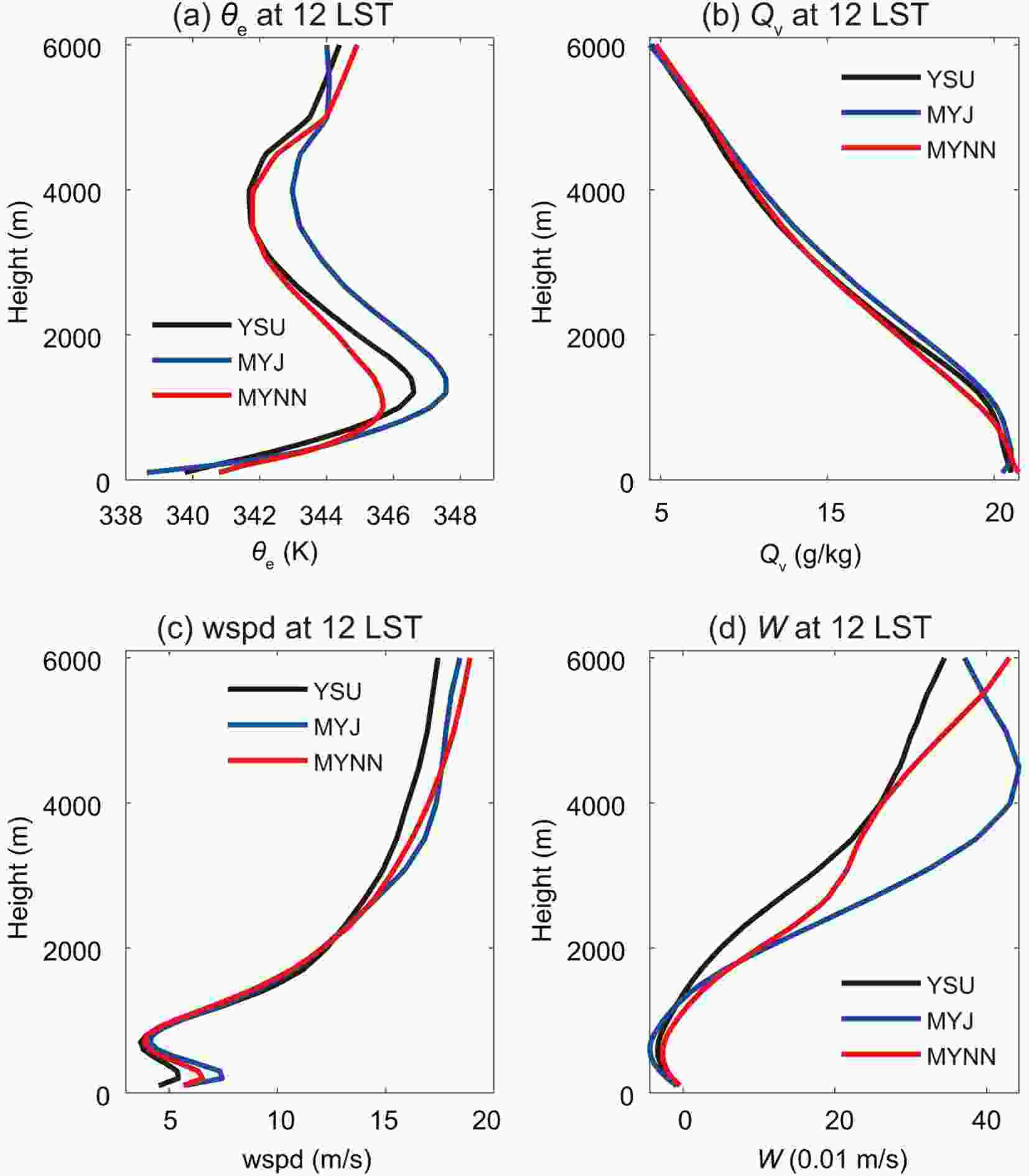Figure9. Profiles of (a) equivalent potential temperature (θe, units: K), (b) water vapor mixing ratio (QV, units: g kg?1), (c) horizontal wind speed (wspd, units: m s?1), and (d) vertical velocity (W, units: m s?1) from 100 to 6000 m over the core rainband at 1200 LST in the 1-km (9-1) grids using YSU, MYJ and MYNN.Therefore, the local MYNN scheme produced the shallowest and most humid inversion layer in the bottom layer, the least warm middle boundary layer, but stronger horizontal wind and upward motion from the top of the boundary layer to the upper levels. YSU produced a deeper inversion layer than MYNN in the bottom layer, a relatively warm and humid middle boundary layer, and the weakest wind fields due to the strongest vertical mixing at the top of the boundary layer. The local MYJ scheme produced an inversion layer with a depth between the other two schemes, but the warmest middle boundary layer, and the wind fields of MYJ at the boundary layer top were strong but quickly weakened above 5000 m. The MYJ scheme had slightly higher wind speeds in the boundary layer compared to the others, but caution should be taken here considering the uncertainty of wind observations and computational errors. In the following we focus on the effects of these different boundary layer structures on the development of convection.
2
5.2. Simulations of convective thermodynamic variations
Figure 10 compares the hourly variations of simulated convective available potential energy (CAPE) and convective inhibition energy (CIN) averaged over the core rainband from the double nesting of 9-1 km simulations with the three PBL schemes. CAPE is defined as the accumulated buoyancy energy from the level of free convection to the equilibrium level, which represents the net kinetic energy that a rising air parcel can gain from the environment and hence reflects the potential strength of convective systems and associated precipitation. CIN is defined as the accumulated negative buoyant energy from the air parcel’s starting position to the level of free convection, which represents the inhibition energy that the rising air parcel has to overcome to become free convection. Under stormy conditions, the PBL height could be defined by some alternative methods such as using a cloud base or lifting condensation level (LCL) (Wisse and de Arellano, 2004; Stull, 2011), and a higher LCL usually denotes a stronger vertical mixing. Table 4 also lists the simulated values of CAPE, CIN and LCL, as well as the horizontal wind speed and upward motions at the top of the boundary layer (around 1500 m), the low-level troposphere (around 2500 m), and the middle troposphere (around 6000 m) at 1200 LST for a quantitative comparison.| PBL | CAPE (J kg?1) | CIN (J kg?1) | LCL (m) | Height of inversion layer (m) | Vertical velocity (m s?1) | Horizontal wind speed (m s?1) | Water vapor mixing ratio (g kg?1) | ||||||||
| 1500 m | 2500 m | 6000 m | 1500 m | 2500 m | 6000 m | 1500 m | 2500 m | 6000 m | |||||||
| YSU | 216.93 | 11.04 | 1438 | 1200 | 0.01 | 0.10 | 0.34 | 9.99 | 13.60 | 17.42 | 13.80 | 10.90 | 4.70 | ||
| MYJ | 402.97 | 7.86 | 1411 | 1300 | 0.02 | 0.21 | 0.37 | 9.63 | 13.93 | 18.44 | 14.10 | 11.40 | 4.70 | ||
| MYNN | 236.6 | 11.08 | 1381 | 1000 | 0.03 | 0.17 | 0.43 | 9.39 | 13.94 | 18.9 | 13.40 | 10.80 | 4.90 | ||
Table4. Simulated values of CAPE, CIN and LCL, as well as the horizontal wind speed, vertical velocity and water vapor mixing ratio, at the top of boundary layer (around 1500 m), the low-level troposphere (around 2500 m), and the middle troposphere (around 6000 m) at 1200 LST.
Figure10. Hourly variations of simulated (a) CAPE (units: J kg?1), (b) CIN (units: J kg?1) and (c) LCL (units: m) averaged over the core rainband at 1-km (9-1) grids on 25 May using three PBL schemes.The nonlocal YSU scheme produced the lowest CAPE peak at around 0800 LST, which was two hours earlier than the primary rainfall peak. Although the YSU scheme produced comparable CIN with the MYNN scheme, it systematically had the highest LCL compared to the other two schemes. This implies that, compared to the local MYNN scheme, the air parcel in the YSU scheme needs to be uplifted to a higher altitude to achieve condensation; nevertheless, the unstable energy in the upper boundary layer is insufficient to sustain the development of convection.
However, the local MYJ scheme systematically produced the largest CAPE and CIN during the morning through the afternoon, indicating that the convection was strongly suppressed and the CAPE was slowly released. The LCL in the MYJ scheme was also higher than in the MYNN scheme. The larger CIN, the slower release rate of CAPE, and the higher LCL with the MYJ scheme all determine that it is more difficult for the convection to initiate and develop compared to using the MYNN scheme. The atmospheric instability, low-level moisture convergence and vertical motion are the prerequisites for the development and maintenance of deep convection and mesoscale convective systems that often lead to heavy rainfall events (Srinivas et al., 2018). Therefore, in the following, we discuss the PBL effects on the large-scale forcings, including the low-level moisture supply and the upward motions.
2
5.3. Simulations of large-scale forcing variations
Figure 11 compares the time?height sections of horizontal and vertical fluxes of water vapor mixing ratio and vertical velocity averaged over the core rainband from the surface to the troposphere in the double nesting of 9-1 km simulations with the three PBL schemes. The water vapor transport simulated by these three PBL schemes mainly differed in its contributions to the primary rainfall peak at noon. The local MYNN scheme systematically produced the strongest horizontal water vapor transport, as well as upward motion from the top of the boundary layer to the middle troposphere during 1000?1200 LST. This can also be identified from Table 4, in which the MYNN scheme shows slightly stronger wind speeds and vertical velocity at the boundary layer top and the middle troposphere at 1200 LST compared to YSU. Although the MYJ scheme produced higher wind speeds and upward motion at 1200 LST at the top of the boundary layer, they weakened rapidly and produced less moisture transport to the upper levels. Therefore, the MYJ scheme also predicted a lower intensity of the primary rainfall peak compared to the MYNN scheme.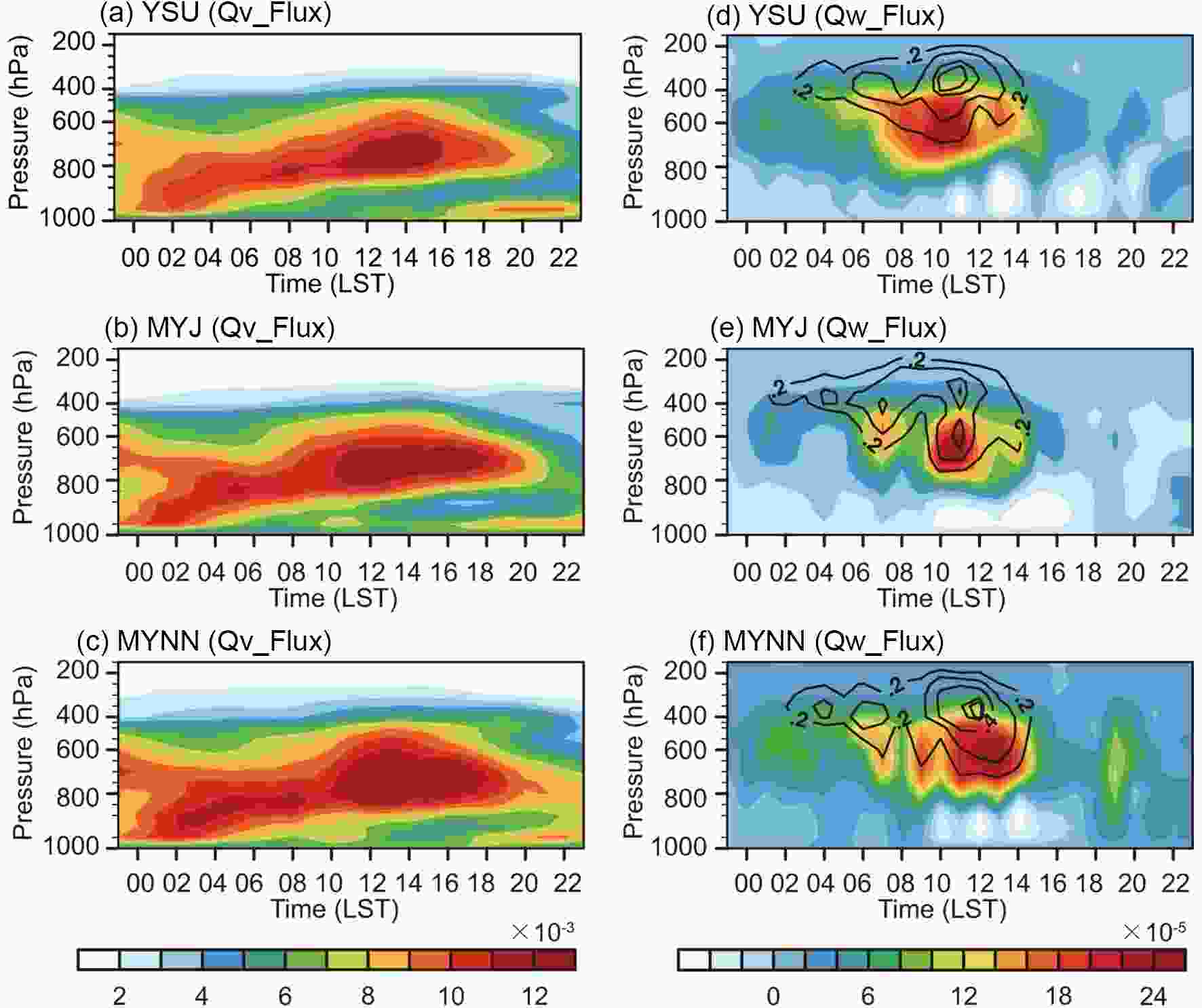
Figure11. Time?height sections of (a?c) horizontal water vapor mixing ratio flux [units: kg (cm hPa s)?1] and (d?f) vertical water vapor mixing ratio flux [units: kg (cm hPa s)?1] and vertical velocity (black solid contours; units: m s?1) averaged over the core rainband on 25 May in the inner 1-km (9-1) grids using YSU, MYJ and MYNN.Figure 12 presents longitude?height sections of moisture convergence and zonal?vertical wind averaged over 31°?33°N in the inner 1-km grid from the double nesting of 9-1 km simulations at 1200 LST and 1400 LST using the three PBL schemes. Here, we chose to demonstrate the moisture convergence at 1400 LST because of the availability of ECMWF reanalysis data. In the ECMWF data, at 1400 LST, there was strong low-level moisture convergence over the region 120°?122°E associated with strong upward motion from the lower to upper troposphere, corresponding to the east rainband. MYNN produced stronger upward motion than the other PBL schemes, which affected the amount of vertical moisture transport and produced the strongest low-level moisture convergence over this region. Weak low-level moisture convergence and upward motion in the lower troposphere were also shown in the ECMWF data over the region 117°?118°E, corresponding to the relatively weak rainfall in the west rainband. However, using the MYNN scheme could only partly capture the upward motion and moisture convergence over this region, and with underestimated intensity; and yet, the other two schemes could barely capture the upward motion, and the MYJ scheme even produced weak moisture divergence in the lower troposphere. This also explains why the experiments with the YSU and MYJ schemes largely underestimated the extreme rainfall over the west rainband. Besides, at 1200 LST, MYNN also produced stronger low-level moisture convergence and upward motion in the lower troposphere over the regions 120°?122°E and 117°?118°E.
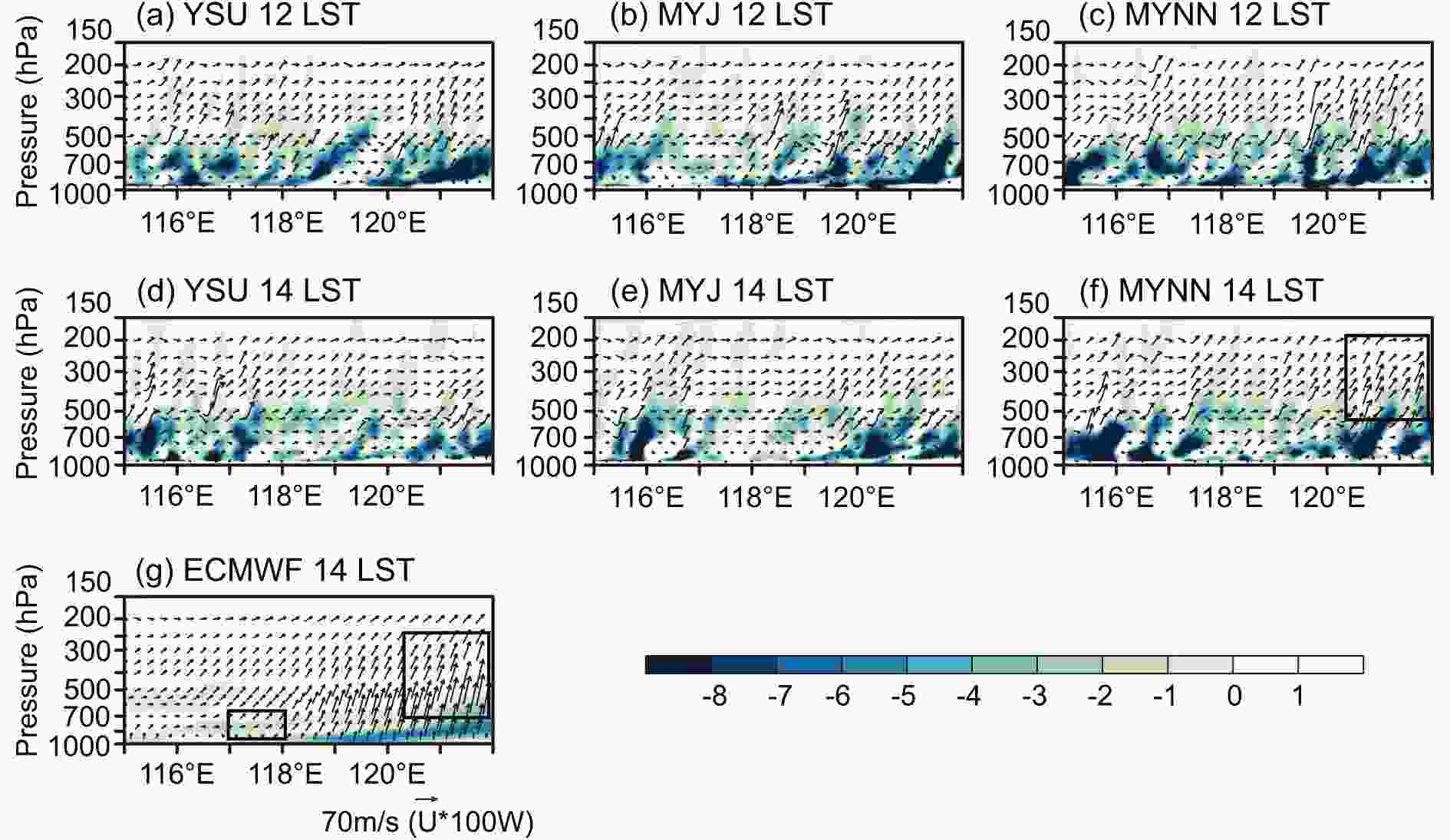Figure12. Longitude?height sections of moisture convergence [shaded; units: 10?7 g (cm2 hPa s)?1] and U-W wind (black vectors; units: U × 100 W m s?1) averaged over 31°?33°N on 25 May in the inner 1-km nested with 9-km grid using three PBL schemes at 1200 LST (a-c) and 1400 LST (d-f).Therefore, the nonlocal YSU scheme, with the strongest vertical mixing, produced the deepest inversion layer in the bottom layer with the highest LCL, the lowest CAPE, and the weakest wind fields, as well as low-level moisture transport. The MYJ scheme, with intermediate vertical mixing, produced larger CIN, slower release of CAPE, and higher LCL compared to the MYNN scheme, which suppressed the development of convection. The wind fields in the MYJ scheme at the low-level troposphere were the strongest but quickly weakened upwards, resulting in less moisture transport and convergence in the lower troposphere, especially over the west rainband. However, the MYNN scheme, with the weakest vertical mixing, produced the shallowest and most humid inversion layer in the bottom layer with the lowest LCL, but stronger wind fields and upward motions from the boundary layer top to upper levels. These all facilitated the development of deep convection and moisture transport for intense precipitation.
First, in the outer mesoscale grids (15 km and 9 km), all experiments failed to capture the location of the observed rainband and the extreme rainfall amount was largely underestimated. The model differences between the three PBL schemes were not significant. In the inner 1-km grid simulations, the model biases in the outer coarser grids were greatly reduced and rainfall-structure simulation was refined. The east rainband was generally underestimated with the YSU scheme, while using both the MYJ and MYNN scheme could capture the general pattern of the core rainband, but the former produced a rainband that deviated further north. Among all the double nesting simulations, using MYNN in the 1-km grid with explicitly resolving convection nested with the 9-km grid with the KF cumulus scheme, produced the best predictive skill for the entire precipitation distribution and the intensity, as well as the size of the core rainband.
Second, in the outer mesoscale grids (15 km and 9 km), all three simulations systematically underestimated the primary and secondary rainfall peaks. In the inner 1-km grid nested with the outer 15-km or 9-km grid, the MYNN scheme showed consistent advantages over the other two PBL schemes in capturing the primary rainfall peak and intensity. Using the MYNN scheme in the double nesting of 15-1 km, however, the peak intensity over the east rain band was overestimated, and an earlier as well as weaker peak over the west rainband was produced. Nevertheless, the MYNN scheme in the double nesting of 9-1 km showed superiority over the other 1-km simulations in predicting the primary rainfall peaks over both the west and east core rainbands.
Third, the three PBL schemes differ in their vertical mixing processes, leading to different vertical profiles of temperature, water vapor and wind fields from the boundary layer to the lower troposphere, which affect the atmospheric stability and moisture transport for the development of convection and precipitation. Among the PBL schemes, for this extreme rainfall event, the local MYNN scheme showed the weakest vertical mixing and produced the shallowest as well as the most humid inversion layer in the bottom layer and the lowest LCL, which are conducive to the development of convection. At the same time, the MYNN scheme produced stronger horizontal winds and upward motion from the top of the boundary layer to the upper levels than the nonlocal YSU scheme, which facilitates the moisture transport and convergence in the lower troposphere for intense precipitation. The combined effects led to the strongest and most realistic rainfall peak in the MYNN scheme. However, the nonlocal YSU scheme, with the strongest vertical mixing, produced a deep inversion layer, the highest LCL and the lowest CAPE, and weaker wind fields, which tend to inhibit the development of convection and moisture transport for heavy rainfall. This explains the largely underestimated primary rainfall peak in the YSU scheme. On the other hand, the MYJ scheme, with intermediate vertical mixing, produced larger CIN and a higher LCL with a slower release of CAPE compared to the MYNN scheme, which also suppressed the development of convection. Although the horizontal winds of the MYJ scheme were comparably strong with the MYNN scheme in the upper boundary layer, it weakened rapidly in the lower troposphere, resulting in less moisture transport than the MYNN scheme. This especially led to the underestimated rainfall amount over the west rainband.
Although our study was based on one single-day case over Shanghai and its adjacent region, the model performances of these three PBL schemes in this case were highly similar to those of previous high-resolution model studies, such as Srinivas et al. (2018), but over different regions. On the other hand, the PBL sensitivities with the varying model resolution and convection treatment also provide a better understanding of the interaction of the boundary layer with the large-scale environment and the organization of mesoscale convective systems. In future work we will conduct high-resolution simulations over a longer period and under different climate regimes to verify the typical characteristics of different PBL schemes. Moreover, the degradation of 1-km simulations downscaled from the coarser grids (15 km and 9 km) in predicting the weak secondary rainfall peak requires further study through improving the cumulus or microphysics representations.
Acknowledgements. This research was supported by the National Natural Science Foundation of China (Grant No. 41730646), National Natural Science Foundation for Young Scientists of China (Grant No. 41605079), and the National Key R&D Program of China (Grant No. 2018YFC1507702). The FNL Operational Global Analysis data at 1° grids provided by NCEP and used in this study can be found at
