HTML
--> --> -->Interpolation is a widely used method for increasing the data resolution in order to obtain more detailed information (Gonzalez and Woods, 2007; Demirel and Anbarjafari, 2011; Azam et al., 2014; Chavez-Roman and Ponomaryov, 2014). Conventional data interpolation methods, such as linear, bicubic, or Cressman interpolation, are the most common spatial domain interpolation methods of weather radar data and have the advantage of high speed but suffer from staircase effects and blurring due to the band limit constraints. A number of methods have been proposed to overcome the shortcomings of these spatial domain interpolation methods based on low-pass filtering (Deidda, 2000; Tao and Barros, 2010; Chavez-Roman and Ponomaryov, 2014; Ruzanski and Chandrasekar, 2015; Jiao et al., 2016). Jiao et al. (2016) proposed an interpolation method for weather radar data based on Fourier spectrum analysis. Ruzanski and Chandrasekar (2015) performed temporal interpolation of meteorological radar data using a kernel-based Lagrangian nowcasting technique with a fast Fourier transform. Tao et al. (2010) used fractal interpolation to enhance the resolution of satellite precipitation products based on iterated function systems and fractal Brownian surfaces. However, the key geometrical and statistical properties of radar precipitation observations have not been explored or included in spatial interpolation algorithms.
The spatial and temporal variabilities of precipitation exhibit distinct statistical space–time structures at multiple scales (Perica and Foufoula-Georgiou, 1996; Harris et al., 2001; Ebtehaj and Foufoula-Georgiou, 2011). Such multiscale statistical characteristics have been studied using several approaches in the frequency and wavelet domain, such as the theory of multifractals, multiplicative cascades, exponential Langevin-type models, and the cascades of Gaussian-scale mixtures (Badas et al., 2006; Deidda et al., 2006; Gupta et al., 2006; Venugopal et al., 2006; Sapozhnikov and Foufoula-Georgiou, 2007; Ebtehaj and Foufoula-Georgiou, 2011). These multiscale representations have proven to be useful for quantifying the precipitation variability at multiple scales and can be exploited as prior information. In view of the sparseness of precipitation in the wavelet domain, Ebtehaj et al. (Ebtehaj et al., 2012, Ebtehaj and Foufoula-Georgiou, 2013) recast precipitation downscaling into an ill-posed inverse problem and estimated the high-resolution information with regularization. Based on the non-Gaussian and local coherent structure of radar reflectivity data in the wavelet domain, Kou et al. (2019) proposed an interpolation algorithm for radar reflectivity data using the Gaussian-scale mixtures model.
Small-scale variability is important for accurate prediction and warning of heavy precipitation. In this study, the multiscale statistical characteristics of radar reflectivity data are studied and modeled using a hidden Markov tree (HMT) in the wavelet domain. A high-resolution interpolation algorithm for spaceborne radar reflectivity based on the HMT model is proposed to enhance the resolution and reproduce the small-scale detailed information. First, the characteristics of the thicker-than-Gaussian structure and interscale dependency of the radar reflectivity data are studied, and these characteristics are matched using the HMT model. Then, the variance decay and multiscale processes controlling parameters across different scales in the HMT model are learned and estimated from a set of matched high-resolution GR reflectivity images dominated by convective precipitation. Furthermore, a Wiener filter is applied locally to each sub-band to obtain the fine-scale coefficients. Finally, high-resolution satellite reflectivity data are generated with an inverse wavelet transform. Case studies are conducted for the proposed method to prove that it can capture and reproduce the small-scale details of the spatial distribution of precipitation, such as sharp variations and extreme values.
2.1. Statistical characteristics of modeling in the wavelet domain
Because of the high precipitation intensity embedded in the lower intensity regions, large gradients and discontinuities are present in precipitation echoes. In other words, the probability distribution of the precipitation reflectivity in the derivative space (e.g., the wavelet domain) has a large mass around zero (nearby pixels with similar values) and a few heavy values (steep gradients), thereby representing a heavy-tailed non-Gaussian distribution. In addition, the evolution of precipitation from coarse to fine scale often displays self-similarity, which can be considered as a self-similar multifractal process (Deidda, 2000; Deidda et al., 2006). Prior information about these multiscale statistics of precipitation is important for reproducing the desired properties of precipitation fields.For remotely sensed precipitation data obtained by ground or spaceborne radar, some common statistical properties and mathematical signatures exist that can be characterized and exploited for precipitation modeling and further applications (Ebtehaj and Foufoula-Georgiou, 2011; Foufoula-Georgiou et al., 2014). The wavelet transform using a multiresolution analysis framework can represent well the multiscale processes of precipitation, and it is useful for quantifying the rainfall variability at multiple scales (Willsky, 2002; Azam et al., 2014). With prior modeling of wavelet coefficients of radar reflectivity data, the estimated finer wavelet coefficients can effectively recover the essential properties of the reflectiviy data.
Before studying the statistical characteristics of the radar reflectivity data, the data from the TRMM PR and the GR were quality controlled and spatiotemporally matched. The level II algorithm of the TRMM PR profile (2A25) was used, which includes ground clutter filtering, attenuation and beam filling correction (Kozu et al., 2001). The GR data from the ground Doppler radar at Longwang Mountain (32.1908°N, 118.6969°E) in Nanjing city, China, were processed with anomalous propagations and ground clutter removal using the NCAR SOLO II algorithm. Using the results in Zhu et al. (2016) that employed 245 TRMM PR and Nanjing GR matchup cases to determine the calibration biases, the system calibration bias of the Nanjing GR was corrected by adding a bias adjustment. The temporal matching was carried out with a 6-min window centered on the TRMM PR overpass time. The spatial matchup scheme was based on the grid matching method (Liao and Meneghini, 2009), in which both sets of data were interpolated to a common 3D Cartesian coordinate system. The gridded GR data were interpolated from the GR spherical coordinate system centered at the GR using a cubic linear interpolation algorithm, with a vertical resolution of about 1 km to a height of 20 km and a horizontal resolution of about 1 km to a horizontal extent of ±150 km. The TRMM PR data were also resampled into Cartesian coordinates with a horizontal resolution of 4 km, and the displacement of the PR samples was corrected as well (Wang and Wolff, 2009; Kou et al., 2018).
After data preprocessing, the statistical characteristics of the high-resolution radar reflectivity data, including non-Gaussian marginal statistics and scale-to-scale dependency, were first studied with convective precipitation cases. Then, the intrascale and interscale statistical characteristics of the reflectivity data were matched using the HMT model. In the wavelet domain of the HMT model, the distribution densities of the wavelet coefficients were approximated by a Gaussian mixture model (GMM), and the dependencies of multiscale wavelet coefficients were represented by a Markov process and state transition parameters (Crouse et al., 1998; Romberg et al., 2001; Li et al., 2010).
The radar data used in this paper are the reflectivity at a height of 3 km in Cartesian coordinates, and a shift-invariant undecimated orthogonal wavelet transform and Haar wavelet were used for wavelet decomposition (Nason and Silverman, 1995). Figure 1a shows the spaceborne radar reflectivity image at 3 km height from TRMM PR at 0456:41 UTC 27 May 2008, and Fig. 1b shows the coincidental high-resolution GR CAPPI (Constant Altitude Plan Position Indicator) at 0459:00 UTC. Figure 1c shows the marginal probability distribution on the log scale of the wavelet coefficient in the horizontal sub-band of the image presented in Fig. 1b, and Fig. 1d is the corresponding statistical histogram of the horizontal wavelet coefficient. It can be seen from Fig. 1d that the wavelet coefficient of the precipitation image has heavy tail that is significantly thicker than those of a Gaussian distribution; this usually corresponds to the heavy precipitation gradients and intensities.
Figure1. (a) Radar reflectivity image from TRMM PR obtained at 0456:41 UTC 27 May 2008, (b) the coincidental reflectivity image captured by the GR in Nanjing at 0459:00 UTC, (c) wavelet coefficients in the horizontal sub-band of the reflectivity image in (b), and (d) the corresponding log histogram (asterisks) of the wavelet coefficients normalized by the standard deviation. A heavier tail than the Gaussian distribution [dotted line in (d)] is clear in the precipitation reflectivity image in the wavelet domain, and the solid line in (d) is the fitted GMM distribution with the EM algorithm.Figure 2 shows another convective precipitation image obtained by the Nanjing GR at 0530:00 15 August 2010. Figure 2b shows the wavelet coefficients in the horizontal band of the radar reflectivity data presented in Fig. 2a, and Fig. 2c is the corresponding probability distribution of the wavelet coefficients, where the asterisk denotes the histogram. It can be seen that the histogram is also significantly different from a Gaussian distribution, with much heavier tails than those of a Gaussian function.
Figure2. (a) Radar reflectivity image of another precipitation case in Nanjing obtained at 0530:00 15 August 2010, (b) wavelet coefficients in the horizontal sub-band of the reflectivity image in (a), and (c) the corresponding log histogram (asterisks) of the wavelet coefficients normalized by the standard deviation.This heavy-tail property implies that most wavelet coefficients contain very little information, while a few wavelet coefficients represent significant information. The Gaussian mixture distribution can be employed to characterize the non-Gaussian marginal statistics and the heavy-tail properties of the radar reflectivity:
where si is the state m of the ith coefficient wi, and
Figure3. Two-state, zero-mean GMM for a random variable used to generate a non-Gaussian probability distribution, where s = 0 or 1 denotes the state 0 or 1, f(w|s=0 or 1) is the Gaussian distribution under state 0 or 1, and f(w) is the generated non-Gaussian distribution.The black solid line in Fig. 1d is the fitted two-state GMM distribution (on the log scale) obtained using the expectation maximization (EM) algorithm (Figueiredo and Nowak, 2003), where the asterisks denote the original probability distribution of wavelet coefficients. The fitted GMM distribution is 0.56N(0, 0.583) + 0.44N(0, 8.2958), where N(0, 0.583) represents the Gaussian distribution function with mean 0 and variance 0.583. The coefficient of determination of the fitted line is 0.9872, and it can be seen from Fig. 1d that the GMM distribution can capture well the sharp peak and heavy tail of the precipitation image in the wavelet domain. By increasing the number of states, the arbitrary probability densities can be generated with a finite number of discontinuities. However, a GMM with more than two states may possess the problem of slow convergence speed and strong dependence on initial values, and it is easy to capture some local optimal values. Developing an optimized algorithm for a GMM with more states is a topic for further research. The two-state, zero-mean GMM is simple, robust, and easy to use, which are attractive features for applications. In this study, a two-state GMM is employed.
In addition to the non-Gaussian and heavy-tail properties of the precipitation reflectivity, the data exhibit an evident interscale dependency because the precipitation fluctuations are similar across scales and the wavelet transform does not completely decorrelate the precipitation images. Figure 4 shows the 2D joint and conditional histograms of the wavelet coefficients in the horizontal sub-band for the reflectivity image presented in Fig. 1b. The shape of the joint histograms in Figs. 4a–c indicates the conditional probability of scale 2 given that scale 1 is not uniform and that a high-order dependency exists. The shape of the conditional histograms in Figs. 4d–f indicates that the variance of scale 2 depends on the magnitudes of scale 1, and larger variance of scale 1 gives rise to scale 2 with larger variance. The tilted bowtie shapes of the horizontal and vertical sub-bands in Figs. 4d and e also represent the presence of off-diagonal nonzero elements on the covariance matrix of the scale-to-scale coefficients.
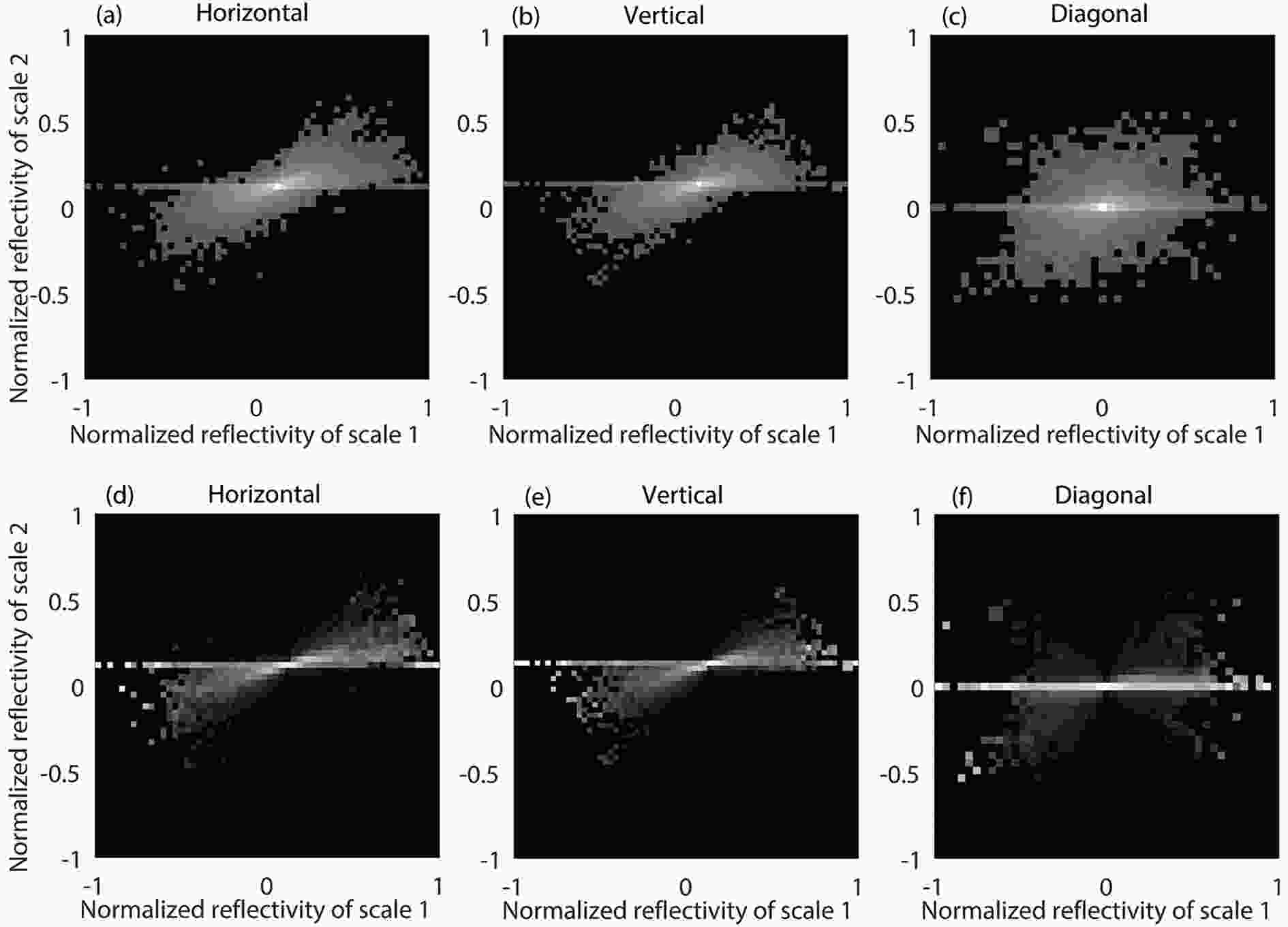Figure4. Joint histogram of the (a) horizontal, (b) vertical and (c) diagonal wavelet coefficients of the precipitation reflectivity image in Fig. 1b, and (d–f) the corresponding conditional histograms. The shape of the joint histograms shows that the conditional probability of scale 2 given scale 1 is not uniform and that a high-order dependency exists. The bowtie shape of the conditional histograms demonstrates the interscale dependency, and the tilted shape indicates a nondiagonal covariance structure.The marginal non-Gaussian distribution and scale-to-scale Markovian dependencies lead to practical HMT modeling for the precipitation reflectivity wavelet coefficients. The structure of the HMT model is shown in Fig. 5, where the solid points represent the wavelet coefficients and the hollow points denote the states of the coefficients. For example, w1 is the wavelet coefficient at the root node and its state is indicated as s1. Every node can be related to the nodes at coarser and finer scales; in particular, the node
Figure5. Quadtree structure used to represent the HMT model, where the black node denotes the wavelet coefficient wi and the white node denotes its state variable s; in particular, w1 and s1 are coefficients and their state at the root node. In the representation, the GMM is used as the PDF for each wavelet coefficient, and every node is related to nodes at the coarser and finer scales (Markov dependency). For example, the state and coefficient at node i depend on its parent node 
The Markov tree structure shown in Fig. 5 has two implications. First, the state of the wavelet coefficients at any node i depends on the state of the coefficients at the parent node
where
where A(i) and B(i) are the parameters that control the scale-to-scale variability of the process, e(i)~N(0,1) is the Gaussian white noise, and the term B(i)e(i) is called “process noise” with covariance
2
2.2. Model parameter estimation
It is necessary to estimate three types of parameters in the HMT model—namely, the state decision, variance of Gaussian distribution, and multiscale process controlling parameters. First, the state probabilities of the GMM for the original (coarser scale) wavelet coefficients are estimated using the EM algorithm. Using the estimated state probabilities, the state of the parent coefficient is then determined by calculating the expectation of the states within a local window:Considering the intrascale dependence of precipitation coefficients, a 5 × 5 window is employed. If
After the decision of the state, the variance of the Gaussian probability distribution is the next important parameter to be estimated. This parameter determines the precision of the shape of the GMM and the estimation of coefficient values. Due to the multifractal behavior and self-similarity of wavelet coefficients across scales (Deidda et al., 2006; Venugopal et al., 2006), the magnitude of variances decays exponentially as they are from coarse scales to finer scales. The relationship between the variances of consecutive scales can be described by
where j denotes the scale,
Decomposing the precipitation reflectivity images at four levels (j = 1–4), the parameters
Figure6. Scaling law (in log form) of the horizontal sub-band wavelet coefficients across scales for the Nanjing GR precipitation reflectivity image obtained at 0456:41 UTC 27 May 2008 (a) and for the precipitation image obtained at 0536:00 UTC 15 August 2010 (b). Variance decay across scales (in log-log scale) for states 0 and 1 follow a linear law and can be used to characterize the evolution of the GMM distribution in the HMT model.The
| H | V | D | |
| ${\alpha _0}$ | 3.1151 (3.0477–3.2701) | 3.0919 (3.0170–3.2545) | 3.8094 (3.7735–3.9369) |
| ${\alpha _1}$ | 2.5803 (2.4555–2.7211) | 2.5022 (2.4738–2.5814) | 2.7362 (2.6437–2.9221) |
Table1. Estimated decay parameters of variances for state 0 (
After the Gaussian mixture probability distribution prior model is obtained, the finer-scale wavelet coefficients of radar reflectivity can be estimated in a multiscale framework using Eq. (3). It can be seen from Fig. 4 that the parameters A(i) depend on the state covariances ∑ρ(i) and scale-to-scale cross covariances ∑(i,ρ(i)):
The B(i) can be estimated from the difference between the fine-scale wavelet coefficient and the coefficient at the next coarser scale of the high-resolution GR reflectivity image,
where Var(w(i)) denotes the variance of the coefficients w(i). B(i) is a function of scale, and the calculation should include the variance exponent decay across the scales.
The proposed interpolation algorithm will first capture and characterize the non-Gaussian structure (e.g., sharp variation and singularity) and interscale dependency (e.g., similarity across scales) of the radar reflectivity data, based on the multiscale wavelet analysis and HMT modeling. This characterization and HMT modeling are then used to estimate the value of the wavelet coefficients at the finest scale. The parameters of the HMT model will be estimated according to the description in section 2.2. Using the estimated parameters in the HMT model, the fine-scale wavelet coefficients for spaceborne radar can be generated according to Eq. (3) with Wiener filtering. The flow chart of the wavelet-based interpolation of spaceborne radar reflectivity data based on the HMT model is shown in Fig.7.
Figure7. Flow chart of the wavelet-based interpolation for spaceborne radar reflectivity with the HMT model as prior informationThe algorithm can be summarized as follows:
A set of matched GR reflectivity images dominated by convective precipitation is decomposed with a shift-invariant undecimated orthogonal wavelet transform and Haar wavelet base, from which the multiscale wavelet coefficients in horizontal, vertical, and diagonal sub-bands are obtained.
Due to the local coherence of the wavelet coefficients, the wavelet coefficients in each sub-band are divided into overlapping 5 × 5 local windows.
The parameters of the state probabilities
Based on the interscale dependence of wavelet coefficients across scales, the self-similarity index of the
Due to the undecimated processing of the wavelet transform used to avoid the aliasing effect, the spaceborne PR reflectivity images are interpolated using a bilinear algorithm to ensure that the pixel size of the interpolated spaceborne PR image is the same as that of the expected high-resolution image.
The interpolated spaceborne radar reflectivity images are decomposed, and the wavelet coefficients in each sub-band are divided with an overlapping 5 × 5 window. Then, the elements of a neighborhood of the wavelet coefficients are stacked according to a fixed order into a vector form y.
Using the prior HMT model parameters, the state m is determined using Eqs. (4) and (5), and the wavelet coefficient vector x at finer scale is estimated locally according to Eq. (9) using Wiener filtering for every neighborhood location that slides over the entire sub-band domain. In Eq. (9),
For all overlapping areas, the estimated coefficients are averaged to obtain the final wavelet coefficients at high-pass sub-bands. The high-resolution spaceborne PR image is obtained with the estimated wavelet coefficients using an inverse wavelet transform.
It is worth noting that the background effect of rainfall fields is significant. At each level of the wavelet decomposition, due to the convolution of the field with the wavelet scaling function, a set of zero values next to edges of the wetted areas becomes nonzero and subsequently the areas of nonzero pixels progressively grow from fine to coarse scales. For resolving this issue, the background pixels (zeros) of the coarse resolution spaceborne radar image remain zero in the finer scale image.
Figure8. Comparisons of radar reflectivity images from the Nanjing GR at 2302:00 UTC 25 July 2011: (a) the original high-resolution GR reflectivity image at resolution 1 km × 1 km; (b) the coarse-scale image at resolution 4 km × 4 km generated by smoothing and downsampling; (c) the GR image with bilinear interpolation; and (d) the high-resolution wavelet-based interpolation result with HMT prior modeling.Table 2 presents a statistical comparison of the images in Fig. 8 in terms of several quantitative parameters—namely, the mean error (MEAN), the root-mean-square error (RMSE), the peak signal-to-noise ratio (PSNR), and the Kullback–Leibler divergence (KLD). These parameters are calculated as follows (Gonzalez and Woods, 2007):
| MEAN | RMSE | PSNR | KLD | |
| GR with bilinear | 1.1242 | 3.6512 | 25.4204 | 0.1028 |
| GR with HMT | 0.2834 | 1.7751 | 28.8759 | 0.038 |
Table2. Error statistics obtained by comparing the original high-resolution GR precipitation reflectivity image obtained on 25 July 2011 (the reference) with the bilinearly interpolated GR image from the smoothed low-resolution GR (GR with bilinear for short) and that obtained by HMT prior modeling in the wavelet domain (GR with HMT for short)
where
For demonstrating the stability and robustness of the algorithm, more different convective precipitation cases from the Nanjing GR during the summer (from May to September) of 2011 were processed in similar way, as shown by the images in Fig. 8, and the statistical comparison results are presented in Table 3. The cases in Table 3 span a wide range of heavy precipitation with different spatial structures and geometrical shapes, ranging from clustered convective cells to frontal convective lines. The first column lists the dates of the precipitation cases. From Table 3, it can be seen that the proposed wavelet-based interpolation method generally outperforms the result obtained via bilinear interpolation. The MEAN decreases by about 60% and the RMSE decreases by about 20% on average, by comparing the results of the proposed method with the results of bilinear interpolation. In terms of the PSNR, the HMT method shows improvement on an order of 2 to 4 dB, and the KLD index is also improved (50%–70%). The wavelet-based HMT method can better reproduce the small-scale structures and variability features compared to the conventional spatial interpolation method, due to the inclusion of prior statistical information, such as the non-Gaussian marginal distribution of convective precipitation. Note that the algorithm can be used for images at other heights or from other radar stations, as long as the model parameters are correctly estimated. The performance for images at 1 km height is similar to those at 3 km height in Table 3 (not shown here). However, it should also be noted that the algorithm’s ability to properly reproduce the high-resolution structures and detailed features may be limited if the original low-resolution image is too smooth with little high-frequency information.
| Case | Methods | MEAN | RMSE | PSNR | KLD |
| 20110617 | GR with bilinear | 1.2530 | 4.5483 | 19.9765 | 0.0981 |
| GR with HMT | 0.3849 | 4.1850 | 22.5394 | 0.0484 | |
| 20110623 | GR with bilinear | 0.8260 | 3.3452 | 23.4702 | 0.1087 |
| GR with HMT | 0.3276 | 3.6212 | 27.3611 | 0.0640 | |
| 20110711 | GR with bilinear | 0.9756 | 3.1947 | 24.8578 | 0.0906 |
| GR with HMT | 0.2925 | 1.8755 | 27.0366 | 0.0583 | |
| 20110718 | GR with bilinear | 1.4812 | 4.1528 | 20.4720 | 0.1138 |
| GR with HMT | 0.4198 | 3.8849 | 22.6933 | 0.0752 | |
| 20110725 | GR with bilinear | 1.1242 | 3.6512 | 25.4204 | 0.1028 |
| GR with HMT | 0.2834 | 1.7751 | 28.8759 | 0.0380 | |
| 20110811 | GR with bilinear | 1.5021 | 4.4328 | 21.5048 | 0.1187 |
| GR with HMT | 0.5277 | 3.6794 | 24.0597 | 0.0445 | |
| 20110817 | GR with bilinear | 0.9565 | 3.8124 | 23.9025 | 0.0899 |
| GR with HMT | 0.3014 | 2.9140 | 26.2355 | 0.0341 | |
| Average | GR with bilinear | 1.1598 | 3.8768 | 22.8006 | 0.1032 |
| GR with HMT | 0.3624 | 3.1336 | 25.5430 | 0.0518 |
Table3. Error statistics obtained by comparing the original high-resolution GR precipitation reflectivity images (Cases) obtained from the Nanjing GR during the summer of 2011 with the bilinearly interpolated GR images from the smoothed low-resolution GR (GR with bilinear for short) and those obtained by HMT prior modeling in the wavelet domain (GR with HMT for short).
To further demonstrate the application of the HMT modeling and the proposed wavelet-based interpolation algorithm on spaceborne radar reflectivity, two cases of convective precipitation from TRMM PR were selected to evaluate the performance quantitatively. Figure 9 shows images for a convective storm that occurred in Nanjing on 27 May 2008. The storm was caused by the joint effects of the eastward movement of a low trough in the upper air, low-level shear, and southward cold air. The storm image obtained by TRMM PR with a resolution of 4 km × 4 km is shown in Fig. 9a, and the coincidental image from the Nanjing GR is shown in Fig. 9b, with a resolution of 1 km × 1 km. For comparison, the TRMM PR image is interpolated using the bilinear method, presented in Fig. 9c. Figure 9d shows the result obtained by the wavelet-based interpolation of the TRMM PR data from the resolution of 4 km × 4 km to the resolution of 1 km × 1 km using the proposed method with HMT prior modeling. It can be seen from Fig. 9c that the bilinear interpolation smooths the image without adequate detailed features of the storm and extreme intensity values, due to its low-pass filtering effect. The result presented in Fig. 9d demonstrates that the proposed method can estimate the small-scale detailed structures of the precipitation and incorporates more information from the TRMM PR data. The 1D reflectivity data shown in Fig. 9e demonstrate that the curve of the original TRMM PR image is relatively smooth, and the reconstructed curve shows more fluctuations, with the result much closer to the high-resolution GR data. This confirms that the reconstructed image can reproduce more detailed information, such as sharp gradients and extreme values, compared to the original low-resolution TRMM PR image.
Figure9. Comparisons of the reflectivity images for the case of convective precipitation in Nanjing at 0459:00 UTC 27 May 2008: (a) TRMM PR; (b) GR; (c) TRMM PR image with bilinear interpolation; (d) wavelet-based interpolated TRMM PR image with HMT prior modeling; (e) reflectivity profiles along the line in (a), where the red, black and blue lines denote the TRMM PR data, the GR data, and the wavelet-based interpolated data, respectively. For quantitative comparison, please refer to Table 3.Table 4 presents a quantitative comparison of the interpolation results for TRMM PR in Fig. 9. Although the reference high-resolution rainfall field is of course not available in practical cases, and differences exist in the reflectivity from the TRMM PR and the GR, it is instructive to make a quantitative assessment by comparing the TRMM PR interpolation results with the spatiotemporally matched GR data [the reference (f0)]. The reflectivity of the original low-resolution TRMM PR (Original PR), bilinearly interpolated TRMM PR (Bilinear), and wavelet-based interpolated TRMM PR with HMT modeling (HMT) methods are compared to the reference GR data. For comparison, the data pairs are selected in the area where both the TRMM PR and GR data are available. Note that to compute the quantitative parameters of the original low-resolution observations of TRMM PR, the size of those fields was extended to the size of the true field using nearest neighborhood interpolation. The results in Fig. 9 and Table 3 show that the proposed method produces high-resolution spaceborne radar precipitation fields that are closer to the structure of the high-resolution GR field, and that the HMT method considerably outperforms the simple spatial interpolation method, such as the result obtained by bilinear interpolation. Due to the difference from the two instruments (TRMM PR and GR), from Table 4 it can be seen that the degree of improvement is lower than the result in Table 2. The PSNR of the spaceborne radar image reconstructed with HMT modeling shows an improvement on the order of approximately 2–3 dB, and the KLD is improved by about 30%.
| MEAN | RMSE | PSNR | KLD | |
| Original PR | 2.8505 | 5.9736 | 19.0184 | 0.1158 |
| Bilinear | 2.7900 | 5.4182 | 19.7585 | 0.0951 |
| HMT | 1.7818 | 4.2253 | 21.9953 | 0.0781 |
Table4. Error statistics obtained by comparing the matched high-resolution GR precipitation reflectivity image obtained on 27 May 2008 (the reference) with the original TRMM PR image (Original PR for short), the interpolated PR image obtained using the bilinear algorithm (Bilinear for short), and that obtained by HMT prior modeling in the wavelet domain (HMT for short)
Figure 10 and Table 5 show the images and the quantitative statistical results for the case on 17 August 2011, when the precipitation was not included in the dataset for HMT modeling. From the interpolation results it can be seen that, with prior knowledge containing important statistical characteristics such as the non-Gaussian structure of convective precipitation data, the high-frequency features and small-scale geometrical structures can be recovered with the proposed method. An examination of the horizontal profiles presented in Fig. 10e shows that the wavelet-based interpolated reflectivity image exhibits obvious fluctuations and gradients compared to the low-resolution TRMM PR data, and its structure is more similar to the high-resolution GR image.
| MEAN | RMSE | PSNR | KLD | |
| Original PR | 3.2823 | 7.5839 | 17.0690 | 0.0848 |
| Bilinear | 2.8304 | 7.6223 | 16.8632 | 0.0754 |
| HMT | 2.4350 | 6.3491 | 18.0984 | 0.0523 |
Table5. Error statistics obtained by comparing the matched high-resolution GR precipitation reflectivity image obtained on 17 August 2011 (the reference) with the original TRMM PR image (Original PR for short), the interpolated PR image obtained using the bilinear algorithm (Bilinear for short), and that obtained by HMT prior modeling in the wavelet domain (HMT for short)
Figure10. Comparisons of the reflectivity images for the case of convective precipitation in Nanjing at 0815:00 UTC 17 August 2011: (a) TRMM PR; (b) GR; (c) TRMM PR image with bilinear interpolation; (d) wavelet-based interpolated TRMM PR image with HMT prior modeling; (e) reflectivity profiles along the line in (a), where the red, black and blue lines denote the TRMM PR data, the GR data, and the wavelet-based interpolated data, respectively. For quantitative comparison, please refer to Table 4.To better illustrate the improvement of the statistical properties of the thicker-than-Gaussian tails of precipitation gradients, in Fig. 11 we compare the probability distribution of the derivatives in the horizontal direction in terms of a Q–Q plot, where the x-coordinates are the standard normal quantiles and the y-coordinates are the quantiles of standardized reflectivity derivatives. All of the PDFs presented in Fig. 11 differ strongly from a Gaussian distribution (black dashed straight line), and the PDF of the high-resolution GR data (black dotted line) shows a more obvious heavy tail compared to the PDF of the low-resolution TRMM PR data (line with red crosses), while the PDF of the wavelet-based interpolated data with HMT modeling (blue diamonds) is in between. It can be seen that the wavelet-based interpolation method with HMT modeling can reproduce the heavy tail of the PDF of precipitation gradients, which are thicker than those of the TRMM PR PDF. It is clear that the high-resolution image is much finer, and the wavelet-based interpolated image is able to enhance the tails of the low-resolution precipitation reflectivity and reproduce the high gradients in the high-resolution precipitation field.
Figure11. Quantiles of the standardized horizontal derivatives versus standard normal quantiles, where red crosses, black circles and blue diamonds denote the original TRMM PR data, the matched high-resolution GR data, and the wavelet-based interpolated TRMM PR data with HMT modeling, respectively: (a) precipitation case on 27 May 2008; (b) precipitation case on 17 August 2011. The dashed straight line represents Gaussian distribution quantiles.In this study, a two-state Gaussian mixture distribution was used in the HMT modeling, which is conditionally Gaussian given another state. The property of the conditional Gaussian distribution is convenient and advantageous for linear optimal estimation problems. However, a two-state Gaussian mixture distribution is not sufficiently flexible. A wavelet-based HMT model with more than two states, and its application to radar reflectivity data, will be studied in further research.
Acknowledgements. This study was funded by the National Natural Science Foundation of China (Grant No. 41975027), the Natural Science Foundation of Jiangsu Province (Grant No. BK20171457), and the National Key R&D Program on Monitoring, Early Warning and Prevention of Major Natural Disasters (Grant No. 2017YFC1501401).
