HTML
--> --> -->Central Asia extends from the Caspian Sea in the west to northwestern China, and includes two of the world’s nine arid and semi-arid regions (Hulme, 1996). Hu et al. (2017) and Chen et al. (2018) found that precipitation exhibits an increasing trend over Xinjiang, but a decreasing trend over five states in Central Asia. Extreme precipitation accounts for 41.9% of the annual precipitation in the Tianshan Mountains (Yang, 2003) and is therefore one of the key factors affecting the security of water resources (Eekhout et al., 2018) and the stability of fragile ecosystems (Holmgren et al., 2006; Pueppke et al., 2018) in Central Asia. Zhang et al. (2017) found that the frequency and intensity of extreme precipitation increased significantly during 1938–2005 over Central Asia. Extreme precipitation in Xinjiang has also shown a significant increasing trend in both frequency and intensity (Yang, 2003; Li et al., 2015; Qi et al., 2015). Owing to the increasing trend of extreme precipitation and its dominant contribution to annual precipitation, it is important to systematically investigate the daily extreme precipitation over Central Asia, including Xinjiang.
Given that Central Asia features complex topography and a predominant rainfall distribution over the mountains (Hu et al., 2016; Guo et al., 2017), high-resolution gridded data or a large number of gauge-observation data is necessary to delineate extreme precipitation properties over Central Asia. However, the gauge-observation daily precipitation data from meteorological stations of the Global Historical Climatology Network—Daily (GHCN-D) are sparse and have declined substantially since 1991 over Central Asia due to the collapse of the Soviet Union (Hu et al., 2016; Zhang et al., 2017). The Asian Precipitation—Highly Resolved Observational Data Integration Towards Evaluation of Water Resources (APHRODITE) precipitation dataset is the only long-term (1950–2015) daily gridded precipitation dataset for Eurasia, and is interpolated from gauge-observation data (Yatagai et al., 2012). Although the faithfulness of APHRODITE precipitation data has been noted for different regions of the world, these studies were primarily based on monthly mean (Yatagai et al., 2012) or index-based (Villafuerte II and Matsumoto, 2015; Singh and Qin, 2019) comparisons, or the frequency of fixed precipitation values (Han and Zhou, 2012; He et al., 2019). Here, we assess the daily extreme precipitation from the APHRODITE dataset with gauge-observation data for the period 1960–90. Since APHRODITE incorporates most gauge-observation data, it is hard to find independent gauge-observation data. Therefore, this study is an analysis of the assimilation technique rather than a validation of the APHRODITE dataset relative to an independent ground truth. We hope the findings can provide some clues for the improvement of algorithms and some helpful information for scientists.
Previous studies have mainly focused on the faithfulness of gridded data in terms of error indices and precipitation hit bias. This study aims to evaluate daily extreme precipitation from the APHRODITE dataset over Central Asia, including Xinjiang, over the 30-year base period of 1961–90 in terms of the extreme precipitation threshold value and total number of extreme precipitation events. Their differences are explained on the basis of precipitation error. The overall performance of APHRODITE for extreme precipitation is given by the probability of detection (POD) and the extremal dependence index (EDI) (Ferro and Stephenson, 2011).
The remainder of this paper is organized as follows: Section 2 describes the data and analysis methods. Section 3 reports the results. Section 4 provides a discussion, followed by a summary of the results in section 5.
2.1. Study area
Figure 1 shows the location of the study area of Central Asia with topographic features and the distribution of the meteorological stations. In this study, Central Asia encompasses five countries—namely, Kazakhstan, Kyrgyzstan, Tajikistan, Turkmenistan and Uzbekistan—as well as the?Xinjiang?Uygur?Autonomous?Region in northwestern China. Central Asia is geographically high in the east and low in the west. The topography mainly includes deserts, plains, hills and mountains. The average altitude of the Pamirs Plateau and Tianshan Mountains is above 4000 m. Three major rivers—the Syr Darya, Amu Darya and Ili rivers—originate from the mountainous regions and flow into the lowlands and basins in the west. The climate of Central Asia is characterized by typical continental climate with annual precipitation ranging from 700 to 1200 mm in the mountainous areas, and semi-arid and desert climates with annual precipitation of about 150 mm in the lowlands and basins (Beck et al., 2018).
Figure1. Topographic features and the distribution of meteorological stations in Central Asia. Colored shading indicates the topography (unit: m). Blue lines indicate the major rivers. KAZ, Kazakhstan; TAD, Tajikistan; TUR, Turkmenistan; KYR, Kyrgyzstan; UZB, Uzbekistan; Xinjiang, Xinjiang Uygur Autonomous Region of China.2
2.2. Data
32.2.1. Gauge-observation precipitation datasets
The observed precipitation data come from two rain-gauge-observation datasets: GHCN-D, version 3.25, and the Chinese Surface Daily Climate Dataset, version 3.0. GHCN-D is an integrated database of daily climate variables summarized from ground stations across the globe, and contains records from over 100 000 stations in 180 countries and regions. The data undergo a series of quality checks before they are collected into the GHCN-D database. However, the GHCN-D dataset includes only 18 meteorological stations in Xinjiang, which is less than the number of Chinese national meteorological stations. To incorporate more meteorological stations, we adopt daily precipitation data from the Chinese Surface Daily Climate Dataset, version 3.0, provided by the China Meteorological Data Service Center (CMDC) (Given the lack of gauge-observation precipitation data over Central Asia since 1991, we focus on the period from 1 January 1961 to 31 December 1990. Furthermore, we chose meteorological stations with data available for at least 90% of the total number of days during 1961–90. With this criterion, we obtained a total of 253 meteorological stations within the five countries from the GHCN-D dataset and 63 meteorological stations in the Xinjiang region from the CMDC dataset (Fig. 1). Figure 2 shows the percentage of the total number of days with available precipitation data in each year for the 316 meteorological stations. The average percentage of the total number of days with available precipitation data is 97.3%. Station No. 51053 and above have a correct data rate of nearly 100%.
Figure2. Percentage of total number of days with available precipitation data in each year for 316 gauge-observation stations in Central Asia over 1961–90.3
2.2.2. Gridded precipitation dataset
The APHRODITE project aims to provide long-term, high-resolution daily gridded precipitation and temperature datasets over Asia. The gridded precipitation dataset is interpolated from Global Telecommunication System (GTS)-based data from gauge observations, data precompiled by other projects or organizations, such as other national hydrological and meteorological services, and data from individual collections. The interpolation of gauge-observation data to gridded data is applied to the ratio of daily precipitation to daily climatology using a Spheremap-type scheme, which considers daily-variation weighting based on the rainfall distribution. Considering the current study period of 1961–90, we use the gridded daily precipitation over Russia/northern Eurasia (APHRO_RU_V1101) from APHRODITE. The APHRO_RU_V1101 daily precipitation dataset is on a 0.25° × 0.25° latitude–longitude grid and covers northern Eurasia for the period 1951–2007. We also use the ratio of 0.05° grid boxes containing stations provided by this dataset.Compared with the GTS analysis and the Global Precipitation Climatology Centre (GPCC) full archive product, version 4 (Schneider et al., 2008), the APHRODITE precipitation data are more accurate over Central Asia and the mountainous areas, as the dataset uses more gauge-observation data. Furthermore, a considerable number of studies have used APHRODITE as a reference dataset for comparison or modeling. Readers are referred to Yatagai et al. (2012) for more information.
2
2.3. Methods
32.3.1. Definition of extreme precipitation
Given the relatively large spatial variation of precipitation over Central Asia, we adopt percentile-based values rather than fixed absolute values to define the extreme precipitation threshold value for each station or grid point. In addition, considering the differences in the general circulation and precipitation phase between summer and winter, we separate each year into the boreal cool (October to April) and warm (May to September) seasons. The percentile-based extreme precipitation threshold value for each station or grid point is defined based on the following procedure:(1) Daily precipitation data of 1.0 mm or more are sorted in ascending order (
(2) The value corresponding to the percentile
where
in which
Noting the complicated interpolation of APHRODITE, we simply pick up the grid point nearest to the gauge-observation station to avoid additional bias induced by our interpolation (Qi et al., 2015; Hu et al., 2018). The average distance between each gauge-observation station and its nearest grid point of APHRODITE is 9.1 km. For the extreme precipitation to be more comparable between two datasets, daily precipitation of an APHRODITE grid point is removed if there is a missing value in its nearest gauge-observation station.
Since this study evaluates the APHRODITE data according to the gauge-observation data, we consider the grid point is identical to its nearest gauge-observation station assuming that the distance between them could be negligible for the extreme precipitation detection. Spatial distributions are generated by interpolating the gauge-observation and the APHRODITE values into a 0.07 × 0.15 latitude/longitude grid using the geographic information of the gauge-observation station regardless of the APRHODITE grid point information. The interpolation method used here is radial basis function interpolation (UCAR Unidata/MetPy:
3
2.3.2. Statistical evaluation metrics
To assess the extreme precipitation detection ability of the APHRODITE dataset, we use the POD and the EDI to evaluate the fidelity of the APHRODITE dataset. The POD, false detection ratio (FDR) and EDI are calculated based on a contingency table, as shown in Table 1, and defined as:| Event observed | Non-event observed | Total | |
| Detected | H | F | H + F |
| Non-detected | M | N | M + N |
| Total | H + M | F + N | $ n $ |
Table1. Contingency table of extreme precipitation detected by the APHRODITE dataset.
where the number of hits of extreme precipitation (H), missing (M), false detections (F) and correct negatives (N) are defined in Table 1.
The POD represents the ratio of the number of extreme precipitation events detected correctly by the APHRODITE dataset; the FDR denotes the proportion of extreme precipitation events in which APHRODITE identifies extreme precipitation when the gauge-observation station does not. Compared with the POD and FDR, the EDI is base-rate independent, asymptotically equitable and non-degenerating (Ferro and Stephenson, 2011). The POD and FDR range from 0 to 1, and the EDI falls between ?1 and 1. For a perfect detection, the POD and EDI is 1, while the FDR is 0.
3.1. Spatial distribution of extreme precipitation
In order to describe the spatial characteristics of extreme precipitation events, we compute probability density function (PDF) distributions of extreme precipitation station numbers on each day for the cool and warm seasons, which are shown in Fig. 3. Daily extreme precipitation station numbers are primarily between 1 and 3 (i.e., below 1% of the total number of stations), with percentages of 59.16% and 70.20% for the cool and warm seasons, respectively. The result suggests that the extreme precipitation events over Central Asia are mainly very localized. In comparison with the cool season, the PDF distribution of the warm season shifts right substantially to the bins with small numbers of stations, indicating more localized extreme precipitation events in the warm season.
Figure3. PDF of extreme precipitation station Nos. on each day for the (a) cool and (b) warm seasons.Figure 4 shows the spatial distribution of extreme precipitation threshold values during the boreal cool and warm seasons for the observations and the APHRODITE data. In general, the maxima of extreme precipitation threshold values are distributed along the mountains in Central Asia in both the observations and the APHRODITE data. In the cool season, the amplitudes of extreme precipitation threshold values are above 6 mm d?1 and reach up to 24 mm d?1 (Fig. 4a). The maxima are situated to the north of the Plateau of Iran, the Hindu Kush Mountains, Pamir, the western Tianshan Mountains, and Kazakhskiy Melkosopochnik. The spatial distribution of APHRODITE basically resembles that of the observations but with smaller threshold values (Fig. 4b). Large biases of APHRODITE with respect to observations mainly occur over the north of the Plateau of Iran, Kazakhskiy Melkosopochnik, and Xinjiang (Fig. 4c). In contrast, the warm season features larger extreme precipitation threshold values and broader maxima areas (Fig. 4d). The maximum over Pamir extends northwestward to the Aral Sea and additional maxima are seen over the east to the Caspian Sea and the eastern Tianshan Mountains. Although the spatial distribution of APHRODITE concurs with the observations, the negative biases in the warm season are nearly double their cool season counterparts (Figs. 4e and f). This underestimation of daily extreme precipitation threshold values agrees with the underestimation of monthly and annual precipitation of the GPCC, Climate Research Unit, and Willmott and Matsuura datasets (Hu et al., 2018). Unlike the monthly and annual precipitation biases, which are the largest over the mountains, the biases in daily extreme precipitation threshold values are smaller over the mountains than the lowlands.
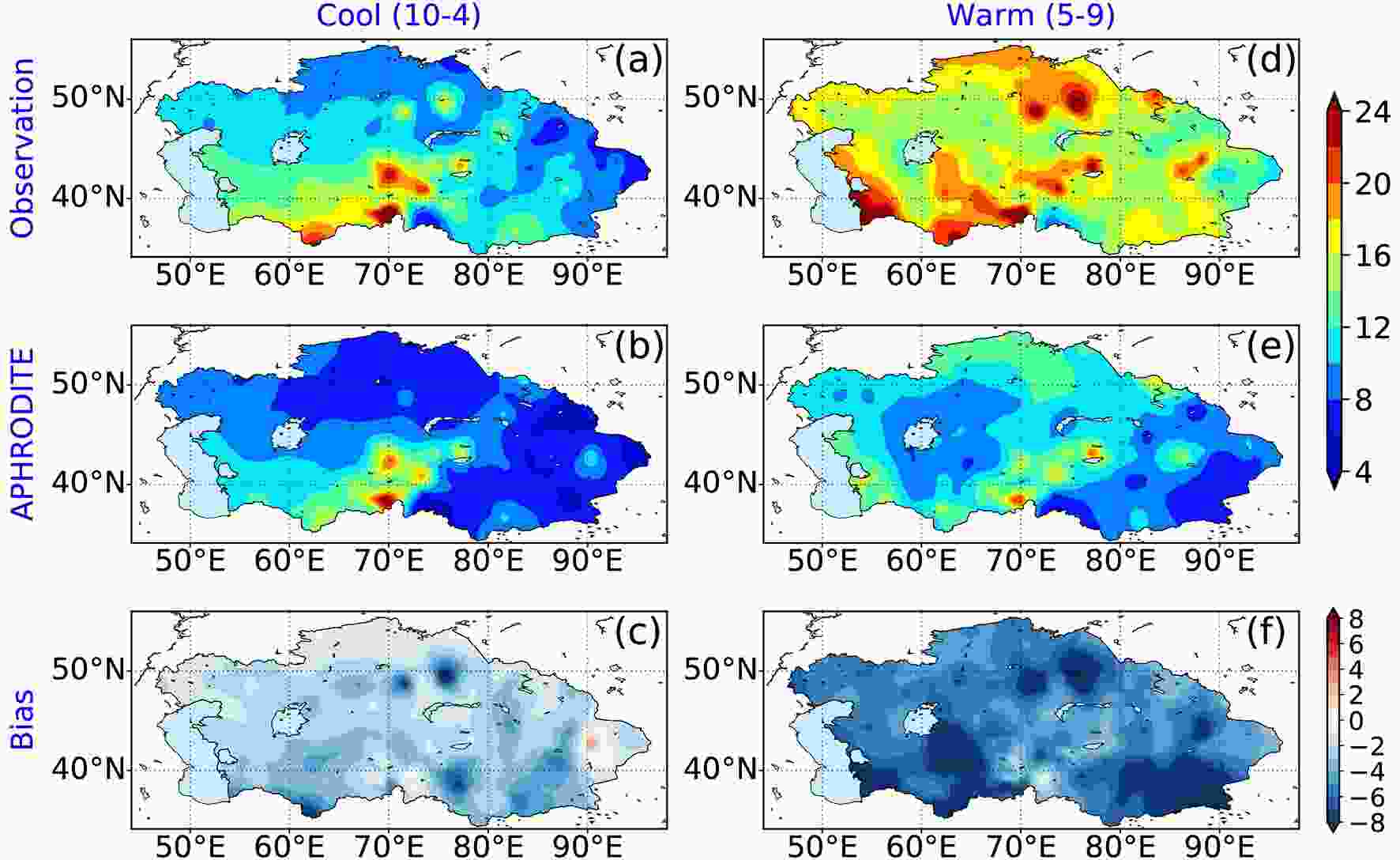Figure4. Spatial distribution of extreme precipitation threshold values (units: mm d?1) in the boreal cool season for (a) observations and (b) APHRODITE, and (c) the bias between (b) and (a). (d–f) As in (a–c) but for the warm season.Figure 5 shows the spatial distribution of the total numbers of extreme precipitation events during the cool and warm seasons over 1961–90 for the observations and the APHRODITE data. Similar to the distribution of extreme precipitation threshold values, extreme precipitation primarily occurs over the mountains. In contrast, the biases mainly occur over the main regions of extreme precipitation. The cool season features a region of abnormally high numbers of extreme precipitation (up to 121 days) extending from the north of the Hindu Kush Mountains via Pamir to the Altai Mountains, with two low centers to its east and west (Fig. 5a). In addition, moderately high numbers of extreme precipitation are observed over Kazakhskiy Melkosopochnik and to the south of the Ural Mountains. The distribution of total numbers of extreme precipitation in the APRHODITE data is consistent with the observations but with a larger magnitude (Fig. 5b). The overestimation regions coincide with the maxima of extreme precipitation occurrence and 29.4% of the total number of grid points have biases above 5 days (Fig. 5c). In the warm season, the distribution of extreme precipitation occurrence numbers is more regional and more northward than the cool season counterparts (Fig. 5d). The maxima are confined to the Tianshan Mountains and the northern border of Kazakhstan. Furthermore, there is a broader small number of extreme precipitation over the Turan Plain. Although the distribution of APHRODITE resembles that of the observations, the biases in the warm season are greater than those in the cool season (Fig. 5f). The percentage of grid points with biases beyond 5 days increases to 38.6%.
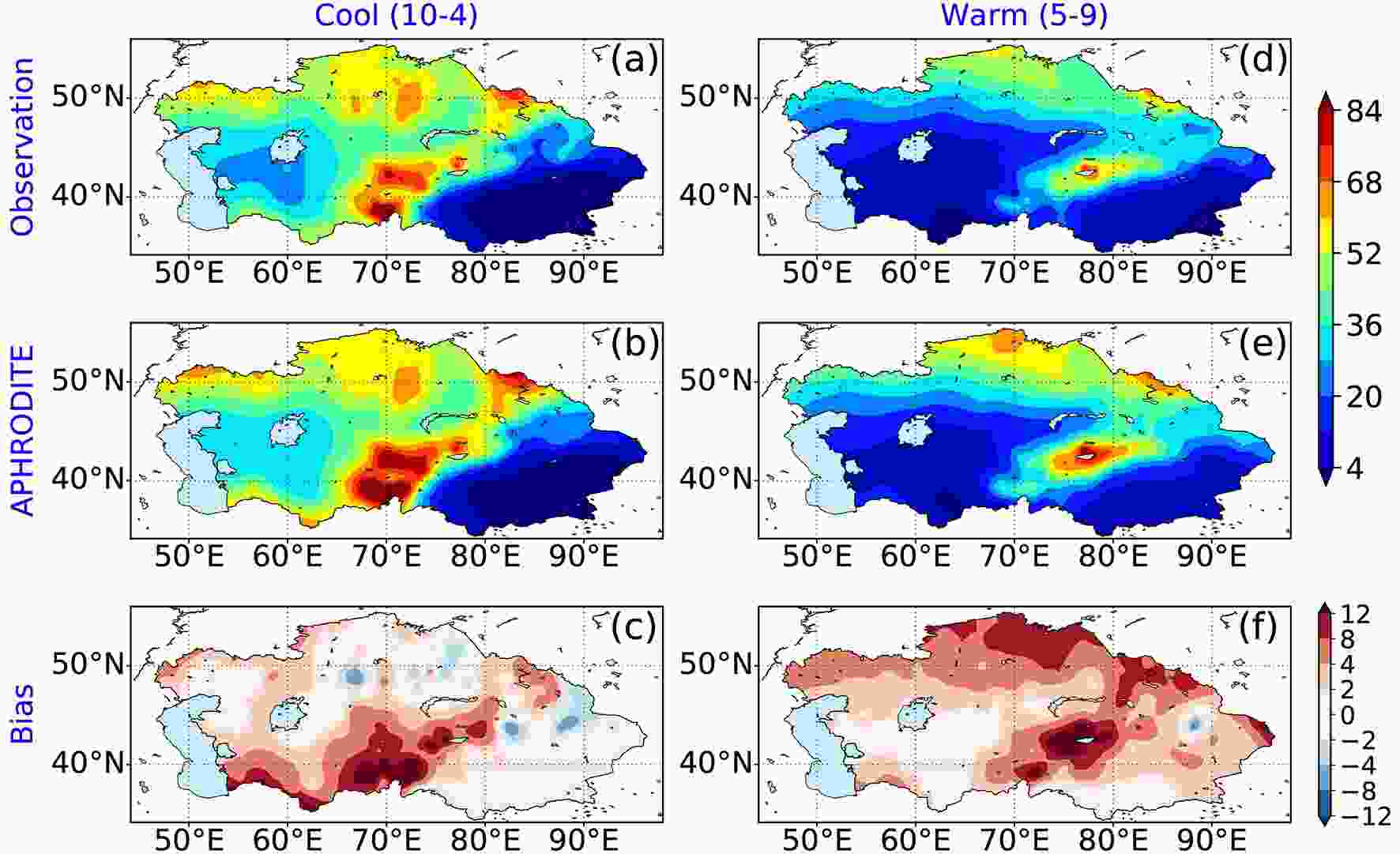Figure5. As in Fig. 4 but for the total numbers of extreme precipitation events over 1961–90.Figure 6 shows time series of the total numbers of extreme precipitation events in each month derived from the 316 gauge-observation stations and APHRODITE grid points for the cool and warm seasons. The time series of APRHODITE are basically consistent with those of gauge observations, with correlation coefficients of 0.98 and 0.95 at the 99.9% confidence level for the cool and warm seasons, respectively. Considering the cool season, APHRODITE tends to overestimate the large numbers of extreme precipitation events, but underestimate the small numbers of events (Fig. 6a). In contrast, the warm season features more evident overpopulation of both the small and large numbers of extreme precipitation events (Fig. 6b).
Figure6. Time series of the total numbers of extreme precipitation events in each month derived from the 316 gauge-observation stations (blue) and APHRODITE grid points (red) for the (a) cool and (b) warm seasons.2
3.2. Possible causes of the bias
To illustrate the potential causative factors of the aforementioned lower threshold values and higher occurrence frequencies of extreme precipitation in APHRODITE relative to the observations, we calculate the PDFs and total number of wet days (> 1 mm d?1) from the two datasets. Figure 7 shows scatterplots and PDFs of the observation and APHRODITE precipitation data during the cool and warm seasons. The APHRODITE daily precipitation is highly correlated with the gauge-observation precipitation, which is significant at the 99% confidence level (
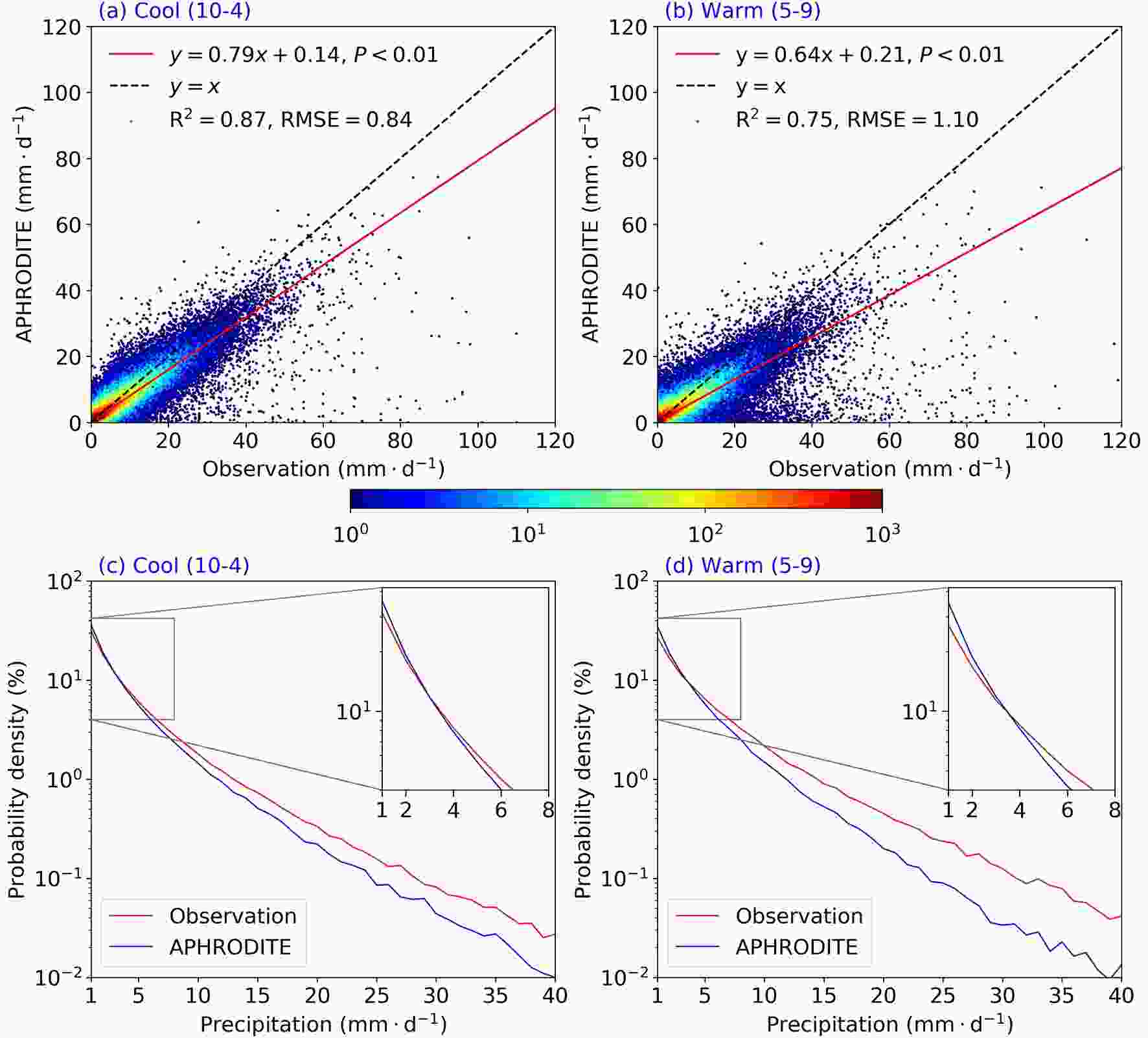Figure7. Density colored scatterplots of precipitation from observations and APHRODITE during the (a) cool and (b) warm seasons. Colors indicate the total numbers and the red line denotes the linear regression between the observed precipitation and the APHRODITE precipitation. PDFs of precipitation for observation (red) and APHRODITE (blue) during the (c) cool and (d) warm season.Figure 8 shows the spatial distribution of the biases in the total number of wet days (> 1 mm d?1) between APHRODITE and the observations. The total number of wet days is generally larger in AHPRODITE, ranging from 20 to 350 days. The spatial distributions strongly resemble the biases of the total numbers of extreme precipitation (Figs. 5c and f). As the interpolation of APHRODITE precipitation is based on the rainfall distribution, the precipitation at gauge-observation stations adjacent to a grid point of APHRODITE could be carried into the grid point even though its nearest gauge-observation station does not have rainfall. However, such interpolation could overestimate the precipitation amplitude at a grid point if there is a precipitation maximum at its nearest gauge-observation station. These two deficits tend to be more pronounced over the regions with larger annual precipitation (i.e., the larger extreme precipitation threshold values), resulting in more evident overestimation of extreme precipitation.
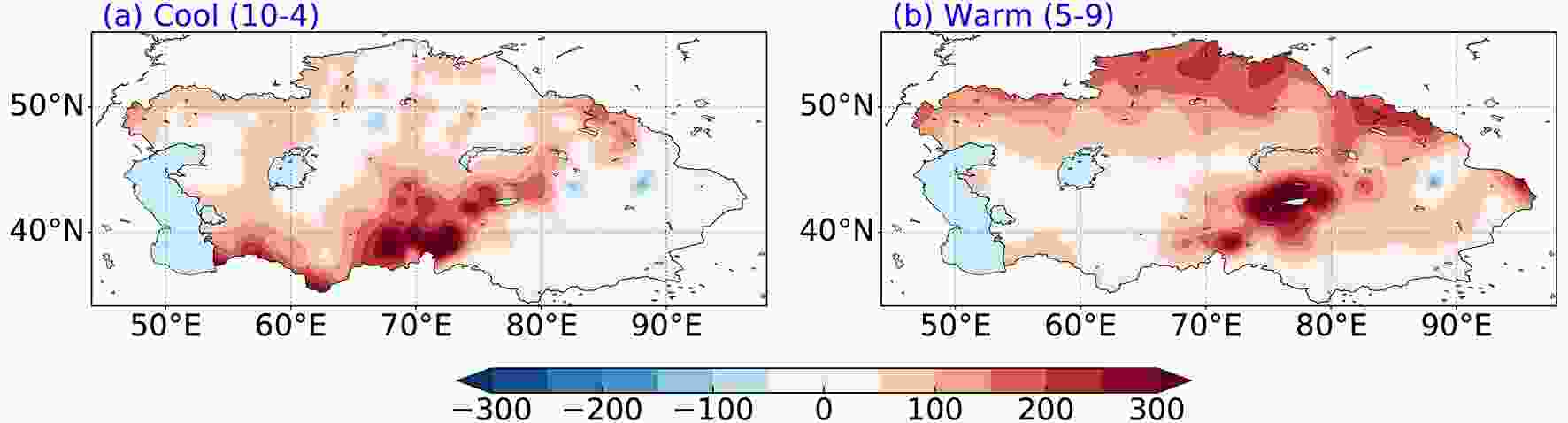Figure8. Spatial distribution of biases in the total number of wet days (>1 mm d?1) between APHRODITE and observations in Central Asia during (a) the cool season and (b) the warm season of 1961–90.Considering the cool season, the average precipitation and standard deviation are 4.4 mm d?1 and 5.53, respectively. In comparison with the cool season, the warm season features more precipitation (5.5 mm d?1) with larger variance (6.67). The interpolation induces a more evident shift of the precipitation distribution “spectrum” to smaller amplitudes for the warm season than for the cool season (Fig. 7), which result in smaller extreme threshold values and stronger overpopulation of extreme precipitation relative to the gauge observations. Therefore, the biases are much higher in the warm season than in the cool season.
2
3.3. Fidelity of the representation of extreme precipitation
Figure 9 shows the spatial distribution of the POD of APHRODITE extreme precipitation in Central Asia. In the cool season, the POD values are generally above 0.70 over most parts of Central Asia except Kazakhskiy Melkosopochnik and the Tianshan Mountains in Xinjiang (Fig. 9a). The mean POD in Central Asia is 0.70, which suggests that 70% of the observed extreme precipitation is captured correctly by APHRODTE. Despite overestimating the number of extreme precipitation events over the mountains (Figs. 5c and f), a maximum above 0.85 is seen over Pamir. As the POD depends on the total number of extreme precipitation events in the observations, the overestimation of extreme precipitation events increases the likelihood of a high POD.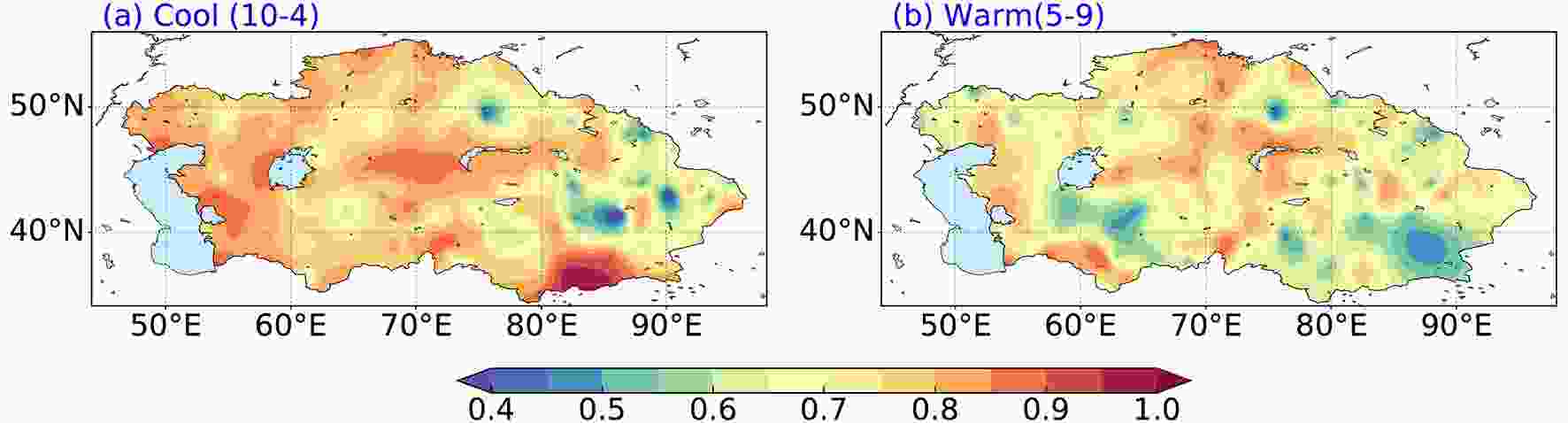
Figure9. Spatial distribution of the POD of extreme precipitation derived from APHRODITE in Central Asia during the (a) cool season and (b) warm season.Similar to the aforementioned larger biases in the warm season, the warm season has smaller POD values than the cool season, with a mean value of 0.65 (Fig. 9b). There are additional minima in the Turan Lowlands (0.53) and the Tarim Basin (0.48), which overlap with small threshold values and low numbers of extreme precipitation events (Figs. 4f and 5f). High PODs corresponding to overestimated extreme precipitation and a low POD corresponding to small numbers of extreme precipitation events suggests that the POD depends on the total number of extreme precipitation events.
Figure 10 shows the spatial distribution of the EDI of extreme precipitation for APHRODITE during the cool and warm seasons. Compared with the POD, the EDI is more comparable between the low and high numbers of extreme precipitation events. The amplitudes of the EDI are obviously larger than the POD. In the cool and warm seasons, 84.2% and 64.6% of grid points have EDI scores above 0.8, respectively. Three minima remain over northern Kazakhstan and central Xinjiang. In general, the identification of extreme precipitation in APHRODITE can be regarded as considerably reliable.
Figure10. As in Fig. 9 but for EDI. Markers in (a) indicate the locations of station No. 36335 (cross), 51581 (circle) and 51655 (triangle).As can be seen from Fig. 1, there are some stations within a single grid box. To quantify the impact of the number of stations included in a single grid box, we compute the averages of the extreme precipitation biases, POD and EDI stratified by different number of stations within each of 316 grid boxes. The grid boxes mainly include 1 and 2 gauge-observation stations, which are 191 and 110, respectively. Besides, 13 grid boxes encompass 3 stations, while only 2 grid boxes include 5 stations. Table 2 shows the averages of extreme precipitation biases, POD and EDI stratified by 1, 2, 3 and 5 stations within a grid box. As subsequently shown in the discussion, there are two stations not incorporated into APHRODITE and two stations with 5-year anomalous values, where the APHRODITE grid points exhibit relatively low performances. These four stations are only related to four grid boxes that include 3 stations. To be more comparable, we have removed these four stations and grid points for the grid box with 3 stations. There is an overall improvement of APHRODITE in representing extreme precipitation if the grid box incorporates 2 and 3 gauge-observation stations. Although the grid boxes with 5 stations have some improvements in POD and EDI with respect to those with 1 station, they exhibit an overall degradation compared to those with 2 and 3 stations. Such degradation could possibly be attributed to the impact of topography since these two grid boxes are both in the Trans-Ili Alatau Mountains with altitudes of 3185 m and 3966 m, respectively.
| Number of stations | Δp95 | ΔEvents | POD | EDI | |||||||
| Cool | Warm | Cool | Warm | Cool | Warm | Cool | Warm | ||||
| 1 | ?2.93 | ?5.98 | 4.13 | 5.83 | 0.74 | 0.68 | 0.84 | 0.78 | |||
| 2 | ?2.10 | ?5.24 | 4.20 | 4.74 | 0.80 | 0.76 | 0.89 | 0.86 | |||
| 3 | ?1.28 | ?3.93 | 4.42 | 6.83 | 0.79 | 0.78 | 0.89 | 0.88 | |||
| 5 | ?3.34 | ?4.60 | 1.50 | 7.00 | 0.79 | 0.72 | 0.90 | 0.85 | |||
Table2. Average biases of extreme threshold values (Δp95) and total number of extreme precipitation events (ΔEvents), POD and EDI stratified by the number of stations within a grid box for the cool and warm seasons.
We compare the gauge-observation precipitation of station No. 36335 with the precipitation of its nearest grid point in APHRODITE in the warm season, which is shown in Fig. 11. Although the number of extreme precipitation events is comparable between the two datasets, the extreme precipitation events do not exactly overlap with each other. The observational data show that extreme precipitation dominates during 1961–65. In APRHODITE, this station is ruled out for this period after a series of quality control checks conducted by the APRHODITE gridding algorithm. As such, the predominant extreme precipitation events in the observations during 1961–65 are absent in APHRODITE. As a result, the extreme precipitation threshold value declines dramatically from 38.2 mm d?1 for the observations to 12.1 mm d?1 for APRHODITE, resulting in more extreme precipitation since 1966 in the APRHODITE dataset. Therefore, station No. 36335 has smaller values for both the POD and EDI. Similarly, the quality control processes of APHRODITE also rule out some of the extreme precipitation in the gauge observations, particularly in the desert areas, which results in relatively lower POD and EDI scores and higher negative biases of the threshold in the Turan Lowlands and the Tarim Basin. We have carefully checked the other 315 stations, and there is another station (No. 35582) similar to No. 36335.
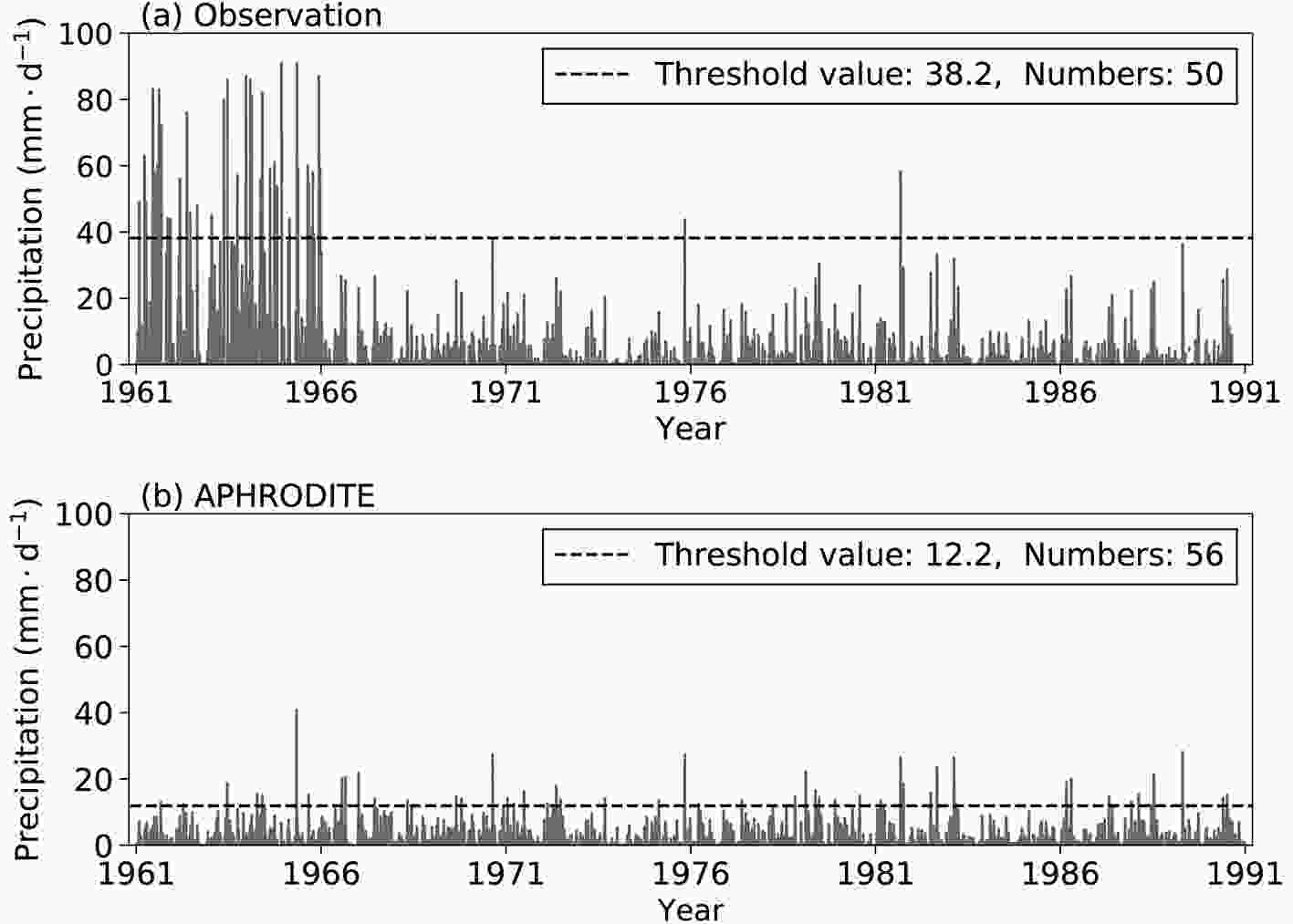Figure11. Time series of daily precipitation for (a) station No. 36335 and (b) its nearest grid point in APHRODITE in the warm season during 1961–90. The dashed lines represent the extreme precipitation criterion.Figure 12 shows the distribution of the distance between each observation station and its nearest grid point in APHRODITE. The distance shows a normal distribution with a mean value of 9.1 km and a standard deviation of 3.6. The magnitude of the distance ranges between 1.1 km and 16.7 km. APHRODITE uses a modified distance-weighting interpolation method (Yatagai et al., 2012, 2018), which partially contributes to the underestimation of precipitation and extreme precipitation extreme values. As we mainly focus on the representation of extreme precipitation rather than the precipitation errors, we assume that such a distance is negligible for the detection of extreme precipitation.
Figure12. Histogram of distance between each observation station and its nearest grid point in APHRODITE. The black line indicates the PDFs derived from a normal distribution fitting method.The number of extreme precipitation days is not comparable between the cool and warm seasons, which are 212 × 30 and 153 × 30, respectively. Strictly speaking, we should not directly compare the distribution of extreme precipitation between two seasons. However, this study compares the distribution of extreme precipitation in the warm season with that in the cool season to highlight the signatures of extreme precipitation and make the study more concise.
The APHRODITE dataset is highly correlated with the gauge-observation precipitation data and can reproduce the spatial distributions of the extreme precipitation threshold value and occurrence number. For the cool season, the maxima of the extreme precipitation threshold value and occurrence number reside over the mountainous areas, such as the Hindu Kush Mountains, Pamir, the western Tianshan Mountains, and Kazakhskiy Melkosopochnik. APHRODITE tends to underestimate the extreme precipitation threshold value, particularly over the regions with moderate threshold values. In contrast, APHRODITE overestimates extreme precipitation over the regions with greater threshold values. Considering the temporal feature, APRHODITE is basically consistent with gauge observation with an overall overpopulation, particularly during the time with large numbers of extreme precipitation events. The distribution-based interpolation of precipitation results in APHRODTE overestimating light rainfall and underestimating heavy rainfall. Therefore, APHRODITE underestimates the extreme precipitation threshold value and overestimates the total number of extreme precipitation events, particularly over the mountainous areas. Since there is a more powerful shift of the precipitation distribution “spectrum” to smaller amplitudes for the warm season than for the cool season, the biases are more evident in the warm season than the cool season.
The POD and EDI reveal that APHRODITE has a fairly good capability of detecting extreme precipitation, particularly in the cool season. The number of sampling grid points with POD values above 0.7 account for 79.7% of the grid points in the cool season and 60.7% in the warm season, while grid points with EDI values above 0.8 account for 84.2% and 64.6% of the grid points in the cool and warm seasons, respectively.
This study has primarily focused on the representation of extreme precipitation in APHRODITE during 1961–90 and interpreted the biases from the perspective of the precipitation distribution. The interannual and interdecadal variabilities of extreme precipitation and the corresponding large-scale meteorological patterns remain to be unexplored. To address these questions, our future work will extend the study period to 2015 to investigate the temporal variability of extreme precipitation on the basis of the current extreme precipitation threshold value, as well as the underlying physical mechanisms, using the APHRODITE dataset with satellite precipitation data instead of gauge observation data. Based on our findings, it is appropriate to perform extreme analysis with APHRODITE in places that incorporate gauge-observation data. Extremes over places without incorporated gauge observations should be examined carefully with atmospheric circulations. The total number of gauge-observation stations over Central Asia experienced two drastic declines in 1991 and 2006, respectively, which is the same situation for APHRODITE (Yatagai et al., 2012, 2018). It is unrealistic to conduct extreme analysis over Central Asia after 2007 using the gauge-observation data. Therefore, it would be better to use the APHRODITE dataset with satellite precipitation data that are calibrated with the APRHRODITE data over their overlapping years, such as 1998–2004 (Yatagai et al., 2014).
Acknowledgements. The authors are grateful to the two anonymous reviewers for their valuable comments and suggestions. This research was funded by the National Key Research and Development Program of China (Grant No. 2018YFC1507101), the National Natural Science Foundation of China (Grant Nos. 41861144014, 41875078 and 41630424) and the National Key Research and Development Program of China (Grant No. 2016YFA0601501). We acknowledge Hirosaki University for providing the APHRODITE precipitation data
