HTML
--> --> -->There have been several generations of coupled climate models (Yu et al., 2002, 2004, 2011; Bao et al., 2013; Li et al., 2014) developed at the State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences (LASG/IAP, CAS). The low-resolution version of the Chinese Academy of Sciences Flexible Global Ocean–Atmosphere–Land System model, version f3-L (CAS FGOALS-f3-L) is one of the latest versions that participated in CMIP6. The CMIP6 historical simulations with this model were completed in 2019, and the model outputs have been submitted to the Earth System Grid (ESG) data server (
Section 2 presents a detailed description of the model and the design of the historical experiments. Section 3 presents the location and format of the datasets. Section 4 presents basic technical validation of the outputs from CAS FGOALS-f3-L. Section 5 provides usage notes. Finally, a summary is given in section 6.
2.1. Model description
CAS FGOALS-f3-L is a fully coupled climate system model that consists of four component models and one coupled module. The atmospheric model is version 2.2 of the Finite-volume Atmospheric Model of the IAP/LASG (FAMIL) (Zhou et al., 2015; Li et al., 2019), which is the latest generation atmospheric general circulation model developed at LASG/IAP, and employs an efficient dynamical core of finite volume (FV3) (Lin, 2004; Putman and Lin, 2007). The oceanic model is the LASG/IAP Climate System Ocean Model, version 3.0 (LICOM3) (Liu et al., 2012; Li et al., 2017), which is the latest generation oceanic general circulation model developed at LASG/IAP and employs the orthogonal curvilinear coordinate. The land model is the Community Land Model, version 4 (CLM4) (Lawrence et al., 2011), and the sea-ice model is the Community Ice Code, version 4 (CICE4) (Hunke and Lipscomb, 2010). All the component models are coupled via the NCAR Coupler 7 (Craig et al., 2011). Compared with the last version FGOALS-s2 (Bao et al., 2013) in CMIP5, the main changes in CAS FGOALS-f3-L are the atmospheric model and oceanic model. The atmospheric model is updated from the Spectral Atmospheric Model of IAP/LASG, version 2 (SAMIL2) (Bao et al., 2010) to FAMIL, and the oceanic model is updated from LICOM2 (Liu et al., 2012) to LICOM3. Besides CAS FGOALS-f3-L, there is another climate system model from LASG/IAP in CMIP6, which is CAS FGOALS-g3. The main difference between the two models is the atmospheric model employed; the atmospheric model of CAS FGOALS-g3 is the Grid-point Atmospheric Model of IAP/LASG (GAMIL) (Li et al., 2013).The atmospheric model of CAS FGOALS-f3-L, FAMIL, is established on a finite volume dynamical core on a cubed-sphere grid, with six tiles across the globe and 96 grid cells (C96) for each tile. Globally, there are 384 grid cells in longitude and 192 grid cells in latitude, making the horizontal resolution approximately equal to 1°. In the vertical direction, there are 32 layers using hybrid coordinates, and the top layer of the model is at 2.16 hPa. Several advanced physical schemes have also been employed in the model, which are specifically documented in He et al. (2019). The outputs of FAMIL uploaded to the ESG are postprocessed and interpolated into a longitude–latitude grid of 288 zonal grid cells and 180 meridional gird cells.
For the oceanic model, LICOM3, since the orthogonal curvilinear coordinate is introduced into this version, a tripolar grid with the North Pole split into two poles on two continents at (35°N, 114°E) and (35°N, 66°W), respectively, can be used, which eliminates the singularity of the primitive equations at the North Pole in the normal longitude–latitude dynamic framework and thus improves the related circulations in the Arctic Ocean (Li et al., 2017). The preserved shape advection and the implicit vertical viscosity are also employed in this version. For physical packages, a tidal mixing (Laurent et al., 2002) and a buoyancy frequency (N2) related thickness diffusivity (Ferreira et al., 2005) are introduced into the model, as well as a new vertical diffusivity (Canuto et al., 2001, 2002) and isopycnal mixing (Gent and Mcwilliams, 1990). The low-resolution LICOM3 used here has 360 grid cells in the zonal direction and 218 grid cells in the meridional direction, which is also a globally horizontal resolution approximately equal to 1°, with uneven enhanced meridional resolution from 0.5° to 1° near the equator. In the vertical direction, the resolution is 30 layers, which is 10 m per layer in the upper 150 m and divided in uneven vertical layers below 150 m.
The land model, CLM4, has a longitude–latitude grid of 288 grid cells in longitude and 192 grid cells in latitude, which is approximately equal to 1° globally. The grid of the sea-ice model, CICE4, is the same as LICOM3, which is also a 360 × 218 tripolar grid. Several codes of CICE4 have been adjusted to adapt the tripolar grid of LICOM3. The sea ice in CICE4 is divided into five categories according to ice thickness in each grid cell to better simulate the freezing and melting processes.
2
2.2. Experiment design
Before the historical experiments, the pre-industrial control experiment (piControl) is conducted using the external forcing fixed at the level before industrialization. The piControl experiment is conducted for a long period such that the deep ocean approaches a steady state. Then, the historical experiments are conducted from the variant stable fields generated in the piControl, using the same historical forcing data provided by CMIP6. In this study, as recommended by CMIP6, three ensemble historical experiments are conducted to more clearly identify forced signals emerging from natural variability (Eyring et al., 2016). The three ensembles, labeled as r1i1p1f1, r2i1p1f1 and r3i1p1f1, start from the restart fields generated in the piControl experiment on 1 January of the 600th, 650th and 700th model year, respectively, as the piControl experiment approaches steady state in the deep ocean after about 500 years. All the experiments are shown in Table 1. The historical forcing data provided by CMIP6 represent the observation-based estimates of solar radiation, GHG concentration, land-use change, etc., which are effective to the external forcing of the climate system (Matthes et al., 2017; Meinshausen et al., 2017). The forcing data cover the period from 1850 to 2014, in which the historical experiments are conducted. The outputs of the three ensembles from 1850 to 2014 are postprocessed according to the standards of ESG and then submitted to CMIP6.| Experiment_id | Label | Initial fields | Period | Forcing |
| historical | r1i1p1f1 | 1 Jan, 600th year in piControl | 1850–2014 | CMIP6 historical forcing data |
| historical | r2i1p1f1 | 1 Jan, 650th year in piControl | 1850–2014 | CMIP6 historical forcing data |
| historical | r3i1p1f1 | 1 Jan, 700th year in piControl | 1850–2014 | CMIP6 historical forcing data |
Table1. Experiment designs.
There are monthly mean outputs and daily mean outputs available in the datasets. The monthly outputs of different component models are stored in different folders with “mon” in its name (e.g., “Amon” is for the monthly outputs of the atmospheric model), and the daily mean outputs are stored in the folder “day”. The monthly mean outputs of the atmospheric model contain 41 variables including air temperature, velocity, precipitation, radiation, etc., and the data size is 101 GB. The monthly mean outputs of the oceanic model contain 44 variables including sea temperature, salinity, currents, meridional stream function and heat transports, etc., and the data size is 152 GB. The monthly mean outputs of the land model contain 11 variables including soil temperature, evaporation, water content and ice etc., and the data size is 2.3 GB. The monthly outputs of the sea-ice model contain 45 variables including sea-ice concentration, thickness, velocity, etc., and the data size is 27 GB. The daily mean outputs contain 24 variables including air temperature, velocity, precipitation, etc., and the data size is 405 GB. The total data size of each ensemble is 687 GB. The full list of all the output variables can be found by visiting the data repository on the ESG node (
4.1. Surface air temperature and precipitation
The surface air temperature and precipitation are the fundamental metrics for the performance of a climate system model. Figure 1 shows the simulated ensemble mean climatology of surface air temperature at 2 m from 1980 to 2014, as well as the observation and the simulated biases. The observed temperature is from the Japanese 55-year Reanalysis (JRA-55) (Kobayashi and Iwasaki, 2016). The original horizontal resolution of the observed data is 288 zonal grids and 145 meridional grids, which has been interpolated into the output grid of FAMIL here. Compared with the observation, the simulated global surface air temperature at 2 m is reasonable and shows a similar spatial pattern, in which the general meridional temperature gradient is well reproduced with a maximum of 30.3°C in tropical Africa (14°N, 33°E) and minimum of ?53.3°C in the Antarctic (75°S, 111°E). Meanwhile, there are still obvious biases, especially at high latitudes. The global mean bias is ?0.9°C and the root-mean-square error (RMSE) is 2.1°C, which are comparable with CMIP5 models (Donner et al., 2011). The biases in the tropics are relatively small (< ±1°C), showing better performance of the model in simulating tropical temperature; the most obvious tropical biases are warm biases in South America. In the midlatitudes, there are mainly cold biases, especially over the Tibetan Plateau, Rocky Mountains and northern Pacific, which are common in CMIP5 models (Donner et al., 2011; Chen et al., 2017). The strongest biases lie at high latitudes; in the Northern Hemisphere (NH), strong cold biases (> ?6°C) exist from the northern Atlantic to the Barents Sea, and these cold biases are larger than in the last version, FGOALS-2, and other CMIP5 models, which is important to note and requires further exploration. In the Southern Hemisphere (SH), strong warm biases (> 6°C) exist around the Antarctic, which is common in CMIP5 models (Donner et al., 2011), while strong cold biases (> ?6°C) exist inside the Antarctic. Considering the large uncertainties of observed data and the different topography of the model at high latitudes, the temperature biases in the SH are generally acceptable.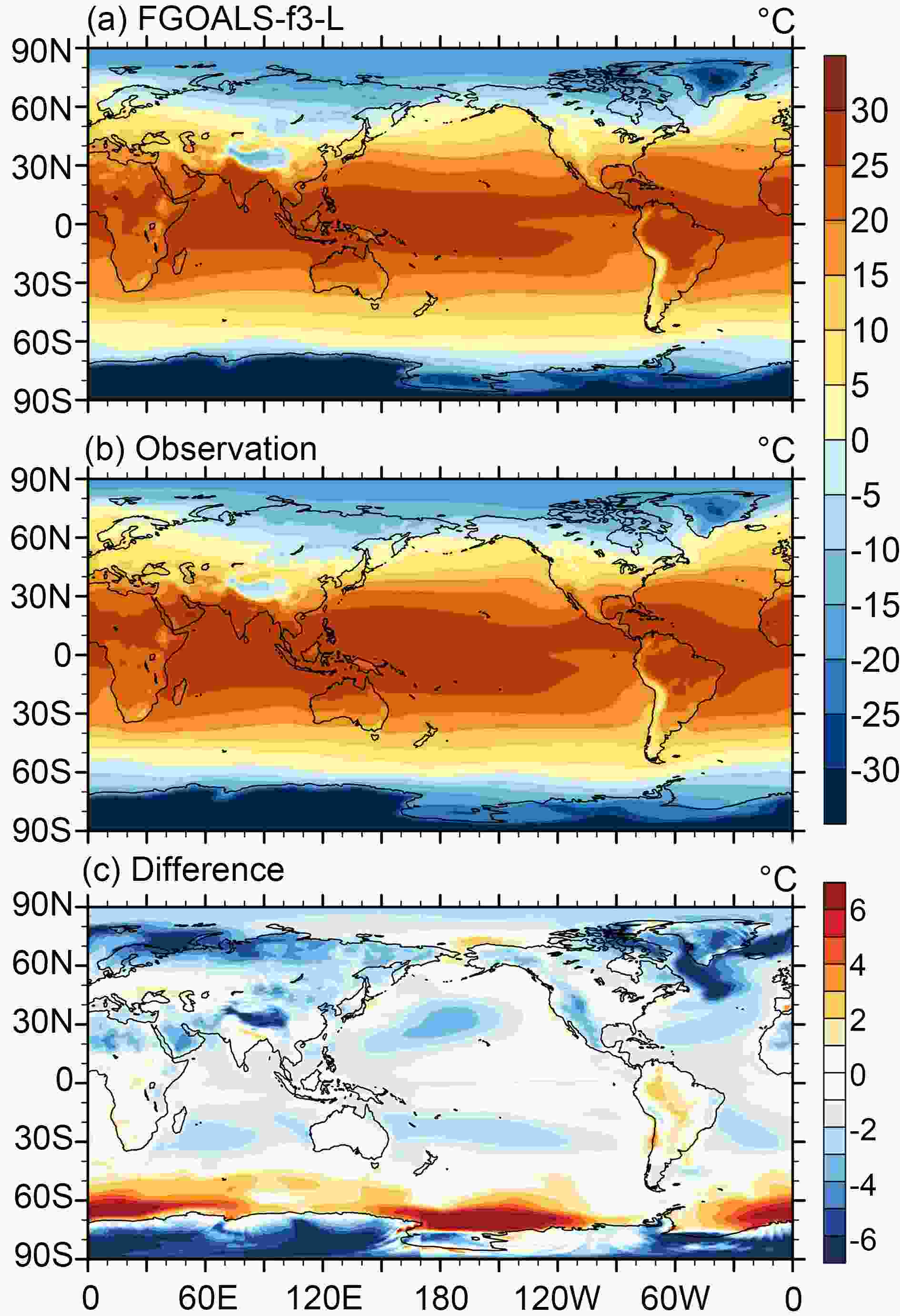
Figure1. The (a) ensemble mean climatology of simulated surface temperature at 2 m, (b) climatology of observed surface temperature at 2 m, and (c) their biases, from 1980 to 2014. The observed temperature is from JRA-55.Figure 2 shows the simulated ensemble mean climatology of precipitation from 1980 to 2014, as well as the observation and the simulated biases. The observed precipitation is from the Global Precipitation Climatology Project, version 2.3 (GPCP v2.3) (Adler et al., 2003); the original horizontal resolution of the observed data is 144 zonal grids and 72 meridional grids, which has also been interpolated into the output grid of FAMIL here. Compared with the observation, the simulated precipitation also shows a similar pattern, with maximum centers in the tropical western Pacific, tropical eastern Indian Ocean and tropical Atlantic, which comprise the Intertropical Convergence Zone (ITCZ). The double ITCZ bias, which widely existed in previous coupled models, is remarkably reduced in CAS FGOALS-f3-L, as the rain belt south of the equator has moved northward by about 5° compared with the last version, FGOALS-s2, and is located at the same place as shown in the observation. The global mean bias is 0.16 mm d?1, with a maximum of 13.5 mm d?1 and minimum of ?7.2 mm d?1, which is comparable with other CMIP5 models (Donner et al., 2011), and an RMSE of 1.2 mm d?1. The large biases (> ±4 mm d?1) are mainly located in the tropics, including positive biases in the western and central Pacific, western Indian Ocean and Atlantic, and negative biases in tropical land areas. The largest positive biases are located in the tropical western Pacific and the strongest negative biases are located in tropical South America. This indicates that some difficulties still exist in simulating tropical precipitation, and the opposite biases in oceanic and land areas are notable.
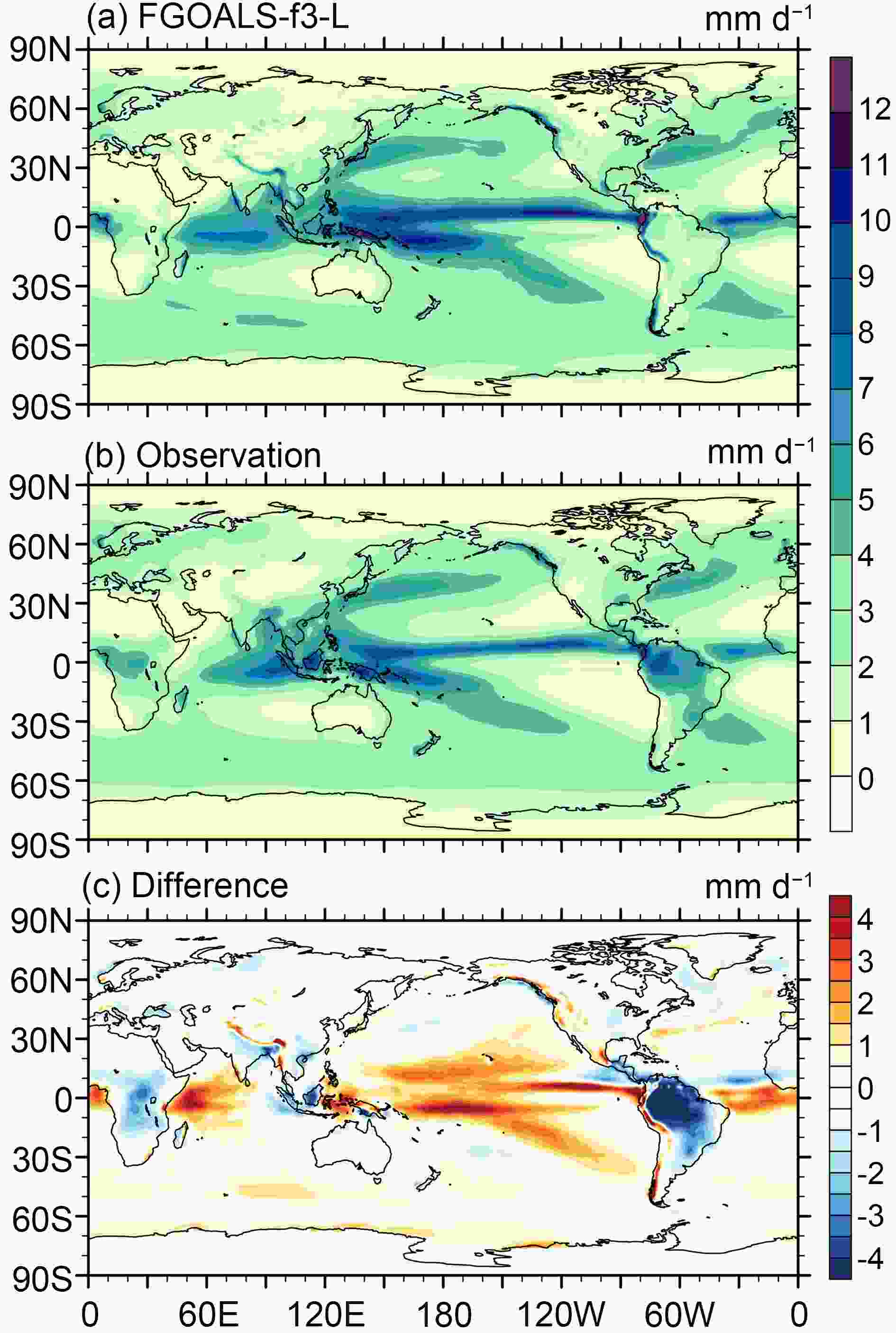Figure2. The (a) ensemble mean climatology of simulated precipitation, (b) climatology of observed precipitation, and (c) their biases, from 1980 to 2014. The observed precipitation is from GPCP v2.3.2
4.2. Long-term trends
The long-term variations in historical experiments are significant measurements of the model’s ability to reproduce the climate and its sensitivity to external forcing. Figure 3a-e shows the annual time series of the global mean surface air temperature anomalies, precipitation anomalies, ocean heat content (OHC) anomalies, and the diagnosed sea surface steric height changes due to heat and salt expansion as suggested by Landerer et al. (2007) from 1850 to 2014 for three ensembles as well as available observations. The global mean sea surface temperatures (SST) in the piControl experiment are also shown, with the starting points of the three historical ensembles, to present the long-term stability of the model (Fig. 3f).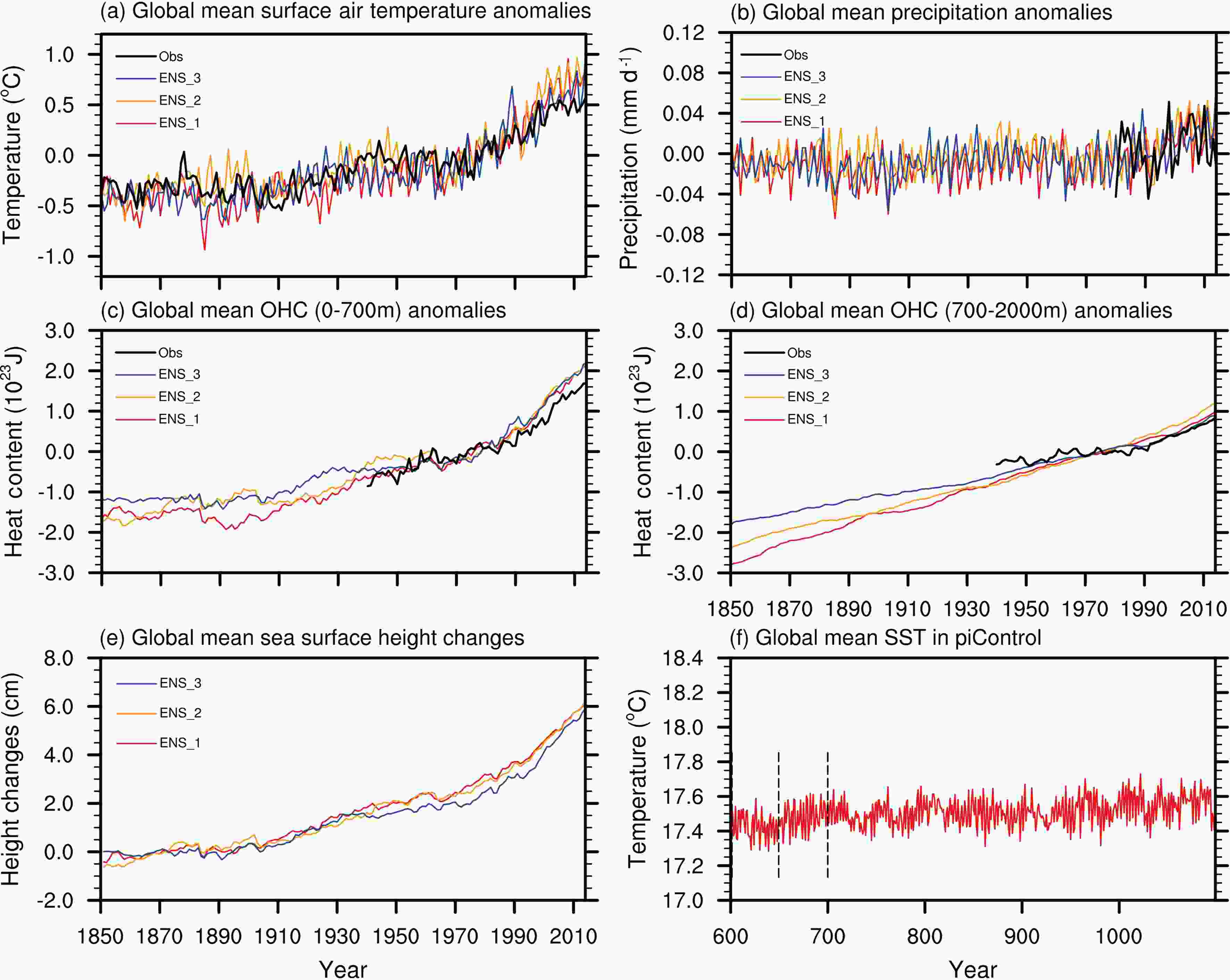
Figure3. The (a) global mean surface air temperature anomalies relative to the period 1961–90 for the ensembles and observation (HadCRUT4), (b) global mean precipitation anomalies relative to the period 1981–2000 for the ensembles and observation (GPCP, available since 1980), (c, d) global mean OHC anomalies within (c) 0–700 m and (d) 700–2000 m relative to the period 1961–90 for the ensembles and observations (IAP_OHC, available since 1940), (e) global mean sea surface steric height changes relative to the period 1850–99 due to heat and salt expansion for the ensembles, and (f) global mean SST from the 600th to 1100th year in the piControl experiment, in which the starting points of the three historical ensembles are shown by the dashed lines.The anomalies of surface air temperature, precipitation and OHC are estimated relative to modern climatology, and the sea surface steric height changes are calculated relative to the 50-year mean of the historical simulations from 1850–1900. The observed surface air temperature anomalies are from the Met Office Hadley Center (HadCRUT4) (Morice et al., 2012), the observed precipitation anomalies are from GPCP v2.3 (available since 1980) (Adler et al., 2003), and the observed OHC anomalies are from the IAP Ocean Gridded Product (IAP_OHC, available since 1940) (Cheng et al., 2017).
For the global mean surface air temperature (Fig. 3a), the three ensembles show similar trends, which are consistent with the observation. The simulations correctly capture the observed warming trend since 1850, although there is inconsistency in terms of the temporal phase between the ensembles and the observation. The average least-squares linear trend of the three ensembles is 0.06°C (10 yr)?1 and the observed trend is 0.05°C (10 yr)?1. The difference in the initial fields does not impact the long-term warming trend of each ensemble, which shows the dominant effect of the historical forcing. All the simulations show the widely recognized rapid increase over the late 20th century in the observation, which shows the model’s ability to accurately respond to the rapid changes of external forcing in the same period. For the global mean precipitation, the simulated global mean precipitation from 1980 to 2014 is higher than the observation by 0.16 mm d?1. The global mean precipitation anomalies in Fig. 3b show that the three ensembles have similar trends. There is no significant trend for the simulations from 1850 to 1980; but since 1980, when the observation is available, the simulations show slightly increasing trends, which are consistent with the observed trend, supporting the reliability of the simulations.
The global mean OHC is divided by depth—one for the OHC within 0 m to 700 m (Fig. 3c), and another for the OHC within 700 m to 2000 m (Fig. 3d), which represent the status of the upper ocean and deep ocean, respectively. It is shown that, either in the upper or deep ocean, the simulated ensembles show similar increasing trends since 1850, which are closely consistent with the observed trend since 1940. The simulated ensemble mean trend of OHC within 0–700 m from 1970 to 2014 is 0.52 × 1022 J yr?1, similar to the observed value of 0.45 × 1022 J yr?1 and the simulated value of 0.49 × 1022 J yr?1 from 40 CMIP5 historical simulations (Taylor et al., 2012). These increasing trends are consistent with the increase of global temperature shown in Fig. 3a, which shows the universal warming in the whole climate system induced by human activity. As shown in Fig. 3d, the initials of OHC in the deep ocean are different since they are branched from a different time in the piControl, but the simulated values get closer along with time, which also shows the dominant effect of the historical forcing. As a result of changes in temperature and salinity (not shown) of the whole ocean, the density of seawater is also changed, which eventually results in heat and salt expansion of seawater. Figure 3e shows the global mean sea surface steric height changes due to heat and salt expansion. The three ensembles show similar increasing trends since 1850, and the rapid increasing appears from the late 20th century, which is consistent with the rapid increase of temperature during the same period.
2
4.3. Spatial distribution of temperature trends
In the context of global climate change, the distribution of surface air temperature trends becomes an issue of great concern. Since the distribution of temperature has obvious seasonal variation, the distributions of the simulated ensemble mean and observed linear trends of surface air temperature in June–July–August (JJA) and December–January–February (DJF) are shown here in Fig. 4. The simulated linear trends are calculated from 1880 to 2014 using the least-squares method, and the observed surface air temperature trends are derived from the Goddard Institute for Space Studies Surface Temperature Analysis, version 4 (GISTEMP v4) (Lenssen et al., 2019), which is available since 1880. The original horizontal resolution of the observed data is 180 zonal grids and 90 meridional grids, which was interpolated into the output grid of FAMIL before calculation.
Figure4. Linear trends of simulated ensemble mean surface temperature at 2 m from 1880 to 2014 in (a) JJA and (b) DJF, and observed linear trends of surface temperature from 1880 to 2014 in (c) JJA and (d) DJF. The observation is from GISTEMP v4.It is shown that the warming trends in JJA (Fig. 4a) are almost universal around the globe, except for slight cooling trends in the northern Atlantic, which is the so-called “warming hole”, and the strongest warming trends [> 0.2°C (10 yr)?1] are located around the Antarctic and over the Norwegian Sea, which is largely consistent with the observed trends in JJA (Fig. 4c). The main differences between the simulated and observed trends in JJA are the slight overestimation in the eastern Pacific, the underestimation in the outer Antarctic, and the absence of decreasing trends on the two sides of the Antarctic Peninsula. The simulated linear trends in DJF (Fig. 4b) also show warming throughout the globe except in the North Atlantic, and the strongest warming [> 0.2°C (10 yr)?1] trends are mainly located in the high-latitude NH. Compared with the observation (Fig. 4d), the simulated linear trends in DJF are overestimated in northern Europe and the Arctic and underestimated in South America and the Antarctic. Generally speaking, the model is able to capture the observed distribution of global temperature trends in JJA and DJF, in which strong warming is mainly located in the high-latitude winter hemisphere, and the main biases are the overestimation in the high-latitude winter hemisphere and opposite trends in the Antarctic.
2
4.4. Vertical temperature trends
Stratification is a remarkable feature of the atmosphere and ocean; hence, the vertical properties are significant measurements of the model’s performance. Figure 5 shows the linear trend of the simulated ensemble mean and observed zonal mean temperature in the atmosphere and ocean from 1960 to 2014. The temperature trends are calculated using the least-squares method, the observed air temperature data are from JRA-55 (Kobayashi and Iwasaki, 2016), and the observed oceanic temperature data are from the IAP Ocean Gridded Product (IAP_TEMP, available since 1940 in upper 2000 m) (Cheng et al., 2017). The resolution of JRA-55 is 145 meridional grids and 37 pressure levels; the resolution of IAP_TEMP is 180 meridional grids and 41 depth layers.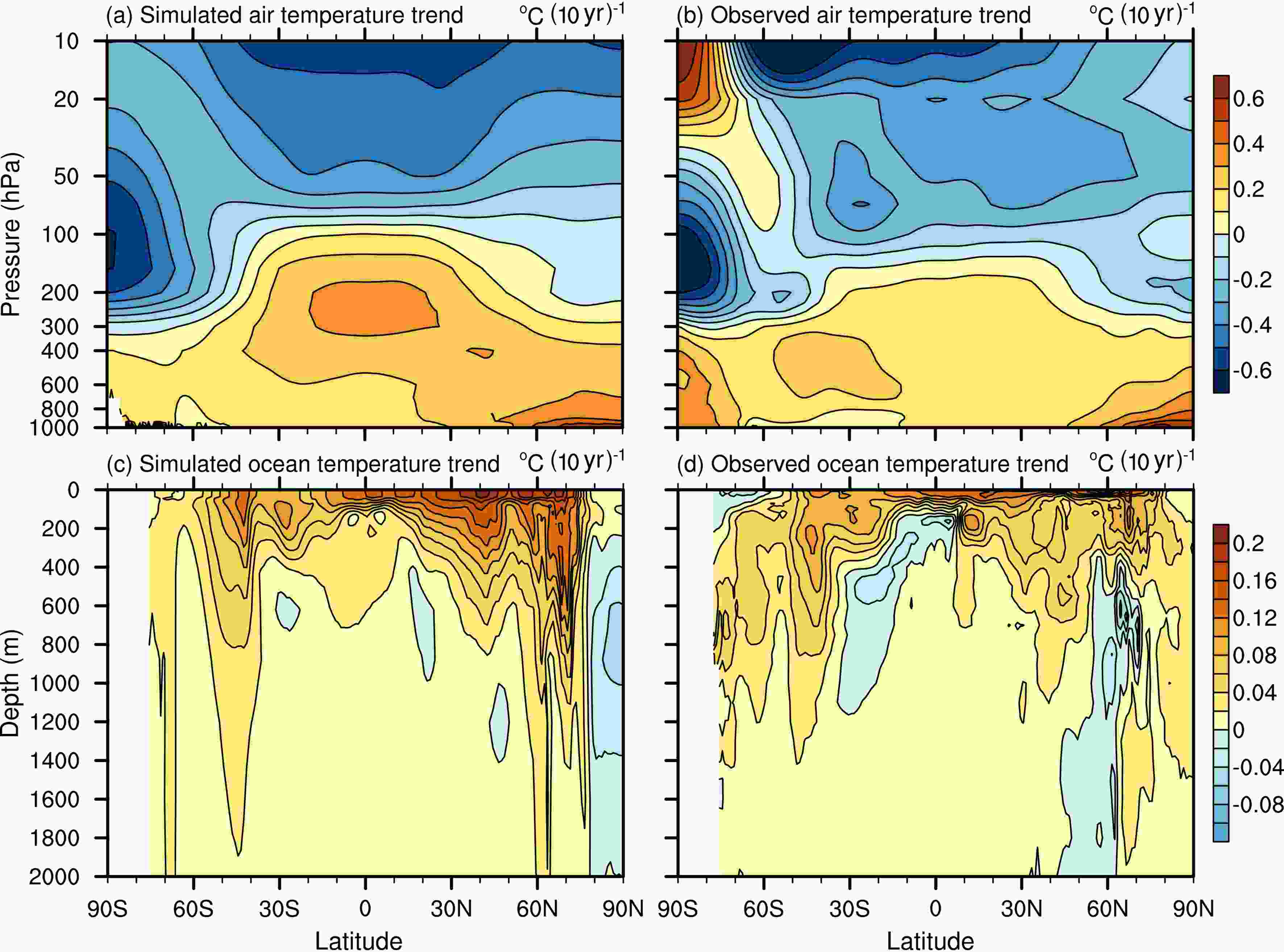
Figure5. Linear trends of the (a) simulated ensemble mean and (b) observed zonal mean air temperature from 1960 to 2014 (observation is from JRA-55); and linear trends of the (c) simulated ensemble mean and (d) observed zonal mean oceanic temperature from 1960 to 2014 (observation is from IAP_TEMP).It is shown that the air temperature trends (Figs. 5a and b) are opposite between the troposphere and stratosphere, which is a typical pattern of vertical temperature trends resulting from the enhanced greenhouse effect. In the troposphere, the simulated and observed temperature trends are dominated by warming signals, while in the stratosphere both the simulated and observed temperature trends are dominated by cooling signals. In the troposphere, the observed warming trends are located under 300 hPa at high latitudes and under 150 hPa at low latitudes, which are correctly captured in the model. The simulated warming trends are weaker and lower than the observation at high latitudes, but stronger and higher at low latitudes. In the high levels, the observed strong cooling trends at 150 hPa in the Antarctic are captured but are weaker in the model, while the observed warming trends at 50 hPa are absent in the simulations. Generally, the model is able to capture the observed vertical temperature trends, but the strength of the trends is slightly underestimated in the model. Considering the uncertainty of observed data at high levels, the biases should be acceptable.
The vertical oceanic temperature trends (Figs. 5c and d) also depend on the depth. The simulated temperature trends are mainly warming signals, except in the Arctic and subtropics under 200 m. The large warming trends are mainly located in the thermocline due to vertical mixing and wind-driven circulations. The observed temperature trends show a similar warming pattern in the ocean. The main differences between the simulated and observed trends are the stronger warming in the thermocline in the model, especially in the NH, the disagreements in the deep layer trends at 60°N and in the Arctic, and the underestimation of cooling in the subtropics under 200 m in the model. Generally, the model is able to capture the observed vertical temperature trends in the ocean, but the strength of warming is overestimated. Considering the relatively low quality of observed data in the deep ocean, the simulated vertical trends should be acceptable.
2
4.5. Distribution of OHC changes
The OHC changes show the response of the ocean to global warming. Figure 6 shows the simulated ensemble mean and observed changes of OHC between the sea surface and 700 m, and between 700 m and 2000 m. The changes are calculated by the 20-year average from 1995 to 2014 minus the 20-year average from 1950 to 1969. The observed OHCs are from the IAP_OHC (Cheng et al., 2017). The horizontal resolution of IAP_OHC is 360 zonal grids and 180 meridional grids.
Figure6. Simulated ensemble mean OHC changes within (a) 0–700 m and (b) 700–2000 m, and observed OHC changes within (c) 0–700 m and (d) 700–2000 m. The observations are from IAP_OHC. The changes are for the period 1995–2014, relative to the period 1950–69.Globally, both the simulated or observed OHC changes within 0–700 m are larger than within 700–2000 m, which indicates that the upper ocean absorbs more heat than the deep ocean in the context of global warming. The observed changes of OHC in the upper 700 m are correctly reproduced by the coupled model (Figs. 6a and c), including the large warming in the northwestern Pacific, northern Atlantic and Southern Ocean. The biases of the model are represented mainly by the stronger warming in the northwestern Pacific and northern Atlantic, the absence of cooling in the northern and western Pacific, and the disagreement in the Arctic. For the OHC changes between 700 m and 2000 m (Figs. 6b and d), the differences between simulation and observation are a bit larger, because of the uncertainties in the model and observation in the deep ocean. The main biases include the disagreements in the Arctic, northern Atlantic and subtropics of the SH. Generally, considering the uncertainty of observation in the deep ocean, the simulated OHC changes are comparable with the observation, and the simulated OHC changes in the upper ocean are better than in the deep ocean.
The data of the oceanic model and sea-ice model uploaded to ESG are on the original tripolar grid. Users can read and visualize the original data by software that supports the curvilinear coordinate like the NCAR Command Language (NCL,
It is found that, in the CMIP6 historical experiments, CAS FGOALS-f3-L is able to reproduce the observed global surface temperature and precipitation, and the double ITCZ is remarkably reduced. The simulated increasing trends of surface temperature, precipitation, OHC and sea level are reasonable and consistent with the available observations. The horizontal and vertical distributions of long-term temperature (OHC) trends in the atmosphere and ocean are comparable with the observed distributions. CAS FGOALS-f3-L performs well in simulating the historical climate.
However, there are still some obvious biases in the CMIP6 historical experiments with CAS FGOALS-f3-L, like most state-of-the-art models. The surface temperature biases are mainly located at high latitudes; especially, the cold biases in the northern Atlantic are larger than the last version, FGOALS-s2, and other CMIP5 models. The simulated tropical precipitation over ocean (land) is overestimated (underestimated). The warming trends of surface temperature in the high-latitude winter hemisphere are overestimated. The simulated OHC in the deep ocean shows larger biases than in the upper ocean.
The CMIP6 historical experiments aim to evaluate the ability of models to reproduce the climate on various time scales, determine the sensitivity of models to the climate model forcing, and provide baseline simulations for detection and attribution studies. In this respect, this paper provides some general guidance and understanding for data users in the scientific community who intend to use these datasets for the aforementioned purposes.
Acknowledgements. This study is jointly supported by the Strategic Priority Research Program of Chinese Academy of Sciences (Grant Nos. XDA19060102 and XDB42010400) and the Natural Science Foundation of China (Grant Nos. 41530426, 91958201 and 41931183).
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (
