李朋磊^,1, 张骁¹, 王文辉¹, 郑恒彪¹, 姚霞^1,2, 朱艳¹, 曹卫星¹, 程涛^,1,21南京农业大学/国家信息农业工程技术中心/江苏省信息农业重点实验室/农业农村部农作物系统分析与决策重点实验室/智慧农业教育部工程研究中心,南京 210095
²江苏省现代作物生产协同创新中心,南京 210095

Assessment of Terrestrial Laser Scanning and Hyperspectral Remote Sensing for the Estimation of Rice Grain Yield

LI PengLei^,1, ZHANG Xiao¹, WANG WenHui¹, ZHENG HengBiao¹, YAO Xia^1,2, ZHU Yan¹, CAO WeiXing¹, CHENG Tao^,1,21Nanjing Agricultural University/National Engineering and Technology Center for Information Agriculture (NETCIA) /Jiangsu Key Laboratory for Information Agriculture/Key Laboratory of Crop System Analysis and Decision Making, Ministry of Agriculture and Rural Affairs/Engineering Research Center of Smart Agriculture, Ministry of Education, Nanjing 210095
²Jiangsu Collaborative Innovation Center for Modern Crop Production, Nanjing 210095

通讯作者: 程涛,E-mail： tcheng@njau.edu.cn

责任编辑: 杨鑫浩
收稿日期:2020-09-1接受日期:2020-11-20

基金资助:

国家重点研发计划.2016YFD0300601 国家自然科学基金.41871259 中国博士后基金.2019M651854

Received:2020-09-1Accepted:2020-11-20
作者简介 About authors
李朋磊,E-mail： 2017101172@njau.edu.cn。










摘要
【背景】快速、准确地估算水稻产量对于肥水精确管理及国家粮食政策的制定至关重要。高光谱与激光雷达遥感作为2种不同的主被动监测技术,为水稻长势信息获取提供了多样化手段。【目的】对比2种遥感监测手段在不同生态点的独立数据集中的验证精度,寻求可移植性强的产量估算模型,对水稻长势监测提供理论与技术支撑,及为精确农业提供科学指导具有重要意义。【方法】本研究通过实施3年（2016—2018年）包含不同地点、不同品种与不同氮素水平的水稻田间试验,在抽穗后各时期同步获取点云数据和光谱数据,结合线性回归与随机森林回归来估算产量,探究抽穗后点云数据与光谱数据估算水稻产量的差异;同时评估产量模型在不同数据集的时空可移植性,寻求可移植性强的产量估算模型。【结果】利用点云数据估算产量的精度（R² = 0.64—0.69）优于光谱数据的估算精度（R² = 0.20—0.58）;基于线性回归的产量估算模型,其验证精度明显优于基于随机森林回归的产量模型;产量模型在同一生态点的可移植性更强（不同生态点：RRMSE 16.69%—17.85%;同一生态点：RRMSE 11.37%—12.41%）。【结论】本研究为抽穗后水稻产量监测提供了新的方法和不同遥感手段的性能比较,为收获前作物产量的实时估算提供重要支撑。激光雷达技术凭借其全天候工作的特点,在长江中下游水稻产量实时监测中有着较好的应用前景。
关键词： 水稻;产量;激光雷达;高光谱;回归模型

Abstract
【Background】Non-destructive and accurate estimation of crop biomass and yield is crucial for the quantitative diagnosis of growth status and planning of national food policies. Hyperspectral and Terrestrial Laser Scanning (TLS) remote sensing provide convenient and effective ways to monitor crop condition.【Objective】The aim of this study was to examine the feasibility of developing models with various independent datasets to build a universal yield monitoring model. The expected results can provide theoretical and technical support for rice growth monitoring and scientific guidance of precision agriculture.【Method】Field plot experiments were conducted in 2016, 2017 and 2018 and involved different study sites, nitrogen (N) rates, planting techniques and rice varieties. Linear regression (LR) and random forest (RF) were evaluated in estimating yield with TLS and spectral data collected since the heading stage, and the feasibility of developing models with various independent datasets was examined to build a universal yield monitoring model.【Result】 The results showed that TLS models exhibited higher estimation accuracies for yield in the heading stage, early-filling stage and late-filling stage (R²: 0.64-0.69) than hyperspectral models (R²: 0.20-0.58). Compared to RF, LR modeling yielded significantly higher validation accuracies for growth stages after heading. While the predictive model was transferred to other datasets, the validation accuracies from the same site (RRMSE: 11.37%-12.41%) were higher than those from a different site (RRMSE: 16.69%-17.85%).【Conclusion】The results suggested that TLS was a promising technique to monitor yield at post-heading stages with high accuracy and to overcome the saturation of canopy reflectance signals encountered in optical remote sensing.
Keywords：rice;yield;LiDAR;hyperspectral;regression model


PDF (2500KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李朋磊, 张骁, 王文辉, 郑恒彪, 姚霞, 朱艳, 曹卫星, 程涛. 基于高光谱和激光雷达遥感的水稻产量监测研究[J]. 中国农业科学, 2021, 54(14): 2965-2976 doi:10.3864/j.issn.0578-1752.2021.14.004
LI PengLei, ZHANG Xiao, WANG WenHui, ZHENG HengBiao, YAO Xia, ZHU Yan, CAO WeiXing, CHENG Tao. Assessment of Terrestrial Laser Scanning and Hyperspectral Remote Sensing for the Estimation of Rice Grain Yield[J]. Scientia Acricultura Sinica, 2021, 54(14): 2965-2976 doi:10.3864/j.issn.0578-1752.2021.14.004


开放科学（资源服务）标识码（OSID）：

0 引言

【研究意义】水稻是当前中国最主要的粮食作物,也是世界上主要的粮食作物之一^[1,2],其产量与国家甚至全世界的粮食安全密切相关,水稻产量的估算对保障农业可持续发展至关重要^[3,4]。实时、准确的地面遥感技术已成为农作物长势及产量监测等农业研究的重要手段^[5,6],同时可为国家粮食安全战略的制定提供参考依据^[7,8]。【前人研究进展】近年来,激光雷达作为一种新兴的遥感技术手段^[9],在全天候作物生长监测中发挥着巨大优势^[10,11]。从激光雷达数据中能够获取作物结构参数,例如高度特征变量、体积等^[11,12],进而准确估算作物生物量^[13,14],然而还很少用于作物产量估算。由于作物生物量与籽粒产量密切相关,部分****尝试利用高度数据估算作物产量,结果发现中等分辨率的全球定位系统高程数据由于精度较差,无法代替由激光雷达技术获取的点云来估算作物产量^[15]。相比定位导航高程数据,无人机激光雷达可以获取精度相对较高的点云数据。有****尝试利用无人机激光雷达来监测作物长势,但是由于激光点云稀疏且激光点云误差较大,导致估算结果并不理想^[16]。利用高光谱遥感估算作物产量,一直是精确农业研究的热点,相关****利用关键生育期的植被指数与产量建立回归关系^[17]。有****还综合环境因子与植被指数来进行作物产量监测^[18],都得到了较为准确的估算结果。还有****从产量要素亩穗数、穗粒数、千粒重的形成过程出发,在综合考虑产量形成生理机制的基础上,建立了较为可靠的基于植被指数的产量估算模型^[19]。作为信号处理领域最有效且常用的方法之一,连续小波变换具有对光谱信号进行多尺度分析的优势,对高光谱数据进行连续小波变换,可以高效提取不同宽度光谱区间的形状信息^[20]。因此,小波变换在遥感监测领域发挥着重要的作用。很多****基于小波变换得到的小波特征进行农学参数反演发现,相比植被指数,小波特征能够进一步提高作物生理生化参数的监测精度^[21,22],有助于叶面积、产量等重要农学参数的估算。【本研究切入点】目前,大部分作物估产研究多基于孕穗期等关键生育期或者孕穗—抽穗期等多生育期复合的光谱数据来估算作物产量^[23],忽视了关键生育期光谱数据缺失时高光谱遥感技术的表现,很少关注抽穗后光谱数据的产量估算性能。作为一种农业应用中使用较多的遥感手段,其水稻产量估算性能与新兴的激光雷达技术相比如何,目前还未见详细报道。【拟解决的关键问题】本研究使用地基激光扫描仪获取高精度、高密度的点云数据,依此来监测水稻产量,明确抽穗后不同时期2种遥感手段的产量估算精度差异,评价不同统计学方法在产量估算建模中的表现,并利用多年多生态点数据集评价产量估算模型的可移植性。

1 材料与方法

1.1 试验地点与设计

试验分别于2016年在江苏省如皋市试验基地,2017年和2018年在江苏省兴化市万亩高产高效粮食产业园进行（图1）。其中,如皋试验包含3个氮梯度,分别为0（N0）、100 kg N·hm^-2（N1）和200 kg N·hm^-2（N2）;2个水稻品种为武运粳24与Y两优1号;播栽方式为旱育秧人工移栽;3次重复。连续2年在兴化进行的水稻互作试验,2年的施氮量设置和品种相同;4个氮肥梯度分别为0（N0）、135 kg·hm^-2（N1）、270 kg·hm^-2（N2）和405 kg·hm^-2（N3）;2个水稻品种分别是南粳9108和甬优2640。2017年水稻试验包含3种水稻播栽方式,分别是机械直播、钵苗移栽和毯苗移栽。如皋市（120°33′E,32°23′N）和兴化市（119°3′E,33°05′N）都属于四季分明的亚热带季风气候。同时,如皋试验和兴化试验在土壤特性、主栽品种以及播栽方式等方面的差异对水稻生长产生较大的影响,这对探索普适性强的产量模型具有重要的指导意义。

图1

新窗口打开|下载原图ZIP|生成PPT
图1研究区地理位置

Fig. 1Geographic location of the experimental sites

1.2 数据获取

本研究所获取的数据包括地面激光雷达数据、冠层高光谱数据与水稻籽粒产量数据3个部分。田间测试及取样的时期包括水稻抽穗期、灌浆前期与灌浆后期。使用的激光扫描设备是RIEGL VZ-1000,在取样当天无风或风速较小的时间段进行激光雷达扫描。2016和2017年的扫描模式为60模式,即角分辨率为0.06°;为获取更精细的水稻冠层结构信息,2018年扫描模式为40模式,即角分辨率为0.04°。2016年如皋试验采用10站点扫描方式;由于小区面积的增加, 2017年和2018年兴化试验均采用21站点扫描方式,具体扫描点的设置情况如图2—3所示。使用的高光谱测试仪是ASD FieldSpec Pro FR 2500便携式高光谱分析仪,在无风、晴朗的中午,当地时间10：00—14：00范围内获取光谱数据。产量是在成熟期通过破坏性取样获得,在成熟期,每个田块设定2个取样点,在每取样点取1 m²,3次重复,从中割取穗子进行脱粒,测量产量构成要素穗数、穗粒数和千粒重,计算得到每个小区的产量。

图2

新窗口打开|下载原图ZIP|生成PPT
图22016年如皋试验小区设置及激光雷达扫描点分布图

氮水平：N0（0）,N1（100 kg·hm^-2）,N2（200 kg·hm^-2）;品种：V1（武运粳24）,V2（Y两优1号）
Fig. 2The design of experimental plots and distribution of terrestrial laser scanning positions of Rugao in 2016

N rates: N0 (0), N1 (100 kg·hm^-2), N2 (200 kg·hm^-2); Varieties: V1 (Wuyunjing 24), V2 (Y Liangyou 1)

图3

新窗口打开|下载原图ZIP|生成PPT
图32017年兴化试验小区设置及激光雷达扫描点分布图

氮水平：N0（0）,N1（135 kg·hm^-2）,N2（270 kg·hm^-2）,N3（405 kg·hm^-2）;品种：V1（南粳9108）,V2（甬优2640）;播栽方式：P1（直播）,P2（钵苗移栽）,P3（毯苗移栽）
Fig. 3The experimental plots and distribution of terrestrial laser scanning positions of Xinghua in 2017

N rates: N0 (0), N1 (135 kg·hm^-2), N2 (270 kg·hm^-2), N3 (405 kg·hm^-2); Varieties: V1 (Nanjing 9108), V2 (Yongyou 2640); Planting techniques: P1 (Direct seeding), P2 (Tray seeding transplanting), P3 (Blanket seeding transplanting)

1.3 特征参数

1.3.1 高光谱数据 基于作物的光谱特性,将多个光谱波段进行线性和非线性组合来构建各种植被指数,能够简单、有效地预测作物产量,本研究归纳了常用的与产量预测相关的植被指数（表1）。

Table 1
表1
表1估算水稻产量的常用植被指数
Table 1Vegetation indices for estimating rice yield

指数 Vegetation index	计算公式 Equation	文献 Reference
差值Deviation
DVI [1200,680]	R1200-R680	[9]
DVI [1200,440]	R1200-R440	[9]
DVI [800,550]	R800-R550	[9]
比值Ratio
SR [609,518]	(R609/R518)-1	[24]
SR [1971,2018]	(R1971/R2018)-1	[25]
SR [750,673]	R750/R673	[26]
归一化Normalization
NDVI [1200,550]	(R1200-R550)/(R1200+R550)	[27]
NDVI[800,680]	(R800-R680)/(R800+R680)	[28]
NDVI [608,518]	(R609-R518)/(R609+R518)	[29]

新窗口打开|下载CSV

连续小波变换的原理是通过平移和缩放母小波函数,与光谱数据进行卷积运算得到小波特征,这些小波特征就可以用于估算产量,连续小波变换的具体公式如下^[20]：

（1）${{\psi }_{\text{a,b}}}\text{(}\lambda \text{)}=\frac{\text{1}}{\sqrt{\text{a}}}\psi \frac{(\lambda -\text{b})}{\text{a}}$
（2）$Wf(\text{a,b})=\int _{0}^{2150}f(\lambda ){{\psi }_{\text{a,b}}}(\lambda )d\lambda$
式中,ψ(λ)表示母小波函数,ψ_a,b(λ)表示平移与缩放后的母小波函数,a表示缩放因子;b表示平移因子,W_f (a,b)表示小波特征。本研究利用连续小波变换对所获取的水稻冠层反射率进行处理,将冠层反射率光谱变换到尺度2³、2⁴、2⁵和2⁶,得到对产量敏感的小波特征。

1.3.2 激光雷达数据 对获取的点云数据进行插值生成数字表面模型,从数字表面模型中减去数字高程模型得到该时期的冠层高度模型,从中提取多个结构参数（表2）。

Table 2
表2
表2基于冠层高度模型提取的特征变量
Table 2Summary of height metrics derived from the canopy height model and their descriptions

结构参数 Structural parameter	描述 Description
Height mean ( Hmean)	高度平均值 Mean of height
Height min (Hmin)	高度最小值 Minimum of height
Height max (Hmax)	高度最大值 Maximum of height
Height standard deviation (Hstd)	高度标准偏差 Standard deviation of height
Height coefficient of variation (Hcov)	高度变异系数 Variable coefficient of height
Height kurtosis (Hk)	高度峰度 Kurtosis of height
Height skewness (Hs)	高度偏度 Skewness of height
Height percentile (H1st, H5th, H10th, H25th, H50th, H75th, H95th, H99th)	高度1st, 5th, 10th, 25th, 50th, 75th, 95th, 和99th 百分位 Percent of 1st, 5th, 10th, 25th, 50th, 75th, 95th, and 99th height

新窗口打开|下载CSV

1.4 回归方法

本研究以2017年兴化数据集训练模型,以2016年如皋数据集和2018年兴化数据集验证模型,各数据集的具体描述见表3。所有的统计分析在Python 3.50软件中进行,画图使用了GraphPad Prism 5.0软件（GraphPad Software,San Diego,CA,USA）。

Table 3
表3
表3数据集描述
Table 3Description of datasets

数据集 Dataset	年份 Year	试验地点 Site	样本数 Number of samples	品种 Variety	播栽方式 Planting technique
训练数据集 Training dataset	2017	兴化Xinghua	72	南粳9108 & 甬优2640 Nanjing 9108 & Yongyou 2640	钵苗移栽Tray seeding transplanting、 毯苗移栽Blanket seeding transplanting、 直播Direct seeding
验证数据集1 Validation dataset 1	2016	如皋Rugao	36	武运粳24 & Y两优1号 Wuyunjing 24 & Y Liangyou 1	旱育秧人工移栽 Dried-seedling manual transplanting
验证数据集2 Validation dataset 2	2018	兴化Xinghua	48	南粳9108 & 甬优2640 Nanjing 9108 & Yongyou 2640	钵苗移栽Tray seedling transplanting、 毯苗移栽Blanket seeding transplanting

新窗口打开|下载CSV

1.4.1 线性回归 线性回归依据最小二乘法对自变量和因变量建模,该方法运用十分广泛。其公式定义为：

（3）Y=AX1+ε
式中,Y表示n×1的矩阵的列向量,即因变量;X1表示n×1个矩阵的列向量,即自变量;A表示回归系数,ε表示误差。在获取植被指数、小波系数与结构参数后,建立3种特征与产量指标的线性关系,进而筛选各变量中最优指标进行籽粒产量估算。

1.4.2 随机森林回归 随机森林（RF）算法^[29]是基于统计学习理论,利用Bootstrap重抽样方法从原始样本中抽取多个样本,对每个Bootstrap样本构建决策树,然后将决策树中出现最好的结果作为最终预测结果,是基于决策树分类器的融合算法。在光谱数据分析的基础上,本研究将获取的最优尺度下的小波特征与产量参数进行相关分析,分析小波特征对产量参数的敏感性,提取排名前1%的小波特征参与随机森林的模型训练。而激光雷达数据的分析则是将所有提取的结构参数用于随机森林的模型训练。

2 结果

2.1 基于光谱及点云数据的产量估算模型构建

2.1.1 光谱估算模型 通过系统分析常用植被指数与水稻产量的相关性发现（表4）,（R₆₀₉/R₅₁₈）-1、R₁₂₀₀-R₄₄₀、R₈₀₀-R₅₅₀分别为抽穗期、灌浆前期与灌浆后期植被指数系列中表现最好的指数,这3种植被指数均与产量显著相关（P<0.001）。不同时期对应的最优植被指数与水稻产量的R²变化范围为0.20—0.52（P<0.001）。

Table 4
表4
表4水稻产量与已有植被指数的相关性
Table 4Coefficient of determination (R²) values for the relationships between rice yield and published vegetation indices

植被指数 Vegetation index	抽穗期 Heading	灌浆前期 Early filling	灌浆后期 Late filling
R1200-R680	0.12*	0.41**	0.23**
R1200-R440	0.10*	0.46**	0.24**
R800-R550	0.17**	0.41**	0.52**
(R609/R518）-1	0.20**	ns	0.01
R750/R673	0.16**	0.29**	0.27**
(R1971/R2018）-1	0.03	0.04	0.02
(R1200-R550)/(R1200+R550)	0.17**	0.31**	0.28**
(R800-R680)/(R800+R680)	0.12**	0.32**	0.23**
(R609-R518)/(R609+R518)	0.16**	ns	0.01

*P<0.01;**P<0.001

新窗口打开|下载CSV

不同时期对产量敏感的最优小波特征分布在不同位置,在抽穗期、灌浆前期、灌浆后期,对产量敏感的小波特征分别分布在730 nm、1 200 nm、1 185 nm的波段,不同尺度的敏感小波特征较为稳定;其中尺度3监测精度最高,故本研究后续分析基于尺度2³的小波特征进行处理（表5）。

Table 5
表5
表5水稻产量与小波特征的相关性
Table 5Coefficient of determination (R²) values for the relationships between wavelet features and yield in rice

	抽穗期 Heading	灌浆前期 Early filling	灌浆后期 Late filing
最优小波特征 Optimal wavelet feature	WF730,3	WF1200,3	WF1185,3
R2	0.34**	0.58**	0.58**

*P <0.01;** P<0.001

新窗口打开|下载CSV

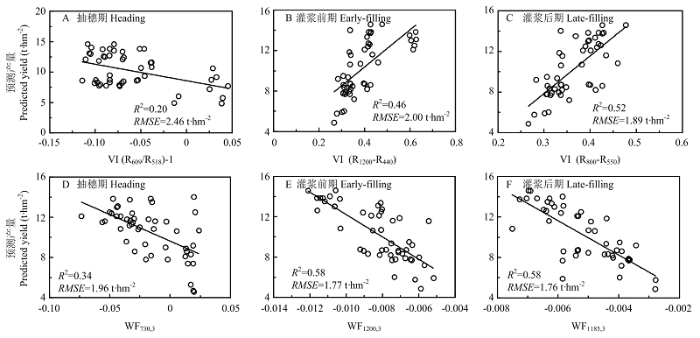
抽穗期、灌浆前期与灌浆后期的最优植被指数及敏感小波特征分别与产量的相关性如图4所示。结果表明,所有时期小波特征与产量的相关性（R² = 0.34—0.58）均优于同时期的植被指数与产量的相关性（R² = 0.20—0.52）。

图4

新窗口打开|下载原图ZIP|生成PPT
图4最优植被指数（A、B、C）及最优小波特征（D、E、F）水稻产量的回归关系

Fig. 4Relationships of optimal spectral features with rice yield (vegetation indices: A, B, C; wavelet features: D, E, F)



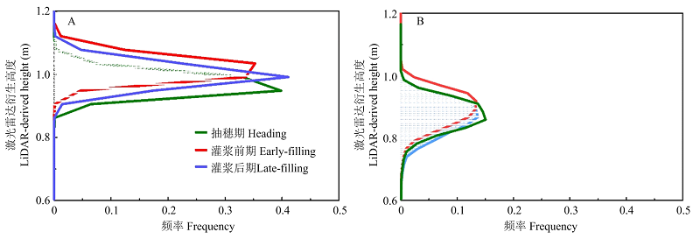
2.1.2 激光雷达估算模型 兴化试验区水稻高于如皋试验区水稻（图5）,且同一研究区在不同生育期获取的点云数据差异不大,植株结构信息较为稳定（图6）。LI等^[30]发现H_95th与水稻器官生物量和地上部生物量表现出明显的相关性,故本研究同样使用H_95th作为水稻产量估算的特征参数。以兴化某小区的数据为例,阐述H_95th的详细含义（图7）。H_95th指高度直方图中的95百分位点,相比极高值与最大值,H_95th 不容易受到环境干扰;相比极低值与最小值,H_95th又包含足够的上部冠层信息,更能真实反映植株的结构信息。

图5

新窗口打开|下载原图ZIP|生成PPT
图5如皋某小区抽穗后（A、B、C）与兴化某小区抽穗后各生育期（D、E、F）的水稻点云数据,颜色依据高度赋值

Fig. 5Three-dimensional view of the point cloud data collected by the TLS instrument for a rice plot at post-heading stages in Rugao (A, B, C) and Xinghua (D, E, F). The data points are color coded by height relative to the soil background in the plot

图6

新窗口打开|下载原图ZIP|生成PPT
图6兴化（A）与如皋（B）某小区的高度直方图

Fig. 6The height histogram of a rice plot in Xinghua (A) and Rugao (B)

图7

新窗口打开|下载原图ZIP|生成PPT
图7结构参数H_min、H_1st、H_95th、H_99th、H_max在高度直方图中的分布

Fig. 7The distribution of structural metrics H_min、H_1st、H_95th、H_99th、H_max in height histogram



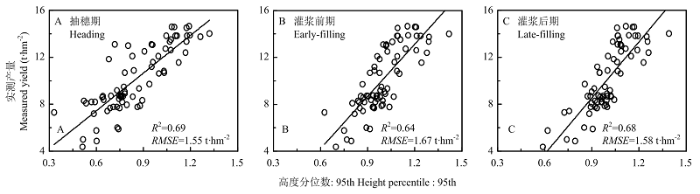
通过系统分析H_95th与水稻产量的相关性（图8）,发现抽穗后各生育期H_95th均与水稻产量具有较高的相关性（R² = 0.64—0.69）,且在抽穗后所有时期结构参数H_95th与产量的相关性,均优于同时期敏感小波特征（R² = 0.34—0.58）和最优植被指数（R² = 0.20—0.52）与产量的相关性。

图8

新窗口打开|下载原图ZIP|生成PPT
图8结构参数在与水稻产量的回归关系

Fig. 8Relationships between structural parameters and rice yield

2.2 光谱估算模型评价

对比不同数据集的检验结果发现,基于植被指数的线性估算模型（M1）在如皋数据集的验证精度（RRMSE = 20.01%—31.17%）,低于在兴化数据集的验证精度（RRMSE = 16.14%—19.31%）。对比M1与M2发现,即线性的产量模型验证效果更准确（表6）。基于小波特征的产量模型验证精度变化规律与基于植被指数的产量模型一致（图9）。

Table 6
表6
表6光谱数据产量模型应用于不同数据集得到的RMSE与RRMSE值
Table 6Accuracy assessments of RMSE(t·hm^-2) and RRMSE(%) values for the estimation of yield in different datasets based on hyperspectral models

模型 Models	如皋Rugao						兴化Xinghua
	抽穗期Heading		灌浆前期Early filling		灌浆后期Late filling		抽穗期Heading		灌浆前期Early filling		灌浆后期Late filling
	RMSE	RRMSE	RMSE	RRMSE	RMSE	RRMSE	RMSE	RRMSE	RMSE	RRMSE	RMSE	RRMSE
M11 (VI & LR)	2.97	31.70	2.01	21.05	1.91	20.01	1.84	17.45	1.70	16.14	2.04	19.31
M2 (VI & RF)	3.07	32.20	2.18	22.90	2.16	22.65	2.14	20.30	3.04	28.84	2.25	21.30
M3 (WF & LR)	1.91	20.04	1.84	19.33	1.67	17.54	1.69	16.02	1.50	14.29	1.42	13.45
M4 (WF & RF)	3.04	31.92	2.37	24.88	2.10	21.10	2.11	20.00	2.05	19.42	1.93	18.29

VI代表植被指数,WF代表小波系数,LR代表线性回归,RF代表随机森林回归
VI = vegetation index, WF = wavelet feature, LR = linear regression, RF = random forest

新窗口打开|下载CSV

图9

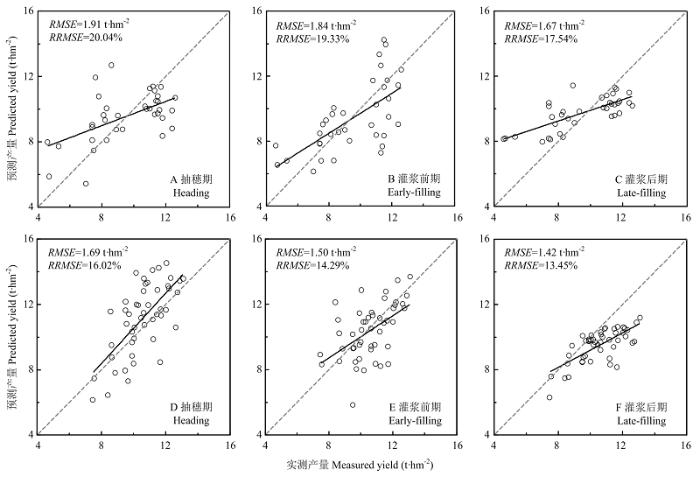新窗口打开|下载原图ZIP|生成PPT
图9基于小波特征的线性估算模型在如皋（A、B、C）以及兴化（D、E、F）数据集的验证结果

Fig. 9The scatter plots of measured and predicted yield of rice with the optimal wavelet feature at different growth stages for the datasets collected in Rugao (A, B, C)and Xinghua (D, E, F)

2.3 激光雷达估算模型评价

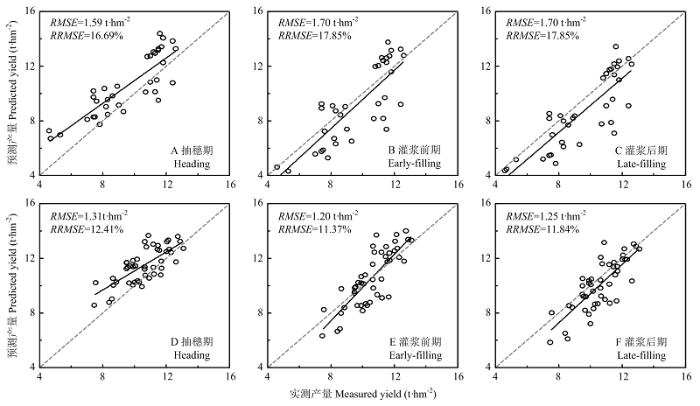
2.3.1 线性回归 对比点云数据模型在不同数据集的检验结果发现,产量模型在兴化数据集的验证精度（RRMSE=11.37 %—12.41%）,明显优于模型在如皋数据集的验证精度（RRMSE= 16.69%—17.85%）（图10）。总体上,基于结构参数的线性估算模型明显优于基于小波特征的线性产量模型。

图10

新窗口打开|下载原图ZIP|生成PPT
图10基于结构参数的线性估算模型在如皋（A、B、C）以及兴化（D、E、F）的验证结果

Fig. 10The scatter plots of measured and predicted yield of rice with TLS-derived height variable (H_95th) at different growth stages in Rugao (A, B, C) and Xinghua (D, E, F)



2.3.2 随机森林回归 对比基于结构参数的随机森林估算模型在不同独立数据集的检验结果发现,产量模型在兴化数据集的验证精度（RRMSE=15.82%—20.75%）,优于模型在如皋数据集的验证精度（RRMSE=19.21%—23.62%）（图11）。对比基于结构参数的估算模型验证结果发现,基于结构参数的线性估算模型验证精度（RRMSE=11.37%—17.85%）,优于随机森林估算模型的验证精度（RRMSE=15.82%—23.62%）。

图11

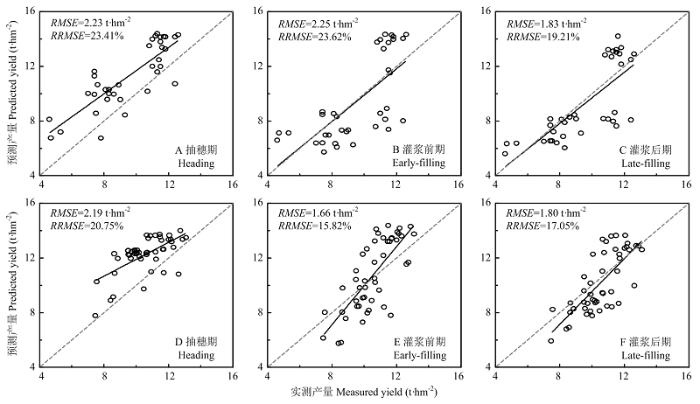新窗口打开|下载原图ZIP|生成PPT
图11基于结构参数的随机森林估算模型在如皋（A、B、C）以及兴化（D、E、F）的验证结果

Fig. 11The scatter plots of measured and predicted yield of rice from the structural metrics with random forest regression in Rugao (A, B, C) and Xinghua (D, E, F)

3 讨论

3.1 激光雷达技术监测产量的优势

在本研究中,植被指数以及小波特征与产量相关性均低于结构参数与产量的相关性,这与预期结果一致。作物所处的生长环境和生化参数（叶绿素、干物质和含水量）影响着作物个体的生长过程和作物的产量^[31]。水稻内部所含的多种色素、植株水分以及其结构控制着水稻特殊的光谱响应^[32]。水稻在生长发育的不同阶段,其内部的结构成分到外部的形态均衡发生一系列变化,因而在不同的生育期选用的光谱指标不同。点云数据可以更准确地估算水稻产量,原因归结于以下2个方面：一是激光雷达技术可以准确地获取作物的三维结构信息,与产量等生物物理参数有很高的相关性^[33]。二是在抽穗后,激光雷达获取到的各生育期的点云数据差异不明显（图6）,因而不同生育期模型较为一致,这使得模型更容易推广,降低了预测滞后性。此外,本研究也比较了不同生育期的激光雷达估算模型,发现分蘖期、拔节期与孕穗期的产量估算RMSE分别为2.03、1.87和1.72 t·hm^-2。与本文结果相比,抽穗后各生育期的产量估算精度更高。尽管光谱与空间维度信息的结合可能有助于提高估产精度,但考虑到技术成本和实用性,目前还是集中在单独使用一种技术,而且如何进行高效融合以显著提高估算精度也值得深入研究,未来在成本更低的情况下可考虑两类信息的融合。

图12

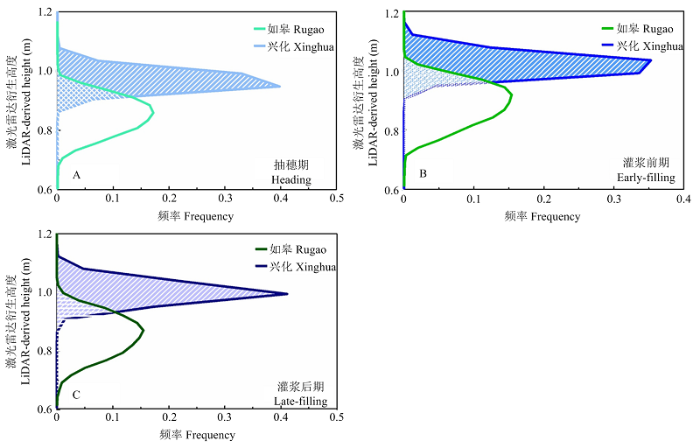新窗口打开|下载原图ZIP|生成PPT
图12如皋与兴化某小区抽穗后各生育期的高度直方图

Fig. 12Height histogram for an example plot at different growth stages in Rugao and Xinghua

3.2 不同条件下的模型可移植性

本研究结果表明,光谱数据的产量模型在如皋数据集的可移植性较差,这是因为光谱数据容易受到多种因素的影响^[34]。本研究在2个生态点进行数据获取,2个生态点在土壤特性、施氮梯度、水稻品种等存在较大差异,这些背景信息会产生光谱叠加,反映在光谱信号中影响数据质量,因而降低了模型的可移植性。

基于点云数据的线性估算模型在兴化数据集的验证精度（RRMSE = 11.37%—12.41%）,明显高于如皋数据集的验证精度（RRMSE = 16.79%—17.85%）,这是因为兴化生态点的品种一致,而如皋小区的水稻植株明显低于兴化小区的水稻植株。同时,如皋与兴化小区在布点方案与种植密度方面存在较大差异,致使激光穿透水稻植株的深度不同,进一步影响了模型精度（图2—3）,所以基于点云数据的线性估算模型在兴化数据集的验证精度更高。

3.3 2种回归方法的比较

基于线性回归与随机森林回归的产量模型的验证结果显示,线性的产量模型验证精度明显优于随机森林产量模型的验证精度,这与部分研究结果不一致^[35]。在本研究中基于随机森林回归的产量模型验证精度较低,可能是以下2个方面的原因导致的。一方面,过多的输入特征使得运行效率降低而且增加了过拟合的风险,同时少数有效特征的作用也会被掩盖在许多无用特征之下^[36]。另一方面,随机森林的回归模型在数据样本不均衡、有效样本较少等情况下难以应用。本研究使用的是独立数据集来评价模型的验证精度,不同数据集间存在差异导致随机森林的产量模型验证精度相对较低,这与部分证明激光雷达技术结合线性回归的生物量模型可移植性强的研究结果类似^[37]。

4 结论

本研究以如皋试验和兴化试验为基础,同步获取点云数据与光谱数据,开展了抽穗后各生育期的水稻光谱数据与点云数据和产量的时空变异特征研究。研究结果表明,基于点云数据的产量模型估算精度,优于基于光谱数据的产量估算模型;线性回归的产量模型较随机森林回归的产量模型更稳定;产量模型在同一生态点的可移植性优于不同生态点的可移植性。激光雷达技术可以在抽穗后直至收获前对产量进行全天候实时监测,该研究结果可以为精确收获和粮食收购政策制定等提供有益的技术支撑。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] ALOLA A, ALOLA U V. The dynamic nexus of crop production and population growth: housing market sustainability pathway
Environmental Science and Pollution Research, 2018, 26:6472-6480.
DOI:10.1007/s11356-018-04074-1URL [本文引用: 1]

[2] UN Food Agriculture Organization. How to feed the word in 2050
Discussion paper prepared for expert forum: 12-13. October 2009, released 23.
[本文引用: 1]

[3] INTERPRETERS S. FAO-food and agriculture organization of the united nations
Science, 2013, 118(3077):13-23.
[本文引用: 1]

[4] JULIAN P, MARK B, SARAH M. Food waste within food supply chains: quantification and potential for change to 2050
Philosophical Transactions of the Royal Society of London, 2010, 365(1554):3065-3081.
[本文引用: 1]

[5] LIU J G, PATTEY E, MILLER J R, MCNAIRN H, SMITH A, HU B X. Estimating crop stresses, aboveground dry biomass and yield of corn using multi-temporal optical data combined with a radiation use efficiency model
Remote Sensing of Environment, 2010, 114(6):1167-1177.
DOI:10.1016/j.rse.2010.01.004URL [本文引用: 1]

[6] MUTANGA O, ADAM E, CHO M A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm
International Journal of Applied Earth Observations and Geoinformation, 2012, 18(1):399-406.
DOI:10.1016/j.jag.2012.03.012URL [本文引用: 1]

[7] 亓雪勇, 田庆久. 光学遥感大气校正研究进展
国土资源遥感, 2005, 45(4):4-9.
[本文引用: 1]

QI X Y, TIAN Q J. The advance in the study of atmospheric correction for optical remote sensing
Remote Sensing for Land and Resources, 2005, 45(4):4-9. (in Chinese)
[本文引用: 1]

[8] 唐延林, 黄敬峰, 王人潮, 王福民. 水稻遥感估产模拟模式比较
农业工程学报, 2004, 3(1):167-172.
[本文引用: 1]

TANG Y L, HUANG J F, WANG R C, WANG F M. Comparsion of yield estimation simulated models of rice by remote sensing
Transactions of The Chinese Society of Agricultural Engineering, 2004, 3(1):167-172. (in Chinese)
[本文引用: 1]

[9] OWERS, C J, ROGERS K, WOODROFFE C D. Terrestrial laser scanning to quantify above-ground biomass of structurally complex coastal wetland vegetation
Estuarine Coastal and Shelf Science, 2018, 204:164-176.
DOI:10.1016/j.ecss.2018.02.027URL [本文引用: 4]

[10] EITEL J U H, MAGNEY T S, VIERLING L A, BROWN T T, HUGGINS D R. LiDAR based biomass and crop nitrogen estimates for rapid, non-destructive assessment of wheat nitrogen status
Field Crops Research, 2014, 159:21-32.
DOI:10.1016/j.fcr.2014.01.008URL [本文引用: 1]

[11] TILLY N, HOFFMEISTER D, CAO Q, LENZ-WIEDEMANN V, BARETH G. Precise plant height monitoring and biomass estimation with Terrestrial Laser Scanning in paddy rice
ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, II-5/W2:295-300.
DOI:10.5194/isprsannals-II-5-W2-295-2013URL [本文引用: 2]

[12] TILLY N, AASEN H, BARETH G. Fusion of plant height and vegetation indices for the estimation of barley biomass
Remote Sensing, 2015, 7:11449-11480.
DOI:10.3390/rs70911449URL [本文引用: 1]

[13] GUO Q H, WU F F, PANG S X, ZHAO X Q, CHEN L H, LIU J, XUE B L, XU G C, LI L, JING H C. Crop 3D: a platform based on LiDAR for 3D high-throughput crop phenotyping
Scientia Sinica, 2016, 12:121-141.
[本文引用: 1]

[14] LUMME J, KARJALAINEN M, KAARTINEN H, KUKKO A, HYYPPÄ J, HYYPPÄ H, JAAKKOLA A, KLEEMOLA J. Terrestrial laser scanning of agricultural crops
International Journal of Remote Sensing, 2008, 26(7):563-566.
DOI:10.1080/01431160512331299270URL [本文引用: 1]

[15] MCKINION J M, WILLERS J L, JENKINS J N. Comparing high density LIDAR and medium resolution GPS generated elevation data for predicting yield stability
Computers and Electronics in Agriculture, 2010, 74(2):244-249.
DOI:10.1016/j.compag.2010.08.011URL [本文引用: 1]

[16] LI Z H, WANG J H, XU X G, ZHAO C J, JIN X L, YANG G J, FENG H K. Assimilation of two variables derived from hyperspectral data into the DSSAT-CERES model for grain yield and quality estimation
Remote Sensing, 2015, 35(9):12400-12418.
[本文引用: 1]

[17] 王延颐. 植被指数与水稻长势及产量结构要素关系的研究
国土资源遥感, 1996, 2(1):56-59.
[本文引用: 1]

WANG Y Y. The relationship between vegetation index and rice growth and rice yield components
Remote Sensing for Land and Resources, 1996, 2(1):56-59. (in Chinese)
[本文引用: 1]

[18] 李卫国, 王纪华, 赵春江, 李存军, 王永华. 基于生态因子的冬小麦产量遥感估测研究
麦类作物学报, 2009, 29(5):213-220.
[本文引用: 1]

LI W G, WANG J H, ZHAO C J, LI C J, WANG Y H. Study on remote sensing estimation of winter wheat yield based on eco-environmental factors
Journal of Triticeae Crop, 2009, 29(5):213-220. (in Chinese)
[本文引用: 1]

[19] 薛利红, 曹卫星, 罗卫红. 基于冠层反射光谱的水稻产量预测模型
遥感学报, 2005, 7(1):102-107.
[本文引用: 1]

XUE L H, CAO W X, LUO W H. Rice yield forecasting model with canopy reflectance spectra
Journal of Remote Sensing, 2005, 7(1):102-107. (in Chinese)
[本文引用: 1]

[20] CHENG T, RIVARD B, SÁNCHEZ-AZOFEIFA A G, FÉRET J B, JACQUEMOUD S, USTIN S L. Deriving leaf mass per area (LMA) from foliar reflectance across a variety of plant species using continuous wavelet analysis
ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 87:28-38.
DOI:10.1016/j.isprsjprs.2013.10.009URL [本文引用: 2]

[21] 宋开山, 刘殿伟, 王宗明, 吕冬梅, 张柏, 任春颖, 杜嘉. 基于小波分析的玉米叶绿素a与LAI高光谱反演模型研究
农业系统科学与综合研究, 2011, 3(2):28-34.
[本文引用: 1]

SONG K S, LIU D W, WANG Z M, LÜ D M, ZHANG B, REN C Y, DU J. Corn chlorophyll-a concentration and LAI estimation models based on wavelet transformed canopy hyperspectral reflectance
System Sciences and Comprehensive Studies in Agriculture, 2011, 3(2):28-34. (in Chinese)
[本文引用: 1]

[22] 宋开山, 张柏, 王宗明, 刘殿伟, 刘焕军. 基于小波分析的大豆叶绿素a含量高光谱反演模型
植物生态学报, 2008, 2(1):157-165.
[本文引用: 1]

SONG K S, ZHANG B, WANG Z M, LIU D W, LIU H J. Soybean chlorophyll a concentration estimation models based on wavelet- transformed, in situ collected, canopy hyperspectral data
Journal of Plant Ecology, 2008, 2(1):157-165. (in Chinese)
[本文引用: 1]

[23] 洪雪. 基于水稻高光谱遥感数据的植被指数产量模型研究
[D]. 沈阳: 沈阳农业大学, 2017.
[本文引用: 1]

HONG X. Rice yield model research based on vegetation index of hyperspectral remote sensing data
[D]. Shenyang: Shenyang Agricultural University, 2017. (in Chinese)
[本文引用: 1]

[24] 王娣. 高光谱与多光谱遥感水稻估产研究
[D]. 武汉: 武汉大学, 2017.
[本文引用: 1]

WANG D. Hyperspectral and multispectral remote sensing study on yield estimation of rice
[D]. Wuhan: Wuhan University, 2017. (in Chinese)
[本文引用: 1]

[25] 黄春燕, 王登伟, 陈冠文, 袁杰, 祁亚琴, 陈燕, 程诚. 基于高光谱植被指数的棉花干物质积累估算模型研究
棉花学报, 2006, 18(2):115-119.
[本文引用: 1]

HUANG C Y, WANG D W, CHEN G W, YUAN J, QI Y Q, CHEN Y, CHENG C. Estimation modeling of cotton dry matter accumulation based on hyperspectral vegetation index
Cotton Science, 2006, 18(2):115-119. (in Chinese)
[本文引用: 1]

[26] 许童羽, 洪雪, 陈春玲, 周云成, 曹英丽, 于丰华, 李娜. 基于冠层NDVI数据的北方粳稻产量模型研究
浙江农业学报, 2016, 28(10):1790-1795.
[本文引用: 1]

XU T Y, HONG X, CHEN C L, ZHOU Y C, CAO Y L, YU F H, LI N. Study on northern japonica rice yield model based on canopy date of NDVI
Acta Agriculturae Zhejiangensis, 2016, 28(10):1790-1795. (in Chinese)
[本文引用: 1]

[27] 宋红燕, 胡克林, 彭希. 基于高光谱技术的覆膜旱作水稻植株氮含量及籽粒产量估算
中国农业大学学报, 2016, 4(8):27-34.
[本文引用: 1]

SONG H Y, HU K L, PENG X. Crop nitrogen content diagnosis and yield estimation in ground cover rice production system based on hyperspectral data
Journal of China Agricultural University, 2016, 4(8):27-34. (in Chinese)
[本文引用: 1]

[28] SHIBAYAMA M. AKIYAMA T. Estimating grain yield of maturing rice canopies using high spectral resolution reflectance measurements
Remote Sensing of Environment, 1991, 36(1):45-53.
DOI:10.1016/0034-4257(91)90029-6URL [本文引用: 1]

[29] BAI J H, LI S K, WANG K R, SUI X Y, CHEN B, WANG F Y. Estimating aboveground fresh biomass of different cotton canopy types with homogeneity models based on hyper spectrum parameters
Agricultural Sciences in China, 2007, 6(4):437-445.
DOI:10.1016/S1671-2927(07)60067-4URL [本文引用: 2]

[30] LI P, ZHANG X, WANG W H, ZHENG H B, YAO X, TIAN Y C, ZHU Y, CAO W X, CHEN Q, CHENG T. Estimating aboveground and organ biomass of plant canopies across the entire season of rice growth with terrestrial laser scanning
International Journal of Applied Earth Observation and Geoinformation, 2020, 91:102-132.
[本文引用: 1]

[31] GITELSON A A, VIÑA A, ARKEBAUER T J, RUNDQUIST D C, KEYDAN G P, LEAVITT B, KEYDAN G. Remote estimation of leaf area index and green leaf biomass in maize canopies
Geophysical Research Letters, 2003, 30:335-343.
[本文引用: 1]

[32] HUDAK A T, LEFSKY M A, COHEN W B, BERTERRETCHE M. Integration of LiDAR and Landsat ETM+ data for estimating and mapping forest canopy height
Remote Sensing of Environment, 2015, 82(2/3):397-416.
DOI:10.1016/S0034-4257(02)00056-1URL [本文引用: 1]

[33] WEI F, HUI F, YANG W N, DUAN L F, CHEN G X, XIONG L Z, LIU Q. High-throughput volumetric reconstruction for 3D wheat plant architecture studies
Journal of Innovative Optical Health Sciences, 2016, 9(5):1650037.
DOI:10.1142/S1793545816500371URL [本文引用: 1]

[34] HUANG J F, BLACKBURN G A. Optimizing predictive models for leaf chlorophyll concentration based on continuous wavelet analysis of hyperspectral data
International Journal of Remote Sensing, 2011, 32(24):9375-9396.
DOI:10.1080/01431161.2011.558130URL [本文引用: 1]

[35] CHEN Q. Modeling aboveground tree woody biomass using national- scale allometric methods and airborne LiDAR
ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 106:95-106.
DOI:10.1016/j.isprsjprs.2015.05.007URL [本文引用: 1]

[36] DAI B, GU C S, ZHAO E, QIN X N. Statistical model optimized random forest regression model for concrete dam deformation monitoring
Structural Control and Health Monitoring, 2018, 25(6):1-15.
[本文引用: 1]

[37] TILLY N, HOFFMEISTER D, CAO Q, LENZ-WIEDEMANN V, MIAO Y X, BARETH G. Transferability of models for estimating paddy rice biomass from spatial plant height data
Agriculture, 2015, 5:538-552.
DOI:10.3390/agriculture5030538URL [本文引用: 1]