吴国雄[4]结合现场调研成果,从理论上分析了水泥混凝土路面的开裂机理和破坏过程。研究结果表明,动荷载对水泥路面的破坏性比普通的交通荷载大得多,是造成路面裂缝出现的主要原因。高哲[5]依据现场监测结果,对落锤式弯沉仪(FWD)荷载作用下沥青路面的沉降进行了分析,发现温度、湿度、结构层厚度对沥青路面的沉降影响较大,而土基模量的影响则相对较小。肖川等[6]采用现场试验的方法,研究了FWD荷载下多种混凝土路面的响应特性,结果表明路面的沉降随荷载的增加显著增加,且增长速率先增大后减小。樊后超[7]结合工程实际,采用数值模拟方法计算了冲击荷载作用位置对水泥混凝土路面的影响。计算结果表明,冲击荷载作用在混凝土面板中部时,对混凝土路面的裂缝扩展影响最大。
值得指出的是,目前已有相关冲击荷载对含初始裂缝的水泥混凝土路面影响的研究成果相对较少。另考虑到数值模拟的可靠性和有效性在很大程度上取决于参数的选定。因此,本文采用文献[8]的计算方法,参考文献[9-10]的研究思路,首先通过将数值模拟和经典的物理试验进行对比,确定出可靠的混凝土数值模拟参数。在此基础上,研究了冲击荷载作用下具有不同初始裂缝长度和位置的水泥混凝土路面的动态响应规律,以望对冲击荷载作用下水泥混凝土路面的动态响应研究有所裨益。
1 数值模拟参数有效性验证 董玉文和任青文[11]已有研究表明:扩展有限元法(Extended Finite Element Method,XFEM)是研究混凝土开裂和裂缝扩展的有效工具。因此,本文采用扩展有限元法分析冲击荷载作用下水泥混凝土路面的开裂过程和影响因素。利用有限元法进行分析,最关键的是参数的可靠性和有效性。因此,在进行系列的数值模拟前,本文首先通过将数值模拟结果与2个经典的试验结果进行对比分析,确定出合理可靠的参数。
第1个经典的试验是文献[12]的三弯梁试验,三弯梁尺寸如图 1[12]所示。图 2给出了加载点荷载-位移曲线的数值模拟与试验结果的对比。由图 2可见,数值模拟的荷载-位移曲线总体上落在试验值包络范围内,尤其是荷载峰值前与试验曲线基本一致,软化段的规律也同试验规律类似,数值模拟能较好地反映试验规律。
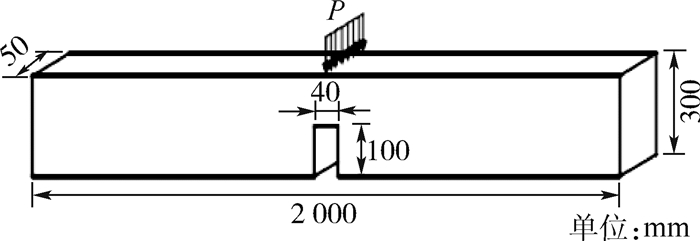 |
| 图 1 Petersson三弯梁尺寸[12] Fig. 1 Dimension of Petersson three bending beam[12] |
| 图选项 |
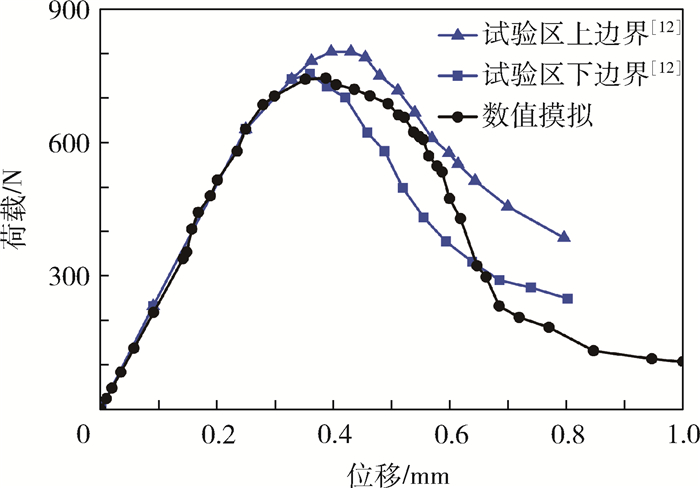 |
| 图 2 加载点荷载-位移曲线 Fig. 2 Load-displacement curves at loading point |
| 图选项 |
第2个经典的试验是文献[13]在1992年进行的混凝土单边缺口三弯梁的动力试验。梁的几何尺寸、应变片布置以及冲击荷载形式分别如图 3[13]和图 4[13]所示, 图 3中SG01、SG02、SG03均为应变片。3个测量点应变随时间变化的数值模拟和试验结果对比曲线如图 5所示。由图 5可见,3个测量点的数值模拟与试验结果变化规律类似,数值模拟能较好地反映冲击荷载作用下不同位置梁体应变的发展过程。
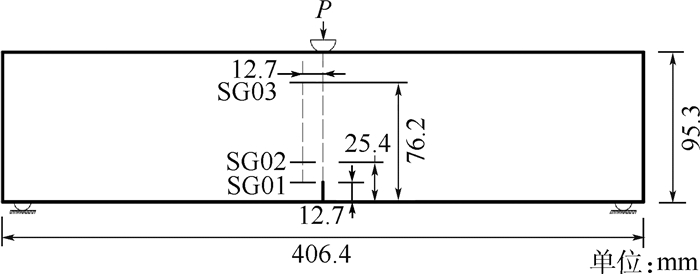 |
| 图 3 动力断裂梁几何尺寸和应变片布置[13] Fig. 3 Geometric dimensions and strain gauge layout of dynamic fracture beam[13] |
| 图选项 |
 |
| 图 4 冲击荷载形式[13] Fig. 4 Type of impact loading[13] |
| 图选项 |
 |
| 图 5 测量点应变随时间变化曲线 Fig. 5 Strain-time curve at measuring points |
| 图选项 |
通过以上将数值模拟与试验结果对比,确定出了较为可靠的混凝土模型主要参数,如表 1所示。
表 1 混凝土参数 Table 1 Parameters for concrete
| 参数 | 弹性模量/ MPa | 泊松比ν | 抗拉强度ft/ MPa | 断裂能 Gf/(N·m-1) |
| 数值 | 30 000 | 0.3 | 3.33 | 124 |
表选项
2 道路数值模型 数值模拟采用的道路结构层由面层水泥混凝土、基层石灰土以及土层黄土组成,各结构层的厚度分别为180 mm、180 mm和3 000 mm。冲击荷载作用在面层的中心,作用区域为圆形。考虑到路面结构和冲击荷载作用的对称性,为提高数值模拟计算的效率[14-15],建立了如图 6所示的2D模型。在该模型中,两侧约束横向(x向)位移,底边约束横向和竖向2个方向(x和y向)的位移。表层水泥混凝土路面采用的基于扩展有限元法的黏聚裂缝模型,基层石灰土采用的摩尔库伦模型,黄土采用的DP模型。各结构层的主要数值模拟参数如表 2所示。
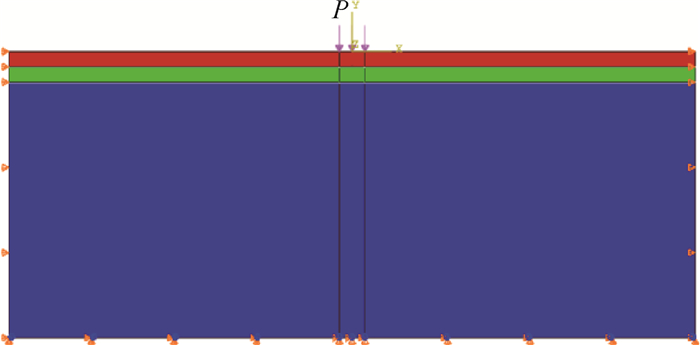 |
| 图 6 路面结构示意图 Fig. 6 Sketch map of pavement structure |
| 图选项 |
表 2 路面结构层数值模拟参数 Table 2 Numerical simulation parameters for pavement structure layer
| 材料 | 弹性模量/ MPa | 密度/ (kg·m-3) | 泊松比 | 内摩擦角/ (°) | 内聚力/ kPa |
| 水泥混凝土 | 30 000 | 2 500 | 0.3 | ||
| 石灰土 | 700 | 1 750 | 0.35 | 32 | 90 |
| 黄土 | 100 | 1 800 | 0.3 | 22 | 56 |
表选项
除弹性模量和泊松比外,水泥混凝土路面的抗拉强度和断裂能均采用的表 1中数值3.33 MPa和124 N/m。
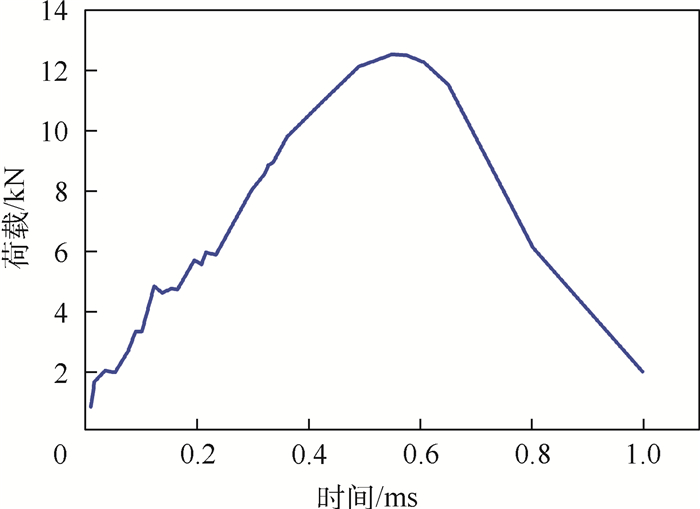
冲击荷载作用在以道路中心为圆心,半径为0.15 m的圆形区域内。图 7所示为冲击荷载的时程曲线,总作用时间为34 ms,峰值为1 400 kN,为标准FWD荷载曲线的2倍。
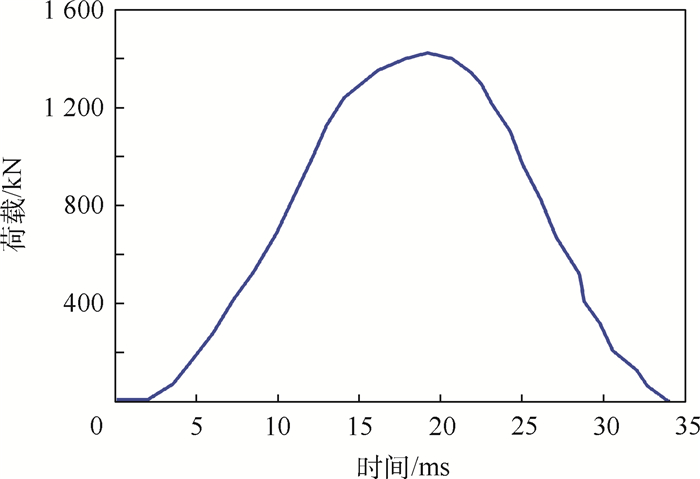 |
| 图 7 FWD荷载作用曲线 Fig. 7 Loading curve of FWD |
| 图选项 |
本文着重探讨水泥混凝土路面在有不同初始裂缝长度和位置的情况下,冲击荷载对裂缝扩展的影响。主要分析了以下2种工况:
1) 初始裂缝长度对裂缝扩展的影响
初始裂缝设置在荷载加载区域中心正下方的面层内,具体位置如图 8所示,其中P为FWD荷载作用区域,分别设置裂缝初始长度l与面层厚度h的比为1/18、1/9、1/6和2/9这4种不同情况。
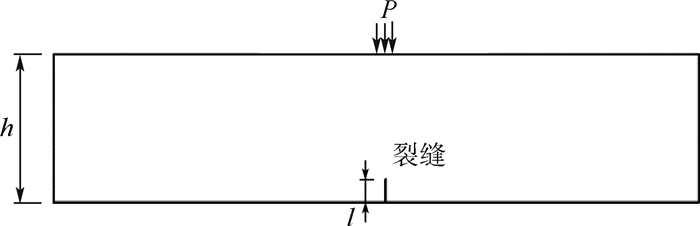 |
| 图 8 初始裂缝位置和长度示意图 Fig. 8 Sketch map of initial crack position and length |
| 图选项 |
2) 初始裂缝位置对裂缝扩展的影响
保持初始裂缝初始长度l与面层厚度h的比为1/9不变,分别设置初始裂缝与荷载作用中心的距离b与板宽B的比为0、0.05、0.10和0.15这4种不同情况,见图 9。
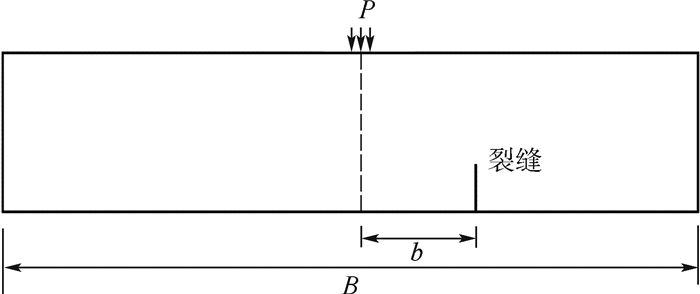 |
| 图 9 初始裂缝位置示意图 Fig. 9 Sketch map of initial crack position |
| 图选项 |
3 计算结果与讨论 3.1 初始裂缝长度对裂缝扩展的影响 图 10所示为初始裂缝长度l与面层厚度h的比l/h分别为1/18、1/9、1/6和2/9时,在冲击荷载作用下最终扩展的裂缝。由图 10可见,当l/h为1/18时,初始裂缝扩展到混凝土面层中部即停止;而在其余3种情况下(l/h为1/9、1/6和2/9),初始裂缝扩展到了水泥混凝土板的顶部,整个水泥混凝土面层产生了贯穿裂缝。
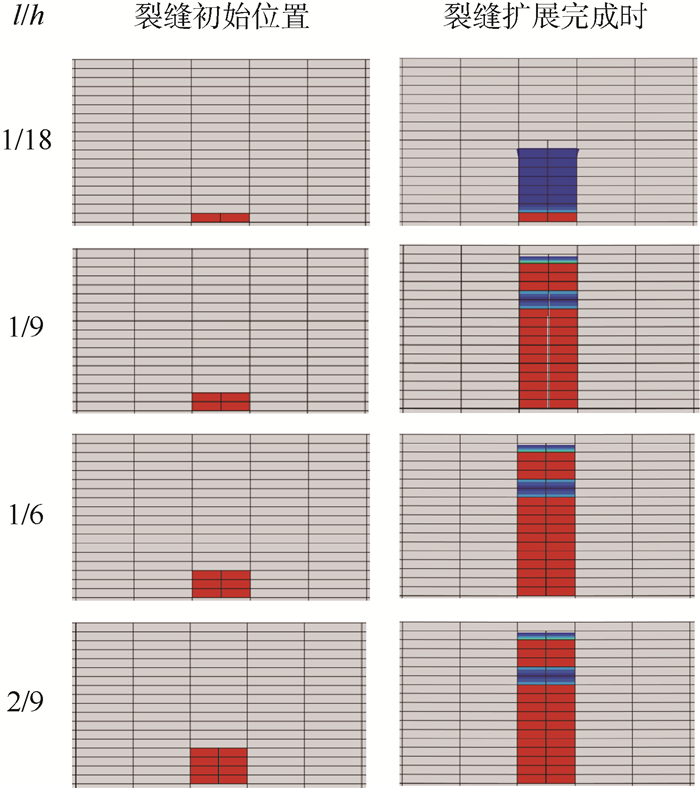 |
| 图 10 不同初始裂缝长度最终扩展的裂缝 Fig. 10 Final crack produced with different initial crack length |
| 图选项 |
图 11(a)、图 11(b)分别给出了水泥混凝土路面冲击荷载作用中心点的沉降时程曲线以及前0.16 s的沉降时程曲线放大图。由图 11可知,在冲击荷载作用下,荷载作用中心点的沉降与冲击荷载作用曲线类似,先迅速达到峰值,然后再回弹到一个稳定值,且达到最大沉降的时间比冲击荷载峰值作用时间有滞后。初始裂缝长度对沉降的影响与最终裂缝扩散长度的影响类似。初始裂缝长度l与面层厚度h的比l/h为1/9、1/6和2/9时,沉降时程曲线几乎一致,且在这3种情况下产生的沉降均大于l/h为1/18时的沉降。
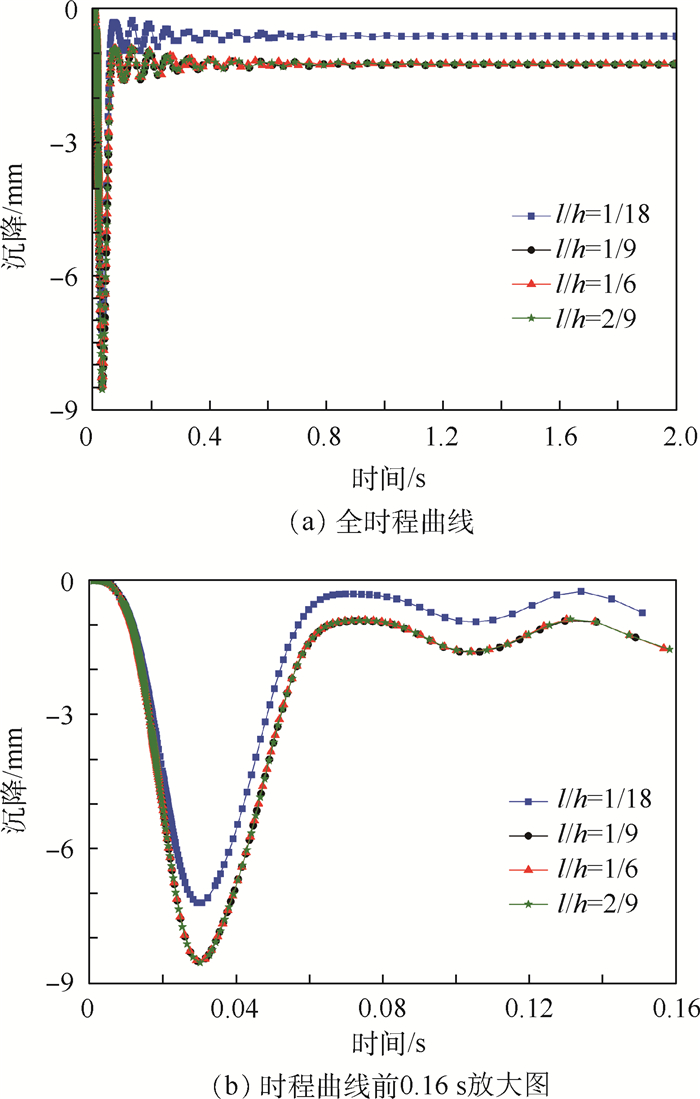 |
| 图 11 不同初始裂纹长度加载中心点沉降随时间变化曲线 Fig. 11 Settlement-time curve at loading center with different initial crack length |
| 图选项 |
图 12所示为冲击荷载作用中心点达到最大峰值沉降时路面弯沉盆曲线。由图 12可见,随着路面点与荷载作用中心点距离的增加,路面的沉降随之减小。初始裂缝长度的不同主要对荷载作用中心1 m范围内的沉降有较大影响。
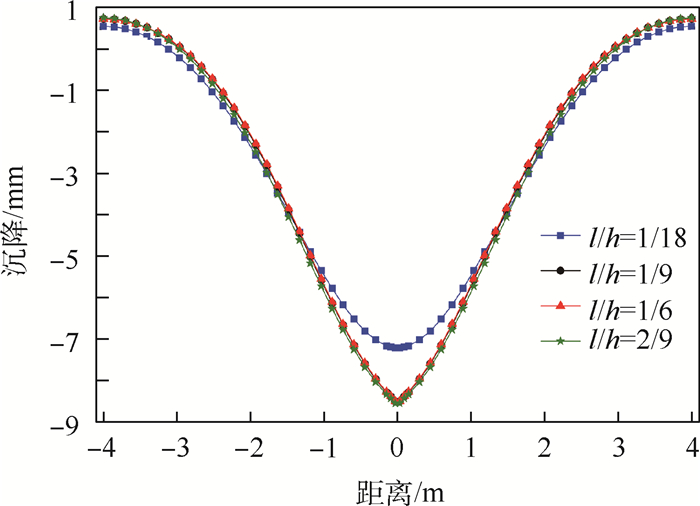 |
| 图 12 不同初始裂纹长度峰值沉降时刻路面弯沉盆 Fig. 12 Pavement deflection basin at moment of maximum settlement with different initial crack length |
| 图选项 |
峰值沉降时刻路面加载中心点沉降随深度的变化曲线如图 13所示。由图 13可知,沉降主要在石灰土和黄土中产生,随深度增加沉降呈递减的趋势。初始裂缝长度的不同主要影响的是面层以下约5倍水泥混凝土面层厚度范围内(水平虚线以上范围)石灰土和黄土的压缩变形。且与荷载作用中心点沉降时程规律类似,初始裂缝长度l与面层厚度h的比l/h为1/9、1/6和2/9时,沉降随深度曲线几乎一致,且在这3种情况下的沉降均大于l/h为1/18时的沉降。
 |
| 图 13 不同初始裂纹长度峰值沉降时刻加载中心点沉降随深度变化曲线 Fig. 13 Settlement-depth curve at loading center at moment of maximum settlement with different initial crack length |
| 图选项 |
3.2 初始裂缝位置对裂缝扩展的影响 保持初始裂缝长度l与面层厚度h的比为1/9不变,初始裂缝与荷载作用中心的距离b与板宽B的比b/B分别为0、0.05、0.10和0.15这4种情况下最终扩展的裂缝如图 14所示。由图 14可知,随初始裂缝位置与荷载作用中心距离的增加,最终扩展的裂缝长度呈递减趋势。当初始裂缝设置在荷载作用中心正下方即b/B=0时,裂缝扩展到混凝土面层顶部,整个水泥混凝土路面产生了贯穿性裂缝;随着初始裂缝远离荷载作用中心,譬如当初始裂缝位置b/B为0.15时,裂缝只扩展到了1/3面板厚度处。
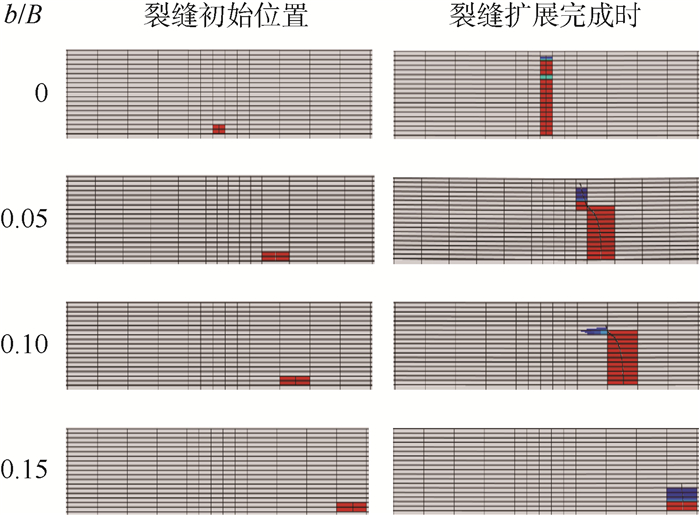 |
| 图 14 不同初始裂缝位置最终扩展的裂缝 Fig. 14 Final crack produced with different initial crack location |
| 图选项 |
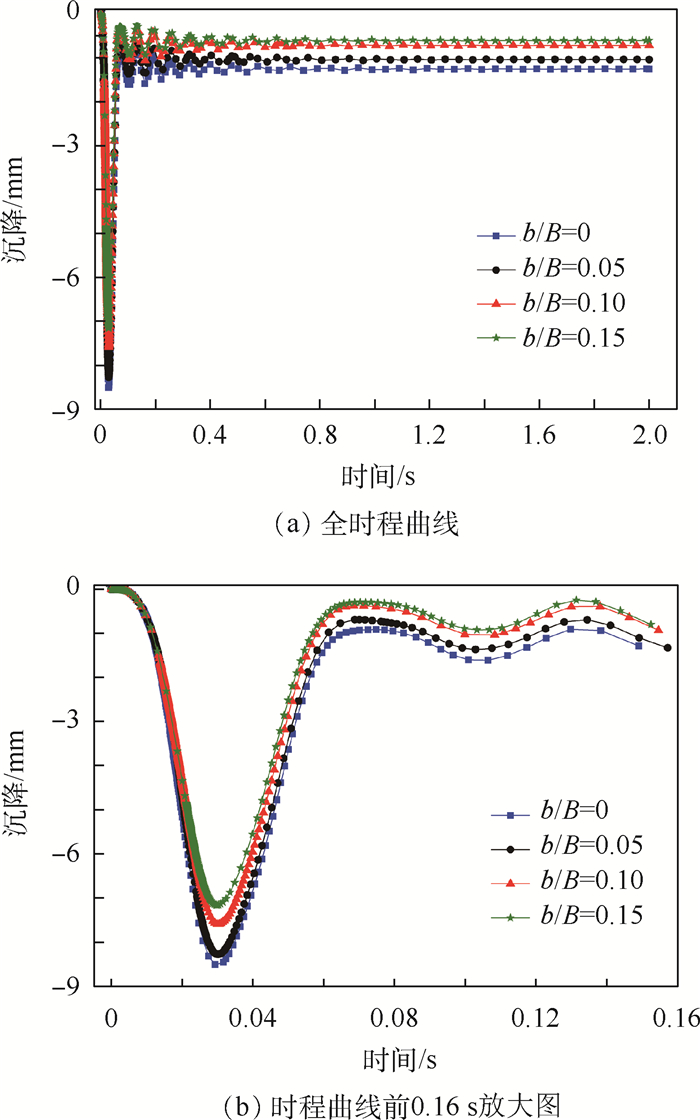
图 15(a)和图 15(b)分别给出了裂缝初始位置不同时水泥混凝土路面冲击荷载作用中心点的沉降时程曲线以及前0.16 s的沉降时程曲线放大图。由图 15可知,不同初始裂缝位置时荷载作用中心点的沉降时程曲线类似,都是先增大后减小,最终趋于稳定。但随初始裂缝位置与荷载作用中心距离的增加,荷载作用中心点的最大沉降和最终稳定的沉降均呈递减趋势。
 |
| 图 15 不同初始裂纹位置加载中心点沉降随时间变化曲线 Fig. 15 Settlement-time curve at loading center with different initial crack location |
| 图选项 |
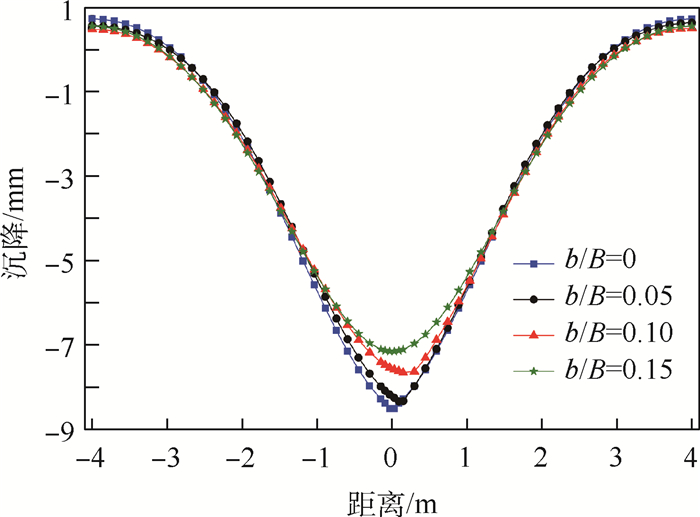
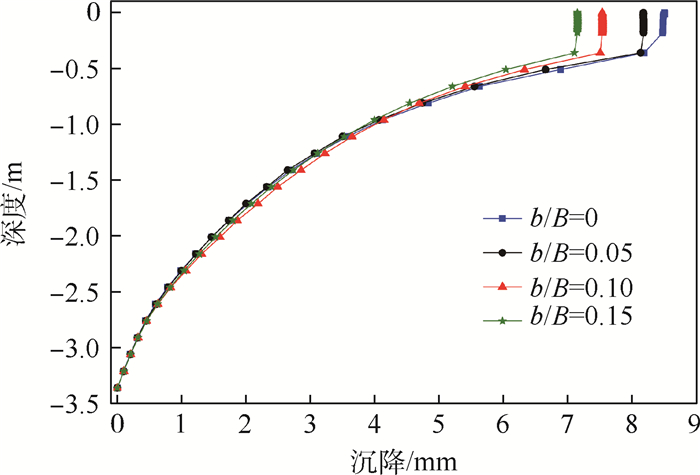
图 16和图 17所示分别为冲击荷载作用中心点达到最大峰值沉降时路面弯沉盆曲线以及沉降随深度的变化曲线。由图 16和图 17可知,沉降随与荷载作用中心距离增加而减小,随深度的增加亦呈递减趋势。初始裂缝位置不同主要对荷载作用中心1 m范围内的沉降有影响,且引起沉降的主要原因是石灰土和黄土的压缩变形。
 |
| 图 16 不同初始裂纹位置峰值沉降时刻路面弯沉盆 Fig. 16 Pavement deflection basin at moment of maximum settlement with different initial crack location |
| 图选项 |
 |
| 图 17 不同初始裂纹位置峰值沉降时刻加载中心点沉降随深度变化曲线 Fig. 17 Settlement-depth curve at loading center at moment of maximum settlement with different initial crack location |
| 图选项 |
4 结论 本文旨在探索冲击荷载作用下含初始裂缝的水泥混凝土路面的动态响应特性。为确保数值模拟的有效性,首先通过将数值模拟和2个经典的物理试验进行比对,确定出了可靠的水泥混凝土参数。在此基础上研究了不同初始裂缝长度和位置的水泥混凝土路面最终扩散的裂缝长度、荷载作用中心点的沉降以及沉降的分布特征。
1) 冲击荷载作用下水泥混凝土路面的沉降时程曲线与冲击荷载作用曲线类似,先快速到达峰值,然后再回弹到一个稳定值。水泥混凝土路面的沉降主要源于基层石灰土和底层黄土的变形。水泥混凝土路面的沉降随与冲击荷载作用中心距离的增大而减小,随深度的增加亦呈递减趋势。
2) 初始裂缝长度的不同主要影响的是面层以下约5倍水泥混凝土面层厚度范围内石灰土和黄土的压缩变形。随初始裂缝长度的增大,水泥混凝土路面的破坏程度会逐渐增大。当裂缝长度与面层厚度的比超过某一值时,水泥混凝土路面会产生贯穿性的裂缝。
3) 水泥混凝土路面最终扩展的裂缝长度和沉降均随初始裂缝与荷载作用中心距离的增加而减小。初始裂缝长度和位置的不同主要影响荷载作用中心1m范围内水泥混凝土面板的沉降。
参考文献
| [1] | 郑玉民, 关庆昌, 旦小伦. 水泥混凝土路面特点分析和施工工艺概述[J]. 科技信息, 2008(30): 125. ZHENG Y M, GUAN Q C, DAN X L. Characteristic analysis and construction technology summary of cement concrete pavement[J]. Science & Technology Information, 2008(30): 125. (in Chinese) |
| [2] | 郝贠洪, 樊磊, 韩燕. 冲击荷载下水泥基材料的冲击损伤研究[J]. 混凝土, 2018, 342(4): 18-20. HAO Y H, FAN L, HAN Y. Study on impact damage of cement-based materials under impact load[J]. Concrete, 2018, 342(4): 18-20. DOI:10.3969/j.issn.1000-4637.2018.04.004 (in Chinese) |
| [3] | 罗立峰, 周建春, 郑国梁. 水泥混凝土路面维修方案的研究[J]. 华南理工大学学报(自然科学版), 1999, 27(6): 123-127. LUO L F, ZHOU J C, ZHENG G L. Research on maintenance methods of the old cement concrete pavement[J]. Journal of South China University of Technology(Natural Science), 1999, 27(6): 123-127. DOI:10.3321/j.issn:1000-565X.1999.06.025 (in Chinese) |
| [4] | 吴国雄.水泥混凝土路面开裂机理及破坏过程研究[D].成都: 西南交通大学, 2003. WU G X.Study on cracking mechanism and failure process of cement concrete pavement[D].Chengdu: Southwest Jiaotong University, 2003(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10613-2004020327.htm |
| [5] | 高哲.基于落锤式弯沉仪(FWD)的半刚性基层沥青路面结构性能评价[D].济南: 山东建筑大学, 2016. GAO Z.Semi-rigid base asphalt pavement structure performance evaluation based on falling weight deflectometer (FWD)[D].Jinan: Shandong Jianzhu University, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10430-1016081495.htm |
| [6] | 肖川, 邱延峻, 曾杰, 等. FWD荷载作用下的沥青路面实测动力响应研究[J]. 公路交通科技, 2014, 31(2): 1-8. XIAO C, QIU Y J, ZENG J, et al. Study on measured dynamic response of asphalt pavement under FWD load[J]. Journal of Highway and Transportation Research and Development, 2014, 31(2): 1-8. DOI:10.3969/j.issn.1002-0268.2014.02.001 (in Chinese) |
| [7] | 樊后超.冲击荷载作用下混凝土路面的损伤分析[D].哈尔滨: 哈尔滨工业大学, 2009. FAN H C.Analysis damage of concrete pavement under impact loading[D].Harbin: Harbin Institute of Technology, 2009(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-2010064297.htm |
| [8] | 余天堂. 扩展有限单元法:理论、应用及程序[M]. 北京: 清华大学出版社, 2012. YU T T. The extended finite element method-theroy, application and program[M]. Beijing: Tsinghua University Press, 2012. (in Chinese) |
| [9] | 潘坚文.高混凝土坝静动力非线性断裂与地基辐射阻尼模拟研究[D].北京: 清华大学, 2010. PAN J W.Nonlinear static and seismic fracture analysis of high concrete dams and modeling of radiation damping for foundation[D].Beijing: Tsinghua University, 2010(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10003-1011280382.htm |
| [10] | 谈至明, 姚祖康, 田波. 水泥混凝土路面的荷载应力分析[J]. 公路, 2002(8): 15-18. TAN Z M, YAO Z K, TIAN B. Load stress analysis of cement concrete pavement[J]. Highway, 2002(8): 15-18. DOI:10.3969/j.issn.0451-0712.2002.08.004 (in Chinese) |
| [11] | 董玉文, 任青文. 基于XFEM的混凝土开裂数值模拟研究[J]. 重庆交通大学学报(自然科学版), 2009, 28(1): 36-40. DONG Y W, REN Q W. Numerical simulation of concrete cracking based on XFEM[J]. Journal of Chongqing Jiaotong University (Natural Science), 2009, 28(1): 36-40. (in Chinese) |
| [12] | PETERSSON P E. Crack growth and development of fracture zones in plain concrete and similar materials: TVBM-1006[R].Lund: University of Lund, 1981. |
| [13] | DU J, YON J H, HAWKINS N M. Fracture process zone for concrete for dynamic loading[J]. ACI Material Journal, 1992, 89(3): 252-258. |
| [14] | REN X F, GUAN X. Three dimensional crack propagation through mesh-based explicit representation for arbitrarily shaped cracks using the extended finite element method[J]. Engineering Fracture Mechanics, 2017, 177: 218-238. DOI:10.1016/j.engfracmech.2017.04.007 |
| [15] | MOTAMEDI D, MOHAMMADI S. Dynamic crack propagation analysis of orthotropic media by the extended finite element method[J]. International Journal of Fracture, 2010, 161(1): 21-39. DOI:10.1007/s10704-009-9423-7 |
