针对连接结构,国内外****从连接界面损伤特征、仿真分析方法等不同方面开展了相关研究。在连接界面损伤失效方面,Truman和Booker[3]研究了配合表面局部小幅相对运动引起微动损伤,得到载荷条件和设计变量对过盈界面失效的影响规律。Wang等[4]为了避免风车叶轮与轴的配合失效并提高连接可靠性,研究了配合紧度和摩擦系数对于盘-轴连接界面接触应力的影响规律,并且对接触应力进行参数化设计和试验验证。笔者团队[5]研究了连接界面的稳健优化方法,基于平均接触应力和最大接触应力对连接界面损伤失效进行有效控制。在连接刚度损失及其对转子动力特性的影响方面,尹泽勇等[6]提出端齿梁元的概念用于端齿轴段刚度与整体轴段刚度的差异,研究结果表明端齿连接结构的存在对结构的模态振型和共振频率均有较大影响。Wang等[7]研究了螺栓连接结构弯曲刚度损失的因素,并采用弹性模量修正方法进行复杂航空发动机转子结构建模分析。Qin等[8]对螺栓松动时连接结构的时变刚度进行有限元法模拟,在考虑螺栓松动及其对转子动力学的影响时,采用非线性角弹簧模拟弯曲刚度非线性特征。
在转子系统动力学的优化设计方面,早期的Shiau和Lin等[9-11]基于动力学方程,采用修正可行性方向法和序列二次规划法等方法对转子系统质量、临界转速分布等动力特性进行了优化。Stocki等[12]考虑了转子系统剩余不平衡量和轴承支承刚度的不确定性,以轴的总重量和转轴形状为目标函数,对离心压气机单盘转子系统进行基于响应面法的稳健优化。杨隽等[13]提出了基于Taguchi方法的容差设计理论,对双转子航空发动机模型初始不平衡量进行了容差设计,以初始不平衡量及相位角差为设计参数,以支承最大振动响应为设计目标。
当前的研究均未考虑由于制造、装配和载荷环境等因素而导致连接结构力学特性和支承刚度的分散性,及其对转子系统动力特性的影响。稳健设计[14]思想源于20世纪70年代田口玄一的三次设计法,其目的在于使产品性能对设计参数的变差不敏感,现广泛应用于工程设计。本文以提高动力涡轮转子结构系统临界转速特性稳健性为目标,对连接界面接触损伤所导致的连接结构力学特性的分散性,及动力特性对各支点支承刚度变化的敏感度进行分析,对动力涡轮转子结构系统动力特性进行优化和稳健设计。
1 典型动力涡轮转子结构系统结构与载荷特征 现代高功重比涡轴发动机转子结构系统一般采用涡轮级间共用承力框架支承方案设计,动力涡轮转子为四支点悬臂支承结构,如图 1所示。动力涡轮转子轴段轴向跨度较大,因受到燃气发生器转子轴承DN值的限制,其外径尺寸较小,弯曲刚性较差。为控制通过多阶临界转速时的振动响应,多采用四支点支承方案,以加强转子局部刚度。动力涡轮位于转子系统的后端,径向尺寸较大,具有很大的质量和转动惯量,导致动力涡轮转子结构系统几何结构特征变化大,质量/刚度分布极不均匀。
 |
| 图 1 典型高功重比涡轴发动机动力涡轮转子结构系统 Fig. 1 Typical power turbine rotor structural system in high power-to-weight ratio turboshaft engine |
| 图选项 |
与整体式转子不同,由于连接界面的存在、几何结构特征突变,动力涡轮转子结构系统在一定载荷环境下其力学特性具有非连续性。如图 2所示,转子结构的连接界面主要分为轴向端面和定心圆柱面。连接界面因装配载荷相互压紧,工作时其力学特性会随转子工作转速、弯曲载荷(机动飞行时的陀螺力矩和惯性载荷等)、气动扭矩等复杂载荷发生变化。随工作载荷变化,可能会引起连接界面变形不协调,作用在连接界面的接触应力发生变化,出现接触损伤特征,其结果可能会使连接结构弯曲刚度发生变化,呈现一定的分布特征,对转子动力特性产生影响。
 |
| 图 2 动力涡轮转子结构系统连接结构 Fig. 2 Joint structures of power turbine rotor structural system |
| 图选项 |
支承结构和承力框架的制造、装配以及不同工作状态造成结构、材料参数变化,转子系统各支点支承刚度具有一定的分布特征。因此,进行支点支承刚度的设计时,需考虑支承刚度是否落入临界转速的敏感区域内,以免临界转速对于支承刚度的变化敏感。
2 连接结构力学特性分散性产生机理 掌握连接界面接触损伤特性对连接结构力学特性分散性影响的内在规律是转子系统连接结构稳健设计的重要前提。如图 3所示,连接结构承受的载荷复杂多变时,其力学特性产生非确定变化。连接界面变形协调性是影响损伤程度的主要原因,由于相互连接的构件变形不协调,在复杂工作载荷环境下,造成连接界面在局部位置产生过度的相互分离或压紧趋势,使得连接界面接触状态和应力分布发生变化,造成连接界面接触损伤、失效,甚至产生连接结构弯曲刚度损失,其力学特性具有非确定性分布特征。
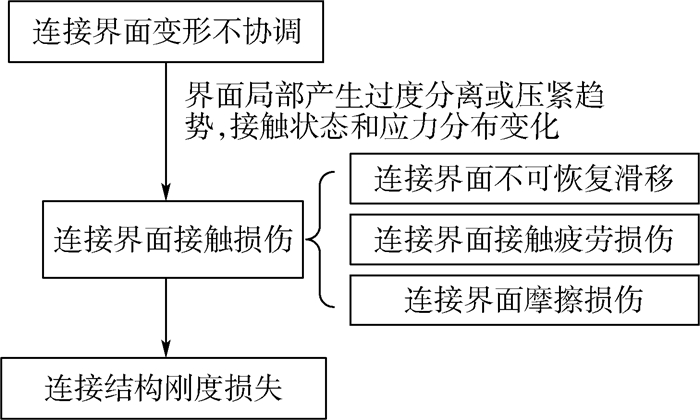 |
| 图 3 连接结构力学特性非确定变化产生机理 Fig. 3 Generation mechanism of non-deterministic change in mechanical properties of joint structure |
| 图选项 |
连接界面接触损伤是连接结构力学特性产生分散性的内在原因,将其机理分为连接界面不可恢复滑移、连接界面接触疲劳损伤和连接界面摩擦损伤3个方面进行分析研究。
2.1 连接界面不可恢复滑移 连接界面不可恢复滑移指连接结构在承受工作载荷时,连接界面切向上产生相对滑移变形,当所承受的工作载荷减小或者进入停车状态时,由于连接界面上摩擦力的存在,连接界面上的一部分滑移变形不可恢复,可能导致转子系统产生附加不平衡量。
针对连接界面不可恢复滑移,提出连接界面接触状态系数Cconta评估损伤程度。接触界面按照其相互约束的紧密程度分为4种接触状态:黏滞和滑移、准接触、张开。其中,只有界面处于黏滞、滑移状态可以传递载荷,提供刚度。为了保证在工作状态下连接界面功能稳定可靠,要求连接界面一部分区域始终稳定压紧,即连接界面黏滞和滑移面积占有一定的比例,即
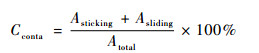 | (1) |
式中:Asticking和Asliding分别为黏滞状态和滑移状态的区域面积;Atotal为连接界面的总面积。
2.2 连接界面接触疲劳损伤 连接界面接触疲劳损伤指连接界面在装配状态和工作状态下承受巨大的法向压力或者产生大的法向压力变化,界面上的局部区域进入塑性变形产生裂纹或破坏,其损伤机理主要是连接界面在接触应力作用下产生微动疲劳。装配或停车状态下,连接界面由于压紧变形会产生较大的法向接触应力。工作状态下,连接结构承受的载荷复杂多变,连接界面接触应力发生变化,如果连接界面上接触应力平均值和变化幅值较大,就容易造成由接触应力导致的连接界面接触疲劳损伤。
针对连接界面接触疲劳损伤,提出连接界面接触应力和不可恢复变形能参数评估其损伤程度。由于连接界面接触应力分布具有不均匀性,同时采用最大接触应力σmax和平均接触应力σaver进行评估。最大接触应力σmax用于评估连接界面疲劳损伤程度,其值不应超过表面微观屈服强度;平均接触应力σaver用于描述连接界面在各工作状态下的压紧程度,其数值越大连接界面越难以松动,应保证其值处于较高水平。基于连接界面疲劳损伤能量理论,疲劳寿命中,每次应力循环产生的耗散能量效应之和为常数。不可恢复变形能E表示每次应力循环损伤能量相对大小,采用数值积分计算接触面的变形能,即
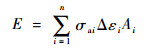 | (2) |
式中:σai、Δεi和Ai分别为接触单元节点法向应力幅值、接触单元节点法向变形量和接触单元面积。连接界面不可恢复变形能需要满足连接结构在疲劳寿命内的使用要求。
2.3 连接界面摩擦损伤 连接界面摩擦损伤指连接界面在工作状态下承受离心和扭转载荷导致界面产生相对滑移趋势或者存在滑移区域,在接触表面上产生巨大的切向摩擦力,造成连接界面摩擦损伤破坏,其损伤机理主要是连接界面在摩擦力作用下产生微动磨损。连接界面摩擦损伤会使得连接结构配合紧度下降,随着损伤积累导致连接结构产生松动,进而产生连接结构弯曲刚度损失和转子系统附加不平衡激励。
针对连接界面摩擦损伤,提出连接界面接触摩擦功W评估其损伤程度。由于接触摩擦功与微动损伤寿命存在反比例关系,采用其作为评估连接界面磨损的参数,反映微动磨损过程对连接界面的损伤程度,采用数值积分计算接触面的摩擦功,即
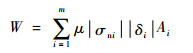 | (3) |
式中:μ、σni和δi分别为接触面摩擦系数、接触单元节点法向接触应力和接触单元节点相对滑移量。在有限元模型中,不能直接显示从装配状态到工作状态的接触摩擦功,因此,该过程的接触摩擦功可以用2个状态的摩擦功作差表示,即
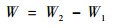 | (4) |
式中:W为从装配状态到施加工作转速的接触摩擦功;W1为加载到装配状态的接触摩擦功;W2为加载到工作状态的接触摩擦功。
3 转子结构系统稳健设计 对于以动力涡轮转子为代表的高速柔性转子系统(见图 4),其稳健性设计包括2个层面:①连接结构力学特性稳健设计,即在工作转速范围内,控制连接界面损伤,避免连接结构力学特性随载荷环境产生剧烈变化,以减弱其对转子系统动力特征的影响;②转子-支承系统动力特性稳健设计,即通过对各支点支承刚度变化下转子-支承系统动力特性变化敏感度的计算分析,优化选取各支点支承刚度,以实现工作过程中,转子动力特性对支承刚度波动的敏感性最低。
 |
| 图 4 多支点高速柔性转子系统稳健设计思路 Fig. 4 Robust design idea of multi-supported high-speed flexible rotor system |
| 图选项 |
3.1 连接结构力学特性稳健性分析及优化 以典型高功重比涡轴发动机动力涡轮盘-轴端齿-法兰-螺栓连接结构为例,对工作转速下连接界面接触特征进行仿真计算、稳健性评估及优化设计。如图 5所示,过渡轴与转接盘间为圆弧端齿连接,以实现自动定心与传递扭矩;转接盘与涡轮盘法兰边为端面-止口配合,由短螺栓提供预紧力、止口圆柱面过盈配合,实现界面压紧。
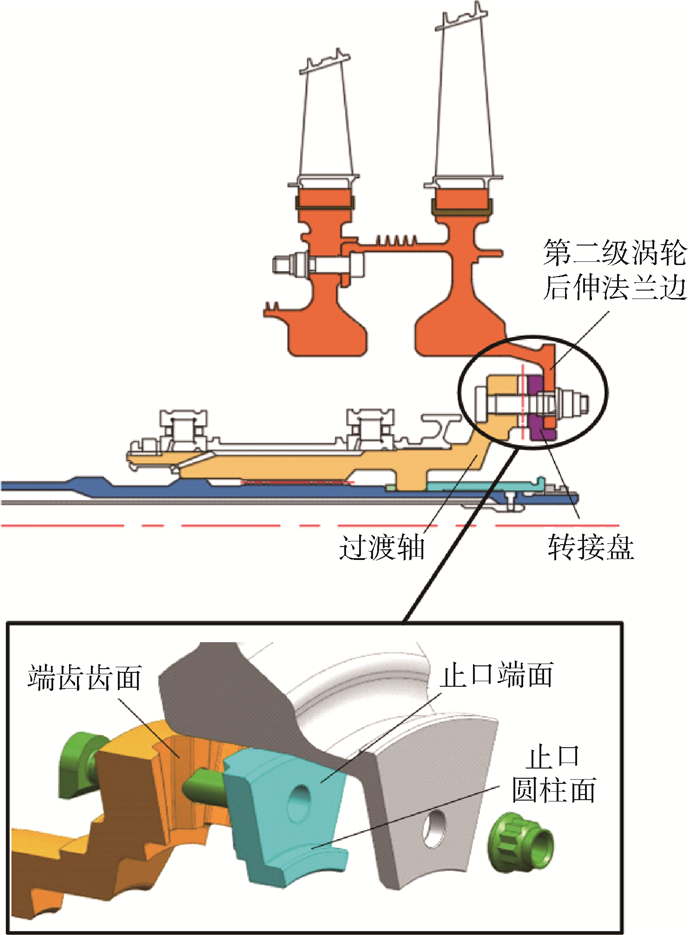 |
| 图 5 典型端齿-法兰-螺栓连接结构 Fig. 5 Typical end tooth-flange-bolt joint structure |
| 图选项 |
动力涡轮盘-轴连接结构主要接触面包括端齿齿面、止口端面、止口圆柱面等,各接触面配合特点及载荷特征不同,主要损伤失效形式亦具有差异。对于端齿齿面、止口端面等接触配合面,沿转子径向具有滑动自由度,在转子离心载荷等作用下,当构件变形存在非协调特征时,易出现连接界面滑移,因而需主要关注其连接界面不可恢复滑移、摩擦损伤等引起的力学特性分散性。而对于止口圆柱面,初始紧配合可产生较大接触应力,而工作过程中,离心载荷作用下配合紧度产生变化,引起应力较大幅度波动,更易造成疲劳损伤,而导致连接结构力学特性的分散性。
采用有限元法,建立带有接触界面的连接结构有限元模型,分别对装配载荷、工作转速下连接界面接触特征进行非线性求解。由于结构和载荷的周期对称性,对于装配载荷、施加工作转速的计算中使用施加周向约束的1/10扇区模型。在支点位置施加相应的位移约束,模拟轴承对于动力涡轮转子的约束作用。只保留端齿-法兰-螺栓连接结构的细节,在端齿齿面、止口端面/圆柱面与螺栓端面之间建立接触单元,模拟连接结构配合面间的接触作用。结构简化适当,并兼顾网格质量,进行网格无关性验证。
在装配状态下,端齿-法兰-螺栓连接结构所受载荷为螺栓的初始轴向预紧力和止口定心圆柱面的配合紧度。采用接触面初始偏移的方式提供螺栓轴向预紧力。在工作转速下,连接结构除了承受上述装配载荷,还要承受离心载荷的影响,对模型施加最大设计转速。计算时采用增广拉格朗日法,选取合理的收敛性判断标准。
对连接结构仅施加装配载荷,端齿齿面和止口端面的接触状态和应力分布如图 6和表 1所示。在螺栓初始预紧力作用下,端齿齿面的大部分面积处于黏滞和滑移状态,端齿结构稳定压紧。止口端面上螺栓孔约2倍孔径的区域范围内处于滑移状态,可以传递轴向载荷。在螺栓轴向预紧力的作用下,刚度较弱的法兰边会产生一定程度的弯曲变形,使得端齿齿面和止口端面上最大接触应力位于半径最小的位置。
 |
| 图 6 装配状态下端齿和止口端面接触状态和应力分布 Fig. 6 Contact state and stress distribution of end tooth and end face of rabbet in assembly condition |
| 图选项 |
表 1 装配状态下端齿和止口端面接触状态系数和应力分布统计 Table 1 Statistical analysis of contact state coefficient and stress distribution of and tooth and end face of rabbet in assembly condition
| 连接界面 | 接触状态系数/% | 最大接触应力/ MPa | 平均接触应力/ MPa | ||
| 黏滞 | 滑移 | 准接触 | |||
| 端齿齿面 (靠近螺栓孔) | 58.0 | 29.7 | 12.3 | 58 | 43 |
| 端齿齿面 (远离螺栓孔) | 78.5 | 21.5 | — | 180 | 90 |
| 止口端面 | — | 53.6 | 46.4 | 96 | 47 |
表选项
对涡轮盘轴组件施加工作转速离心载荷,端齿齿面和止口端面的接触状态和应力分布如图 7和表 2所示。端齿结构受到了止口法兰边局部弯曲变形的影响,接触状态发生变化,靠近螺栓孔的端齿齿面约64.8%处于黏滞状态,而远离螺栓孔的齿面上只有半径较小的区域约占10.8%处于黏滞状态,大部分区域发生分离,界面承载能力下降且容易造成接触损伤。止口端面在离心载荷下产生相对滑移变形,容易导致连接界面摩擦损伤。端齿齿面最大接触应力位于半径最小的位置,止口端面上接触应力分布相对均匀。
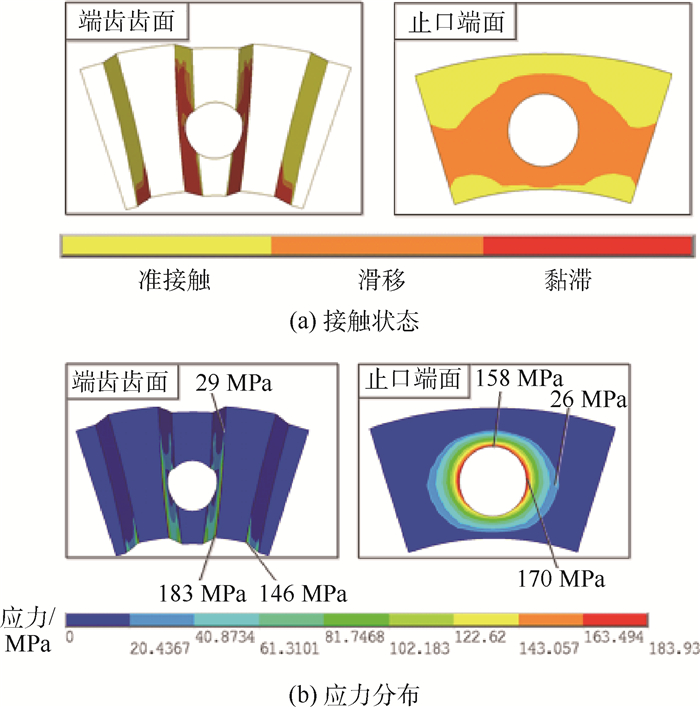 |
| 图 7 工作转速下端齿和止口端面接触状态和应力分布 Fig. 7 Contact state and stress distribution of end tooth and end face of rabbet at working speed |
| 图选项 |
表 2 工作转速下端齿和止口端面接触状态系数和应力分布统计 Table 2 Statistical analysis of contact state coefficient and stress distribution of end tooth and end face of rabbet at working speed
| 连接界面 | 接触状态系数/% | 最大接触应力/ MPa | 平均接触应力/ MPa | ||
| 黏滞 | 滑移 | 准接触 | |||
| 端齿齿面 (靠近螺栓孔) | 64.8 | 24.0 | 11.2 | 183 | 42 |
| 端齿齿面 (远离螺栓孔) | 10.8 | 3.9 | 85.3 | 146 | 35.8 |
| 止口端面 | — | 56.9 | 43.1 | 170 | 39 |
表选项
分别提取装配载荷和工作转速下止口端面的接触参数分布情况,如图 8和图 9所示。装配状态和工作状态止口端面接触状态系数分别为53.6%和56.9%;从装配载荷到施加工作转速的过程中,止口端面上产生的连接界面接触摩擦功为4.59×10-2 J。分别提取装配载荷和工作转速状态下止口圆柱面的接触参数分布情况,如图 10和图 11所示。从装配载荷到施加工作转速的过程中,止口圆柱面最大接触应力的变化范围很小,为431~441 MPa,产生的不可恢复变形能为3.47×10-3 J。
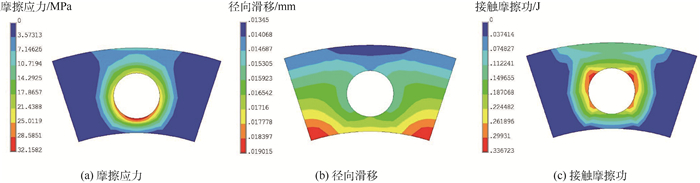 |
| 图 8 装配状态下止口端面的接触参数分布 Fig. 8 Distribution of contact parameters of end face of rabbet in assembly condition |
| 图选项 |
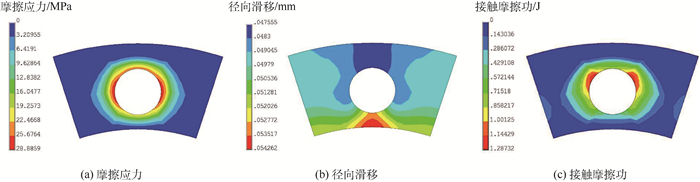 |
| 图 9 工作转速下止口端面的接触参数分布 Fig. 9 Distribution of contact parameters of end face of rabbet at working speed |
| 图选项 |
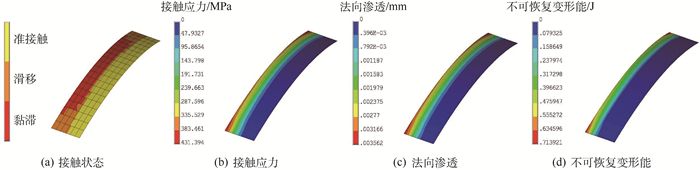 |
| 图 10 装配状态下止口圆柱面的接触参数分布 Fig. 10 Distribution of contact parameters of cylindrical surface of rabbet in assembly condition |
| 图选项 |
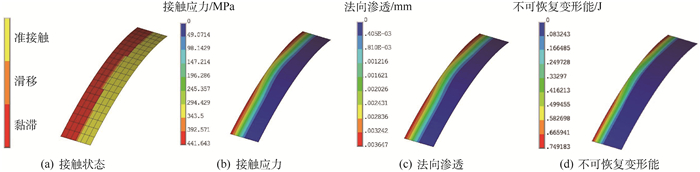 |
| 图 11 工作转速下止口圆柱面的接触参数分布 Fig. 11 Distribution of contact parameters of cylindrical surface of rabbet at working speed |
| 图选项 |
通过对典型盘-轴端齿-法兰-螺栓连接结构界面力学特性分析,可知在工作转速状态下,端齿齿面接触状态差;由于受到变形不协调的影响,连接界面易产生损伤。可初步通过结构改进的方式提高连接结构的稳健性,如图 12所示。改变第2级涡轮后轴颈倾斜角度,将第2级涡轮后的锥壳轴颈替换为一段鼓筒,以减弱径向变形的耦合。在涡轮法兰边后增加一个实心压紧盘,形成环腔结构,提高连接结构抗变形能力,改善连接界面接触状态,控制连接界面损伤。
 |
| 图 12 结构改进示意图 Fig. 12 Schematic of structural improvement |
| 图选项 |
对于本文所提出的接触状态系数、接触应力、不可恢复变形能和接触摩擦功等工程适用的定量评估参数,尚未建立稳健性评判通用标准,只能根据工程经验粗略判断连接结构设计方案的稳健程度。在有限元计算时,只考虑了装配载荷、工作转速下连接界面接触参数分布,未考虑发动机实际工作过程中由于转速变化等动态载荷而造成的连接界面损伤积累对连接界面力学特性稳健性的影响。开展相关试验验证工作,试验器设计成本较高,且很难保证改进前后试验条件完全一致。对比不同结构形式的有限元计算结果,可大致评估不同结构形式下其连接结构力学特性的稳健程度,为结构构型改进提供方向。
3.2 转子-支承系统动力特性稳健设计 如图 1所示,动力涡轮转子采用四支点支承,1#、2#支点位于转子前部,支承功率输出端;5#、6#支点位于转子后部,支承动力涡轮端。为考虑各支点支承刚度变化对转子-支承系统动力特性的影响,建立转子结构整体有限元模型,采用有限元法计算转子-支承系统各阶临界转速对各支点支承刚度变化的敏感度,结果如图 13所示。综合考虑支承刚度和支点对应转子轴段截面的等效刚度,定义当量刚度系数kr[15]对支承刚度进行无量纲化处理:
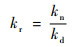 | (5) |
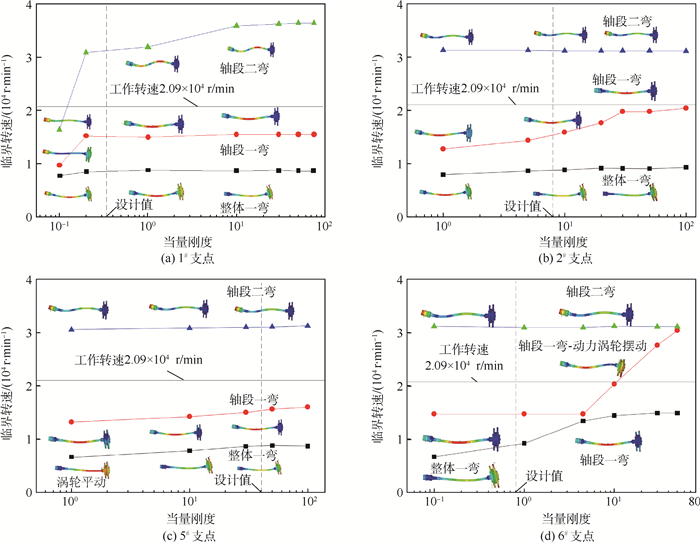 |
| 图 13 各支点支承刚度变化对各阶临界转速的影响 Fig. 13 Influence of bearing stiffness of various supporting points on critical speeds of various orders |
| 图选项 |
式中:kn为支承刚度;kd为支点位置处转子截面的等效刚度。
临界转速随支点当量刚度变化曲线的斜率反映出转子-支承系统动力特性对支承刚度系数的敏感度。由计算结果可以看出:1#支点当量刚度系数为0.1~0.2时,前3阶临界转速对于其支承刚度变化敏感度较高。2#支点当量刚度系数为5~30时,第2阶临界转速对于其支承刚度变化敏感度较高。前3阶临界转速对5#支点当量刚度系数变化的敏感度较小。前两阶临界转速对6#支点支承刚度变化较为敏感。6#支点当量刚度系数在4附近时,前两阶振型会发生变化。轴段一弯、轴段二弯振型对应的临界转速对6#支点当量刚度系数的变化不敏感。
通过对各个支点支承刚度变化对临界转速的影响的分析,可知现有的支承刚度设计是否处于临界转速高敏感区,并因此提出支承刚度初步优化方案。在1#支点支承刚度设计值附近,各阶临界转速对其支承刚度变化敏感度相对较低,但其距高敏感区较近,在支承结构具有较大刚度损失时,可能使支承刚度落入高敏感区,可适当提高1#支点支承刚度。2#支点支承刚度设计值处于第二阶临界转速高敏感度区间。在满足结构加工装配及基本强度要求的前提下,可尽量降低2#支点支承刚度。5#支点是转子后支承的主支点,转子各阶临界转速对其刚度变化的敏感度均较小,只要具有足够的安全裕度即可。在6#支点支承刚度设计值附近,各阶临界转速具有很低的敏感度,只要控制支点刚度不过大,即可保证不落入弯曲振型临界转速的敏感区域。
此外,对于多支点转子系统在装配和使用中会出现支承同心度及其振动控制问题,为了有效抑制高速柔性转子系统振动响应过大,可以在2#支点处采用无定心油膜阻尼结构设计,以提供必要的阻尼抑制转子振动。
4 结论 本文以动力涡轮转子结构系统为研究对象,根据转子结构系统具有多连接界面、几何结构突变所产生的结构非连续性特点,从控制连接结构界面损伤和降低临界转速对多支点支承刚度变化的敏感度两方面,对连接结构力学特性、转子系统动力特性进行降低载荷环境敏感度的优化设计。以保证连接结构力学特性在复杂载荷条件下变差较小,转子系统动力特性在连接结构力学特性、支承刚度发生变差的情况下仍保持稳定,提高转子结构系统稳健性。主要结论如下:
1) 连接界面接触损伤是产生力学特性分散性的内在原因,其产生机理分为连接界面不可恢复滑移、连接界面接触疲劳损伤和连接界面摩擦损伤3个方面。针对典型涡轮盘-轴连接结构定量评估连接界面损伤程度,并通过调整结构构形和关键几何尺寸有效控制连接界面损伤,提高连接结构稳健性。
2) 对于多支点、高转速、工作转速在弯曲振型临界转速以上的柔性转子-支承系统,各阶临界转速对不同位置的支点支承刚度变化的敏感度不同。在转子系统动力学设计中,可以在满足避开共振安全裕度的基础上,降低临界转速对支点刚度的敏感度,以提高转子-支承系统动力特性的稳健性。
参考文献
| [1] | 洪杰, 马艳红, 张大义. 航空燃气轮机总体结构设计与动力学分析[M]. 北京: 北京航空航天大学出版社, 2014: 436. HONG J, MA Y H, ZHANG D Y. Structure design and dynamic analysis of aero gas turbine engines[M]. Beijing: Beihang University Press, 2014: 436. (in Chinese) |
| [2] | 付才高, 郑大平, 欧园霞. 航空发动机设计手册第19册:转子动力学及整机振动[M]. 北京: 航空工业出版社, 2000. FU C G, ZHENG D P, OU Y X. Aero engine design manual 19th:Rotordynamics and whole engine vibration[M]. Beijing: Aviation Industry Press, 2000. (in Chinese) |
| [3] | TRUMAN C E, BOOKER J D. Analysis of a shrink-fit failure on a gear hub/shaft assembly[J]. Engineering Failure Analysis, 2007, 14(4): 557-572. DOI:10.1016/j.engfailanal.2006.03.008 |
| [4] | WANG J, KANG J, TANG L. Theoretical and experimental studies for wind turbine's shrink disk[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2014, 229(2): 325-334. |
| [5] | 洪杰, 徐筱李, 梁天宇, 等. 转子结构系统界面失效分析及稳健设计方法[J]. 航空动力学报, 2018, 33(3): 649-656. HONG J, XU X L, LIANG T Y, et al. Interface failure analysis and robust design methodology in rotor structural system[J]. Journal of Aerospace Power, 2018, 33(3): 649-656. (in Chinese) |
| [6] | 尹泽勇, 欧圆霞, 李彦, 等. 端齿轴段刚度及其对转子动力特性的影响[J]. 振动工程学报, 1993, 6(1): 63-67. YIN Z Y, OU Y X, LI Y, et al. Stiffness of a shaft section with end tooth and its effect on dynamic characteristic of a rotor[J]. Journal of Vibration Engineering, 1993, 6(1): 63-67. (in Chinese) |
| [7] | WANG C, ZHANG D, ZHU X, et al.Study on the stiffness loss and the dynamic influence on rotor system of the bolted flange joint[C]//ASME Turbo Expo 2014: Turbine Technical Conference and Exposition.New York: ASME, 2014: V07AT31A020. |
| [8] | QIN Z, HAN Q, CHU F. Bolt loosening at rotating joint interface and its influence on rotor dynamics[J]. Engineering Failure Analysis, 2016, 59: 456-466. DOI:10.1016/j.engfailanal.2015.11.002 |
| [9] | SHIAU T N, HWANG J L. Minimum weight design of a rotor bearing system with multiple frequency constraints[J]. Journal of Engineering for Gas Turbines and Power, 1988, 110(4): 592-599. DOI:10.1115/1.3240176 |
| [10] | LIN Y H, LIN S C. Optimal weight design of rotor systems with oil-film bearings subjected to frequency constraints[J]. Finite Elements in Analysis and Design, 2001, 37(10): 777-798. DOI:10.1016/S0168-874X(00)00072-X |
| [11] | SHIAU T N, CHANG J R. Multiobjective optimization of rotor-bearing system with critical speeds constraints[J]. Journal of Engineering for Gas Turbines and Power, 1991, 2(2): 246-255. |
| [12] | STOCKI R, SZOLC T, TAUZOWSKI P, et al. Robust design optimization of the vibrating rotor-shaft system subjected to selected dynamic constraints[J]. Mechanical Systems and Signal Processing, 2012, 29: 34-44. DOI:10.1016/j.ymssp.2011.07.023 |
| [13] | 杨隽, 臧朝平, 刘永泉, 等. 基于Taguchi方法的转子系统动力学容差设计[J]. 航空动力学报, 2014, 29(7): 1583-1590. YANG J, ZANG C P, LIU Y Q, et al. Taguchi method based to-lerance design for rotor system dynamics[J]. Journal of Aerospace Power, 2014, 29(7): 1583-1590. (in Chinese) |
| [14] | 陈立周. 稳健设计[M]. 北京: 机械工业出版社, 2000. CHEN L Z. Robust design[M]. Beijng: China Machine Press, 2000. (in Chinese) |
| [15] | 于欢, 马艳红, 肖森, 等. 高速柔性转子支承松动力学特征及动力特性[J]. 北京航空航天大学学报, 2017, 43(8): 1677-1683. YU H, MA Y H, XIAO S, et al. Mechanical and dynamic cha-racteristics of bearing with looseness on high-speed flexible rotor[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(8): 1677-1683. (in Chinese) |
