作为一个航天大国,中国****在航天充液系统的刚-弹-液耦合机理研究和大规模刚-弹-液耦合模型建模计算的应用研究方面,已经进行了一些有益的探索,并且取得了丰硕的研究成果。杜建镔和王勖成[3]针对具有旋转周期性的含液容器,将旋转周期方法引入液固耦合动力特性分析,开发出一套有效的液固耦合有限元分析方法。刘习军等[4]研究了壳液耦合系统的自激振动问题和重力波现象。马兴瑞等[5]将流固耦合问题作为一个专题进行了研究。邢景棠、周盛和崔尔杰[6]全面综述了流固耦合力学及其特点、研究分支、一些进展及进一步发展,并重点阐述了国外****在这一学科领域的研究成果。王勖成[7]研究了流固耦合的有限单元法,采用一种简化的方式处理弹-液耦合问题。李磊等[8]研究了运动圆筒内液体流动不稳定的非线性特征。席如青和曲广吉[9]研究了充液航天器任意旋转对称偏置贮箱在低微重力情况下的小幅液体晃动问题, 并编制了具有工程实用性和通用性的计算机分析软件。李英波和冯正进[10]建立了三轴定向充液卫星在二维平动和二维摆动扰动作用下的空间摆等效力学模型。王佳栋等[11]研究了带有环形刚性隔板的部分充液刚性圆柱罐中液体的微幅晃动特性。黄华等[12]建立了三维质心面等效模型, 将贮箱内液体等效为位于液体质心处的质点。贺元军等[13]建立了在微重力环境、横向激励下圆柱贮箱液固耦合系统的动力学方程,并得到了耦合系统的幅频特性曲线。包光伟和王政伟[14]通过建立液体晃动特征问题的泛函极值原理, 计算了平放圆柱腔内三维液体晃动的特征频率, 并与解析解、实验结果和二维有限元数值解进行了比较。陈建平等[15]提出了刚-弹-液耦合系统的液体-多体耦合力学模型。高索文等[16]分析了俯仰激励下矩形贮箱类液固耦合系统动力学特性。苟兴宇等[17]研究了弹簧-质量系统与圆柱贮箱类液体有限幅晃动系统间的非线性耦合动力学问题, 在建立了六自由度非线性耦合动力学模型的基础上, 导出了液体有限幅晃动力和力矩解析表达式, 说明在终了构形上积分及压力表达式中的非线性项是有限幅晃动作用力、作用力矩非线性的根源。李青等[18]分别综述了国内外****在充液航天器液体晃动和液固耦合动力学方面的研究进展,并重点阐述了国外****在这一学科领域的研究成果。
在刚-弹-液耦合动力学中,存在刚-弹耦合、刚-液耦合、弹-液耦合,它们是互相联系和相互影响的。笔者分别研究了非线性刚-弹耦合动力学[19]和刚-液耦合动力学[20],为研究刚-弹-液耦合动力学中存在的刚-弹耦合、刚-液耦合提供了重要的参考。在此基础上,还研究了刚-弹-液耦合动力学[21],但是没有专门研究弹-液耦合问题。所以,本文重点研究刚-弹-液耦合动力学中的弹-液耦合问题,这是一个关系到航天充液系统液固耦合机理研究和大规模液固耦合模型建模计算研究方面的重要问题。
1 刚-弹-液耦合中的刚-弹耦合、刚-液耦合和弹-液耦合特点 设有如图 1所示的刚-弹-液耦合系统。文献[21]给出了刚-弹-液耦合动力学一类变量的Hamilton型的拟变分原理,这里给出一类变量的Hamilton型的拟变分原理改进形式为(用实体张量符号书写)
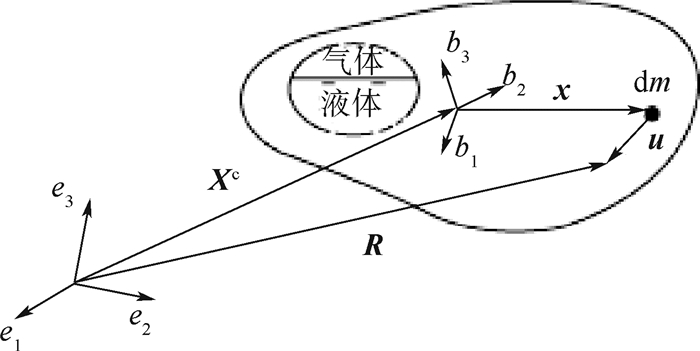 |
| 图 1 参考标架 Fig. 1 Frame of reference |
| 图选项 |
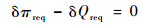 | (1) |
式中:
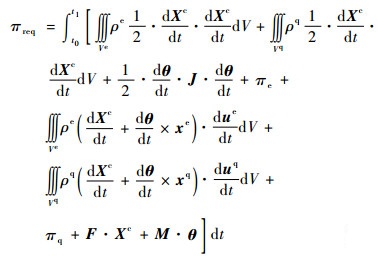 | (2) |
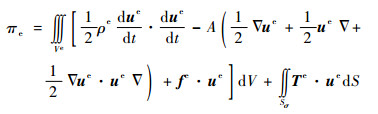 | (3) |
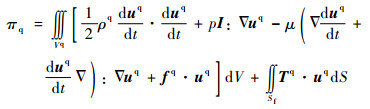 | (4) |
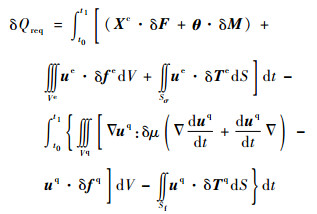 | (5) |
先决条件为
 | (6) |
式中:ρe为弹性体的质量密度;ρq为液体的质量密度;uq为流体位移;fq为流体所受的体积力;μ为黏性系数;I为单位张量;p为流体的压强;Tq为流体的面积力;?为梯度算子;Sf为力学边界面;fe为弹性体所受的体积力;ne为外法线;Te为弹性体的面积力;Sσ为应力边界面;Su为位移边界面;Xc为质心矢径;θ为角位移;F为外力主矢;M为外力主矩;Ve为弹性体的体积;Vq为液体的体积,认为气体的体积很小,可以忽略,V为系统的总体积; A为弹性体的应变能函数;J为对质心的转动惯量; xe为质心到弹性体中任意一点的矢径; xq为质心到液体中任意一点的矢径。另外,nq为单位外法线,ue为弹性体位移,ue为弹性体的边界位移。
δπreq为刚-弹-液耦合动力学一类变量的拟变分原理的定积分形式泛函的变分;πe为πreq的一个组成部分(
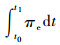
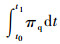
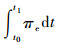
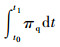
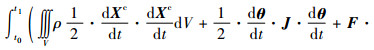

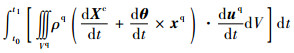
该变分原理的泛函隐含弹-液耦合,这是因为弹-液耦合是在弹-液交界面处出现的[6],在弹-液交界面处,按照一般的力学原理,位移满足协调关系,应力满足平衡关系,这便是刚-弹-液耦合中的弹-液耦合的特点。因为这一问题的重要性,将在第2节结合研究弹-液耦合的机理,做进一步的说明。
2 刚-弹-液耦合动力学中弹-液耦合的机理 对于刚-弹-液耦合系统而言,弹-液交界面是整个系统内部出现的。假想将弹-液耦合体划分为2个元素,其弹-液交界面Sw是无际边界(inter-element boundary)[23-24],无际边界条件为
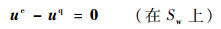 | (7) |
应用钱伟长先生倡导的Lagrange乘子法[23, 25]来处理无际边界条件的问题。为此,将式(1)写成展开形式,引入Lagrange乘子λ,将无际边界条件式(7)纳入泛函中,可得
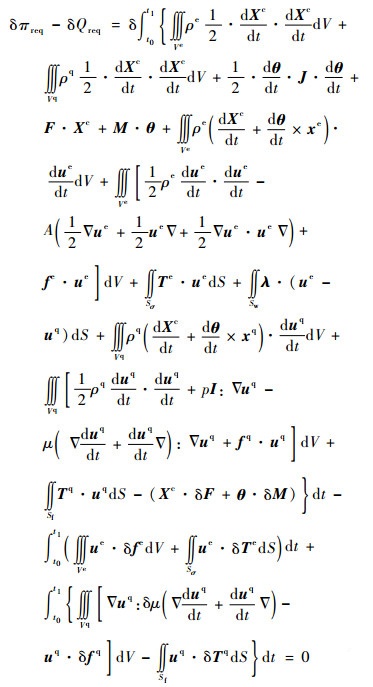 | (8) |
其先决条件为式(6)。
进行分部积分,可得
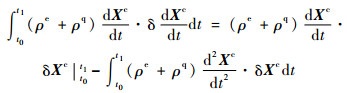 | (9) |
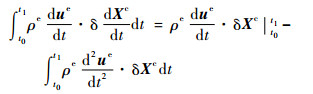 | (10) |
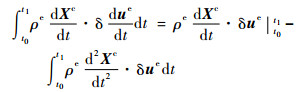 | (11) |
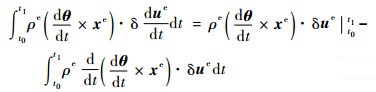 | (12) |
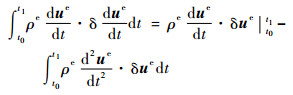 | (13) |
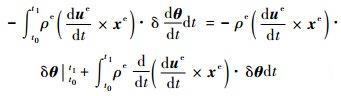 | (14) |
 | (15) |
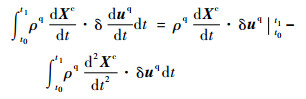 | (16) |
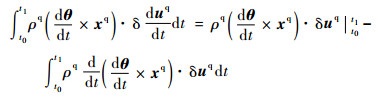 | (17) |
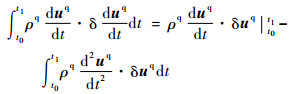 | (18) |
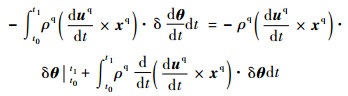 | (19) |
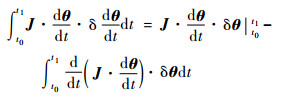 | (20) |
应用Green定理,可得
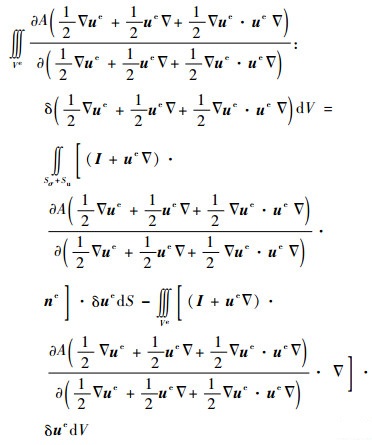 | (21) |
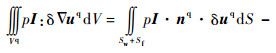 |
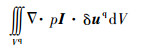 | (22) |
 | (23) |
将式(9)~式(23)代入式(8)的变换式中,考虑到位移边界条件的变分式为δue=0,并且按惯例在时域边界t=t0和t=t1处取δXc、δθ、δue、δuq等于零,可得
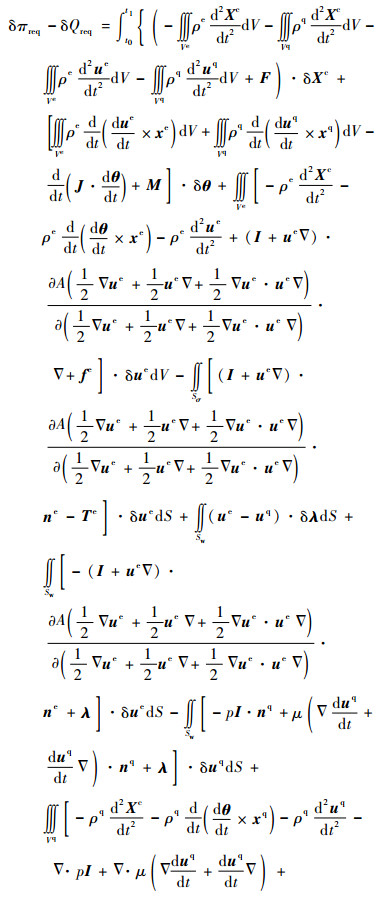 |
 | (24) |
由于δXc、δθ、δue、δuq和δλ的任意性,故由式(24)可得拟驻值条件为
 | (25-1) |
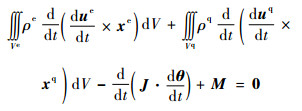 | (25-2) |
 | (25-3) |
 | (25-4) |
 | (25-5) |
 | (25-6) |
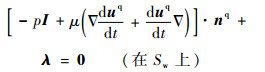 | (25-7) |
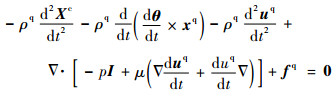 | (25-8) |
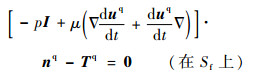 | (25-9) |
由式(25-6)和式(25-7)解得
 | (26) |
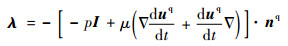 | (27) |
分析式(26)和式(27)的物理意义。不难看出,式(26)表示在Sw处弹性体所承受的应力,式(27)表示在Sw处液体所承受的应力。并且式(26)和式(27)都与经典分析力学中Lagrange乘子是约束力的论述相吻合。将式(26)代入式(27),或者将式(27)代入式(26),均可得到
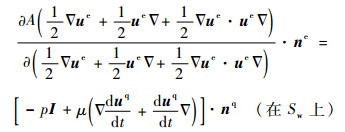 | (28) |
认为弹性体和液体以无际边界面为接触面,二者在此处相互作用,式(28)的物理意义可以解释为:在无际边界Sw处,弹性体对液体的作用力和液体对弹性体的作用力大小相等,方向相反。
式(28)又可写为另一种形式:
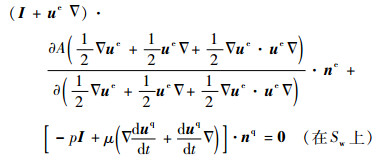 | (29) |
认为弹性力和液体力共同作用在无际边界Sw处的无限薄的一层物质面上,式(29)表明:由于刚-弹耦合动力学导致的应力和由于刚-液耦合动力学导致的应力在无际边界面Sw处构成平衡应力系。
在以上分析中,建议注意:在无际边界面Sw处,ne+nq=0。
刚-弹-液耦合动力学的拟变分原理式(8)的丰富的内涵反映在其驻值条件中:驻值条件式(25-6)和驻值条件式(25-7)经变换得到式(29),反映弹-液耦合的力的平衡关系;驻值条件式(25-5)反映弹-液耦合的位移协调关系;这是本文的主要研究内容。驻值条件式(25-3)和驻值条件式(25-4)反映刚-弹耦合特性;驻值条件式(25-8)和驻值条件式(25-9)反映刚-液耦合特性;驻值条件式(25-1)和驻值条件式(25-2)反映连续介质动力学对刚体动力学的影响。由如上论述可以看出,刚-弹-液耦合中弹-液耦合的平衡方程式(29)中的变量,不仅受到弹-液耦合的影响,还受到刚-液耦合(式(25-8)、式(25-9))和刚-弹耦合(式(25-3)、式(25-4))的影响。反之,刚-液耦合(式(25-8)、式(25-9))和刚-弹耦合(式(25-3)、式(25-4))的变量,也要受到弹-液耦合式(29)的影响。
综合以上分析,可以明确刚-弹-液耦合动力学中弹-液耦合的机理。刚-弹-液耦合动力学中弹-液耦合发生在弹、液两相的无际边界面上, 在该边界面上,位移满足协调关系式(25-5),应力满足平衡关系式(29)。
应当注意到,虽然刚-弹-液耦合动力学中弹-液耦合是在弹-液交界面实现的,但是,弹-液耦合是受到控制方程式(25-1)~式(25-9)的制约的。
3 弹-液耦合机理与建模计算相结合 关于弹-液耦合的建模计算研究,首先会想到有限元建模计算问题。
结合第2节的研究,由拟驻值条件式(25-5)可以看出,通过应用Lagrange乘子法,已经将无际边界条件转化为泛函的拟驻值条件;从有限元建模计算方面考虑问题,这一研究进展实现了从协调元(compatible model)到杂交元(hybrid model)的过渡。国外****应用Lagrange乘子法研究有限元素法基本上到此为止。
按照中国著名应用数学和力学专家钱伟长院士的理论,还要在上述研究的基础上,进一步识别Lagrange乘子,即将Lagrange乘子用泛函中原有的变量来表示,然后将已经识别的Lagrange乘子代入泛函中,用来减少有限元素法的计算自由度。
将Lagrange乘子的表达式(26)代入泛函式(8)中,可得
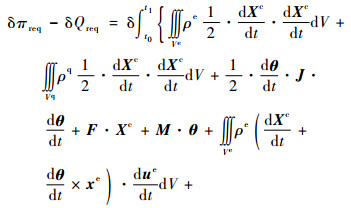 |
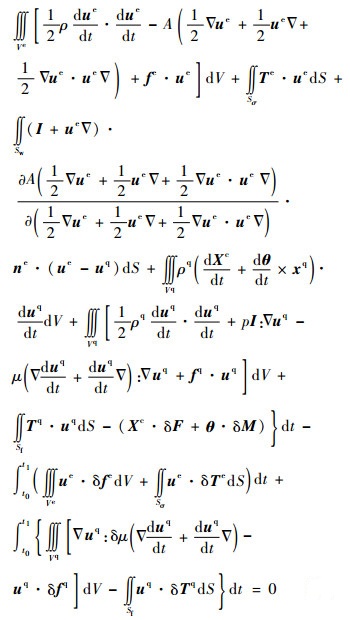 | (30) |
应用与第2节相同的方法,不难求得,其驻值条件为
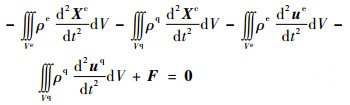 | (31-1) |
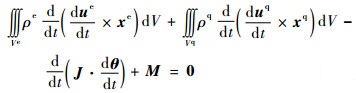 | (31-2) |
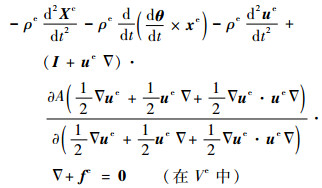 | (31-3) |
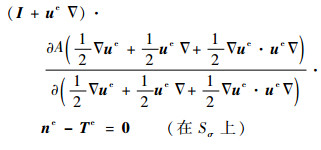 | (31-4) |
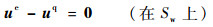 | (31-5) |
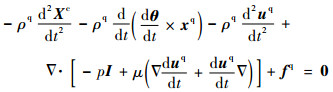 | (31-6) |
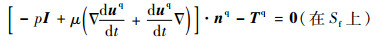 | (31-7) |
比较式(31)和式(25)可以发现,识别Lagrange乘子之后,可以减少计算自由度。具体地说,式(25)和式(8)的Lagrange乘子尚未识别,它们仍然作为计算自由度存在于控制方程中;由于这里的Lagrange乘子λ是矢量,需要计算其3个分量方可确定,即其占用3个计算自由度。式(30)和式(31)的Lagrange乘子已经识别,即Lagrange乘子已经应用泛函中原有的变量表达出来,从而减少3个计算自由度。注意到,这是将刚-弹-液耦合系统划分为弹性体和液体2个元素,来处理其无际边界条件问题得到的结果。在有限元建模计算中,弹-液交界面可以离散为很多个元素的无际边界面,因此明确弹-液耦合机理之后,可以有效地减少计算自由度。具体地说,假设弹-液交界面可以离散为100个元素的无际边界面,根据前面的分析,明确弹-液耦合机理之后,可以减少300个计算自由度。
再引申一步,在有限元建模中,除了以弹-液交界面作为元素的无际边界面之外,还有更多的元素的无际边界面不是弹-液交界面,它们也存在用识别Lagrange乘子法减少计算自由度的问题。这样一来,减少的计算自由度就更多了。结合以上2种因素,可以大大减少计算自由度。这是中国****对应用数学和力学的一大贡献。
最后说明,在刚-弹-液耦合动力学的建模计算研究中,存在弹-液交界面处的无际边界条件。把弹-液交界面处的无际边界条件处理好了,其余部分的有限元建模计算与一般的有限元建模计算便没有多大差别了,也就比较容易处理了。二者相结合,便是一个比较完整的刚-弹-液耦合动力学的建模计算研究。对于如何实现有限元计算的问题,可以参阅著名流固耦合专家英籍华人****邢景棠先生的近期著述[26]。
4 结论 航天刚-弹-液耦合动力学是航天器动力学领域最具有挑战性的研究方向之一。
1) 通过分析刚-弹-液耦合动力学拟变分原理的泛函,说明了刚-弹耦合、刚-液耦合和弹-液耦合的特点。
2) 通过识别Lagrange乘子,逐步说明了弹-液耦合的机理。
3) 通过分析识别Lagrange乘子前后泛函的驻值条件,明确了识别Lagrange乘子可以有效地减少计算自由度。
研究工作处于该研究方向的理论基础层面,具有较好的理论意义,对这类系统有限元建模、计算及结果分析、讨论具有重要的参考价值。
参考文献
| [1] | 王照林, 刘延柱. 充液系统动力学[M]. 北京: 科学出版社, 2002. WANG Z L, LIU Y Z. Fluid filling system dynamics[M]. Beijing: Science Press, 2002. (in Chinese) |
| [2] | 梁立孚, 宋海燕, 李海波. 航天分析动力学[M]. 北京: 科学出版社, 2016. LIANG L F, SONG H Y, LI H B. Aerospace analytical dynamics[M]. Beijing: Science Press, 2016. (in Chinese) |
| [3] | 杜建镔, 王勖成. 旋转周期性含液容器的流固耦合动力学特性分析[J]. 清华大学学报(自然科学版), 1999, 39(8): 108-116. DU J B, WANG X C. Fluid solid coupling dynamic characteristics of rotating periodic liquid containing containers[J]. Journal of Tsinghua University (Natural Science Edition), 1999, 39(8): 108-116. DOI:10.3321/j.issn:1000-0054.1999.08.028 (in Chinese) |
| [4] | 刘习军, 张素侠, 刘国英, 等. 矩形弹性壳液耦合系统中的重力波分析[J]. 力学学报, 2006, 38(1): 106-112. LIU X J, ZHANG S X, LIU G Y, et al. Gravity wave analysis in rectangular elastic shell and fluid coupling system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 106-112. DOI:10.3321/j.issn:0459-1879.2006.01.014 (in Chinese) |
| [5] | 马兴瑞, 王本利, 苟兴宇. 航天器动力学——若干问题进展及应用[M]. 北京: 科学出版社, 2001. MA X R, WANG B L, GOU X Y. Some problems of spacecraft dynamics:Development and applications[M]. Beijing: Science Press, 2001. (in Chinese) |
| [6] | 邢景棠, 周盛, 崔尔杰. 流固耦合力学概述[J]. 力学进展, 1997, 27(1): 19-38. XING J T, ZHOU S, CUI E J. Fluid solid coupling mechanics[J]. Advances in Mechanics, 1997, 27(1): 19-38. DOI:10.3321/j.issn:1000-0992.1997.01.002 (in Chinese) |
| [7] | 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003. WANG X C. The finite element method[M]. Beijing: Tsinghua University Press, 2003. (in Chinese) |
| [8] | 李磊, 任业军, 蔡斌, 等. 进动圆筒内液体流动不稳定的非线性特征[J]. 力学学报, 2005, 37(1): 64-72. LI L, REN Y J, CAI B, et al. Nonlinear characteristics of liquid flow instability in precession cylinders[J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(1): 64-72. (in Chinese) |
| [9] | 席如青, 曲广吉. 在低微重力下卫星液体晃动力学应用研究[J]. 航天器工程, 1997, 6(1-2): 18-26. XI R Q, QU G J. Application of liquid sloshing dynamics in satellite under low gravity[J]. Spacecraft Engineering, 1997, 6(1-2): 18-26. (in Chinese) |
| [10] | 李英波, 冯正进. 充液航天器液体晃动等效力学模型的建立[J]. 上海航天, 2003(4): 1-5. LI Y B, FENG Z J. Establishment of equivalent mechanical model for liquid sloshing in liquid filled spacecraft[J]. Aerospace Shanghai, 2003(4): 1-5. DOI:10.3969/j.issn.1006-1630.2003.04.001 (in Chinese) |
| [11] | 王佳栋, 周叮, 刘伟庆. 带环形隔板圆柱形储液罐中液体晃动的解析研究[J]. 振动与冲击, 2010, 29(2): 54-59. WANG J D, ZHOU D, LIU W Q. Analytical study of liquid sloshing in cylindrical tank with annular baffles[J]. Journal of Vibration and Shock, 2010, 29(2): 54-59. DOI:10.3969/j.issn.1000-3835.2010.02.013 (in Chinese) |
| [12] | 黄华, 杨雷, 张熇, 等. 航天器贮箱大幅液体晃动三维质心面等效模型研究[J]. 宇航学报, 2010, 31(1): 55-59. HUANG H, YANG L, ZHANG H, et al. The equivalent model of three dimensional centroid surface for large liquid sloshing in spacecraft tanks[J]. Journal of Astronautics, 2010, 31(1): 55-59. DOI:10.3873/j.issn.1000-1328.2010.01.008 (in Chinese) |
| [13] | 贺元军, 马兴瑞, 王本利. 微重环境下平移圆柱贮箱液固耦合系统的动力响应研究[J]. 西安交通大学学报, 2006, 40(9): 1083-1087. HE Y J, MA X R, WANG B L. Research on dynamic response of liquid-solid coupling system of translational cylindrical tanks under microgravity environment[J]. Journal of Xi'an Jiao Tong University, 2006, 40(9): 1083-1087. DOI:10.3321/j.issn:0253-987X.2006.09.022 (in Chinese) |
| [14] | 包光伟, 王政伟. 液体三维晃动特征问题的有限元数值计算方法[J]. 力学季刊, 2003, 24(2): 185-190. BAO G W, WANG Z W. Finite element numerical method for three-dimensional sloshing characteristics of fluids[J]. Chinese Quarterly of Mechanics, 2003, 24(2): 185-190. DOI:10.3969/j.issn.0254-0053.2003.02.006 (in Chinese) |
| [15] | 陈建平, 周儒荣, 虞伟建. 充液系统液体-多体耦合动力响应分析[J]. 力学学报, 2004, 36(6): 724-731. CHEN J P, ZHOU R R, YU W J. Fluid multi-body coupling dynamic response analysis of fluid filled system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(6): 724-731. DOI:10.3321/j.issn:0459-1879.2004.06.012 (in Chinese) |
| [16] | 高索文, 尹立中, 王本利, 等. 矩形贮箱类液固耦合系统转动特性分析[J]. 振动与冲击, 2000, 19(3): 17-19. GAO S W, YIN L Z, WANG B L, et al. Analysis of rotation characteristics of liquid solid coupling system for rectangular tanks[J]. Journal of Vibration and Shock, 2000, 19(3): 17-19. DOI:10.3969/j.issn.1000-3835.2000.03.005 (in Chinese) |
| [17] | 苟兴宇, 李铁寿, 马兴瑞, 等. 液固耦合系统中液体的有限幅晃动力及晃动力矩[J]. 应用数学和力学, 2001, 22(5): 465-476. GOU X Y, LI T S, MA X R, et al. Finite amplitude sloshing power and sloshing torque in liquid solid coupling system[J]. Applied Mathematics and Mechanics, 2001, 22(5): 465-476. DOI:10.3321/j.issn:1000-0887.2001.05.004 (in Chinese) |
| [18] | 李青, 王天舒, 马兴瑞. 充液航天器液体晃动和液固耦合动力学的研究与应用[J]. 力学进展, 2012, 42(4): 471-480. LI Q, WANG T S, MA X R. Research and application of liquid sloshing and liquid-solid coupling dynamics in liquid filled spacecraft[J]. Advances in Mechanics, 2012, 42(4): 471-480. (in Chinese) |
| [19] | LIANG L F, SONG H Y. Non-linear and non-conservative quasi-variational principle of flexible body dynamics and application in spacecraft dynamics[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(11): 2192-2199. DOI:10.1007/s11433-013-5316-x |
| [20] | 梁立孚, 刘宗民, 郭庆勇. 充液系统刚-液耦合动力学功能型拟变分原理[J]. 哈尔滨工程大学学报, 2013, 34(12): 1514-1519. LIANG L F, LIU Z M, GUO Q Y. The rigid liquid coupled dynamic functional quasi variational principle of the fluid system[J]. Journal of Harbin Engineering University, 2013, 34(12): 1514-1519. (in Chinese) |
| [21] | 冯晓九, 梁立孚, 宋海燕. 刚-弹-液耦合动力学功能型拟变分原理[J]. 中国科学E辑, 2017, 46(2): 195-203. FENG X J, LIANG L F, SONG H Y. Rigid, elastic fluid coupling dynamics, functional quasi variational principles[J]. Chinese Science E Series, 2017, 46(2): 195-203. (in Chinese) |
| [22] | 梁立孚, 郭庆勇. 刚体动力学的拟变分原理及其应用[J]. 力学学报, 2010, 42(2): 300-305. LIANG L F, GUO Q Y. Quasi variational principles for rigid body dynamics and their applications[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(2): 300-305. (in Chinese) |
| [23] | 钱伟长. 广义变分原理[M]. 北京: 知识出版社, 1985. QIAN W C. Generalized variational principle[M]. Beijing: Knowledge Press, 1985. (in Chinese) |
| [24] | WASHIZU K. Variational method in elasticity and plasticity[M]. New York: Pergamon Press, 1982. |
| [25] | 钱伟长. 弹性理论中广义变分原理的研究及其在有限元计算中的应用[J]. 力学与实践, 1979, 1(1): 16-24. QIAN W C. The study of the principle of generalized variational principles in elastic theory and its application in finite element calculation[J]. Mechanics in Engineering, 1979, 1(1): 16-24. (in Chinese) |
| [26] | XING J T. Developments of numerical method for linear and nonlinear fluid-solid interaction dynamics with applications[J]. Advances in Mechanics, 2016, 46(2): 95-139. |
