最近几十年中有多项关于加速度变化对心血管系统影响的研究。Sud和Sekhon[1]研究了加速度对人体动脉树模型中血流的影响。Chaturani和Majhi[2-4]等提出了加速度对生理脉动状态下血液流动影响的数学模型。Chakravarty和Mandal等[5-6]研究了加速度对简化的动脉狭窄模型中血流特征的影响。
近年来,随着医学影像技术和计算机技术的快速发展,基于医学影像建立人体血管真实3D构型并进行血流状态准确仿真成为可能。本文建立了人体右侧颈动脉真实血管的3D模型,并利用计算机模拟了加速度作用对颈动脉中血液流动的影响。之所以选择颈动脉,主要原因是:①颈动脉是为脑部供血的主要动脉血管;②颈动脉分叉处血流容易紊乱,根据血流动力学原理和临床统计观察,此部位易发生动脉粥样硬化斑块和狭窄;③颈动脉分叉处有颈动脉窦,属于动脉系统中的压力感受器,主要发挥监测血压异常以及触发心血管系统心率、心输出量等生理参数调整性改变的生理作用。
目前,还未发现有关加速度影响颈动脉3D模型内生理脉动流变化的文章。本文通过计算机模拟研究,选取了一个向前的均匀加速度作为加载条件,考察加速度对颈动脉分叉处血流动力学环境的影响。发现了加速度作用情况下颈动脉内血流变化的一些现象,并讨论分析了加速度变化可能对颈动脉生理、病理现象的影响。
1 研究方法 1.1 模型建立与网格划分 基于中日友好医院采集的人体CT断层图像,导入Mimics v9.0软件后经图像手动分割、3D重建等步骤,建立了一个具有在体真实血管空间构型的右颈动脉模型(见图 1)。为了后续网格划分和血流模拟的需要,还对模型进行了表面平滑,对颈总动脉、颈内动脉和颈外动脉进行了延长。
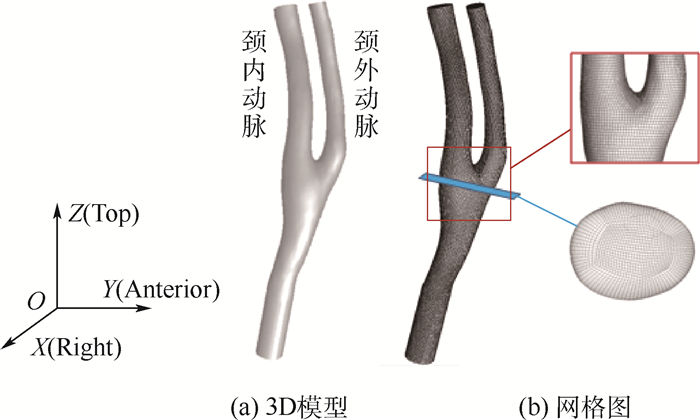 |
| 图 1 右侧颈动脉血管3D模型及网格图 Fig. 1 Right carotid artery 3D model and meshes |
| 图选项 |
模型网格划分在ICEM中进行,控制六面体网格最大尺寸0.1 mm。为了准确获得模型表面(血管内壁面)的血流动力学参数,在划分网格时专门设置了4层边界层,第1层厚度为0.01 mm,逐层增长率为1.2。模型网格如图 1(b)所示。
1.2 边界条件 为了更加真实地反映在体血流情况,本文采用生理脉动流动条件,同时对整个系统坐标系施加特定加速度运动条件。分别采用速度入口和压力出口边界条件,参数从已有文献获得[7-9]:平均入口血流量为6 mL/s,平均出口压力为13 300 Pa(约100 mmHg),波形如图 2所示。除了主动脉入口和颈内、颈外动脉出口外,其余表面规定为刚性无滑动边界条件,这也符合体内血液流动与血管内壁面的运动关系。
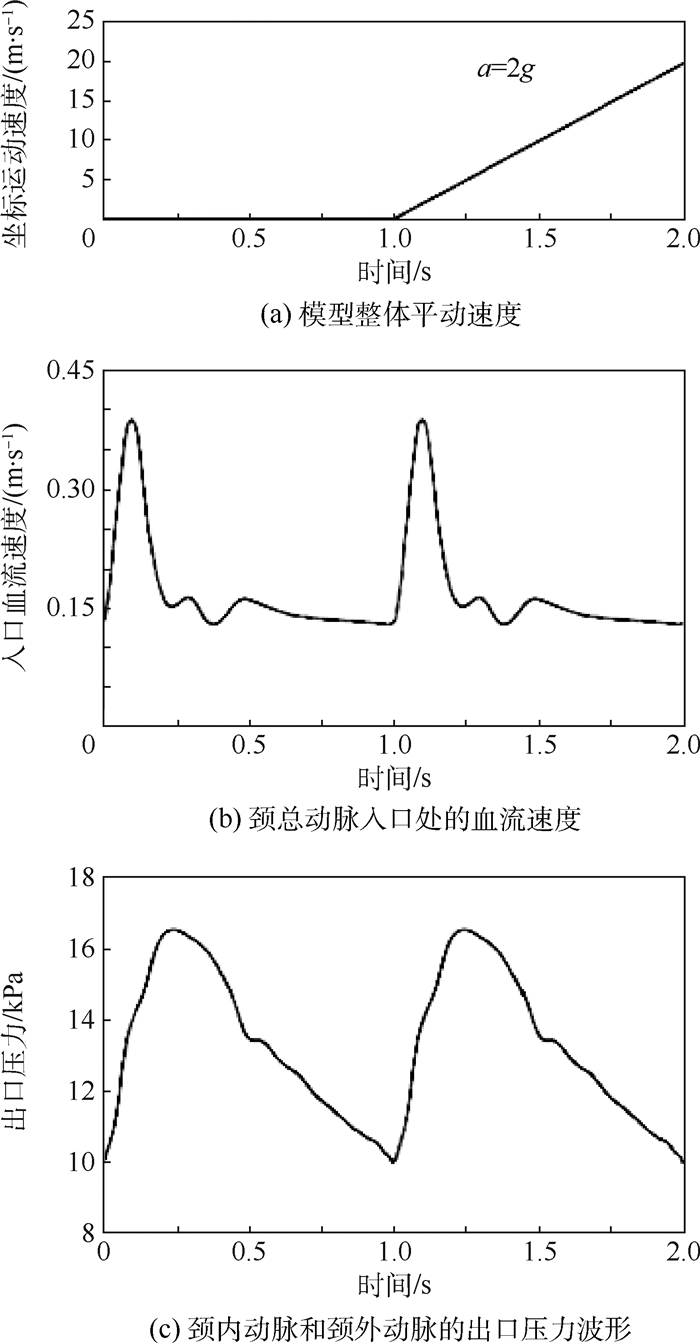 |
| 图 2 模型的边界条件 Fig. 2 Boundary conditions of model |
| 图选项 |
整个模型施加平动加速度条件,t = 0~1 s阶段,模型速度为0 m/s,模型保持静止状态。t = 1~2 s阶段,模型直线速度遵循式(1),即保持19.6 m/s2(约2g)的水平匀加速度运动状态。加速度方向为+y方向。加速度条件如图 2所示。
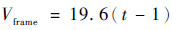 | (1) |
1.3 假设与计算 流动仿真计算中将血液假设为各向同性、牛顿、不可压缩流体[10-11],控制方程为动量守恒方程(3D不可压缩Navier-Stokes方程)与流体连续性方程。
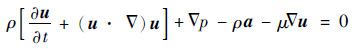 | (2) |
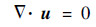 | (3) |
式中:u为血液相对颈动脉模型的流动线速度;p为压力;a为整个颈动脉模型的+y向加速度
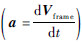
利用有限体积法CFD求解软件包ANSYS Fluent 15.0对血液域进行流动仿真模拟计算。
在非定常计算3个周期后从第4个周期末开始记录每个时间步长计算数值。每个心动周期假设为1 s,每个心动周期均匀分为100个时间步。计算收敛条件为连续性项残差小于等于1×10-4。
1.4 结果 在记录结果的2个心动周期内选取8个时间点,对结果进行对比分析。T1、T5在心脏收缩期血液流速上升阶段,T2、T6为收缩期血液流速峰值时刻,T3、T7在血液流速下降阶段,T4、T8为舒张期血流低值阶段(见表 1)。
表 1 T1~T8代表的具体时刻(记录周期初始时刻为T = 0) Table 1 Specific time represented by T1-T8 (beginning of cycle is defined as T = 0)
| 时间点 | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 |
| 时间/s | 0.05 | 0.1 | 0.15 | 0.7 | 1.05 | 1.1 | 1.15 | 1.7 |
表选项
图 3为颈动脉壁面压力梯度云图。可以看出,T5~T8阶段颈动脉壁面压力梯度明显高于T1~T4阶段。此外,压力梯度的空间分布特征也存在明显的区别。在T1~T4阶段,压力梯度主要沿血流方向变化。而在T5~T8阶段,压力梯度的条带大致与血液流动方向平行,且相对较高的压力梯度在模型的两侧部位(颈动脉模型的左右两侧)。
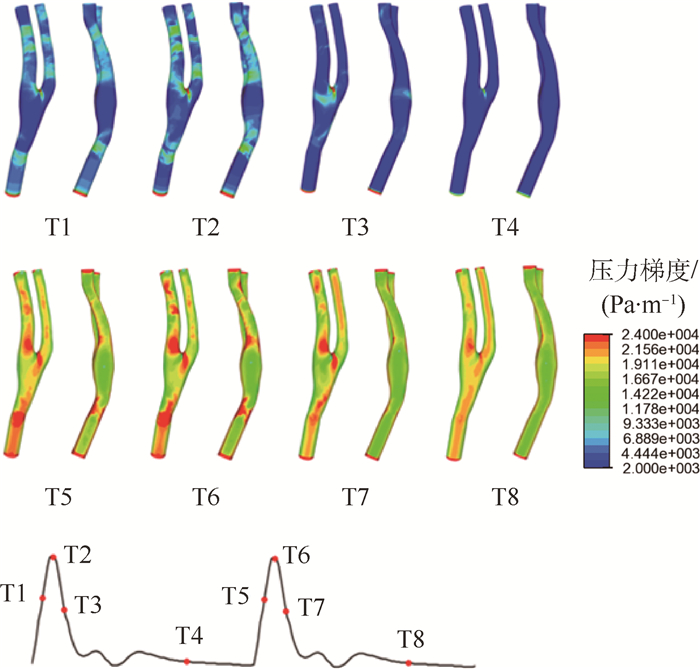 |
| 图 3 颈动脉模型壁面压力梯度分布云图 Fig. 3 Contours of wall pressure gradient distribution of carotid artery model |
| 图选项 |
图 4为颈动脉模型表面各点相对出口的压力云图(图中压力值为相对出口的压力值)。在T1~T4阶段,沿着血液的流动方向压力逐渐降低。而在T5~T8阶段,当模型处在加速度运动环境中时,压力分布特征发生了明显变化。相对较高的压力值主要分布在颈动脉模型的后方区域,相对较低的压力值主要分布在颈动脉模型前方区域。
 |
| 图 4 颈动脉模型相对压力云图 Fig. 4 Contours of relative pressure of carotid artery model |
| 图选项 |
图 5反映的是颈动脉模型壁面剪切应力分布情况,2个心动周期颈动脉壁面剪切应力的区别主要体现在颈内和颈外动脉上。相对第1个心动周期(颈动脉模型无加速度),在第2个心动周期(模型受到2g加速度)内,颈外动脉壁面剪切应力降低,而颈内动脉壁面剪切应力升高。
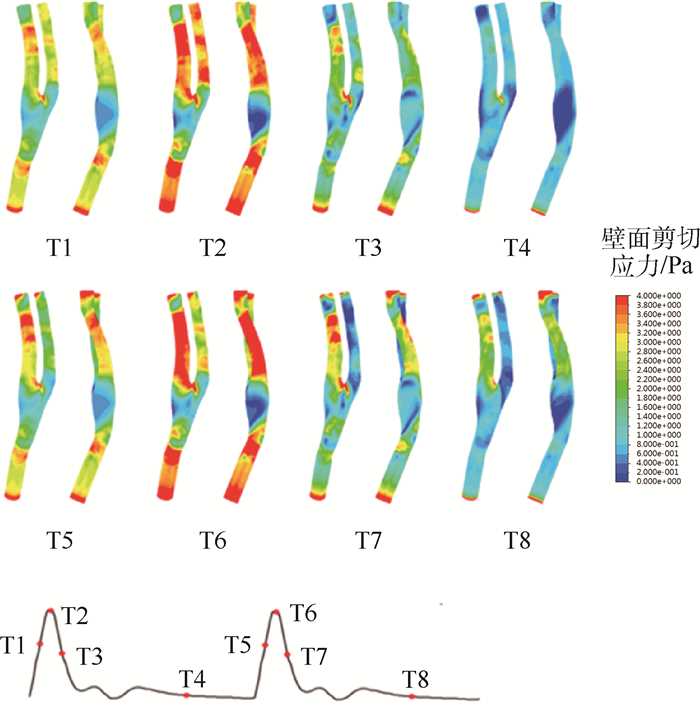 |
| 图 5 颈动脉模型壁面剪切应力分布云图 Fig. 5 Contours of wall shear stress distribution of carotid artery model |
| 图选项 |
颈动脉分叉处的颈动脉窦部位分布着丰富的压力感受器,是人体进行压力调节的重要压力感受部位。为了研究加速度环境对颈动脉窦部位压力的影响,将颈动脉分叉部位分为4个区域,分别命名为AN区(前部区域)、PO区(后部区域)、L区(左侧区域)、R区(右侧区域),如图 6所示。这4个区域上压力及压力梯度平均值随时间变化的曲线如图 7所示。在第2个心动周期(2g加速度),4个面上压力梯度均发生明显提高,尤其是左侧区域(L区)和右侧区域(R区)压力梯度的增加值更大。而对平均压力而言,加速度的影响相对较小。后部区域(PO区)压力平均值发生少量增加,前部区域(AN区)压力平均值发生少量降低。左侧区域(L区)和右侧区域(R区)压力值无明显变化。
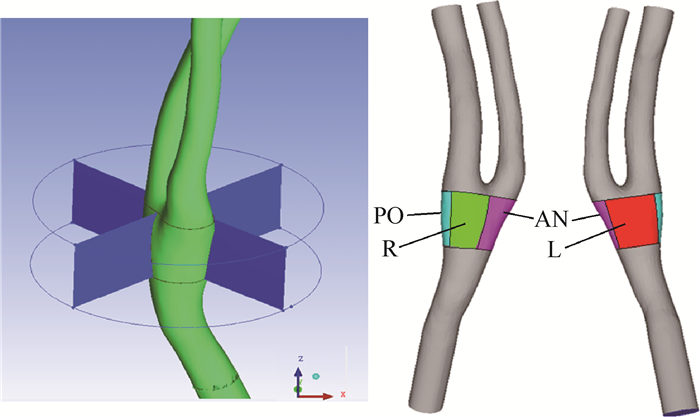 |
| 图 6 颈动脉分叉处4个分区示意图 Fig. 6 Schematic of four areas at carotid branch |
| 图选项 |
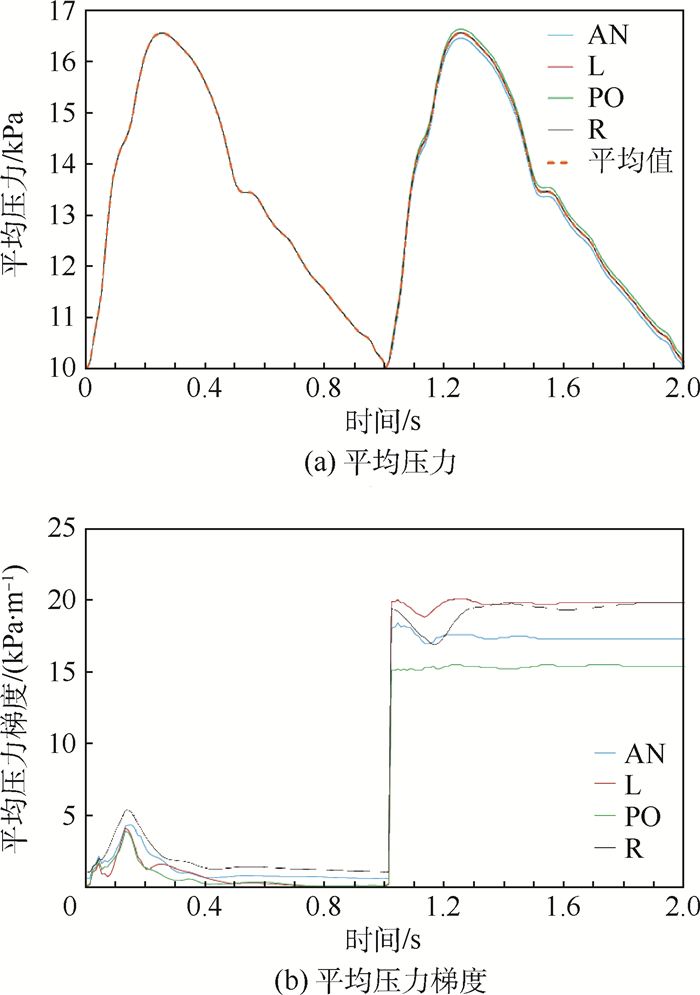 |
| 图 7 颈动脉分叉处4个分区上平均压力和压力梯度变化曲线 Fig. 7 Average pressure and pressure gradient curves of four areas at carotid branch |
| 图选项 |
图 8展示了颈内动脉和颈外动脉血液流量变化情况。颈内动脉内血液流量在第2个心动周期内增加到第1个周期的约2倍。而在颈外动脉内,血液流量降低到0以下,说明出现暂时的血液返流现象。
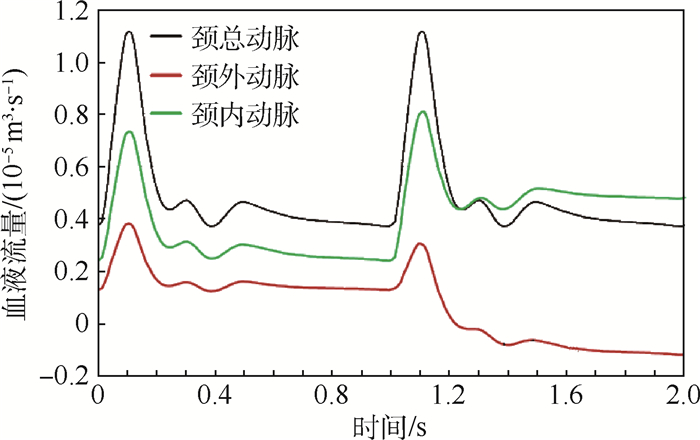 |
| 图 8 颈动脉内血液流量变化曲线 Fig. 8 Blood flow rate curves of carotid arteries |
| 图选项 |
2 讨论 人类日常生活或工作中经常要面临加速度环境,特别是在一些特殊领域和情况下(如航空航天领域),加速度环境更加恶劣。由于血液的易流动性,加速度对心血管系统的影响是显而易见的。之前已有关于加速度影响动物机体功能的动物实验研究。例如,Shahed等[12]发现多次+Gz加速度可以引起小鼠大脑水肿。Oyama和Platt[13]研究了在突然的加速度作用情况下小鼠新陈代谢获得的改变。Erickson等[14]则研究了在持续+Gz加速度情况下狗的心血管系统功能的改变。还有一些临床病例报道,在受到剧烈攻击或车祸撞机后,人体血管会发生损伤性破裂或夹层发生,其中加速度起到了关键的作用[15-17]。
因此,有必要研究人体面临减速环境时心血管系统发生了怎样的改变。为此,选取了一个向前的均匀加速度作为加载条件,考察加速度对颈动脉分叉处血流动力学环境的影响,旨在发现基本规律,为更加复杂的加速度条件对不同部位血流动力学环境的影响研究做基础。本文采用计算流体力学的方法,选择典型的颈动脉模型,对加速度引起的血流动力学参数变化进行了详细模拟。这里的颈动脉3D模型基于医学影像重建获得,计算中采用了在体生理条件下的入口和出口边界条件,从而保证计算结果更加真实地反映在体情况。
数值模拟结果表明,加速度可以显著影响血管内壁面剪切应力的梯度值,并改变应力分布规律;加速度可以改变血管内压力分布特征,降低前部壁面压力,提高后部壁面压力,改变压力分布云图条带的方向;加速度可以改变颈动脉分叉处流向颈内动脉和颈外动脉的血液流量比,即改变分叉血管的流量分配。
此外,大量已有研究揭示了压力、压力梯度、壁面剪切应力等血流动力学参数与动脉血管疾病之间的高度相关性。动脉内压力升高是动脉斑块破裂、动脉瘤扩展等临床症状的诱发力学因素[18-20]。血管内压力梯度还与动脉粥样硬化斑块扩展和破裂存在密切的关系[21-22]。本文发现,加速度可以显著改变颈动脉血管内压力和压力梯度,这就有可能对动脉的生理功能产生直接影响。因此笔者据此推测,临床中遇到的外伤性心血管损伤(如动脉破裂、夹层等)很可能是由于动脉内压力或压力梯度突然变化引起的,而长期的加速度暴露也可能对心血管系统带来潜在的危害。
加速度对颈内动脉和颈外动脉血流量分配比例的影响同样具有重要的生理意义。颈动脉是为头部供血的主要动脉血管,如为大脑、眼睛供血。本文发现,在向前加速度情况下,颈外动脉血流量降低、颈内动脉血流量增加。如果加速度方向改变,血流量分配比例一定也会发生相应改变。动脉血管内血流量的变化会影响下游器官的供血量,进而影响其生理功能,引起下游器官适应性调整和重建。例如,飞行员做机动动作,暴露在+Gz时常常发生的短时间内意识丧失和视觉功能丧失就是由大脑和眼部缺血引起的[23-24]。因此,对加速度引起局部血管(特别是脑部血管)血流量变化的深入研究对研究和预防飞行员暂时性意识丧失、一过性失明等现象具有重要意义。
本文对模型进行了部分简化,如将血管壁假设为刚性壁面。这一简化将导致无法获得壁面弹性变形及其对局部流动的影响。由于颈动脉处血管壁在一个脉动周期内变形量很小,参照已有文献报道的常用做法,认为这一简化对结果趋势的影响很小。再进一步详细探讨管壁内应力分布,以及讨论血流-管壁间流固耦合计算时,则需要将管壁弹性体现到计算模型中。
3 结论 本文以颈动脉为例,通过数值模拟研究,分析了加速度环境下人体颈动脉内血液流动的变化规律。结果表明,加速度环境下动脉血管内压力、壁面剪切应力、分叉血管流量比等流动参数均会受到影响。这些结论有利于更加全面分析人体动脉系统生理、病理变化的生物力学机理,也对航空、航天等特殊环境下人员防护提供有力的理论参考。
参考文献
| [1] | SUD V K, SEKHON G S. Analysis of blood flow through a model of the human arterial system under periodic body acceleration[J]. Journal of Biomechanics, 1986, 19(11): 929-941. DOI:10.1016/0021-9290(86)90188-0 |
| [2] | CHATURANI P, PALANISAMY V. Casson fluid model for pulsatile flow of blood under periodic body acceleration[J]. Biorheology, 1990, 27(5): 619-630. DOI:10.3233/BIR-1990-27501 |
| [3] | CHATURANI P, PALANISAMY V. Pulsatile flow of blood with periodic body acceleration[J]. International Journal of Engineering Science, 1991, 29(1): 113-121. DOI:10.1016/0020-7225(91)90081-D |
| [4] | MAJHI S N, NAIR V R. Pulsatile flow of third grade fluids under body acceleration-Modelling blood flow[J]. International Journal of Engineering Science, 1994, 32(5): 839-846. DOI:10.1016/0020-7225(94)90064-7 |
| [5] | CHAKRAVARTY S, DATTA A, MANDAL P K. Effect of body acceleration on unsteady flow of blood past a time-dependent arterial stenosis[J]. Mathematical and Computer Modelling, 1996, 24(2): 57-74. DOI:10.1016/0895-7177(96)00090-8 |
| [6] | MANDAL P K, CHAKRAVARTY S, MANDAL A, et al. Effect of body acceleration on unsteady pulsatile flow of non-Newtonian fluid through a stenosed artery[J]. Applied Mathematics and Computation, 2007, 189(1): 766-779. DOI:10.1016/j.amc.2006.11.139 |
| [7] | JOU L D, BERGER S A. Numerical simulation of the flow in the carotid bifurcation[J]. Theoretical and Computational Fluid Dynamics, 1998, 10(1-4): 239-248. DOI:10.1007/s001620050061 |
| [8] | HOLDSWORTH D W, NORLEY C J, FRAYNE R, et al. Characterization of common carotid artery blood-flow waveforms in normal human subjects[J]. Physiological Measurement, 1999, 20(3): 219-240. DOI:10.1088/0967-3334/20/3/301 |
| [9] | DE SANTIS G, CONTI M, TRACHET B, et al. Haemodynamic impact of stent-vessel(mal)apposition following carotid artery stenting:Mind the gaps![J]. Computer Methods in Biomechanics and Biomedical Engineering, 2013, 16(6): 648-659. DOI:10.1080/10255842.2011.629997 |
| [10] | PATEL D J, VAISHNAV R N. Basic hemodynamics and its role in disease processes[M]. Baltimore: University Park Press, 1980. |
| [11] | WANG Z, SUN A, FAN Y, et al. Comparative study of Newtonian and non-Newtonian simulations of drug transport in a model drug-eluting stent[J]. Biorheology, 2012, 49(4): 249-259. |
| [12] | SHAHED A R, BARBER J A, WERCHAN P M. Multiple +Gz exposures cause brain edema in rats[J]. Aviation, Space, and Environmental Medicine, 1994, 65(6): 522-526. |
| [13] | OYAMA J, PLATT W T. Metabolic alterations in rats exposed to acute acceleration stress[J]. Endocrinology, 1965, 76: 203-209. DOI:10.1210/endo-76-2-203 |
| [14] | ERICKSON H H, SANDLETR H, STONE H L. Cardiovascular function during sustained +Gz stress[J]. Aviation, Space, and Environmental Medicine, 1976, 47(7): 750-758. |
| [15] | KRISTOFFERSEN S, VETTI N, MORILD I. Traumatic dissection of the vertebral artery in a toddler following a short fall[J]. Forensic Science International, 2012, 221(1-3): E34-E38. DOI:10.1016/j.forsciint.2012.04.023 |
| [16] | KAISER C, SCHNABEL A, BERKEFELD J, et al. Traumatic rupture of the intracranial vertebral artery due to rotational acceleration[J]. Forensic Science International, 2008, 182(1-3): E15-E17. DOI:10.1016/j.forsciint.2008.10.001 |
| [17] | SALVATORI M, KODIKARA S, POLLANEN M. Fatal subarachnoid hemorrhage following traumatic rupture of the internal carotid artery[J]. Legal Medicine, 2012, 14(6): 328-330. DOI:10.1016/j.legalmed.2012.06.004 |
| [18] | LI Z, TAVIANI V, TANG T, et al. The mechanical triggers of plaque rupture:Shear stress vs pressure gradient[J]. British Journal of Radiology, 2009, 82(1): S39-S45. |
| [19] | MENDELL J T, OLSON E N. MicroRNAs in stress signaling and human disease[J]. Cell, 2012, 148(6): 1172-1187. DOI:10.1016/j.cell.2012.02.005 |
| [20] | KOUGIAS P, BISMUTH J, HUYNH T T, et al. Symptomatic aneurysm rupture without bleeding secondary to endotension 4 years after endovascular repair of an abdominal aortic aneurysm[J]. Journal of Endovascular Therapy, 2008, 15(6): 702-705. DOI:10.1583/08-2391.1 |
| [21] | SAMESHIMA N, YAMASHITA A, SATO S, et al. The values of wall shear stress, turbulence kinetic energy and blood pressure gradient are associated with atherosclerotic plaque erosion in rabbits[J]. Journal of Atherosclerosis and THombosis, 2014, 21(8): 831-838. DOI:10.5551/jat.23093 |
| [22] | FOLTS J. Arterial blood pressure gradient across vulnerable plaque might increase rupture[J]. Journal of the American College of Cardiology, 2007, 50(25): 2440. |
| [23] | SALIOU G, LEBLANC P E, CAUQUIL C, et al. Sudden loss of consciousness during a flight[J]. Cerebrovascular Diseases, 2014, 37(6): 470-471. DOI:10.1159/000363370 |
| [24] | WHINNERY J E, WHINNERY A M. Acceleration-induced loss of consciousness:A review of 500 episodes[J]. Archives of Neurology, 1990, 47(7): 764-776. DOI:10.1001/archneur.1990.00530070058012 |
