航天飞行器壳体的套装过程要求装置调整位姿精确,抗阻能力强,因此要求推进机构必须具有刚度大和精度高这2个特点,同时位姿调整的范围不大,而并联机构具有刚度大、精度高、响应快的优点[4],在位姿调整、部件对接等领域应用较多。
针对少自由度并联机构构型的设计,国内外****通过螺旋理论[5]、群论[6]、机构拓扑学[7]等方法对3T2R机构进行了构型综合,如唐卫星[8]、李秦川[9]等,但通过该类方法得出的构型往往支链杆件数目过多,结构十分繁杂,难以应用于实际生产应用中。针对上述问题,****们采用了新的设计方法,可归纳为以下2种:①串并混联形式,如Song[10]、Dong[11]等在三自由度并联机构末端串联两自由度转头,Xu等[12]为三自由度机构增加两自由度的操作转台,该方法有效解决了结构复杂和控制难的问题,但串联部分结构强度较弱;②在六自由度机构中添加被动支链的形式,如刘建坤[13]用CPU支链取代一条六自由度支链作为主动支链,Sun[14]、杨会[15]等直接在机构中间添加约束支链作为被动支链,Xie等[16]添加被动支链并对支链结构进行了改进,该方法利用被动支链限制了动平台的自由度,发挥了五自由度机构的优势,但动平台的约束力或力偶完全由一条支链承担,需要该支链有较高的强度。
本文就如何提高飞行器套装位姿调整机构的刚度和精度提出了一种新型的5-U(RRP)S/(8U)PU并联机构,并开展了相关研究。
1 机构结构配置 由于机构对刚度有较高的要求,故以5条六自由度支链作为主动支链,添加1条五自由度约束支链作为被动支链,以此作为机构的基本配置方式。
对于主动支链,机构设计流程如图 1所示。为提高刚度,在传统的UPS支链上附加一条UPS支链并简化运动副。该方法构造的闭环结构本质是一个五杆机构,因此需要同时添加2个驱动才能保证机构运动的唯一性,这就使得整个机构为冗余驱动并联机构,增加了质量,也增加了控制难度,违背了支链构型的初衷。在该机构的基础上,将一条支链上的移动(P)副舍去,则闭环结构为四杆机构,拥有1个自由度,结合球(S)副及底部的转动(R)副共拥有5个自由度,因此整个支链的自由度数目减少为5。为满足六自由度,在底部R副处再增加一个R副构成虎克铰(U)。该闭环三角形支链与UPS支链相比,极大地提高了机构的稳定性和强度。
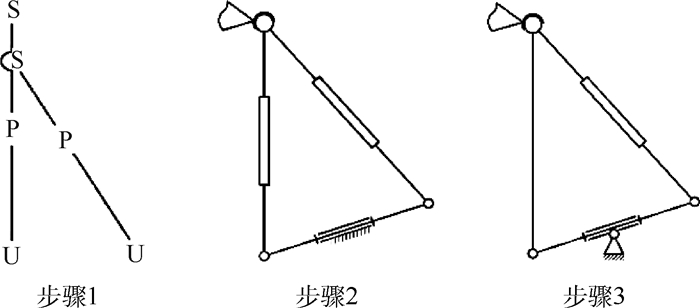 |
| 图 1 主动支链结构设计流程 Fig. 1 Design flow of active limb structure |
| 图选项 |
被动支链结构如图 2所示,底部采用平行六面体结构(以下简称8U结构)[17],顶部为U副和P副,该结构用R副代替P副,使得结构更加紧凑,有效提高了支链的强度,同时避免过多的P副产生自锁。
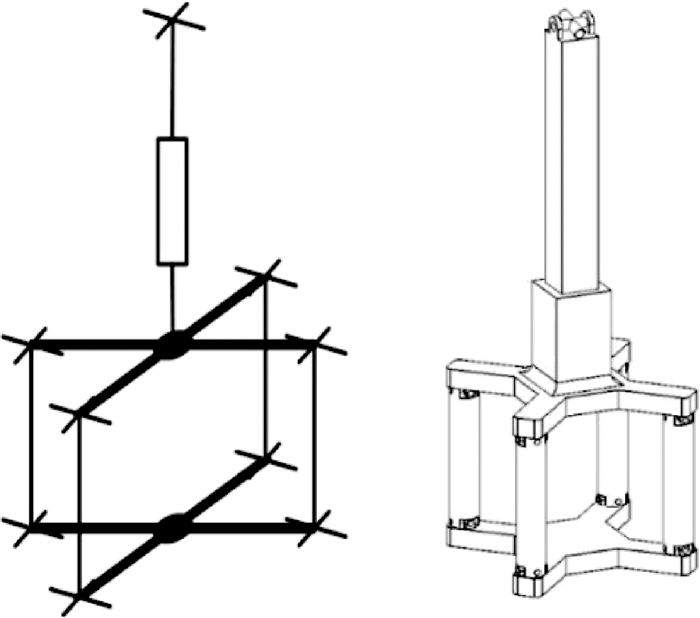 |
| 图 2 被动支链结构示意图 Fig. 2 Schematic of passive limb structure |
| 图选项 |
图 3为新型5-U(RRP)S/(8U)PU并联机构的三维结构。该机构由动平台、静平台、5条主动支链和1条被动支链组成。主动支链依次由虎克铰(U)、2个R副、P副和复合S副组成,其中U副与静平台相连,每个P副为驱动副,复合S副与动平台相连;被动支链依次由8U结构、P副、U副组成,其中8U结构与静平台相连,U副与动平台相连。静平台为等边五边形,动平台为对称五边形,该设计可以保证选择主动支链的P副作为驱动副时各主动支链的等效运动具有线性无关性。
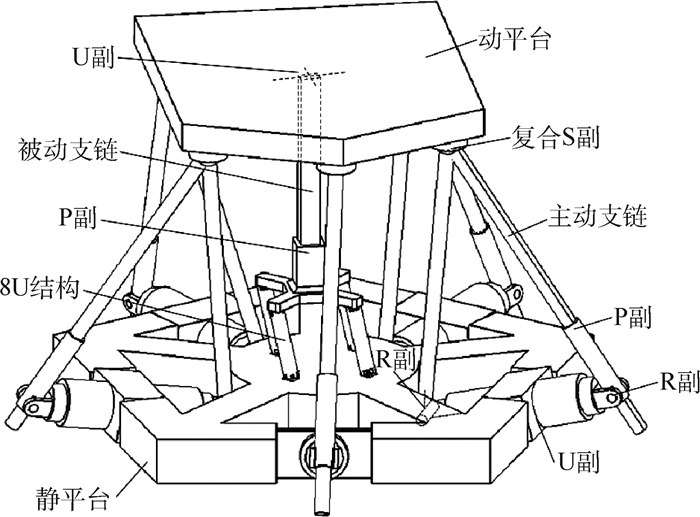 |
| 图 3 新型5-U(RRP)S/(8U)PU并联机构结构示意图 Fig. 3 Schematic of a new type of 5-U(RRP)S/(8U)PU parallel mechanism |
| 图选项 |
图 4为新型5-U(RRP)S/(8U)PU并联机构的结构简图。动平台的形状可由参数a、b、c表示,静平台的顶点到中心的距离为r;主动支链的复合S副为点Ci,2个R副分别为点Ai和点Bi,U副为点Di,Di为AiBi的中点,P副位于杆BiCi;被动支链的U副为点P(与动平台C2C5的中点重合),8U结构的等效中心为点O(与静平台的中心重合);初始安装时,点P与点O位于同一铅垂线,点C1与点D1位于同一铅垂面,动平台与静平台平行且距离为z0。以此建立如图 4所示的坐标系:Puvw为动系,固结于动平台点P,其中坐标轴v为

 |
| 图 4 新型5-U(RRP)S/(8U)PU并联机构结构简图 Fig. 4 Structure diagram of a new type of 5-U(RRP)S/(8U)PU parallel mechanism |
| 图选项 |
2 自由度计算 新型5-U(RRP)S/(8U)PU并联机构的主动支链和被动支链的结构形式不同,因此自由度计算需要分别考虑2种支链。
对于被动支链(8U)PU,U副的轴线分别沿x和y方向;8U结构的自由度数目为2,具体为沿x和y方向的移动,但这2个移动耦合了沿z方向的移动。因此,当8U机构和轴线沿z方向的P副连接时,可等效看作空间内沿x、y和z方向的3个P副,那么原(8U)PU支链在运动学上可等效为UPPP支链。对于该支链,易得到其自由度数目为5,分别为沿x、y、z方向的移动和绕x、y方向的转动。
对于主动支链U(RRP)S,由于5条支链结构相同,故取支链1进行分析。图 5为支链1的结构简图。支链1在初始位姿时位于定系yOz平面内,现以点D为原点建立坐标系Dxyz,并对各运动副进行如图 5所示的编号。设支链1中各个参数如下:AD=DB=l1/2, AC=l2, BC=l3,杆AB初始仰角为γ;在一般位置时,虎克铰D转过的角度分别为θ1和θ2,杆AB与杆BC夹角为θ3。利用螺旋理论[18]可以分别求得各运动副的运动螺旋如下:
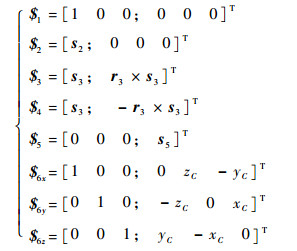 | (1) |
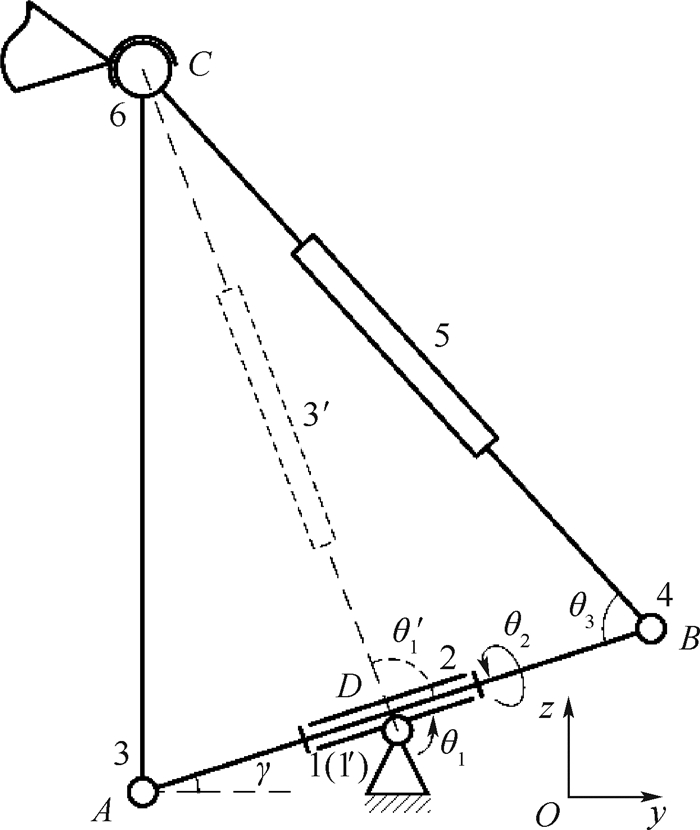 |
| 图 5 支链1结构简图 Fig. 5 Structure diagram of limb 1 |
| 图选项 |
式中:
 |
将式(1)组合后即可得到支链1的运动螺旋系为
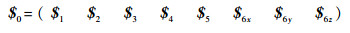 | (2) |
求解后可得该运动螺旋系的反螺旋$0r=0,即该支链不存在约束,其自由度为6。
综上所述,由于每条主动支链的自由度为6,对动平台不提供约束,所以动平台和中间被动支链具有相同的自由度数,即沿x、y、z方向的移动和绕x、y方向的转动。
3 运动学分析 3.1 位置反解 已知动平台的位姿,以初始位姿为基准,可给出动平台在某一时刻的位姿参数如下:(x, y, z)为动系原点P沿x、y、z轴移动的距离;α为动平台绕u轴转过的角度;β为动平台绕v轴转过的角度。现求解驱动P副的位置即求解杆BiCi的长度。
由图 4可建立第i(i=1, 2, …, 5)条支链的封闭矢量方程为
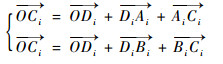 | (3) |
因为Di为AiBi的中点,所以
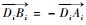
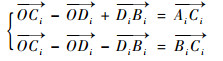 | (4) |
首先,利用坐标变换可得Ci在定系的坐标为
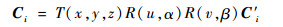 | (5) |
式中:C′i 为Ci在动系中的坐标。
然后,求出Di在定系的坐标为
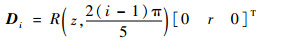 | (6) |
最后,求得向量
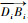
 | (7) |
式中:θ1, i为未知量,表征第i条支链绕U副一条转动轴线的转角。
将式(5)~式(7)代入式(4),由于AiCi为固定杆长l2,BiCi为所需求的位置l3, i,利用杆长条件可得方程组,未知量为θ1, i、l3, i,即可解得l3, i。
3.2 位置正解 已知各驱动P副的位置,即杆BiCi的长度l3, i,现求解动平台的位姿参数(x, y, z, α, β)。
当杆BiCi的长度已知时,三角形AiBiCi各边长确定,为固定桁架结构,可等效看作固定杆CiDi,利用三角形中线定理可求得
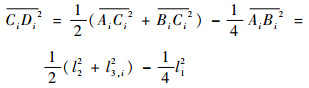 | (8) |
写成坐标点的形式为
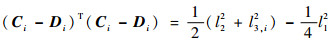 | (9) |
将式(5)和式(6)代入式(9)中,其中未知量为(x, y, z, α, β),共可得到5个方程,则可唯一求解出动平台的位姿。
3.3 求解雅可比矩阵 采用螺旋理论进行雅可比矩阵的求解[19]。共分为2个部分:约束雅可比矩阵和运动雅可比矩阵。各运动副的运动螺旋表示如图 6所示,图中sj, i表示第i支链的第j个运动副的轴线方向。
 |
| 图 6 各运动副的运动螺旋 Fig. 6 Twist of each kinematic pair |
| 图选项 |
首先,求解约束雅可比矩阵。由于主动支链对动平台不提供约束,因此仅考虑被动支链。由第2节可知,(8U)PU支链可等效为UPPP支链,易得到其自由度分别为沿x、y、z方向的移动和绕x、y方向的转动。动平台的瞬时速度$P可表示为
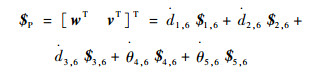 | (10) |
式中:
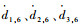
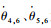
 |
求得其反螺旋为
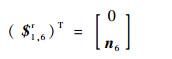 | (11) |
式中:n6为s4, 6和s5, 6公垂线方向。
将式(10)与式(11)做互易积并整理得
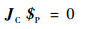 | (12) |
式中:JC为该机构的约束雅可比矩阵,即
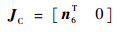 | (13) |
其次,求解运动雅可比矩阵。由于被动支链不存在驱动副,因此仅考虑主动支链。对于主动支链,支链本身为闭环结构,需等效为开环结构才可用螺旋理论进行求解雅可比矩阵。根据第2节的自由度计算和支链的运动形式不难发现,闭环四杆机构AiBiCi的运动可等效成如图 5所示的P副3′、R副1′,其中1′与U副的转动轴线1共轴。
将式(8)对时间t求导得
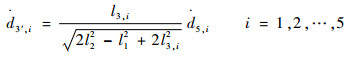 | (14) |
式中:
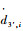
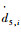
设等效R副1′的速度为
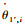
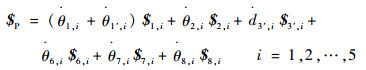 | (15) |
将驱动P副刚化,驱动支链为US结构,因此该支链会产生一个额外的反螺旋为
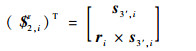 | (16) |
式中: ri为方向矢量

将式(15)与式(16)做互易积得
 | (17) |
将式(14)代入式(17)整理,将5条支链叠加后得
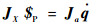 | (18) |
式中:
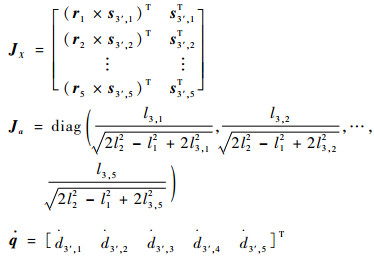 |
综上所述,将式(13)与式(18)叠加即可得机构的完整雅可比矩阵为
 | (19) |
4 工作性能分析 4.1 定姿态工作空间
4.1.1 理论分析 在实际工程应用中,对于新型5-U(RRP)S/(8U)PU并联机构动平台的调姿转角要求很小,因此仅分析该机构的定姿态工作空间。
该机构的主动支链和被动支链的运动具有解耦特性,整个机构的工作空间可看作是主动支链和被动支链独立工作空间的公共重合区域,因此需分别计算2个独立定姿态工作空间。
对于被动支链,影响工作空间的主要因素有P副的移动距离和8U结构中U副的转角限制。
设每个U副转角为θ6,其约束条件可表示为
 | (20) |
设P副的移动距离为l6,其约束条件可表示为
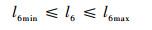 | (21) |
如图 7所示,8U结构点O′处的工作空间是以O为原点、d为半径的球冠面。
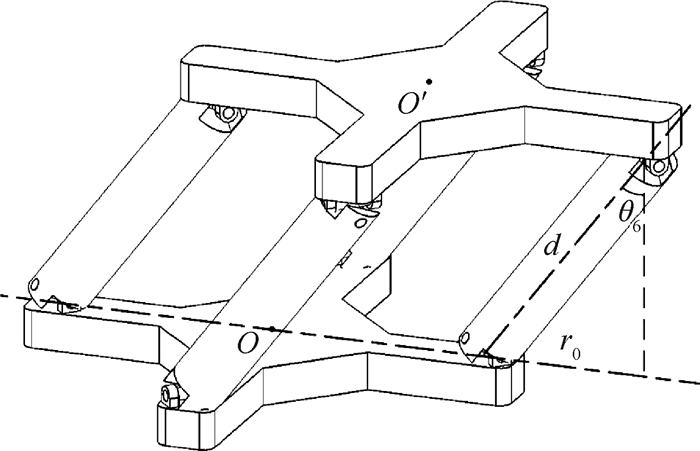 |
| 图 7 8U结构工作空间示意图 Fig. 7 Schematic diagram of workspace of 8U structure |
| 图选项 |
对于主动支链,影响工作空间的主要因素有P副的移动距离及复合S副处杆AiCi和杆BiCi的相对转角限制。
设P副的移动距离为l3, i,其约束条件可表示为
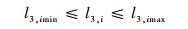 | (22) |
设杆AiCi和杆BiCi的相对转角为θi,其约束条件可表示为
 | (23) |
式中:

4.1.2 计算实例 对该机构的尺寸参数及约束范围进行赋值后整理如表 1所示。
表 1 并联机构尺寸参数 Table 1 Dimension parameters of parallel mechanism
| 参数 | 数值 |
| a/mm | 200 |
| b/mm | 160 |
| c/mm | 160 |
| d/mm | 100 |
| r/mm | 215 |
| l1/mm | 220 |
| l2/mm | 340 |
| θ6m/(°) | 60 |
| l6min/mm | 100 |
| l6max/mm | 800 |
| l3, imin/mm | 150 |
| l3, imax/mm | 550 |
| θimin/(°) | 15 |
| θimax/(°) | 45 |
表选项
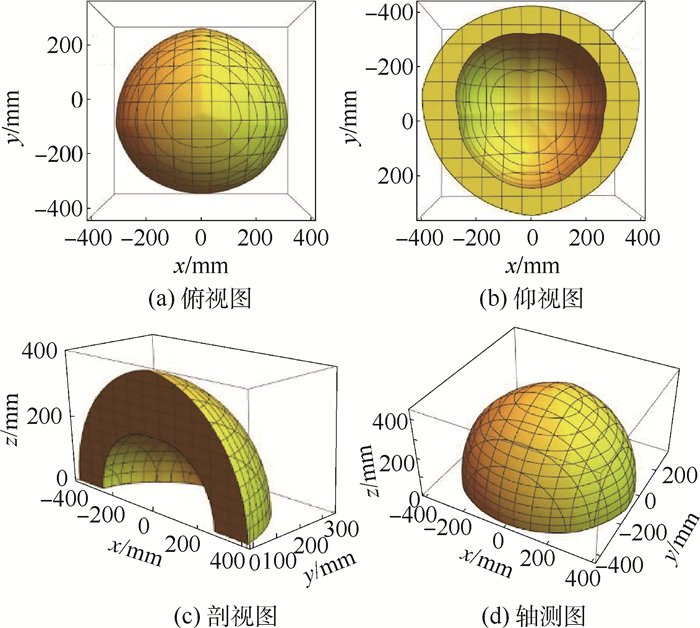
设初始位置时z=300 mm,在不考虑杆件干涉的情况下,根据表 1可分别绘制出z≥0时主动支链和被动支链的定姿态工作空间,如图 8和图 9所示,将2个工作空间取交集后得到机构的工作空间如图 10所示。
 |
| 图 8 主动支链工作空间 Fig. 8 Workspace of active limb |
| 图选项 |
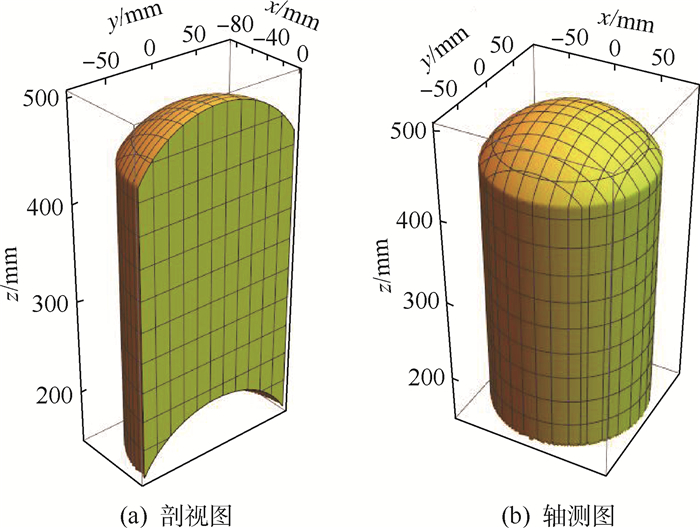 |
| 图 9 被动支链工作空间 Fig. 9 Workspace of passive limb |
| 图选项 |
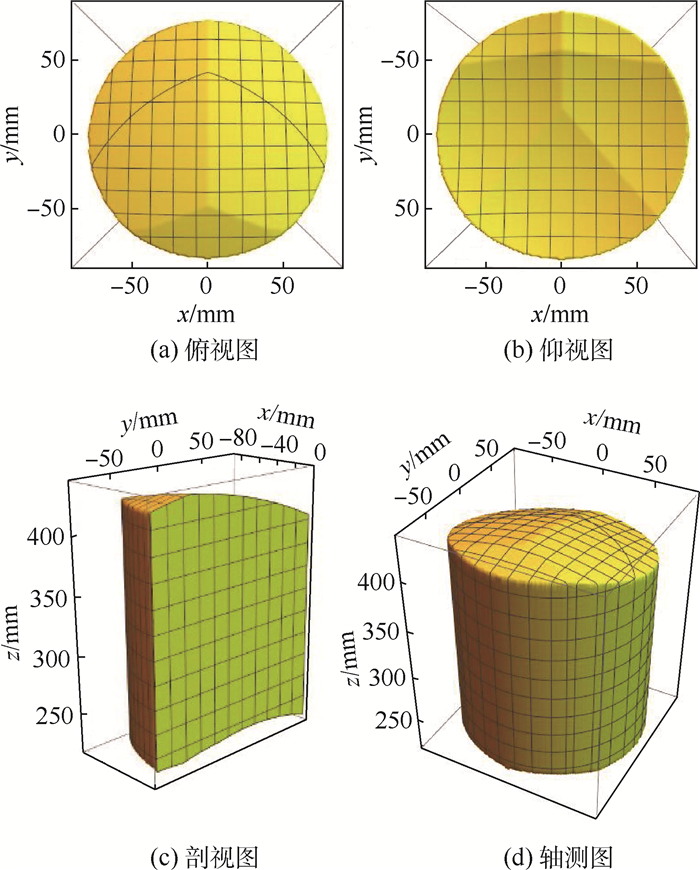 |
| 图 10 整体机构工作空间 Fig. 10 Workspace of whole mechanism |
| 图选项 |
由此可见,在尺寸约束等条件下,该机构的定姿态工作空间由8U结构的转角范围(即被动支链工作空间的粗细)和三角形结构的最大、最小伸缩量(即主动支链工作空间类球壳体的厚度)决定。
4.2 静刚度分析 机构在运动过程中刚度随位姿参数的变化而产生的变化趋势是衡量该机构是否具有高刚度的一个重要指标。
根据文献[20],静刚度矩阵为
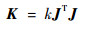 | (24) |
式中:k为各关节的等效弹簧系数;J为机构的雅可比矩阵。
动平台的等效力螺旋F与其微小变形量Δx的关系为
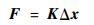 | (25) |
现选用将静刚度矩阵K的最小特征值λmin作为评价静刚度性能的指标。
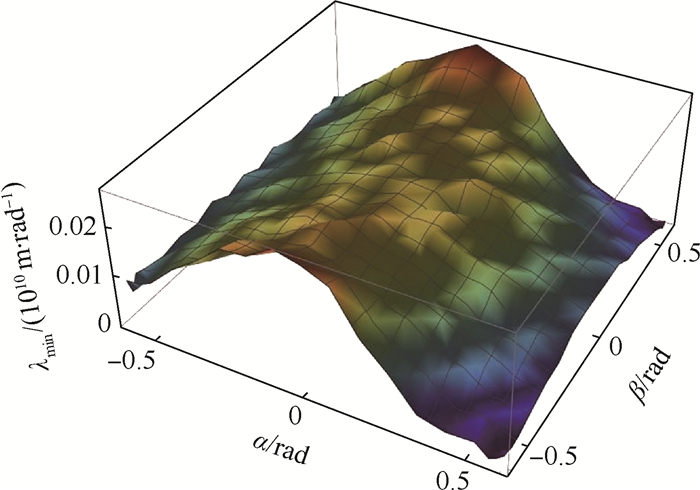
当机构动平台位置固定,即x=0, y=0,z=300 mm时,动平台的刚度随其转角α、β的分布如图 11所示。
 |
| 图 11 定位置下刚度随转角的分布 Fig. 11 Distribution of stiffness with rotation angle under fixed position |
| 图选项 |
当机构动平台姿态固定,即α=0,β=0时,动平台的刚度随其位移x、y、z的分布如图 12所示。
 |
| 图 12 定姿态下刚度随位移的分布 Fig. 12 Distribution of stiffness with displacement under fixed posture |
| 图选项 |
从图 11中可以看出,当α一定时,刚度随β绝对值的增大或增或减,但变化不明显;当β一定时,刚度随α绝对值的增大而减小。
从图 12中可以看出,刚度随x绝对值的增大而减少,随y绝对值的增大变化不明显,随z的增大而增大。
5 对比与仿真 为验证新型5-U(RRP)S/(8U)PU并联机构的可行性以及其主动支链的结构形式相对于一般机构是否具有优势,现选择与之相似的5-UPS/(8U)PU机构(见图 13)与之进行对比。
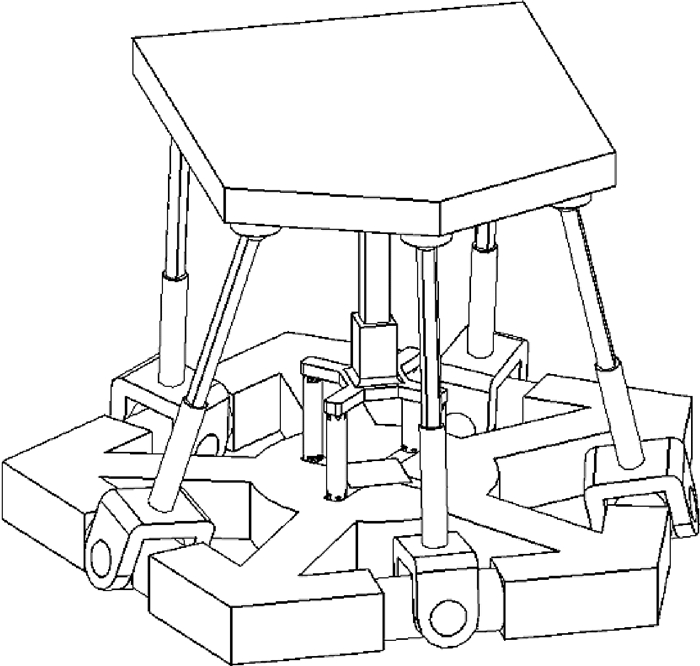 |
| 图 13 5-UPS/(8U)PU并联机构结构示意图 Fig. 13 Schematic of 5-UPS/(8U)PU parallel mechanism |
| 图选项 |
5-UPS/(8U)PU机构由5条主动支链和1条被动支链构成,其主动支链为常见的UPS结构,被动支链则选择与新机构相同的(8U)PU结构,以减少其他因素对结果的影响。赵永生等[21]对5-UPS/PRPU机构进行了运动学分析等研究,该机构与5-UPS/(8U)PU机构类似,由于被动支链上不含有驱动副,对机构的运动学特性影响较小,因此其运动学分析方法可用于5-UPS/(8U)PU机构,此处不再赘述,并最终得出5-UPS/(8U)PU机构可控性好的特点。
对于新型5-U(RRP)S /(8U)PU机构,从图 6中不难看出,式(8)中的等效杆CiDi即为5-UPS/(8U)PU机构的主动支链,因此CiDi的长度可看作5-UPS/(8U)PU机构中移动驱动副的变化量,设新机构的驱动副的变化量为L,对比机构的驱动副的变化量为LC,由式(8)可得两者关系为
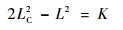 | (26) |
式中:K为常数。
由此可见,L与LC满足双曲函数关系,当两者都大于0时,L随LC单调递增。结合式(14),新机构中驱动副速度与对比机构中驱动副速度呈线性关系。
因此,当5-UPS/(8U)PU机构具有良好的可控性时,新型5-U(RRP)S/(8U)PU机构也具有较好的可控性。
接下来验证新型5-U(RRP)S/(8U)PU机构是否具有更高的精度和刚度。利用ADMAS软件对该机构和对比机构进行仿真。
用于对比的机构结构除了主动支链采用UPS结构外,机构的尺寸参数、结构布局和初始位姿等都与本文机构相同,以此减少除构型以外的因素产生的误差。
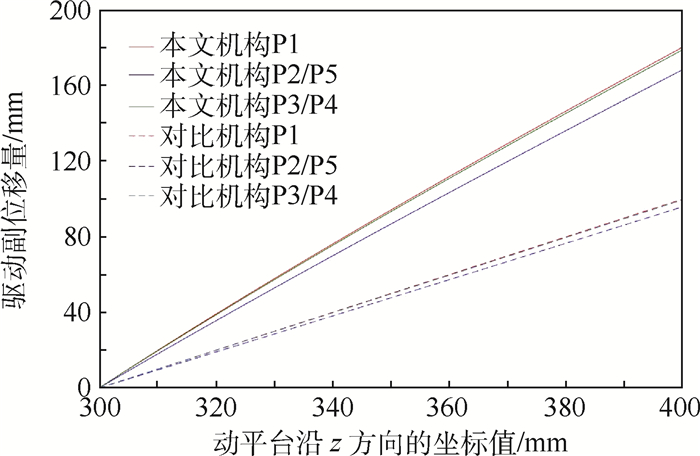
首先验证本文机构的精度。将2种机构的动平台运动进行轨迹规划,为保证对比的准确性,动平台的运动应尽可能简单,现规划2种机构的动平台运动为从初始位姿沿z轴方向移动100 mm,通过仿真后得到的2种机构各驱动P副的位移数据如表 2所示,整理后如图 14所示。
表 2 各支链驱动副位移量 Table 2 Displacement of driving joint on each limb
| 动平台沿z方向的坐标值/mm | P1位移量/mm | P2/P5位移量/mm | P3/P4位移量/mm | |||||
| 本文 | 对比 | 本文 | 对比 | 本文 | 对比 | |||
| 300 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 310 | 18.03 | 10.04 | 18.03 | 10.01 | 16.85 | 9.74 | ||
| 320 | 36.07 | 20.03 | 36.06 | 19.96 | 33.63 | 19.32 | ||
| 330 | 54.15 | 30.18 | 54.12 | 30.11 | 50.55 | 29.07 | ||
| 340 | 72.26 | 40.14 | 72.19 | 40.08 | 67.32 | 38.66 | ||
| 350 | 90.48 | 50.18 | 90.37 | 50.06 | 84.26 | 48.31 | ||
| 360 | 108.65 | 60.16 | 108.56 | 60.11 | 101.05 | 58.15 | ||
| 370 | 126.88 | 70.11 | 126.74 | 70.09 | 117.76 | 67.63 | ||
| 380 | 144.81 | 80.18 | 144.73 | 80.12 | 134.54 | 77.24 | ||
| 390 | 162.93 | 90.01 | 162.75 | 89.95 | 151.38 | 96.99 | ||
| 400 | 180.11 | 100.04 | 179.94 | 100.00 | 168.01 | 96.51 | ||
表选项
 |
| 图 14 驱动副位移量变化曲线 Fig. 14 Changing curves of driving joints' displacement |
| 图选项 |
从图 14中可以看出,当动平台进行相同运动时,本文机构驱动副的位移量相比于一般机构要增加近100%。因此,本文机构通过增加驱动副的变化量使得驱动电机对动平台的控制精度提高了近1倍。
其次,验证本文机构的刚度。当动平台受到外界的阻力时,各驱动副所承受力的大小可以作为评价机构刚度的标准。现设定2种机构各个驱动副的运动速度相同,具体数值如表 3所示。
表 3 各支链驱动副电机运行速度 Table 3 Motor operation speed of driving joint on each limb
| 支链驱动副编号 | 速度/(mm·s-1) |
| P1 | -2 |
| P2 | 2 |
| P3 | 4 |
| P4 | 4 |
| P5 | 2 |
表选项
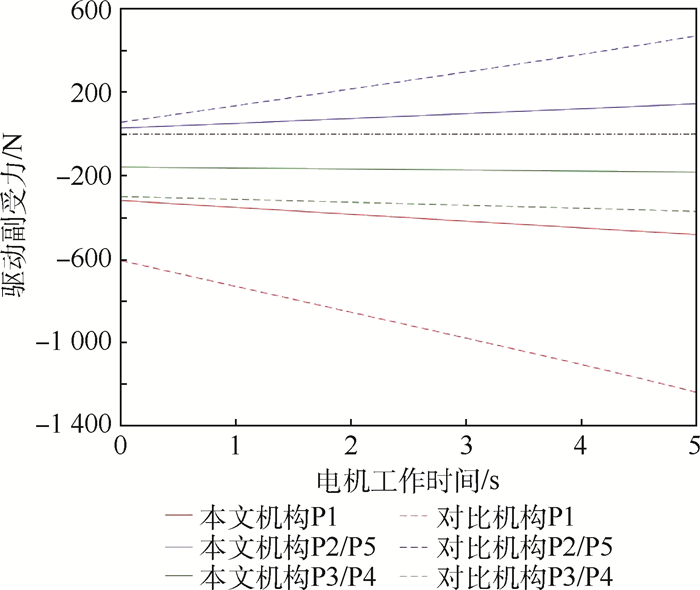
给2种机构的动平台施加相同的外界压力,大小为800 N,方向始终沿重力方向。在保持上述速度下2种机构的驱动电机同时运行5 s,通过仿真后得到2种机构各驱动P副的受力大小,如表 4所示,整理后如图 15所示。
表 4 各支链驱动副受力 Table 4 Force of driving joint on each limb
| 电机工作时间/s | P1受力/N | P2/P5受力/N | P3/P4受力/N | |||||
| 本文 | 对比 | 本文 | 对比 | 本文 | 对比 | |||
| 0 | -323.29 | -610.14 | 38.46 | 72.19 | 158.15 | -291.08 | ||
| 0.5 | -338.51 | -673.73 | 49.51 | 113.77 | 159.93 | -298.71 | ||
| 1.0 | -354.46 | -737.49 | 61.43 | 155.43 | 161.85 | -306.40 | ||
| 1.5 | -365.83 | -801.16 | 72.59 | 197.16 | 163.71 | -314.15 | ||
| 2.0 | -385.18 | -864.83 | 84.16 | 238.86 | 165.65 | -321.84 | ||
| 2.5 | -400.57 | -1928.53 | 95.54 | 280.52 | 167.58 | -329.53 | ||
| 3.0 | -416.16 | -992.24 | 107.37 | 322.24 | 169.41 | -337.27 | ||
| 3.5 | -431.19 | -1055.96 | 118.51 | 363.93 | 171.35 | -344.91 | ||
| 4.0 | -447.74 | -1119.67 | 130.74 | 405.66 | 173.25 | -352.62 | ||
| 4.5 | -462.57 | -1183.34 | 141.53 | 447.31 | 175.17 | -360.30 | ||
| 5.0 | -478.15 | -1247.18 | 153.44 | 489.25 | 177.06 | -368.43 | ||
表选项
 |
| 图 15 驱动副受力变化曲线 Fig. 15 Changing curves of driving joints under force |
| 图选项 |
从图 15中可以看出,当动平台受力相同且驱动副运动相同时,本文机构驱动副的受力约为一般机构的1/3。因此,本文机构使得驱动副的结构刚度提高了近2倍。
6 结论 为解决导弹壳体的自动套装要求,本文提出了一种用于位姿调整的新型5-U(RRP)S/(8U)PU并联机构。采用被动支链进行约束,同时主动支链采用三角形闭环结构,以提高机构的精度、刚度和稳定性。
1) 进行了自由度计算及运动学分析,利用位置关系分别绘制了主动支链与被动支链的工作空间并综合,利用全雅可比矩阵建立了刚度模型。
2) 选取主动支链为UPS支链的机构作为对比机构,利用ADAMS软件同时对2种机构进行仿真,一方面验证了机构运动的可行性,另一方面通过软件仿真初步得出本文机构相比于对比机构的精度提高了近1倍,刚度提高了近2倍。
参考文献
| [1] | 谷良贤, 龚春林. 航天飞行器设计[M]. 西安: 西北工业大学出版社, 2016: 37-40. GU L X, GONG C L. Design of aerospace vehicle[M]. Xi'an: Northwestern Polytechnical University Press, 2016: 37-40. (in Chinese) |
| [2] | 刘鹏程, 杜毅民. 导弹总体测试工程化的几个问题[J]. 航空兵器, 2006(4): 50-53. LIU P C, DU Y M. Problems of engineering design for missile system test[J]. Aero Weaponry, 2006(4): 50-53. DOI:10.3969/j.issn.1673-5048.2006.04.013 (in Chinese) |
| [3] | 马政伟, 李卫东, 万敏, 等. 飞机侧壁部件装配调姿机构的设计与分析[J]. 北京航空航天大学学报, 2014, 40(2): 280-284. MA Z W, LI W D, WAN M, et al. Design and analysis of flexible fixture for aircraft side panels[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 280-284. (in Chinese) |
| [4] | 文福安, 杨光. 并联机器人机构概述[J]. 机械科学与技术, 2000, 19(1): 69-72. WEN F A, YANG G. Summary of parallel robot mechanism[J]. Mechanical Science and Technology, 2000, 19(1): 69-72. DOI:10.3321/j.issn:1003-8728.2000.01.026 (in Chinese) |
| [5] | KONG X. Type synthesis of 5-DOF parallel manipulators based on screw theory[M]. New York: John Wiley & Sons, 2005. |
| [6] | LI Q C, HUANG Z, HERV J M. Displacement manifold method for type synthesis of lower-mobility parallel mechanisms[J]. Science in China, 2004, 47(6): 641-650. DOI:10.1360/03ye0352 |
| [7] | 杨廷力. 机器人机构拓扑结构学[M]. 北京: 机械工业出版社, 2004: 12-16. YANG T L. Topology structure design of robot mechanisms[M]. Beijing: China Machine Press, 2004: 12-16. (in Chinese) |
| [8] | 唐卫星, 马履中, 石奇端, 等. 3T-2R五自由度并联机构的型综合[J]. 中国机械工程, 2007, 18(20): 2460-2463. TANG W X, MA L Z, SHI Q D, et al. Type synthesis of 3T-2R parallel mechanism[J]. China Mechanical Engineering, 2007, 18(20): 2460-2463. DOI:10.3321/j.issn:1004-132x.2007.20.016 (in Chinese) |
| [9] | 李秦川.对称少自由度并联机器人型综合理论及新机型综合[D].秦皇岛: 燕山大学, 2003: 57-68. LI Q C.Type synthesis theory of lower-mobility parallel mechanisms and synthesis of new architectures[D].Qinhuangdao: Yanshan University, 2003: 57-68(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10216-2004061702.htm |
| [10] | SONG Y M, LIAN B B, SUN T, et al. A novel five-degree-of-freedom parallel manipulator and its kinematic optimization[J]. Journal of Mechanisms and Robotics, 2014, 6(4): 041008. DOI:10.1115/1.4027742 |
| [11] | DONG C, LIU H, YUE W, et al. Stiffness modeling and analysis of a novel 5-DOF hybrid robot[J]. Mechanism and Machine Theory, 2018, 125: 80-93. DOI:10.1016/j.mechmachtheory.2017.12.009 |
| [12] | XU P, CHEUNG C F, LI B, et al. Kinematics analysis of a hybrid manipulator for computer controlled ultra-precision freeform polishing[J]. Robotics and Computer-Integrated Manufacturing, 2017, 44: 44-56. DOI:10.1016/j.rcim.2016.08.003 |
| [13] | 刘建坤.基于五自由度并联机构的隔振平台研究[D].哈尔滨: 哈尔滨工业大学, 2013: 7-19. LIU J K.Research of a vibration isolation platform based on 5-DOF parallel mechanism[D].Harbin: Harbin Institute of Technology, 2013: 7-19(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10213-1014080959.htm |
| [14] | SUN T, SONG Y M, DONG G, et al. Optimal design of a parallel mechanism with three rotational degrees of freedom[J]. Robotics and Computer-Integrated Manufacturing, 2012, 28: 500-508. DOI:10.1016/j.rcim.2012.02.002 |
| [15] | 杨会, 房海蓉, 李典, 等. 一种新型并联灌注机器人运动学分析和多目标优化[J]. 北京航空航天大学学报, 2018, 44(3): 568-575. YANG H, FANG H R, LI D, et al. Kinematics analysis and multi-objective optimization of a novel parallel perfusion robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 568-575. (in Chinese) |
| [16] | XIE F, LIU X J, WANG J, et al. Kinematic optimization of a five degrees-of-freedom spatial parallel mechanism with large orien-tational workspace[J]. Journal of Mechanisms and Robotics, 2017, 9(5): 051005. DOI:10.1115/1.4037254 |
| [17] | LIU C H, LI R M, YAO Y A. An omnidirectional rolling 8U parallel mechanism[J]. Journal of Mechanisms and Robotics, 2012, 4(3): 034501. DOI:10.1115/1.4006657 |
| [18] | KONG X, GOSSELIN C M. Type synthesis of parallel mechanisms[M]. Berlin: Springer, 2007. |
| [19] | JOSHI S A, TSAI L W. Jacobian analysis of limited-DOF parallel manipulators[J]. Journal of Mechanical Design, 2002, 124(2): 254-258. DOI:10.1115/1.1469549 |
| [20] | TSAI L W. Robot analysis and design:The mechanics of serial and parallel manipulators[M]. New York: John Wiley & Sons, 1999. |
| [21] | 赵永生, 郑魁敬, 李秦川, 等. 5-UPS/PRPU 5自由度并联机床运动学分析[J]. 机械工程学报, 2004, 40(2): 12-16. ZHAO Y S, ZHENG K J, LI Q C, et al. Kinematic analysis of 5-UPS/PRPU 5-DOF parallel machine tool[J]. Journal of Mechanical Engineering, 2004, 40(2): 12-16. (in Chinese) |
