鉴于此,本文以典型高推重比涡扇发动机高压转子的结构构型为例,探索了航空发动机转子结构布局优化设计的方法流程。首先,对各设计变量进行参数关联性研究,对各个待优化的构型参数对结构力学特性的敏感度进行统计分析;然后,在此基础上对结构的构型进行基于响应面的布局优化设计;最后,通过随机验证点充分验证优化结果的准确性。本文方法可以为结构改型提供指导方向,较大程度地摆脱转子结构的经验设计。
1 结构布局优化设计的定义及算例模型 结构布局设计是指基于某些数学优化算法使能够自动识别系统中构型参数的最优或次优布置的技术,由此充分展示结构构型所带来的力学特征的变化。简言之,即是通过建立转子构型和其力学特征之间的关联性,进而揭示结构构型和尺寸效应所引起的力学特性的变化,同时附加先进的优化算法,实现转子结构与力学特征一体化设计。结构布局设计可以为航空燃气轮机总体结构初始设计阶段进行结构构型和尺寸控制,提供设计指导的理论依据。本文以典型的高推重比涡扇发动机高压转子结构为例,论述布局优化设计的流程、布局设计方法的可靠性及布局设计的重要意义。
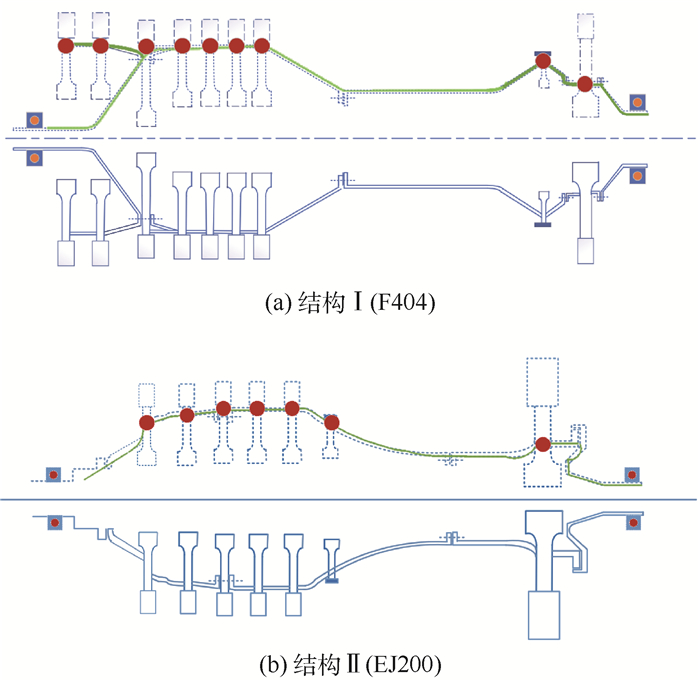
结构布局优化设计可以为结构改型提供指导。图 1为2种典型的高推重比涡扇发动机高压转子结构,二者均为1-0-1支承方案。结构Ⅰ为7级压气机和1级涡轮,前2级压气机为悬臂结构,靠近涡轮处存在一个封沿盘。结构Ⅱ为5级压气机和1级涡轮,无悬臂结构,封沿盘靠近压气机。通过这2种典型结构构型,可以衍生出其他类型高压转子结构。例如,同结构Ⅰ相比,F110高压转子总体上是将压气机增加2级,并在压气机后增加封沿盘;结构Ⅱ则是不存在悬臂的一类结构。以上这些转子结构的改型设计均可以在布局优化设计中得到完整的体现。当然,每家航空发动机集团公司在结构方案的选择上都有着较强的继承性,有着各自不同的设计风格。在布局优化设计时,应充分考虑传统工程经验和技术的积累,在此基础上进行布局的优化设计,这一点在布局设计中是需要充分考虑的。
 |
| 图 1 典型转子结构 Fig. 1 Typical rotor structure |
| 图选项 |
图 1中,实线勾勒出了转子大概的结构布局线路,盘和叶片等转子构件按照一定的规则分布其上,实心圆点代表构件的集中质量。值得注意的是,转子的结构布局优化设计是对整体构型进行优化设计,并不涉及具体构件的尺寸设计。例如,涡轮盘的构型属于强度设计问题,不在转子结构布局设计范畴。
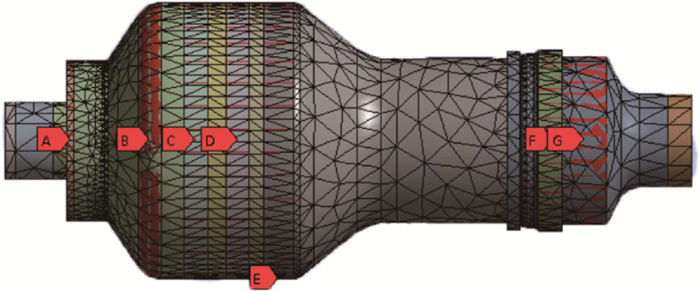
目前,转子的力学特性计算多为传递矩阵法及有限元法,考虑到传递矩阵法程序的通用性和可扩展性均较差,较难在工程中广泛使用,本文优化示例过程均采用有限元法进行计算,所建立的有限元模型如图 2所示。盘和叶片的等效分布质量和转动惯量已经加到相应的位置处(mass21单元),如图 2中的A、B、C、D、E、F、G所指。前、后支承位置在抗变形能力优化设计时为简支约束,在力学环境适应能力优化设计时采用弹性支承(combin214轴承单元),其支承刚度如表 1所示。其余构型全部采用三维实体solid189高阶单元,不计阻尼。
 |
| 图 2 有限元模型 Fig. 2 Finite element model |
| 图选项 |
表 1 支承刚度 Table 1 Supporting stiffness
| 107 N/m | |
| 支点 | 刚度 |
| 前支点 | 2.5 |
| 后支点 | 25 |
表选项
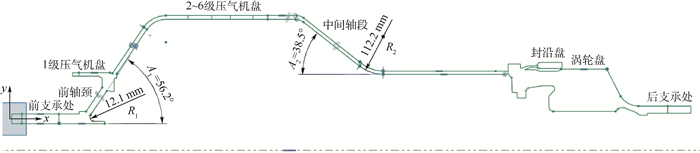
2 关键特征参数及其确定方法 关键特征参数的探索是布局设计的首要任务。所谓关键特征参数,是指对转子的力学性能(刚度特征和模态特征等)具有明显影响的构型参数。由于很难把握构型参数相互之间的约束规律,对全体构型参数进行优化设计是不现实的,同时,在后续试验设计(DOE)研究中,设计点的数量会随着输入参数的数量增加而迅速增加,严重降低DOE计算效率。因此,首先需要以一个较优的转子构型参数为基础(可直接由工程实际确定),对各个参数之间进行关联性研究,确定对转子力学性能有明显影响的关键特征参数。图 3为转子结构布局的构型尺寸工程图,由于结构的构型尺寸及约束条件参数繁多,图中仅标出了待优化的部分参数。其中,A1为前轴颈与水平线的倾角,R1为其倒角半径;A2为中间轴段与水平线的倾角,R2为其倒角半径,为方便叙述,各构型参数在本文里均用其代号表示,对应位置已标于图 3中。原始构型参数归纳如表 2所示。
 |
| 图 3 布局尺寸 Fig. 3 Layout size |
| 图选项 |
表 2 待优化的原始构型参数 Table 2 Original configuration parameters for subsequent optimization
| 参数 | 数值 |
| A1/(°) | 56.2 |
| A2/(°) | 38.5 |
| R1/mm | 12.1 |
| R2/mm | 112.2 |
表选项
统计学中的参数关联性研究有多种方法[9-10],已广泛应用于优化设计。本文通过拉丁超立方(Latin hypercube)法布置样本点,使用斯珀曼(Spearman)法进行数据之间的关联性分析。斯珀曼法是在基于蒙特卡罗关系下,检查2个变量之间的单调关系,比线性关系限制较少,具有较高的准确度。通过该方法从众多构型变量中选出较少的参数作为关键特征参数,这些参数也是后续待优化的设计变量。
得到关键特征参数的目的之一是进行DOE[11]。DOE是研究正确的设计试验计划,分析试验数据的理论和方法,通过改变过程的输入因素,观察其相应的输出响应变化,从而获取关于此过程的知识,确定各个输入因素的重要性以及各输入因素如何影响输出响应,并如何达到最优化的目的。DOE类型分为很多种,常见的如稀疏网格设计[12]、Box-Behnken试验设计[13]、田口静态试验设计[14]、拉丁超立方试验设计[15]等。DOE是获取响应面的前提条件,合适的DOE方法不仅可以提高计算效率,而且可以有效提高响应面的拟合精度。为了最大程度提高响应面拟合精度,本文采用稀疏网格响应面法。稀疏网格响应面是一种自适应响应面,可以对数据点进行自动细化,精度很高。当然,每一次细化都需要对构型参数改变的有限元模型进行重启动分析,这是以牺牲计算效率为代价的。
转子系统结构效率[16]内容主要包括承载能力、抗变形能力和力学环境适应能力三方面。承载能力属于强度优化设计,不属于布局优化设计范畴。布局优化设计主要是针对转子系统的抗变形能力和力学环境适应能力进行构型的寻优设计。由于本文目的仅为阐述转子结构布局优化设计的方法、方法可靠性和重要意义,不针对某型号的发动机转子,不针对具体的工程结构,另外考虑到优化过程中,为了便于寻找各构型参数对某个力学特征是否存在影响及影响的程度,因此本文将抗变形能力的寻优目标参数只定义了惯性载荷下的最小等效刚度,力学环境适应能力的寻优目标参数只定义了一阶弯曲共振时的转子转速,同时兼顾总质量的变化情况。本文给出了工程综合仿真示例。值得注意的是,寻优目标参数应该在结构效率的定义范围内,需要依据实际情况而变化。
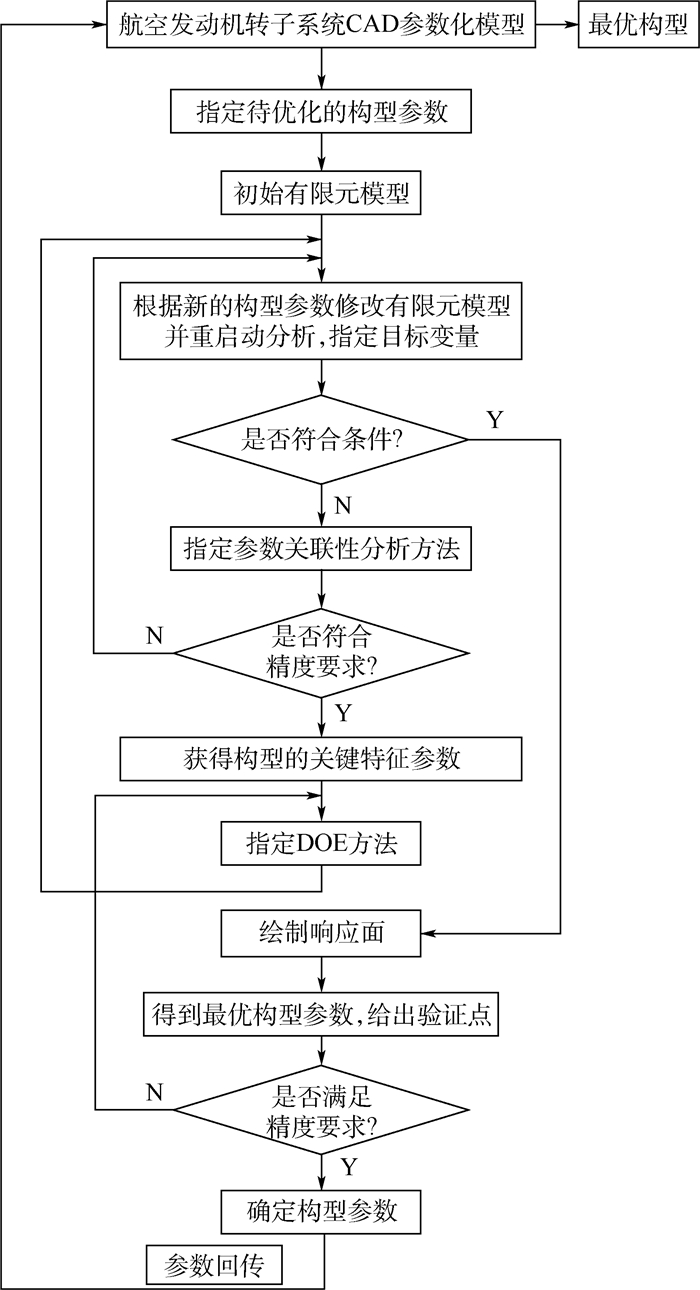
3 基于响应面法的结构布局优化设计方法流程 航空发动机转子系统结构布局优化设计方法流程如图 4所示。
 |
| 图 4 结构布局优化设计方法流程 Fig. 4 Flow of structure layout optimization design method |
| 图选项 |
步骤1 ??建立原始CAD参数化模型,并初步判断对结构力学特征有明显影响的构型参数作为待优化的设计变量,这是依据技术积累和工程经验得出的。建立模型时应注意图形元素之间的约束条件,避免构型参数改变时,转子结构模型的严重失真,否则将导致结构布局优化设计的失败。
步骤2 ??建立有限元模型,进行有限元求解,指定优化目标(如结构效率相关评估参数),将有限元求解器与CAD关联。这里主要是为了使构型参数改变时,利用CAD快速建模和利用有限元求解器快速求解,以期实现迭代计算。
步骤3 ??参数关联性分析,确定关键特征参数。从步骤1选取的待优化设计变量中,进一步确定哪些是对力学特征有显著影响的构型参数,作为关键特征参数,这是后续优化迭代中的设计变量。
步骤4 ??进行DOE,绘制响应面。确定响应面的拟合优度,确保数据的准确性。
步骤5??基于某些数学优化算法,找到最优或次优的构型参数。
步骤6??与原构型对比,验证优化结果。
4 基于结构效率的结构布局优化设计 为了充分证明航空发动机转子系统结构布局优化设计方法的可行性,本节以典型高推重比涡扇发动机高压转子构型(见图 3)为例,分别从抗变形能力和力学环境适应能力两方面对转子结构进行结构布局优化设计。构型参数波动的上下限均为在原始构型的基础上±10%。
4.1 抗变形能力 根据航空发动机转子系统的结构特征,在设计中对转子系统抗变形能力的要求有:①具有良好的横向弯曲刚度;②盘轴连接处具有良好的角向刚度。在转子系统刚度设计中,常采用的大比刚度材料有利于提高结构的抗变形能力,但是材料的选取通常根据强度设计准则来确定,对于给定的材料,通过转子轴截面结构形状和面积的优化,可以进一步提高转子系统的刚度,从而达到提高其抗变形能力的目的。虽然连接结构处存在的刚度损伤,对转子结构的力学特征存在较大影响,但是由于其力学特征计算的复杂性,在结构构型设计初期的布局优化中一般不予考虑。
为此,对转子结构横向施加1个重力加速度,此时转子将发生弯曲变形,计算整体转子结构横向变形的最大值(TD_Max)和转子结构的质量(TM),通过寻找合适构型的设计参数,使得最大变形量和总质量最小。
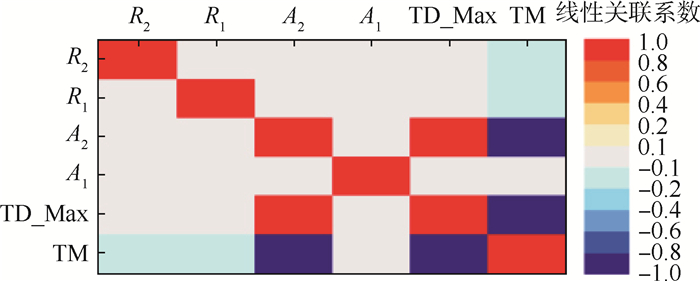
基于斯珀曼[17]法的参数关联性分析(进行了100组构型参数计算)可以得到如表 3所示的各参数间的相关性矩阵,绘制出相应的参数关联性云图,如图 5所示,其中颜色的深浅表示关联度的强弱。
表 3 抗变形能力优化相关性矩阵 Table 3 Correlation matrix of anti-deforming ability optimization
| 参数 | R2 | R1 | A2 | A1 | TD_Max | TM |
| R2 | 1 | 0.006 8 | -0.01 | 0.041 418 | -0.017 436 | -0.155 |
| R1 | -0.006 80 | 1 | 0.007 8 | 0.095 346 | 0.010 111 | -0.144 |
| A2 | -0.014 19 | 0.007 8 | 1 | -0.010 88 | 0.998 7 | -0.954 |
| A1 | 0.041 418 | 0.095 3 | -0.01 | 1 | -0.001 296 3 | 0.094 6 |
| TD_Max | -0.017 43 | 0.010 1 | 0.998 | -0.001 29 | 1 | -0.953 |
| TM | -0.155 04 | -0.145 | -0.95 | 0.094 633 | -0.953 4 | 1 |
表选项
 |
| 图 5 抗变形能力优化参数关联性云图 Fig. 5 Contour of parameter correlation about anti-deforming ability optimization |
| 图选项 |
从图 5中可以较为清晰地看出各参数之间的关联性强弱,严重影响最大变形量(即转子结构的抗变形能力)的参数为高压转子构型参数A2,对最大变形量的线性关联系数为0.998 7,对总质量线性关联系数为-0.954,均接近1,明显高于其他值。其次,构型参数R1和R2的变化对总体质量稍有影响。综上,可以初步断定,对转子系统抗变形能力具有显著影响的关键特征参数为A2。
为了减少设计变量个数,略去一些对力学特征影响不敏感的参数,同时兼顾对实际转子力学特征的影响。因为2个倒角半径(R1和R2)只对结构质量有少许影响,且影响程度大体相当,因此将这2个构型参数一起去掉。接下来只研究2个锥角(A1和A2)的变化对转子系统的抗变形能力和总质量的影响程度。
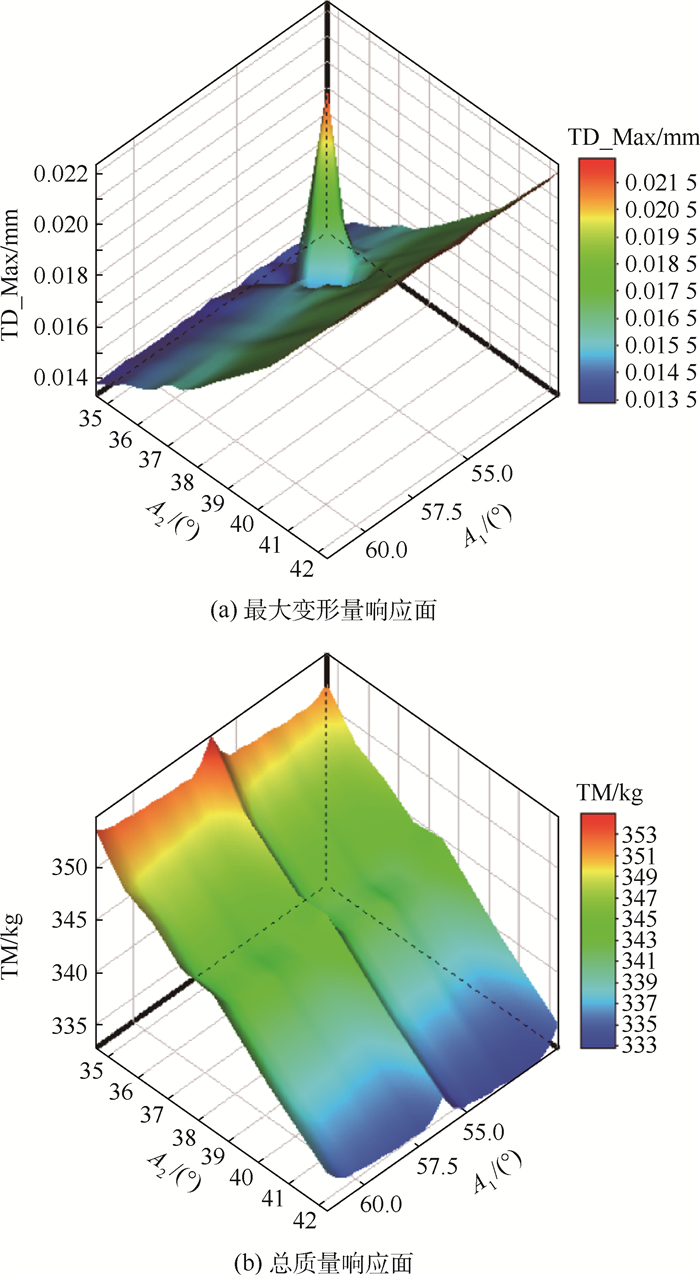
通过有限元迭代计算,可以得到总质量和最大变形量相对于2个锥角(A1和A2)的稀疏网格响应面,如图 6所示。
 |
| 图 6 抗变形能力优化响应面 Fig. 6 Response surface of anti-deforming ability optimization |
| 图选项 |
从响应面可以直观地找出使最大变形量和总质量最小时所对应的构型参数。图 6(a)所示的最大变形量相对于2个锥角的响应面有着很高的“尖点”,存在迅速上升或下降的最大值点,一定程度上可以反映出,假如构型参数选取的不合理,可能会对转子系统的力学特性产生严重影响。为了验证响应面的准确性,给出了5个验证点,如表 4所示。
表 4 抗变形能力响应面误差验证 Table 4 Error verification of response surface of anti-deforming ability
| 编号 | 优化变量 | 验证点(有限元计算) | 响应点(响应面计算) | 相对误差/% | |||||||
| A1/(°) | A2/(°) | TD_Max/mm | TM/kg | TD_Max/mm | TM/kg | TD_Max | TM | ||||
| 1 | 61.162 | 40.402 | 0.019 226 | 340.94 | 0.019 409 | 347.24 | 0.95 | 1.8 | |||
| 2 | 58.68 | 40.591 | 0.019 436 | 336.93 | 0.019 601 | 341.92 | 0.85 | 1.5 | |||
| 3 | 52.027 | 39.633 | 0.018 195 | 343.12 | 0.018 297 | 351.98 | 0.56 | 2.6 | |||
| 4 | 52.043 | 41.095 | 0.020 178 | 335.41 | 0.020 183 | 340.56 | 0.02 | 1.5 | |||
| 5 | 57.758 | 39.611 | 0.018 13 | 350.49 | 0.018 293 | 355.54 | 0.90 | 1.4 | |||
表选项
从随机选取的5个验证点所统计出的相对误差来看,该响应面拟合度很高,几乎零误差,可以为下一步优化提供数据支持。响应面拟合程度的优劣直接影响后续优化结构,影响结构的可靠性,若误差统计数据存在较大的值,则应以更多的数据点对响应面进行细化,直到误差在允许的范围内为止。
通过响应面的优化是基于某些先进算法实现,如多目标遗传算法[18]、自适应多目标[19]等,相比于有限元计算耗时很少。遗传算法是一种通过模拟自然进化过程搜索最优解的方法, 在优化方法中具有独特的优越性,通过前面得到的响应面,基于多目标遗传算法最终得到3组候选设计点,如表 5所示,表中“☆”表示优化后总质量最小的一组参数。
表 5 抗变形能力优化设计结果 Table 5 Design results of anti-deforming ability optimization
| 编号 | 优化变量 | 验证点(有限元计算) | 响应点(响应面计算) | 相对误差/% | |||||||
| A1/(°) | A2/(°) | TD_Max/mm | TM/kg | TD_Max/mm | TM/kg | TD_Max | TM | ||||
| 1 | 51.278 | 38.531 | 0.016 908 | 345.57 | 0.016 859 | 346.91☆ | 0.29 | 0.4 | |||
| 2 | 57.409 | 37.955 | 0.016 546 | 361.77 | 0.016 267 | 350.65 | 1.69 | 3.1 | |||
| 3 | 50.646 | 37.806 | 0.016 264 | 360.55 | 0.016 174☆ | 351.24 | 0.55 | 2.6 | |||
表选项
从表 5可以看到,若以最大变形量最小为优化目标,应选择第3组构型参数,即A1=50.646°,A2=37.806°,此时具有较强的抵抗惯性载荷的能力。若以总质量最小为优化目标,应选择第1组构型参数,即A1=51.278°,A2=38.531°。若折中选取,则应选择第2组构型参数。从表 5中的数据也可以发现,虽然前后锥角仅有1°左右的变化,却可以引起最大变形量和总质量的显著改变,特别是质量的变化,大约4 kg。
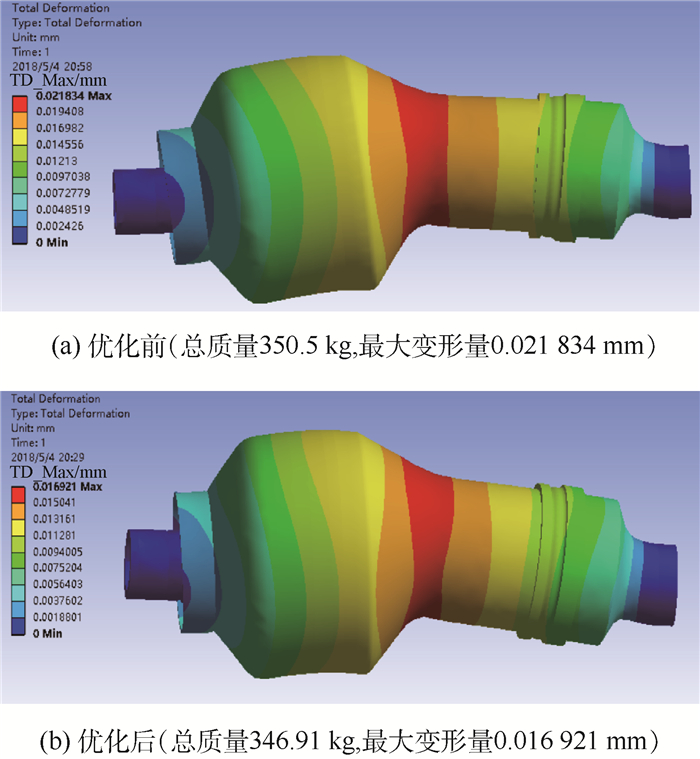
考虑第1组误差较小,若选取第1组设计点,与原始构型对比,质量减少3.59 kg,在惯性载荷作用下,最大变形量减少0.004 913 mm,如图 7所示。值得注意的是,本算例计算的是在1个重力加速度下的变形量,若在更大的惯性载荷作用下,优化效果会更加明显。
 |
| 图 7 抗变形能力优化前后对比 Fig. 7 Comparison of results before and after anti-deforming ability optimization |
| 图选项 |
由此可得,经过结构布局优化设计后的转子结构,在惯性力下的最小等效刚度为
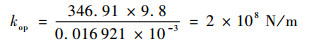 |
优化前的等效刚度为
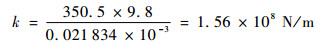 |
优化前后相比提高了4.4×107 N/m,整体提升了近28%的惯性刚度,可见转子结构布局优化设计的显著效果。
4.2 力学环境适应能力 转子系统的工作转速相对于共振频率之间的稳定裕度一直是结构设计需要考虑的重要问题,在航空发动机转子结构设计初期,常因为结构布局设计的不合理而达不到裕度要求(一般为20%)。例如,高压转子在工作转速范围内往往存在2个共振转速,较低的共振转速是由静不平衡引起的,较高的共振转速是由力偶不平衡引起的。工作转速距离较近的一阶弯曲振型和俯仰振型均应有一定的裕度,这就需要将一阶弯曲共振频率最大化设计。工程上一般通过调节支承处刚度来调节共振转速,但若是构型设计严重不合理,单凭调节支承刚度是达不到要求的。
仍以图 3所示的高压转子结构构型为例,以一阶弯曲共振频率最大、振幅最小且结构总质量最小为优化目标,通过对4个构型参数(见表 2)的选取使结构趋于“合理化设计”。结构布局优化流程同第3节,基于斯珀曼法可以得到参数关联性矩阵(见表 6)及对应的云图(见图 8),观察可知,关键特征参数依旧是A1和A2。
表 6 力学环境适应能力优化相关性矩阵 Table 6 Correlation matrix of mechanical environment adaptability optimization
| 参数 | R2 | R1 | A2 | A1 | TD_Max | TM | C_S |
| R2 | 1 | 0.024 | -0.050 | 0.000 6 | -0.372 73 | -0.17 | 0.050 649 |
| R1 | 0.024 | 1 | 0.003 8 | -0.012 | -0.128 57 | 0.175 | -0.129 87 |
| A2 | -0.05 | 0.003 | 1 | -0.007 | -0.589 61 | -0.94 | -0.961 04 |
| A1 | 0.006 | -0.01 | -0.007 | 1 | -0.463 64 | 0.042 | -0.171 43 |
| TD_Max | -0.37 | -0.12 | -0.589 | -0.463 | 1 | 0.679 | 0.703 9 |
| TM | -0.17 | 0.175 | -0.949 | 0.042 8 | 0.679 22 | 1 | 0.927 27 |
| C_S | 0.051 | -0.13 | -0.961 | -0.171 | 0.703 9 | 0.927 | 1 |
| ??注:C_S—临界转速。 | |||||||
表选项
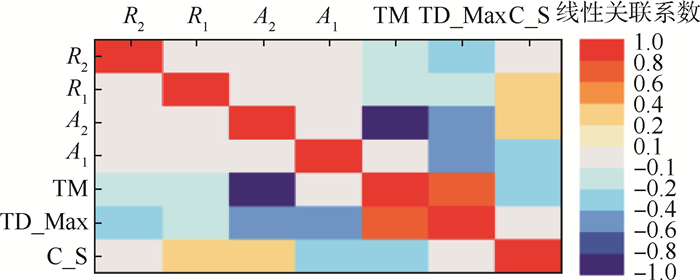 |
| 图 8 力学环境适应能力优化参数关联性云图 Fig. 8 Contour of parameter correlation about mechanical environment adaptability optimization |
| 图选项 |
通过有限元迭代计算,可以得到结构总质量、一阶弯曲临界转速和一阶弯曲共振最大变形量相对于2个锥角(A1和A2)的稀疏网格响应面,如图 9所示。
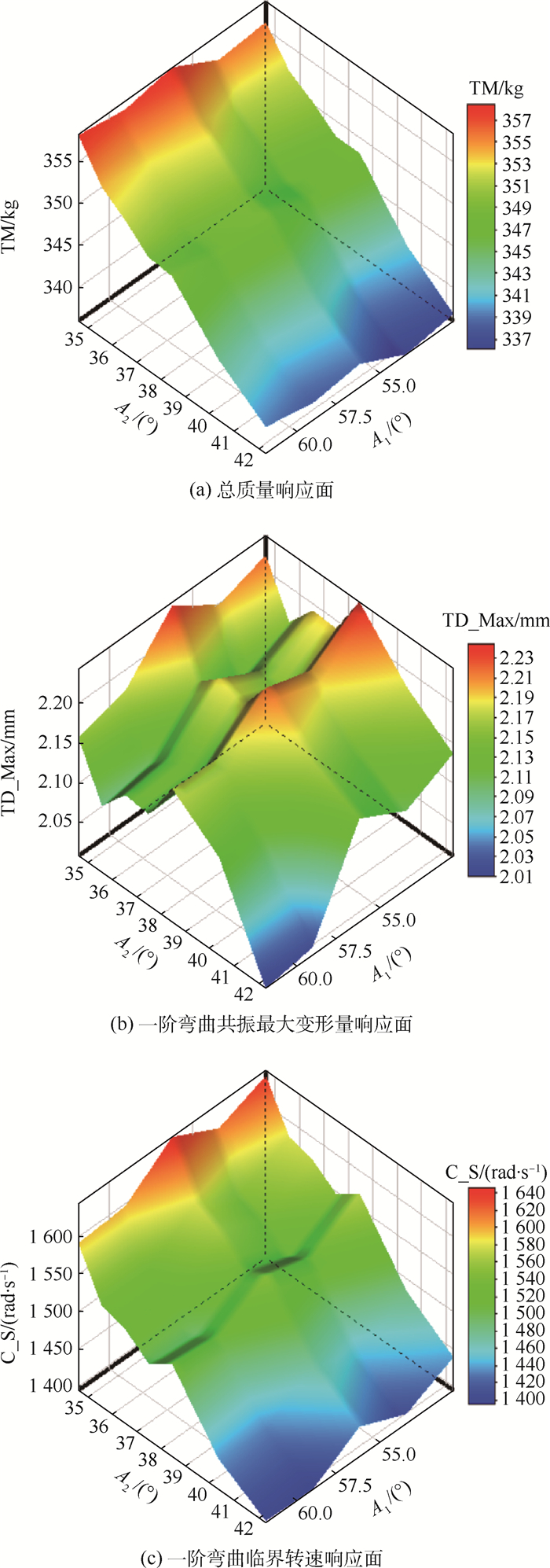 |
| 图 9 力学环境适应能力优化响应面 Fig. 9 Response surface of mechanical environment adaptability optimization |
| 图选项 |
响应面误差验证如表 7所示。可以看出,响应面误差较小,拟合精度较高,可以为后续优化提供数据支持。基于多目标遗传算法,最终得到了3组候选设计点,如表 8所示。
表 7 力学环境适应能力响应面误差验证 Table 7 Error verification of response surface of mechanical environment adaptability
| 编号 | 优化变量 | 验证点(有限元计算) | 响应点(响应面计算) | 相对误差/% | ||||||||||
| A1/(°) | A2/(°) | TD_Max/mm | TM/kg | C_S/(r·min-1) | TD_Max/mm | TM/kg | C_S/(r·min-1) | TD_Max | TM | C_S | ||||
| 1 | 52.929 | 36.22 | 2.144 6 | 353.95 | 14 543 | 2.154 8 | 350.05 | 14 769 | 0.48 | 1.10 | 1.55 | |||
| 2 | 52.953 | 40.724 | 2.175 4 | 342.91 | 13 536 | 2.142 2 | 339.45 | 13 812 | 1.53 | 1.01 | 2.04 | |||
| 3 | 59.483 | 36.251 | 2.103 8 | 354.49 | 14 146 | 2.123 4 | 351.71 | 14 555 | 0.93 | 0.78 | 2.89 | |||
| 4 | 59.015 | 40.384 | 2.185 5 | 344.37 | 13 391 | 2.110 5 | 341.85 | 13 672 | 3.43 | 0.73 | 2.10 | |||
| 5 | 50.621 | 40.172 | 2.113 | 343.94 | 14 662 | 2.186 | 341.87 | 14 255 | 3.45 | 0.60 | 2.78 | |||
表选项
表 8 力学环境适应能力优化设计结果 Table 8 Design results of mechanical environment adaptability optimization
| 编号 | 优化变量 | 验证点(有限元计算) | 响应点(响应面计算) | 相对误差/% | ||||||||||
| A1/(°) | A2/(°) | TD_Max/mm | TM/kg | C_S/(r·min-1) | TD_Max/mm | TM/kg | C_S/(r·min-1) | TD_Max | TM | C_S | ||||
| 1 | 60.774 | 42.296 | 2.135 7 | 340.04 | 13 620 | 2.013 2 | 338.79 | 13 342 | 5.7 | 0.37 | 2.04 | |||
| 2 | 59.369 | 42.266 | 2.124 1 | 339.97 | 13 662 | 2.019 8☆ | 338.29☆ | 13 335 | 4.91 | 0.49 | 2.39 | |||
| 3 | 56.195 | 41.615 | 2.159 7 | 341.37 | 14 307 | 2.080 6 | 343 | 14 569☆ | 3.66 | 0.48 | 1.83 | |||
表选项
从表 8可以看到,优化结果误差较小,第2组设计点的总质量和转子在一阶弯曲共振时的最大变形量较小,第3组的一阶弯曲临界转速最大,可以考虑选择这2组设计点。若选择第3组为设计点,优化前后临界转速如图 10所示。
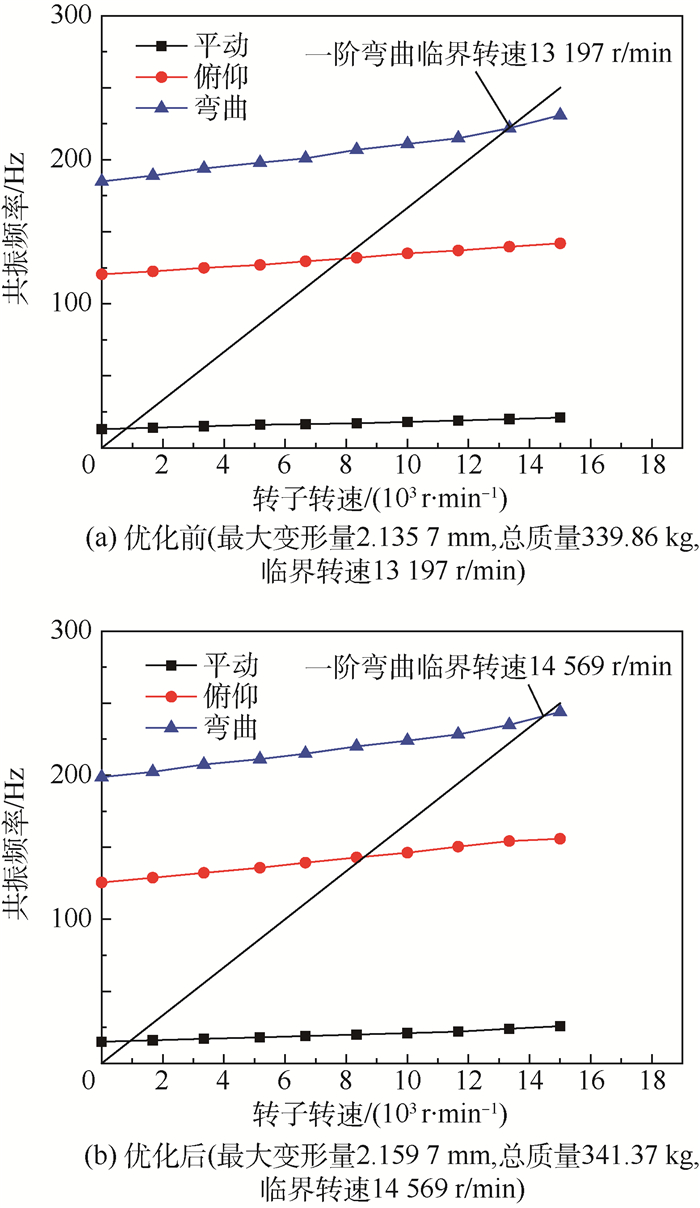 |
| 图 10 力学环境适应能力优化前后对比 Fig. 10 Comparison of results before and after mechanical environment adaptability optimization |
| 图选项 |
可以看出,相比于优化前,一阶弯曲临界转速增加1 372 r/min,但是这是以质量和一阶弯曲共振幅值的增加为代价的,其中质量增加1.51 kg, 一阶弯曲共振最大变形量增加0.024 mm。在实际工程中,可以根据要求进行取舍。
需要说明的是,工程中转子结构动力学优化设计包含着更多的内容。例如,在航空发动机转子结构设计中,转子结构的平衡配重是在有限个转速下进行的,因此在飞行包线内仍存在一定的不平衡响应,这时为了保证转子具有足够的抗变形能力,需要结构对不平衡量的敏感性降到最低,即结构对不平衡量的低敏感性设计。例如,低压转子的动挠度曲线形状和弯曲程度随转速而变化,当转速接近某阶临界转速时,该阶阵型分量最大。如果轴承支点位置布置不合理,距离振型节点较远,将会大大增加轴承的支反力,转子系统可靠性急剧降低,这就需要通过调整局部构型以期改变振动振型,从而达到降低轴承支反力的目的。本文所涉及的构型优化仅是为了阐述布局优化设计的实现方法、可行性和重要意义,并不针对具体型号的发动机转子及其出现的具体问题做分析,所以计算结果可能与实际发动机转子存在偏差。同时,为了节省篇幅和简化计算,略去了工程上其他诸多方面的布局优化仿真。
5 工程结构综合优化示例 以两支点高速转子结构系统为背景,为了建立具有通用性的优化流程,掌握结构几何构形和尺寸变化对转子力学特性的影响规律,本节以转子结构的结构效率为目标,对其进行多目标综合优化设计,使本文提出的结构布局设计方法更具工程应用价值。
对高压转子初始施加国军标所要求的横向过载载荷和机动飞行的角加速度,高压转子工作转速为12 000 r/min,通过有限元法综合考虑结构的抗变形能力和力学环境适应能力,优化的目标是控制转子系统结构总质量的前提下,使转子结构效率损失降到最低。定义结构布局优化的数学表达式如下:
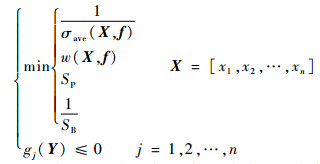 | (1) |
式(1)即为目标函数。式中:X为关键设计参数组成的参数向量;f为环境载荷;w(X,f)为径向挠曲变形;SP为转子俯仰振型对应的临界转速;SB为一阶弯曲对应的临界转速;Y为结构力学特征参数;σave(X, f)为外加环境载荷下结构的平均应力系数,表达式如下:
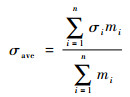 | (2) |
其中:σi为第i个结构单元的应力;mi为第i个单元的质量。平均应力系数反映了材料的使用效率。
式(1)是一个多参数、多目标的优化问题,也可以在结构效率的意义下,将其合并成一个参数,定义为结构效率损失系数:
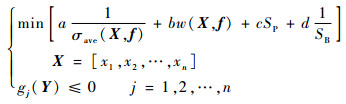 | (3) |
式中:a、b、c、d为加权系数,可根据工程实际进行适当选取。可把结构效率损失系数作为结构合理性的度量。以此为目标函数,首先基于斯珀曼法的参数关联性分析得到如表 9所示的参数关联性矩阵。可以看出,对结构效率损失系数影响较大的2个构形参数为A1和A2,故选定A1和A2作为关键特征参数。
表 9 参数关联性矩阵 Table 9 Parameter correlation matrix
| 参数 | A1 | A2 | R1 | R2 | TD_Max |
| A1 | 1 | 0.275 | -0.028 6 | -0.125 | 0.214 286 |
| A2 | 0.275 | 1 | -0.032 1 | -0.003 5 | 0.785 71 |
| R1 | -0.028 571 | -0.032 143 | 1 | -0.171 4 | 0.203 57 |
| R2 | -0.125 | -0.003 571 | -0.171 4 | 1 | -0.046 42 |
| TD_Max | -0.214 286 | 0.785 71 | 0.203 57 | -0.046 4 | 1 |
表选项
基于有限元法,采用稀疏网格响应面对试验点数据拟合,得到如图 11所示的响应面,图中S_E为结构效率损失系数。基于多目标遗传算法,通过响应面可以较为容易地找到极小值点(A1, A2)=(49.6°, 37.5°),该点即是优化后的最优构形点。优化前后的总变形如图 12所示。
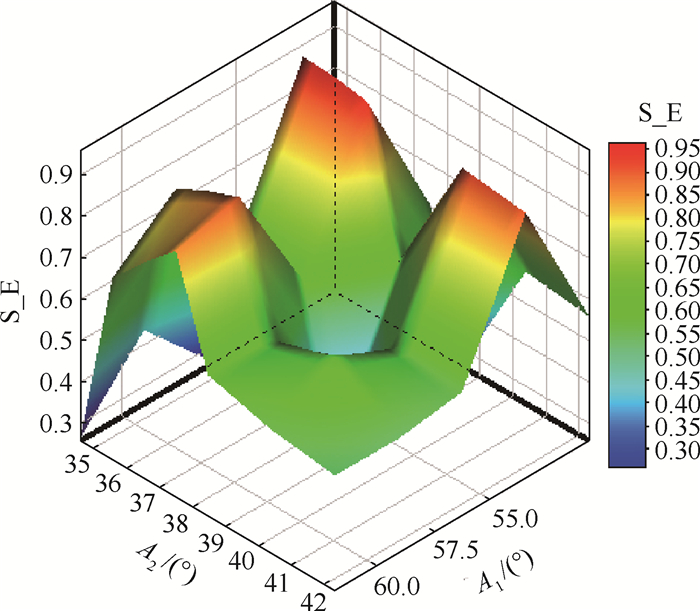 |
| 图 11 拟合响应面 Fig. 11 Fitting response surface |
| 图选项 |
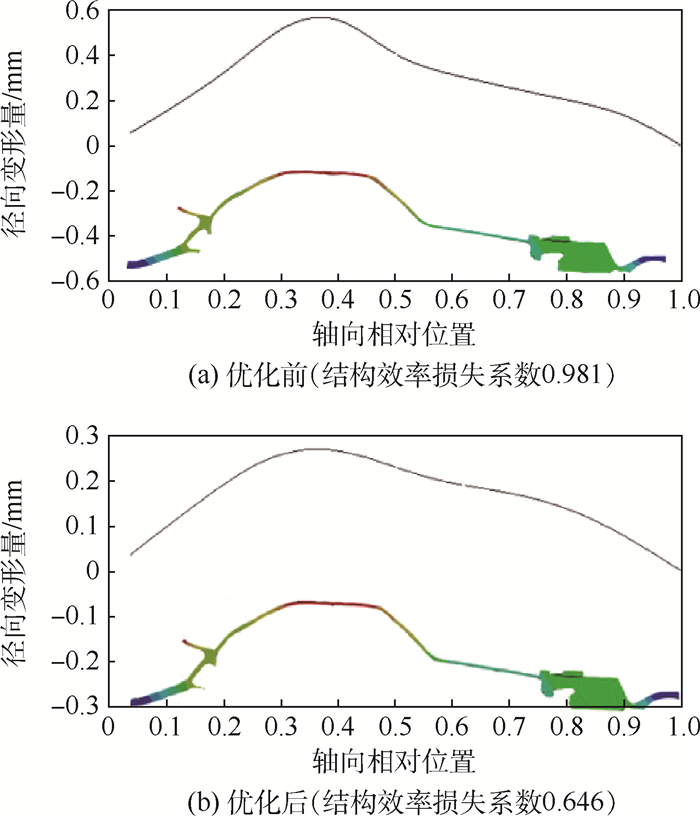 |
| 图 12 优化前后结构总体变形 Fig. 12 Overall structure deformation before and after optimization |
| 图选项 |
按照式(3)定义的结构效率损失系数为目标函数,优化后的结构效率损失系数(0.646)同优化前(0.981)相比,下降0.335,使结构总质量基本不变的条件下,转子刚度特性大幅提高。从参数关联性矩阵也可以看出,中间轴段倾角(A2)对转子刚度特性产生较大影响,合理的倾角选取可以有效提升结构的抗变形能力。从总体变形云图(见图 12)上也可以看出,不仅结构效率损失系数有所下降,而且整体变形的分布形式并没有较大变化,这对结构整体性能提升是有意义的。
6 结论 本文提出的航空发动机转子结构布局设计方法是为适应新一代先进航空发动机转子结构研制顺势而出,是摆脱过多依靠传统设计经验,实现其先进性的有效途径,该方法不仅适合涡扇发动机,对涡轴、涡桨等同样适用。同时,转子结构布局设计方法补充了原转子结构效率的内容,在对转子结构力学特征定量评估的基础上,提供了最优或次优的结构布局易行方法。
1) 航空发动机转子构型的合理设计,特别是中间轴段的合理设计,可以有效提升转子的抗变形能力和力学环境适应能力。算例结果表明,通过对结构构型的布局优化设计,与原始结构相比,抗变形能力优化设计使高压转子整体提升了近28%的惯性刚度,力学环境适应能力优化设计使转子系统的一阶弯曲临界转速提高1 372 r/min,同时给出了多目标综合优化设计方法,最大程度降低了结构效率损失系数。通过对转子结构布局优化设计,完全可以达到将不合理的结构构型最大程度合理化的效果,这对航空发动机转子系统结构改进设计,乃至整机结构布局优化设计具有着重要的借鉴意义。
2) 在航空发动机转子结构布局优化设计时,除了要考虑优化目标达到技术要求外,同时需要兼顾其他力学特征是否发生严重改变,是否依然符合技术要求。例如,本文在力学环境适应能力优化时,虽然一阶弯曲临界转速实现了1 372 r/min的增加,但是结构总质量也和一阶弯曲时的最大变形量均有少许增加。
本文仅以航空发动机高压转子构型为例,探索其结构关键特征参数,并对转子结构抗变形能力和力学环境适应能力进行了布局优化设计。实际工程中,可能需要考虑更多的实际环境因素,如在高温、高压、流固耦合等复杂环境下对航空发动机双转子系统和整机的结构布局优化设计,这仍有待进一步的研究。
参考文献
| [1] | 郑华强, 彭刚, 马艳红, 等. 航空发动机结构力学性能定量分析方法[J]. 推进技术, 2018, 39(3): 645-652. ZHENG H Q, PENG G, MA Y H, et al. Quantitative analysis method for mechanical characteristics of structure system in aero-engine[J]. Journal of Propulsion Technology, 2018, 39(3): 645-652. (in Chinese) |
| [2] | ARNE S, JULIAN B, SASCHA K, et al. Conceptual investigation of a propulsive fuselage aircraft layout[J]. Aircraft Engineering and Aerospace Technology, 2014, 86(6): 464-472. DOI:10.1108/AEAT-06-2014-0079 |
| [3] | LUO Q, WEN Z H. Application of garden design style in Tang dynasty to the design of modern city public gardens:A case study of Tang paradise[J]. Journal of Landscape Research, 2018, 10(2): 11-14. |
| [4] | LIU S, QIAO H. Topology optimization of continuum structures with different tensile and compressive properties in bridge layout design[J]. Structure and Multidisciplinary Optimization, 2011, 43(3): 369-380. |
| [5] | GUTTA P R, CHITHALA V S, MANCHOJU R V, et al. A review on facility layout design of an automated guided vehicle in flexible manufacturing system[J]. Materialstoday:Proceedings, 2018, 05(2): 3981-3986. |
| [6] | WANG Y K, LIAO M F, ZHANG J H. Dynamic load reduction design for inter-shaft bearing of aircraft engine[J]. Journal of Aerospace Power, 2017, 32(2): 492-499. |
| [7] | FU C, REN X M, YANG Y F, et al. An interval precise integration method for transient unbalance response analysis of rotor system with uncertainty[J]. Mechanical System and Signal Processing, 2018, 107: 137-148. DOI:10.1016/j.ymssp.2018.01.031 |
| [8] | WHANG C, CHOY K L, BACK J. Development and experimental vertification of counter-rotating dual rotor/dual generator wind turbine:Generating, yawing and furling[J]. Renewable Energy, 2017, 114(B): 644-654. |
| [9] | 刘子君. 统计学[M]. 北京: 清华大学出版社, 2017: 148-156. LIU Z J. Statics[M]. Beijing: Tsinghua University Press, 2017: 148-156. (in Chinese) |
| [10] | 鹏翔.复杂产品设计中参数关联和等效简化方法激起应用[D].杭州: 浙江大学, 2014: 92-145. PENG X.Method and its application of parameter correlation and equivalent simplification in complex product design[D].Hangzhou: Zhejiang Uiversity, 2014: 92-145(in Chinese). |
| [11] | 闵亚能. 试验设计(DOE)应用指南[M]. 北京: 机械工业出版社, 2011: 5-17. MIN Y N. Application guide of DOE[M]. Beijing: China Machine Press, 2011: 5-17. (in Chinese) |
| [12] | XIONG F F, XIONG Y, GREENE S, et al.A new sparse grid based method for uncertainty propagation[C]//International Design Engineering Conference & Computers and Information in Engineering Conference.New York: ASME, 2009: 1-11. |
| [13] | FERREIRA S L C, BRUNS R E, MATOS G D, et al. Box-Behnken design:An alternative for the optimization of analytical methods[J]. Analytica Chimica Acta, 2007, 597(2): 179-186. DOI:10.1016/j.aca.2007.07.011 |
| [14] | 文放怀. 田口方法[M]. 广州: 广东经济出版社, 2006: 43-101. WEN F H. Taguchi method[M]. Guangzhou: Guangdong Economic Press, 2006: 43-101. (in Chinese) |
| [15] | HELTON J C, DAVIS F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability Engineering & System Safety, 2003, 81(1): 23-69. |
| [16] | 马艳红, 陈璐璐, 张大义, 等. 航空发动机转子系统结构效率评估参数及计算方法[J]. 航空动力学报, 2013, 28(7): 1598-1606. MA Y H, CHEN L L, ZHANG D Y, et al. Assessment parameters and calculation methods of structural efficiency on rotor system in aero engine[J]. Journal of Aerospace Power, 2013, 28(7): 1598-1606. (in Chinese) |
| [17] | OSCAR L, OLVERA A, BRUNO D. Population models and simulation methods:The case of the spearman rank correlation[J]. Mzthematical and Statistical Psychology, 2017, 70(6): 347-367. |
| [18] | 玄光男. 遗传算法与工程优化[M]. 北京: 清华大学出版社, 2004: 76-88. XUAN G N. Genetic algorithm and engineering optimization[M]. Beijing: Tsinghua University Press, 2004: 76-88. (in Chinese) |
| [19] | 左益.基于全局优化和局部学习的进化多目标优化算法[D].西安: 西安电子科技大学, 2016: 29-47. ZUO Y.Evolutionary multi-objective algorithms based on global optimization and local learning[D].Xi'an: Xidian University, 2016: 29-47(in Chinese). |
