高速柔性转子一般工作在多阶临界转速之上，且工作转速范围内存在以转子弯曲振型为主的临界转速，为控制其转子变形而常采用多支点支承方案。高速柔性转子在起动工作过程中需要通过多阶临界转速，会产生较大弯曲变形，对各支点动载荷及整机振动水平有很大影响。在工作循环中，支承结构和转子连接结构承载界面的损伤不断积累，易产生轴承组件界面磨损和转子连接界面接触损伤等问题。
高速柔性转子的质量、刚度分布极不均匀，通过若干界面配合、连接而成，转子产生弯曲变形时，连接结构处的应变能会导致转子弯曲刚度存在一定的分散性^[1]，同时考虑到支承结构的装配误差和工作载荷波动，支承刚度同样具有一定的分散度，导致临界转速分布、转子振幅等呈现区间分布特征。在转子弯曲变形不大，不考虑连接结构刚度损失时，可基于转子连续力学模型，通过确定性方法进行临界转速设计^[2]，以实现避开有害振动的设计目的。随着转子转速负荷的加大，在工作载荷环境下转子应变能比例的增加，使得必须考虑转子连接界面所产生的结构非连续性的影响，即在工作载荷环境下转子系统动力特性具有低敏感度的稳健设计方法。
近年来，国内外****关于转子动力特性设计方法的研究主要有两方面：设计目标函数的合理选取及非确定设计方法的研究。在设计目标函数的合理选取方面，Shiau和Chang^[3]以转子质量和支点动载荷为目标函数，分别采用多种优化算法对支承刚度、轴承位置等变量进行优化，验证了同时降低质量和减小支点动载荷的可行性；Lin等^[4]以转子总应变能为目标函数，对支承刚度和挤压油膜阻尼器的油膜间隙进行优化，通过转子总应变能分布反映转子变形及运动状态。在非确定设计方法研究方面，Zang等^[5]提出稳健设计方法的本质是多目标非确定优化设计，核心是降低目标函数的敏感度和分散度；Li等^[6]在考虑转速、滑油温度等工作状态具有非确定性的前提下，验证了凸方法在提高转子平衡精度稳健性方面的可行性；Ma等^[7]和陈萌^[8]将区间数学引入转子振动方程的各矩阵中，采用摄动理论建立了用于转子系统动力特性分析的区间摄动法，并通过试验验证了该方法在转子分析中的有效性；Ritto等^[9]在考虑支承刚度等参数具有非确定性的基础上，假设了多种概率分布，采用概率性优化方法对临界转速共振裕度进行了稳健设计，验证了此稳健设计方法的有效性。
综上，国内外****在转子动力特性设计方法方面开展的研究工作，大多基于连续模型假设，未考虑转子应变能分布对转子连接结构弯曲刚度的影响，而这正是柔性转子系统动力特性稳健设计中必须考虑的问题。本文根据带有连接结构非连续柔性转子结构的特征，考虑支承刚度和转子弯曲刚度等参数分散性，引入区间变量对转子系统动力特性进行非确定性设计方法研究。以全转速区域转子振幅和支点动载荷为控制优化目标，采用罚函数定量描述临界转速分布特征，进行基于临界转速分布优化和振动响应低分散性的高速柔性转子稳健设计方法研究。
1 柔性转子系统动力学模型 图 1为典型高速柔性转子的动力学模型，其主要结构特征为质量、刚度沿轴向分布极不均匀，采用多支点支承，通过界面连接而成。在工作转速范围附近存在多阶临界转速，其动力特性主要由支承特性、转子质量/刚度分布以及连接结构刚度特性等因素决定。需要注意的是，转子连接结构处的弯曲变形会导致转子弯曲刚度产生变化，其数值取决于转子工作状态，这使转子刚度特性表现出非确定性。

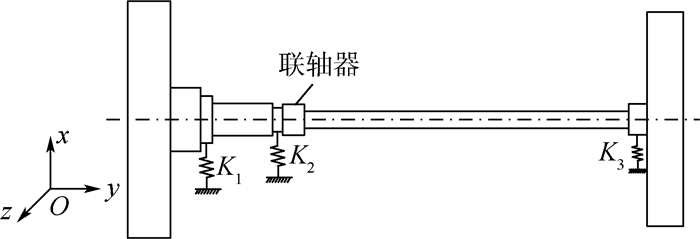图 1 典型高速柔性转子系统非确定动力学模型 Fig. 1 Uncertain dynamic model of typical high-speed flexible rotor system

图选项

1.1 运动方程 为准确反映柔性转子的动力特性，可通过有限元素法对转子动力学模型进行离散^[10-11]，各节点的位移和转角构成了系统的广义坐标q。

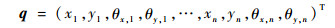(1)

式中：x_n和y_n分别为第n个截面的x和y方向位移；θ_{x, n}和θ_{y, n}分别为第n个截面绕x轴和y轴的角向位移。
利用Lagrange能量法建立其动力学方程为

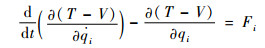(2)

式中：T为转子系统动能；V为转子系统势能；F_i为外力；q_i为广义坐标。
柔性转子系统一般由轮盘、弹性轴和支承3种单元组成。在建模时，将柔性转子系统中的连接结构(也即联轴器)等效为等截面弹性轴，通过调整密度与内外轴径以保证其质量与局部弯曲刚度相同。转子系统的动能表达式为

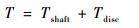(3)

式中：刚性轮盘的动能T_disc为

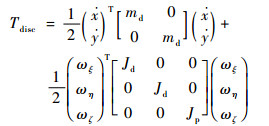(4)

其中：x、y、m_d、ω_ξ、ω_η、ω_ζ、J_d和J_p分别为轮盘质心的x向位移、y向位移、轮盘质量、轮盘绕x轴转速、绕y轴转速、绕z轴转速、直径转动惯量和极转动惯量。
弹性轴的动能T_shaft为

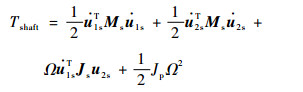(5)

式中：u_1s和u_2s为轴段两端的节点位移；M_s为考虑平动质量和转动惯量在内的一致质量矩阵；J_s为转动惯量矩阵；Ω为公转角速度。
转子系统的势能表达式为

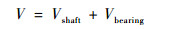(6)

式中：弹性轴和轴承的势能表达式分别为

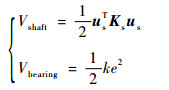(7)

式中:u_s为弹性轴两端点的节点位移组成的向量; K_s为弹性轴的刚度矩阵; k为轴承的支承刚度; e为轴承的变形量。
将上述动能表达式T、势能表达式V代入Lagrange方程中，可得转子系统动力学方程为

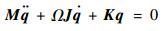(8)

式中:M、J和K分别为转子系统动力学方程的质量矩阵、转动惯量矩阵和刚度矩阵。
令Ω=ω，即可得到临界转速满足的方程，解方程可得临界转速。

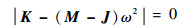(9)

1.2 应变能分布特性 应变能是指结构在外力作用下发生形变时，外力在形变位移上所做的功，这些功以能量的形式储存在结构内部，故称作应变能，可用于定量描述外力作用下结构的损伤情况^[12]。转子系统在刚体模态振动时，转子自身不发生变形，刚体位移仅使支承结构产生变形，即应变能均集中于支承结构中，只有当转子在靠近弯曲振型共振转速时，转子弯曲变形使应变能聚集在转子上。由于转子质量/刚度分布不均匀性以及轮盘的惯性力矩载荷的变化，使得转子连接结构处的应变能分布在工作过程中存在分散性，造成连接结构界面约束失效，表现为转子弯曲刚度区间分布特征。因此，转子应变能分布可表征转子结构的变形和受力状态，定量反映连接结构弯曲刚度损失程度。
转子应变能的定义式为

(10)

式中:σ、ε和dv分别为微元体的应力、应变和体积。
应变能可以分为体积改变能和畸变能，即

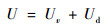(11)

根据材料力学第四强度理论，只有畸变能会导致结构发生失效，同时在细长轴段中，体积改变能的数值较小，因此本文中的轴段应变能仅考虑畸变能，利用广义坐标Q可表示为

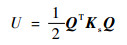(12)

在计算轴段应变能时，先对式(8)的各阶模态振型进行归一化，并提取出轴段的广义位移Q，再按照式(12)计算得到轴段应变能。
支承结构的应变能为其自身因变形积累的势能，按照式(7)计算，即

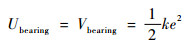(13)

2 基于区间分析的稳健设计方法 稳健设计目的是优化目标函数的中值(或称均值)，同时减小因非确定因素引起的分散度^[3]。图 2为本文提出的高速柔性转子系统动力特性稳健设计方法框图。考虑到转子应变能分布可能导致转子弯曲刚度产生分散性，以及多支点转子结构中弹性支承刚度的分散性^[13]，会影响转子系统动力特性随转子转速变化的稳健性，故采用区间分析方法描述转子动力特性的非确定性，通过合理选择设计变量的中值，以优化临界转速分布，并控制弯曲应变能在转子连接结构处的分布，减小动力特性参数分散度，实现转子系统动力特性稳健设计。

图 2 高速柔性转子系统动力特性稳健设计思路 Fig. 2 Robust design concept of dynamic properties of high-speed flexible rotor systems

图选项

2.1 区间分析 实际工程应用中，通常无法给出非确定参数的概率分布和隶属函数，仅能确定参数的波动范围。区间分析方法可不对其分布规律进行任何人为假设，用区间数描述参数非确定性并经过区间运算得到振动响应的变差范围，并以此开展稳健设计。对于带有连接界面的高速柔性转子系统，考虑转子结构参数、支承结构参数区间分布特征，以及在求解转子系统各阶临界转速、应变能等动力特性时，需要在确定性优化方法的基础上，提出基于区间分析的稳健设计流程。
以临界转速为例，由于非确定性因素是支承刚度和转子弯曲刚度，将导致方程式(8)中的刚度矩阵K为非确定参数，可通过区间参数加以表示：

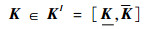(14)

式中：K为具有非确定性的刚度矩阵的上界矩阵；K为具有非确定性的刚度矩阵的下界矩阵。
引入列向量，并设Z=ψe^λt，对应的广义特征值问题为

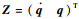
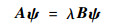(15)

(16)

式中：ψ为特征值λ的右特征向量；υ^T为特征值λ的左特征向量。

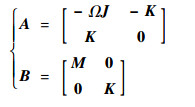(17)

其中:M、J、K为式(8)中对应的物理量。
方程式(15)两端同时左乘B^-1，可以表示为

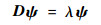(18)

(19)

经过推导，转子系统固有频率所在的区间为

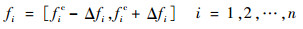(20)

式中：f_i^c为固有频率的区间中值，由常规方法求解；Δf_i为固有频率非确定量，表达式^[7]为

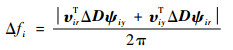(21)

其中：υ_ir为第i个左特征向量的实部；ψ_iy为第i个右特征向量的虚部；ΔD为区间矩阵D的非确定量。
2.2 设计流程 为定量描述临界转速的集中程度，定义临界转速分布罚函数，以前两阶临界转速中值为例。

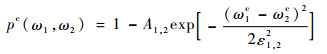(22)

式中：ω₁^c、ω₂^c分别为第一、二阶临界转速中值；A_1，2和ε_1，2可以控制罚函数的形状。罚函数的函数图形如图 3所示。此罚函数的性质为：当两阶临界转速互相靠近时，罚函数值急剧减小，可用于定量表示临界转速的集中程度。

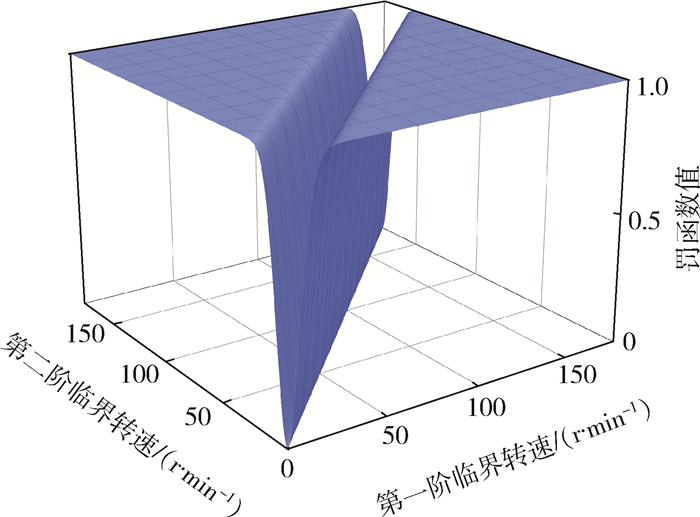图 3 罚函数图形 Fig. 3 Graph of penalty function

图选项

针对本文提出的转子系统动力特性稳健设计思想，建立基于区间分析方法的高速柔性转子系统动力特性稳健设计流程，如图 4所示。

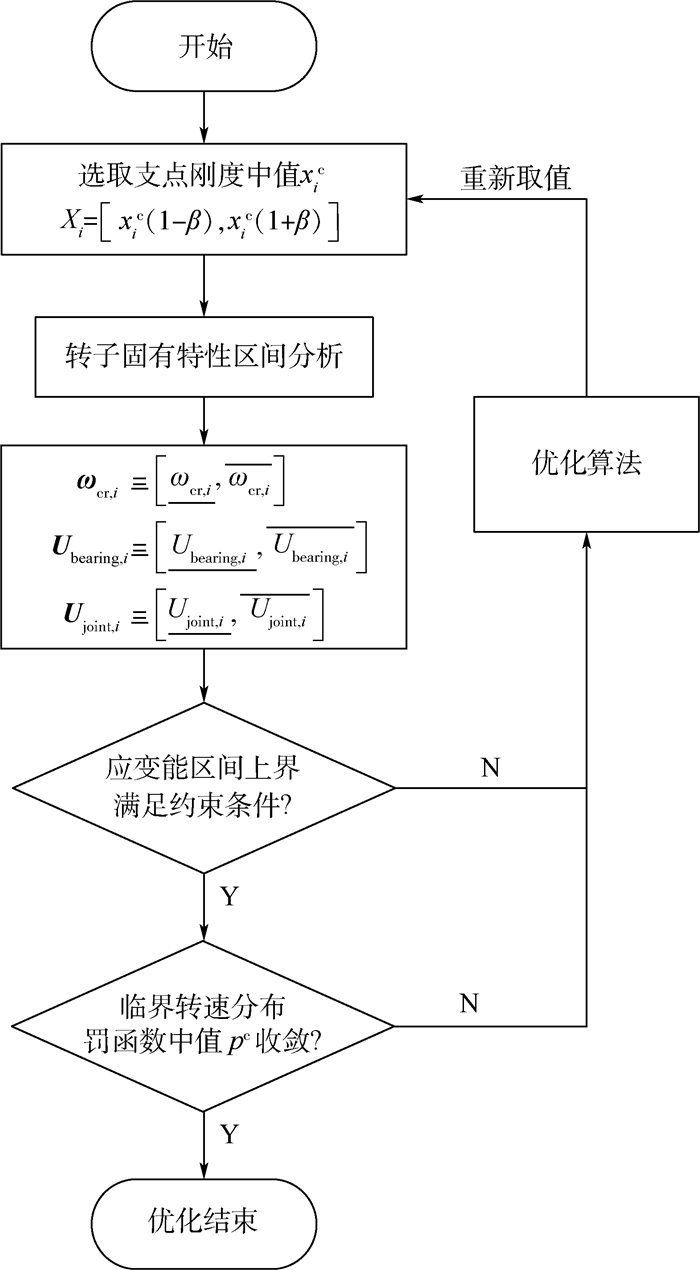图 4 高速柔性转子系统动力特性稳健设计流程 Fig. 4 Robust design process for dynamic properties of high-speed flexible rotor systems

图选项

由图 4可知，高速柔性转子系统动力特性稳健设计可分为以下4个步骤：
步骤1??试取一组设计变量x_i的中值。
步骤2??将设计变量代入方程式(8)，通过区间分析方法求得各阶临界转速及应变能分布的区间解。
步骤3??对控制点应变能的区间上界进行评估，若满足设计要求，则进行步骤4，若不满足则利用优化算法进行重新取值，重复步骤2、步骤3。
步骤4??对临界转速分布罚函数的区间中值进行评估，如区间中值满足收敛条件，则完成该稳健优化，如不收敛则利用优化算法重新取值，重复步骤2、步骤3，直至优化结束。
2.3 优化算法及其参数选择
2.3.1 优化算法的选择 依据优化算法中可行域是否具有非确定性，优化算法可分为2类：确定性算法与非确定性算法(也称随机优化算法)^[14]。确定性算法是指遵循严格数学规划的算法，其中不涉及任何非确定元素，如牛顿法、梯度下降法等；非确定性算法是指寻优过程中会产生随机性参数的算法，如模拟退火算法、遗传算法等。优化算法的选择及其参数设置会影响能否得到全局最优解。本文以遗传算法为例进行最优解的求解。遗传算法是在模拟达尔文的进化论基础上建立的，利用概率方法生成一定数量的样本，并选取较优的个体继续逐代演化，直至得到近似最优解。

2.3.2 设计变量及目标函数的选择 在柔性转子的结构参数设计中，转子的几何尺寸、支点位置、轮盘位置通常由整机性能、结构与强度设计要求所决定，一般不由动力学特性所决定，故选取各支承刚度的中值为设计变量。
不同于传统临界转速设计方法，本文以临界转速的分布特征作为目标函数，即在进行临界转速分布特征设计时，主要从转子通过多阶临界转速时支点动载荷的抑制出发，尽可能将多阶临界转速集中于较小的转速范围内，当转子通过多阶临界转速时，由于各阶模态振动相位的不同而产生了相互制约作用，使得支点动载荷得到抑制。

2.3.3 约束条件的选择 为使转子系统在满足一般性的设计准则的基础上，提高转子系统动力特性稳健性，以临界转速安全裕度的区间下界、连接结构处应变能的区间上界作为约束条件。考虑到固有特性分析中，应变能的绝对值并没有实际意义，故本文以应变能比例作为衡量应变能多寡的判据，以柔性转子系统连接结构处的应变能比例作为约束条件。
计算约束函数表达式时，由于支承刚度和连接结构弯曲刚度等参数具有区间分布特征，因此通过动力学方程式(8)计算出的临界转速式(9)及连接结构应变能式(12)均以区间参数的形式表示，类似于刚度矩阵的区间形式(式(14))，由区间上界和区间下界组成。临界转速安全裕度的区间下界、连接结构处应变能比例的区间上界如下：

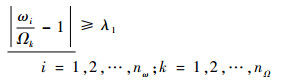(23)

式中：λ₁为临界转速安全系数；ω_i为第i阶临界转速；Ω_k为第k个工作转速。

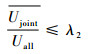(24)

式中：U_joint为连接结构处应变能；U_all为转子系统的总应变能；λ₂为连接结构应变能稳健系数。
故柔性转子动力特性的稳健设计模型为

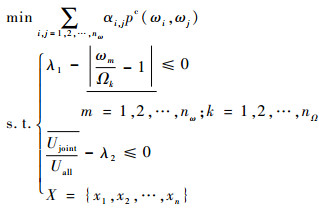(25)

式中：α_{i, j}为第i，j阶临界转速分布罚函数中值的关注系数；x₁, x₂, …, x_n为各设计变量的取值。
3 算例分析 图 5为三支点高速柔性转子系统结构示意图，其工作转速为30 000 r/min，主要由压气机叶盘、涡轮叶盘、压气机轴和涡轮轴组成，两轴段通过联轴器相连，压气机叶盘后及涡轮叶盘前均布置一个支点，同时在联轴器附近布置一个支点，以控制细长轴段的变形。该转子系统的具体参数如表 1所示。

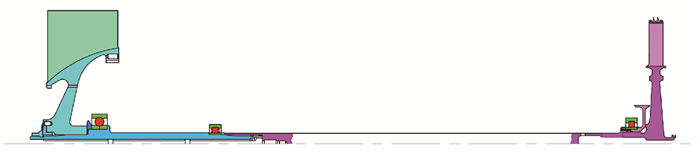图 5 三支点高速柔性转子系统结构示意图 Fig. 5 Schematic of three-support high-speed flexible rotor system structure

图选项

表 1 算例转子系统参数 Table 1 Parameters of example rotor system

参数	数值
轴段密度/(kg·m-3)	7 820
轴段弹性模量/GPa	195
轴段内径/m	0.006
轴段外径/m	0.022
转子总长/m	0.598
风扇等效集中质量/kg	3.583
风扇绕轴线转动惯量/(kg·m2)	0.024
涡轮等效集中质量/kg	3.135
涡轮绕轴线转动惯量/(kg·m2)	0.017

表选项






采用本文提出的转子系统动力特性稳健设计方法对该转子的支承刚度进行优化设计。以支点刚度作为非确定变量，用区间参数形式表示，并依据工程经验给定支承刚度的分散度β。对此转子系统进行固有特性的区间分析，并采用遗传算法进行支承刚度中值的优化选取，表 2为优化过程的控制参数。
表 2 优化参数选取 Table 2 Choice of optimization parameters

参数	数值
支承刚度分散度β/%	5
临界转速分布罚函数幅值Ai, j	1
临界转速分布罚函数标准差εi, j	2 400
临界转速分布罚函数中值的关注系数αi, j	1
临界转速安全系数λ1/%	20
连接结构应变能稳健系数λ2/%	2
遗传算法初代样本数	100
遗传算法子代样本数	20
遗传算法的可容忍收敛误差/%	2
注：i, j=1, 2, 3, 4。

表选项






依照表 2给出的优化参数，在约束条件的约束下，对目标函数进行遗传优化。首先在整个可行域内随机生成100个样本点，并进行个体筛选，保留较优秀的样本，进行逐代优化，每代个体数为20个，优化过程如图 6所示。可以看出，经过6代进化，逐步逼近最优解。

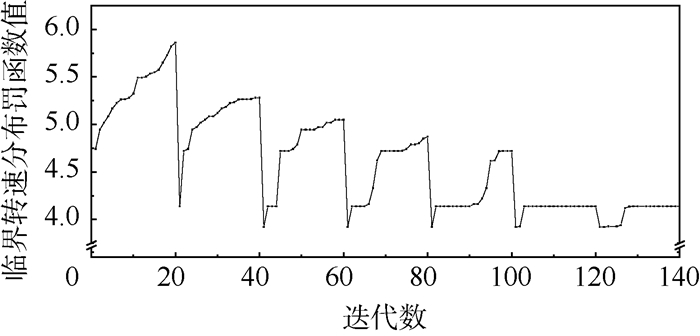图 6 目标函数的优化过程 Fig. 6 Optimization process of objective function

图选项

表 3为优化前后支点刚度中值、前四阶临界转速及连接结构处的应变能比例。图 7为2种方案对应的具有区间分布特征的Campbell图。从表 3和图 7中可以看出，通过降低前支点和中支点的支承刚度，并提高后支点的支承刚度，使得转子结构的刚度分布更加均匀。将初始方案中分散的前三阶临界转速集中在[13 180, 15 818]r/min的转速区间内，并将连接结构处的应变能比例由11.15%降低至1.93%，验证了优化算法选取的有效性。
表 3 不同支点刚度组合及其临界转速 Table 3 Different support stiffness combinations and their critical speeds

方案	前支点刚度 中值/(N· mm-1)	中支点刚度 中值/(N· mm-1)	后支点刚度 中值/(N· mm-1)	第一阶 临界转速/ (r·min-1)	第二阶 临界转速/ (r·min-1)	第三阶 临界转速/ (r·min-1)	第四阶 临界转速/ (r·min-1)	连接结构 应变能 比例上限/%
初始方案	20 250	42 694	1 955	6 771±146	16 323±597	22 748±621	51 849±30	11.15
最优方案	9 750	2 858	8 723	13 300±120	15 479±178	15 594±224	50 353±7	1.93
注：连接结构应变能比例上限为工作转速范围内的应变能比例最大值。

表选项

图 7 不同支点刚度组合下的Campbell图 Fig. 7 Campbell diagram under different support stiffness combinations

图选项

由于考虑了动力特性的非确定性，因此各阶临界转速随工作转速的变化曲线应扩展为变化条带，条带的宽度表示其分散度的大小。从表 3和图 7中可以看出，虽然2个方案均能满足临界转速安全裕度的约束，但相比于初始方案，最优方案的前三阶临界转速分布较为集中，各阶临界转速的分散度也较小，其动力特性的稳健性更高，同时由于在优化过程中增设了针对连接结构应变能比例的约束条件，可有效降低连接结构应变能比例，降低转子弯曲刚度的分散度，提高转子系统的稳健性。
对上述2种方案进行不平衡响应计算，可得到各支点动载荷随转子转速的变化曲线，如图 8所示。虽然初始方案的临界转速分布满足安全裕度的要求，但由于各阶临界转速分布较为分散，工作转速范围内，随着转速增加，支点动载荷体现出多峰值特征，而最优方案的支点动载荷则体现出单峰值特征，利用转子连续通过多阶临界转速时阻尼滞后和响应滞后的特性，使不同相位的振型叠加，使得最优方案的支点动载荷最大值相比初始方案较小。考虑到支点动载荷导致的结构损伤主要分为2个方面：轴承的损伤与承力框架的损伤，其中轴承的损伤可由滚动轴承的寿命计算公式体现^[15]，其寿命与轴承当量动载荷呈三次方反比关系，因此最优方案由于支点动载荷较小，在多个工作循环内积累的轴承损伤较小；同时考虑到，在承力框架的温度载荷等相同时，支点动载荷越小，有利于抑制承力框架连接界面的滑移及微动磨损等情况的发生，且对静子承力结构的激励幅值较小，有利于提高整个转子系统及静子结构动力特性的稳健性。

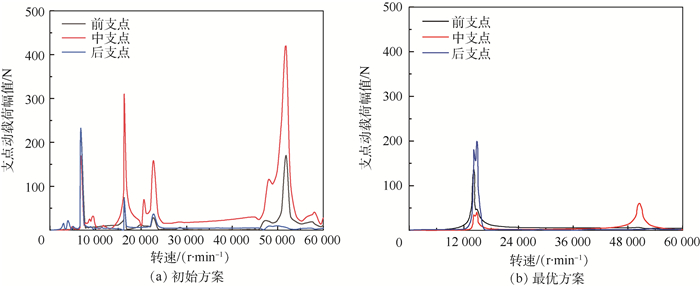图 8 不同支点刚度组合下的支点动载荷 Fig. 8 Support dynamic load under different support stiffness combinations

图选项

4 结论 1) 考虑转子结构参数及动力特性参数具有非确定性，本文提出了控制转子振动响应的稳健设计思路，利用转子不同共振转速下振动相位及阻尼滞后特性，将多阶临界转速集中于一定区间，可以有效降低转子通过临界转速时的振动响应。
2) 采用区间分析方法描述转子动力特性的非确定性，提出临界转速分布罚函数，用于定量评估临界转速的分布特征，当临界转速分布罚函数取值最小化，并满足共振安全裕度要求时，高速柔性转子动力特性具有良好的稳健性。
3) 通过算例验证了本文提出的动力特性稳健设计方法的有效性，算例表明，临界转速分布罚函数可有效表征临界转速的分布特征，通过临界转速的合理分布，并控制连接结构应变能，可有效控制转子振动响应，同时减小转子动力特性参数的分散度，可切实提高柔性转子动力特性的稳健性。

参考文献

[1]	LIU S, WANG J, HONG J, et al.Dynamics design of the aero-engine rotor joint structures based on experimental and numerical study[C]//ASME Turbo Expo 2010: Power for Land, Sea, and Air.New York: ASME, 2010: 49-60.
[2]	RAJAN M, RAJAN S D, NELSON H D, et al. Optimal placement of critical speeds in rotor-bearing systems[J]. Journal of Vibration and Acoustics, 1987, 405(1-6): 417-419.
[3]	SHIAU T N, CHANG J R. Multi-objective optimization of rotor-bearing system with critical speeds constraints[J]. Journal of Engineering for Gas Turbines and Power, 1991, 115(2): 246-255.
[4]	LIN Y, CHENG L, HUANG T P. Optimal design of complex flexible rotor-support systems using minimum strain energy under multi-constraint conditions[J]. Journal of Sound and Vibration, 1998, 215(5): 1121-1134. DOI:10.1006/jsvi.1998.1690
[5]	ZANG C, FRISWELL M I, MOTTERSHEAD J E. A review of robust optimal design and its application in dynamics[J]. Computers & Structures, 2005, 83(4-5): 315-326.
[6]	LI G, LIN Z, ALLAIRE P E. Robust optimal balancing of high-speed machinery using convex optimization[J]. Journal of Vibration and Acoustics, 2008, 130(3): 263-269.
[7]	MA Y, CAO P, WANG J, et al.Interval analysis method for rotor dynamics with uncertain parameters[C]//ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition.New York: ASME, 2011: 307-314.
[8]	陈萌.航空发动机转子系统动力特性区间分析理论与方法研究[D].北京: 北京航空航天大学, 2012. CHEN M.Investigation on interval analysis theory and method of aero-engine rotor dynamics[D].Beijing: Beihang University, 2012(in Chinese).
[9]	RITTO T G, LOPEZ R H, SAMPAIO R, et al. Robust optimization of a flexible rotor-bearing system using the Campbell diagram[J]. Engineering Optimization, 2011, 43(1): 77-96.
[10]	顾家柳, 等. 转子动力学[M]. 北京: 国防工业出版社, 1985. GU J L, et al. Rotordynamics[M]. Beijing: National Defense Industry Press, 1985. (in Chinese)
[11]	NELSON H D, MCVAUGH J M. The dynamics of rotor-bearing systems using finite elements[J]. Journal of Engineering for Industry, 1976, 98(2): 593-600. DOI:10.1115/1.3438942
[12]	单辉祖. 材料力学[M]. 北京: 高等教育出版社, 2009. SHAN H Z. Mechanics of materials[M]. Beijing: High Education Press, 2009. (in Chinese)
[13]	洪杰, 于欢, 肖森, 等. 高速柔性转子系统非线性振动响应特征分析[J]. 北京航空航天大学学报, 2018, 44(4): 653-661. HONG J, YU H, XIAO S, et al. Nonlinear vibration response characteristics of high-speed flexible rotor system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(4): 653-661. (in Chinese)
[14]	CAVAZZUTI M. Optimization methods[M]. Berlin: Springer, 2013.
[15]	《航空发动机设计手册》总编委会. 航空发动机设计手册第12册传动及润滑系统[M]. 北京: 航空工业出版社, 2000.
[16]	The Editorial Board of Design Manual of Aero Engines. Design manual of aero engines Vol.12, Transmission and lubrication system[M]. Beijing: Aviation Industry Press, 2000.