铌酸锂(LiNbO₃)晶体具有优异的电光和声光等特性，被广泛用于制备各种光波导器件^[1-2]。LiNbO₃光波导是高精度光纤陀螺系统的核心器件，LiNbO₃光波导的大批量生产是实现光纤陀螺产业化的关键之一。质子交换炉是用质子交换法制备LiNbO₃光波导的主要设备，为了提高生产效率，往往将批量LiNbO₃基底同时放到质子交换炉中进行质子交换以制备光波导。若炉内轴向温度分布不均匀，将导致不同温度梯度下进行质子交换时LiNbO₃光波导的薄膜厚度会有所不同，会对同一批次制备的光波导的性能一致性造成影响，因此提高质子交换炉的温度场均匀性很有必要^[3]。目前对质子交换炉的要求为：质子交换炉轴向均匀温区长度≥200 mm，均匀温区内的最大温差在5 min内≤1℃。
目前国内外对质子交换炉内部温度的研究重点大多在于温度的精确控制^[4-5]，而对炉内温度分布均匀性的相关研究较少，导致现有的质子交换炉很难用于大批量LiNbO₃光波导的制备。质子交换炉内存在热传导、热对流等多种传热方式，十分复杂，难以建立精确的数学模型。面对复杂的质子交换炉系统设计，一般采用模仿或经验改进等方法对质子交换炉进行设计，不仅成本高而且研究周期长，生产出来的质子交换炉往往不能达到理想的温度分布。随着计算机技术的发展，计算流体力学(CFD)的出现给质子交换炉的设计提供了极大的方便^[6-7]。FLUENT是国际上流行的CFD软件包，它提供了用户自定义函数(UDF)作为FLUENT的二次开发，当标准的FLUENT界面不能满足用户需求时，用户可以编写UDF程序并动态地连接到FLUENT求解器上以实现期望的控制算法、模型方程等^[8]。1994年，Chicatelli等^[9]首次将CFD和控制方法相结合，用于高速推进系统的模拟和控制。Yang等^[10]针对垃圾焚烧炉难以测量内部温度的问题，通过CFD建模研究前馈控制效果，并将数值模拟结果作为控制系统信息数据库。Gao等^[11]针对PID控制器参数整定时难以评估整体控制效果的问题，提出了一种基于FLUENT的PID控制器参数整定评估方法，验证了该方法的有效性。这些成果为本文模拟质子交换炉的控温奠定了一定的基础。本文采用基于FLUENT的PID控制方法，利用FLUENT模拟控制对象，编写UDF控温程序，使用FLUENT UDF进行闭环控制，模拟质子交换炉炉温的PID控制。与传统的PID控制器不同之处在于基于FLUENT的PID控制器不需要建立被控对象的传递函数模型，而是建立被控对象的网格模型，利用FLUENT对网格计算求解得到最终的控制效果。
本文基于质子交换炉提出了多种加热控温方案，利用FLUENT对质子交换炉加热过程的温度场进行仿真，分析此过程中温度场分布特点，研究质子交换炉控温方式、传感器位置布置、加热丝布置对炉内温度场均匀性的影响，找到最佳加热方案，提高炉内温度场均匀性。
1 模型建立 1.1 物理模型 本文研究的质子交换炉采用圆筒结构，立式放置，炉体结构由外至内分别有保温层、加热丝、炉壁，如图 1所示，炉体高H=0.8 m，炉膛内径为0.12 m。加热丝均匀缠绕在炉壁四周，将产生的热量传递给炉壁，炉壁与炉膛内的空气主要以传导和对流的方式进行热量传递，由于冷热空气密度不同，炉膛内的热气流会向上流动。炉体壁面和底部有保温结构，为方便工艺过程中打开炉口送料，炉顶一般没有保温结构，故炉顶处主要以对流的方式与外界环境进行换热。图 1中炉膛内的箭头代表热量流动。

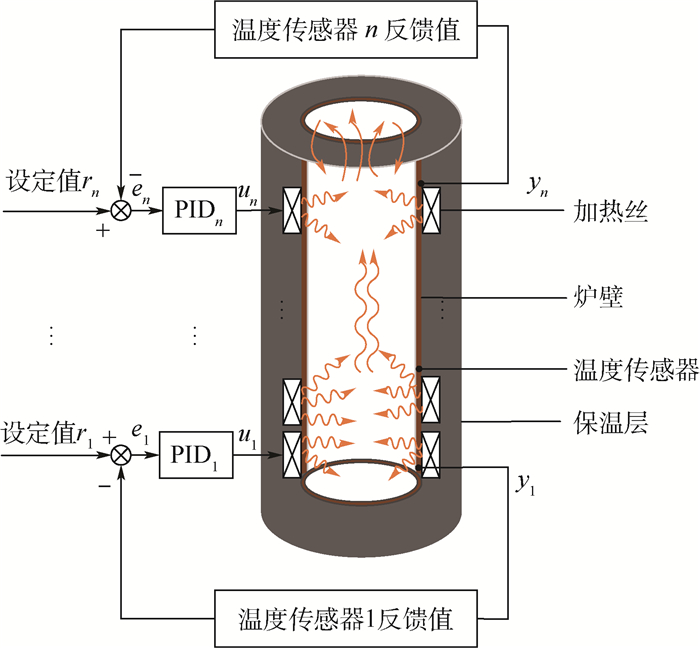图 1 质子交换炉系统实际模型 Fig. 1 Practical model of proton exchange furnace system

图选项

质子交换炉的炉温是通过改变加热丝的控制电流来调节的，综合考虑控制精度、炉温均匀性等多方面因素，可将加热丝分为多段，每段加热丝对应一个温区，构成多个加热回路，并在每个区安装温度传感器(通常采用热电偶)用于反馈各区温度，各区的控制回路根据目标设定温度值与实时反馈的温度值之差调整相应的控制器输出以控制加热丝加热, 如图 1所示，r_i为设定温度值，y_i为反馈温度值，e_i为温度偏差，PID_i代表控制器，u_i为控制器的输出值(其中i为控制回路的个数，i=1, 2, …, n)。
由于本文的研究重点在于质子交换炉内部的温度场分布，故对实际模型作如下简化：
1) 炉膛内的温度是本文的研究重点，故将模型简化为内径0.12 m，高0.8 m的圆柱体。
2) 加热丝均匀缠绕在炉膛周围，可假设壁面热流量是均匀的。
质子交换工艺的目标温度为240℃，安装在炉壁外表面的温度传感器将采集的温度信号发送给控制器，控制器将采集温度值与目标温度值进行比较后经PID计算输出控制量，并由继电器控制加热丝的电流通断来调节发热量，使炉膛的温度稳定在目标温度值。
1.2 数学模型
1.2.1 质子交换炉内空气的传热模型 炉膛内的空气和炉壁之间的热量传递主要靠热传导和热对流的方式进行，由能量守恒原理和傅里叶定律可得柱坐标系下空气的传热微分方程^[12]：

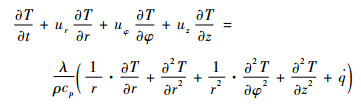(1)

式中:T为空气的温度；t为时间；u_r、u_φ和u_z分别为径向、圆周和轴向的空气流速；λ、ρ和c_p分别为空气的导热率、密度和比热容；为内热源强度。
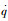
为简化式(1)，现做如下合理假设：①由于空气是完全透明体，因此可以忽略辐射换热；②空气是不可压缩的流体，空气的流速是固定的；③径向空气流量可忽略不计；④内热源生成热为0。
实际上空气的流速在径向上不为零，但是空气在轴向上的速率比径向上快的多，因此可忽略不计。上述假设下的空气瞬态热传导模型如下：

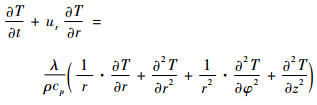(2)

对于轴对称的炉体，变量T与φ无关，因此上述模型可简化为

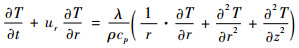(3)

初始条件和边界条件为

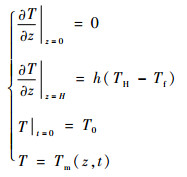(4)

式中：h为表面对流传热系数；T_H为炉体顶部的温度；T_f为周围流体的温度，为已知量；T₀为初始温度；T_m为空气温度。

1.2.2 CFD模型 CFD模型是基于微元内的质量守恒、动量守恒和能量守恒确定的一组偏微分方程。基本控制方程包括质量守恒方程、动量守恒方程和能量守恒方程，数学表达式为^[13]
质量守恒方程：

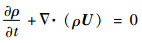(5)

x方向动量守恒方程：

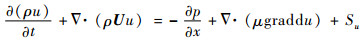(6)

y方向动量守恒方程：

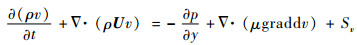z方向动量守恒方程：

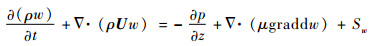(7)

能量守恒方程：

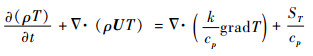(8)

式中：U=(u, v, w)，u、v、w分别为U在x、y、z方向的分速度；S_u、S_v、S_w、S_T均为广义源项；k为传热系数；μ为动力黏度系数; p为压强。
2 FLUENT仿真 2.1 网格划分及边界条件设置 进行CFD分析的第1步是划分网格^[14]。其主要思想是将空间连线的计算区域分割成足够小的计算区域，然后在每一计算区域里应用流体控制方程，求解所有区域的流体计算方程，最终获得整个计算区域的物理量分布^[15]。本文针对不同的方案分别采用Gambit生成圆柱体的结构化网格。
边界条件的设置如表 1所示。
表 1 边界条件的设置 Table 1 Boundary condition setting

边界名称	边界类型	边界条件	参数
炉顶	壁面	对流	传热系数=10W/(m2·K)自由流体温度为300K
炉壁	壁面	热流量	没有加热丝覆盖的壁面：热流量=0；有加热丝覆盖的壁面：热流量=UDF flux
炉底	壁面	热流量	热流量=0

表选项






表 1中的UDF flux表示使用UDF编写的热流量输出函数。炉壁的边界条件分为2种情况，有加热丝的部分设为壁面wall，热流量通过调用UDF编写的热流量输出函数来获得；没有加热丝的部分设为壁面wall，由于有保温层，热流量设为0。
2.2 模拟监测点设置 质子交换炉内的轴向温度分布是影响LiNbO₃光波导生产质量的关键。由于研究重点是质子交换炉内轴向方向的温度场分布，炉口没有保温结构，受外界环境影响较大，故均匀温区在炉底。工艺要求均匀温区长度Δh≥200 mm，故在均匀温区从炉底依次沿轴向方向均匀布置了5个监测点，间距l=0.05 m，其位置坐标分别为(0，0，0)m、(0，0，0.05) m、(0，0，0.1)m、(0，0，0.15)m、(0，0，0.2)m。质子交换炉内均匀温区温度分布用这5个测点的温度分布来描述。
2.3 求解器的设置 激活能量模型，湍流模型选择标准k-ε模型，壁面函数选为标准壁面函数，求解方法选择SIMPLEC，湍流动能与湍流耗散选择二阶差分，湍流黏度和能量的松弛因子选为0.8，其他保持默认值。质子交换炉内空气初始温度设为300 K，预期达到的温度设为513 K，根据温度传感器采集到的温度，控制壁面热流量的变化。对于瞬态求解，时间步长是一个重要的概念，时间步长设置太大会导致计算难以收敛，设置太小会增加迭代次数，计算时间过长。为了尽量减少计算时间而不降低计算精度，在仿真中设时间步长为0.5 s，时间步数为800，即仿真时间为400 s。始终采用上述设置完成以下仿真内容。
3 不同方案下的仿真结果与对比分析 本文提出3种控温方式，分别为整段控温、两段控温、三段控温。整段控温即加热丝为一整段，传感器位置布置在整段加热丝上，由其反馈的温度经过PID处理后控制整段加热丝的热流量；两段控温即将均匀缠绕在炉膛周围的加热丝均匀分为2段，2个传感器位置分别布置在每段加热丝上，其反馈的温度经过PID处理后分别控制每段加热丝的热流量；三段控温即将均匀缠绕在炉膛周围的加热丝均匀分为3段，3个传感器位置分别布置在每段加热丝上，其反馈的温度经过PID处理后分别控制每段加热丝的热流量。
本文在提出的3种控温方式下分别设计了不同的传感器位置布置，如图 2所示。在每种传感器位置布置下通过改变加热丝布置高度h，即h=2Δh、h=3Δh，可得出表 2中18种设计方案，利用FLUENT分别模拟这18种方案下的温度场。

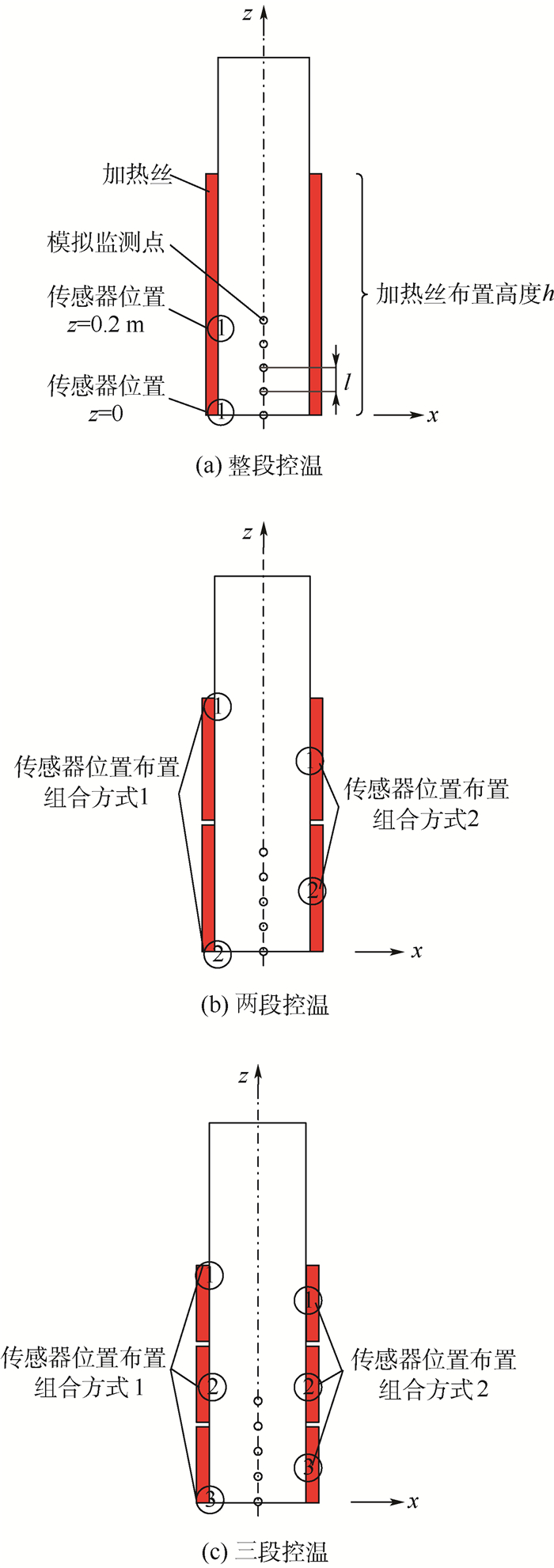图 2 3种控温方式的传感器位置布置 Fig. 2 Sensor position arrangement of three kinds of temperature control methods

图选项

表 2 18种设计方案 Table 2 18 kinds of design schemes

序号	控温方式	传感器位置布置	加热丝布置高度/m
1	整段控温	z=0	h=2Δh=0.4
2			h=3Δh=0.6
3			h=4Δh=0.8
4		z=0.2m	h=2Δh=0.4
5			h=3Δh=0.6
6			h=4Δh=0.8
7	两段控温	组合方式1	h=2Δh=0.4
8			h=3Δh=0.6
9			h=4Δh=0.8
10		组合方式2	h=2Δh=0.4
11			h=3Δh=0.6
12			h=4Δh=0.8
13	三段控温	组合方式1	h=2Δh=0.4
14			h=3Δh=0.6
15			h=4Δh=0.8
16		组合方式2	h=2Δh=0.4
17			h=3Δh=0.6
18			h=4Δh=0.8

表选项






为准确描述温度场的均匀性，采用在同一时刻所有监测点温度的最高温度与最低温度之差，即最大偏差来衡量温度场均匀性的好坏，其表达式为

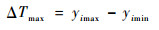(9)

式中：y_imin为第i时刻所有监测点的最低温度值；y_imax为第i时刻所有监测点的最高温度值。
对以上18种方案分别仿真400 s，经过100 s后炉内温度基本上达到动态平衡，本文选取100 ~400 s之间的最大温差ΔT_max来分析各种方案的均匀性好坏，所得结果如图 3~5所示。

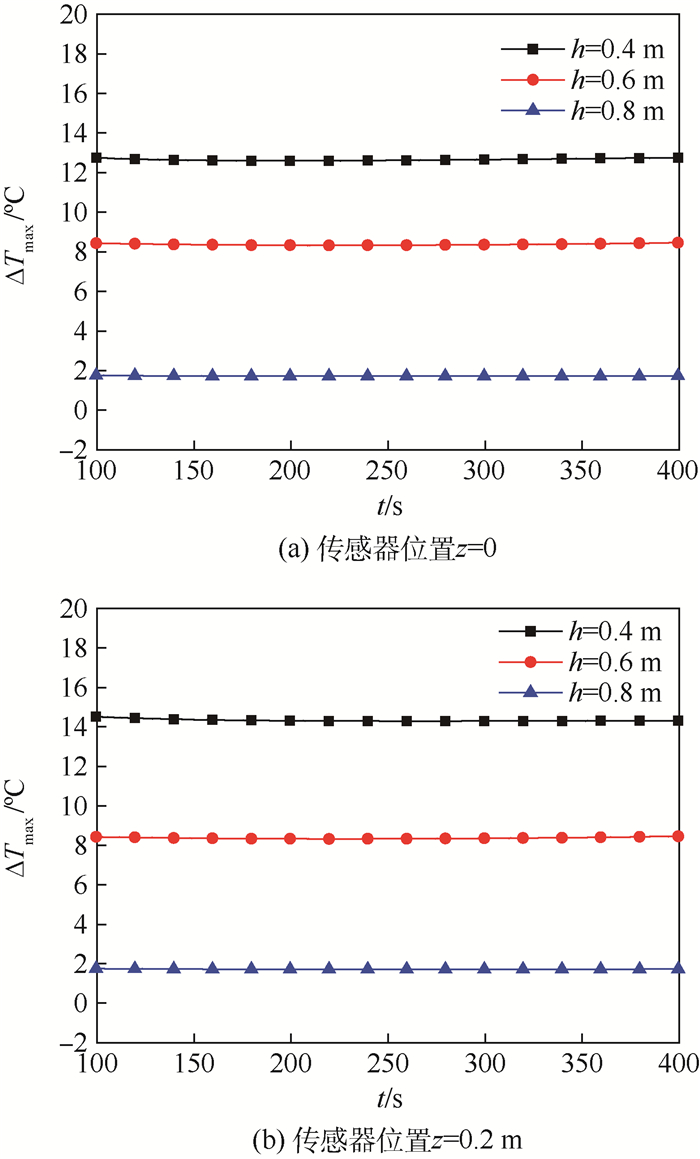图 3 整段控温时传感器位置对质子交换炉均匀性的影响 Fig. 3 Effect of sensor position on uniformity of proton exchange furnace under only one temperature controller

图选项

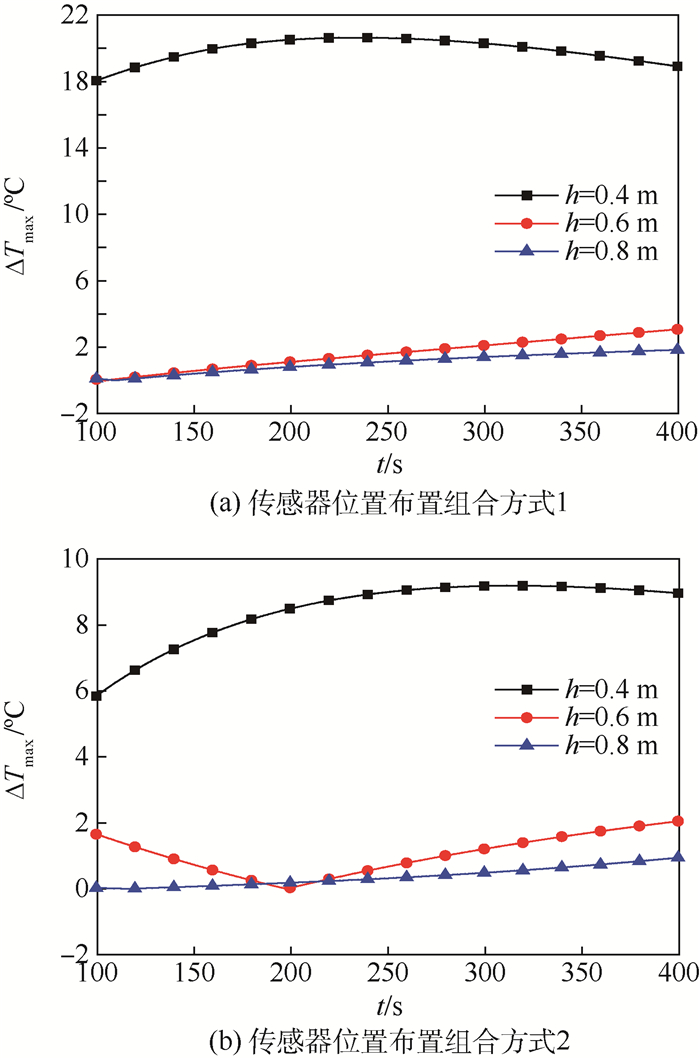图 4 两段控温时传感器位置对质子交换炉均匀性的影响 Fig. 4 Effect of sensor position on uniformity of proton exchange furnace under two temperature controllers

图选项

图 5 三段控温时传感器位置对质子交换炉均匀性的影响 Fig. 5 Effect of sensor position on uniformity of proton exchange furnace under three temperature controllers

图选项

对比图 3(a)和(b)可以发现，采用整段控温方式时改变传感器的位置对加热丝布置高度h=2Δh的均匀性影响较大，对于h=3Δh和h=4Δh的均匀性几乎没有影响；由图 3(a)可以看出，传感器位置在z=0时，加热丝布置高度h=2Δh时炉内温度场均匀性最差，而h=4Δh时炉内温度场均匀性最好。这是由于加热丝布置的高度过低时，没有布置加热丝的炉壁热流量为0，不能完全补偿炉顶的对流换热作用引起的热量散失，导致炉底均匀温区长度变短，达不到期望的均匀温区长度。因此整段控温方式下的最佳方案为方案3，即传感器位置z=0，加热丝布置高度h=4Δh。
对比图 4(a)和(b)可以看出，采用两段控温方式时改变传感器位置对加热丝布置高度h=2Δh的均匀性影响很大，与组合方式1相比，采用组合方式2时h=2Δh的均匀性提高了2~3倍，对于h=3Δh和h=4Δh的均匀性也有一定提高；由图 4(b)可以看出，传感器位置布置均采用组合方式2时，加热丝布置高度h=2Δh时炉内均匀温区的均匀性最差，而h=4Δh时炉内均匀温区的均匀性最好。因此两段控温方式下的最佳方案为方案12，即传感器位置布置组合方式2，加热丝布置高度h=4Δh。
对比图 5(a)和(b)可以看出，采用三段控温方式时，传感器位置布置采用组合方式2可以更好地改善均匀温区的均匀性；图 5(b)中传感器位置布置均采用组合方式2时，加热丝布置高度h=4Δh时炉内温度场均匀性最好。因此三段控温方式下的最佳方案为方案18，即传感器位置布置组合方式2，加热丝布置高度h=4Δh。
对以上3种控温方式下的最佳方案进行进一步对比，取400 s时刻y=0截面的温度分布云图，如图 6所示，从左到右依次为方案18、方案12、方案3对应温度范围512.5~513.5 K的温度分布，可见三段控温下的最佳方案对应的均匀温区长度最长，整段控温下的最佳方案对应的均匀温区最短。

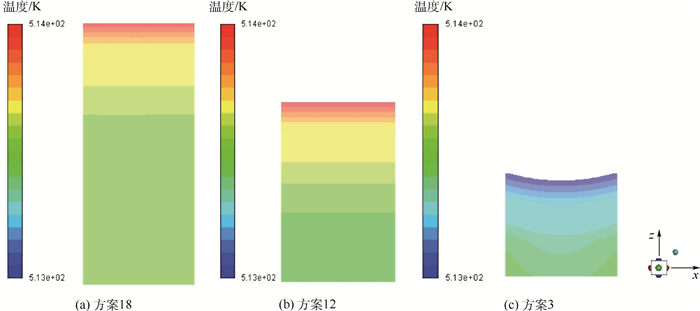图 6 方案18、方案12、方案3的y=0截面的温度分布云图 Fig. 6 Temperature distribution contour of y=0 cross-section for Scheme 18, Scheme 12 and Scheme 3

图选项

在100~400 s时间段内对3种控温方式下的最佳方案进行最大偏差的对比，如表 3所示。
表 3 3种控温方式下的最佳方案对比 Table 3 Comparison of the best solutions under three temperature control methods

序号	最佳方案	最大偏差ΔTmax/℃
3	整段控温，传感器位置布置在z=0，加热丝布置高度h=4Δh	1.73
12	两段控温，传感器位置布置组合方式2，加热丝布置高度h=4Δh	0.95
18	三段控温，传感器位置布置组合方式2，加热丝布置高度h=4Δh	0.03

表选项






表 3中，采用方案18炉内均匀温区的均匀性最好，即三段控温、传感器位置布置采用组合方式2、加热丝布置高度h=4Δh时最大温度偏差最小，ΔT_max可达0.03℃，满足生产工艺的要求。由表 3可以看出，当加热丝布置高度均为h=4Δh时，随着控温分段数目的增加，均匀温区的最大温度偏差越小。这是由于炉内温度分布存在梯度时，整个壁面热流量的不同位置需要不同程度的调整，而整段控温会同时改变整个壁面热流量，且改变程度相同，这就导致有些位置会有热量积累而有些位置散失的流量得不到补偿，炉内温度分布均匀性较差；随着控温分段数目的增加，炉内温度分布存在梯度时，壁面热流量可以分时进行不同程度的调整，快速补偿散失的热量，因此炉内温度分布越均匀。但是控温段数越多，生产成本也会越高，而且各个控制回路之间的耦合效应也越来越严重，提高炉温均匀性的同时有可能会降低控温精度。因此满足生产工艺均匀性要求的前提下，三段控温的方式较好。
4 结论 1) 整段控温、两段控温、三段控温下改变传感器位置布置对加热丝布置高度h=2Δh的均匀性影响最大，优化传感器的位置可以改善炉内温度场的均匀性。
2) 在相同的控制方式下，加热丝布置高度越高，炉内均匀温区长度越长。
3) 对比分析18种设计方案的仿真结果，采用三段控温、3个传感器位置分别布置在3段加热丝中间、加热丝布置高度h=4Δh时炉内温度场均匀性最好，长度为200 mm的均匀温区内最大温度偏差为0.03℃，满足生产工艺的要求。
4) 利用FLUENT软件对设计方案进行仿真，这种方法可缩短设备调试周期，节约成本，同时该方法也为同类电加热炉的温度场均匀性优化设计提供了思路。

参考文献

[1]	FAKHRI M A, AL-DOURI Y, HASHIM U, et al. Optical investigation of nanophotonic lithium niobate-based optical waveguide[J]. Applied Physics B, 2015, 121(1): 107-116. DOI:10.1007/s00340-015-6206-x
[2]	CAO L, ABOKETAF A, WANG Z H, et al. Hybrid amorphous silicon(a-Si:H)-LiNbO3 electro-optic modulator[J]. Optics Communications, 2014, 330: 40-44. DOI:10.1016/j.optcom.2014.05.021
[3]	FAKHRI M A, AL-DOURI Y, HASHIM U, et al. Annealing temperature effects on morphological and optical studies of nano and micro photonics lithium niobate using for optical waveguide applications[J]. Australian Journal of Basic & Applied Sciences, 2015, 9(12): 128-133.
[4]	SHEN L, HE J J, YANG C H, et al. Temperature uniformity control of large-scale vertical quench furnaces for aluminum alloy thermal treatment[J]. IEEE Transactions on Control Systems Technology, 2015, 24(1): 24-39.
[5]	EMADI A, SABOONCHI A, TAHERI M, et al. Heating characteristics of billet in a walking hearth type reheating furnace[J]. Applied Thermal Engineering, 2014, 63(1): 396-405. DOI:10.1016/j.applthermaleng.2013.11.003
[6]	LING Z, CHEN J, FANG X, et al. Experimental and numerical investigation of the application of phase change materials in a simulative power batteries thermal management system[J]. Applied Energy, 2014, 121: 104-113. DOI:10.1016/j.apenergy.2014.01.075
[7]	PANG L, WANG M, WANG W, et al. Optimal thermal design of a stacked mini-channel heat sink cooled by a low flow rate coolant[J]. Entropy, 2013, 15(11): 4716-4731.
[8]	唐家鹏. ANSYS FLUENT 16.0超级学习手册[M]. 北京: 人民邮电出版社, 2016: 502-507. TANG J P. ANSYS FLUENT 16.0 super study manual[M]. Beijing: People's Posts and Telecommunications Press, 2016: 502-507. (in Chinese)
[9]	CHICATELLI A, HARTLEY T T, COLE G, et al.Interdisciplinary modeling using computational fluid dynamics and control theory[C]//American Control Conference.Piscataway, NJ: IEEE Press, 1994, 3: 3438-3443.
[10]	YANG Y, REUTER M A, HARMAN D T M. CFD modelling for control of hazardous waste incinerator[J]. Control Engineering Practice, 2003, 11(1): 93-101.
[11]	GAO X J, WANG S Y, WANG P.The evaluation method of PID controller parameter tuning based on FLUENT[C]//Control and Decision Conference.Piscataway, NJ: IEEE Press, 2015: 4850-4854. https://ieeexplore.ieee.org/document/7162784
[12]	李友荣, 吴双应, 石万元, 等. 传热分析与计算[M]. 北京: 中国电力出版社, 2013: 3-15. LI Y R, WU S Y, SHI W Y, et al. Heat transfer analysis and calculation[M]. Beijing: China Electric Power Press, 2013: 3-15. (in Chinese)
[13]	王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 7-11. WANG F J. Computational fluid dynamics analysis:Principles and applications of CFD software[M]. Beijing: Tsinghua University Press, 2004: 7-11. (in Chinese)
[14]	朱能伟, 方晓东. 基于FLUENT的准分子激光器气体流场数值仿真[J]. 中国激光, 2016, 43(9): 44-49. ZHU N W, FANG X D. Numerical simulation of gas flow field in excimer laser based on FLUENT[J]. Chinese Laser, 2016, 43(9): 44-49. (in Chinese)
[15]	胡坤, 李振北. ANSYS ICEM CFD工程实例详解[M]. 北京: 人民邮电出版社, 2014: 34-39. HU K, LI Z B. Detailed explanation of ANSYS ICEM CFD project[M]. Beijing: People's Posts and Telecommunications Press, 2014: 34-39. (in Chinese)