从目前公开的文献资料看,大多数的研究工作是基于建立的Winged-Cone刚体模型上开展的[4-6],一般很难反映出高超声速飞行器的结构动力学特性。Bolender与Doman[7]则在以上研究的基础上,通过分别建立弹性动力学模型、气动力模型与发动机模型,最终得到了一个气动/推进/结构耦合的纵向一体化解析式系统模型。Parker等[8]则在Bolender与Doman[7]的工作基础上,通过忽略模型中的一些弱耦合关系,建立了一个面向控制的高超声速飞行器参数拟合模型。目前已有相当多的控制算法被应用于控制器的设计。经典的鲁棒控制在本质上是考虑不确定性为最坏情况时优化解的求取情况,文献[9]通过反馈线性化和极点配置的方法设计了标称控制器,通过鲁棒补偿器来抑制参数不确定和外界扰动带来的不利影响;滑模控制对模型本身的不确定与外部扰动都不敏感,具有良好的鲁棒性,文献[10]设计了一种多输入、多输出的自适应滑模控制律,确保了速度与高度跟踪误差指数收敛的滑模面,但控制输入存在高频抖振;文献[11]设计弹性自适应控制律,减弱了系统的抖振,跟踪效果较好,但控制律设计是基于刚体模型建立的且并未分析系统的弹性状态影响;反演控制能充分利用系统有用的非线性项,将非匹配不确定系统转化为匹配不确定系统,这已成为高机动飞行器控制系统设计的主流方法[12-13]。文献[14]针对飞行器弹性模型设计了一种鲁棒反演控制器,虽然对指令输入跟踪效果较好,但是由于未考虑到加入干扰观测器后使得对模型的不确定项估计变得相对平滑,在后期鲁棒性能上无法确保。
虽然对于高超声速飞行器的参考轨迹跟踪研究已有大量的较好成果,但是考虑不确定扰动下跟踪误差的瞬态性能(如超调量、跟踪误差等)研究却少之又少[15-16]。2008年,希腊****Bechlioulis和Rovithakis[15]提出了一种控制策略-预设性能控制,较好地实现了对跟踪误差瞬态性能的范围约束。预设性能控制方法的主要思路是通过设计预设性能函数对轨迹跟踪误差进行相应转化,从而保证误差能够以预期的瞬态性能收敛至预设范围内。文献[17]设计了一种预设性能的鲁棒反演控制,完成了控制任务且对未知随机扰动有较强的鲁棒性,但误差收敛速度较慢。文献[18]对于全状态的预设性能设计了一种受限指令的反演控制器,在输出和中间状态稳态分析的基础上,对全状态信号的瞬时性能进行了分析。
本文针对高超声速飞行器巡航段纵向动力学模型设计了一种新型预设性能神经反演控制方法。首先,将纵向运动模型分解为速度和高度子系统,并分别进行控制器设计,引入预设性能函数及转化误差来满足预先设定的瞬态性能和稳态精度。在设计控制器过程中引入径向基函数(RBF)神经网络对模型不确定项进行补偿和逼近,有效提高了控制精度。然后,分别对速度和高度子系统构造Lyapunov函数进行系统稳定性分析。最后,通过仿真对所设计控制器的可行性和有效性进行验证。
1 高超声速飞行器建模 1.1 高超声速飞行器纵向平面运动学方程 高超声速飞行器轨迹控制系统的任务是在保持飞行姿态稳定的前提下,通过调节燃料-空气比Φ和升降舵偏角δe在纵向平面内实现对速度参考指令和高度参考指令的有效跟踪。高超声速飞行器受力情况示意图如图 1所示,其在纵向平面内的运动模型为[7-8, 19-20]
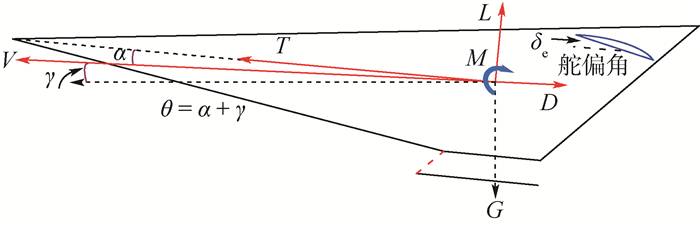 |
| 图 1 高超声速飞行器受力示意图 Fig. 1 Force map of hypersonic flight vehicle |
| 图选项 |
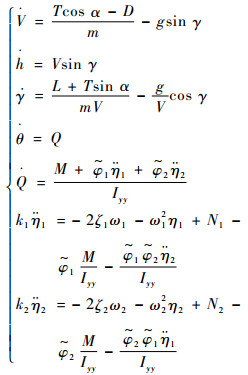 | (1) |
式中:V为飞行速度;γ为飞行航迹角;h为飞行高度;θ为俯仰角;g为重力加速度;Q为俯仰角速率;m和Iyy分别为飞行器的质量和俯仰转动惯量;L、T、D和M分别为升力、推力、阻力和俯仰力矩;攻角α=θ-γ;ηi为弹性状态量;ζi和ωi分别为第i阶弹性模态的阻尼系数和自然频率;Ni为第i阶广义弹性力;
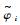
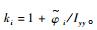
式(1)中L、T、D、M的拟合式如下:
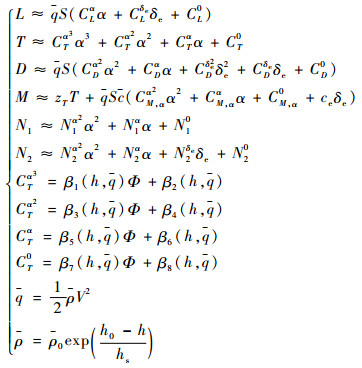 | (2) |
式中:q为空气动压;ρ为空气密度;S和c分别为飞行器参考气动面积和气动弦长;Φ和δe分别为燃料-空气比和升降舵偏角;zT为推力力矩耦合系数。式(1)和(2)中飞行器几何参数和气动参数见文献[21]。
注1??本文所采用的Parker弹性体模型相比于文献[22-23]中采用的刚体模型更能准确地模拟出飞行器的真实飞行状态。本文所采用模型的气动力拟合公式中充分考虑了弹性状态的影响,将弹性状态视为系统的不确定项处理,因此相应的控制难度加大。
由式(1)和式(2)可以看出,速度的变化主要与燃料-空气比Φ相关,而高度的变化主要与舵偏角δe相关。因此控制输入选择燃料-空气比Φ和升降舵偏角δe,输出为速度V和高度h。
由式(1)和式(2)可以看出,飞行器弹性体状态通过气动力L、T、D、M严重地同刚体状态耦合,如果抑制弹性状态的效果不明显,将会对刚体状态的控制产生较大影响。因此,控制系统的任务除了保证刚体系统稳定跟踪参考输入外,还要保证弹性状态最终是收敛的。
为便于控制律设计,通常先将高超声速飞行器的运动模型分解为速度子系统与高度子系统,再分别对其设计相应控制律。这里已将2个子系统的耦合考虑在内[14]。
1.2 RBF神经网络 引入如下RBF神经网络用来逼近模型不确定项:
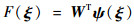 | (3) |
式中:F∈R和ξ∈Rn分别为神经网络的输出和输入;W∈Rn为权值向量;ψ(ξ)=[ψ1(ξ), ψ2(ξ), …, ψn(ξ)]T为径向基函数。通常情况下,将ψi(ξ)选取成如下高斯基函数:
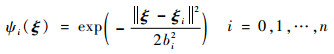 | (4) |
式中:ξi∈Rn为高斯基函数中心向量;bi∈R+为高斯基函数的宽度。
引理1[24]??给定任意连续函数F(ξ)是定义在紧集Ωξ上的实函数以及任意常数
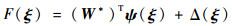 | (5) |
式中:

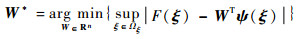 | (6) |
2 控制器设计与稳定性分析 2.1 预设性能分析 定义1??连续函数ρ(t):R+→R+,若同时满足以下条件[25]:①ρ(t)是严格单调递减的正函数;②
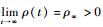
基于定义1,本文选取如下预设性能函数:
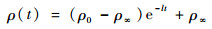 | (7) |
式中:ρ0, ρ∞, l∈R+为待设计参数且ρ0>ρ∞,ρ0为函数ρ(t)的初值,ρ∞为函数ρ(t)的稳态值,l为函数ρ(t)的下降速率。
可以看出,ρ(t)具有如下性质:①ρ(t)为正的单调递减函数;②ρ(0)=(ρ0-ρ∞)+ρ∞=ρ0>ρ∞;
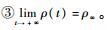
跟踪误差e(t)应满足下述定义不等式:
 | (8) |
式中:κ和λ为正参数。
则对于任意未知但有界的e(0),均有
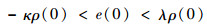 | (9) |
由式(8)可以看出,ρ∞表示e(t)稳态值的上界,即-κρ∞ < e(∞) < λρ∞,故可通过选取合适的ρ∞来保证e(t)具有理想的稳态精度。ρ(0)表示e(t)所允许的最大超调量。
在设计控制系统的过程中,直接对不等式约束(式(8))进行处理的难度非常大,因此可以先将不等式约束转化为等式约束再进行设计,这里定义一个误差转换函数H(ε(t)):
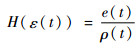 | (10) |
式中:ε(t)为转换误差。
H(ε(t))平稳递增,则有
 | (11) |
那么H(ε(t))的逆可以写成
 | (12) |
这里将ε(t)选取为如下形式:
 | (13) |
对式(13)求导可得
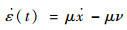 | (14) |
式中:
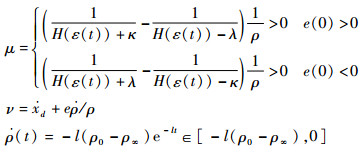 |
显然,μ和ν是有界的。
定理1??若ε(t)有界,则有-κρ(t) < e(t) < λρ(t)。
证明??当e(0)>0时,因为ε(t)有界,必存在有界正数εM使得|ε(t)|≤εM。这样,式(13)的逆变换为
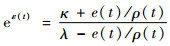 | (15) |
由式(15)可得
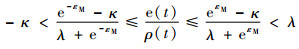 | (16) |
也即
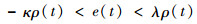 |
反之可得e(0) < 0的情况。????证毕
下文的控制器设计将基于转换误差ε(t)。定理1表明,只要ε(t)有界,误差e(t)便可被限定在式(8)所定义的预设区域内。通过为ρ(t)设计合适的参数,便可保证e(t)具有预期的瞬态性能与稳态精度。
2.2 速度控制器设计与稳定性分析 根据文献[14]中的时间刻度原理,由于速度的动态变化比高度角及角速率(γ、θ、Q)更慢,可以认为速度和高度属于长周期模态,高度角属于短周期模态,这样在设计控制器时就可以将高超声速飞行器运动模型分解为速度子系统和高度子系统。因此将式(1)中
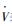
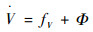 | (17) |
式中:
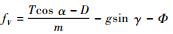
定义速度跟踪误差为
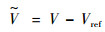 | (18) |
将式(18)求导,得到
 | (19) |
根据式(13),速度的转换误差εV可以表示为
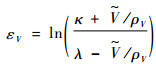 | (20) |
式中:ρV=(ρV0-ρV∞)e-lVt+ρV∞,ρV0、ρV∞、lV均为正的待设计参数。
结合式(19)对式(20)求导可得
 | (21) |
若假设μV>μV0>0,式(21)可以进一步写成
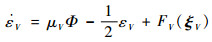 | (22) |
式中:

基于反演理论,将实际控制律Φ设计为
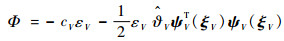 | (23) |
对于式(5)中未知的最优权值向量,定义
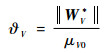 | (24) |
根据式(24)可得
 | (25) |
式中:
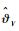
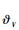
证明??选取如下Lyapunov函数:
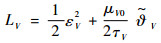 | (26) |
式中:
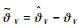
对式(26)求导可得
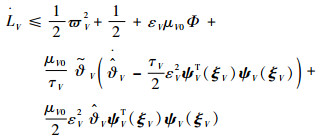 | (27) |
将式(23)和式(25)代入式(27)可得
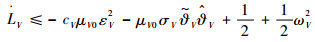 | (28) |
又有不等式
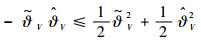 | (29) |
将不等式(29)代入式(28)可得
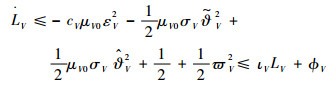 | (30) |
式中:
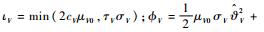
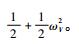
结合式(29)可得
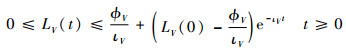 | (31) |
显然,εV、
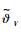
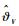
2.3 高度控制器设计与稳定性分析 为了便于控制器设计,根据式(1)将高超声速飞行器高度子系统改写为如下形式:
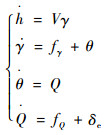 | (32) |
式中:
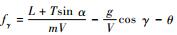
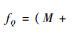
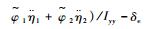
定义高度跟踪误差为
 | (33) |
将式(33)求导并结合式(32),得到
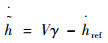 | (34) |
根据式(13),高度的转换误差函数εh可表示为
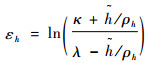 | (35) |
式中:ρh=(ρh0-ρh∞)e-lht+ρh∞,ρh0、ρh∞、lh均为正的待设计参数。
类似的,航迹角的转换误差函数εγ可表示为
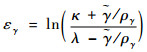 | (36) |
式中:ργ=(ργ0-ργ∞)e-lγt+ργ∞,ργ0、ργ∞、lγ均为正的待设计参数。
俯仰角的转换误差函数εθ可表示为
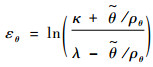 | (37) |
式中:ρθ=(ρθ0-ρθ∞)e-lθt+ρθ∞,ρθ0、ρθ∞、lθ均为正的待设计参数。
俯仰角速率的转换误差函数εQ可表示为
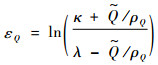 | (38) |
式中:ρQ=(ρQ0-ρQ∞)e-lQt+ρQ∞,ρQ0、ρQ∞、lQ均为正的待设计参数。
结合式(34)对式(35)求导可得
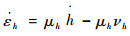 | (39) |
若假设μh>μh0>0,式(39)可以进一步写成
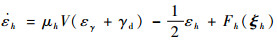 | (40) |
式中:
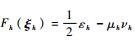
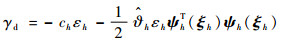 | (41) |
其中:
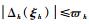
基于反演理论,将虚拟控制律γd设计为
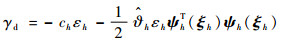 | (42) |
同时
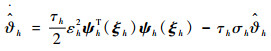 | (43) |
式中:
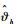
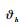
选取如下Lyapunov函数:
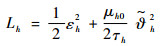 | (44) |
对式(44)求导可得
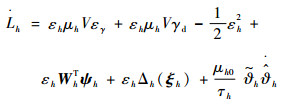 | (45) |
根据Yong不等式,有
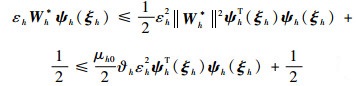 | (46) |
又有不等式
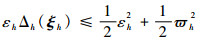 | (47) |
因此
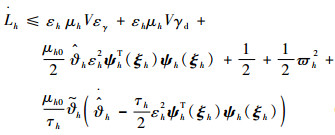 | (48) |
将式(42)、式(43)代入式(48)可得
 | (49) |
定义航迹角误差为
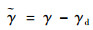 | (50) |
将式(50)求导并结合式(32),得到
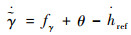 | (51) |
结合式(51)对式(36)求导可得
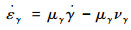 | (52) |
若假设μγ>μγ0>0,式(52)可以进一步写成
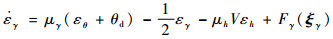 | (53) |
式中:
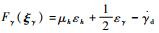
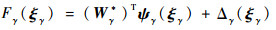 | (54) |
其中:

基于反演理论,将虚拟控制律θd设计为
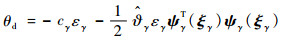 | (55) |
同时
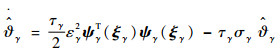 | (56) |
式中:
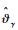
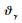
选取如下Lyapunov函数:
 | (57) |
对式(57)求导可得
 | (58) |
与式(46)和式(47)类似可得
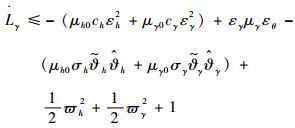 | (59) |
定义俯仰角误差为
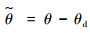 | (60) |
将式(60)求导并结合式(32),得到
 | (61) |
结合式(61)对式(37)求导可得
 | (62) |
若假设μθ>μθ0>0,式(62)可以进一步写成
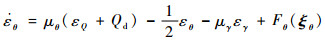 | (63) |
式中:
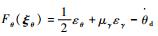
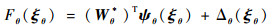 | (64) |
其中:
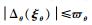
基于反演理论,将虚拟控制律Qd设计为
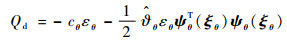 | (65) |
同时
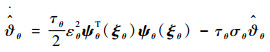 | (66) |
式中:
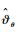
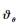
选取如下Lyapunov函数:
 | (67) |
对式(67)求导可得
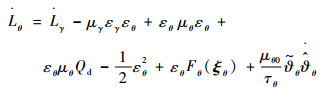 | (68) |
与式(46)和式(47)类似可得
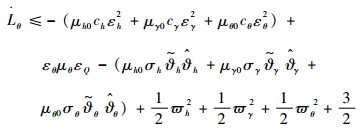 | (69) |
定义俯仰角速率误差为
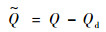 | (70) |
将式(70)求导并结合式(32),得到
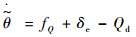 | (71) |
结合式(71)对式(38)求导可得
 | (72) |
若假设μQ>μQ0>0,式(72)可以进一步写成
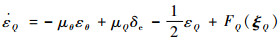 | (73) |
式中:
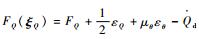
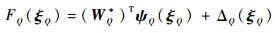 | (74) |
其中:
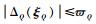
基于反演理论,将实际控制律δe设计为
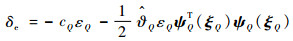 | (75) |
同时
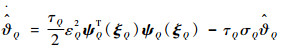 | (76) |
式中:
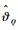
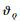
证明??选取如下Lyapunov函数:
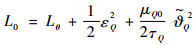 | (77) |
对式(77)求导可得
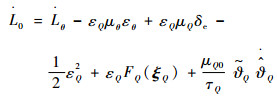 | (78) |
与式(46)和式(47)类似可得
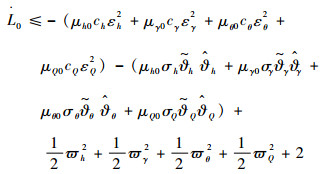 | (79) |
注2??RBF神经网络具有补偿和逼近系统的不确定项的能力,这样一来避免了虚拟控制量的重复求导问题。在每一步设计控制律中,通过引入神经网络权值的估计值,使得只有一个参数需要在线更新,这样简化了参数设计降低了计算量。同时考虑到RBF神经网络的估计性能是建立在紧集Ω上的,这里只能保证控制系统的局部稳定。
应用如下不等式:
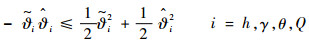 | (80) |
将式(79)写成如下形式:
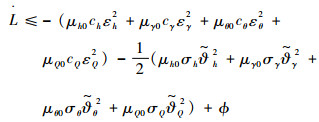 | (81) |
式中:
 | (82) |
令ι=min{2ciμi, τiσi},式(81)变为
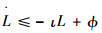 | (83) |
则由式(83)可得
 | (84) |
式(84)表明了L(t)是有界的,又有εi、
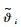
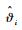
3 仿真与分析 针对高超声速飞行器动力学模型进行速度与高度的闭环仿真实验。速度与高度参考输入均由图 2所示的二阶参考模型给出。该二阶参考模型的传递函数为[26]
 | (85) |
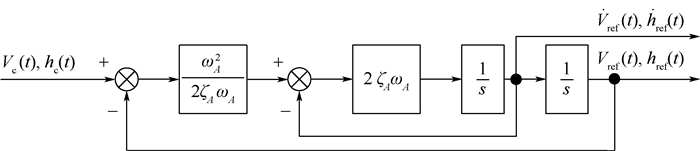 |
| 图 2 参考输入二阶模型结构 Fig. 2 Second-order model structure of reference input |
| 图选项 |
二阶参考模型参数取为:ζA=0.9,ωA=0.1。RBF神经网络的输入ξV、ξh、ξγ、ξθ、ξQ以及非线性函数的高斯基宽度均为1。定义的自适应律的初值为:
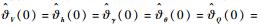
表 1 高超声速飞行器的状态初值 Table 1 Hypersonic flight vehicle state initial value
| 参数 | 数值 |
| V/(m·s-1) | 2 500 |
| h/m | 27 000 |
| γ/(°) | 0 |
| θ/(°) | 1.529 5 |
| Q/((°)·s-1) | 0 |
| η1 | 0.285 7 |
| η2 | 0.235 0 |
表选项
通过MATLAB/Simulink搭建控制系统,采用步长为0.01 s的四阶Runge-Kuta法验证本文控制方法的有效性。在保持动压q=90 148 Pa不变的前提下,要求巡航阶段高超声速飞行器在速度阶跃100 m/s, 高度阶跃100 m作用下。控制的目的是要求系统输出跟踪给定的速度和高度参考指令并保证跟踪误差稳定在给定的预设性能范围内。为了检验控制律的鲁棒性,假设高超声速飞行器模型气动系数存在±40%的摄动量,定义
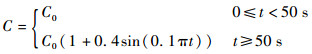 | (86) |
式中:C0为高超声速飞行器气动系数的标称值。
为了验证本文方法的优越性,将其与文献[27]中传统反演控制方法进行对比仿真,仿真结果如图 3~图 9所示。由图 3和图 4可见,速度与高度均能准确跟踪参考输入,采用预设性能控制方法时的速度跟踪误差与高度跟踪误差均能够被限定在预设的区域内;与文献[27]方法相比,本文方法能够保证速度跟踪误差与高度跟踪误差具有较好的瞬态性能和稳态性能;当存在气动参数摄动时,本文方法的控制精度更高,也具有更强的鲁棒性。图 5表明,2种控制方法的航迹角控制效果并无很大差别,但本文方法的航迹角响应更平滑。虽然文献[27]方法的俯仰角与俯仰角速率响应更平滑,但采用本文方法时,这2个角度响应没有出现高频抖振,并且本文方法能够保证俯仰角以及俯仰角速率跟踪误差具有更好的动态性能与稳态精度。由图 6~图 8可见,2种控制方法的弹性状态与控制输入均没有高频抖振现象。图 9表明,误差转换函数εV(t)、εh(t)、εγ(t)、εθ(t)与εQ(t)均有界。
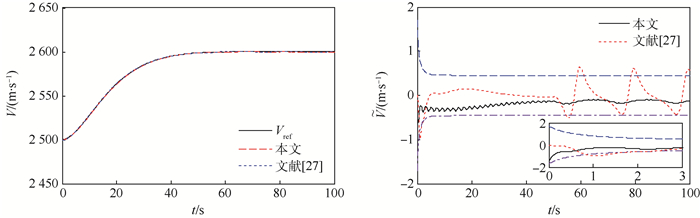 |
| 图 3 速度跟踪响应 Fig. 3 Velocity tracking performance response |
| 图选项 |
 |
| 图 4 高度跟踪响应 Fig. 4 Altitude tracking performance response |
| 图选项 |
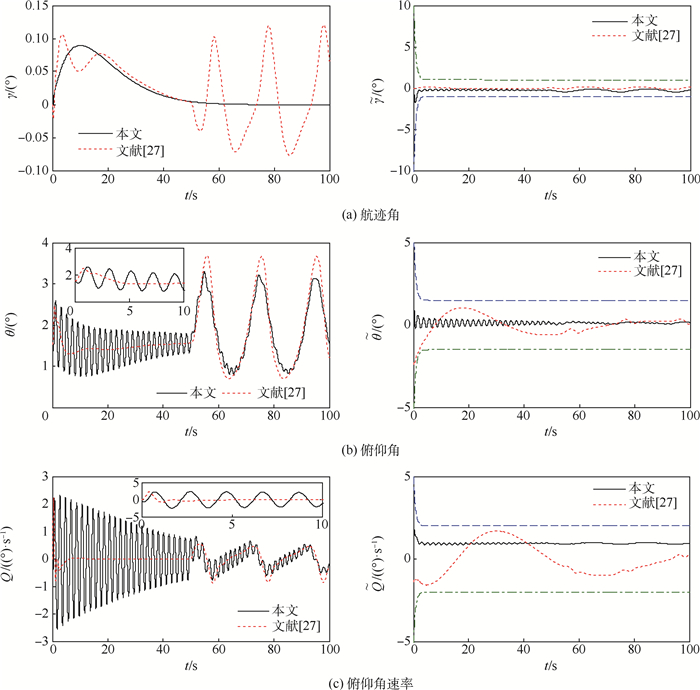 |
| 图 5 高度角曲线 Fig. 5 Curves of altitude angle |
| 图选项 |
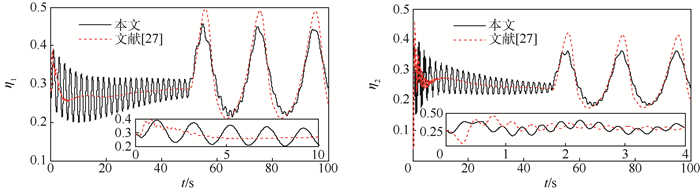 |
| 图 6 弹性状态 Fig. 6 Flexible states |
| 图选项 |
 |
| 图 7 燃料-空气比 Fig. 7 Fuel-to-air ratio |
| 图选项 |
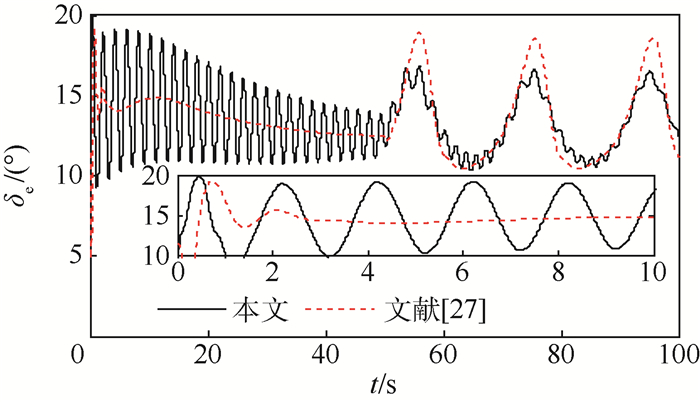 |
| 图 8 升降舵偏角 Fig. 8 Elevator declination |
| 图选项 |
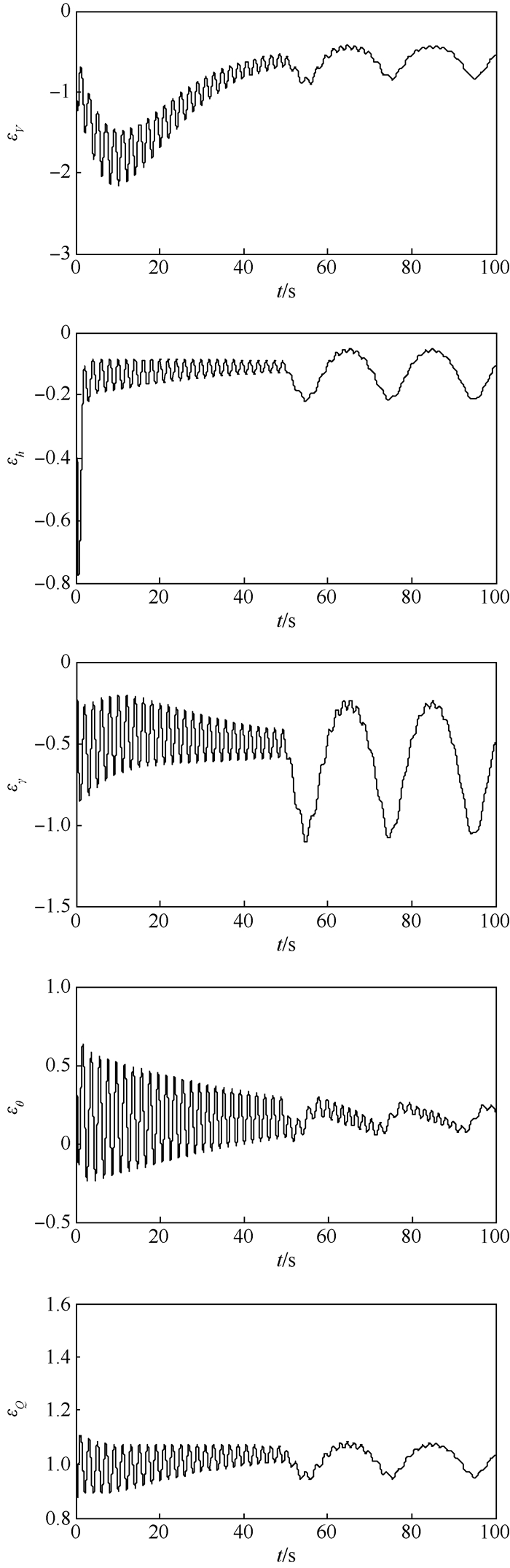 |
| 图 9 转换误差函数 Fig. 9 Conversion error function |
| 图选项 |
4 结论 针对高超声速飞行器纵向动力学模型设计了一种预设性能神经反演控制方法。
1) 通过构造预设性能函数,使得速度跟踪误差和高度跟踪误差能够同时满足预先设定的瞬态性能和稳态精度。
2) 为了保证系统具有足够的鲁棒性应对参数及模型的不确定,在每个子系统反演控制器设计过程中的未知非线性函数引入RBF神经网络估计,在对不确定项逼近的过程中仅有一个参数需要实时更新,既有效将控制精度提高,又顺利避免了反演控制方法中的“微分膨胀问题”,并降低了计算量。
3) 基于Lyapunov函数证明了所有闭环系统均是有界的。仿真结果表明,同现有的反演控制器相比,本文所设计的控制方法可以很好地实现控制目标,满足预设性能且对未知的随机扰动具有较强的鲁棒性。
参考文献
| [1] | 孙长银, 穆朝絮, 余瑶. 近空间高超声速飞行器控制的几个科学问题研究[J]. 自动化学报, 2013, 39(11): 1901-1913. SUN C Y, MU C X, YU Y. Some control problems for near space hypersonic vehicles[J]. Acta Automatica Sinica, 2013, 39(11): 1901-1913. (in Chinese) |
| [2] | 黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战[J]. 控制理论与应用, 2011, 28(10): 1496-1505. HUANG L, DUAN Z S, YANG J Y. The challenge to control science of near space hypersonic vehicles[J]. Control Theory and Application, 2011, 28(10): 1496-1505. (in Chinese) |
| [3] | SOLOWAY D I, OUZTS P J, WOLPERT D H, et al.The role of guidance, navigation, and control in hypersonic vehicle multidisciplinary design and optimization: AIAA-2009-7329[R].Reston: AIAA, 2009. |
| [4] | 董朝阳, 路遥, 王青. 高超声速飞行器指令滤波反演控制[J]. 宇航学报, 2016, 37(8): 957-963. DONG Z Y, LU Y, WANG Q. Command filtered backstepping control for hypersonic vehicles[J]. Journal of Astronautics, 2016, 37(8): 957-963. DOI:10.3873/j.issn.1000-1328.2016.08.008 (in Chinese) |
| [5] | FIORENTINI L.Nonlinear adaptive controller design for air-breathing hypersonic vehicles[D].Columbus: The Ohio State University, 2010. |
| [6] | FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 401-406. |
| [7] | BOLENDER M A, DOMAN D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 374-387. DOI:10.2514/1.23370 |
| [8] | PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856-869. DOI:10.2514/1.27830 |
| [9] | 李昭莹, 余令艺, 刘昊, 等. 高超声速飞行器非线性鲁棒控律设计[J]. 控制理论与应用, 2016, 33(1): 62-69. LI Z Y, YU L Y, LIU H, et al. Nonlinear robust controller design for hypersonic vehicles[J]. Control Theory & Applications, 2016, 33(1): 62-69. (in Chinese) |
| [10] | XU H J, MIRMIRANI M D, IANNOU P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 829-838. DOI:10.2514/1.12596 |
| [11] | 余朝军, 江驹, 甄子洋, 等. 高超声速飞行器弹性自适应控制方法[J]. 哈尔滨工程大学学报, 2018, 39(6): 1026-1031. YU C J, JIANG J, ZHEN Z Y, et al. A novel resilient adaptive control scheme for hypersonic vehicles[J]. Journal of Harbin Engineering University, 2018, 39(6): 1026-1031. (in Chinese) |
| [12] | ZONG Q, WANG F, SU R, et al. Robust adaptive backstepping tracking control for a flexible air-breathing hypersonic vehicle subject to input constraint[J]. Journal of Aerospace Engineering, 2015, 229(1): 10-25. |
| [13] | GAO D X, WANG S X, ZHANG H J. A singularly perturbed system approach to adaptive neural back-stepping control design of hypersonic vehicles[J]. Journal of Intelligent and Robotic Systems, 2014, 73(1): 249-259. |
| [14] | BIN X. Robust adaptive neural control of flexible hypersonic flight vehicle with dead-zone input nonlinearity[J]. Nonlinear Dynamics, 2015, 80(3): 1509-1520. DOI:10.1007/s11071-015-1958-8 |
| [15] | BECHLIOULIS C P, ROVITHAKIS G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J]. IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099. DOI:10.1109/TAC.2008.929402 |
| [16] | BECHLIOULIS C P, ROVITHAKIS G A. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems[J]. Automatica, 2009, 45(2): 532-538. DOI:10.1016/j.automatica.2008.08.012 |
| [17] | 王鹏飞, 王洁, 时建明, 等. 高超声速飞行器预设性能反演鲁棒控制[J]. 电机与控制学报, 2017, 21(2): 94-102. WANG P F, WANG J, SHI J M, et al. Prescribed performance back-stepping robustness control of a flexible hypersonic vehicle[J]. Electric Machines and Control, 2017, 21(2): 94-102. (in Chinese) |
| [18] | 张扬, 吴文海, 胡云安, 等. 基于全状态预设性能的受限制令反演控制器设计[J]. 控制与决策, 2018, 33(3): 479-485. ZHANG Y, WU W H, HU Y A, et al. Constrained command backstepping controller design under full state prescribed performance[J]. Control and Decision, 2018, 33(3): 479-485. (in Chinese) |
| [19] | 卜祥伟. 高超声速飞行器纵向运动非线型控制技术[M]. 西安: 西安电子科技大学出版社, 2018: 16-18. BU X W. Nonlinear control technology for longitudinal motion of hypersonic vehicles[M]. Xi'an: Xidian University Press, 2018: 16-18. (in Chinese) |
| [20] | BU X W, WU X Y, HUANG J Q, et al. Minimal-learning-parameter based simplified adaptive neural back-stepping control of flexible air-breathing hypersonic vehicles without virtual controllers[J]. Neurocomputing, 2016, 175: 816-825. DOI:10.1016/j.neucom.2015.10.116 |
| [21] | 李惠峰. 高超声速飞行器制导与控制技术(下)[M]. 北京: 中国宇航出版社, 2012: 469-473. LI H F. Hypersonic vehicles guidance and control technology(Ⅱ)[M]. Beijing: China Aerospace Press, 2012: 469-473. (in Chinese) |
| [22] | 唐意东, 李小兵, 夏训辉. 高超声速飞行器弱抖振反演滑模控制律设计[J]. 导弹与航天运载技术, 2014, 17(6): 17-30. TANG Y D, LI X B, XIA X H. Design of weak buffet back stepping sliding mode control law for hypersonic vehicles[J]. Missiles and Space Vehicles, 2014, 17(6): 17-30. (in Chinese) |
| [23] | 高道祥, 孙增圻, 罗熊, 等. 基于Back-stepping的高超声速飞行器模糊自适应控制[J]. 控制理论与应用, 2008, 25(5): 805-810. GAO D X, SUN Z Y, LUO X, et al. Fuzzy adaptive control for hypersonic vehicle via Back-stepping method[J]. Control Theory and Application, 2008, 25(5): 805-810. (in Chinese) |
| [24] | SANNER R M, SLOTINE J E. Gaussian networks for direct adaptive control[J]. IEEE Transactions on Neural Networks, 1992, 3(6): 837-863. DOI:10.1109/72.165588 |
| [25] | 胡云安, 耿宝亮, 盖俊峰. 初始误差未知的不确定系统预设性能反演控制[J]. 华中科技大学学报(自然科学版), 2014, 42(8): 43-47. HU Y A, GENG B L, GAI J F. Prescribed performance backstepping control for uncertain systems with unknown initial errors[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2014, 42(8): 43-47. (in Chinese) |
| [26] | 卜祥伟, 吴晓燕, 马震, 等. 基于状态重构的吸气式高超声速飞行器鲁棒反演控制器设计[J]. 固体火箭技术, 2015, 38(3): 314-319. BU X W, WU X Y, MA Z, et al. State-reconstruction-based robust backstepping controller of air-breathing hypersonic vehicles[J]. Journal of Solid Rocket Technology, 2015, 38(3): 314-319. (in Chinese) |
| [27] | BU X W, WU X Y, ZHANG R, et al. Tracking differentiator design for the robust backstepping control of a flexible air-breathing hypersonic vehicle[J]. Journal of the Franklin Institute, 2015, 352(4): 1739-1765. DOI:10.1016/j.jfranklin.2015.01.014 |
