近年来,研究者针对系统的可靠性分配问题做了一定的研究。Amari和Hegde[7]将平均分配法、考虑重要度复杂度等分配方法进行改进,使其适用于可修系统的可靠性分配,但仅适用于串联系统。冯川等[8]根据重要程度因素,构建了重要度相同和不同的2种使用可用度模型,并提出了分配过程,但该方法解算过于复杂,且不适用于包含复杂故障逻辑的模型。Elegbede和Adjallah[9]提出了基于遗传算法的可修系统的分配方法,该方法实现了将多目标优化问题转化为单目标优化问题,但该方法计算复杂,较难进行实际操作。以上文献中提出的可修系统的分配方法或需要一定的约束条件,或在算法上过于复杂,因此无法有效应用于可修复杂系统的任务可靠性分配。
可修系统由于存在维修的影响,在工程应用中通常有2种分配方法:一是将可用度看作可靠度并将其转化为故障率,然后运用基于不可修复系统的可靠性分配方法进行分配,该方法没有考虑到维修的影响,导致分配结果误差较大; 二是将可用度直接等分分配给各单元,然后依据指定的MTTR计算MTBF,但该方法只能适用于串联系统,没有考虑到包含复杂故障逻辑的系统。对于不可修系统的故障率目标值,通常假设组件一旦故障系统就故障,而对于可修系统中的故障率则为严重故障率,即组件故障在允许的修复时间内修复完成即可认定无故障。因此,对于同一个系统,具有维修条件的系统故障率目标值要低于没有维修条件的系统故障率目标值,两者的区别在于是否具有维修的影响。因此本文以系统故障率和系统修复率为分配目标提出了一种考虑维修、故障逻辑等多因素影响的可修系统任务可靠性分配方法,该方法首先将故障率目标转化为去除维修影响的故障率目标值;然后将传统的评分分配法进行改进,使其能够对具有包含串联、并联、表决等复杂故障逻辑的任务可靠性模型进行分配,并依据各单元故障率分配结果计算各单元的修复率;最后通过备件因子对分配值进行修正,可以得到各单元的故障率。该方法简单易操作,便于工程中使用。
1 可修系统任务可靠度分配流程 对于可修系统提出的任务可靠性目标值通常包含了维修的影响,因此大多数不可修系统的分配方法无法适用于可修系统的分配。若不考虑维修特性将导致各单元的分配结果误差过大。
本文提出的可修系统任务可靠性分配方法综合考虑了维修因素、复杂任务可靠性逻辑因素以及备件因素的影响,因此分配主要分为3步:对规定的任务剖面顶层指标进行转化,考虑故障逻辑的评分分配,以及对有备件库的单元进行修正,分配流程如图 1所示。
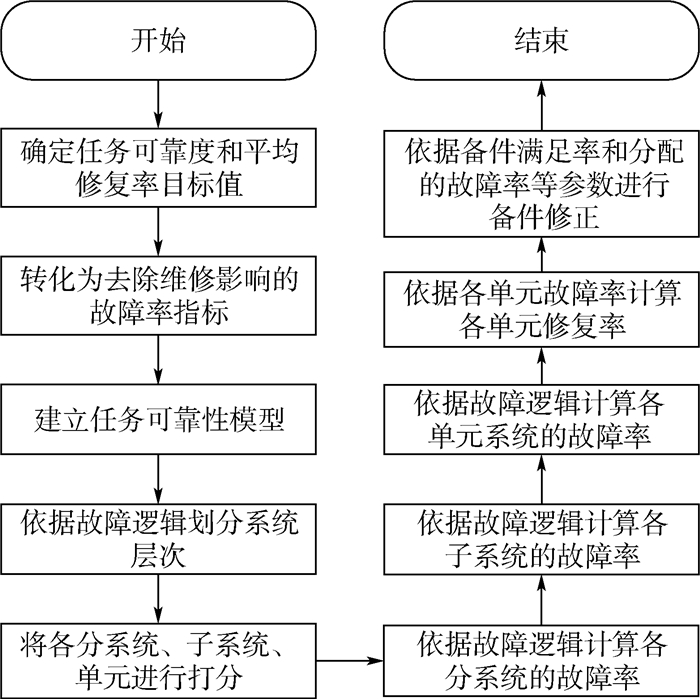 |
| 图 1 可修系统任务可靠度分配流程 Fig. 1 Process of mission reliability allocation for repairable system |
| 图选项 |
具体步骤如下:
1) 顶层指标转化。首先,明确可修系统顶层待分配的系统故障率和系统修复率的目标值;然后,将已知的故障率转化为去除维修影响的故障率目标值,使其能够适用于不可修系统的分配方法。
2) 依据故障逻辑进行评分分配。首先,依据故障逻辑将系统由上而下进行层次划分,并聘请专家对各层级对象进行打分。然后,用改进的评分分配法对系统自上而下逐层进行评分分配,其中,不同层级对象的综合得分依据其对应的故障逻辑进行计算。最后,根据各底层单元的故障率计算各单元的修复率。
3) 对具有备件库的单元进行修正。根据备件满足率和分配的故障率等参数对单元进行故障率修正,最终得到所有单元的故障率分配值。
2 顶层指标转化计算 考虑维修的任务可靠度[10-11]是产品在允许的维修时间内,在规定的任务剖面中的任一随机时刻,能够使用且完成规定功能的概率。一般考虑任务可靠性和维修性对完成任务的影响,表达式为
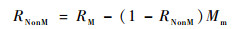 | (1) |
式中:RNonM为去除维修影响下的任务可靠度,RM为考虑维修下的任务可靠度,如果在不允许维修的情况下,RNonM=RM;Mm为维修度,假设维修时间服从参数为μ的指数分布:
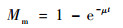 | (2) |
其中:t为任务期间内允许的维修时间;μ为平均故障修复率。
从式(1)和式(2)可以看出,对于同一系统或单元,有维修影响的可靠度要高于去除维修影响的可靠度,将可修复系统可靠度的分配按照不可修复系统的分配方法进行分配,显然会导致各单元分配的可靠度过高,造成指标浪费。因此,在分配之前将可修复系统的故障率指标转化为去除维修影响下的故障率指标,通过指标转化从而使分配结果更加合理。假设系统寿命服从指数分布,综合式(1)和式(2)则得到去除维修影响下待分配的系统故障率为
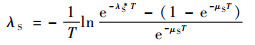 | (3) |
式中:λS为去除维修影响的可修系统S的故障率;λS*为已知的可修系统S待分配的故障率;μS为已知的S系统待分配的平均故障修复率;T为系统工作时间。
3 基于故障逻辑的评分分配法 任务可靠度分配要综合考虑系统各单元之间的关系和故障逻辑,因此需要根据不可修复系统的任务可靠性模型对评分分配法中的综合得分计算公式进行修改,使其能够进行除串联以外其他模型的可靠度分配。
3.1 分层评分 鉴于当前系统通常不再是由单一故障逻辑组成的简单系统,而是由存在串联、并联、表决以及旁联等故障逻辑组成的大型复杂系统,传统的单层评分分配方法会极大增加计算的复杂性,因此应将系统根据故障逻辑情况由上而下进行层级划分,使某一层级各组成部分只具有单一任务可靠性逻辑。如图 2所示示例中,系统级是由分系统A、B、Z组成的串联系统。分系统是由各子系统组成,其中,分系统A是由子系统A1到An组成的并联系统,分系统B是由子系统B1到Bn组成的表决系统,分系统Z是由子系统Z1到Zn组成的旁联系统。各子系统则是由各单元组成的系统,以子系统A1、B1、Z1为例,子系统A1是由单元A11到A1n组成的并联系统,子系统B1是由单元B11到B1n组成的表决系统,子系统Z1是由单元Z11到Z1n组成的旁联系统。
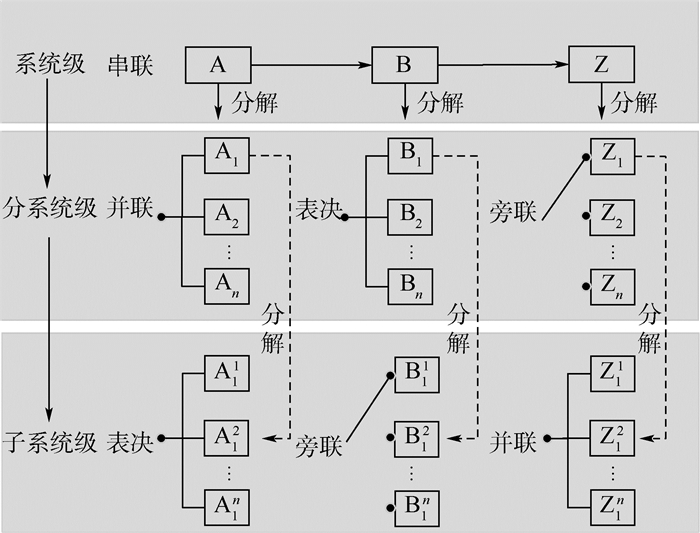 |
| 图 2 分层模型 Fig. 2 Hierarchical model |
| 图选项 |
对分层后的系统自上而下对每一层级的系统或单元进行评分。以图 2示例中的分系统A为例,建立评分表如表 1所示。
表 1 评分表示例 Table 1 Score form example
| 分系统A | πf | πj | πt | πe | 得分 |
| 子系统A1 | af1 | aj1 | at1 | ae1 | wA1 |
| 子系统A2 | af2 | aj2 | at2 | ae2 | wA2 |
| | | | | | |
| 子系统Ai | aif | aij | ait | aie | wAi |
表选项
表 1中,πf为复杂度;πj为技术发展水平;πt为工作时间;πe为环境条件;wSi为第i个子系统Ai的得分,计算公式为
 | (4) |
3.2 按照故障逻辑实施分配 评分分配法的核心思想是权重分配,分配公式为
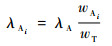 | (5) |
式中:λAi为A系统下的第i个分系统或单元被分配的故障率;λA为A系统的顶层故障率目标值;wAi为A系统第i个分系统或单元的得分,计算方法如式(4)所示;wT为系统A的综合得分。
传统的评分分配法只能够对串联系统进行分配,在串联系统中,总故障率为各单元故障率的总和,因此系统的综合得分为各单元的评分加和。因此,本文考虑将综合得分的计算公式进行扩展,使其能够对其他故障逻辑的系统也进行分配。
以并联系统为例,假设系统S包含n个不同的单元,失效率为λ1到λn,系统的故障率λS与各单元失效率之间的关系式为
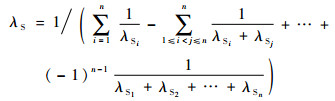 | (6) |
式中:λSi为第i个子系统的第i个单元初步被分配的故障率。
若系统S的综合得分为wSP,n个单元的相对评分分别为wS1到wSn,二者关系式为
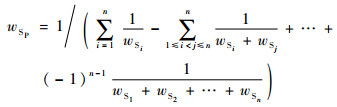 | (7) |
依据上述方法也可以得到具有表决、旁联等其他逻辑关系系统的综合得分计算方法。将具有不同故障逻辑的系统以综合得分的形式展现出来,可以将适用于单一串联系统的评分分配法扩展至适用于具有多种故障逻辑的复杂系统。以此方法为基础,对系统进行自上而下的任务可靠性指标分配。假设系统具有分系统、子系统、单元三层,计算方法如下:
1) 分配各分系统的故障率
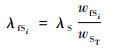 | (8) |
式中:λfSi为系统S第i个分系统初步被分配的故障率;wST为系统S的综合得分;wfSi为系统S第i个分系统的打分。
2) 分配各子系统的故障率
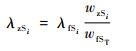 | (9) |
式中:λzSi为第i个分系统的第i个子系统初步被分配的故障率;wfST为分系统的综合得分;wzSi为第i个分系统的第i个子系统的打分。
3) 分配各单元的故障率
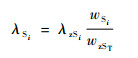 | (10) |
式中:wzST为子系统的综合得分;wSi为子系统第i个单元的打分。
4) 分配各单元的修复率
各单元的维修性分配采用依据故障率的分配方法,计算公式为
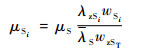 | (11) |
式中:μSi为S系统第i个单元的平均修复率;λS为S系统各单元的故障率的平均值。
4 备件因子修正 第2节和第3节首先将可修系统的顶层任务可靠性指标去除维修的影响,然后运用基于逻辑关系的评分分配法对故障率和维修率进行了初步分配。然而,通常部件发生故障时,会利用其备件进行更换,以使部件及其系统迅速恢复功能,一定数量的备件会显著影响可靠度[12],备件数量越多,可靠度越高。在实际工程中一些单元会配备相应的备件库来保障单元的可靠度,但在第2节和第3节提出的分配方法中未考虑备件因素的影响,因此会导致有备件的单元被分配的可靠度要求过低。本文考虑利用备件修正因子对具有备件单元的初始可靠度分配结果进行修正。
如果已知某单元具有备件库,且备件完好,则经过分配后该单元整体的可靠度RN[13]为
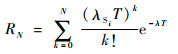 | (12) |
式中:k为取值范围为0到N的变量;N为备件数量;λ为故障率。
如果单元无备件库,则该单元的可靠度可以表示为
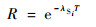 | (13) |
则备件修正系数α1可以用有备件下单元可靠度与无备件下单元可靠度的比例关系表示:
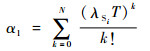 | (14) |
在设计阶段初期通常会给定备件满足率作为保障资源配备的要求。其中,备件满足率Pf与任务期间的故障次数X有如下关系[13]:
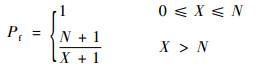 | (15) |
为计算方便,故障次数X可以用单元在任务时间T内的平均故障次数近似表达,即
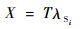 | (16) |
因此备件数量与备件满足率的关系可以近似表示为
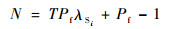 | (17) |
将式(17)代入式(14)可以得到备件修正系数α1为
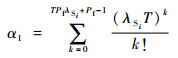 | (18) |
则修正后的故障率可以表示为
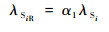 | (19) |
5 案例分析 以某可修系统为例,该系统由5个分系统组成,分系统1、2、3、4、5整体为串联系统,分系统3是由单元3A、3B组成的并联系统,分系统5是由单元5A、5B、5C组成的2/3的表决系统。其中,分系统1和分系统2有备件库,备件满足率要求为1,如图 3所示。假设更换备件时间忽略不计。故障率分配目标λS *=0.001/h,修复率μ=0.5/h,系统工作时间T=100 h,任务期间内允许维修时间t=0.5 h。
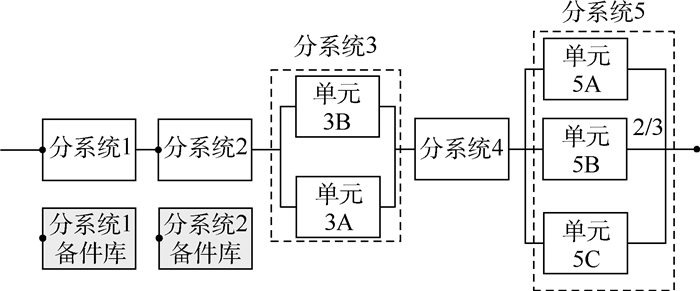 |
| 图 3 某生产系统任务可靠性模型 Fig. 3 Mission reliability model for a production system |
| 图选项 |
1) 计算去除维修影响下任务可靠性指标
根据式(3)可计算出去除维修影响下的待分配的故障率为λS=0.001 3/h。
2) 依据基于故障逻辑的评分分配法进行分配
由图 3可知该系统可分为2层,第1层是由分系统1~5组成的串联系统。第2层分为两部分:一部分是由单元3A、3B组成的并联系统,另一部分是由单元5A、5B、5C组成的表决系统。专家分层打分情况如表 2所示。
表 2 第1层总系统打分汇总 Table 2 First-level score for whole system
| 系统 | 编号 | 复杂度 | 技术水平 | 工作时间 | 环境条件 |
| 串联系统 | 分系统1 | 10 | 7 | 5 | 4 |
| 分系统2 | 10 | 6 | 6 | 6 | |
| 分系统3 | 8 | 8 | 8 | 8 | |
| 分系统4 | 8 | 9 | 9 | 5 | |
| 分系统5 | 6 | 10 | 6 | 6 | |
| 并联系统 | 单元3A | 10 | 8 | 7 | 5 |
| 单元3B | 10 | 9 | 8 | 6 | |
| 表决系统 | 单元5A | 10 | 8 | 7 | 5 |
| 单元5B | 10 | 9 | 8 | 6 | |
| 单元5C | 10 | 7 | 8 | 5 |
表选项
以故障率0.001 3/h为顶层指标,根据3.2节所述方法计算得出第1层各分系统的故障率如表 3所示。
表 3 第1层任务可靠性分配结果 Table 3 Mission reliability allocation results of the first level
| 系统编号 | 被分配的故障率/h-1 |
| 分系统1 | 0.000 139 |
| 分系统2 | 0.000 215 |
| 分系统3 | 0.000 408 |
| 分系统4 | 0.000 323 |
| 分系统5 | 0.000 215 |
表选项
分别以故障率0.000 408、0.000 215/h为目标,计算得出第2层并联系统及表决系统各单元的故障率分别如表 4所示。
表 4 第2层任务可靠性分配结果 Table 4 Mission reliability allocation results of the second level
| 系统 | 编号 | 被分配的故障率/h-1 |
| 并联系统 | 单元3A | 0.000 833 |
| 单元3B | 0.001 285 | |
| 表决系统 | 单元5A | 0.000 216 |
| 单元5B | 0.000 333 | |
| 单元5C | 0.000 216 |
表选项
根据式(11)计算各底层单元的平均故障修复时间和修复率如表 5所示。
表 5 维修性分配结果 Table 5 Results of maintenance allocation
| h-1 | ||
| 编号 | 分配的修复率 | 分配的MTTR |
| 分系统1 | 0.268 1 | 3.73 |
| 分系统2 | 0.413 6 | 2.41 |
| 分系统4 | 0.620 4 | 1.61 |
| 单元3A | 0.616 7 | 1.62 |
| 单元3B | 0.951 4 | 1.05 |
| 单元5A | 0.350 2 | 2.85 |
| 单元5B | 0.540 3 | 1.85 |
| 单元5C | 0.350 2 | 2.85 |
表选项
3) 备件修正
依据式(18)和式(19)对分系统1和2进行备件修正,修正后各系统与单元的故障率如表 6所示。
表 6 任务可靠度分配结果 Table 6 Mission reliability allocation results
| h-1 | ||
| 编号 | 备件修正前故障率分配值 | 备件修正后故障率最终分配值 |
| 分系统1 | 0.000 139 | 0.000 141 |
| 分系统2 | 0.000 215 | 0.000 220 |
| 分系统4 | 0.000 323 | 0.000 323 |
| 单元3A | 0.000 659 | 0.000 659 |
| 单元3B | 0.001 017 | 0.001 017 |
| 单元5A | 0.000 216 | 0.000 216 |
| 单元5B | 0.000 333 | 0.000 333 |
| 单元5C | 0.000 216 | 0.000 216 |
表选项
从表 6可以看出,备件修正后,系统1和系统2由于存在备件,故障率分配值相对较高,可靠度要求相应降低。
以λS=0.001/h为目标按照文中所述方法进行分配, 将分配结果与以λS=0.001 3/h为目标的分配结果作对比,结果如表 7所示。
表 7 可靠度分配结果对比 Table 7 Comparison of mission reliability allocation results
| h-1 | ||
| 编号 | 忽略维修影响的故障率分配值 | 考虑维修影响的故障率分配值 |
| 分系统1 | 0.000 107 | 0.000 141 |
| 分系统2 | 0.000 165 | 0.000 220 |
| 分系统4 | 0.000 248 | 0.000 323 |
| 单元3A | 0.000 641 | 0.000 659 |
| 单元3B | 0.000 989 | 0.001 017 |
| 单元5A | 0.000 166 | 0.000 216 |
| 单元5B | 0.000 256 | 0.000 333 |
| 单元5C | 0.000 166 | 0.000 216 |
表选项
由表 7可以看出,各单元在考虑维修影响下的故障率分配值高于不考虑维修影响下的故障率分配值,任务可靠性要求均有所降低。将分配结果作为输入,运用任务可靠性预计软件BlockSim[14-15]对系统进行任务可靠性建模和预计,最终得到系统的故障率为0.000 1/h,满足系统任务可靠性指标要求。因此,利用本文提出的方法进行任务可靠性分配不仅使分配结果更符合可修系统的特点,而且有效降低了设计难度。
6 结论 在工程中,传统的任务可靠性分配方法使分配结果过于保守。本文提出的可修系统的任务可靠性分配方法充分考虑了维修、复杂故障逻辑及备件因素对系统任务可靠性的影响,能够广泛应用于包括船舶、石油、电网等大型复杂系统,整体具有以下3点优势:
1) 通过有无维修影响下故障率的转换从而完成对可修系统任务可靠性的分配,分配方法简单实用。
2) 考虑故障关系的评分分配法实现了对复杂系统可靠度的分配。
3) 对具有备件库的单元进行备件修正,降低了设计难度,更贴近工程实际。
参考文献
| [1] | KAPUR K C, LAMBERSON L R. Reliability in engineering design[M]. Washington, D.C.: John Wiley & Sons, 1977: 405-414. |
| [2] | KECECIOGLU D. Reliability engineering handbook[M]. 2nd ed.Englewood: PTR Prentice Hall, 1991: 363-399. |
| [3] | CLEMENT L M. Reliability of military electronic equipment[J]. Journal of the British Institution of Radio Engineers, 1956, 16(9): 488-495. DOI:10.1049/jbire.1956.0050 |
| [4] | FALCONE D, SILVESTRI A, BONA D.Integrated factor method (IFM): A new reliability allocation technique[C]//Proceedings of the IASTED International Conference on Software Engineering and Applications, 2002: 166. |
| [5] | SILVESTRI A, FALCONE D, BONA G D, et al. A new method for reliability allocation:Critical flow method[J]. Lecture Notes in Control & Information Sciences, 2015, 20: 249-261. |
| [6] | CHANG Y C, CHANG K H, LIAW C S. Innovative reliability allocation using the maximal entropy ordered weighted averaging method[J]. Computers & Industrial Engineering, 2009, 57(4): 1274-1281. |
| [7] | AMARI S V, HEGDE V.New allocation methods for repairable systems[C]//Reliability & Maintainability Symposium.Piscataway: IEEE Press, 2006: 290-295 |
| [8] | 冯川, 汪文峰, 杨建军. 使用可用度分配模型研究[J]. 电子产品可靠性与环境试验, 2009, 27(6): 49-53. FENG C, WANG W F, YANG J J. Research on the use of availability allocation model[J]. Electronic Product Reliability and Environmental Testing, 2009, 27(6): 49-53. DOI:10.3969/j.issn.1672-5468.2009.06.012 (in Chinese) |
| [9] | ELEGBEDE C, ADJALLAH K. Availability allocation to repairable systems with genetic algorithms:A multi-objective formulation[J]. Reliability Engineering & System Safety, 2003, 82(3): 319-330. |
| [10] | DUGAN J B. Automated analysis of phased-mission reliability[J]. IEEE Transactions on Reliability, 1991, 40(1): 45-52. DOI:10.1109/24.75332 |
| [11] | TESSERON J M. Mission:Reliability[J]. Power & Energy Magazine IEEE, 2008, 6(1): 42-48. |
| [12] | GHODRATI B, KUMAR U. Reliability and operating environment-based spare parts estimation approach[J]. Journal of Quality in Maintenance Engineering, 2005, 11(2): 169-184. DOI:10.1108/13552510510601366 |
| [13] | 张志华, 应新雅, 费广玉. 串联系统备件满足率分配及配置优化[J]. 系统工程理论与实践, 2015, 35(11): 2987-2992. ZHANG Z H, YING X Y, FEI G Y. Spare part rate allocation and configuration optimization of series system[J]. Systems Engineering-Theory & Practice, 2015, 35(11): 2987-2992. DOI:10.12011/1000-6788(2015)11-2987 (in Chinese) |
| [14] | CHEN C H, YANG Z J, CHEN F, et al. The study of reliability modeling of machining center based on Blocksim and Weibull++[J]. Applied Mechanics & Materials, 2013, 274: 49-52. |
| [15] | CARLUCCI E, TOGNARELLI L.Mixed Weibull distribution as best representative of forced outage distribution to be implemented in BlockSim[C]//ASME 2014 Power Conference.New York: ASME, 2014: V001T06A009. |
