重要性分析主要研究输出不确定性向输入不确定性的逆向分配问题,一般包含2种,即局部重要性分析和全局重要性分析。其中,局部重要性分析定义为结构系统输出响应函数在输入参数名义值点处的偏导数,而全局重要性分析则衡量输入参数在其整个取值区间内对结构系统输出不确定性的平均影响程度。一旦得知输入变量的不确定性排序,就可以在工程优化设计中忽略低重要性参数,关注高重要性参数,从而提供有益的指导信息[3]。相对于局部灵敏度,全局灵敏度能够反映设计变量的随机性,而局部灵敏度则不能,因此,全局重要性分析的应用相对更广泛[4]。当前,多种全局重要性分析方法已经发展开来,包括非参数方法[5-6]、扫描法[7]、微分法[8]、基于方差的重要性分析[9-10]、矩独立重要性分析[11-12]和随机森林[13]等,其中应用最为广泛的为基于方差的重要性分析和矩独立重要性分析。
本文重点关注设计变量对结构系统失效概率的重要性分析。Cui等[14]提出了基于失效概率的矩独立重要性指标,王文选[15]和Zhou[16]等提出了求解矩独立重要性指标的点估计法和稀疏网格法,Li和Lu[17]在Cui等[14]基础上作出了改进,并证明其指标可以转化为Sobol基于方差的重要性指标,Wei等[18]则将单层Monte Carlo方法用于Sobol指标求解中。本文在Li和Lu[17]所提指标的基础上作出扩展,分析输入参数的方差变化对结构系统失效概率的影响程度,即开展一种新的重要性分析方法,将输入变量方差缩减的百分比作为一个随机输入变量,得到一个重要性指标函数,其平均值作为平均矩独立重要性指标。尽管Sobol方法可以高效地计算Li和Lu[17]提出的指标,然而在计算平均矩独立重要性指标时需要不断重复抽样,计算成本在工程中依然无法接受。本文引入拒绝抽样(Rejection Sampling,RS)方法来求解所提矩独立重要性指标函数和平均矩独立重要性指标,该方法可通过使用Sobol方法中产生的一组样本获取更多的信息,不需要重复抽样,因此大大节约了计算成本,提高了计算效率。本文所提指标的有效性以及所提方法的高效性和准确性均可通过数值、工程算例加以验证。
1 平均矩独立重要性指标 1.1 矩独立重要性指标 假设结构系统模型为Y=g(X1, X2, …, Xn),其中g(·)为响应函数,Y为模型输出,X=(X1, X2, …, Xn)为一组相互独立的随机变量,其联合概率密度函数为f(x1, x2, …, xn)=f(x)=
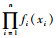
 | (1) |
式中:XI为一个输入变量Xi或一组输入变量(Xi1, Xi2, …, Xig), 1≤i1≤i2≤…≤ig≤n;E[·]为期望函数。
ηI反映了输入变量XI在其整个取值区间内的不确定性对失效概率的影响程度。由于式(1)中定义的指标不便求解,Li和Lu[17]提出了一种新的重要性指标δIP,即在原有指标的基础上将绝对值形式转化为方差形式,其定义如下:
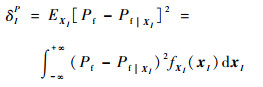 | (2) |
此外,Li和Lu[17]还证明式(2)中的指标可转化为相应的基于方差的重要性指标,即
 | (3) |
式中:
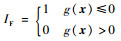
明显可以看出,式(2)中定义的重要性指标为矩独立重要性指标,但若将IF看作模型输入,它可以等效为Sobol基于方差的指标。因此,δIP可以用求解Sobol指标的方法进行求解,也为矩独立重要性指标的求解提供了一种新的可选择方法。
Wei等[18]提出了一种可以高效求解条件方差的方法,那么矩独立重要性指标δIP可以改为
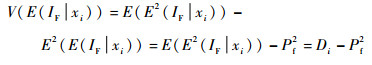 | (4) |
式中:Di=E(E2(IF|xi)),且Pf2和Di的数值计算方法分别为
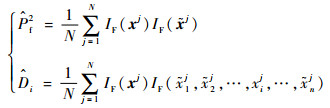 | (5) |
那么,δIP可以用式(6)计算得到:
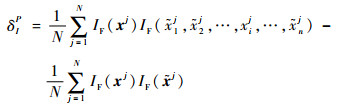 | (6) |
式中:xij和
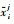
1.2 平均矩独立重要性测度 假定Xio为参数Xi在原始分布下的随机变量,X′i为参数Xi在开展进一步研究后的新分布下的随机变量,它们对应的重要性指标分别为δiPo和δiP′。那么,本文可以定义新分布下参数方差与原始分布下参数方差的比值为λi=var(X′i)/var(Xio)。由于开展进一步研究的目的在于减小参数Xi的方差,那么有λi∈[0, 1]。然而,由于研究深入使得参数原始分布的方差减小程度未知,可以假定λi为在[0, 1]区间服从均匀分布的随机变量,也就给出了λi取值的最大熵分布。
假定参数Xi的方差在原方差基础上缩减的倍数为Λi,那么缩减后的方差为原始分布方差的1-Λi,可以定义如下矩独立重要性指标:
 | (7) |
式中:λi∈[0, 1];Λi=λi表示参数Xi的方差在原方差基础上缩减λi倍;δiPo为参数Xi的初始矩独立重要性指标;δiP′为参数Xi的方差由V[Xio]缩减为λiV[Xio](即V[X′i])时对应的矩独立重要性指标。
假设任一参数Xi的方差可以被缩减为0,即λi=0,也就意味着参数Xi变为一常数,即δiP′=0。因此,当λi=0时,ζi=δiPo。类似地,若λi=1,也就意味着参数的方差没有被缩减,那么δiP′=δiPo。因此,当λi=1时,ζi=0。
由于矩独立重要性指标可以转化为基于方差的重要性指标进行求解,那么ζi可以被等效转化为如下基于方差重要性指标函数的形式:
 | (8) |
那么可以定义ζi在λi取值范围内的平均值为参数Xi的平均矩独立重要性指标τi,其定义为
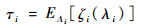 | (9) |
平均矩独立重要性指标τi可以量化地反映当对模型中参数Xi作进一步研究时,δiP可被减小的平均程度。
需要指出的是,给定某参数Xi的初始分布和一些λi值,可能存在不止一种分布满足随机变量新分布下方差为原始分布下方差的λi倍。Allaire和Willcox[19]提出了一种针对初始均匀分布和正态分布如何得到合理新分布的方法。
2 拒绝抽样方法 RS方法可以从某给定分布产生理想分布样本,该技术对于伪随机样本[20-21]和随机样本已经得到较好应用,本文将该方法用于失效概率函数的求解中。
根据文献[20],假设理想一维分布参数θ*下随机变量p的概率密度函数(PDF)为fP|θ*(p),而分布参数θ下随机变量X的PDF为fX|θ(x),而fX|θ(x)符合下面条件:对任意X的一实现值x,存在常数r,满足rfX|θ(x)≥fP|θ*(x)对于所有x均成立。那么,RS方法就可以用来产生J个服从fP|θ*(p)分布的样本。下面分别对随机分布和低偏差序列的普通一维样本使用RS方法进行介绍。
步骤1??1)随机分布:根据fX|θ(x)产生一列随机样本xi(i=1, 2, …, M)。
2) 低偏差序列:产生低偏差序列的点(ξi, νi)∈[0, 1]2, i=1, 2, …, M。将ξi映射到xi,使用累积分布函数(CDF)的反变换xi=Fxi-1(ξi)来得到输入变量xi的样本(其中Fxi为xi的CDF)。
步骤2??1)随机分布:产生一列在[0, 1]上均匀分布的样本ui(i=1, 2, …, M)。
2) 低偏差序列:ui=νi。
步骤3??当i从1到M取值时,若fP|θ*(x)/fX|θ(x)≥rui,则pj=xi,j=j+1;否则拒绝xi。
一般情况下,取r=max(fP|θ*(x)ui/fX|θ(x))。
RS方法可以用来求解式(8)中转化后的基于方差的重要性指标,从而得到式(9)中的平均矩独立重要性指标,步骤如下:
步骤1??产生2列随机输入变量矩阵XN×n和
步骤2??在区间[0, 1]上产生Λi=λi的均匀分布样本,对给定λi,列出所有更新后的分布如下:
1) 对于均匀分布U(a, b),在区间[a+λi1/2·(b-a), b]上产生b′的均匀分布样本,并使a′=b′-λi1/2(b-a)。
2) 对于正态分布N(μ, σ2),令μ′=μ,σ′=λ1/2σ。
步骤3??对于Λi=λi对应的可能的更新后的分布,使用分布1)或者分布2)选择初始样本的子样,并使用步骤1求解δiP′。
步骤4??重复步骤3直到Λi=λi对应的所有更新后的分布分析完成,然后使用式(7)对ζi进行求解。
步骤5??重复步骤4直到Λi对应的所有值分析完成,然后使用式(9)对τi进行求解。
由上述求解步骤可以看出,根据输入变量{x(1), x(2), …, x(N)}的一组初始分布参数θ,采样得到2组N维输入样本及相应的输出样本,利用式(6)对矩独立重要性指标δiPo进行求解,计算成本为N(2+n)。利用RS方法,可以从初始的输入样本{x(1), x(2), …, x(N)}中根据更新后的分布fX|θ*(x)筛选出符合条件的样本x(k)*,并得到相应的输出样本y(k)*,然后计算矩独立重要性指标ζi,从而得到平均矩独立重要性指标τi。
3 算例 3.1 数值算例——Ishigami函数 Ishigami函数被广泛用于可靠性分析中,首先被Ishigami和Homma引入,然后被用于测试重要性和不确定性分析技术中[2, 22],可表示为
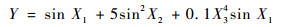 | (10) |
式中:X1、X2、X3 3个输入变量互相独立且服从均匀分布Xi~U(-π, π)(i=1, 2, 3)。使用1 000个随机序列得到它们的矩独立重要性指标δiP分别为0.047 9、0.025 8和0.010 7。
要实现参数优化,根据重要性指标δiP的排序可以看出,首先要重点关注参数X1。为了说明矩独立重要性指标函数的优点,现分别采用Sobol和RS方法对各输入参数在λi=0, 0.05, 0.10, …, 1时开展分析,λi=1时对应的即为δiP,如图 1(a)和图 2(a)所示。由图中可以看出,当输入参数的方差缩减时,对失效概率的影响呈现高度的非线性。而δiP指标的结果很可能误导工程分析人员,使其在决定如何合理分配资源以降低失效概率时做出不合理决策。举例来说,当参数X1方差减小10%时,失效概率实际上增大了;当参数X1方差减小50%以上时,失效概率才开始减小。分析参数X2和X3可以得到类似的结论。
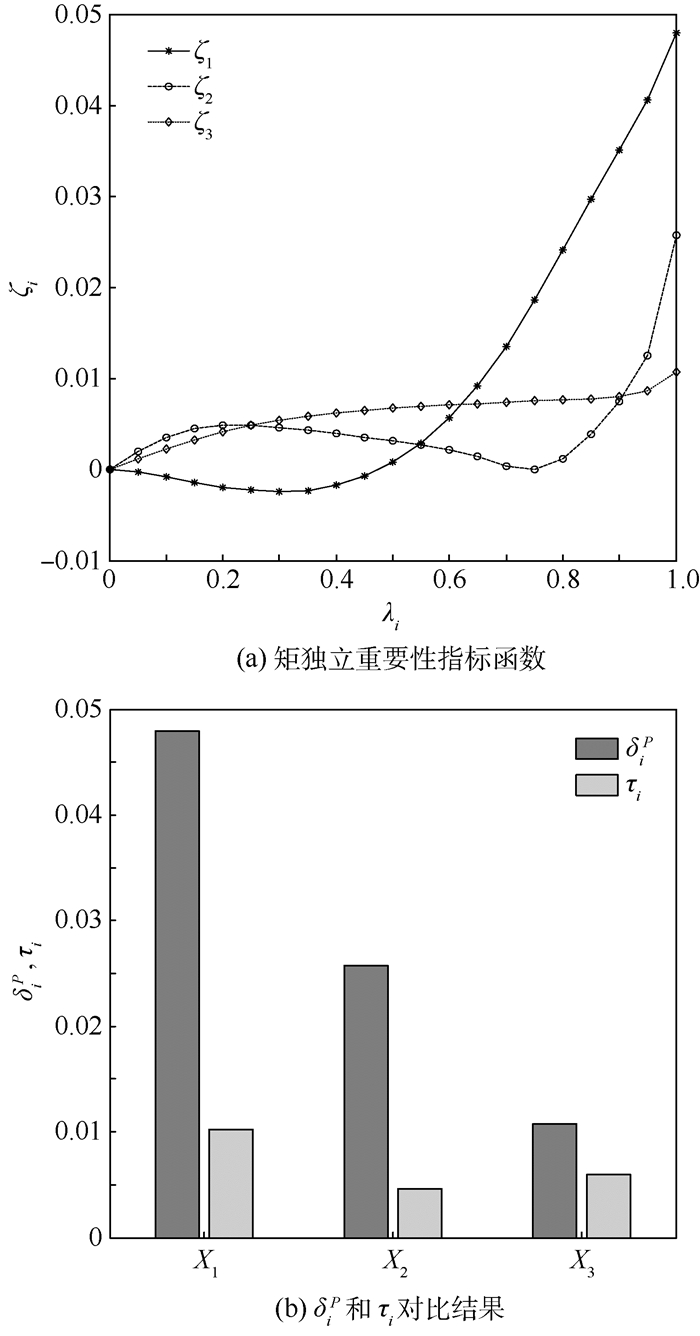 |
| 图 1 Sobol方法求解的Ishigami测试函数重要性指标结果 Fig. 1 Importance index results solved by Sobol's method for Ishigami test function |
| 图选项 |
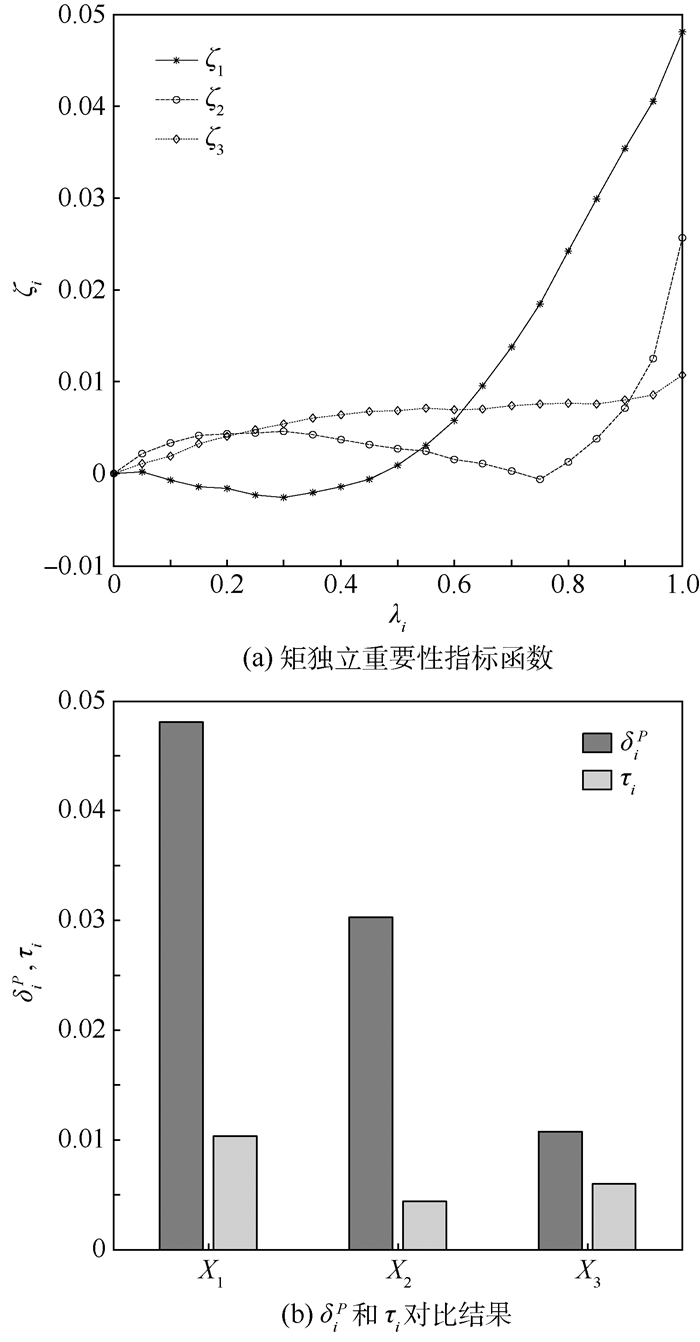 |
| 图 2 RS方法求解的Ishigami测试函数重要性指标结果 Fig. 2 Importance index results solved by RS method for Ishigami test function |
| 图选项 |
根据矩独立重要性指标函数可以计算得到平均矩独立重要性指标,如图 1(b)和图 2(b)所示。不难看出,若假设所有参数的不确定性均可以被消除,矩独立重要性指标函数度量的是哪个参数的方差的可以被进一步减缩,这也是平均矩独立重要性指标与当前矩独立重要性指标的区别。
若使用Sobol方法,那么矩独立灵敏度指标和图 1结果的调用功能函数的次数分别为103和21×103,而RS方法则大大节约了模型计算量。利用求解δiPo时产生的输入输出样本,RS就可以在保证精度的前提下提供矩独立重要性指标函数及平均矩独立重要性指标等额外信息,图 2中结果证明了RS方法的有效性和准确性。
3.2 工程算例——屋架结构 屋架上弦杆和其他压杆均采用钢筋混凝土杆,下弦杆和其他拉杆则采用钢杆,见图 3[17]。假定屋架结构承受均布载荷q,将其转化成节点载荷后可得P=ql/4,l为杆长。用结构力学分析可得C点沿垂直地面方位移为ΔC=
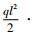
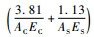
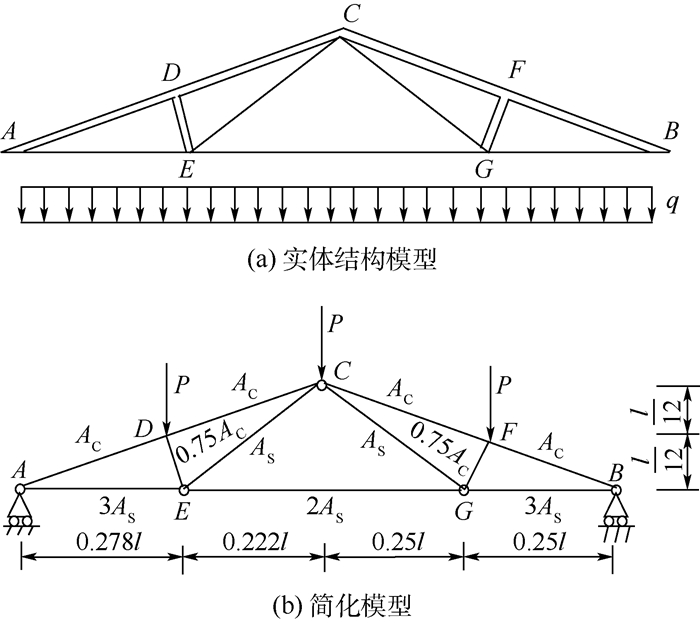 |
| 图 3 屋架结构模型的示意图[17] Fig. 3 Schematic diagram of a roof truss structure model[17] |
| 图选项 |
表 1 屋架结构模型中输入变量的分布参数 Table 1 Distribution parameters of input variables of roof truss structure model
| 分布参数 | 均值 | 变异系数 |
| q | 20 000 N/m | 0.07 |
| l | 12 m | 0.01 |
| AS | 9.82×10-4 m2 | 0.06 |
| AC | 0.04 m2 | 0.12 |
| ES | 1×1011 N/m2 | 0.06 |
| EC | 2×1010 N/m2 | 0.06 |
表选项
使用Sobol方法和RS方法分别计算的矩独立重要性指标函数和平均矩独立重要性指标分别如图 4和图 5所示,其调用功能函数的次数分别为5×103和21×5×103。矩独立重要性指标函数曲线说明通过每个输入参数是否被进一步研究取决于其本身的方差可减少程度。本算例中可以看出,通过减小任一输入参数的方差,由于矩独立重要性指标函数的曲线单调递增,均可以达到降低结构系统失效概率的目的。此外,明显可以看出,RS方法和Sobol方法所得结果的一致性。
 |
| 图 4 Sobol方法求解的屋架结构模型重要性指标结果 Fig. 4 Importance index results solved by Sobol's method for roof truss structure model |
| 图选项 |
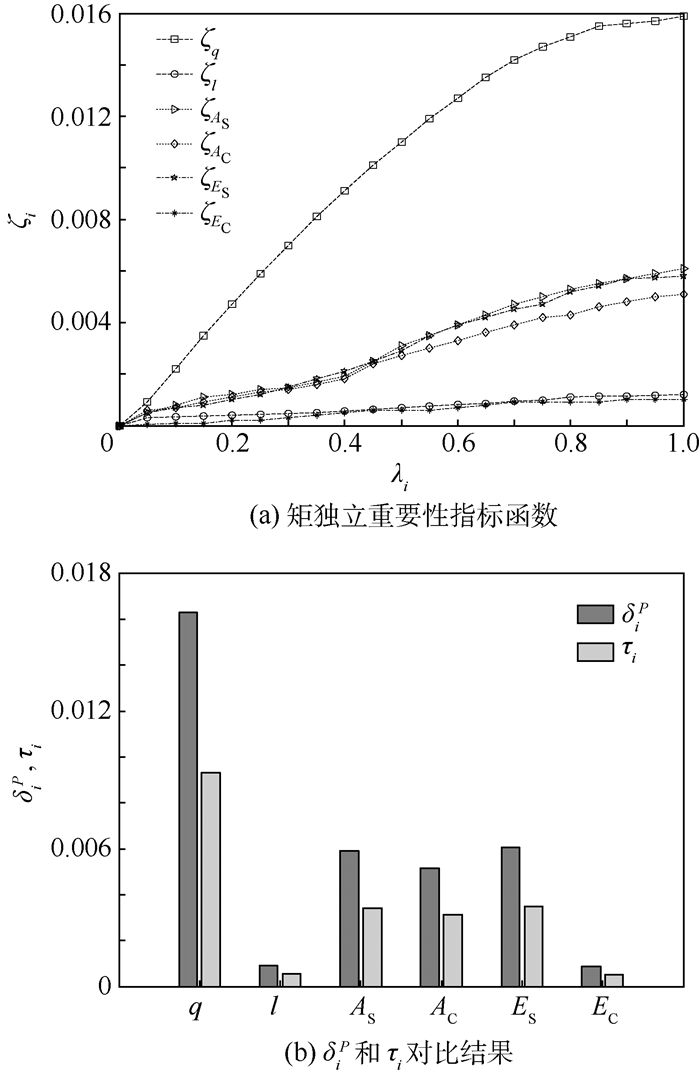 |
| 图 5 RS方法求解的屋架结构模型重要性指标结果 Fig. 5 Importance index results solved by RS method for roof truss structure model |
| 图选项 |
3.3 工程算例——十杆桁架结构 考虑图 6(a)中的平面十杆桁架结构模型[23],水平杆和竖直杆的长度和弹性模量均为L和E,每根杆的横截面积为Ai(i=1, 2, …, 10),载荷作用在节点2和节点3处。设L、E、Ai(i=1, 2,…, 10)和Pi(i=1, 2, 3)为15个相互独立服从正态分布的随机变量,分布参数见表 2。以节点3的纵向位移不超过0.004 m为约束条件,那么结构系统的功能函数为gf=0.004-Δy,其中Δy为隐式功能函数,即Δy=Δ(Ai, L, P1, P2, P3, E)(i=1, 2, …, 10)。
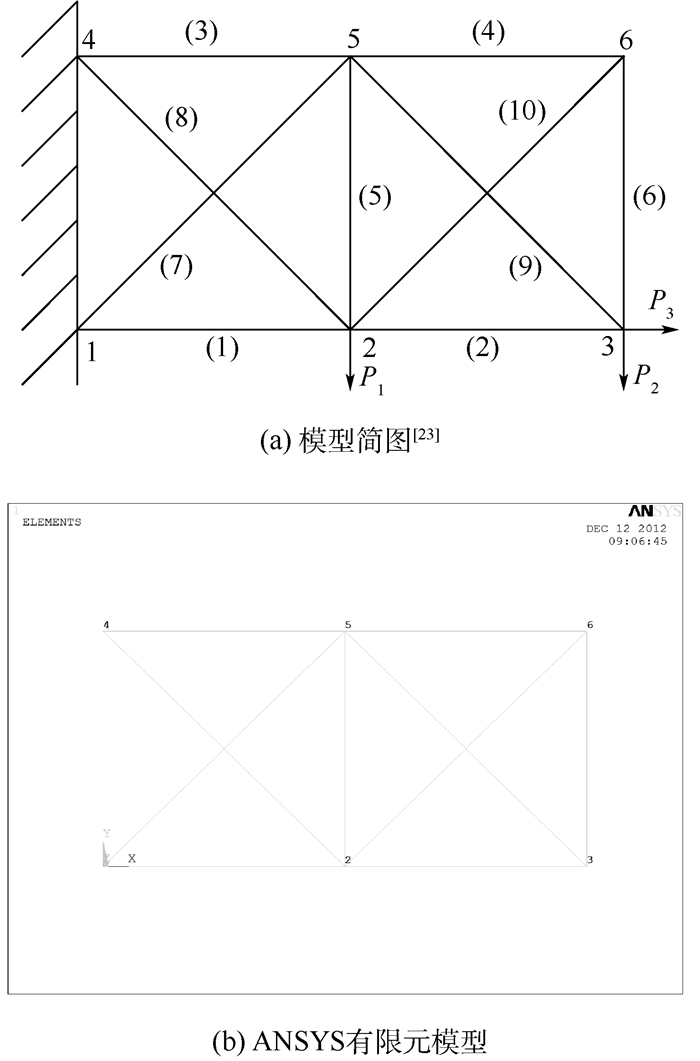 |
| 图 6 平面十杆桁架结构模型示意图 Fig. 6 Schematic diagram of a planar ten-bar truss structure model |
| 图选项 |
表 2 十杆桁架结构模型中输入变量的分布参数 Table 2 Distribution parameters of input variables of ten-bar truss structure model
| 分布参数 | 均值 | 变异系数 |
| L | 1 m | 0.05 |
| E | 100 GPa | 0.05 |
| P1 | 80 kN | 0.05 |
| P2 | 10 kN | 0.05 |
| P3 | 10 kN | 0.05 |
| Ai | 0.001 m2 | 0.15 |
表选项
本算例中假设输入参数的方差不可减缩,然而输入参数的均值可以在一定范围内移动。这里假设λi=(μi-μio)/μio, λi∈[-0.15, 0.15],那么使用Sobol方法和RS方法计算得到的矩独立指标函数和平均矩独立重要性指标分别见图 7和图 8,其调用功能函数的次数分别为104和21×104。从图中可以看出,当λi=0时,参数的均值没有移动,且δiP′=δiPo,那么ζi=0。同时,输入参数L、E和P1的矩独立重要性指标函数的非线性程度最高,也就说明工程人员可以针对这几个参数的均值移动作进一步研究和探索。根据矩独立重要性指标函数,就可以对平均矩独立重要性指标进行求解。本算例中的结果再次证明了RS方法的高效性和准确性。
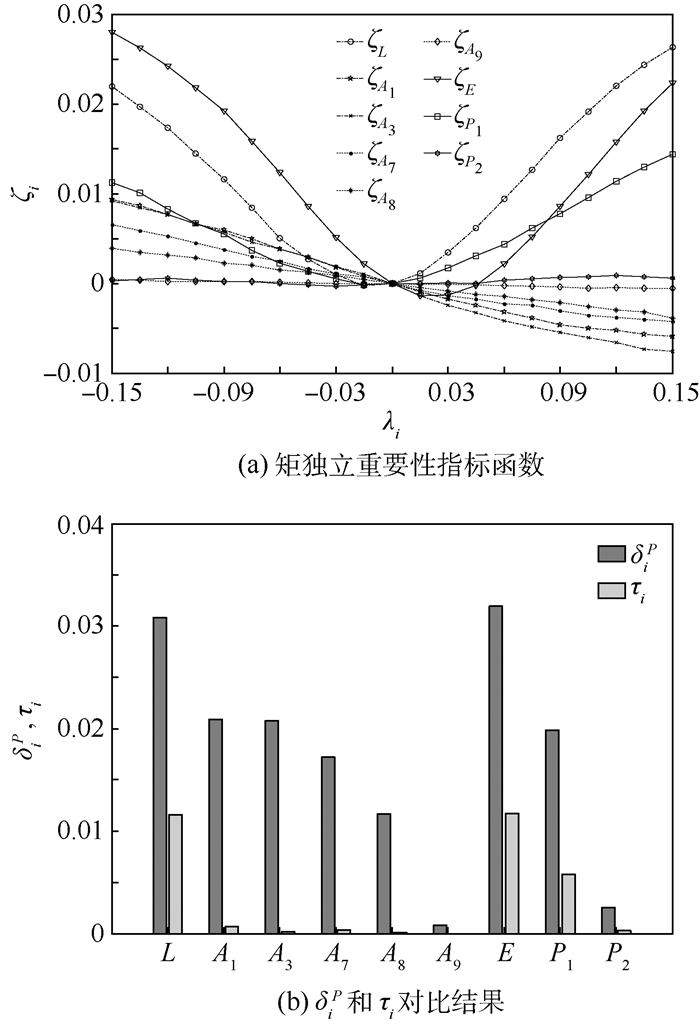 |
| 图 7 Sobol方法求解的十杆桁架结构模型重要性指标结果 Fig. 7 Importance index results solved by Sobol's method for ten-bar truss structure model |
| 图选项 |
 |
| 图 8 RS方法求解的十杆桁架结构模型重要性指标结果 Fig. 8 Importance index results solved by RS method for ten-bar truss structure model |
| 图选项 |
4 结论 矩独立重要性分析被广泛应用于工程结构分析中,然而当前存在的指标是建立在假设输入参数的不确定性不能被减小或消除的基础上。实际上,输入参数的方差/均值(或其他分布参数)的被减缩量是未知的,因此得到如下结论:
1) 输入变量分布参数发生变化时,各个变量对应的全局矩独立重要性指标也发生变化,而本文提出的平均矩独立重要性指标可以衡量输入变量分布参数变化时对输出响应的平均影响。
2) RS方法可以使用原始全局重要性分析中的样本,额外获取输入变量分布参数发生变化时的矩独立重要性指标,从而计算得到平均矩独立灵敏度指标。这样在不增加额外计算成本的情况下获取更多的信息,为研究人员进一步进行工程设计和优化提供了丰富的指导信息。
参考文献
| [1] | 吕震宙, 宋述芳, 李洪双, 等. 结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009: 2-7. LU Z Z, SONG S F, LI H S, et al. Reliability and reliability analysis for structure and mechanics[M]. Beijing: Science Press, 2009: 2-7. (in Chinese) |
| [2] | SALTELLI A, TARANTOLA S, CAMPLONGO F, et al. Sensitivity analysis in practice:A guide to assessing scientific models[M]. New York: Wiley, 2004: 3-10. |
| [3] | WANG W, ZHOU C, GAO H, et al. Application of non-probabilistic sensitivity analysis in the optimization of aeronautical hydraulic pipelines[J]. Structural and Multidisciplinary Optimization, 2018, 57(6): 2177-2191. DOI:10.1007/s00158-017-1848-4 |
| [4] | BORGONOVO E. Measuring uncertainty importance:Investigation and comparison of alternative approaches[J]. Risk Analysis, 2006, 26(5): 1349-1361. DOI:10.1111/risk.2006.26.issue-5 |
| [5] | HELTON J C, DAVIS F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability Engineering & System Safety, 2003, 81: 23-69. |
| [6] | SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output:A comparison of selected techniques[J]. Reliability Engineering & System Safety, 1990, 28: 229-253. |
| [7] | MORRIS M. Factorial sampling plans for preliminary computational experiments[J]. Technometrics, 1991, 33(2): 161-174. DOI:10.1080/00401706.1991.10484804 |
| [8] | LAMBONIA M, IOOSS B, POPELIN A L, et al. Derivative-based global sensitivity measures:General links with Sobol' indices and numerical tests[J]. Mathematics and Computers in Simulation, 2013, 87: 45-54. DOI:10.1016/j.matcom.2013.02.002 |
| [9] | SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathmatics and Computers in Simulation, 2001, 55(1): 221-280. |
| [10] | CASTILLO E, MINGUEZ R, CASTILLO C. Sensitivity analysis in optimization and reliability problems[J]. Reliability Engineering & System Safety, 2008, 93(12): 1788-1800. |
| [11] | BORGONOVO E. A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92(6): 771-784. |
| [12] | CHUN M H, HAN S J, TAK N I. An uncertainty importance measure using a distance metric for the change in a cumulative distribution function[J]. Reliability Engineering & System Safety, 2000, 70(3): 313-321. |
| [13] | ARCHER K J, KIMES R V. Empirical characterization of random forest variable importance measures[J]. Computational Statistics & Data Analysis, 2008, 52(4): 2249-2260. |
| [14] | CUI L J, LU Z Z, ZHAO X P. Moment-independent importance measure of basic random variable and its probability density evolution solution[J]. Science China Technological Sciences, 2010, 53: 1138-1145. DOI:10.1007/s11431-009-0386-8 |
| [15] | 王文选, 高行山, 周长聪. 基于点估计的矩独立重要性测度分析方法[J]. 机械工程学报, 2017, 53(8): 16-24. WANG W X, GAO H S, ZHOU C C. The moment-independent importance measure analysis method based to point-estimate[J]. Chinese Journal of Mechanical Engineering, 2017, 53(8): 16-24. (in Chinese) |
| [16] | ZHOU C, LU Z, LI W. Sparse grid integration based solutions for moment-independent importance measures[J]. Probabilistic Engineering Mechanics, 2015, 39: 46-55. DOI:10.1016/j.probengmech.2014.12.002 |
| [17] | LI L Y, LU Z Z. Moment-independent importance measure of input variable and its state-dependent parameter solution[J]. Structrual Safety, 2012, 38: 40-47. DOI:10.1016/j.strusafe.2012.04.001 |
| [18] | WEI P F, LU Z Z, HAO W R, et al. Efficient sampling methods for global reliability sensitivity analysis[J]. Computer Physics Communications, 2012, 183: 1728-1743. DOI:10.1016/j.cpc.2012.03.014 |
| [19] | ALLAIRE D L, WILLCOX K E. A variance-based sensitivity function for factor prioritization[J]. Reliability Engineering & System Safety, 2012, 107: 107-114. |
| [20] | DEGROOT M, SCHERVISH M. Probability and statistics[M]. 3rd ed. Boston: Addison-Wesley, 2002: 35-40. |
| [21] | WANG X. Improving the rejection sampling method in quasi-Monte Carlo methods[J]. Journal of Computational & Applied Mathematics, 2000, 114: 231-246. |
| [22] | STORLIE C, SWILER L, HELTON J, et al. Implementation and evaluation of nonparametric regression procedures for sensitivity analysis of computationally demanding models[J]. Reliability Engineering & System Safety, 2009, 94: 1735-1763. |
| [23] | LU Z Z, LIU C L, YUE Z F. Probabilistic safe analysis of the working life of a powder-metallurgy turbine disk[J]. Materials Science and Engineering:A, 2005, 395: 153-159. DOI:10.1016/j.msea.2004.12.008 |
