利用空间系绳系统执行碎片在轨捕获任务时一般可以分为捕获前系绳的展开、交会捕获以及捕获后系统回稳、回收、拖拽等不同阶段。捕获前系绳展开到平衡位置、交会捕获以及捕获后系统回稳是后续回收、拖拽任务的前提。然而,由于太空环境复杂,展开结束后可能存在一定的长度及摆角误差;而捕获完成后由于目标物与捕获机构构成统一整体,质量突变、捕获位置不理想等问题,系统不可避免地会出现摆动。因此,需要对上述情况进行控制使其回到稳定状态即平衡位置。
目前,国内外****对系绳平衡位置附近的稳定性问题进行了大量研究。Pasca[1]研究了系绳卫星系统在状态保持阶段的运动,并提出了利用子星推力来控制系绳的面内振荡。Williams等[2]提出了通过电动力和偏置控制来控制系绳的振荡。Mankala和Agrawal[3]设计了一套边界控制器将系统控制到了径向相对平衡的位置。Larsen和Blanke[4]设计了一套非线性控制器,并利用电动力系绳注入阻尼的方法将系绳卫星系统控制到一个渐进稳定的平衡位置。余本嵩等[5]通过雅可比矩阵对处于平衡位置的绳系卫星的稳定性进行了研究,提出了通过在子星一端安装喷气力控制装置的含约束条件的PID控制律[6]。庞兆君[7]针对位于圆轨道上和椭圆轨道上的系绳卫星的混沌运动进行了分析,并通过Melnikov方法给出圆轨道下含阻尼系统的混沌域,采用延迟反馈控制,将欠驱动系绳卫星系统的混沌运动稳定到周期运动。
而对于系绳系统,捕获后系统稳定控制问题则更为复杂。孙亮等[8-9]针对空间系绳系统面内转移过程中的系统的摆振特性及稳定性进行了研究,指出面内轨道转移过程中面内角会以固定的频率绕平衡位置往返摆动,并且这种摆动受轨道高度、系绳长度、推力加速度等影响,提出了连续常值推力系绳系统的轨道转移策略和基于系绳张力系统的摆振抑制策略。张帆和黄攀峰[10]针对非合作目标抓捕后保持阶段的振动特性参数辨识方法,提出了非合作目标被系绳系统抓捕后处于保持阶段的姿态运动振动特性参数辨识方法。赵国伟等[11]在考虑捕获平台与目标物的姿态运动基础上,提出了留位和阻尼控制相结合的张力复合控制方法。张宇靖和钟睿[12]以模型预测控制方法为基础设计了稳定系绳摆动的非线性模型预测控制算法。
上述文献在设计控制器时,多采用施加外力矩的方式(如电动力、喷管推力等),或通过输入外部能量来控制系统的面内运动。施加外力矩的方式能够快速抑制面内运动,且精度较高,这对于要求定绳长的高精度任务场合尤其重要[13]。然而,电动力系绳在地磁场中由于洛伦兹力的作用会使得系统轨道能量减少,轨道高度降低,对于状态保持阶段并不适用;喷管能够有效产生交会捕获时目标逼近、跟踪所需要的摆动,但要不断消耗燃料,然而系统在轨时间较长,若从始至终一直通过喷管来控制子星的运动需要消耗大量燃料,十分不经济。
对于本文所研究的展开后状态保持以及捕获结束后回稳的过程,由于轨道周期较长,对任务的时间要求并不强烈,则通过张力控制使系统缓慢回到稳态也是可行的。例如,王班等[14]针对捕获完成后提出了一种在最大摆角处收紧系绳、平衡位置处释放系绳的面内摆动抑制控制方法,但仅在面内角速率大于零的条件下有效。李超等[15]针对圆轨道下系绳系统的状态保持阶段提出了基于标准系绳法的稳定控制方法。但上述方法对系绳张力机构提出了系绳面内、面外角姿态可测、绳长可测和系绳张力可控可测等要求。
系绳系统测量姿态角的主要方式是GPS干涉法[16],对姿态测量系统提出了较高要求。通过张力对系统进行控制时,一旦角度和角速率反馈失效,将会对系统造成严重影响。例如1988年发射的ECHO-7、2003年发射的DTUsat-1、2006年发射的CUTE-1.7以及2007年发射的YES-2卫星都出现了传感器及控制器故障,对任务造成了不同程度的影响[17-18]。因此,设计在角度和角速率反馈失效时仍能够使用的控制器,对于系绳展开后的面内保持以及捕获后系统的回稳具有重要意义。此外,面内运动反馈被证明对系统稳定性没有本质影响[19],因此在仅反馈长度和速率信号的情况下设计控制律同样可行。
针对状态反馈不完全问题,目前较为常用的方法为线性二次调节器(LQR)+降维观测器方法,除此之外,矩阵分解也为控制律的设计提供了一种良好的选择,其思想为:针对线性系统,通过配置反馈矩阵使其闭环特征方程配置到指定位置,从而使特征方程与具有较好性能的指定标准特征多项式具有相同的系数。本文在设计控制律时,结合标准系数法将系统特征多项式设计为确定形式,在矩阵分解基础上利用相容性原理解决由不完全状态反馈所带来的相容性问题,从而将控制器参数计算出来,此时由于系统特征多项式确定,故其闭环特性也将比较理想,控制效果可预期。
基于上述考虑,本文针对系绳展开后状态保持阶段以及捕获后系统的回稳任务,设计仅反馈长度和速率信号的张力控制律,从而对系统的绳长、面内角误差以及面内摆动进行有效控制。在设计不完全状态反馈的控制律时,本文基于矩阵分解方法,结合标准系数法通过简单的代数运算计算出控制器参数,控制律结构简单,无需复杂的参数调整。
1 动力学模型 考虑系绳系统为有质量弹性杆模型。有以下4点假设:①捕获平台(母星)和捕获前/后的捕获机构(子星)通过弹性系绳连接,系统质心在未受扰动的开普勒圆轨道上运行。②将母星和子星视为质点,且母星质量远大于子星,即系统质心位于母星上。系绳未释放前卷轴位于母星内。③系绳视为质量分布均匀的弹性杆,只考虑沿其自身的纵向振动,不计入系绳的扭转刚性及各向异性等。④所有影响系统的外部作用力中,只考虑重力的影响,忽略太阳光压、大气阻力、日月引力等扰动的影响。
定义地心轨道坐标系和绳系坐标系如图 1所示。其中,地心轨道坐标系OXYZ为惯性坐标系,OXY平面与轨道平面一致,OX轴指向轨道近地点(对于圆轨道,沿地心指向轨道升交点方向),OZ轴与轨道平面正交并沿航天器的动量矩方向,OY轴按右手坐标系原则确定。轨道运动坐标系CXoYoZo与系统质心C固联,CXo轴沿航天器矢径方向,CZo轴和OZ轴平行。坐标系CXoYoZo相对于坐标系OXYZ以轨道角速率Ω旋转。绳系坐标系坐标原点C位于航天器质心处,CXt轴沿着卫星拉紧绳系的反方向,CYt轴和CZt轴的位置由相对于坐标系CXoYoZo的面内角θ和面外角φ确定。空间系绳系统所在轨道与目标物所在轨道在同一平面内,惯性系下目标物的真近点角为η。
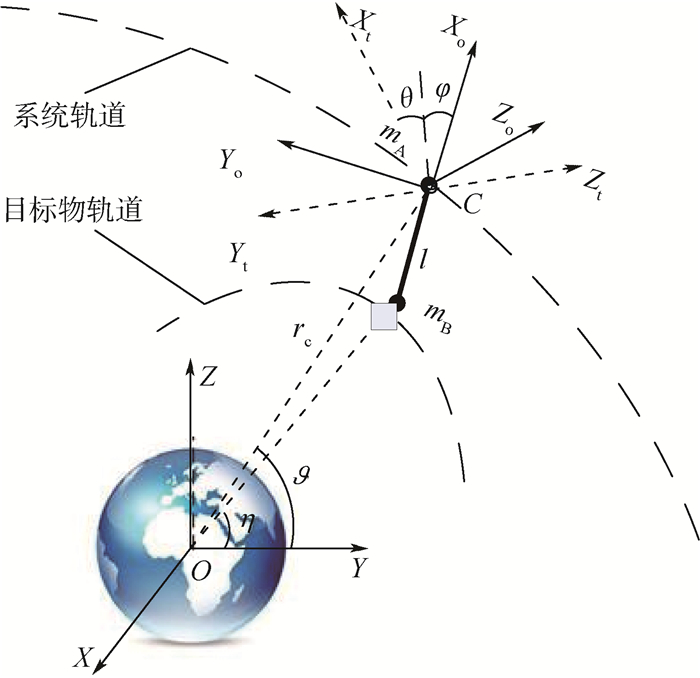 |
| 图 1 系绳系统捕获过程示意图 Fig. 1 Schematic of capture process with tether system |
| 图选项 |
空间系绳系统的状态可以用5个广义坐标描述:系绳系统质心距地心距离rc、系统质心的真近点角?、面内角θ、面外角φ和系绳弹性应变ε。根据拉格朗日方程,推导出有质量系绳的空间系绳系统的微分方程为
 | (1) |
式中:“·”表示对时间t求导;mA和mB分别为母星和子星的质量,mA?mB;mt=ρl0为系绳质量,ρ为系绳线密度,l0为系绳原长,系绳当前长度为l=l0(1+ε);T为系绳张力;μ为地球引力常量;?1、?2、?3、?4为质量项。
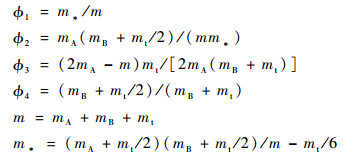 |
2 线性化处理及开环稳定性分析 由于系绳密度较小(约为10-4 kg/m),且假设展开后所出现的非标称行为及捕获后所出现的摆动等扰动情况下,系绳均在平衡位置附近摆动,故系绳长度基本不变,出于控制律设计方便,此时忽略系绳质量、弹性伸长量变化带来的影响。即式(1)中的质量系数?2≈?4≈1,
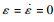

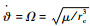
引入无量纲时间τ=Ωt,则
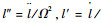
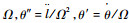
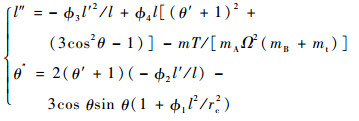 | (2) |
式中:“′”表示对无量纲时间τ=Ωt求导。
对于系绳系统,稳定的平衡位置沿轨道的径向方向,即θ1, 2=0, π。将方程式(2)在平衡点附近线性化,并引入无量纲长度,忽略高阶小量可得
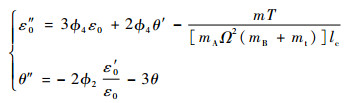 | (3) |
式中:ε0=l/lc为系绳无量纲长度,lc为系绳展开的最终长度即标称长度。
因此,平衡点附近系统的状态空间方程为
 | (4) |
式中:
 |
经计算可知,线性化系统式(4)可观可控。
由式(3)可得系统面内角运动的特征方程为
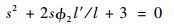 | (5) |
该特征方程的解为
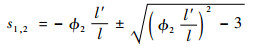 | (6) |
显然,当处于平衡位置(l′=0, l=const)时,特征根位于虚轴上,即系统临界稳定。此外,由式(2)可以看出,如果调节系绳长度l和速率
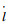
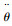
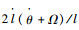
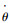
3 捕获后面内扰动情况分析 系统展开完成后被控处于平衡位置,而当捕获机构与目标物即将交会对接时,将通过喷管使系绳摆动从而实现捕获机构对目标物的跟踪。文献[20]指出,理想捕获位置(近地点或远地点)交会时,空间碎片与捕获机构的速度大小和方向完全一致。
然而,出于捕获安全性考虑,通常设计理想捕获时刻附近数十秒的捕获窗口,此时空间碎片和捕获机构仍在理想捕获位置附近运动。捕获机构速度矢量已不再沿OY轴互相平行,故此时执行捕获任务会对系统的相对运动产生扰动,因此被称为非理想捕获。本文欲针对捕获后系绳的面内摆动进行控制,故首先需对非理想捕获所带来的扰动情况进行计算分析。
由于本文假设捕获前后捕获平台的轨道运动不受空间碎片和系绳质量的影响,即其质心变化忽略不计。此外,忽略空间碎片对系绳纵向振荡所产生的扰动,仅考虑系绳的面内摆动。且为了简化捕获过程,将其视为恒定速率运动[13],利用刚体动量守恒原理对非理想位置进行扰动分析,并计算捕获后捕获机构与空间碎片构成的统一整体绕地垂线运动的角速率。
捕获平台在惯性坐标系下的矢径和速度分别为
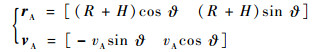 | (7) |
目标物的轨道运动可表示为
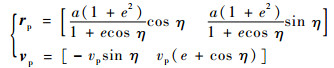 | (8) |
式中:vA=Ω(R+H), R和H分别为地球半径和捕获平台轨道高度;

惯性坐标系下目标物相对捕获平台的矢径和运动速度为
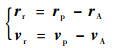 | (9) |
则绳系坐标系下目标物相对捕获平台的相对矢径和相对速度为
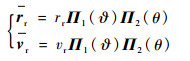 | (10) |
式中:


系统动量守恒过程如下:
 | (11) |
式中:mp和Ip分别为目标物的质量和角动量;Ibefore、Iafter分别为捕获前、后系统的角动量;Jbefore=mBlc2、Jafter=(mB+mp)lc2分别为捕获前、后捕获机构转动惯量;ωbefore、ωafter分别为捕获前、后系绳摆动角速度;Jt=mtlc2/3为系绳的转动惯量。
定义捕获机构能够允许的距离误差Rcap为
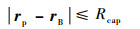 | (12) |
式中:rB为捕获机构(子星)矢径。
此外,由式(1)可得,系绳完全展开后其面内摆动方程为
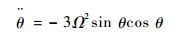 | (13) |
积分可得面内自由摆动最大摆角应为
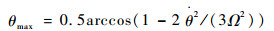 | (14) |
可通过式(7)~式(14)计算并分析捕获过程刚体碰撞所带来的系绳面内运动情况,进而确定控制器所要克服的扰动大小。
4 控制律设计 对于线性系统式(4),其开环传递函数可表示为
 | (15) |
式中:F(s)=det(sI-A),I为n阶单位矩阵;M(s)=[m11+…+m1nsn-1, …, mr1+…+mrn·sn-1]T,n为矩阵A的维数。
系统闭环传递函数为
 | (16) |
式中:P为不完全不状态反馈下反馈矩阵,P∈R1×r,r为反馈状态量的个数。
系统闭环特征方程为
 | (17) |
因此,通过配置反馈矩阵,理论上可将系统闭环特征方程的根配置在任意位置上,全状态反馈下一般配置方法参见文献[15]。
由闭环特征多项式可得
 | (18) |
比较方程两端相同阶次s的系数,可得
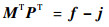 | (19) |
式中:f和j分别为多项式H(s)和F(s)的系数,且f, j∈Rn×1。此外,
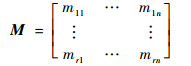 |
对于式(19),可列出具有r个未知数的n个方程。对完全反馈的系统(r=n),式(19)有唯一解;对不完全反馈的系统(r < n),除满足期望特征方程外,还需要满足相容性条件,即由r个线性无关的方程组所构成的子系统的解必须同时符合剩余n-r个方程。
将式(18)中M(s)分解为
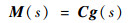 | (20) |
式中:g(s)=[1, s, …, sn-1]T。
将式(19)代入式(18),可得
 | (21) |
式中:
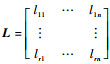
从矩阵CT中取r个线性无关的行组成r阶矩阵CBT,并从单位矩阵I中选取相应行组成r×n阶矩阵IB,CHT、IH则由各自矩阵的剩余部分组成。则式(21)可分解为
 | (22) |
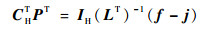 | (23) |
解方程式(22)并将结果代入式(23)中,得到相容性条件为
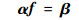 | (24) |
式中:α=S(LT)-1,β=αj,S∈R(n-r)×n,仅与矩阵C有关,β∈R(n-r)×1。对于单输入对象来说,矩阵CB可逆,即矩阵C中元素不全为0。
达到相容性条件后,计算矩阵P使特征根达到事先选定的值,得到期望配置的特征根系数。以期望的特征方程(包含未知量ω的系数矩阵)代入相容性方程,解出ω,从而确定系数矩阵。以空间系绳系统为例选取四阶标准型:
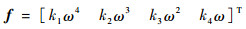 | (25) |
此处ω的值可以根据相容性条件αf=αj得出,这样既确定了ω的范围,又满足了相容性条件的要求。通过相容性条件解出ω的值以后,一般得到不同的值,当ω的取值范围为0.5~2.5时,系统的性能最理想。
如果式(24)中向量f的约束能够满足,那么反馈矩阵P为
 | (26) |
式中:K=(CBT)-1IB。
计算系统的反馈矩阵P时,本文的期望特征方程以ITAE标准型为参考,当状态方程为四阶时,可得期望的特征根系数表示为[15]:f=[ω4??2.7ω3??3.4ω2??2.1ω]T。
代入相容性条件可得ω为±1.527、±3.19 i和0。选择ω在0.5~2.5附近的值(ω=1.527)代入到ITAE的标准传递系数中,得到期望的系数值。
由式(26)计算可得反馈矩阵为:P=[4.812 3.207 0 0]T,将其代入式(17)得
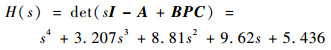 | (27) |
值得注意的是,二次项与标准型系数有一定出入。当设计的系统各阶次系数与标准型完全一致时,控制效果最好,但高阶情况下很难全部成立,因此应使各系数尽可能相近。在设计计算时,当(Z′/Z)≥0.8同时成立时就可满足要求,Z′和Z分别为设计系统和标准型的各阶系数。因此,设计的反馈矩阵P满足相容性要求,且满足ITAE标准型设计要求,反馈系数矩阵设计成功。
5 仿真分析 由于空间碎片所处的高度越高,在地球轨道中存在的时间越长。高度大于800 km的空间碎片需要几百年的时间方可回到地球空间销毁,且大部分空间碎片凝聚在800~850 km的高度上,尤其是倾角在71°~74°和81°~83°的低轨道和太阳同步轨道上。
本文假设质量mA=1 600 kg的母星(捕获平台)处于高度H=900 km的太阳同步圆轨道上,利用lc=30 km的系绳和质量m2=50 kg的捕获机构对处于偏心率为e=0.01的椭圆轨道上质量mp=100 kg的目标物进行捕获。地球半径R=6 371 km,地球引力常量μ=398 600 km3/s3。系绳选用迪尼玛材料,线密度ρ=0.198 kg/km。捕获前需将系绳展开至标称长度,理想状态下,系绳向地垂线方向展开完成后,系统处于平衡位置,无量纲坐标下对应的状态量为ε0=1,ε′0=0,θ=0,θ′=0。
此外,为检验本文设计控制律是否具有预期的控制效果,首先在线性化模型中进行验证,同时设计了LQR+降维观测器作为对比。其中,LQR控制器的Q矩阵选取为[2, 2, 1, 1],降维观测器的特征根为[-0.5, -3.3]。仿真均采用无量纲形式。
5.1 系绳展开后非标称行为抑制 由于太空环境复杂,在大气阻力、太阳光压等扰动作用下,系绳的最终展开状态可能并不理想。如YES-2任务由于控制机构出现了非致命故障,使得其第一阶段的展开出现了12 m的长度误差(约为标称长度的0.4%)和10°的面内角误差[21]。因此本文在考虑系统存在系绳长度、面内角存在初始偏差值的情况下,检验稳态保持控制系统的有效性。假设展开后存在面内角约为10°(0.174 5 rad)、绳长为100 m的初始误差,此时不加控制系统会始终处于幅值为10°的周期摆动运动。无量纲下仿真初始条件为:ε0=0.996 7,ε′0=0,θ=0.174 6,θ′=0。
在利用矩阵分解方法设计控制参数时,所使用的系统状态方程是在空间系绳系统有质量弹性杆模型归一化处理、平衡点附近线性化处理的基础上得到的。因此,所得到的控制参数是在线性化模型条件下忽略了系统各部分质量变化。为进一步验证矩阵分解方法所设计的控制器的有效性,采用实际的非线性模型式(1)来验证线性化条件下得出的控制参数的控制效果。
利用传统的LQR+降维观测器对线性化系统进行控制,同时分别在线性化模型式(4)和非线性模型式(1)下对比,检验所设计的控制律的有效性,仿真结果如图 2所示,相应的控制力(系绳张力)变化曲线如图 3所示。
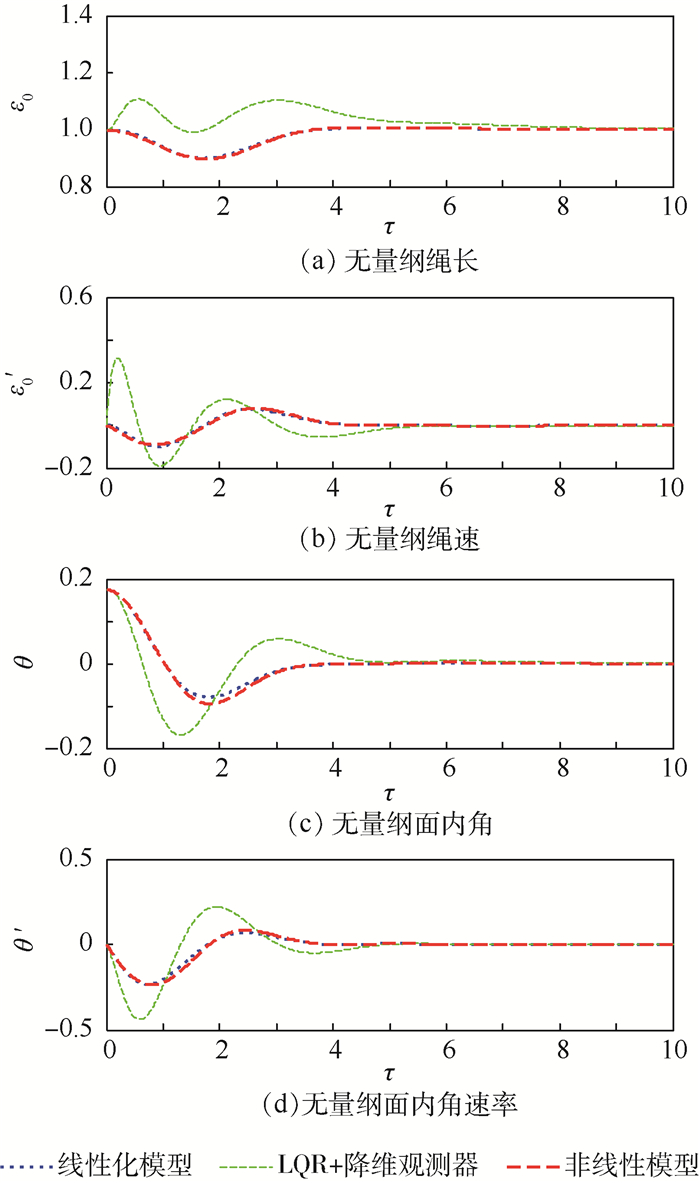 |
| 图 2 系绳展开后各状态量受控变化曲线 Fig. 2 Changing curves of state variables under control after tether deployment |
| 图选项 |
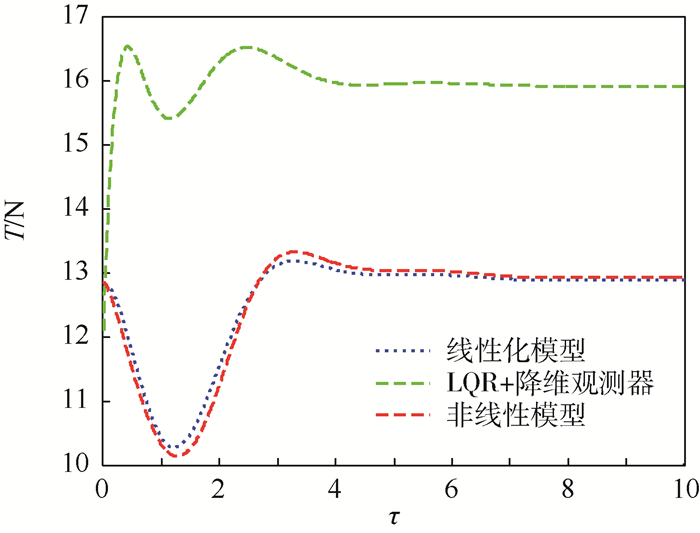 |
| 图 3 系绳展开后系绳张力变化曲线 Fig. 3 Variation curves of tether tension after tether deployment |
| 图选项 |
如图 2所示,利用矩阵分解方法设计的控制器对线性化模型和非线性模型进行控制,其仿真曲线基本重合。非线性模型下,4个状态量的超调量略高于线性化模型,这是由于线性化过程中忽略了系绳长度、质量以及面内摆动运动等因素的影响,因此,后续针对捕获后面内摆动问题采用非线性模型式(1)进行仿真验证。此外,由图 3可以看出,3种情况下系绳张力变化均相对平稳,张力保持在十几牛的大小附近(远小于极限张力T*=σ*S=54×109×2×10-7=10 800 N)。
线性化模型下,根据矩阵分解方法设计的控制器与LQR+降维观测器对比可知, 2种方法都能够有效控制系统的长度和角度误差,且调节时间相差不大,系统的4个状态量在5个无量纲时间(约0.8个轨道周期)时间前后全部回到了稳态值。然而,利用LQR+降维观测器方法时,绳长、速率、面内角及面内角速率的超调量均远高于基于矩阵分解方法设计的控制器,即基于矩阵分解方法的模态控制器不仅能有效抑制系统展开后所出现的非标称行为,使系统回到平衡位置,同时,与常用的LQR+降维观测器相比,其平稳性和静差消除都更为理想,能够满足空间系绳系统稳态保持控制的要求。
5.2 捕获后系绳面内摆动抑制 以轨道高度H=900 km、捕获窗口30 s为例,捕获后瞬间系统以5.786 5×10-4 rad/s的角速率摆动,则由式(14)计算可知,系绳不受控下最大摆角θmax可达到0.33 rad(约18.9°),故利用本文设计的控制律针对捕获任务完成后系统出现的面内摆动,对其进行控制使其回到稳定状态即平衡位置。根据式(11)计算非理想情况下捕获后面内角速率,根据计算结果结合式(14)计算捕获后面内最大摆角,并将其转换为无量纲形式,可得仿真初始条件为:ε=1,ε′=0,θ=8.68×10-3,θ′=5.786 5×10-4/Ω。与各模型、控制律相对应的控制力变化曲线如图 4所示,仿真结果如图 5所示。
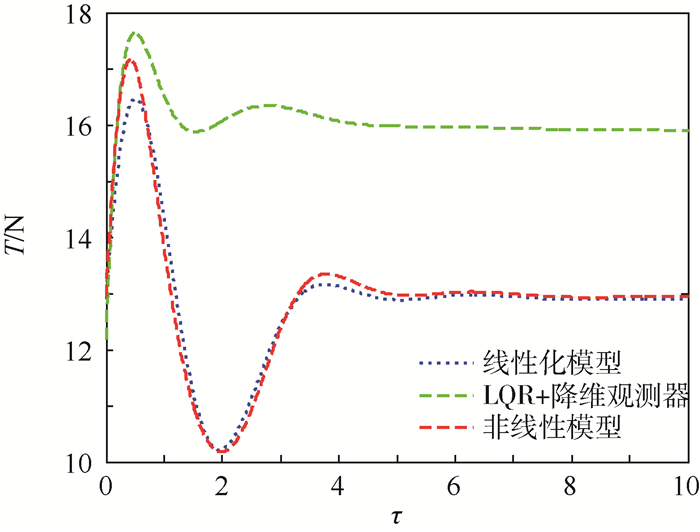 |
| 图 4 捕获后系绳张力变化曲线 Fig. 4 Variation curves of tether tension after capture |
| 图选项 |
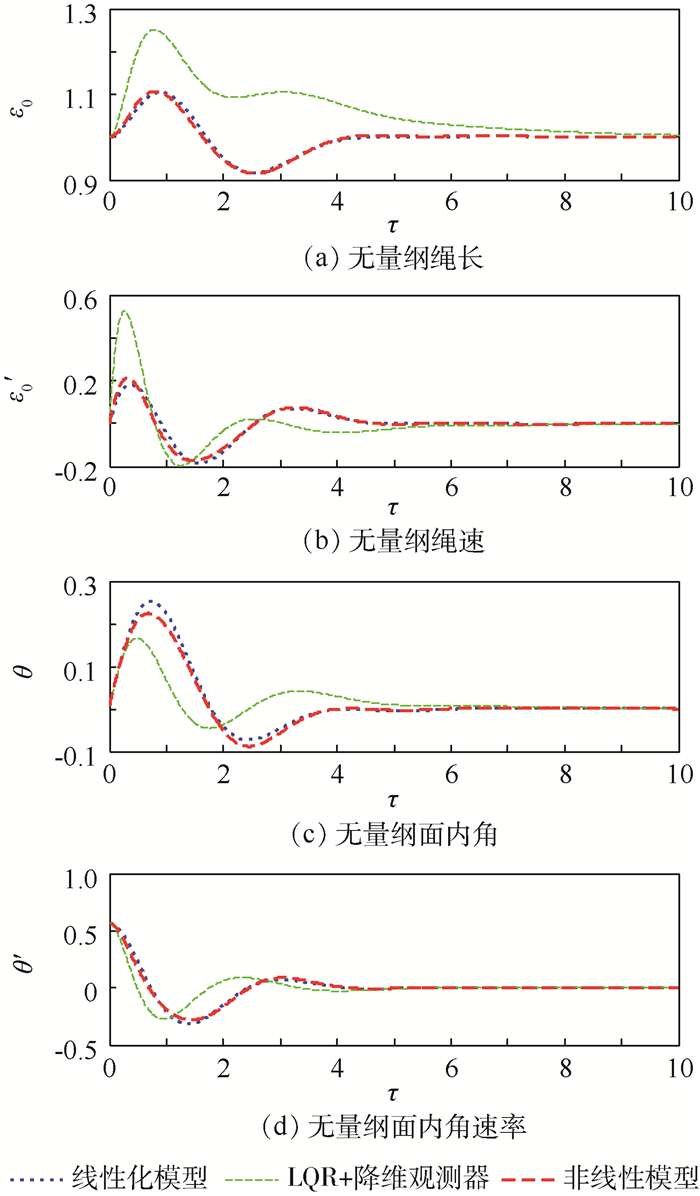 |
| 图 5 捕获后各状态量受控变化曲线 Fig. 5 Changing curves of state variables under control after capture |
| 图选项 |
由图 5可以看出,线性化系统初始时刻存在面内摆动时,基于矩阵分解的模态控制和LQR+降维观测器作用下速率、面内角和面内角速率的变化趋势大致相近,LQR+降维观测器对面内角和面内角速率的控制略优于基于矩阵分解设计的控制器,但绳长和速率的变化差异较大。基于矩阵分解模态控制器下绳长、速率最终全部回到稳态值1和0(无静差),系统回复到了平衡位置,快速性和平稳性较好;而LQR+降维观测器对绳长和速率控制的平稳性较差,控制效果并不理想。绳长超调量达到了21.59%,是基于矩阵分解控制方法的2倍;峰值速率为0.44(13.442 m/s),对系绳机构的要求更为严苛。
基于矩阵分解方法设计的控制器对线性化模型和非线性模型的控制曲线基本重合。故基于线性化模型设计的模态控制律在实际非线性模型下也具有标称的控制效果,其对非线性模型的控制效果与对线性化模型控制的效果基本相同,绳长、速率、面内角及面内角速率最终都在有限时间内回到平衡位置附近,过渡过程相对平稳,没有对控制机构提出额外的要求,从而表明利用矩阵分解方法设计的控制律对于捕获后系统的面内摆动抑制是有效的。
由式(11)可知,捕获完成后系绳的面内摆动角速率的大小直接或间接受到目标物的质量以及捕获瞬间二者的距离(即绳长)的影响;与此同时,系统各部分质量变化会直接改变非线性模型中参数?1、?2、?3、?4。因此,需计算目标物、系绳质量不同时捕获后系统的角速率,并在新的初始条件下进行仿真对比,进一步检验本文设计的控制器对系统的控制效果。
质量mA=1 600 kg捕获平台利用lc=30 km的系绳对不同质量的目标物进行捕获时,利用式(11)计算捕获前后角速率以及捕获窗口结束时系绳的面内角的大小,并将捕获后角速率化为无量纲形式作为仿真初始条件进行仿真,系统各状态量变化曲线如图 6所示。尽管仿真初始条件根据目标物质量变化而有所改变,但系统的过渡过程平稳,4个状态量出现波峰和波谷的时间相差无几,且长度、速率、面内角的超调量均随目标物质量的增加而微弱增加。
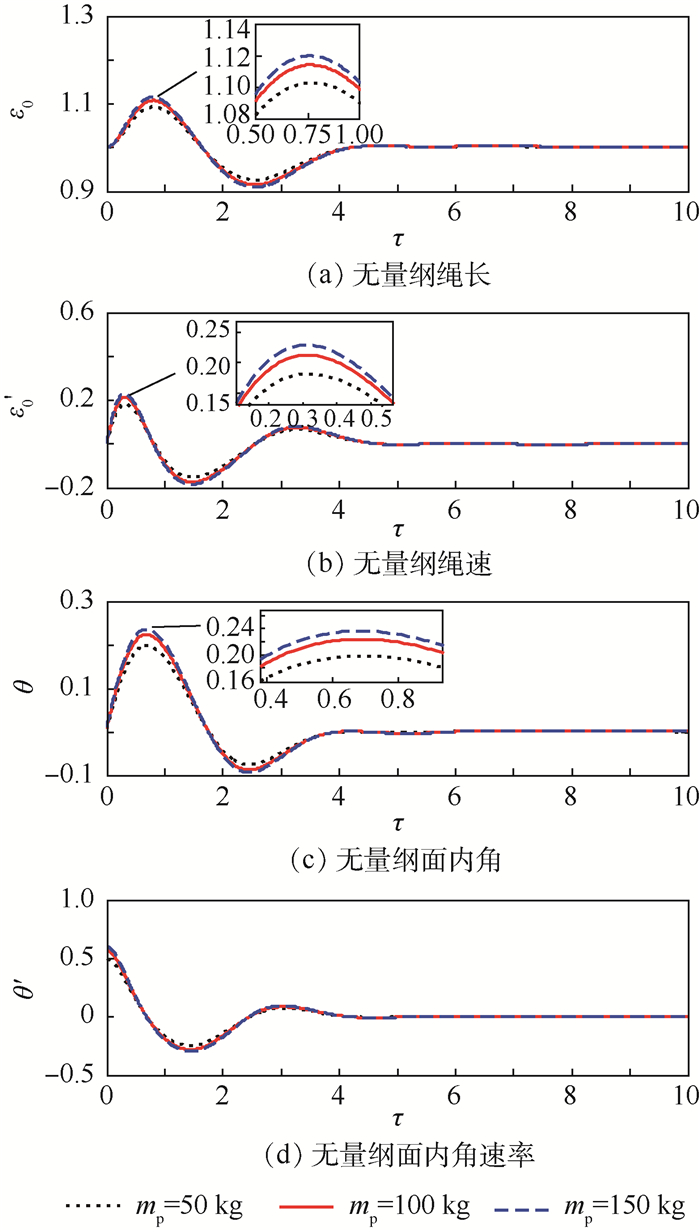 |
| 图 6 捕获不同目标物后各状态量受控变化曲线 Fig. 6 Changing curves of state variables under control with different captured debris |
| 图选项 |
质量mA=1 600 kg捕获平台利用不同的长度系绳对质量mp=100 kg的目标物进行捕获时,系统各状态量变化曲线如图 7所示。与捕获平台和目标物的质量变化相比,绳长变化对仿真初始条件的影响更为明显,而对系统控制效果的影响也更为剧烈。系统状态量的波峰/波谷都会随系绳长度增加而更高/低,即在一定程度上系绳长度越长,系统平稳性越好。
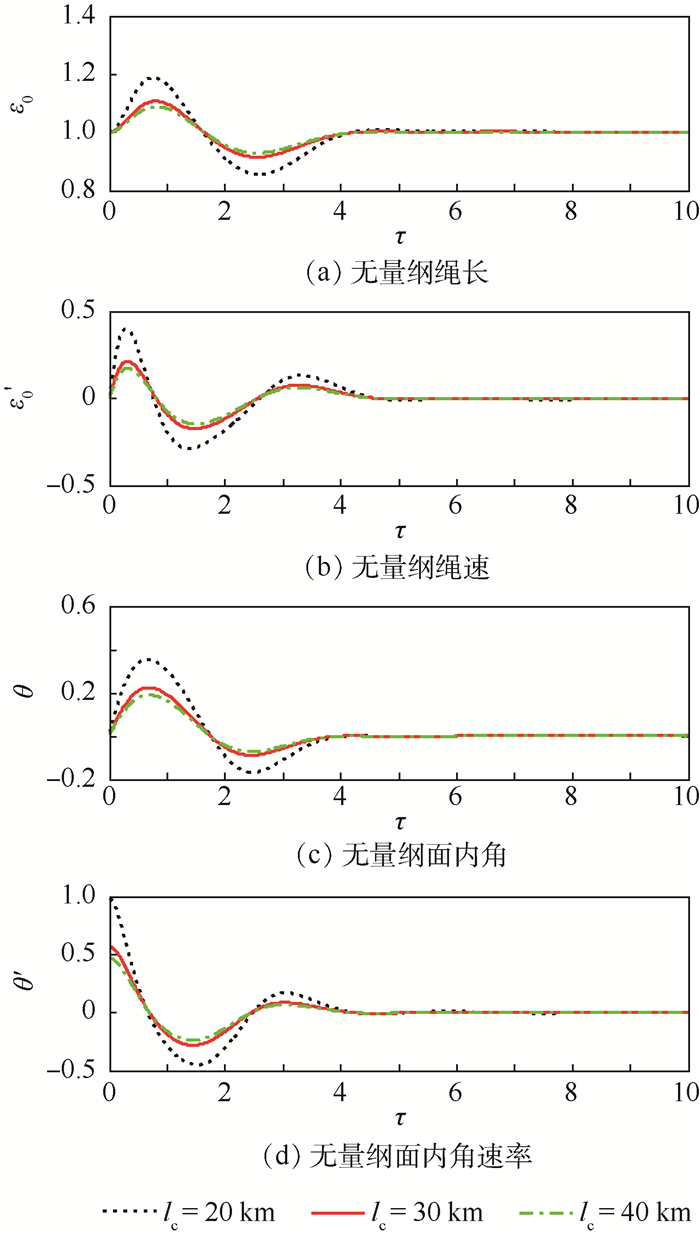 |
| 图 7 不同长度系绳完成捕获后各状态量受控变化曲线 Fig. 7 Changing curves of state variables under control with different length of tether after capture |
| 图选项 |
综合上述分析可以看出,相比LQR控制器繁琐的调参工作,以及降维观测器设计中观测器矩阵特征值复杂的选定工作,矩阵分解方法根据较为理想的参考传递函数,直接设计出了控制效果较为理想的控制器,省去了相应的调参工作。本文设计的控制律能够有效解决捕获后系绳面内摆动的抑制任务,过渡过程平稳,其状态量出现波峰波谷的时间相近,大小变化不大,控制效果良好,任务适应性强。因此,基于矩阵分解方法设计的控制器能够有效地将空间系绳系统控制在期望的稳定状态,同时设计简便,没有繁琐的调参环节。
6 结论 1) 基于矩阵分解设计的控制律能够有效控制系绳展开非标称行为及捕获后面内扰动,超调量较小,过渡过程平稳且调节时间相对较短;此外,该控制律在模型质量参数存在大范围不确定性的情况下同样具有较好的控制效果和抗干扰能力。
2) 本文设计的控制律相比于常见的LQR+降维观测器方法,具有更好的控制效果,且将闭合特征方程设计为标准系数法中指定形式,其控制效果可预期。此外,设计过程简单,避免了繁琐的调参工作。
3) 仿真表明,本文设计的控制律对于目标物以及系绳质量(长度)大范围变化的系统同样适用,故可以适用于一大类大质量捕获平台捕获小质量目标物的系绳系统状态保持和摆动抑制的问题,为利用空间系绳系统进行捕获的回稳控制提供了有用参考。
参考文献
| [1] | PASCA M. Nonlinear control of tethered satellite system oscillations[J]. Nonlinear Analysis, 1997, 30(6): 3867-3878. DOI:10.1016/S0362-546X(97)00114-4 |
| [2] | WILLIAMS P, WATANABE T, BLANKSBY C, et al. Libration control of flexible tethers using electromagnetic forces and movable attachment[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 882-897. DOI:10.2514/1.1895 |
| [3] | MANKALA K K, AGRAWAL S K.A boundary controller based on linear infinite dimensional system for station keeping of a tethered satellite system[C]//American Control Conference.Piscataway, NJ: IEEE Press, 2006: 9036818. |
| [4] | LARSEN M B, BLANKE M.Control by damping injection of electrodynamic tether system in an inclined orbit[C]//American Control Conference.Piscataway, NJ: IEEE Press, 2009: 4824-4829. |
| [5] | YU B S, JIN D, WEN H. Nonlinear dynamics of flexible tethered satellite system subject to space environment[J]. Applied Mathematics and Mechanics(English Edition), 2016, 37(4): 485-500. DOI:10.1007/s10483-016-2049-9 |
| [6] | 余本嵩.复杂太空环境下柔性绳系卫星动力学与控制[D].南京: 南京航空航天大学, 2011: 91-94. YU B S.Dynamics and control of flexible tethered satellite in complex space environment[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2011: 91-94(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1012033381.htm |
| [7] | 庞兆君.绳系卫星状态保持阶段运动分析与控制[D].南京: 南京航空航天大学, 2015: 39-42. PANG Z J.Motions and their controls of tethered satellite systems during station-keeping[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2015: 39-42(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D820835 |
| [8] | SUN L, ZHAO G W, HUANG H. Stability and control of tethered satellite with chemical propulsion in orbital plane[J]. Nonlinear Dynamics, 2013, 74(4): 1113-1131. DOI:10.1007/s11071-013-1028-z |
| [9] | 孙亮, 赵国伟, 黄海, 等. 面内轨道转移过程中的绳系系统摆振特性研究[J]. 航空学报, 2012, 33(7): 1245-1254. SUN L, ZHAO G W, HUANG H, et al. Analysis of librational and vibrational characteristics for tethered systems during orbital transfer in plan[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1245-1254. (in Chinese) |
| [10] | 张帆, 黄攀峰. 空间绳系机器人抓捕非合作目标的质量特性参数辨识[J]. 宇航学报, 2015, 36(6): 630-639. ZHANG F, HUANG P F. Inertia parameter estimation for an noncooperative target captured by a space tethered system[J]. Journal of Astronautics, 2015, 36(6): 630-639. DOI:10.3873/j.issn.1000-1328.2015.06.003 (in Chinese) |
| [11] | 赵国伟, 张兴民, 唐斌, 等. 空间绳系拖拽系统摆动特性与平稳控制[J]. 北京航空航天大学学报, 2016, 42(4): 694-702. ZHAO G W, ZHANG X M, TANG B, et al. Properties of pendulum motion of tether tugging system and its stable control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(4): 694-702. (in Chinese) |
| [12] | 张宇靖, 钟睿. 基于非线性模型预测的绳系系统系绳摆振控制[J]. 北京航空航天大学学报, 2018, 44(10): 2200-2207. ZHANG Y J, ZHONG R. Tether swing control of tether system based on nonlinear model prediction[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(10): 2200-2207. (in Chinese) |
| [13] | LORENZINI E C. Error-tolerant technique for catching a spacecraft with a spinning tether[J]. Journal of Vibration and Control, 2004, 10(10): 1473-1491. |
| [14] | 王班, 易琳, 郭吉丰, 等. 一种基于摆长反复小幅改变的面内摆动抑制方法[J]. 四川大学学报(工程科学版), 2014, 46(6): 191-197. WANG B, YI L, GUO J F, et al. An in-plane swing damping method based on pendulum length changed repeatedly[J]. Journal of Sichuan University(Engineering Science Edition), 2014, 46(6): 191-197. (in Chinese) |
| [15] | 李超, 王长青, 李爱军, 等. 基于标准系数法的空间系绳系统状态保持稳定控制[J]. 航天控制, 2014, 32(2): 73-77. LI C, WANG C Q, LI A J, et al. Stability control for station-keeping phase of space tether system based on standard coefficient method[J]. Aerospace Control, 2014, 32(2): 73-77. DOI:10.3969/j.issn.1006-3242.2014.02.013 (in Chinese) |
| [16] | BANGHAM M E, LORENZINI E C, VESTAL L.Tether transportation system study: NASA/TP-1998-206959[R].Washington, D.C.: NASA, 1998. |
| [17] | CHEN Y, HUANG R, REN X, et al. History of the tether concept and tether missions:A review[J]. ISRN Astronomy and Astrophysics, 2013, 2013: 502973. |
| [18] | ASHIDA H, FUJIHASHI K, INAGAWA S, et al. Design of Tokyo tech nano-satellite CUTE-1.7+APD Ⅱ and its operation[J]. Acta Astronautica, 2010, 66(9): 1412-1424. |
| [19] | WEN H, ZHU Z H, JIN D, et al. Space tether deployment control with explicit tension constraint and saturation function[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(4): 916-921. DOI:10.2514/1.G001356 |
| [20] | WILLIAMS P, BLANKSBY C, TRIVAILO P, et al. In-plane payload capture using tethers[J]. Acta Astronautica, 2005, 57(10): 772-787. DOI:10.1016/j.actaastro.2005.03.069 |
| [21] | KRUIJFF M, VAN DER HEIDE E, OCKELS W, et al.First mission results of the YES2 tethered SpaceMail experiment[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Reston: AIAA, 2008: 7385. |
