2007年,国际系统工程协会(International Council on Systems Engineering, INCOSE)给出了MBSE的定义[3]:基于模型的系统工程(Model-Based Systems Engineering,MBSE)理论用于支持系统需求捕获、设计、分析和验证活动,这些活动从概念设计阶段开始,一直延续至整个系统开发及后续生命周期阶段[4]。
近年来,MBSE理论在系统工程领域得到越来越广泛的关注和应用。美国国家航空航天局(NASA)、空客和波音均已在多个项目中成功应用了MBSE方法[5]。IBM公司基于MBSE方法开发出载有需求分析模块的Rhapsody软件,得到广泛应用[6]。MEL (Michigan Exploration Lab)实验室成功使用MBSE和SysML对标准立方体卫星进行建模,并应用于实际的立方体卫星任务中[7]。Perez[8]将MBSE理论成功应用到风险信息设计中。Fusaro等[9]基于MBSE开发了有效的超高音速轨道交通系统。国内张绍杰等[5]结合民机设计通用规范,提出了一种基于模型的系统工程对飞机安全关键系统进行分析和设计的方法。傅有光等[10]基于MBSE理论在达索V6的环境平台验证了两型雷达研发的完整过程,全面实现了由传统基于文档的研发模式向基于模型的MBSE研发模式转变。
本文引入MBSE理论开展民用飞机设计方法研究。研究起始于基于用户需求的自顶向下的民机系统产品顶层用例,基于关键子对象用例展开“需求—功能分析”,进一步构建可进行逻辑仿真的黑盒状态机。在黑盒功能架构的基础上驱动基于人机交互系统模型的民机功能架构“正向设计”过程。对黑盒进行解白,基于建模分析和数值仿真结果,构建实现相关飞机级需求的系统功能白盒架构的“正向设计”。研究表明基于MBSE的民用飞机功能架构设计方法可以充分保证需求分析和功能架构设计的紧密结合。
1 MBSE理论概述与民机系统功能需求分析实例 本文展开基于MBSE的民机系统功能需求分析工作。从用例出发,进行MBSE方法和SysML模型的实例分析。
1.1 MBSE方法概述 Harmony SE(Harmony for Systems Engineering)是MBSE方法中的一种。Harmony SE的系统工程工作流是增量迭代式的周期活动流,它可分为需求分析、系统功能分析和设计综合3个设计阶段:
1) 需求分析[11]。此阶段是将初始用户需求转化为系统需求初稿,同时定义系统用例详细描述系统的行为。
2) 系统功能分析[12]。此阶段的重点是把系统功能性需求转化为一个连贯的系统功能描述。该阶段将系统功能性需求转化为一个可执行模型,通过3个SysML图形(活动图、顺序图、状态机)来展现用例模型的内容。
3) 设计综合[13]。此阶段分为2个大的子阶段:架构分析与架构设计阶段。架构分析阶段是通过一系列的系统评估分析, 确定最佳的解决方案。架构设计阶段是分配功能性和非功能性需求到架构结构中,将系统功能分析阶段的“黑盒”模型逐渐转变为“白盒”模型。
图 1为Rational集成系统开发流程Harmony图。V模型的左边是在设计前期,模型自顶向下推动后续设计的进展,V模型的右边是在设计后期自底向上对系统进行验证与测试[14]。
 |
| 图 1 Rational集成系统开发流程Harmony图 Fig. 1 Harmony diagram of Rational integrated system development process |
| 图选项 |
1.2 基于用例的民机飞机级需求分析 MBSE方法从导入用户的原始需求出发,形成系统顶层用例模型[15]。随后对系统顶层需求进行捕获和分解得到系统子用例。国际民用航空组织(the International Civil Aviation Organization, ICAO)年度安全性报告显示[16],最后进近着陆阶段是事故率高发时期。图 2为民机系统最后进近着陆场景顶层用例模型。图中,矩形表示系统边界,系统内部椭圆表示系统具有的一个功能即用例,“人形”图标表示系统与外界的交互。控制飞机完成最后进近着陆飞行任务,其中用例为完成最后进近着陆任务,外部使用者为飞机本身。民机系统可以接受通信导航信息,用例为接受通信信息,外部使用者为地面站。飞机系统可以接受执行控制操作,用例为执行控制操作,外部使用者为飞行员。
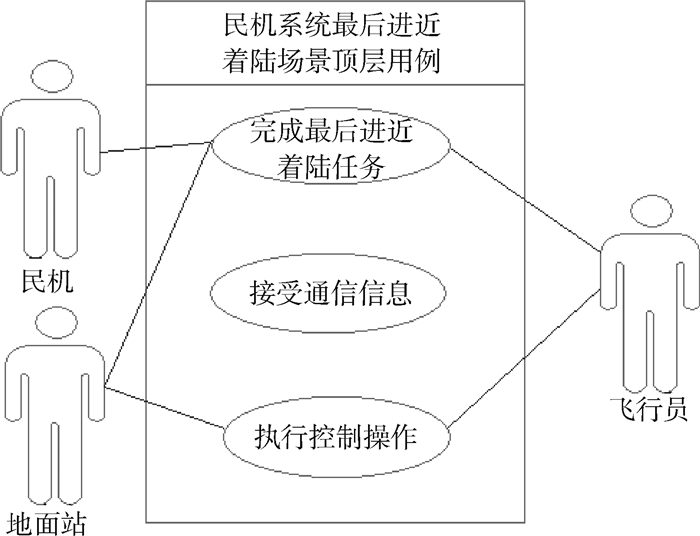 |
| 图 2 民机系统最后进近着陆场景顶层用例模型 Fig. 2 Top-level use case model of civil aircraft system in final approach and landing scenario |
| 图选项 |
在完成最后进近着陆任务、接受通信信息和执行控制操作3个用例中,完成最后进近着陆任务是用户基于典型场景对飞机系统提出的首要需要,即完成最后进近着陆任务的颗粒度最大,优先级最高。对于优先级高的用例继续分解细分,可分为完成起始进近,完成五边进近,完成着陆或复飞3个二级子用例如图 3所示。
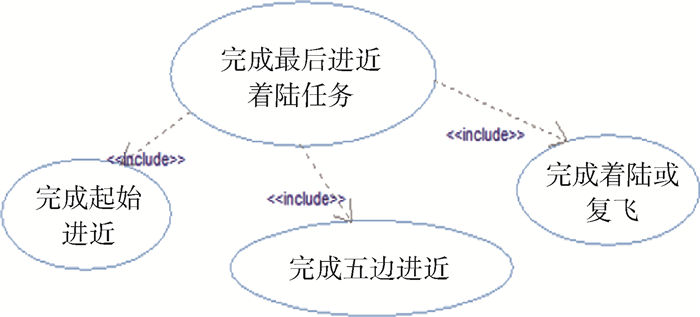 |
| 图 3 民机系统二级子用例 Fig. 3 Second-level sub-use case of civil aircraft system |
| 图选项 |
图 4将事故率最高的着陆或复飞子用例进一步划分为3层子用例,包括调定速度、调整高度、着陆滑行和复飞4个三级子用例。
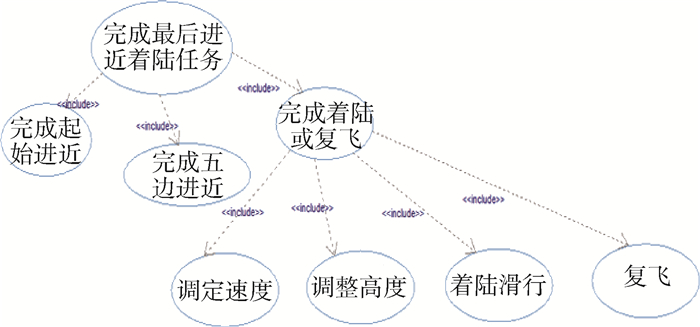 |
| 图 4 民机系统三级子用例 Fig. 4 Third-level sub-use case of civil aircraft system |
| 图选项 |
1.3 基于流图的系统黑盒功能架构辨识 在功能分析阶段,形成能描述系统功能及其相互影响的一系列模型,即把在前面需求分析阶段确认的用例翻译成一个可执行模型。模型和相关需求由模型的执行来验证,主要包括活动图、顺序图和状态机。其中活动图用于规定功能之间的逻辑关系,描述工作流或是分解执行流到一系列的活动和子活动中的运算法则。图 5为最后进近着陆过程的黑盒活动图[17]。
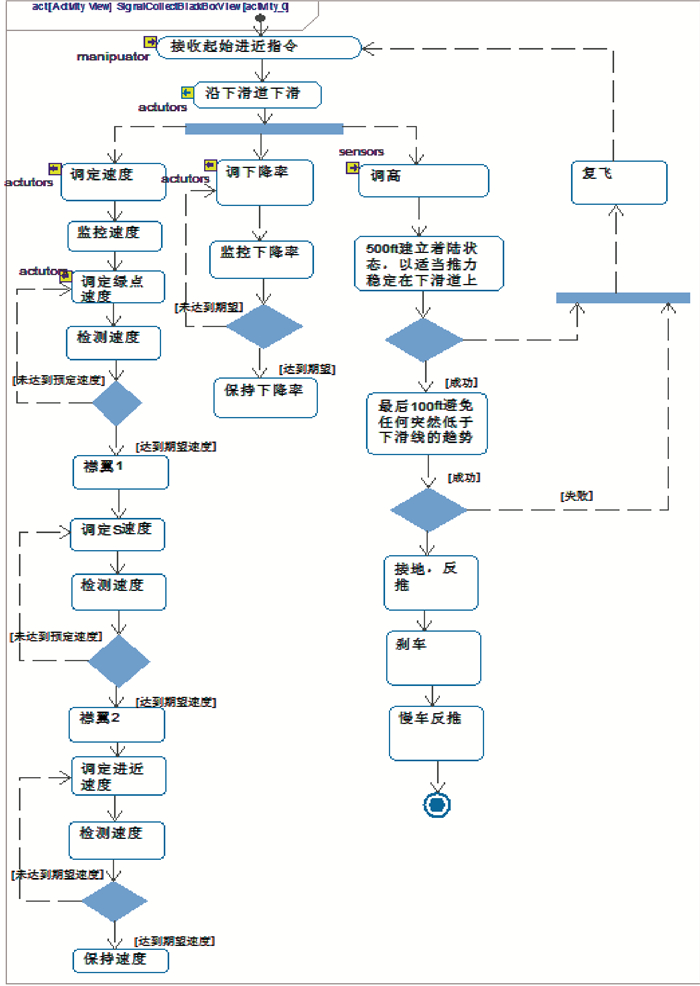 |
| 图 5 最后进近着陆过程黑盒活动图[17] Fig. 5 Black box activity diagram of final approach and landing process[17] |
| 图选项 |
由图 5的最后进近着陆过程黑盒活动图,抽象出调定速度顺序图如图 6所示。其他活动的顺序图也可同理得到此处不再赘述。顺序图是由伴随角色和模块的垂直生命线,以及这些实体在一段时期内所形成的有顺序的系列信息构成[18]。顺序图可以清晰地展现出系统与外界的交互内容,在顺序图基础上可以产生系统功能的基本操作、交互事件以及接口等。
 |
| 图 6 调定速度用例顺序图 Fig. 6 Sequence diagram of set speed use case |
| 图选项 |
1.4 基于接口的系统级功能需求捕获 汇总以上具体用例中得到的需求分析,通过将相似需求的功能进行归类,得到民机子系统划分表,如表 1所示。
表 1 子系统划分 Table 1 Subsystem partition
| 具体功能 | 子系统 |
| 监控速度 | 监控子系统 |
| 监控高度 | |
| 监控下降率 | |
| 接受指令 | |
| 报告飞行状态信息 | |
| 报告飞行状态信息 | |
| 调整速度 | 油门控制子系统 |
| 保持速度 | |
| 刹车 | |
| 慢车反推 | |
| 调整滚转平衡 | 舵面调节子系统 |
| 调整滚转角 | |
| 调节下降率 | |
| 保持下降率 | |
| 复飞 | |
| 襟翼收放 | 襟翼系统 |
| 感知飞行状态信息 | 指令计算子系统 |
| 沿下滑道下滑 | |
| 对准跑道 | |
| 生成预测航迹 | |
| 调定速度 | |
| 调整下降率 |
表选项
1.5 基于MBSE仿真的飞机级需求确认
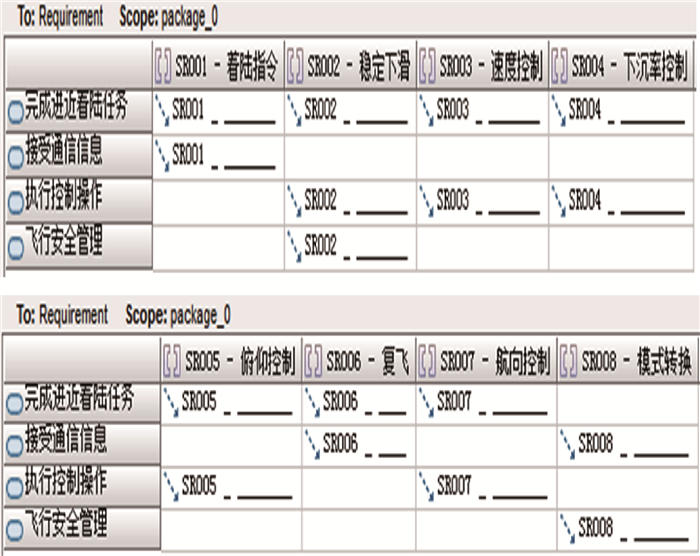
1.5.1 基于用例——需求矩阵的需求完整性确认 本节将对1.2~1.4节得到的民机系统最后进近着陆过程的需求进行追溯和确认。需求追溯的过程是检查设计的系统是否满足用户需要,Rhapsody软件中gateway插件可以实现需求的追溯[19]。图 7为Rhapsody需求确认矩阵,可以将用例和需求进行关联,确认提取的功能需求是满足用户原始需要的。
 |
| 图 7 需求确认矩阵 Fig. 7 Requirement confirmation matrix |
| 图选项 |
图 7中,横轴是民机系统的系统级功能需求,纵轴是用户原始需求。在需求确认矩阵中,添加能满足用户需求的对应系统级功能需求与用户需求之间的关系,图中展示的4条用户需求:完成最后进近着陆任务、接受通信信息、执行控制操作与飞行安全管理均被关联。表明设计的系统是满足用户原始需求的,需求得到追溯。
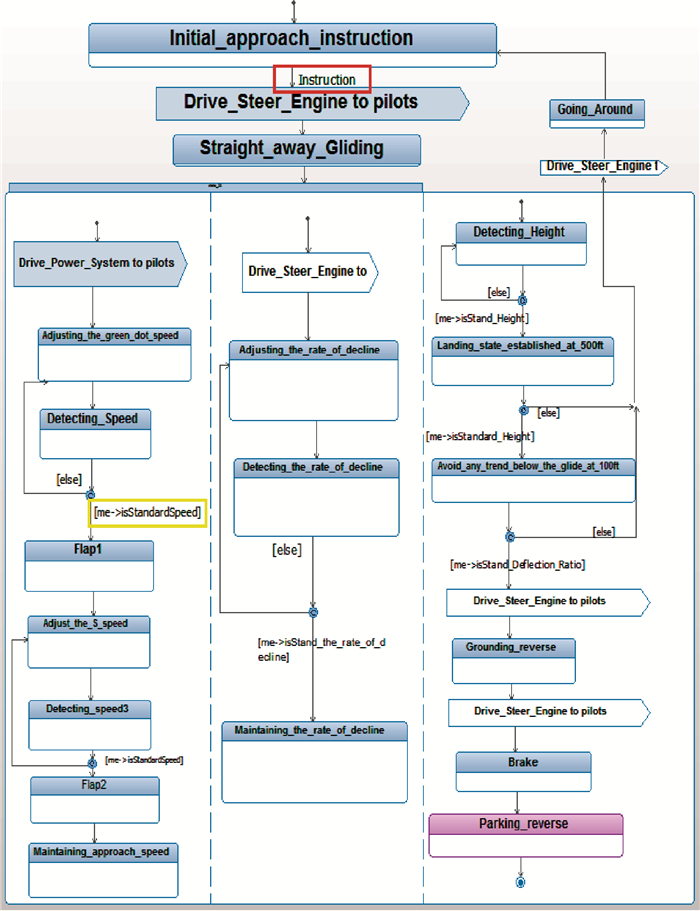
1.5.2 基于黑盒状态机仿真的飞机级需求正确性确认 使用Rhapsody软件绘制民机系统的状态机图如图 8所示[11]。状态机描述了系统的状态行为、分析活动图、顺序图以及列出的子系统划分表,得到系统的状态变换描述。首先民机通信系统收到最后进近着陆指令,经指令计算系统计算,飞机沿下滑道下滑。飞机同时发出调整速度、调下降率和调高的指令。接下来分别进入相应的子系统执行系统功能直至飞行任务完成。
 |
| 图 8 最后进近着陆过程状态机图[11] Fig. 8 State machine diagram in final approach and landing process[11] |
| 图选项 |
状态机的运行结果是检验系统设计是否符合需求的重要手段。在状态机模型中,红色方框代表外部触发事件,当且仅当触发事件发生时,状态机才会向下执行。黄色方框([me->is])代表不同的任务场景,状态机执行到此处时,通过系统不同场景的选择执行不同支路。蓝色的矩形(如图 8中的Drive_Steer_Engine to pilots)表示外部系统参与的事件,即仅当外部系统作用时才会触发。粉色框图代表系统当前所处的状态。如图 8所示的状态机中,触发事件Instruction生成后,状态机即向下执行,当状态机执行到分支场景时,将通过飞行状态判断执行相应支路。图 8中系统进入着陆过程的刹车与反推阶段,最终完成典型飞行场景任务流程。功能逻辑设计合理,用户期望的飞机完成最后进近着陆典型飞行场景的需求得以完整实现。
2 基于人机交互系统建模的民机功能白盒架构设计 设计综合的目标是整合功能分析阶段的模型元素, 设计系统架构[11]。由于本文选取的机型Boeing 747系统架构已成熟,因此在设计综合阶段主要的工作是对已形成的功能进行分析,对需求进行追溯与确认工作,将系统功能分析阶段的“黑盒”模型逐渐转变为“白盒”模型。
2.1 基于认知架构的人机交互系统开发 本节基于Harmony SE的民用飞机功能架构的“正向设计”过程,搭建基于认知架构的人机系统模型验证功能设计过程面向功能需求的可追溯性与合理性。开发人机系统的直接目的是根据各种机型以及人机环参数下的多种飞行条件快速实现基于各种飞行场景的飞行任务。人机交互系统快速自动产生的飞行数据经与在高仿真驾驶舱中真实机组执行相同的飞行任务产生的飞行数据的比较,经验证是可靠且全面的。人机交互系统可以用于描述在各种飞行条件下飞行任务与机组干预、工作负荷分配和异常事件的处置程序等因素之间的动态关系与适应性。
人机交互系统中的飞机模型基于六自由度飞机模型搭建。飞机在空中的运动可看成具有六自由度的刚体,其中包括以牛顿第二定律为基础的3个平动向量和以欧拉方程为基础的3个转动向量。在仿真中,基于波音747-400系列飞机动力学模型[20]的机身参数、气动力系数和气动力矩系数等相关参数进行实验。相关飞机参数的设置如表 2~表 4所示。表 3中,CL0、CL_α、CL_adot、CL_q、CL_de分别为零升系数、升力线斜率、升力对迎角变化率的导数、升力对俯仰角速度的导数和升力对升降舵偏角的导数,CDo和CD_α分别为零升阻力系数和阻力对迎角变化率的导数,侧力系数CY_beta、CY_p和CY_dr分别为侧力对侧滑角的导数、侧力对滚转角速度的导数和侧力对方向舵偏角的导数。表 4中,Cl_r为滚转力矩系数对偏航角速度的导数; CN_r为偏航(方向)力矩系数对无量纲偏航角速度的导数。
表 2 波音747-400机身参数 Table 2 Boeing 747-400 aircraft parameters
| 参数 | 数值 | |
| 翼展c/m | 59.74 | |
| 翼展b/m | 8.32 | |
| 参考面积s/m2 | 510.97 | |
| 起飞质量m/kg | 288 775 | |
| 最大推力T/kg4 | 28 803 | |
| Ix | 24 675 887 | |
| Iy | 44 877 574 | |
| 转动惯量/(kg·m2) | Iz | 67 384 152 |
| Ixz | 1 315 143 |
表选项
表 3 波音747-400气动力系数 Table 3 Boeing 747-400 aerodynamic coefficient
| 参数 | 数值 | |
| 升力系数 | CL0 | 0.21 |
| CL_α | 4.40 | |
| CL_adot | 7.0 | |
| CL_q | 6.6 | |
| CL_de | 0.32 | |
| 阻力系数 | CD0 | 0.016 4 |
| CD_α | 0.2 | |
| 侧力系数 | CY_beta | -0.9 |
| CY_p | 0 | |
| CY_dr | 0.12 |
表选项
表 4 波音747-400气动力矩系数 Table 4 Boeing 747-400 aerodynamic moment coefficient
| 参数 | 数值 | |
| 滚转力矩l | Cl_beta | -0.16 |
| Cl_p | -0.34 | |
| Cl_r | 0.13 | |
| Cl_da | -0.013 | |
| Cl_dr | 0.008 | |
| 俯仰力矩M | CM0 | 0 |
| CM_a | -1.0 | |
| CM_adot | -4 | |
| CM_q | -20.5 | |
| CM_de | -1.3 | |
| 偏航力矩N | CN_beta | 0.16 |
| CN_p | -0.026 | |
| CN_r | -0.280 | |
| CN_da | -0.001 8 | |
| CN_dr | -0.1 |
表选项
系统中的模拟飞行员认知模型可分为3个模块:飞行状态信息获取、决策和控制[21]。
1) 飞行状态信息获取模块:指飞行员的情景意识,即在飞行中对周围环境信息以及飞行动态的即时感知过程。
通过串行自终止搜索模型(SSTS)[22]得到N个仪器的搜索时间ST与N成正比:
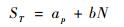 | (1) |
式中:ap为在一个信息搜索过程中的固有时间;b为单个仪器的搜索时间,它随着仪器的不同而变化。在此飞行员模型中,定义变量ST等于在信息获取阶段的认知时延。
2) 决策模块:指飞行员获得信息感知模块得到的信息后,根据飞行经验等对目前的飞行状况做出评估与预测,并生成一组可执行的预期操作程序。
反应时间可以由Hick-Hyman-law定理[23]测量,它与该模块中包含的信息量成正比:
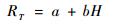 | (2) |
式中:a为与不确定性降低无关的时延总和;H是由式(3)计算出的平均信息量:
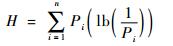 | (3) |
其中:Pi为在飞行中第i个信息出现的概率,所有信息出现的概率总和为1。
3) 控制模块:指飞行员在决策模块得到一组预期的操作程序后,执行程序的结果。通常控制模块包括油门的加减、升降舵的偏转和起落架收放等动作。
控制模块的时延与操作精度的关系可以用速度-精度操作特性(SAOC)[24]表示:
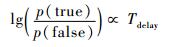 | (4) |
式中:p(true)+p(false)=1,操作精度用随机变量的形式表示; Tdelay为控制模块的时延。若设升降舵操作精度为99%,可得
 | (5) |
其中:δeac为升降舵的实际操作量;δeex为升降舵的期望操作量。模拟飞行员认知过程模型如图 9所示。结合飞机六自由度模型实现人机交互系统开发平台。
 |
| 图 9 模拟飞行员模型框架 Fig. 9 Simulated pilot model framework |
| 图选项 |
人机交互系统采用MATLAB/Simulink和C#混合编程方法搭建。其中在MATLAB/Simulink中实现飞机的非线性动力学模型,该模型会根据舵面和油门的控制量输入解算出飞机状态量的变化,并能外接自动控制器进行联合数值仿真。在C#中主要完成座舱系统显示平台的界面设计以及功能划分等工作。模型中自动控制器控制的操作机理可类似于飞行员对飞机的操作,即用于纵向控制的升降舵,油门杆和用于横向/舵向控制的方向舵和副翼。系统针对座舱系统中自动驾驶仪的高度保持、俯仰姿态保持和速度保持3种控制,在MATLAB/Simulink中设计了相应的自动控制器。
统计数据显示最后进近着陆阶段是飞行事故的高发阶段,本文针对最后进近着陆阶段典型飞行场景用例进行详细分析,并在民机系统的功能需求分析中进行迭代,形成较为完整的需求分析结果。
2.2 基于典型飞行场景仿真的功能黑盒解白 选取如图 10所示的最后进近着陆阶段典型飞行场景,将着陆过程细分为飞机沿下滑道直线下滑、拉平飘落、滑行停车阶段。
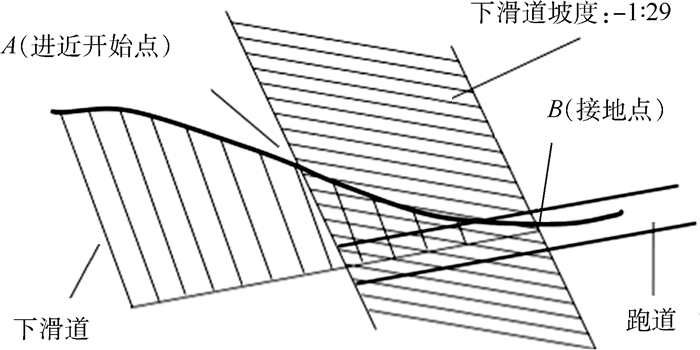 |
| 图 10 最后进近着陆阶段典型飞行场景 Fig. 10 Typical flight scenario of final approach and landing phase |
| 图选项 |
截取图 5黑盒活动图中正常进近着陆的部分进行相关从MBSE方法对应到相关人机系统设计的叙述。图 11为基于MBSE的民用飞机功能需求方法中正常进近着陆包含的主要活动产生的需求映射到相应的控制器设计过程演示图。
 |
| 图 11 需求映射到控制器演示图 Fig. 11 Demonstration diagram of requirements mapped to controller |
| 图选项 |
基于MBSE分析得到的活动图,在最后进近着陆阶段,有调定速度、调下降率和调高的3个基本需求。将需求反应到人机系统的实际建模中,本文设计了速度保持控制器、俯仰姿态保持控制器和高度保持控制器以实现相关调速、调高以及调整俯仰姿态需求的功能黑盒解白。
1) 速度保持控制器:本文设计的速度保持控制器控制律为
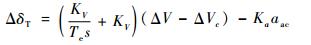 | (6) |
式中:KV为速度环比例系数;ΔVc为平衡点处的飞机空速;ΔV为飞机实际空速;aac为飞机实际加速度;Ka为加速度反馈系数;Te为积分环节时间常数。
2) 俯仰姿态保持控制器:针对下降率的调节与保持需求,系统中设计了俯仰姿态控制器。比例-积分控制器是目前工程中最广泛使用的姿态控制器[25]。系统设计的俯仰姿态保持控制器控制律为
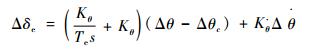 | (7) |
式中:Kθ为俯仰角比例环节系数;Δθc为平衡点处的俯仰角;Δθ为飞机实际俯仰角;Kθ·为俯仰角速度反馈环节系数;

3) 高度保持控制器:高度保持控制器是以俯仰姿态保持控制器为内环,在外环加一层对高度的比例-积分控制器实现的[25]。高度保持控制器控制律为
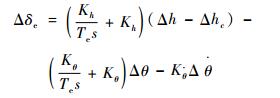 | (8) |
式中:Kh为高度环比例系数;Δhc为平衡点处的飞行高度;Δh为飞机实际飞行高度。
基于最后进近着陆阶段的典型飞行场景,在人机模拟座舱系统中分布配置不同的飞行员操作时延以及升降舵和油门控制精度快速进行仿真模拟实验。基础实验以及对照实验的设置方法如表 5所示,TSA为系统模拟飞行员认知阶段飞行状态获取时延,TMD为系统模拟飞行员认知阶段决策时延,TAC为系统模拟飞行员认知阶段控制时延。其中飞行员操作时延的设置是依据相关文献及飞行经验设置的,具体设置方法本文不进行赘述[21]。
表 5 基础实验及对照实验仿真方法 Table 5 Basic experiment and control experiment simulation method
| 实验组别 | 参数设置 |
| 基础实验 | 时延:TSA~U(0, 1), TMD~N(1, 1), TAC~T(1, 2) 升降舵控制精度IδE和油门控制精度IδT: IδE~RandomInteger(1, 5) IδT=U(1/50, 1/10) 高度控制灵敏度: 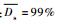 |
| 对照实验1 | 时延:TSA~U(1, 2), TMD~N(2, 1), TAC~T(2, 3) 其他参数设置与基础实验相同 |
| 对照实验2 | 控制精度: IδE~RandomInteger(1, 10) IδT=U(1/50, 1/5) 其他参数设置与基础实验相同 |
表选项
每组仿真实验进行1 000次,每组实验中选取1 000次飞行轨迹的中线。3组实验得到的飞行轨迹中线图如图 12所示(1 ft =0.304 8 m)。
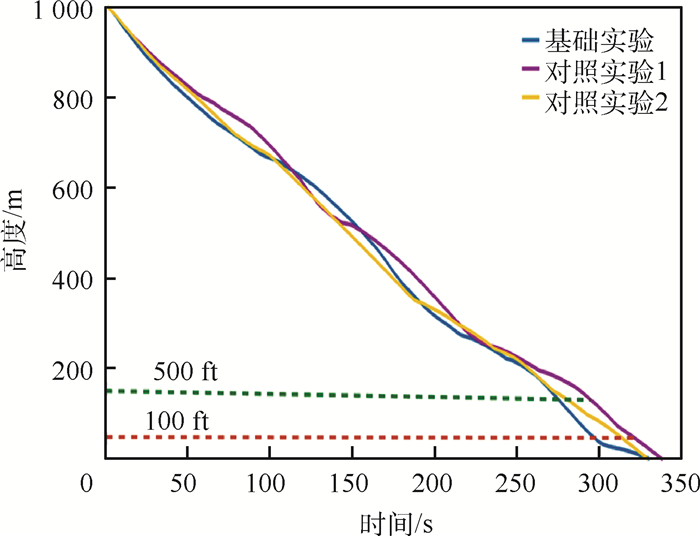 |
| 图 12 模拟飞机轨迹 Fig. 12 Simulated aircraft trajectory |
| 图选项 |
根据仿真产生的最后进近着陆阶段飞行数据,本文选取基础实验组中一次典型飞行任务中起始进近指令开始点,离地500 ft高度点,最后离地100 ft高度点以及接地点的飞行状态数据进行分析。模拟飞行状态轨迹中飞行状态信息的变化直观体现了通过白盒仿真实现解白飞机级功能架构的黑盒过程。
1) 起始进近点:起始进近高度h=1 000.00 m, 空速v=100.00 m/s, 飞机平飞,迎角α=0,期望飞行下滑道平面倾斜坡度-1:29,升降舵操纵量δE=0,油门操纵量δT=0.3。
2) 离地500 ft高度点:飞行高度h=152.40 m, 空速v=76.91 m/s, 飞机迎角α=0.056 rad,δE=2, δT=0.05。
3) 离地100 ft高度点:飞行高度h=30.48 m, 空速v=72.52 m/s, 飞机迎角α=0.024 rad, δE=9,δT=0.05。
4) 接地点:飞行高度h=0 m, 空速v=70.92 m/s, 飞机迎角α=0.027 rad, δE=16, δT=0.21。
通过对比基础实验与受控实验结果,可以得出飞行员对飞机精确,及时操作对于飞行安全具有重要意义。图 5黑盒活动图设计的合理性在仿真系统中得到了验证。本节在已经获得的黑盒功能架构的基础驱动基于人机系统模型仿真的民用飞机功能架构的“正向设计”过程,对黑盒进行解白,基于建模分析和数值仿真结果,构建实现相关飞机级需求的系统功能白盒架构的“正向设计”。同时通过人机系统基于飞行任务产生的飞行数据验证了基于模型的民用飞机功能需求方法研究的有效性与合理性。经过人机系统模型的真实模拟飞行验证,基于模型的民用飞机功能需求方法是行之有效的系统设计方法,符合系统设计需求分析方法与实际飞行任务的需求。
3 结论 本文将MBSE理论应用在民用飞机功能结构研究中,得到了民机系统最后进近着陆场景的飞机系统级功能需求,飞机系统功能架构以及描述最后进近着陆过程的图形化模型,并通过人机系统仿真验证了功能设计过程面向功能需求的合理性。本文的主要研究工作有:
1) 引入MBSE理论开展民用飞机功能设计方法研究,该方法起始于基于用户需求的自顶向下的民机系统产品顶层用例,辨识相关关键子用例,进一步基于对象用例展开“需求—功能分析”,构建黑盒活动图、顺序图表达实现相关飞机级需求的黑盒功能流,从而明确系统接口和辨识子系统,构建可进行逻辑仿真的黑盒状态机,结合“用例—需求矩阵”验证系统级功能架构所捕获的需求的完整性和正确性。
2) 基于黑盒功能架构驱动基于人机交互系统模型仿真的民用飞机功能架构的“正向设计”过程,对黑盒进行解白,基于建模分析和数值仿真结果,构建实现相关飞机级需求的系统功能白盒架构的“正向设计”。
3) 相比传统研究方法,本文提出的基于MBSE理论的民用飞机功能架构设计充分保证了需求分析和功能架构设计的紧密结合,正向构建了以满足民机产品需求为导向的结构化系统设计方法。
未来的研究工作可以从以下两方面展开:
1) 基于MBSE理论,进行民机其他关键系统的系统设计工作,并开展SysML模型与其他数值仿真软件的集成,联合仿真等工作,进行一些产品研发的尝试。
2) 基于民用飞机高安全性要求的特殊性,进一步展开功能失效与关键系统安全性分析的研究工作,确保航空安全。
参考文献
| [1] | 卢艺, 郝莲, 李承立, 等. 基于构型项目分类的民机系统适航符合性证据体系结构研究[J]. 民用飞机设计研究, 2017(3): 26-30. LU Y, HAO L, LI C L, et al. Research on airworthiness compliance evidence architecture of civil aircraft system based on configuration item classification[J]. Civil Aircraft Design and Research, 2017(3): 26-30. (in Chinese) |
| [2] | 汤超, 方俊伟, 谢陵, 等. MBSE在民机起落架系统设计中的应用[J]. 民用飞机设计与研究, 2015(3): 56-60. TANG C, FANG J W, XIE L, et al. Application of MBSE method during landing gear system design for civil aircraft[J]. Civil Aircraft Design & Research, 2015(3): 56-60. (in Chinese) |
| [3] | KARBAN R, HAUBER R, WEILKIENS T. MBSE in telescope modeling[J]. Insight, 2009, 12(4): 24-31. DOI:10.1002/inst.v12.4 |
| [4] | ESTEFAN J A, 张新国. 基于模型的系统工程(MBSE)方法论综述[M]. 北京: 机械工业出版社, 2014: 1-20. ESTEFAN J A, ZHANG X G. Survey of model-based system engineering methodology[M]. Beijing: China Machine Press, 2014: 1-20. (in Chinese) |
| [5] | 张绍杰, 李正强, 海晓航, 等. 基于MBSE的民用飞机安全关键系统设计[J]. 中国科学:技术科学, 2018(3): 299-311. ZHANG S J, LI Z Q, HAI X H, et al. Design of safety critical system for civil aircraft based on MBSE[J]. Chinese Science:Technical Science, 2018(3): 299-311. (in Chinese) |
| [6] | GERY E, HAREL D, PALACHI E.Rhapsody: A complete life-cycle model-based development system[C]//International Conference on Integrated Formal Methods.Berlin: Springer, 2002, 2335: 1-10. https://link.springer.com/chapter/10.1007%2F3-540-47884-1_1 |
| [7] | SPANGELO S C, KASLOW D, DELP C, et al.Applying model based systems engineering (MBSE) to a standard cubesat[C]//Proceedings of IEEE Symposium on Aerospace Conference Aerospace Conference.Piscataway, NJ: IEEE Press, 2012, 1-20. https://www.researchgate.net/publication/254026905_Applying_Model_Based_Systems_Engineering_MBSE_to_a_standard_CubeSat |
| [8] | PEREZ R M.Application of MBSE to risk-informed design methods for space mission applications[C]//AIAA Space 2014 Conference and Exposition.Reston: AIAA, 2014: 1-47. |
| [9] | FUSARO R, FERRETTO D, VIOLA N.MBSE approach to support and formalize mission alternatives generation and selection processes for hypersonic and suborbital transportation systems[C]//IEEE International Systems Engineering Symposium.Piscataway, NJ: IEEE Press, 2017: 1-8. |
| [10] | 傅有光, 储晓彬, 李明. 基于MBSE的雷达数字化系统设计方法[J]. 现代雷达, 2017, 39(5): 1-7. FU Y G, CHU X B, LI M. Design method of radar digital system based on MBSE[J]. Modern Radar, 2017, 39(5): 1-7. (in Chinese) |
| [11] | 汉斯-彼得·霍夫曼. 基于模型的系统工程最佳实践[M]. 北京: 航空工业出版社, 2014: 1-40. HOFFMAN H P. Model-based system engineering best practices[M]. Beijing: Aviation Industry Press, 2014: 1-40. (in Chinese) |
| [12] | ESTEFAN J. MBSE methodology survey[J]. Insight, 2009, 12(4): 16-18. DOI:10.1002/inst.v12.4 |
| [13] | 朱静, 杨晖, 高亚辉, 等. 基于模型的系统工程概述[J]. 航空发动机, 2016, 42(4): 12-16. ZHU J, YANG H, GAO Y H, et al. An overview of model-based system engineering[J]. Aeroengine, 2016, 42(4): 12-16. (in Chinese) |
| [14] | WIBBEN D R, FURFARO R. Model-based systems engineering approach for the development of the science processing and operations center of the NASA OSIRIS-REx asteroid sample return mission[J]. Acta Astronautica, 2015, 115: 147-159. DOI:10.1016/j.actaastro.2015.05.016 |
| [15] | WEILKIENS T. Systems engineering with SysML/UML[M]. Burlington: Morgan Kanfmann SMG Press, 2008: 18-22. |
| [16] | GLOWACKI P, BALICKI W. ICAO aviation occurrence categories significantly affecting aviation safety in poland from 2008 to 2015[J]. Scientific Journal of Silesian University of Technology, 2017, 94: 47-56. |
| [17] | WU Q, GOUYON D, HUBERT P, et al. Towards model-based systems engineering (MBSE) patterns to efficiently reuse know-how[J]. Insight, 2017, 20(4): 31-33. DOI:10.1002/inst.12178 |
| [18] | 杜伟, 刘传会, 张红安, 等. 基于顺序图的fadec软件需求状态图模型验证[J]. 测控技术, 2016, 35(4): 109-112. DU W, LIU C H, ZHANG H A, et al. Fadec software requirements state diagram model validation based on sequence diagram[J]. Observation and Control Technology, 2016, 35(4): 109-112. DOI:10.3969/j.issn.1000-8829.2016.04.027 (in Chinese) |
| [19] | MORDECAI Y, ORHOF O, DORI D. Model-based interoperability engineering in systems-of-systems and civil aviation[J]. IEEE Transactions on Systems Man and Cybernetics Systems, 2018, 48(4): 637-648. DOI:10.1109/TSMC.2016.2602543 |
| [20] | ROSKAM J. Airplane flight dynamics and automatic flight controls, part ⅰ & ⅱ[M]. Lawnence: Design, Analysis and Research Corporation, 2001. |
| [21] | YANG C P, YIN T W, ZHAO W, et al. Modeling the uncertain effects of human factors upon the safety of airport approaches via pilot modeling[J]. Journal of Aeronautics, Astronautics and Aviation, 2013, 45(4): 249-57. |
| [22] | STERNBERG S. High-speed scanning in human memory[J]. Science, 1966, 153(3736): 652-654. DOI:10.1126/science.153.3736.652 |
| [23] | HYMAN R. Stimulus information as a determinant of reaction time[J]. Journal of Experimental Psychology, 1953, 45(3): 188-196. DOI:10.1037/h0056940 |
| [24] | DRURY C G. The speed-accuracy trade-off in industry[J]. Ergonomics, 1994, 37(4): 747-763. DOI:10.1080/00140139408963686 |
| [25] | 郭锁凤, 申功璋, 吴成富. 先进飞行控制系统[M]. 北京: 国防工业出版社, 2003. GUO S F, SHEN G Z, WU C F. Advanced flight control system[M]. Beijing: National Defence Industry Press, 2003. (in Chinese) |
