浮空器一般指飞行高度在海拔20~30 km之间的临近空间低动态飞行器,通过携带光学、微波等遥感载荷和无线通信载荷,可实现对特定区域的长期、实时、全天候、全天时的高分辨率对地观测和高速移动通信,可为空天预警、战场侦察监视、实时监视、反恐维稳、防灾减灾、环境监测和高速通信等应用需求提供崭新的技术手段[3]。
针对准零风层现象,通过控制浮空器上升或下降可以使其进入不同的风层,借助相应风层的风场,使浮空器以期望的方向和速度进行飞行,理论上能以较小的能源和动力代价实现区域驻留。近年来,这种基于风场环境利用的临近空间浮空器在民用和军事上取得了突破性的进展。民用上,谷歌公司提出的“Project Loon”项目采取超压球体制,通过调节副气囊内空气量对2 km范围内不同高度风层的利用进行飞行轨迹设计,通过对气球组网的控制进行区域连续覆盖,目的是为偏远地区提供网络服务[4]。军事上,诺斯罗谱·格鲁曼(Northrop Grumman)公司提出的“STRATACUS”项目采用零压球体制的诺格气球通过控制氦气温度对不同高度层风场的利用进行飞行轨迹设计,目的是通过跨多网协作的平流层气球群为战区提供C4ISR服务[5]。国内西北工业大学常晓飞等[6]通过控制轨迹控制器姿态调整浮空气球高度,利用准零风层上下区域纬向风反向的特点实现东西方向控制;利用轨迹控制器产生经向控制力,通过系绳拖动气球实现南北方向控制。
综上所述,基于风场利用的临近空间浮空器是当前研究前沿,通常采取借助平流层底部准零风层纬向风相反的特点实现在一定区域的驻留。因此,对平流层风场环境的研究是开展浮空器轨迹控制和区域驻留研究的前提和保障。本文以长沙地区风场数据为例,研究平流层风场随空间和时间的变化特点,通过本征正交分解(Proper Orthogonal Decomposition,POD)方法对风场数据进行降阶处理;在此基础上,分别采用Fourier级数与BP神经网络算法对平流层风场进行预测,并分析了基于2种平流层风场预测模型对浮空器轨迹控制的影响。
1 平流层风场预测模型 POD方法是风场建模中常用的一种方法,本文在采用POD方法对风场数据进行降阶处理的基础上,分别采用Fourier级数与BP神经网络算法对风场进行预测,风场预测模型原理如图 1所示。
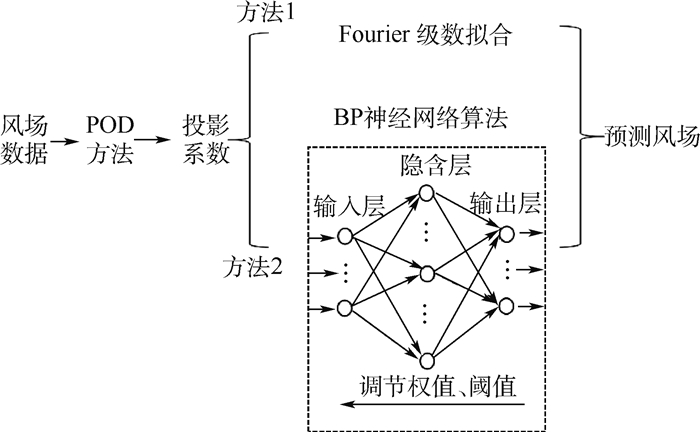 |
| 图 1 风场预测模型原理图 Fig. 1 Schematic of wind field prediction model |
| 图选项 |
1.1 基于POD方法的风场降阶模型 建立海拔高度h1~hL的风场模型,即
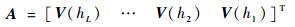 | (1) |
式中:V为风速。假设风场模型统计天数为Md,则A∈RL×M,通常Md≥L。
定义相关矩阵[7]:
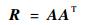 | (2) |
则R∈RL×L,显然R是实对称正定矩阵,可分解为
 | (3) |
式中:Λ为L个由大到小排列的特征值(λ1>λ2>…>λL)组成的对角阵;D为L个列为互相正交的特征向量dk(k=1, 2, …, L),它是L维向量的一组基,称为最优POD基,又称为POD模态。
矩阵A的md(md=1, 2, …, Md)列(即第md天的风场)AmT可以表示为
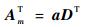 | (4) |
式中:系数矩阵a由L个值组成,计算式为
 | (5) |
若要提取主要的物理信息,利用截断后的前r阶POD模态较全阶模态所捕获的能量比求出需要选取的POD模态阶数,将特征值从大到小排列,模态能量比公式为
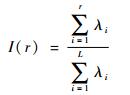 | (6) |
以长沙地区为例,采用2005-01-01—2010-12-31每天00:00所测量的风场数据,风场数据由国防科技大学气象海洋学院提供,数据记录了长沙地区00:00(世界时)的风速、湿度、温度和气压等气象要素,数据覆盖海拔高度0~60 km每隔0.5 km所对应的天气数据。考虑到临近空间低动态飞行器驻空期间的工作高度范围,本文针对海拔高度10~30 km进行研究,下面分别从东西和南北方向进行分析。
相对模态能量分布主要用于识别数据降阶处理所需的模态数量。图 2(a)给出了东西方向风场各阶POD模态的相对模态能量,前5种模态能量所占的比重相对于其他模态能量具有明显的区别,图 2(b)表示POD模态的累积模态能量,显示前6阶POD模态可以捕获到东西方向风场总特征性的99.24%。
 |
| 图 2 东西方向风场POD模态的相对和累积模态能量 Fig. 2 Relative and cumulative modal energy of east-west wind field POD modes |
| 图选项 |
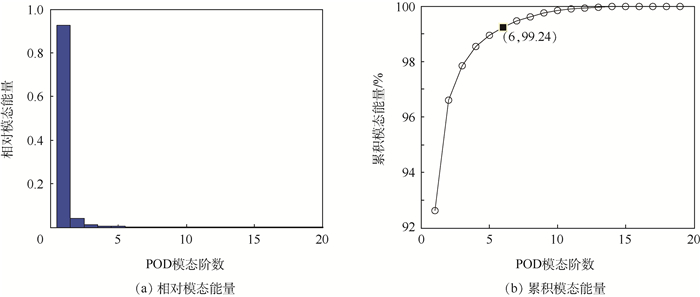
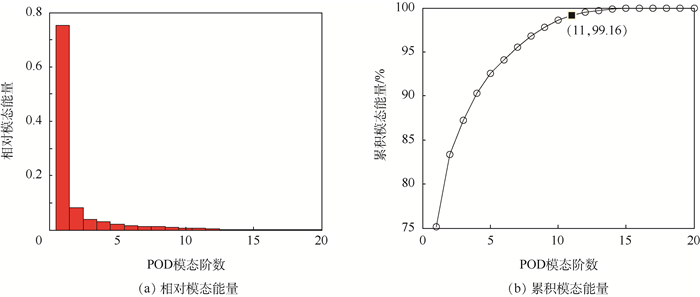
由图 3(a)可知,南北方向风场的相对模态能量分布除第1阶POD模态之外,其余模态能量呈逐渐下降的趋势,若只选取前5种模态进行降阶处理,不足以表现出风场的主要特征,因此,南北方向风场不能像东西方向一样高效地进行降阶建模。图 3(b)显示出前11阶POD模态能够捕获到南北方向风场总特征性的99.16%。东西方向上前6阶POD模态的风场模型如图 4(a)所示,南北方向上前11阶POD模态的风场模型如图 4(b)所示。
 |
| 图 3 南北方向风场POD模态的相对和累积模态能量 Fig. 3 Relative and cumulative modal energy of north-south wind field POD modes |
| 图选项 |
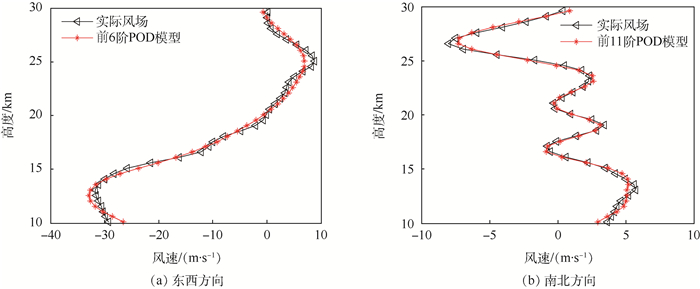 |
| 图 4 POD降阶模型 Fig. 4 POD reduced order model |
| 图选项 |
1.2 基于Fourier级数的风场预测模型 通过POD方法可以获得风场数据在最优POD基上的投影系数,若每一阶POD模态的投影系数都具有明显的空间相关性和周期性,可采用Fourier级数直接进行表示。通过最优POD基与Fourier级数所表示的投影系数可计算出风速随时间的变化情况,从而可对未来风场进行预测[8],其计算式为
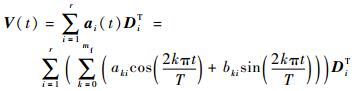 | (7) |
式中:t为时间,d;mf为Fourier级数展开的项数;aki和bki为Fourier系数;T为投影系数的振荡周期。
通过POD方法对2005-01-01—2009-12-31五年风场数据进行降阶处理,得到相应的投影系数,分别以东西和南北方向的第1阶POD模态的投影系数为例,根据投影系数存在的规律性和周期性,采用Fourier级数进行拟合,如图 5所示。
 |
| 图 5 Fourier级数拟合 Fig. 5 Fourier series fitting |
| 图选项 |
由图 5可知,相对于南北方向,东西方向的第1阶POD模态的投影系数更紧凑、周期性更强,其Fourier级数拟合度高达91.1%,而南北方向上的拟合度只达到32.2%,因此东西方向上的预测风场更能体现出实际风场的变化趋势。如图 6所示,基于Fourier级数预测出的风场与实际风场具有一定的误差,预测精度不高。除此之外,风场预测误差具有随机性,表现在Fourier级数拟合系数与实际投影系数两者之间的偏差。
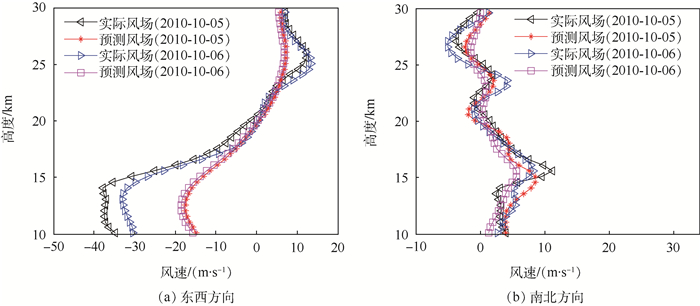 |
| 图 6 基于Fourier风场预测 Fig. 6 Prediction of wind field based on Fourier |
| 图选项 |
1.3 基于BP神经网络的风场短期预测模型 针对Fourier预测模型预测精度不高的问题,在对风场数据进行POD方法降阶处理后,采用BP神经网络算法对风场进行短期预测,将投影系数进行BP神经网络建模,通过训练好的网络对投影系数进行预测。
BP神经网络模型一般分为3层前馈网或3层感知器:输入层、中间层(也称隐含层)和输出层。主要特点:各层神经元只与相邻层神经元相连接,同层的内神经元彼此独立没有连接,同时各层神经元之间也不存在反馈连接,从而构成了层次分明的前馈型神经网络系统[9-10],BP神经网络拓扑结构如图 1中虚线框图所示。
BP算法的实质是将一组输入、输出问题转化成非线性映射问题,并通过梯度下降算法迭代求解权值[11-13]。平流层风场短期预测中,对于输出层有
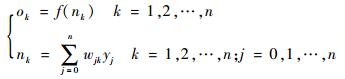 | (8) |
对于隐含层有
 | (9) |
式中:变量含义见文献[11-13]。
设输出层和隐层的转移函数为单极性S型函数
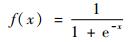 | (10) |
当网络输出与实际输出不等时,存在输出误差E,定义如下:
 | (11) |
将以上误差定义展开至隐含层有
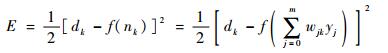 | (12) |
进一步展开至输入层有
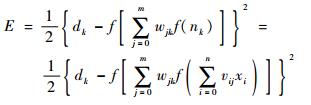 | (13) |
网络输入误差是各层权值wjk、vij的函数,因此调整权值可改变误差E。显然,调整权值的原则是使误差不断的减小。因此在本文所建立的预测模型中将采用一个常用而又有效的方法——快速梯度下降法,使权值的调整量与误差的负梯度成正比:
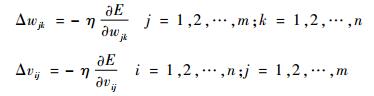 | (14) |
式中:负号表示梯度下降;η∈(0, 1)为学习速率。
引入误差信号:
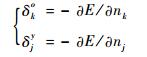 | (15) |
可推导出误差调整公式为
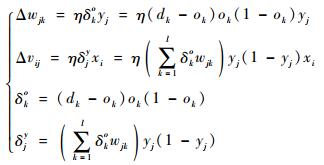 | (16) |
为了预测2010-10-05的风场,通过POD方法对10月5日以前的风场数据进行降阶处理,得到相应的投影系数,分别以东西和南北方向的第1阶POD模态的投影系数为例,通过BP神经网络算法对投影系数的变化进行预测,如图 7所示。
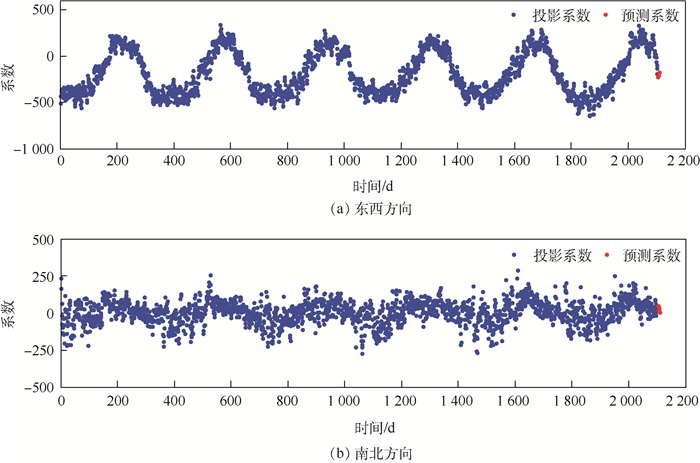 |
| 图 7 基于BP神经网络预测系数 Fig. 7 Prediction of coefficients based on BP neural network |
| 图选项 |
将最优POD基与通过BP神经网络算法预测出的系数结合可对未来的风场进行预测,如图 8所示,东西方向上的预测风场能够大致体现出实际风场的变化趋势,南北方向上的预测精度虽然不高,但由于南北方向上的风速较小,随高度的变化比较复杂,因此其预测风场具有一定的参考价值。BP神经网络算法是一种误差反向传播算法,不依赖于数据的周期性和规律性,因此基于BP神经网络算法只能对未来短期内的风场进行预测。
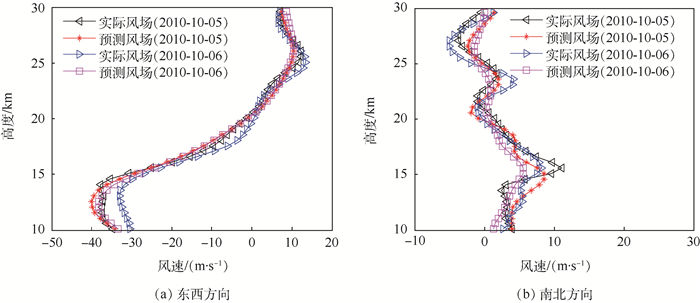 |
| 图 8 基于BP神经网络风场预测 Fig. 8 Prediction of wind field based on BP neutral network |
| 图选项 |
2 风场预测误差分析 分别将东西和南北方向的预测风场与实际风场进行比较,对风场预测误差进行分析,如图 9所示。随高度的变化,基于BP神经网络算法的风场预测误差在-5~5 m/s小范围波动,而基于Fourier级数拟合的风场预测误差范围较大。在高度20 km附近,2种风场预测模型的预测误差都接近于0;在15 km附近,基于Fourier级数拟合的预测风场与实际风场相差约20 m/s,因此基于BP神经网络算法的预测风场与实际风场更吻合,其风场预测精度更高。
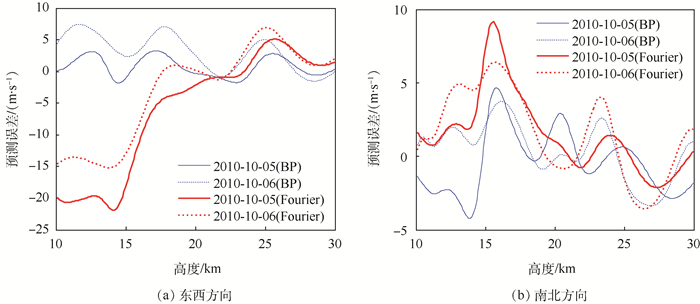 |
| 图 9 风场预测误差 Fig. 9 Wind field prediction errors |
| 图选项 |
2种风场预测方法采取的POD降阶阶数一致,降阶模型导致的误差也一致,因此风场预测精度与投影系数的拟合程度有直接的关系。分别将2种预测模型的拟合系数与实际投影系数进行比较分析,以第1阶POD模态的投影系数为例,如图 10和图 11所示。相对于Fourier级数拟合误差,基于BP神经网络所获取的系数拟合误差范围更小,误差值的分布更加平整、均匀,说明采用BP神经网络算法的系数拟合程度更高,可信度更强。
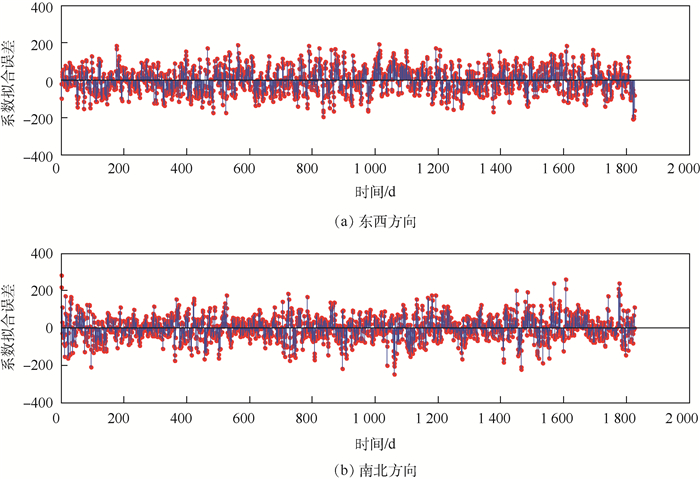 |
| 图 10 Fourier级数拟合误差 Fig. 10 Fourier series fitting errors |
| 图选项 |
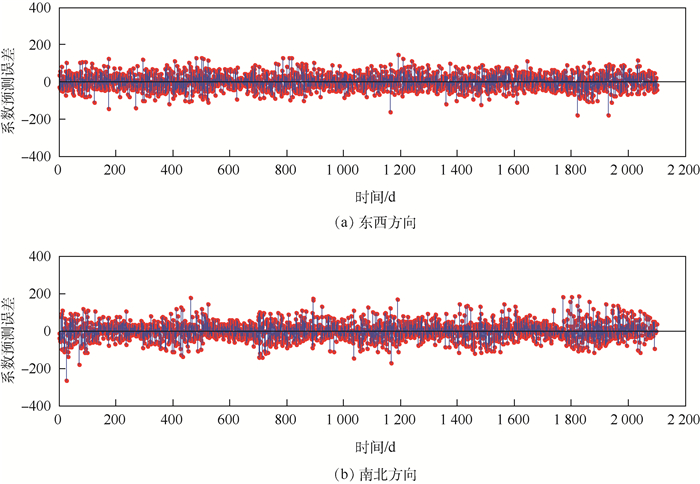 |
| 图 11 BP神经网络预测误差 Fig. 11 Prediction errors of BP neural network |
| 图选项 |
3 动力学建模 对不同高度纬向风场综合利用,通过高度调控对浮空器进行东西方向的飞行控制,建立浮空器系统的质点模型,忽略球体弹性变形和姿态变化的影响[14]。下面分别对竖直和水平方向建立动力学模型。
由牛顿第二定律,竖直方向动力学方程为
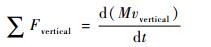 | (17) |
式中:M为浮空器总质量和附加惯性质量的总和; vvertical为升降速度。附加惯性质量为飞行器由于运动所排开空气对其反作用效应,对于体积小的飞行器,其作用可以忽略,但对于体积较大的浮空类飞行器,应考虑附加惯性质量的影响:
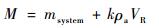 | (18) |
其中:msystem为浮空器系统各部分的质量之和;k为附加惯性质量系数;VR为浮空器体积。
浮空器内气体状态方程:
 | (19) |
式中:mHe为浮空器内氦气质量;RHe为氦气常数;mair为浮空器内空气质量;Ra为空气常数;T为气体温度,由于系统高度变化远快于温度变化,假定氦气温度与环境温度相同。浮空器在竖直方向所受外力包括浮力Fb、重力G、气动阻力Fd:
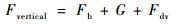 | (20) |
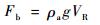 | (21) |
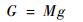 | (22) |
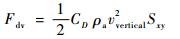 | (23) |
式中:ρa为大气环境密度;Sxy为参考面积。本文采用正球形浮力体,其阻力系数CD经验公式为[15]
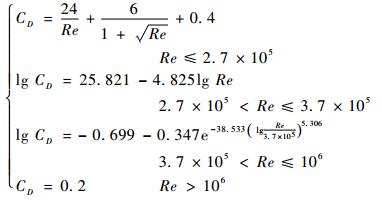 | (24) |
其中:Re为雷诺数。
由牛顿第二定律,水平方向动力学方程为
 | (25) |
在水平方向只受气动阻力Fdh:
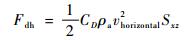 | (26) |
式中:vhorizontal为水平方向空速;Sxz为参考面积。
浮空器通过高度调控主要是对不同高度风层的风进行有效利用。高度调控分系统通过将空气排出或压入副气囊,改变浮空器的总重量,进而调整驻空浮重平衡状态。当需要提升浮空器的飞行高度时,开启排气阀,副气囊中空气受内外压差作用而排出,减少浮空器总重,在到达预期飞行高度时控制浮重平衡。反之,当需要降低浮空器的飞行高度时,鼓风机作功,将环境空气压入副气囊,增加浮空器总重,在到达预期飞行高度时控制浮重平衡即可。
当浮空器处于上升调控过程,空气阀门打开,副气囊中空气被排出,空气质量的变化[16]为
 | (27) |
式中:mair为副气囊空气质量;ΔP为超压气球与大气环境压差;Rair为阀门开口半径;K为阀系数。
当浮空器处于下降调控过程,鼓风机做功将外界空气压入副气囊,空气质量变化[17]为
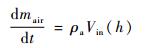 | (28) |
式中:Vin为单位时间进气量。
4 飞行仿真与分析 根据长沙地区风场数据统计,在10~11月的时间段内,平流层20 km附近存在风速较小的准零风层,因此,通过对临近空间浮空器的飞行高度进行调控,综合利用平流层风场能量,可实现在一定区域内驻留。浮空器高度调控的范围越大,外界压强的影响越大,对其材料要求、技术水平越高,因此,通过上述所说的2种风场预测方法对18~22 km高度范围2010-09-29—2010-10-03五天的东西方向风场进行预测,如图 12所示,从其中的实际风场轮廓线可看出,在19 km高度附近存在零风层,在其上下存在风向相反的风层。
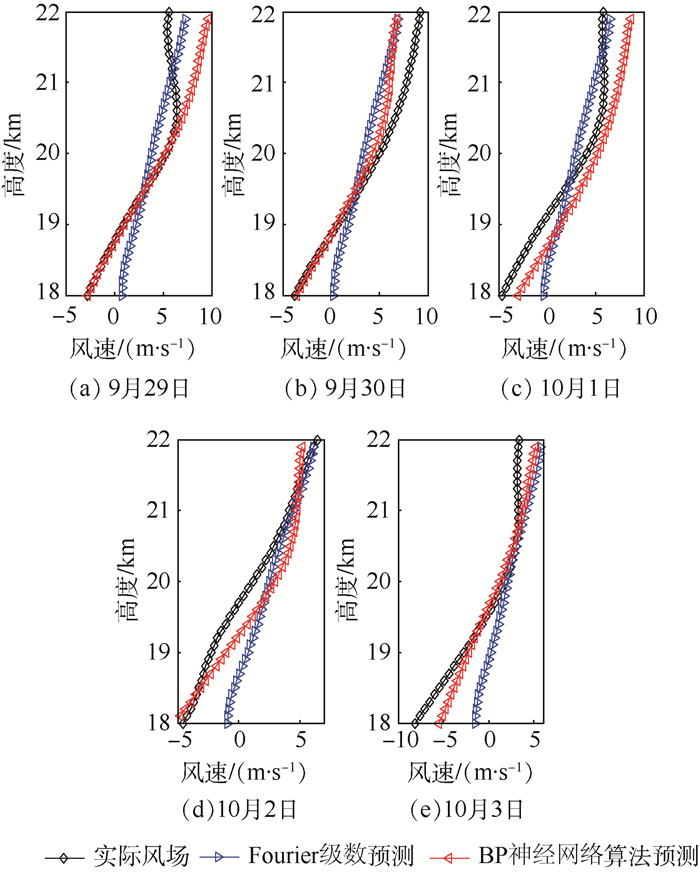 |
| 图 12 五天风场预测 Fig. 12 Wind field prediction for 5 days |
| 图选项 |
根据9月29日的预测风场轮廓线,通过高度调控,将浮空器飞行在风速为零的高度,由于预测风场与实际风场具有偏差,浮空器将会偏离起始位置,随风自由飘行,因此,计算出这一天实际的飞行位移,再根据9月30日的预测风场轮廓线,搜索出需要的风速所在高度,并对浮空器进行高度调控。依次反复进行调控,具体工作流程如图 13所示。
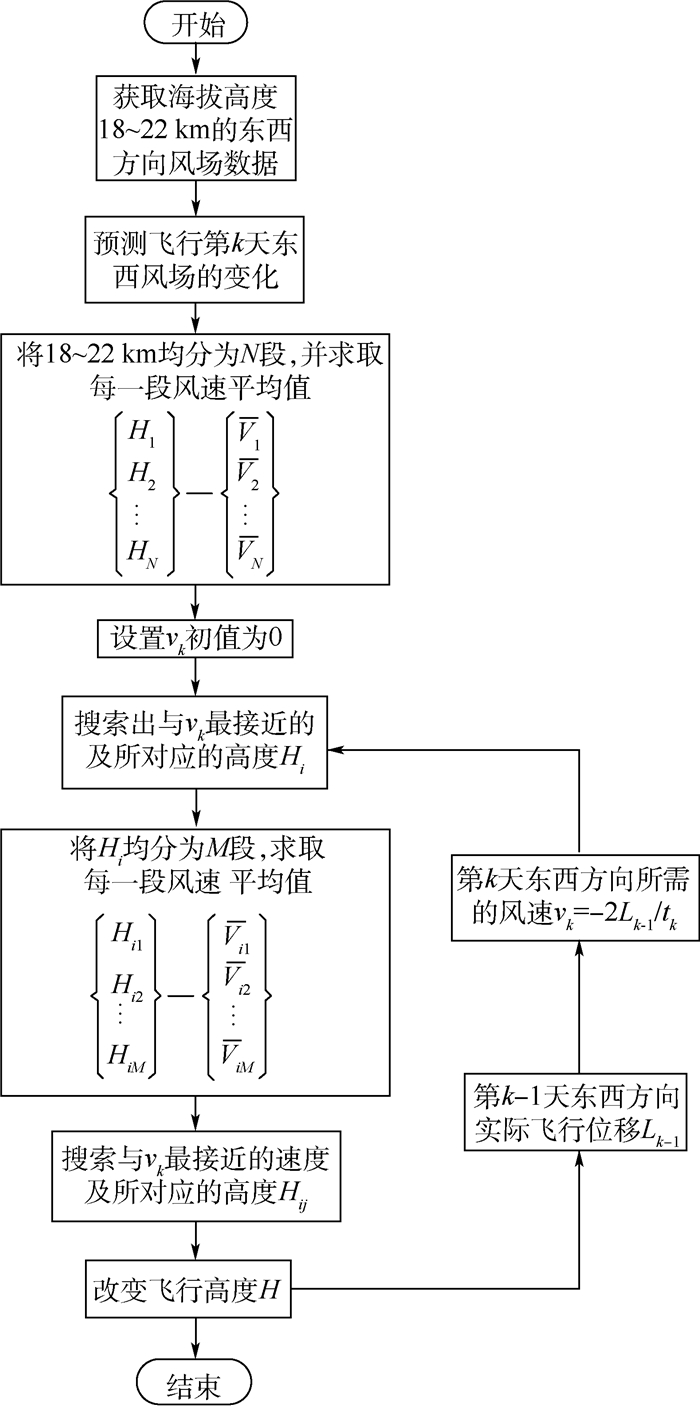 |
| 图 13 工作流程图 Fig. 13 Diagram of work process |
| 图选项 |
分别以Fourier级数预测风场与BP神经网络算法预测风场作为参考,根据工作流程,通过仿真,得到浮空器飞行过程中竖直方向的运动状态如图 14所示。从图 14(a)可看出,基于Fourier级数预测风场,浮空器五天飞行从18 km高度调节到了22 km,调控范围较大,基于BP神经网络算法预测风场,大大减少了浮空器的调控范围,从而可以增强浮空器的使用寿命,减小对浮空器材料与技术的要求。相对于Fourier级数预测风场,基于BP神经网络算法预测风场的高度调控范围较小,则高度调控过程中所消耗的时间较短,大大减小了对浮空器排气阀和鼓风机的要求性能,如图 14(b)所示。
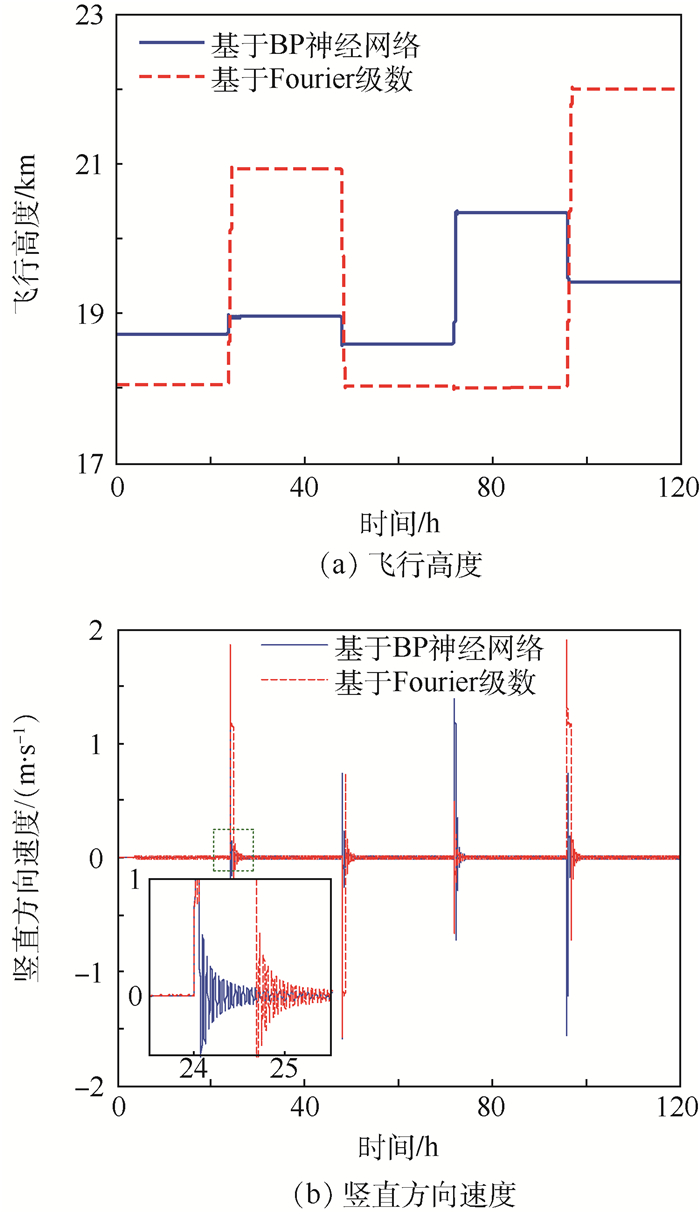 |
| 图 14 竖直方向运动状态 Fig. 14 Motion state in vertical direction |
| 图选项 |
相对于Fourier级数预测模型,基于BP神经网络算法预测模型的预测精度更高,因此,以BP神经网络算法预测风场作为参考更为准确,浮空器在东西方向上将随较小的风速来回飘行,使其在东西方向上的驻空范围较小,能够充分利用经向风场能量,实现在一定区域内驻留,如图 15所示。
 |
| 图 15 水平方向运动状态 Fig. 15 Motion state in horizontal direction |
| 图选项 |
5 结论 本文通过POD方法将平流层风场数据进行高精度高效率降阶处理后,采用了2种预测模型对风场进行预测,分别考虑了2种风场预测模型对浮空器轨迹控制的影响,得出:
1) 以长沙地区为例,选取海拔高度10~30 km五年风场数据,采用了一种对平流层风场数据进行降阶处理的POD方法,在此基础上,分别采用了Fourier级数与BP神经网络算法对平流层风场进行预测。
2) 对2种模型的预测精度进行了比较分析,通过建立临近空间浮空器的动力学模型和高度调控模型,分析了2种风场预测模型对浮空器轨迹控制的影响。
3) 相对于Fourier预测模型,基于BP神经网络预测模型的预测预测误差波动的范围更小,误差值的分布更加平整、均匀,预测精度更高,可信度更强,能够更好地为浮空器飞行轨迹控制提供参考价值。
参考文献
| [1] | 王彦广, 李健全, 李勇, 等. 近空间飞行器的特点及其应用前景[J]. 航天器工程, 2007, 16(1): 50-57. WANG Y G, LI J Q, LI Y, et al. Characters and application prospects of near space flying vehicles[J]. Spacecraft Engineering, 2007, 16(1): 50-57. DOI:10.3969/j.issn.1673-8748.2007.01.010 (in Chinese) |
| [2] | 陶梦初, 何金海, 刘毅. 平流层准零风层统计特征及准两年周期振荡对其影响分析[J]. 气候与环境研究, 2012, 17(1): 92-102. TAO M C, HE J H, LIU Y. Analysis of the characteristics of the stratospheric quasi-zero wind layer and the effects of the quasi-biennial oscillation on it[J]. Climatic and Environmental Research, 2012, 17(1): 92-102. DOI:10.3878/j.issn.1006-9585.2011.10087 (in Chinese) |
| [3] | 李春霖, 罗蓉媛, 陈彤曦. 平流层通信新思路-谷歌气球计划[J]. 通信技术, 2015, 48(2): 125-129. LI C L, LUO R Y, CHEN T X. New idea for stratospheric communications-Google Loon[J]. Communications Technology, 2015, 48(12): 125-129. (in Chinese) |
| [4] | ATHAR R, MATTHEWS T, LAVIGNE J, et al.Stratospheric C4ISR unmanned station (STRATACUS)[C]//AIAA Balloon Systems Conference.Reston: AIAA, 2017: 1-25. |
| [5] | 王艳奎. 临近空间飞行器应用前景及发展分析[J]. 国防科技, 2009, 30(2): 20-24. WANG Y K. An analysis on application prospects and development of near-space vehicles[J]. National Defense Science & Technology, 2009, 30(2): 20-24. (in Chinese) |
| [6] | 常晓飞, 白云飞, 符文星, 等. 基于平流层特殊风场的浮空器定点方案研究[J]. 西北工业大学学报, 2014, 32(1): 12-17. CHANG X F, BAI Y F, FU W X, et al. Research on fixed-point aerostat based on its special stratosphere wind field[J]. Journal of Northwestern Polytechnical, 2014, 32(1): 12-17. (in Chinese) |
| [7] | 陈兴权, 王解先, 谷川. 基于主成分分析的BP神经网络在形变预测中的应用[J]. 大地测量与地球动力学, 2008, 28(3): 72-76. CHEN X Q, WANG J X, GU C. Application of BP neural network based on principal component analysis in deformation forecasting[J]. Journal of Geodesy and Geodynamics, 2008, 28(3): 72-76. (in Chinese) |
| [8] | HEIKKIL? U, SHI X, PHIPPS S J, et al. 10Be in late deglacial climate simulated by ECHAM5-HAM-Part 2:Isolating the solar signal from 10Be deposition[J]. Climate of the Past Discussions, 2013, 9(5): 5627-5657. DOI:10.5194/cpd-9-5627-2013 |
| [9] | 杨晓亮, 徐建源, 林莘.主成分BP神经网络预测模型在风电场输出功率中的应用[C]//2010输变电年会论文集, 2010. YANG X L, XU J Y, LIN X.Application of principal component bp neural network prediction model to output power of wind farm[C]//2010 Annual Conference of Power Transmission and Transformation, 2010(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=7358704 |
| [10] | 范高锋, 王伟胜, 刘纯, 等. 基于人工神经网络的风电功率预测[J]. 中国电机工程学报, 2008, 28(34): 118-123. FAN G F, WANG W S, LIU C, et al. Wind power prediction based on artificial neural network[J]. Chinese Journal of Electrical Engineering, 2008, 28(34): 118-123. DOI:10.3321/j.issn:0258-8013.2008.34.019 (in Chinese) |
| [11] | 农吉夫, 黄文宁. 基于主成分分析的BP神经网络长期预报模型[J]. 广西师范学院学报(自然科学版), 2008, 25(4): 46-51. NONG J F, HUANG W N. Long-term prediction model of BP neural networks based on principle component analysis[J]. Journal of Guangxi Normal University(Natural Science Edition), 2008, 25(4): 46-51. DOI:10.3969/j.issn.1002-8743.2008.04.012 (in Chinese) |
| [12] | 李春祥, 牛东晓, 孟丽敏. 基于层次分析法和径向基函数神经网络的中长期负荷预测综合模型[J]. 电网技术, 2009, 33(2): 99-104. LI C X, NIU D X, MENG L M. A comprehensive model of medium and long term load forecasting based on analytic hierarchy process and radial basis function neural network[J]. Power System Technology, 2009, 33(2): 99-104. (in Chinese) |
| [13] | 张明理, 杨晓亮, 滕云, 等. 基于主成分分析与前向反馈传播神经网络的风电场输出功率预测[J]. 电网技术, 2011, 35(3): 183-187. ZHANG M L, YANG X L, TENG Y, et al. Wind farm output power prediction based on principal component analysis and forward feedback propagation neural network[J]. Power System Technology, 2011, 35(3): 183-187. (in Chinese) |
| [14] | 常晓飞, 尚妮妮, 符文星, 等. 平流层浮空器快速部署平台的建模与仿真[J]. 宇航学报, 2014, 35(10): 1135-1140. CHANG X F, SHANG N N, FU W X, et al. Modeling and simulation of rapid deployment system for stratospheric aerostat[J]. Journal of Astronautics, 2014, 35(10): 1135-1140. DOI:10.3873/j.issn.1000-1328.2014.10.005 (in Chinese) |
| [15] | 吕明云, 巫资春. 高空气球热力学模型与上升过程仿真分析[J]. 北京航空航天大学学报, 2011, 37(5): 505-509. LV M Y, WU Z C. Thermodynamic model and numerical simulation of high altitude balloon ascending process[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(5): 505-509. (in Chinese) |
| [16] | 苗景刚, 周江华, 杨新. 动态过程的飞艇排气特性分析[J]. 宇航学报, 2016, 37(2): 153-158. MIAO J G, ZHOU J H, YANG X. Analysis of airship exhaust characteristics in dynamic process[J]. Journal of Astronautics, 2016, 37(2): 153-158. DOI:10.3873/j.issn.1000-1328.2016.02.003 (in Chinese) |
| [17] | 凡永华, 于云峰, 闫杰. 高空飞艇高度控制系统设计及仿真[J]. 科学技术与工程, 2011, 11(24): 5957-5961. FAN Y H, YU Y F, YAN J. High altitude airship altitude control system design and simulation[J]. Science Technology and Engineering, 2011, 11(24): 5957-5961. DOI:10.3969/j.issn.1671-1815.2011.24.051 (in Chinese) |
