随着航空结构设计与制造水平的不断提高，现代飞机尤其是军用飞机的任务剖面越来越复杂，模块化飞机设计作为一种可同时兼顾多任务需求和经济性约束的飞机设计思想而得到了国内外****的广泛关注^[1-4]。模块化飞机是指将飞机主要结构划分成相对独立的模块进行设计、制造和使用的设计理念，基于模块化的飞机设计思想产生了飞机族的概念^[5-7]，通过开发系列化飞机产品，可满足用户不同的需求，既能占有市场，同时又能缩短产品开发周期，降低生产成本，从而提高企业的竞争力。例如，波音737有600/700/800/900型, 4种机型间具有98%的机械零部件通用性和100%的发动机通用性^[8]。美国F35战斗机在同一平台下实现了A、B、C 3种可满足不同任务需求的机种，通用性超过80%^[9-10]。
模块化结构相比于传统结构有诸多优势，但其设计需要满足多种任务需求，并考虑不同模块接口的包容性。目前工程可用的结构优化设计方法以传统单机型方案为主，专用于模块化飞机结构的优化设计技术成熟度较低。Pate等建立了任务-模块响应矩阵，并采用多级优化算法完成了模块化可重构无人机的优化设计^[11]。Cetin和Saitou利用基于模块分解思想的优化方法完成了模块化结构通用模块的设计^[12]。Souma等对协调设计模型进行了改进，并成功应用于一款双尾撑可重构无人机的设计^[13]。张立丰等采用等效多工况法对模块化可重构机翼结构进行了优化设计^[14]。范林和王哲对模块化技术在飞机研制中的应用情况进行了分析^[15]。董云峰等通过引入Agent概念和基于Agent的协商算法，提出了一种基于劝说式多Agent协商的协同优化设计算法^[16]。马树微等建立了多级固体运载火箭多学科优化模型，采用分级优化思想完成了固体火箭多学科优化问题^[17]。已有研究包含了机身、机翼等主要结构件的优化设计，对复杂结构的多级优化技术也有较多涉及，但对于模块化可重构机翼优化时不同方案的设计变量、约束条件和分析工况的差异化带来的耦合影响研究不足。
本文以满足不同飞行任务需求的无人机模块化可重构机翼结构为研究对象，对3种机翼重构方案的载荷相关性进行分析，通过建立分步补偿优化方法来解决模块化可重构机翼优化设计问题，并以某无人机模块化可重构机翼为例对本文方法的正确性与实用性进行验证。
1 模块化可重构机翼优化问题 模块化可重构机翼应用对象为一款双尾撑无人机，该无人机采用同一套机身、尾撑、尾翼、机翼机身连接、尾撑机翼连接、发射回收装置及接口，通过分别安装翼展为11、8和6 m的机翼来形成3种无人机重构方案，从而实现不同的飞行性能来满足多种任务需求。图 1给出了3种构型机翼的外形尺寸，3种无人机方案的总体设计参数和最大过载系数如表 1所示。

图 1 三种翼展机翼外观及尺寸 Fig. 1 Appearance and dimension of airfoils with three kinds of wingspan

图选项

表 1 无人机3种重构方案总体设计参数 Table 1 General design parameters of three UAV reconfiguration schemes

飞机参数	重构方案1	重构方案2	重构方案3
起飞重量/kg	680	625	600
实用升限/m	8 000	6 500	5 000
机翼面积/m2	7.5	6.1	5
机翼翼展/m	11	8	6
最大正过载	3.8	3.5	4.5
最大负过载	-2.5	-2.7	-3.5
安全系数	1.3	1.3	1.3

表选项






图 2给出了本文模块化可重构机翼的主要结构件布置情况，机翼沿弦向布置了前后两根翼梁，沿展向布置了10个翼肋，根肋为1号肋，翼尖为10号肋。为控制研制成本，该无人机机翼采用模块化设计，如图 2所示，将翼展11 m的机翼沿展向剪裁成3个模块，相邻模块连接面的弦长和翼型自然保持一致。则11 m翼展可通过3个模块连接得到，8 m翼展方案通过模块1和模块2连接得到，6 m翼展方案只包括模块1。

图 2 机翼主要结构件布置和模块划分 Fig. 2 Airfoil's main structural component layout and module partition

图选项

从表 1可知，3种重构无人机的飞行过载差距较大，如果不考虑模块间的重用性，对3个机翼单独进行优化，模块1有3种设计方案，模块2有两种设计方案，模块3有一种，对应不同翼展的同一模块其尺寸参数可能差异明显，对最终生产工艺和模块之间的连接设计带来极大难度，甚至导致设计方案被否定，这有悖于模块化飞机设计的初衷。模块化可重构设计就是要在优化设计环节充分考虑各重构方案的载荷和约束，最终给出一套能够同时满足3种无人机飞行指标的机翼结构最优设计方案。
为便于模型描述，本文作如表 2中的符号定义。
表 2 符号及定义 Table 2 Definition of symbols

符号	定义
V1	模块1的结构设计变量
V2	模块2的结构设计变量
V3	模块3的结构设计变量
CON1	机翼重构方案1的约束条件
CON2	机翼重构方案2的约束条件
CON3	机翼重构方案3的约束条件
W1	模块1的重量
W2	模块2的重量
W3	模块3的重量
LC1	机翼重构方案1对应的工况
LC2	机翼重构方案2对应的工况
LC3	机翼重构方案3对应的工况

表选项






则本文所述及的模块化可重构机翼优化设计问题可表示为

模块化可重构机翼不同重构方案包含的其设计变量、设计工况、约束条件、优化目标均不相同，需要在优化过程中分别考虑，具备这种特征的优化问题比较适合采用分级优化的思想来解决，但需要对各级设计变量和约束条件的影响关系进行深入分析，才能够形成适用于本文模块化可重构机翼结构的优化方法。
2 考虑载荷相关性的模块化可重构机翼结构分步补偿优化方法 分步补偿法是解决变设计空间优化问题的有效方法。该方法通过对不同设计空间的优化问题进行排序，首先解决排名第一(设计空间最大)的优化问题，随后，在同时考虑第一和第二优化问题约束前提下解决第二优化问题，以此类推，下一级优化需要在考虑之前所有约束的前提下对专有设计空间进行只增不减的补偿优化，即设计空间不断减小，设计约束不断增加。此外，为消除后一级优化可能对之前优化结果产生的不利影响，需要进行反向补偿设计。
针对本文模块化可重构机翼优化问题，建立三级分步补偿优化模型，如式(1)所示：

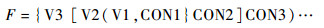(1)

从花括号到圆括号，三级优化设计空间依此减小，设计约束逐级增加。11 m翼展的机翼重构方案其优化和加载区域最大，因此，考虑先在其对应工况下对3个模块进行优化设计，在此基础上，保持模块1和模块2的设计变量不能下调，只能增加，然后依次在后2种重构方案对应工况下开展相应模块2和模块1的补偿优化。由于模块2和模块1的尺寸改变后对机翼传力路径产生影响，将补偿优化结果赋予内侧模块1和模块2以后，再由内向外依次对模块2和模块3进行优化。上述优化过程循环进行，直至收敛。在完成机翼重构方案1优化后不允许模块2和模块3的变量下调是考虑到内侧2个模块必须能够承受对其施加的所有工况中的最大载荷，因此模块2和模块3的优化是限制变量空间的分步补偿方法。
优化流程如图 3所示，其中：V2表示模块2的结构设计变量，变量值只能增加或不变，V1表示模块1的结构设计变量，变量值只能增加或不变。每一轮优化包含5个阶段，其中第1、4和5阶段为常规全域优化，第2和3阶段为补偿优化。优化收敛判断是根据相邻两轮迭代的最大翼展结构重量差距小于2%来确定。

图 3 考虑载荷相关性的模块化可重构机翼结构补偿优化流程 Fig. 3 Modular reconfigurable airfoil's structure compensation optimization flow considering load correlation

图选项

优化步骤如下：
步骤1??在11 m翼展对应工况下对3个模块进行常规优化设计，强度约束为所有属性区，刚度约束为10号翼肋与前后梁交点的升力方向位移。
步骤2??在8 m翼展对应工况下对模块1和模块2进行补偿优化设计，强度约束施加在模块1和模块2对应单元，刚度约束为8号翼肋与前后梁交点的升力方向位移，设计变量下限为步骤1的优化值。
步骤3??在6 m翼展对应工况下对模块1进行补偿优化设计，强度约束施加在模块1，刚度约束为6号翼肋与前后梁交点的升力方向位移，设计变量下限为步骤2的优化值。
步骤4??在8 m翼展对应工况下对模块2进行常规优化设计，强度约束施加在模块1和模块2，刚度约束为8号翼肋与前后梁交点的升力方向位移，设计变量下限为步骤3的优化值。
步骤5??在11 m翼展对应工况下对模块3进行常规优化设计，强度约束为所有模块，刚度约束为10号翼肋与前后梁交点的升力方向位移。
步骤6??判断最大翼展结构重量是否收敛。否则返回到步骤1重新开始；是则结束优化输出结果。
3 模块化可重构机翼优化设计 模块化可重构机翼设计变量包括上下蒙皮厚度、翼肋腹板厚度、翼梁腹板厚度、翼梁缘条截面面积和翼肋缘条截面面积。由于实际工程机翼沿展向和弦向的结构尺寸是连续变化的，为了更好地接近工程，本文以翼肋和翼梁站位为边界对蒙皮和翼梁进行分区，相邻两个翼肋之间的上下蒙皮、前后梁腹板和前后梁缘条分别用1个设计变量表示，每个翼肋的腹板和缘条分别用1个设计变量表示。整个模型包含110个设计变量，变量分布和编号情况为：
1) 上蒙皮27个分区，厚度变量为TU1~TU27。
2) 下蒙皮27个分区，厚度变量为TD1~TD27。
3) 前梁9个分区，腹板厚度变量为TF1~TF9，缘条截面面积变量为AF1~AF9。
4) 后梁9个分区，腹板厚度变量为TB1~TB9，缘条截面面积变量为AB1~AB9。
5) 翼肋共10个，腹板厚度为TR1~TR10，缘条截面面积变量为AR1~AR10。
约束条件包括强度约束和刚度约束2类。其中强度约束为：壳单元von Mises应力≤441.0 MPa，梁单元轴向拉压应力≤441.0 MPa。刚度约束为：翼尖升力方向位移≤10%的机翼半展长(重构方案1位移≤550 mm，重构方案2位移≤400 mm，重构方案3位移≤300 mm)。优化目标为机翼结构重量最小。
分析工况：按照无人机3种重构方案对应的过载，首先采用军用飞机强度规范给出的载荷设计方法，用每种翼展无人机起飞重量、过载系数和安全系数的乘积得到总的气动载荷；再选择飞行剖面A、A′、D、D′四个设计点的载荷分布形式，展向均按椭圆分布，A′和D′弦向按矩形分布，A和D在10%弦长范围按矩形分布，剩余90%弦长按三角形线性衰减；最后，将分布在弦平面的载荷按50%和50%的比例分别投影到上下翼面的有限元节点上，这样每种翼展可以得到4套工况作为机翼强度分析和优化设计载荷工况。
分别采用本文考虑载荷相关性的模块化可重构机翼结构分步补偿优化方法和传统单方案优化方法对该模块化可重构机翼进行优化设计，2种方法均能够收敛并给出相应的优化方案。优化后参与优化的机翼模块重量统计结果如表 3所示。
表 3 优化目标结果统计 Table 3 Optimization objective result statistics

模块编号	本文方法模块重量/ kg	单方案优化重构方案1			单方案优化重构方案2			单方案优化重构方案3
		模块重量/kg	比率/ %		模块重量/kg	比率 /%		模块重量/kg	比率 /%
1	49.03	47.16	3.81		46.65	4.85		46.73	4.69
2	8.94	8.33	6.82		7.90	11.63		—	—
3	6.64	6.64	0		—	—		—	—

表选项






表 3中“—”表示该模块未参与优化。比率表示与本文方法相比较，采用单方案优化后相同模块的减重百分比。
从优化结果来看，采用本文方法能够较好地收敛到满足所有约束的最优解，但从重量统计结果来看，为了实现机翼的模块化设计，保持模块通用性，各翼段均不同程度的付出了重量代价，3种单方案优化结果相对于本文方法的减重率分别为3.81%、4.85%和4.69%。由于模块3只用于11 m翼展方案的重构，本文方法和单独11 m翼展方案优化的最优解都是6.64 kg。
由于优化模型变量数较多，这里对3种重构方案都用到的模块1的上蒙皮变量优化结果进行说明进一步说明，如表 4所示。
表 4 模块1上蒙皮厚度设计变量优化结果统计 Table 4 Optimization result statistics of thickness design variables belonging to top skin of Module 1

变量编号	上蒙皮厚度设计变量值/mm
	本文方法	单方案优化重构方案1	单方案优化重构方案2	单方案优化重构方案3
TU1	4.22	4.13	4.26	4.05
TU2	4.71	4.66	4.58	4.61
TU3	4.14	3.91	4.11	4.06
TU4	3.75	3.65	3.55	3.71
TU5	3.81	3.77	3.71	3.77
TU6	3.45	3.22	3.42	3.44
TU7	2.84	2.64	2.62	2.71
TU8	3.16	3.04	2.94	2.85
TU9	2.55	2.55	2.45	2.46
TU10	2.54	2.34	2.42	2.34
TU11	2.73	2.62	2.52	2.42
TU12	2.41	2.31	2.38	2.31
TU13	2.31	2.24	2.14	2.05
TU14	2.70	2.56	2.46	2.17
TU15	2.30	2.26	2.23	2.04

表选项






从表 4的变量统计结果来看：同一设计区在3个单方案优化后的结果存在一定的差异，这与各重构方案所选工况压心分布和总载大小有关系。本文方法优化后各变量值基本覆盖了其余3个单方案优化的结果，这是符合常理也满足模块化结构设计要求的。
4 结论 本文建立了适用于变设计空间优化问题的分步补偿优化方法，并分别采用本文方法和传统单方案优化方法对某无人机模块化可重构机翼结构进行了优化设计。结果表明：
1) 本文方法能够较好地解决模块化可重构机翼结构的优化设计问题，优化后各模块满足强度刚度等设计要求。
2) 本文方法优化结果与单方案优化结果相比重量略有增加，但设计和加工更加方便，经济性更好。

参考文献

[1]	BROWN R B.Low cost innovative design for new commercial transport family: AIAA-2002-5830[R].Reston: AIAA, 2002.
[2]	FUNK J E, HARBER J R, MORIN L.Future military common aircraft development opportunities: AIAA-2006-1514[R].Reston: AIAA, 2006.
[3]	DE WECK O L, NADIR W D, WONG J G, et al.Modular structures for manned space exploration: The truncated octahedron as a building block: AIAA-2005-2764[R].Reston: AIAA, 2005.
[4]	SIMPSON T W. Product platform design and customization:Status and promise[J]. Artificial Intelligence for Engineering Design, Analysis and Manufacturing, 2004, 18(1): 3-20. DOI:10.1017/S0890060404040028
[5]	雍明培, 余雄庆. 一种面向飞机族的结构优化方法[J]. 航空学报, 2008, 29(3): 664-669. YONG M P, YU X Q. A structural optimization method for aircraft family[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 664-669. DOI:10.3321/j.issn:1000-6893.2008.03.021 (in Chinese)
[6]	ALLISON J, ROTH B, KOKKOLARAS M, et al.Aircraft family design using decomposition-based method: AIAA-2006-6950[R].Reston: AIAA, 2006.
[7]	WILLCOX K, WAKAYAMA S. Simultaneous optimization of a multiple-aircraft family[J]. Journal of Aircraft, 2003, 41(4): 616-622.
[8]	李苏杭.飞机模块化结构优化设计的满约束并行优化方法[D].南京: 南京航空航天大学, 2014. LI S H.Full-constraint parallel optimization method for aircraft modular structure design[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2014(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D672751
[9]	BEVILAQUA P M.Future applications of the JSF variable propulsion cycle: AIAA-2003-2614[R].Reston: AIAA, 2003.
[10]	FULLER J.The role of manned aircraft in the future: AIAA-2003-2860[R].Reston: AIAA, 2003.
[11]	PATE D J, PATTERSON M D, GERMAN B J. Optimizing families of reconfigurable aircraft for multiple missions[J]. Journal of Aircraft, 2012, 49(6): 1988-2000. DOI:10.2514/1.C031667
[12]	CETIN O L, SAITOU K. Decomposition-based assembly synthesis for structural modularity[J]. Journal of Mechanical Design, 2004, 126(2): 234-243. DOI:10.1115/1.1666890
[13]	SOUMA C, VICTOR M, WEI Y T, et al. New modular product platform planning approach to design macroscale reconfigurable unmanned aerial vehicles[J]. Journal of Aircraft, 2016, 53(2): 309-322. DOI:10.2514/1.C033262
[14]	张立丰, 姚卫星, 邹君. 模块化飞机结构优化设计的等效多工况法[J]. 航空学报, 2015, 36(3): 834-839. ZHANG L F, YAO W X, ZOU J. Equivalent multi-case optimization architecture for modular aircraft structures[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 834-839. (in Chinese)
[15]	范林, 王哲. 模块化技术在飞机研制中的应用[J]. 航空科学技术, 2010(3): 19-21. FAN L, WANG Z. Application of modularization technology at each development stage of aircraft[J]. Aeronautical Science & Technology, 2010(3): 19-21. DOI:10.3969/j.issn.1007-5453.2010.03.007 (in Chinese)
[16]	董云峰, 卫晓娜, 郝朝. 引入多Agent协商的协同优化在卫星设计中的应用[J]. 北京航空航天大学学报, 2016, 42(5): 1055-1064. DONG Y F, WEI X N, HAO Z. A multi-Agent negotiation based collaborative optimization application in satellite design[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(5): 1055-1064. (in Chinese)
[17]	马树微, 李静琳, 陈曦, 等. 多级固体运载火箭分级多学科设计优化[J]. 北京航空航天大学学报, 2016, 42(3): 542-550. MA S W, LI J L, CHEN X, et al. Stage-wise multidisciplinary design optimization for multi-stage solid launch vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(3): 542-550. (in Chinese)