机场道面结构承载能力动态检测方法因其不损坏道面、简便快速、对机场运行影响小等优势，逐渐成为道面无损检测的主要研究方向，但动态承载能力检测通常获取道基动模量，而中国相关设计规范将道基静模量作为机场道面工程设计施工和检测维护的重要指标，因此如何确定道基动静模量相关分析模型，通过实测的道基动模量求解道基静模量，进而科学地指导机场道面工程的建设和维修，逐渐成为有关****们的研究热点和机场道面承载能力检测的技术重点。如Xenaki和Athanasopoulos^[1]分析了围压、含水率和循环应变幅值影响下黏土动静模量的变化规律。Ling等^[2]探究了5种温度、5种围压、5种含水率对最大动模量和静模量的影响，结果表明最大动模量和静模量随着温度增加而减小，随着围压增大而增大，且含水率不小于0.21%时对最大动模量影响很小。Guisasola等^[3]研究了动静模量随着土类型、含水率、应力历史和荷载比变化的规律，结果表明含水率能够降低黏土的动静模量。Sitharam等^[4]研究表明动静模量随着非塑性组分百分比的增加而降低。Wang等^[5]分析含水率、围压、固结比和循环次数对动静模量影响，结果表明动静模量随着固结比和围压增加而增加，随着含水率增加而降低。Deng等^[6]通过动静三轴试验探究了围压和频率对粗颗粒土动静模量的影响。Bao和Mohajerani^[7]探讨了动静模量与含水率、围压、偏应力关系，发现含水率和偏应力对动静模量影响大，围压对动静模量影响不大。蔡良才等^[8]基于静态三轴试验探究了围压、偏应力、含水量和干容重对机场刚性道面下土基弹性模量的影响，提出基于回弹模量-偏应力曲线确定机场刚性道面下土基弹性模量的方法。邢耀忠和刘洪兵^[9]基于运动荷载下黏弹性Winkler地基板的力学模型，利用最小二乘方准则提出基于挠度的机场刚性道面地基模量识别方法。宋花玉等^[10]借助BP神经网络提出了不同含水量、干容重和偏应力下机场水泥混凝土道面土基模量的计算方法。郑刚等^[11]针对天津临港工业区典型黏土进行了动三轴试验，结果表明不同频率下，饱和软黏土的动模量随应变的增加均有所下降，在相同轴向应变下，动模量随振动频率的增加而增大。罗汀等^[12]在ABAQUS软件中引入超固结土统一硬化(UH)模型来表征道基土的应力应变关系，并在此基础上探究飞机荷载下机场刚性道面的不同位置处应力、应变和位移响应规律，最后将数值模型的计算值与模型试验的实测值进行对比，表明引入UH模型的数值模型能够可靠地预测实际机场道面道基受力变形。陈章毅等^[13]采用DDS-70型号电磁式动三轴仪分析海洋软土在动力作用下的动力特性，发现加载频率、围压和干密度越大，动模量越高。郝斌等^[14]针对唐山曹妃甸地区滨海软土进行动静模量试验研究，发现滨海软土的动静模量随着围压的增大而增大。
模量作为机场道面道基的重要参数，存在显著的应力依赖性^[15-17]。但已有的研究没有充分考虑机场道面工程的特殊性，如飞机荷载的多轮叠加效应、飞机荷载重量远远大于车辆荷载重量，以及道面结构性能有别于道路工程等^[18-19]；除此之外，对于道基强度指标(压实度和含水率)研究较少，对于飞机荷载动态特性(频率)的研究几乎空白，没有形成飞机滑行下道基动静模量相关分析模型，难以满足机场道面工程设计和检测的要求。鉴于粉质黏土道基应用较为广泛，如上海浦东国际机场第一跑道^[20]、四川九寨机场^[21]、云南泸沽湖机场^[22]等，本文结合飞机滑行下的道基应力水平、道基压实度和含水率取值范围，以及飞机滑行时频率区间，进行道基动静模量影响规律的研究，并建立多因素综合作用下动静模量相关分析模型，为机场场道工程设计与检测评估提供依据。
1 试验参数确定 以客机B737-800建立整个飞机模型，用弹性层状半空间体理论建立机场道面模型，基于飞机-道面的振动响应模型，选取距离机场道基顶面5.0 m为飞机荷载的作用深度^[23]，来研究飞机滑行下道基的应力分布水平，以及不同滑行速度下的振动频率。
1.1 飞机-道面响应模型 飞机在道面上滑行时产生的随机动荷载有别于车辆动荷载，它受到道面平整度、滑行速度以及飞机升力等因素的综合作用，可表示为

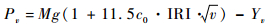(1)

式中：P_v为飞机滑行时道面承受的实际荷载；M为飞机荷载的质量；g为重力加速度；c₀为系数，取10^-3m^-0.5·s^0.5；IRI为国际平整度指数；v为飞机滑行速度；Y_v为飞机滑行时的升力。
当飞机的滑行速度达到离地速度时，道面承受的实际荷载P_v为0，此时

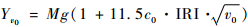(2)

式中：v₀为飞机离地速度；Y_v0为飞机离地时的升力。
结合式(1)和式(2)可得飞机的动荷载系数为

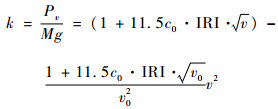(3)

B737-800的相关参数见表 1^[23-24]，在ANSYS15.0中选用刚性梁单元MPC184模拟飞机机身，用结构质量单元Mass21模拟飞机悬挂系统质量、非悬挂系统质量及转动惯量，用弹簧-阻尼单元Combine14来模拟飞机的弹簧和阻尼，用结构瞬态求解中的完全法来求解道面不平整度影响下的飞机随机动荷载。
表 1 B737-800参数^[23-24] Table 1 Parameters of B737-800 ^[23-24]

参数	数值
最大起飞重量/kN	792.60
主起落架荷载分配系数	0.95
主起落架间距/m	5.72
主起落架轮距/m	0.86
胎压/MPa	1.47
轮印面积/m2	0.125
轮印长度/m	0.45
轮印宽度/m	0.30

表选项






为了确定飞机-道面动态响应时的最不利平整度和滑行速度，对飞机动荷载系数进行了研究(见图 1)。

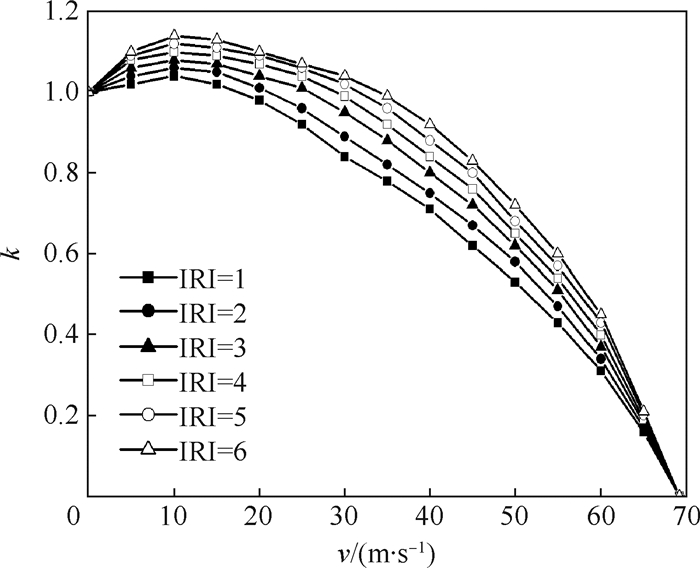图 1 IRI和v影响下的动荷载系数 Fig. 1 Dynamic load coefficient influenced by IRI and v

图选项

从图 1中可以看出，当滑行速度为0时，飞机处于静止状态(即动荷载系数为1)；当滑行速度达到69.2 m/s时，飞机处于离地状态(即动荷载系数为0)；当滑行速度处于0~69.2 m/s时，飞机处于滑行状态，动荷载系数呈现先增后减的趋势。因为飞机刚开始滑行时速度较低，升力较小，对道面的冲击作用较大，道面表现为高幅低频的应力形式；随着飞机滑行速度的增加，升力增加，对道面冲击作用减弱，道面表现为高频低幅的应力形式。滑行速度一定时，动荷载系数随着平整度指数的增加而增加；不同平整度指数下的动荷载系数均在10 m/s左右取得最大值，而且当滑行速度为10 m/s时，随着IRI从1到6动荷载系数变化量约0.1。依据MH/T5024—2009^[25]规定：IRI < 2.0时平整度等级为好，2.0≤IRI≤4.0时平整度等级为中，IRI>4.0时平整度等级为差；而大多数机场场道的平整度等级为中以上，考虑到一般性，在后续的飞机-道面响应研究中，选取平整度指数为3且滑行速度为10 m/s的飞机随机动荷载。
依据弹性层状半空间体理论的基本假设，建立由面层、基层和道基组成，平面尺寸45 m×15 m(长×宽)的机场道面结构模型(具体道面结构层参数见表 2^{[23, 26-27]})。其中面层和基层的单元网格尺寸分别为0.1 m和0.3 m，沿深度均为该层厚度的一半；道基的单元网格尺寸为0.3 m，沿深度为0.5 m。道基底部为完全固定约束，x=0及x=45 m处只约束x方向，z=0及z=15 m处只约束z方向。飞机沿面层z方向的中心线进行滑行。
表 2 道面结构参数^{[23, 26-27]} Table 2 Parameters of pavement structure ^{[23, 26-27]}

结构层	弹性模量/ GPa	厚度/m	密度/ (kg·m-3)	泊松比	阻尼
水泥混凝土面层	30~42	0.2~0.5	2 300	0.15	0.05
水泥稳定碎石基层	1~2.2	0.2~0.5	1 900	0.25	0.05
道基	0.02~0.08	10	1 650	0.35	0.05

表选项






1.2 飞机滑行下频率分析 选取面层、基层和道基模量分别为38 GPa、1.4 GPa和80 MPa，面层和基层厚度均为0.4 m，平整度指数为6，分析不同滑行速度下的频率f，见图 2。从图 2中可知，飞机滑行下的频率范围为1.11~5.46 Hz，因此动三轴试验时选取的频率区间为0.5~6 Hz。

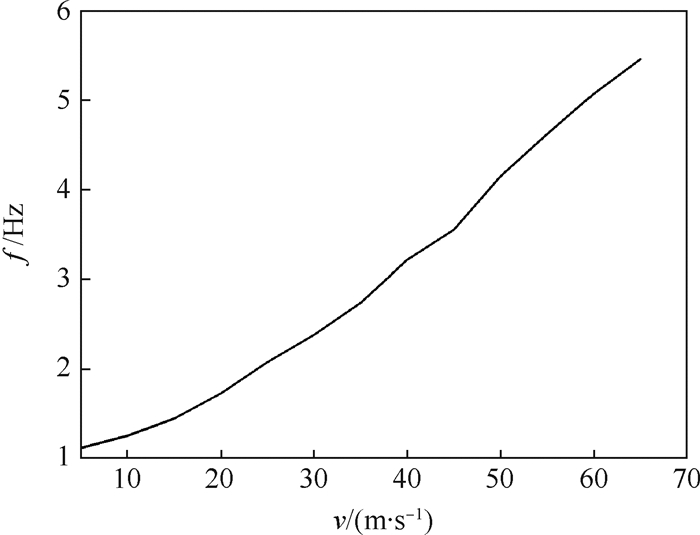图 2 不同滑行速度下的频率 Fig. 2 Frequency under different taxiing speed

图选项

1.3 道基应力水平分析 上覆结构自重引起的竖向应力为

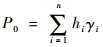(4)

式中：h_i和γ_i分别为第i层的层厚和容重(i=1，2，…，n)。
计算点处的总竖向应力为

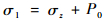(5)

式中：σ_z为飞机荷载产生的竖向应力。
计算点处的总侧向应力(围压)为

(6)

式中：σ_{x, y}为飞机荷载产生的x和y方向水平应力的平均值；k₀为侧压系数，参考文献[28]选取0.6。
基于飞机-道面响应模型，分析不同结构层参数对道基总竖向应力、围压及偏应力的影响规律，见表 3和表 4。
表 3 道基应力水平(距道基顶面5.0 m) Table 3 Stress level of subgrade (5.0 m away from top surface of subgrade)

Ec/GPa	hc/m	E2/GPa	h2/m	E0/GPa	σ1/kPa	σ/kPa	σd/kPa
30	0.4	1.4	0.4	0.08	102	60	42
34	0.4	1.4	0.4	0.08	102	60	42
38	0.4	1.4	0.4	0.08	102	60	42
42	0.4	1.4	0.4	0.08	102	60	42
38	0.2	1.4	0.4	0.08	98	58	40
38	0.3	1.4	0.4	0.08	100	59	41
38	0.5	1.4	0.4	0.08	103	60	43
38	0.4	1.0	0.4	0.08	102	60	42
38	0.4	1.8	0.4	0.08	102	60	42
38	0.4	2.2	0.4	0.08	102	60	42
38	0.4	1.4	0.2	0.08	98	58	40
38	0.4	1.4	0.3	0.08	100	59	41
38	0.4	1.4	0.5	0.08	103	60	43
38	0.4	1.4	0.4	0.06	102	60	42
38	0.4	1.4	0.4	0.04	102	60	42
38	0.4	1.4	0.4	0.02	102	60	42
注：Ec—面层模量；hc—面层厚度；E2—基层模量；h2—基层厚度；E0—道基模量；σd—偏应力。

表选项






表 4 道基应力水平(道基顶面) Table 4 Stress level of subgrade (top surface of subgrade)

Ec/GPa	hc/m	E2/GPa	h2/m	E0/GPa	σ1/kPa	σ/kPa	σd/kPa
30	0.4	1.4	0.4	0.08	104	34	70
34	0.4	1.4	0.4	0.08	99	32	67
38	0.4	1.4	0.4	0.08	96	31	65
42	0.4	1.4	0.4	0.08	93	30	63
38	0.2	1.4	0.4	0.08	158	56	102
38	0.3	1.4	0.4	0.08	134	39	95
38	0.5	1.4	0.4	0.08	75	28	47
38	0.4	1.0	0.4	0.08	93	30	63
38	0.4	1.8	0.4	0.08	98	33	65
38	0.4	2.2	0.4	0.08	100	35	65
38	0.4	1.4	0.2	0.08	134	32	102
38	0.4	1.4	0.3	0.08	116	31	85
38	0.4	1.4	0.5	0.08	82	30	52
38	0.4	1.4	0.4	0.06	87	31	56
38	0.4	1.4	0.4	0.04	78	35	43
38	0.4	1.4	0.4	0.02	69	35	34

表选项






由表 3、表 4知，在距道基顶面5.0 m处的总竖向应力、围压和偏应力变化均小，而且道面结构层模量对应力水平的影响甚微；但在道基顶面处的总竖向应力和偏应力变化显著，围压的变化较大，而且均比距道基顶面5.0 m处显著。因为随着距道基顶面距离的增加，道面结构自重产生的应力逐渐增加，飞机荷载产生的附加应力逐渐减小，对总竖向应力、围压起决定性作用的因素逐渐由附加应力转变为自重应力；由式(5)、式(6)可知，自重应力仅受结构层厚度和容重的影响，不受结构层模量的影响，且总竖向应力受自重应力的影响程度比围压要大。
与此同时，表 3、表 4表明道基总竖向应力分布范围为69~158 kPa，围压分布范围为28~56 kPa，偏应力分布范围为34~102 kPa。因此动静三轴试验选取的围压为15~60 kPa，偏应力为30~105 kPa。
2 动静三轴试验 本文所采用的三轴试验仪参数为：最大轴向荷载1 kN，最大围压300 kPa，频率范围0~20 Hz，详见图 3。本文试验土样为河北沧州地区的粉质黏土，其物理参数详见表 5，依据重塑土样的制备方法^[29]，采用三瓣模人工击实成型法，制备直径为61.8 mm、高度为125 mm的圆柱体土样，并迅速用保鲜膜将其密封，见图 4。

图 3 三轴试验系统 Fig. 3 Triaxial test system

图选项

表 5 土样的物理参数 Table 5 Physical parameters of soil sample

参数	液限/%	塑限/%	塑限指数/%	最佳含水率/%	最大干密度/(g·cm-3)
数值	33.39	16.79	16.60	14.89	1.75

表选项

图 4 三瓣模成型土样 Fig. 4 Soil sample of three-section mould

图选项

本文重点研究应力水平、含水率、压实度和频率对道基动静模量的影响。鉴于规范要求道基含水率波动范围不超过±2%，选取含水率为10.89%、12.89%、14.89%、16.89%、和18.89%。因为机场道基的压实度均大于90%，同时考虑实际试验条件限制，选取压实度为90%、93%、94%、96%和98%。结合数值模型结果选取频率为0.5、1、2、3、4、5和6 Hz；围压为15、30、45和60 kPa，偏应力为30、55、75和105 kPa。与此同时，选取预压阶段围压为30 kPa，偏应力为55 kPa，预压循环1 000次，来模拟施工期间的应力历史，消除试样端部与压盘间的不良接触^[30]；选取半正弦波形循环加载100次，来模拟飞机荷载滑行时对道基的影响，详见表 6。其中应力水平、含水率和压实度都适用于动静三轴试验，频率仅适用于动三轴试验。
表 6 加载序列 Table 6 Loading sequence

加载序列号	围压/kPa	偏应力/kPa	作用次数
0	30	55	1 000
1	60	30	100
2	60	55	100
3	60	75	100
4	60	105	100
5	45	30	100
6	45	55	100
7	45	75	100
8	45	105	100
9	30	30	100
10	30	55	100
11	30	75	100
12	30	105	100
13	15	30	100
14	15	55	100
15	15	75	100
16	15	105	100

表选项






3 试验结果分析 3.1 动模量分析 动模量定义为

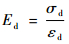(7)

式中：σ_d=σ_max-σ_min，σ_max和σ_min分别为循环偏应力的最大值和最小值；ε_d=ε_max-ε_min，ε_max和ε_min分别为相应循环偏应力作用下应变最大值和最小值。
依据式(7)对动三轴试验测得的应力应变数据进行处理，选取每个加载序列最后5次循环加载的动模量平均值为重塑粉质黏土试样的动模量，见图 5。

图 5 动模量曲线 Fig. 5 Dynamic modulus curves

图选项

由图 5(a)知，当应力水平(围压和静偏力)、压实度和频率一定时，动模量随着含水率增加而逐渐降低，与文献[1, 7]的结论相一致；当含水率低于最佳含水率时，动模量的增长幅度逐渐减弱。因为随着含水率的增加，土样颗粒间的黏结作用减弱，润滑作用增强，土样的强度和刚度降低，进而削弱了动模量；因此规范中要求道基的含水率接近最佳含水率有助于保证道基的强度。
由图 5(b)知，当应力水平、含水率和频率一定时，动模量随着压实度的增加而逐渐增加；因为随着压实度增加，土样内部的孔隙减少，整体结构强度和刚度增加，进而提高了土样的动模量。但考虑到工程实际和建设费用的要求，应在满足道基强度的情况下合理选择道基压实度。
由图 5(c)知，当应力水平、含水率和压实度一定时，动模量随着频率的增加而逐渐增加，在频率低于3 Hz时，动模量增长显著，在频率高于3 Hz时，动模量增长缓慢；因为频率较低时，加载时间较长，土样的黏塑性能较充分的发挥出来，但频率较高时，加载时间较短，土样的黏塑性无法充分发挥，并表现出很好的弹性性能。因此，进行动模量试验时不能忽略频率的影响。
由图 5可知，当含水率、压实度和频率一定时，动模量随着围压的增加而增加，随着循环偏应力的增加而降低。因为围压增加提高了土样的侧向约束，土样中的微裂隙在侧向约束下逐渐闭合，土样逐渐被压密实，土样的强度和刚度均增加，进而促进了土样动模量的增加。
3.2 静模量分析 将试样的静模量定义为应力-应变曲线的斜率，通过对土样静三轴试验的应力应变数据分析得到不同含水率和压实度下的静模量，见图 6。

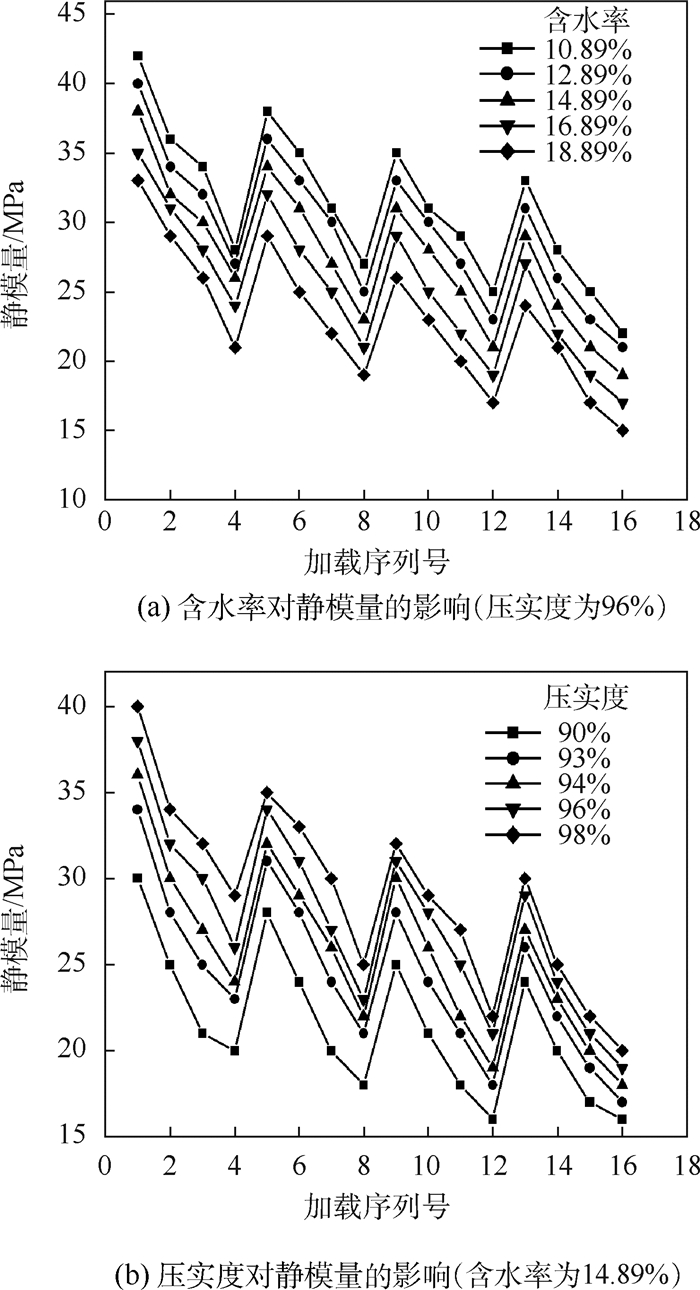图 6 静模量曲线 Fig. 6 Static modulus curves

图选项

由图 6知，土样静模量随含水率、压实度和应力水平(围压和偏应力)的变化规律与动模量相似，即当其他因素一定时，含水率的增加导致土样静模量降低，压实度和围压的增加均引起土样静模量的增加。
3.3 动静模量关系 鉴于动静回弹模量随含水率、压实度以及应力水平的变化规律一致，可以建立动静回弹模量相关分析模型如下：

(8)

式中：E′_d为频率为1 Hz时动模量；E_s为静模量; ω为含水率; K为压实度。
通过比较幂函数、指数函数、对数函数、线性函数等对试验数据的拟合效果，本文首先选取线性函数对1 Hz频率下动模量和静模量建立动静回弹模量相关分析模型为

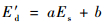(9)

式中：a和b均为回归系数，其中：

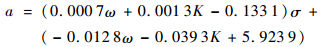(10)

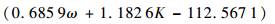(11)

为了考虑飞机滑行速度对道基动静模量相关分析模型的影响，在式(9)~式(11)的基础上，引入了不同频率下动模量与1 Hz频率下动模量的比值k′，见图 7(其中图例中的1~16对应于表 6中的加载序列)。

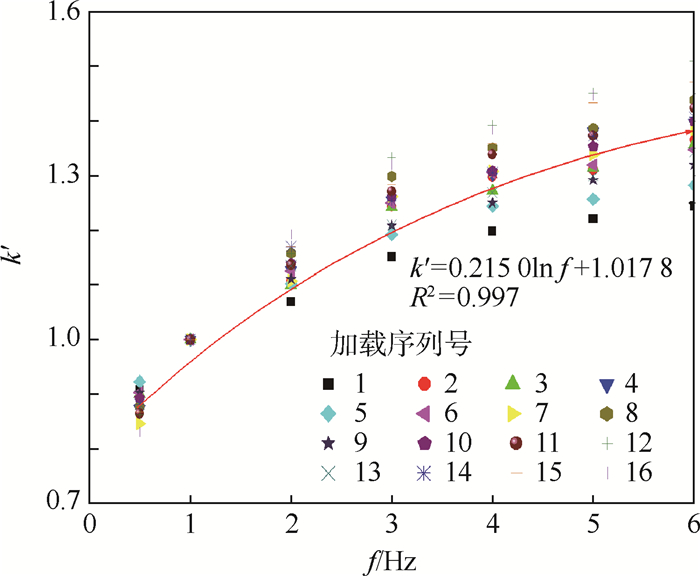图 7 k′-f回归曲线 Fig. 7 k′-f regression curve

图选项

结合式(9)~式(11)和图 7得不同频率下动静模量相关分析模型如下：

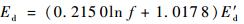(12)

将式(9)~式(11)代入式(12)即可得到基于静模量、围压、含水率、压实度和频率的动模量。为了验证本文动静模量相关分析模型的可靠性，进行了基于静模量的动模量计算值与实测值的对比，见表 7，土样为张家口粉质黏土。
表 7 动模量计算值与实测值对比 Table 7 Comparison between calculated and measured values of dynamic modulus

围压/ kPa	含水率/ %	压实度/ %	频率/ Hz	静模量/ MPa	动模量
					计算值/ MPa	实测值/ MPa	相对误差/%
60	15.77	90	1	31.03	72.09	72.06	0.04
45	15.77	93	1	47.53	105.11	105.05	0.06
30	15.77	96	1	52.17	114.75	114.34	0.36
15	13.77	96	1	56.39	122.13	122.77	0.52
60	17.77	96	1	46.44	105.01	102.87	2.08
45	15.77	96	0.5	54.99	105.32	112.98	6.78
30	15.77	96	2	52.17	133.89	128.28	4.37
15	15.77	96	3	50.17	138.09	130.31	5.97
45	15.77	96	4	54.99	159.52	154.68	3.13
30	15.77	96	5	52.17	156.49	151.56	3.26
15	15.77	96	6	50.17	154.50	148.34	4.15

表选项






由表 7可知，对于张家口粉质黏土本文动静模量相关分析模型的计算值与动三轴试验的实测值误差不超过10%。因为本文的动静模量相关分析模型是针对沧州粉质黏土建立的，仅考虑了应力水平、含水率、压实度和频率的影响；但实际道基土体性能还受黏粒含量、液塑限、塑性指数等影响，而且不同测试点的土样具有区域效应。
4 结论 本文结合飞机滑行下道基应力水平、典型道基压实度和含水率、飞机荷载滑行时常见频率范围，针对重塑粉质黏土进行了不同含水率、压实度、频率和应力水平下的动静三轴试验；不仅分析了含水率、压实度、频率和应力水平对动静模量的影响规律，而且建立了多因素综合作用下动静模量相关分析模型，具体结论如下：
1) 当压实度和应力水平一定时，动静模量均随着含水率的增加而降低；当含水率和应力水平一定时，动静模量均随着压实度的增加而增加；当压实度和含水率一定时，动静模量均随着围压的增加而增加。
2) 当应力水平、含水率和压实度一定时，动模量随着频率的增加而增加，当频率低于3 Hz时，动模量增加显著；当频率高于3 Hz时，动模量增加缓慢。
3) 分别建立了基于应力水平、含水率、压实度和频率的动静模量相关分析模型，并通过不同地区的土样进行了动模量计算值与实测值的对比验证，为机场道面工程的设计和检测提供依据。
4) 因为道基土体的复杂性和测试点土样的区域效应，道基土体的动静模量不仅受到含应力水平、含水率、压实度和频率的影响，而且受到黏粒含量、液塑限、塑性指数等作用，因此需要通过更多地三轴试验和工程实践进一步修正完善本文的模型，进而更好的满足机场道面工程的应用要求。

参考文献

[1]	XENAKI V C, ATHANASOPOULOS G A. Dynamic properties and liquefaction resistance of two soil materials in an earth-fill dam-Laboratory test results[J]. Soil Dynamics & Earthquake Engineering, 2008, 28(8): 605-620.
[2]	LING X Z, ZHU Z Y, ZHANG F, et al. Dynamic elastic modulus for frozen soil from the embankment on Beiluhe Basin along the Qinghai-Tibet Railway[J]. Cold Regions Science & Technology, 2009, 57(1): 7-12.
[3]	GUISASOLA I, JAMES I, STILES V, et al. Dynamic behaviour of soils used for natural turf sports surfaces[J]. Sports Engineering, 2010, 12(3): 111-122. DOI:10.1007/s12283-010-0036-1
[4]	SITHARAM T G, RAVISHANKAR B V, VINOD J S. Dynamic properties of sandy soils at large shear strains with special reference to the influence of non-plastic fines[J]. International Journal of Geotechnical Earthquake Engineering, 2011, 2(2): 16-28. DOI:10.4018/IJGEE
[5]	WANG Z J, LUO Y S, GUO H, et al. Effects of initial deviatoric stress ratios on dynamic shear modulus and damping ratio of undisturbed loess in China[J]. Engineering Geology, 2012, 143(11): 43-50.
[6]	DENG G, ZHANG J, WANG J, et al. Experimental study on coarse-grained soil about the relationships among dynamic strain, dynamic elastic modulus and damping ratio[J]. Electronic Journal of Geotechnical Engineering, 2014, 19(2): 313-326.
[7]	BAO T N, MOHAJERANI A. Resilient modulus of fine-grained soil and a simple testing and calculation method for determining an average resilient modulus value for pavement design[J]. Transportation Geotechnics, 2016, 7(5): 59-70.
[8]	蔡良才, 余定选, 杜俭. 机场刚性道面下土基模量取值方法研究[J]. 中国公路学报, 1992, 5(2): 8-12. CAI L C, YU D X, DU J. On the evaluation of subgrade modulus under rigid airfield pavement[J]. China Journal of Highway and Transport, 1992, 5(2): 8-12. (in Chinese)
[9]	邢耀忠, 刘洪兵. 机场刚性道面地基参数识别研究[J]. 公路工程, 2006, 31(4): 52-54. XING Y Z, LIU H B. Foundational parameter identification research of airport rigid pavement[J]. Central South Highway Engineering, 2006, 31(4): 52-54. DOI:10.3969/j.issn.1674-0610.2006.04.013 (in Chinese)
[10]	宋花玉, 蔡良才, 韶斌. BP神经网络在道面土基模量取值中的应用[J]. 路基工程, 2008(4): 36-38. SONG H Y, CAI L C, SHAO B. BP neural network application in the subgrade modulus of the pavement[J]. Subgrade Engineering, 2008(4): 36-38. DOI:10.3969/j.issn.1003-8825.2008.04.018 (in Chinese)
[11]	郑刚, 霍海峰, 雷华阳, 等. 振动频率对饱和黏土动力特性的影响[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(1): 38-43. ZHENG G, HUO H F, LEI H Y, et al. Contrastive study on the dynamic characteristics of saturated clay in different vibration frequencies[J]. Journal of Tianjin University(Science and Technology), 2013, 46(1): 38-43. (in Chinese)
[12]	罗汀, 张海鹏, 郭全全, 等. 基于UH模型的机场道基道面受力变形分析[J]. 建筑科学, 2014, 30(增刊2): 315-320. LUO T, ZHANG H P, GUO Q Q, et al. Analysis of interaction of airplane pavement and foundation based on unified hardening model[J]. Building Science, 2014, 30(Supplement 2): 315-320. (in Chinese)
[13]	陈章毅, 宋金良, 刘文程, 等. 珠江口海洋软土动三轴试验分析[J]. 华南地震, 2014, 34(s1): 204-207. CHEN Z Y, SONG J L, LIU W C, et al. Dynamic triaxial test analysis of marine soft soil of the pearl river estuary[J]. South China Journal of Seismology, 2014, 34(s1): 204-207. (in Chinese)
[14]	郝斌, 赵玉成, 刘珍岩, 等. 唐山曹妃甸滨海软土的动模量和阻尼比测试[J]. 土工基础, 2016, 30(4): 520-523. HAO B, ZHAO Y C, LIU Z Y, et al. Dynamic shear modulus and damping ratio of soft soils of Tangshan Caofeidian coastal area[J]. Soil Engineering and Foundation, 2016, 30(4): 520-523. (in Chinese)
[15]	周正峰, 凌建明. 机场水泥混凝土道面土基强度和变形标准分析[J]. 同济大学学报(自然科学版), 2008, 36(11): 1516-1520. ZHOU Z F, LING J M. Study on criteria for subgrade strength and deformation of airport concrete pavement[J]. Journal of Tongji University (Natural Science), 2008, 36(11): 1516-1520. DOI:10.3321/j.issn:0253-374X.2008.11.012 (in Chinese)
[16]	弋晓明, 李术才, 王松根, 等. 非饱和粉土模量的应力依赖性与水敏感性耦合分析[J]. 山东大学学报(工学版), 2013, 43(2): 84-88. YI X M, LI S C, WANG S G, et al. Coupling analysis of stress dependence and water sensitivity for the resilient modulus of unsaturated silt soil[J]. Journal of Shandong University (Engineering and Science), 2013, 43(2): 84-88. (in Chinese)
[17]	张凡.飞机单轮荷载作用下山区机场跑道道面道基动力响应研究[D].杭州: 浙江大学, 2016. ZHANG F.Study on dynamic response in pavement and subgrade of airport in mountainous area subjected to aircraft single-wheel load[D].Hangzhou: Zhejiang University, 2016(in Chinese).
[18]	GUO L, WANG J, CAI Y, et al. Undrained deformation behavior of saturated soft clay under long-term cyclic loading[J]. Soil Dynamics & Earthquake Engineering, 2013, 50(7): 28-37.
[19]	SALOUR F, ERLINGSSON S. Resilient modulus modelling of unsaturated subgrade soils:Laboratory investigation of silty sand subgrade[J]. Road Materials & Pavement Design, 2015, 16(3): 553-568.
[20]	杨斐, 杨宇亮, 孙立军. 飞机起降荷载作用下的场道地基沉降[J]. 同济大学学报(自然科学版), 2008, 36(6): 744-748. YANG F, YANG Y L, SUN L J. Settlement of runway subgrade under moving aircraft loads[J]. Journal of Tongji University(Natural Science), 2008, 36(6): 744-748. DOI:10.3321/j.issn:0253-374X.2008.06.007 (in Chinese)
[21]	王云龙.飞机移动荷载作用下机场跑道动力响应研究[D].杭州: 浙江大学, 2017. WANG Y L.Study on dynamic response of pavement and subgrade under the moving load of aircraft[D].Hangzhou: Zhejiang University, 2017(in Chinese).
[22]	王祺, 韩文喜. 泸沽湖机场场区工程地质评价[J]. 土工基础, 2011, 25(2): 76-79. WANG Q, HAN W X. Engineering geological evaluation of Lugu lake airport[J]. Soil Engineering and Foundation, 2011, 25(2): 76-79. DOI:10.3969/j.issn.1004-3152.2011.02.018 (in Chinese)
[23]	张献民, 薛华鑫, 董倩. 飞机跑道荷载响应深度变化规律[J]. 北京航空航天大学学报, 2014, 40(4): 427-432. ZHANG X M, XUE H X, DONG Q. Influencing depth under aircraft loads of runway[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(4): 427-432. (in Chinese)
[24]	薛华鑫.飞机滑行状态下振动频率响应分析[D].天津: 中国民航大学, 2014. XUE H X.Analysis on vibration frequency response of rigid pavement in conditions of aircraft taxing[D].Tianjin: Civil Aviation University of China, 2014(in Chinese).
[25]	中国民用航空局. 民用机场道面评价管理技术规范:MH/T5024-2009[J]. 北京:中国民用航空局, 2009. Civil Aviation Administration of China. Technical specifications of aerodrome pavement evaluation and management:MH/T5024-2009[J]. Beijing:Civil Aviation Administration of China, 2009. (in Chinese)
[26]	中国民用航空局.民用机场水泥混凝土道面设计规范: MH/T5004-2010[S].北京: 中国民用航空局, 2010. Civil Aviation Administration of China.Specifications for airport cement concrete pavement design: MH/T5004-2010[S].Beijing: Civil Aviation Administration of China, 2010(in Chinese).
[27]	翁兴中. 机场道面设计[M]. 北京: 人民交通出版社, 2014: 130-208. WENG X Z. Design of airport pavement[M]. Beijing: China Communications Press, 2014: 130-208. (in Chinese)
[28]	张亚娟.山西省黄土道基模量研究[D].西安: 长安大学, 2015. ZHANG Y J.The research of the loess subgrade modulus of resilience[D].Xi'an: Chang'an University, 2015(in Chinese).
[29]	中华人民共和国交通部.公路土工试验规程: JTG E40-2007[S].北京: 人民交通出版社, 2007. The Ministry of Transport of the People's Republic of China.Test methods of soils for highway engineering: JTG E40-2007[S].Beijing: China Communications Press, 2007(in Chinese).
[30]	GUO L, WANG J, CAI Y, et al. Undrained deformation behavior of saturated soft clay under long-term cyclic loading[J]. Soil Dynamics & Earthquake Engineering, 2013, 50(7): 28-37.