随着场面航空器数量的不断增加,航空器在滑行道区域涌现出特有的交通流特性。纵观国内外****的研究,对于航空器交通流研究大多集中在空域,Menon[1-2]、Robelin[3]和Saraf[4]等分别建立空域交通流网络模型,许炎等[5]对空域交通流的时序分布和参数关系基本图进行了分析,张洪海等[6]进一步剖析了不同交通组织、间隔标准和流控策略下空域交通流的相变规律。尹苏皖等[7-8]研究大型机场离场交通流运行特征,剖析离场交通流特征参量关联演变规律,但对于滑行道交通流演变特性并未深入分析。随着元胞传输模型(Cell Transmission Model,CTM)的广泛应用,Tessellation模型[1]将空域系统分割为二维元胞,研究航空器在元胞间的传输和流动;Robelin[3]和Sun[9]等采用CTM离散化交通流连续方程的方法进行求解,利用时间离散的差分方程描述元胞中航空器的线性流动。在交通流仿真工具方面,相比于SIMMOD[10]、TAAM[11]等高成本仿真工具,AnyLogic[12-14]、Netlogo[15-16]等综合仿真平台上也开发了系统模块。Netlogo以模块化的形式直接进行系统动力学建模仿真,通过定义系统中不同个体之间的联系得到系统内个体的变化情况,在验证和调试方面优于其他仿真软件。
本文从滑行道区域航空器运行特性和交通流时空特性出发,结合CTM,建立滑行道交通流元胞传输模型,在NetLogo系统动力学仿真平台基础上,推演滑行道交通流相态的演变过程,为优化大型机场场面航空器运行效率提供理论基础。
1 基于CTM的滑行道交通流元胞传输建模 1.1 滑行道交通流基本参数定义 1) 滑行道交通流流量:单位时间内经过滑行道元胞的航空器数量的总和。
2) 滑行道交通流密度:单位时间内滑行道元胞中的航空器数量总和与滑行道总长度的比值。
3) 滑行道交通流流速:单位时间内在滑行道元胞中所有航空器的平均速度。
1.2 模型假设 1) 场面滑行道交通流是连续的,在划定的元胞内均匀分布,以满足流体假设。
2) 在跑道和停机位分配确定的情况下,航空器进离场滑行路径相对固定。
3) 航空器起降过程中,主要考虑跑道容量限制,不考虑空域条件限制。
4) 场面航空器运行过程中,进离场航空器具有相同的优先级。
1.3 机场场面离散化元胞传输网络 本文以中国某大型机场场面资源布局结构为例,将跑道、滑行道和停机坪离散化,构建场面离散化元胞传输网络如图 1所示。该传输网络具有链路、汇聚和分散等物理特性。机场场面由跑道元胞、滑行道元胞和停机坪元胞组成。停机坪分为G1、G2、G3和G4 4个区域。本文针对4个停机坪区域的进离场滑行道,将部分滑行道结构简化,验证元胞传输建模的可行性,更复杂的网络拓扑结构可在本文基础上进一步实现。进场过程中,航空器推出跑道1,通过滑行道进入停机坪区域;离场过程中,航空器推出停机坪区域,通过滑行道进入跑道2。进离场路径与跑道、滑行道和机坪区域,共同组成机场场面离散化元胞传输网络。
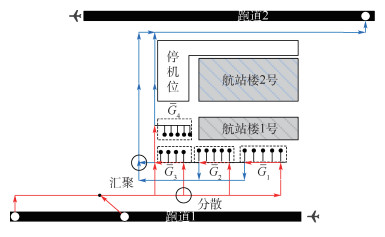 |
| 图 1 中国某大型机场场面离散化元胞传输网络 Fig. 1 Discretized cell transmission network on ground of a large airport in China |
| 图选项 |
1.4 模型建立 航空器在滑行道的滑行传输模式可以分为3类:链路滑行、分散滑行和汇聚滑行。根据3种传输模式,将滑行道交通流元胞传输模型分为链路滑行道元胞传输模型、分散滑行道元胞传输模型和汇聚滑行道元胞传输模型。
1.4.1 链路滑行道元胞传输模型 将滑行道划分为相互连接的元胞,在滑行道元胞内,航空器通过链路在各个元胞间均匀流动。链路滑行道元胞传输模型如图 2所示。
 |
| 图 2 链路滑行道元胞传输模型 Fig. 2 Taxiway cell link transmission model |
| 图选项 |
因为模型将空间、时间离散化,所以在一个步长后,元胞i内的容量变化与流量有关。
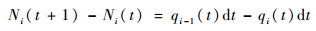 | (1) |
式中: qi-1(t)和qi(t)分别为单位时间内元胞i中流入和流出的航空器数量;Ni(t+1)和Ni(t)分别为单位步长dt前后的元胞i内航空器的数量,满足流量守恒定理。流体qi(t)满足:
 | (2) |
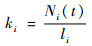 | (3) |
 | (4) |
其中:vi为滑行元胞内航空器的平均滑行速度;ki为滑行元胞内航空器的密度;li为滑行元胞的长度。除了受到自身均质流体的影响,还受到下级元胞容量的限制:
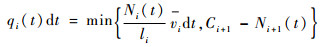 | (5) |
式中:Ci为元胞的容量,由元胞长度li、航空器长度Hflight和安全距离Dsafe决定,即
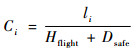 | (6) |
其中:Hflight与机型有关,根据飞机手册确定;而Dsafe与管制速度、管制间隔有关,根据前后航空器的类型、航空器的滑行速度等参数可以确定安全距离:
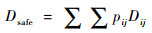 | (7) |
其中:pij表示前机的机型为i,后机的机型为j的概率;Dij表示前机的机型为i,后机的机型为j时的前后航空器的安全间隔。
同样可以得到qi-1(t)的流量表达式。如果上级元胞的流出流量超出了下级元胞容量的限制,那么上级元胞内的部分航空器就要减速或者停止等待,从而降低进入下级元胞的航空器流量,元胞i内需要等待的航空器数量为
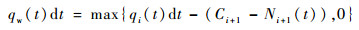 | (8) |
式(1)~式(8)表示链路滑行道元胞传输模型。
1.4.2 分散滑行道元胞传输模型 分散滑行主要发生在进场过程中,航空器脱离跑道后,通过平行滑行道元胞分散到不同的联络滑行道元胞从而进入不同停机坪区域。分散滑行道元胞传输模型如图 3所示。
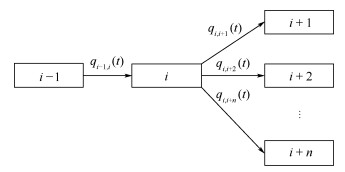 |
| 图 3 分散滑行道元胞传输模型 Fig. 3 Taxiway cell divergence transmission model |
| 图选项 |
滑行道元胞i内的航空器通过滑行道元胞i+1,i+2,…,i+n分散传输,单位时间后,元胞i内的航空器数量变化为
 | (9) |
 | (10) |
 | (11) |
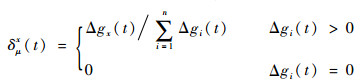 | (12) |
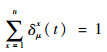 | (13) |
式中:x为1~n中任意数值;δμx(t)为从元胞i流入元胞i+x的分流比;Δgx(t)为停机坪元胞Gx中空闲机位的数量。分流比δμx(t)由元胞i+x连接的停机坪区域内空闲机位数量与所有停机坪内空闲机位总量的比值决定。式(9)~式(13)表示分散滑行道元胞传输模型。
1.4.3 汇聚滑行道元胞传输模型 航空器离场过程中,离场滑行道交通流通过不同停机坪区域的联络滑行道元胞,汇聚到平行滑行道元胞,从而进入跑道。汇聚滑行道元胞传输模型如图 4所示。
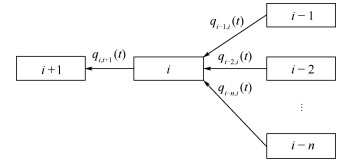 |
| 图 4 汇聚滑行道元胞传输模型 Fig. 4 Taxiway cell convergence transmission model |
| 图选项 |
滑行道元胞i-1~i-n汇聚传输到滑行道元胞i内,其元胞内的航空器数量变化为
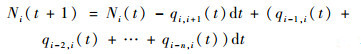 | (14) |
 | (15) |
 | (16) |
 | (17) |
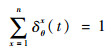 | (18) |
式中:x为1~n中任意数值;δθx(t)为元胞i-x流入元胞i的汇流比,由元胞i-x连接的停机坪区域内航空器数量与所有停机坪内航空器总量的比值决定。当元胞i-1~i-n的汇流流量超过元胞i的容量限制时,流量qi-x, i(t)应按照一定的比例δθx(t)汇聚到元胞i内。式(14)~式(18)表示汇聚滑行道元胞传输模型。
2 仿真验证 设置单位仿真步长为1 min。根据前后2架航空器降落在同一条跑道的最小尾流时间间隔,以及该机场每天的航空器平均进场率,确定该机场的航空器进场率为0.4架次/min保持不变,设置航空器离场率为0.15架次/min,模拟由于恶劣天气等引起的离场航班流控、管制情况下,滑行道交通流相态的演变过程。参考航空器在场面的实际运行过程,设置平行滑行道元胞内的航空器滑行速度为20 m/s,联络滑行道的航空器滑行速度为10 m/s,机坪滑行道的航空器滑行速度为2 m/s。在CTM中,元胞长度li、时间步长dt和速度vi之间需要满足vidt≤li的关系式,否则元胞间的流量传输不守恒。
基于NetLogo软件的系统动力学仿真平台,对所建滑行道交通流元胞传输模型进行宏观仿真,如图 5所示。图中,N0和Nair表示该机场终端区元胞;Nin和Nout分别表示进场跑道元胞和离场跑道元胞;N1和N6表示平行滑行道元胞,N2~N5表示联络滑行道;NA1~NA4表示进场机坪滑行道元胞;ND1~ND4表示离场机坪滑行道元胞;NG1~NG4表示该机场的4个停机坪元胞;方块表示“stock”,代表模型中的一个元胞,存储在其中的流体数量表示元胞中航空器的数量;箭头表示“flow”,代表不同元胞之间流量流动的方向,根据1.4节中建立的场面宏观交通流模型确定元胞之间的流量公式,通过NetLogo软件编程实现对元胞之间的流量控制,进而模拟推演滑行道区域的交通流运行特性。
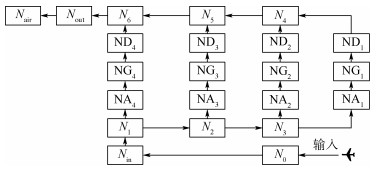 |
| 图 5 基于NetLogo系统动力学平台的交通流元胞传输模型宏观仿真 Fig. 5 Traffic flow cell transmission model macroscopic simulation based on system dynamic platform NetLogo |
| 图选项 |
3 数据分析 本文选取中国某大型机场07:30~08:30的航空器运行数据进行模拟仿真,该时段为机场的高峰时段,通过比较实际推出流量和仿真推出流量的差值,验证本文模型是否合理,如表 1所示。
表 1 实际推出流量和仿真推出流量的比较 Table 1 Comparison of actual and simulated departure flux
| 时间/ min | 实际推出流量/ (架次·min-1) | 仿真推出流量/ (架次·min-1) |
| 10 | 0 | 0.008 |
| 20 | 0.097 | 0.096 |
| 30 | 0.139 | 0.136 |
| 40 | 0.167 | 0.146 |
| 50 | 0.167 | 0.149 |
| 60 | 0.167 | 0.149 |
表选项
通过比较发现,航空器在高峰时段的实际推出流量和仿真推出流量的最大差值控制在0.02架次/min,表明本文模型合理,可以用来模拟场面运行。
3.1 滑行道交通流特性分析 在保持航空器进场率qin和离场率qout不变的情况下,随着航空器数量的不断增加,滑行道上的航空器呈现交通流特性。利用NetLogo系统动力学进行滑行道交通流宏观仿真,得到离场滑行道交通流的基本参数之间的关系如图 6所示。其中,qmax为最大流量,qjam为阻塞流流量,qsyn为同步流临界流量,vfree为自由流最大速度,vsyn为同步流临界速度,vjam为阻塞流速度,kfree为自由流临界密度,ksyn为同步流临界密度,kjam为阻塞流密度。
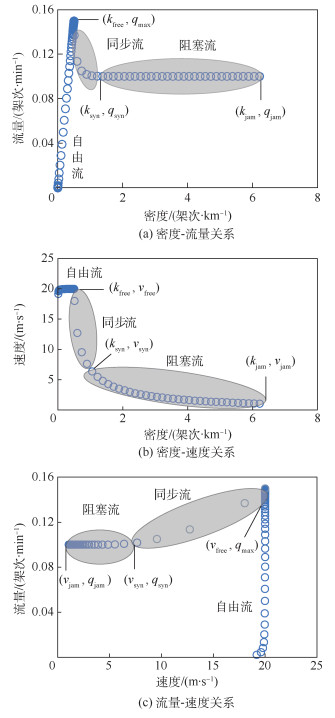 |
| 图 6 滑行道交通流的密度、流量和速度的关系 Fig. 6 Relationship among density, flux and velocity of taxiway traffic flow |
| 图选项 |
本文参考地面交通流基本相态的不同特性,将滑行道交通流划分为3种相态:自由流、同步流和阻塞流。不同相态的基本特性如图 6(a)所示。
滑行道交通流密度-流量曲线是交通流的基本图表,根据图 6(a)可以得到密度-流量曲线的拟合公式为
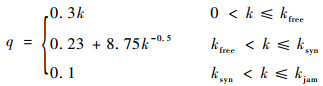 | (19) |
对式(17)进行F检验,判断其函数关系是否成立。
从表 2显著性检验的结果可以看出回归效果显著(置信度α=95%),密度-流量之间可以满足拟合公式(19)。根据两者之间的关系曲线及拟合公式,可知:
表 2 密度-流量函数关系显著性检验结果(α=95%) Table 2 Significance test results of density-flux functional relationship (α=95%)
| 相态 | 样本数 | R2相关系数 | F检验 |
| 自由流 | 64 | 1 | 0.924 6 |
| 同步流 | 10 | 0 | 0.075 4 |
表选项
1) 在自由流状态下,当交通流密度为0时,滑行道流量也为0。流量随着密度的增加而呈线性增长;自由流临界密度kfree=0.50架次/km,自由流最大流量达到qmax=0.15架次/min;在自由流相态下,航空器运行效率很高,场面不会产生拥堵。
2) 在同步流相态下,交通流流量对于密度的变化十分敏感,随着滑行道上的航空器数量进一步积累,场面航空器交通流密度增加至同步流临界密度ksyn=0.88架次/km;在同步流相态下,场面航空器积累产生局部拥堵,导致场面交通流流量迅速下降,从qmax下降至qsyn=0.10架次/min。
3) 在阻塞流相态下,此相态下场面航空器不断累积导致场面拥堵加剧,滑行道交通流密度继续增加至阻塞流密度kjam=6.21架次/km,交通流流量保持不变;机场场面滑行道的运行效率逐渐达到了饱和,此时场面运行效率主要受进场率和离场跑道容量的限制。
图 6(b)为滑行道交通流的密度-速度曲线,根据此图可以得到密度-速度曲线的拟合公式为
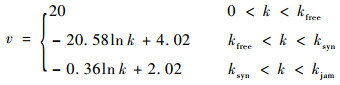 | (20) |
对式(20)进行F检验,结果如表 3所示。
表 3 密度-速度函数关系显著性检验结果(α=95%) Table 3 Significance test results of density-velocity functional relationship (α=95%)
| 相态 | 样本数 | R2相关系数 | F检验 |
| 同步流 | 10 | 0.920 8 | 0.969 5 |
| 阻塞流 | 32 | 0.009 7 | 0 |
表选项
由以上显著性检验结果可知,同步流和堵塞流下的密度-速度关系满足拟合公式,回归效果显著。在自由流状态下,航空器的滑行速度保持自由流最大速度vfree=20 m/s不变;在同步流阶段,随着交通流密度的增加,交通流的滑行速度不断下降,从自由流最大速度vfree下降至同步流临界速度vsyn=7.64 m/s,同步流情况下速度对于密度的敏感性很强,速度下降明显;在阻塞流相态下,交通流的滑行速度继续下降至堵塞流速度vjam=1.07 m/s左右,不再变化。
图 6(c)为滑行道交通流的流量-速度曲线,根据此图可以得到流量-速度曲线的拟合公式为
 | (21) |
对式(21)进行F检验,判断结果见表 4。
表 4 流量-速度函数关系显著性检验结果(α=95%) Table 4 Significance test results of flux-velocity functional relationship(α=95%)
| 相态 | 样本数 | R2相关系数 | F检验 |
| 同步流 | 10 | 0.986 1 | 0.002 0 |
表选项
从以上显著性检验的结果可以看出,流量-速度参数关系满足拟合公式。在自由流相态下,交通流的速度保持在自由流速度vfree,交通流流量随着密度增加而不断增大至qmax;在同步流相态下,受到离场跑道容量的限制,场面部分航空器受到管制,导致场面航空器密度增加,此时交通流速度开始明显下降至vsyn,交通流量也减少至qsyn;在堵塞流相态下,场面拥堵越发严重,交通流速度降低到堵塞流速度vjam,交通流量保持不变。
根据图 6的滑行道交通流参数关系曲线,得到滑行道交通流在自由流、同步流和阻塞流等3个不同相态的演变过程中关键特征参数,具体如表 5所示。
表 5 滑行道交通流的关键特征参数 Table 5 Key characteristic parameters of taxiway traffic flow
| 参数 | 数值 | |
| 流量/(架次·min-1) | qmax | 0.15 |
| qsyn | 0.10 | |
| qjam | 0.10 | |
| 速度/(m·s-1) | vfree | 20.00 |
| vsyn | 7.64 | |
| vjam | 1.07 | |
| 密度/(架次·km-1) | kfree | 0.50 |
| ksyn | 0.88 | |
| kjam | 6.21 |
表选项
综上所述,当进场率为0.4架次/min、离场率为0.15架次/min时,由于场面航空器的增多,交通流密度增大,滑行道交通流会经历自由流-同步流-阻塞流的相变过程,在各个相态下,交通流有其自身的特性;进场率和离场率是直接影响滑行道交通流相变的重要因素,通过改变两者的比例,仿真分析两因素对滑行道交通流的影响机理。
3.2 进场率和离场率影响下的交通流演变 本文固定进场率qin=0.4架次/min不变,设置离场率低于进场率,模拟空中交通管制或由于其他情况,航空器滞留机场而产生的场面拥堵;设置离场率qout=0.4,0.2和0.15架次/min,3种情况下,得到不同的离场率与进场率比例,基于NetLogo系统动力学仿真平台,得到滑行道交通流的3个基本参数之间关系的变化趋势如图 7所示。
 |
| 图 7 不同比例下的滑行道交通流密度、流量和速度的关系 Fig. 7 Relationship among densty, flux and velocity of taxiway traffic flow under different ratios |
| 图选项 |
根据图 7的仿真结果,得到不同离场率和进场率比例下的滑行道交通流关键特征参数如表 6所示。
表 6 不同比例下的滑行道交通流关键特征参数 Table 6 Key characteristic parameters of taxiway traffic flow under different ratios
| qout/qin | 流量/(架次·min-1) | 速度/(m·s-1) | 密度/(架次·km-1) | ||||||||
| qmax | qsyn | qjam | vfree | vsyn | vjam | kfree | ksyn | kjam | |||
| 1.00 | 0.15 | 20.0 | 0.52 | ||||||||
| 0.20 | 0.15 | 0.10 | 0.10 | 20.0 | 7.64 | 1.07 | 0.50 | 0.88 | 6.21 | ||
| 0.15 | 0.13 | 0.05 | 0.05 | 20.0 | 0.88 | 0.25 | 0.46 | 3.77 | 13.17 | ||
表选项
在滑行道交通流关键特征参数的演变过程中,当进场率和离场率相同或者进场率大于离场率时,滑行道交通流速度保持在自由流速度vfree不变,滑行道交通流流量增加至最大流量qmax后也不再变化,这说明此时滑行道交通流一直保持在自由流的相态,进场航空器在场面运行过程中不会产生拥堵,场面航空器运行效率很高。离场率小于进场率时,随着运行时间推移,滑行道航空器逐渐积累,相态从自由流逐渐向阻塞流过渡:
1) 在自由流相态中,qout/qin比例越大,场面航空器推进越多,自由流临界密度kfree和最大流量qmax随着比例增加而增大,不断趋近于滑行道的最大容量;由于自由流相态下场面航空器较少,不会产生拥堵,滑行道交通流的自由流速度vfree是相同的,交通流速度与参数定义的元胞滑行速度一致。
2) 在同步流相态中,qout/qin比例越大,场面航空器吞吐量增加,qsyn随之增加,航空器能够在较短时间内推进推出,滑行道内累积的航空器数量减少,同步流临界密度ksyn减小;场面航空器不容易积累,航空器不需要制动或减速滑行,大部分航空器能够按照参数设定的速度进行滑行,所以同步流临界速度vsyn较大。
3) 在阻塞流相态中,qout/qin比例越大,滑行道内航空器推进推出越多,阻塞流量qjam越大;场面中积累的航空器数量随着qout/qin增加而减少,所以阻塞流密度kjam减小;且受拥挤需要等待的航空器数量越少,所以阻塞流速度vjam增加。
综上所述,进场率和离场率决定了滑行道交通流参数之间的关系,同时自由流临界速度、临界密度和同步流临界速度、临界密度等关键特征参数也受其影响。
4 结论 1) 本文结合机场场面布局结构,建立机场场面离散化元胞传输网络,结合CTM,建立滑行道交通流元胞传输模型,利用NetLogo系统动力学仿真平台推演场面滑行道交通流的相态从自由流向拥堵流逐渐演变的过程。
2) 本文分析了滑行道交通流的基本参数间的关系,并根据密度-流量曲线对场面滑行道上的滑行道交通流相态进行划分,阐明了不同相态下滑行道交通流的特性;并且在此基础上进一步探究进场率和离场率对场面滑行道交通流相态的影响。
3) 本文研究可以为由于空中管制或恶劣天气下,离场航空器无法准时离场而导致的场面拥堵情况下,交通流相态演变提供理论基础,在交通流相态特性的基础上,为场面交通管制提供决策支持。
4) 在本文研究的基础上,未来可将交通流宏观模型概念扩展至整个机场场面;逐步健全场面交通流理论,科学地指导智能化场面交通系统的建设发展。
参考文献
| [1] | MENON P K, SWERIDUK G D, LAM T, et al. Computer-aided eulerian air traffic flow modeling and predictive control[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(1): 12-19. DOI:10.2514/1.13496 |
| [2] | MENON P K, SWERIDUK G D, BILIMORIA K. New approach for modeling, analysis and control of air traffic flow[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 737-744. DOI:10.2514/1.2556 |
| [3] | ROBELIN C, SUN D, WU G, et al.En-route air traffic modeling and strategic flow management using mixed integer linear programming[C]//Proceedings of the 2006 American Control Conference.Piscataway, NJ: IEEE Press, 2006: 5257-5262. |
| [4] | SARAF A P, SLATERG L. Adaptive eulerian modeling for air traffic flow management[J]. Journal of Aircraft, 2015, 45(5): 1585-1600. |
| [5] | 许炎, 张洪海, 杨磊, 等. 基于实测数据的终端区空中交通流特性分析[J]. 交通运输系统工程与信息, 2015, 15(1): 205-211. XU Y, ZHANG H H, YANG L, et al. Analysis of air traffic flow characteristics in airport terminal area based on observed data[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(1): 205-211. DOI:10.3969/j.issn.1009-6744.2015.01.034 (in Chinese) |
| [6] | 张洪海, 杨磊, 别翌荟, 等. 终端区进场交通流广义跟驰行为与复杂相变分析[J]. 航空学报, 2015, 36(3): 949-961. ZHANG H H, YANG L, BIE Y H, et al. Analysis on generalized following behavior and complex phase-transition law of approaching traffic flow in terminal airspace[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 949-961. (in Chinese) |
| [7] | 尹苏皖.大型机场离场运行分析与机位协同管控研究[D].南京: 南京航空航天大学, 2015. YIN S W.Research on departure operation analysis and gate collaborative control at mega-airport[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. |
| [8] | 杨磊, 胡明华, 尹苏皖, 等. 大型繁忙机场场面离场交通流拥堵特征分析[J]. 航空学报, 2016, 37(6): 1921-1930. YANG L, HU M H, YIN S W, et al. Characteristics analysis of departure traffic flow congestion in mega-airport surface[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1921-1930. (in Chinese) |
| [9] | SUN D F, BAYEN A M. A new Eulerian-Lagrangian large-capacity cell transmission model for en route traffic[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(3): 616-628. DOI:10.2514/1.31717 |
| [10] | 侯文涛. 基于SIMMOD仿真的机场拥挤时段推出率控制策略研究[J]. 中国民航飞行学院学报, 2015, 26(1): 38-42. HOU W T. Research on strategy of pushback rate control for airport congestion time based on SIMMOD simulation[J]. Journal of Civil Aviation Flight University of China, 2015, 26(1): 38-42. DOI:10.3969/j.issn.1009-4288.2015.01.008 (in Chinese) |
| [11] | ZHANG X H. Analysis of KATL operation simulated by TAAM[J]. Applied Mechanics & Materials, 2015, 713-715: 1601-1604. |
| [12] | BRAILSFORD S, CHURILOV L, DANGERFIELD B. Discrete-event simulation and system dynamics for management decision making[M]. Hoboken: Wiley, 2014: 248-279. |
| [13] | WAI P A, OSTROUKH A V. Development of simulation model mixed system in the AnyLogic software[J]. International Journal of Advanced Studies, 2015, 4(4): 48-53. DOI:10.12731/2227-930X-2014-4-7 |
| [14] | LI J, YANG Y, ZHAO Q. Study on passenger flow simulation in urban subway station based on AnyLogic[J]. Journal of Software, 2014, 9(1): 140-146. |
| [15] | CHIACCHIO F, PENNISI M, PENNISI M, et al. Agent-based modeling of the immune system:NetLogo, a promising framework[J]. Biomed Research International, 2014, 2014: 907171. |
| [16] | KAHN K. An Introduction to agent-based modeling:Modeling natural, social, and engineered complex systems with NetLogo[J]. Physics Today, 2015, 68(8): 55. |
