自Reuschel[4]和Pipes[5]首次提出单车道跟随引导模型以来,在过去几十年中,已经开发了多种的跟驰模型。其中大多数都是仅考虑到周围车辆带来的影响。例如,Chandler等[6]提出了“加利福尼亚”模型,该模型考虑了车辆在跟驰行为中存在的延迟时间; Newell[7]利用速度-车头间距关系的一般数学方程来模拟车辆跟驰行为;Bando等[8]开发了最优速度(OV)模型,该模型由于其简单、直观和创新性而被广泛采用; Jiang等[9]通过考虑正速度差异因子,建立了全速差(FVD)模型,FVD模型因可用于表征较为真实的汽车跟踪行为,而被认为优于OV模型和广义力(GF)模型[10]。因此,许多研究人员都是通过改进FVD模型,来更好地描述真实的交通环境。例如,Zhou[11]通过引入驾驶员的视角来扩展FVD模型,通过有效地解释一些复杂的交通现象,使新模型显得更加符合实际。Yu和Shi[12]将相对速度波动纳入其中对FVD模型进行改进,使得能满足先进自适应巡航控制系统的设计。
最近十年来,人车混合交通的情况引起****的兴趣,但其中的大多数都专注于不受控制的十字路口和人行横道。例如,Helbing等[13]通过观察过马路的行人,从宏观动态的角度研究了行人和车辆流动的振荡和延迟;Chen等[14]开发了一种改进的双向行人模型来描述不受控制的中间人行横道上车辆和行人之间的相互作用;Zhang和Chang[15]设计了一个合作规划模型,将行人和车辆纳入疏散网络; Ito和Nishinari[16]基于元胞自动机(CA)模型描述了拥挤交叉路口的车辆和行人之间的相互作用。
毋庸置疑,横跨公路的行人肯定会对车辆的行为产生影响,而行走在相邻车道上的行人也会对驾驶行为产生一些影响。行驶过程中驾驶员必须注意周围车辆以及相邻车道上的行人或自行车,以避免任何潜在的冲突。在机动车和非机动车混合行驶的复杂环境中,驾驶行为可能有很大差异。驾驶员会依据车辆与行人之间距离的变化来调整相应的速度,以此保证车辆的安全驾驶。然而目前在这个方向存在的研究工作很少。虽然Jiang和Wu[17-18]使用格子模型模拟了进入狭窄通道的汽车中的类似现象,但因为他们的关注点在疏散时行人的行为,所以并不能获取混合交通流中车辆的动态特征。
考虑到在相邻车道上存在行人或自行车的情况在城市中很常见,因此,有必要研究这种人车行为。本文提出一种改进跟驰模型,该模型考虑了行人和自行车在邻车道上对跟驰车辆产生的影响。改进后的模型对城市复杂混合车辆-行人交通的安全性和控制性有很大的帮助。例如,由于在这种复杂的驾驶环境中存在异常驾驶行为,该模型可用于确定更适合于由行人和自行车包围的城市街道的限制车速。此外,该模型还可用于改善对行人和自行车在相邻车道上行驶的旅行时间估计。这对于城市交通的控制是非常必要的。
1 模型构建 在本节中,假设车辆与行人混合行驶在同一条道路上,并且二者之间无任何显著的物理隔离,如图 1所示, 其中xn和sm分别为汽车n和行人m的位置;Δxn=xn+1-xn为汽车n(即跟驰车辆)与汽车n+1(即前向车辆)之间的距离;Δxn, mW为车辆n与行人m之间的横向行驶距离; Δxn, mL=sm-xn为车辆n与行人m之间的纵向行驶距离。
 |
| 图 1 行人车辆混合流的示意图 Fig. 1 Sketch map of pedestrian-vehicle mixed flow |
| 图选项 |
本文基于Newell[7]和Whitham[19]提出的优化速度模型,引入车辆与横向行人之间的横向与纵向车头间距,得到如下改进跟驰模型:
 | (1) |
式中:V为考虑连续车辆的车间距与相对速度,以及车与邻道行人的横向与纵向距离的最优速度函数;Δvn(t)=vn+1(t)-vn(t)为前车与后车的速度差(即相对速度);τ为延迟时间。
对式(1)进行显式化,本文采用文献[20]中提到的最优速度函数:
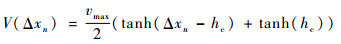 | (2) |
式中:hc为安全距离;vmax为车辆最大速度。可知V(Δxn)为单调递增函数,因为
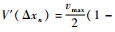


正如Sawada[21]和Li等[22]所提出的理论,多参数最优速度函数可以通过在单个参数的最优速度函数中加入可调权值来进行线性化。因此,将式(1)的右侧线性化可以得到
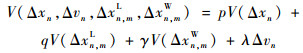 | (3) |
式中:p、q和γ分别为连续车辆车头间距、车辆和行人之间的横向间距以及纵向间距的最优函数的权重; λ为连续车辆之间相对速度的响应系数。注意:λ为一个与时间、速度和位置都无关的常数。
将式(1)进行泰勒展开,可以得到以下微分方程:
 | (4) |
式中:α为驾驶员反应度,且α=1/τ, μ=λ/τ。
注意,p+q+γ=1。同时本文假设:
 |
式中:lc和dc分别为观察到的车辆与行人之间预定的临界纵向和横向间距。如果跟驰车辆和前方行人之间的横向行驶距离太大(即大于临界距离dc),则当车辆超过行人时,行人对车辆没有影响。类似地,如果观察到的汽车与前方行人之间的纵向行驶距离大于临界距离lc,则相邻道路上的行人对驾驶员没有影响。p+q+γ=1表明除了这3个参数之外,驾驶员不会考虑周围其他影响因素[23]。
为了计算方便,式(4)需要使用非对称前向离散化方法,得到如下差分方程:
 | (5) |
2 线性稳定性分析 在稳定性分析中,首先假定车辆和行人的流量是均匀的,不存在换道和超车行为。根据文献[10]所述,在一个理想的均匀状态下,每个行人和车辆将保持一定的空间留给前面和后面的行人。因此,本文给出式(5)的均匀稳态解如下:
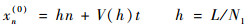 | (6) |
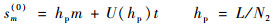 | (7) |
式中:h和hp分别为连续车辆和连续行人之间的间距; N1和N2分别为混合流动中车辆和行人的数量;V和U分别为车辆和行人的最优速度;L为道路长度。
通过在式(6)和式(7)的解中添加小偏差yn(t)和δm(t),给出车辆和行人位置的方程分别为
 | (8) |
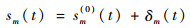 | (9) |
式中:

为了更好地分析线性稳定性,式(5)可以改写为
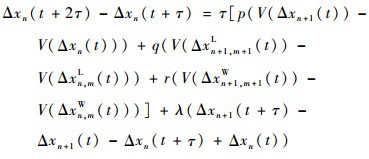 | (10) |
基于式(5)、式(6)和式(8),可将式(10)改写为
 | (11) |
式中:V′为V(Δxn)在Δxn=h时的一阶导;β为平均强度系数,描述了连续车辆的车头间距与观察到的汽车和前方行人的纵向间距之间的干扰关系;η为描述观察到的汽车与前方行人之间的干扰关系的平均强度系数。注意:本文也应用了平均场理论,该理论把任何一个因子的所有相互作用替换为平均或有效的单一相互作用,可以将2种类型的粒子(即行人和车辆)从宏观视角合并成单个物体[24]。
假设一个显式函数Δyn(t)=Aexp(ikn+zt),方程式(11)可写为
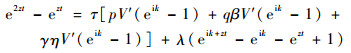 | (12) |
式中:A为波动幅度;k为波数,其取值范围是0≤k≤π;z=-iω,ω为波动的角频率。
通过将z展开为z=z1(ik)+z2(ik)2+…[25],式(12)可转换为
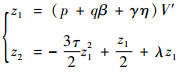 | (13) |
对于长波模式,如果z2为负,则均匀稳定流会变得不稳定; 如果z2为正,则均匀流保持稳定状态。在z2=0时设置中性稳定条件
 | (14) |
式中:延迟时间τ称为临界值,通常写为τc。它的倒数被称为临界敏感度(αc=1/τc)。对于长波小扰动,可以导出以下不稳定和稳定的条件:
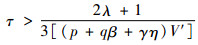 | (15) |
 | (16) |
在式(1)中,最优速度V的导数V′有一个最大值,即vmax/2。将车辆最大速度输入式(16),发现当满足如下不等式
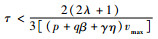
图 2显示了具有(λ, p, q, γ)不同组合的中性稳定性曲线,vmax=3 m/s, hc=4 m, β=0.5,η=0.1。实线对应于(0, 1, 0, 0),与OV模型一致;虚线对应于(0.2, 1, 0, 0),与RV模型一致;圆线对应于(0.2, 0.8, 0.1, 0.1),考虑了相邻行人的相互作用。从这3条曲线中可以看出,改进模型的特征曲线(即带有圆圈标记的线)具有最大的稳定区域(即最小的不稳定区域)。该发现意味着考虑相邻车道行人影响的跟驰模型将比传统跟驰模型具有更好的稳定性。
 |
| 图 2 不同参数组合(λ, p, q, γ)下的中性稳定性曲线 Fig. 2 Neutral stability curves with different parameter sets of (λ, p, q, γ) |
| 图选项 |
在图 3中为车头间距-敏感度的中性稳定性曲线,每条曲线的顶点表示临界点。在图中呈现为当p=0.6是定值时,随着q的增大以及γ的减小,稳定区域增大。曲线以外的区域表示交通流畅通的稳定状态; 曲线以内区域表示交通流量拥挤的不稳定状态。图 3表明相对于横向的行人影响因素,驾驶员更关注前车的运动变化行为。
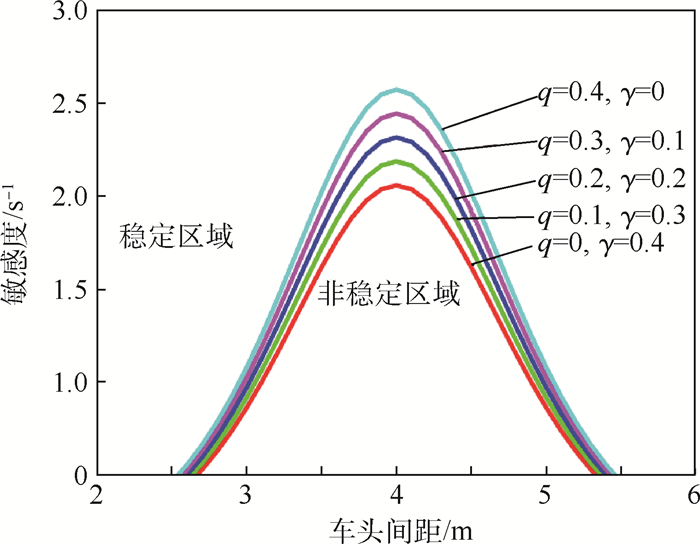 |
| 图 3 不同q和γ值的中性稳定性曲线(vmax=3 m/s, hc=4 m) Fig. 3 Neutral stability curves with different values of q and γ (vmax=3 m/s, hc=4 m) |
| 图选项 |
3 仿真实验 为了更好地模拟真实的交通行为,本文应用了Konishi等[27]提出的另一个最优速度函数,具体方程如下:
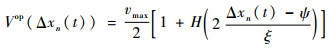 | (17) |
式中:ξ为距离参数;ψ为车辆安全距离;饱和度函数H(x)被描述为
 | (18) |
实际上,方程式(17)是由V(Δx)=16.8×(tanh(0.086(Δx-25)+0.913))推导出来的,其来源于文献[28-30]中提到的日本高速公路上的观测数据。这些值与本文中车辆的仿真参数一致,如表 1所示。表 2是行人的相关仿真参数。
表 1 车辆仿真参数 Table 1 Simulation parameters of vehicles
| 参数 | 数值 | 物理意义 |
| ψ/m | 25.0 | 车辆安全距离 |
| ξ/m | 23.3 | 距离参数 |
| vmax/(m·s-1) | 33.6 | 车辆最大速度 |
| v/(m·s-1) | 20 | 车辆初始化速度 |
| αc/s-1 | 2.0 | 敏感度 |
| ymin/m | 7.02 | 最小车头时距 |
| T/s | 0.1 | 抽样时间 |
表选项
表 2 行人仿真参数 Table 2 Simulation parameters of pedestrians
| 参数 | 数值 | 物理意义 |
| vp/(m·s-1) | 1.5 | 行人初始速度 |
| vmaxp/(m·s-1) | 3 | 行人最大速度 |
| φ/m | 7.6 | 行人安全距离 |
表选项
假设一个由11辆车组成的车队在混合行人车道上行驶,用以验证受到相邻道路行人影响的交通模式的变化。为了更好地验证所提出的模型,提供了2种模拟情景:
情景1??街道上只有少数行人的情景。车队中车辆逐个经过前向相邻的行人。在这种情况下,本文研究了几个受相邻行人影响的车辆特征的变化。这种情况适用于在夜间或雨天在路边行走的少数行人的实际交通情况。
情景2??大量行人行走的情景。在这种情况下,本文提出研究以下的3个时间间隔内受相邻行人影响的车辆行为:车辆开始进入,车辆驶过,车辆离开。适用于行人较多的道路。
对于这2种情况,初始条件设置为:vn(0)=20 m/s, x11(0)=0(即车队的最后一辆车位于原点),当n≠1, Δx1(t)=vξ/vmax-ξ/2+ψ,Δxn(0)=vξ/vmax-ξ/2+ψ。假设所有车辆在接近相邻行人之前具有相同的初始速度和车头间距。也就是说,所有车辆在早期均匀运行且没有额外的干扰。当它们开始超过考虑了行人道的相邻行人时,交通流的特征将发生巨大变化。
3.1 情景1 图 4和图 5分别通过假设p=0.6, q=0.3, γ=0.1和p=0.6, q=0.2, γ=0.2时第2、第5、第8和第11辆(即最后一辆汽车)的速度随时间的变化情况。
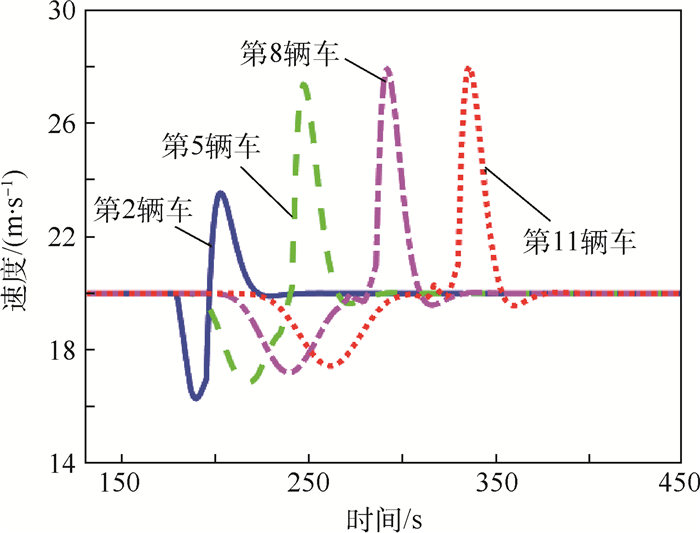 |
| 图 4 当p=0.6, q=0.3, γ=0.1时,车辆速度随时间变化曲线 Fig. 4 Variation curves of vehicle velocity with time for p=0.6, q=0.3, γ=0.1 |
| 图选项 |
 |
| 图 5 当p=0.6, q=0.2, γ=0.2时,车辆速度随时间变化曲线 Fig. 5 Variation curves of vehicle velocity with time for p=0.6, q=0.2, γ=0.2 |
| 图选项 |
图 4与图 5表示当车辆超过相邻行人时,均匀行驶车辆的交通冲击波产生波动,且所选择的车辆的速度变化是不同的。该图基本上可证明振荡行为和交通拥堵的演变。可以看到在p=0.6, q=0.2, γ=0.2的条件下(图 5),速度波动的幅度相对较小。这表明与图 4中的情况相比,汽车能更平稳地运行并且恢复稳定状态。
3.2 情景2 假设行人沿着路边均匀且稳定地行走。当领先的车辆遇到行人队尾时,车辆的振荡行为发生。为了更好地观察和分析,本文只选择其中的4辆车,图 6为情景2下的第2、第5、第8和第11辆车的速度随时间的变化。
 |
| 图 6 场景2下的车辆速度随时间变化曲线 Fig. 6 Variation curves of vehicle velocity with time in scene 2 |
| 图选项 |
在100~400 s期间,车辆遇到行人,然后车速减慢。在400~700 s期间,所有车辆都在人群队列旁行驶,其速度仍然相对较低。在这个阶段,行人之间的间距比车辆车头间距小得多,车速比所有行人都快。从宏观角度来看,行人流可以看作是一个长长的障碍。事实上,在这个时期车流受到每个行人的影响,由于间隔极短(行人间距离短),因此每辆车的速度波动曲线看起来像一条直线。在700~1 000 s期间,汽车连续经过人群,并通过一系列复杂的速度波动后将其速度恢复到初始速度。
为了进一步分析交通流量行为,图 7显示了随着时间的变化,第1辆车和其余每辆跟驰车之间的距离变化。如图 7所示,左边第1条线为第2辆车与第1辆车的距离差,向右以此类推,由于距离波动,每条曲线有2个凸起。当第1辆车遇到行人并且必须降低速度时,发生第1次扰动导致前车和后车之间的距离变小。当前车离开人群并恢复到其初始速度时,发生第2次扰动,导致前车和后车之间的距离变大。
 |
| 图 7 通过行人人群时的车队时空图 Fig. 7 Space-time plots for a motorcade passing by pedestrian crowd |
| 图选项 |
经仿真实验发现,在行人与车辆混合车道上,交通流会受到相邻行人的影响。速度和车头间距随着时间的推移而变化。结果表明,当行人在邻近的车道上行走时,司机通常会放慢车速,以确保行人和车辆自身的安全。这表明,通过考虑相邻行人的横向和纵向影响,可以改善交通安全,有助于解决交通拥堵问题。
4 结论 1) 本文提出了一种改进跟驰模型,该模型考虑了基于OV模型的行人和自行车在相邻车道上行走时对行驶车辆产生的影响。特别地,将车辆与行人之间的横向和纵向距离引入到传统的跟驰模型中。
2) 利用所提出的新模型,进一步进行线性稳定性分析,获得一系列中性稳定性曲线。
3) 通过仿真评估2种实际场景的模型能够成功描述混合交通流量行为,提高交通流量,避免交通事故和堵塞。
参考文献
| [1] | NAGATANI T. The physics of traffic jams[J]. Reports on Progress in Physics, 2002, 65(9): 1331. DOI:10.1088/0034-4885/65/9/203 |
| [2] | TREIBER M, KESTING A, HELBING D. Delays, inaccuracies and anticipation in microscopic traffic models[J]. Physica A:Statistical Mechanics and Its Applications, 2006, 360(1): 71-88. DOI:10.1016/j.physa.2005.05.001 |
| [3] | NGODUY D. Analytical studies on the instabilities of heterogeneous intelligent traffic flow[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(10): 2699-2706. DOI:10.1016/j.cnsns.2013.02.018 |
| [4] | REUSCHEL A. Vehicle movements in a platoon with uniform acceleration or deceleration of the lead vehicle[J]. Zeitschrift des Oesterreichischen Ingenieur-und Architekten-Vereines, 1950, 95: 50-62. |
| [5] | PIPES L A. An operational analysis of traffic dynamics[J]. Journal of Applied Physics, 1953, 24(3): 274-281. DOI:10.1063/1.1721265 |
| [6] | CHANDLER R E, HERMAN R, MONTROLL E W. Traffic dynamics:Studies in car following[J]. Operations Research, 1958, 6(2): 165-184. |
| [7] | NEWELL G F. Nonlinear effects in the dynamics of car following[J]. Operations Research, 1961, 9(2): 209-229. |
| [8] | BANDO M, HASEBE K, NAKAYAMA A, et al. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51(2): 1035-1045. DOI:10.1103/PhysRevE.51.1035 |
| [9] | JIANG R, WU Q, ZHU Z. Full velocity difference model for a car-following theory[J]. Physical Review E, 2001, 64(1): 017101. DOI:10.1103/PhysRevE.64.017101 |
| [10] | HELBING D, TILCH B. Generalized force model of traffic dynamics[J]. Physical Review E, 1998, 58(1): 133-138. DOI:10.1103/PhysRevE.58.133 |
| [11] | ZHOU J. An extended visual angle model for car-following theory[J]. Nonlinear Dynamics, 2015, 81(1): 549-560. |
| [12] | YU S, SHI Z. An improved car-following model considering relative velocity fluctuation[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 36: 319-326. DOI:10.1016/j.cnsns.2015.11.011 |
| [13] | HELBING D, JIANG R, TREIBER M. Analytical investigation of oscillations in intersecting flows of pedestrian and vehicle traffic[J]. Physical Review E, 2005, 72(4): 046130. DOI:10.1103/PhysRevE.72.046130 |
| [14] | CHEN P, WU C, ZHU S. Interaction between vehicles and pedestrians at uncontrolled mid-block crosswalks[J]. Safety Science, 2016, 82: 68-76. DOI:10.1016/j.ssci.2015.09.016 |
| [15] | ZHANG X, CHANG G. A dynamic evacuation model for pedestrian-vehicle mixed-flow networks[J]. Transportation Research Part C:Emerging Technologies, 2014, 40: 75-92. DOI:10.1016/j.trc.2014.01.003 |
| [16] | ITO H, NISHINARI K. Totally asymmetric simple exclusion process with a time-dependent boundary:Interaction between vehicles and pedestrians at intersections[J]. Physical Review E, 2014, 89(4): 042813. DOI:10.1103/PhysRevE.89.042813 |
| [17] | JIANG R, WU Q. The moving behavior of a large object in the crowds in a narrow channel[J]. Physica A:Statistical Mechanics and Its Applications, 2006, 364: 457-463. DOI:10.1016/j.physa.2005.08.060 |
| [18] | JIANG R, WU Q. Interaction between vehicle and pedestrians in a narrow channel[J]. Physica A:Statistical Mechanics and Its Applications, 2006, 368(1): 239-246. DOI:10.1016/j.physa.2005.12.071 |
| [19] | WHITHAM G B.Exact solutions for a discrete system arising in traffic flow[C]//Proceedings of the Royal Society of London.Series A, Mathematical and Physical Sciences.London: The Royal Society of London, Mathematical, Physical and Engineering Sciences, 1990: 49-69. |
| [20] | GE H X, DAI S Q, DONG L Y, et al. Stabilization effect of traffic flow in an extended car-following model based on an intelligent transportation system application[J]. Physical Review E, 2004, 70(6): 066134. DOI:10.1103/PhysRevE.70.066134 |
| [21] | SAWADA S. Generalized optimal velocity model for traffic flow[J]. International Journal of Modern Physics C, 2002, 13(1): 1-13. DOI:10.1142/S0129183102002894 |
| [22] | LI Y, ZHANG L, ZHENG H, et al. Evaluating the energy consumption of electric vehicles based on car-following model under non-lane discipline[J]. Nonlinear Dynamics, 2015, 82(1): 629-641. |
| [23] | PENG G H, SUN D H. A dynamical model of car-following with the consideration of the multiple information of preceding cars[J]. Physics Letters A, 2010, 374: 1694-1698. DOI:10.1016/j.physleta.2010.02.020 |
| [24] | TANG T, HUANG H, GAO Z. Stability of the car-following model on two lanes[J]. Physical Review E, 2005, 72(6): 066124. DOI:10.1103/PhysRevE.72.066124 |
| [25] | LI Z P, LIU Y C. Analysis of stability and density waves of traffic flow model in an its environment[J]. The European Physical Journal B:Condensed Matter and Complex Systems, 2006, 53(3): 367-374. DOI:10.1140/epjb/e2006-00382-7 |
| [26] | YU X. Analysis of the stability and density waves for traffic flow[J]. Chinese Physics, 2002, 11(11): 1128-1134. DOI:10.1088/1009-1963/11/11/307 |
| [27] | KONISHI K, KOKAME H, HIRATA K. Coupled map car-following model and its delayed-feedback control[J]. Physical Review E, 1999, 60(4): 4000-4007. DOI:10.1103/PhysRevE.60.4000 |
| [28] | BANDO M, HASEBE K, NAKANISHI K, et al. Analysis of optimal velocity model with explicit delay[J]. Physical Review E, 1998, 58(5): 5429-5450. DOI:10.1103/PhysRevE.58.5429 |
| [29] | BANDO M, HASEBE K, NAKANISHI K, et al. Phenomenological study of dynamical model of traffic flow[J]. Journal de Physique I, 1995, 5(11): 1389-1399. DOI:10.1051/jp1:1995206 |
| [30] | TADAKI S, KIKUCHI M, SUGIYAMA Y, et al. Coupled map traffic flow simulator based on optimal velocity functions[J]. Journal of the Physical Society of Japan, 1998, 67(7): 2270-2276. DOI:10.1143/JPSJ.67.2270 |
